Complexity of 2-Rainbow Total Domination Problem

Abstract

In this paper, we extend the findings of recent studies on k-rainbow total domination by placing our focus on its computational complexity aspects. We show that the problem of determining whether a graph has a 2-rainbow total dominating function of a given weight is NP-complete. This complexity result holds even when restricted to planar graphs. Along the way tight bounds for the k-rainbow total domination number of rooted product graphs are established. In addition, we obtain the closed formula for the k-rainbow total domination number of the corona product $G*H$, provided that H has enough vertices.

1 Introduction and Preliminaries

The remarkable growth and widespread recognition of domination in graphs are vividly illustrated by the following data. Since the introduction of domination as a fundamental graph-theoretical parameter by Berge [1] in 1958, the researchers community has produced a substantial body of literature. Prior to the seminal survey [13, 14] published in 1998, over 1200 articles had been dedicated to this field. Moreover, as of the year 2022, when a comprehensive book [12] together with its two companion books [10, 11] were released on the subject, the number of articles had surged to exceed 5000. This number is not surprising, considering the pervasive nature of domination, a field renowned for its practical applications. Over time, motivated by real-world challenges, various adaptations and extensions of domination have emerged, leading to a diverse spectrum of related concepts.

In this paper, we further explore the notion of k-rainbow total domination, introduced in [21] and further explored in [17], by directing our attention towards its computational complexity aspects. We show that the problem of determining whether a graph has a 2-rainbow total dominating function of a given weight is NP-complete, even when restricted to the class of planar graphs. Through our exploration of NP-completeness in Sect. 3, we noted the significance of graphs constructed as rooted products. Consequently, in Sect. 2, we dedicated a segment of our research to determining tight bounds for the k-rainbow total domination number of rooted product graphs. As a side result, we derived the k-rainbow total domination number of the corona product graph, under the condition that the second graph in this product possesses a sufficient number of vertices.

To ensure a comprehensive understanding of the paper, we commence by elucidating definitions and laying out preliminary concepts. The graphs examined herein are finite, simple and undirected. For a graph G, V(G) denotes its set of vertices and E(G) is the set of its edges. We use the notation $n_G$ for the order of a graph G, i.e. $n_G=|V(G)|$. If $n_G>1$, G is a nontrivial graph. The notation $N_G(v)$ stands for the open neighborhood of a vertex v in G, that is the set of vertices in G which are adjacent to v. The minimum degree of G, $\delta (G)$, is the degree of a vertex with the least number of edges incident to it. Recall that a support vertex in a graph is a vertex that is adjacent to a leaf, i.e. a vertex with degree equal to 1.

A dominating set of a graph G is a subset D of V(G) such that every vertex not in D is adjacent to some vertex in D. The domination number, $\gamma (G)$, is the minimum cardinality of a dominating set of G. If every vertex of G is adjacent to a vertex in D, then D is called a total dominating set of G, and the minimum cardinality of a total dominating set of G is the total domination number, ${\gamma }_t(G)$, [15].

For a positive integer k, a k-rainbow dominating function (or simply referred to as kRDF) of a graph G is a function $f: V(G) \rightarrow 2^{[k]}$, such that for any vertex v with $f(v)=\emptyset$ we have $\bigcup _{u\in N(v)} f(u) = [k]$. Let $||f||=\sum _{v\in V(G)}|f(v)|$; we refer to ||f|| as the weight of f. The k-rainbow domination number, $\gamma _{\textrm{r}k}(G)$, of a graph G is the minimum value of ||f|| over all k-rainbow dominating functions of G. A kRDF of weight $\gamma _{\textrm{r}k}(G)$ is called a $\gamma _{\textrm{r}k}$-function. Since its inception in the seminal paper [4], this invariant has undergone extensive analysis, exemplified in works such as [3, 6, 7, 18,19,20, 22], to name a selection, while a comprehensive survey on the topic can be found in [2]. The definition of the k-rainbow domination number was motivated by wanting to understand domination in generalized prisms (i.e. Cartesian products of arbitrary graphs with complete graphs).

Similarly, with the aim of enhancing comprehension of total domination in generalized prisms, k-rainbow total domination was defined in [21]. A k-rainbow total dominating function f of a graph G (or simply referred to as kRTDF) was introduced as a k-rainbow dominating function satisfying an additional condition that for every $v\in V(G)$ such that $f(v)=\{i\}$ for some $i\in [k]$, there exists some $u\in N(v)$ such that $i\in f(u)$. The weight of a kRTDF is $||f||=\sum _{v\in V(G)}|f(v)|$, and the minimum weight of a kRTDF is called the k-rainbow total domination number of G, $\gamma _{k\textrm{rt}}(G)$. In particular, a kRTDF of weight $\gamma _{k\textrm{rt}}(G)$ is called a $\gamma _{k\textrm{rt}}$-function. For a positive integer k, let $[k]=\{1,2,\ldots , k\}$. For easier argumentation, we refer to elements of [k] as to colors, and to sets in $2^{[k]}$ as to labels. In addition, to enhance the clarity of figures, we use colors only instead of labels (for instance, we simply write 1 instead of $\{1\}$, and 12 instead of $\{1,2\}$, see Fig. 2). Moreover, we do not label vertices if they are empty, i.e. if their label is $\emptyset$. If $A\subseteq V(G)$ then $w(A)=\sum _{v\in A}|f(v)|$ will be referred to as the contribution of vertices in A to the weight of f.

Bounds on the k-rainbow total domination number in terms of the total domination number, the k-rainbow domination number, the k-rainbow total domination number, as well as the usual domination number, were presented in [17]. In the same paper it was shown that in the case of bipartite graphs a Vizing-like conjecture for 2-rainbow total domination coincides with the famous original Vizing’s conjecture. Also, closed formula for the k-rainbow total domination number for complete bipartite graphs was given. Such formulae for paths and cycles were obtained in [21], where also graphs G with $\gamma _{k\textrm{rt}}(G) = k$ were characterized.

Proposition 1

Let k and n be positive integers such that $n>k>1$. For a connected graph G of order n we have $\gamma _{k\textrm{rt}}(G) = k$ if and only if G contains a spanning subgraph isomorphic to a complete bipartite graph $K_{s,n-s}$ where $s\le \lfloor \frac{k}{2}\rfloor$.

We conclude this section with several observations that will be necessary in the main two sections. If G is an arbitrary graph with no isolated vertices, then clearly $\gamma _{k\textrm{rt}}(G)\le |V(G)|$. In [21] it was shown that $\gamma _{k\textrm{rt}}(G) = |V(G)|$ for a nontrivial graph G of order n as soon as $k \ge 2\Delta (G)$. The following was observed as well.

Observation 2

If G is a graph without isolated vertices and $k\ge |V(G)|$, then $\gamma _{k\textrm{rt}}{(G)}=|V(G)|$.

Observation 3

For a nontrivial graph G, $\gamma _{2\textrm{rt}}(G)=2$ if and only if G contains a universal vertex.

While the above observation is straightforward, we need the following argumentation to show that there is no graph with 2-rainbow total domination number equal to 3.

Observation 4

There is no graph G with $\gamma _{2\textrm{rt}}(G)=3$.

Proof

Suppose G is a graph with $\gamma _{2\textrm{rt}}(G)=3$. Clearly such graph is nontrivial and connected. Moreover, it contains more than 3 vertices. Therefore there exists an empty vertex v. The existence of labels $\{1\}$ and $\{2\}$ of vertices in $N_G(v)$ implies $\gamma _{2\textrm{rt}}(G)\ge 4$. Thus v has a neighbor u with label $\{1,2\}$. Then there is another nonempty vertex with label $\{1\}$ (or $\{2\}$), clearly adjacent to u. Note that all other vertices have label $\emptyset$ and are therefore adjacent to u, so u is a universal vertex, a contradiction by Observation 3. $\square$

To facilitate referencing, we formally write also the last direct observation on rainbow total domination for general k.

Observation 5

Let f be a kRTDF of G, and H an induced subgraph of G such that $f(v)=\emptyset$  for each v in $V(G)\setminus V(H)$ having a neighbor in V(H). Then the contribution of vertices in H to ||f|| is at least $\gamma _{k\textrm{rt}}(H)$. Consequently, $\gamma _{k\textrm{rt}}(G)\ge \gamma _{k\textrm{rt}}(H)$.

2 Rooted Product

The concept of rooted product graph was introduced in 1978 by Godsil and McKay [9]. Kuziak et al. [16] proved that there are two possibilities for the domination number of a rooted product graph. Cabrera Martínez and Rodríguez-Velázquez [5] characterized graphs reaching the two expressions, and provided closed formulae for the total domination number of rooted product graphs. Our attention was drawn to the construction of rooted graphs upon realizing its utility in establishing the NP-completeness of the 2-rainbow total domination problem. This motivation prompted us to derive results in this section.

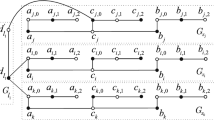
Given a graph G with vertex set $V(G)=\{g_1,g_2,\ldots , g_{n_G}\}$, and a graph H with the root vertex v, the rooted product graph $G\circ _v H$ is defined as the graph obtained from G and H by taking one copy of G and $n_G$ copies of H, and for every $i\in [n_G]$ identifying $g_i\in V(G)$ with the root vertex v in the i-th copy of H, which we denote by $H_i$. See for example Fig. 1, where the rooted product of a star $K_{1,4}$ and a graph H containing a universal vertex (taking the role of v in the definition) is depicted. If G or H is a trivial graph, then $G\circ _v H$ is equal to H or G, respectively, therefore we only consider graphs of order at least 2.

In the next theorem we identify extreme values of $\gamma _{k\textrm{rt}}(G\circ _v H)$ under the assumption that $k < n_G n_H$. Namely, by Observation 2, $\gamma _{k\textrm{rt}}(G\circ _v H)=n_G n_H$, if $k \ge n_G n_H$.

Theorem 6

Let $2\le k < n_G n_H$ and let G and H be arbitrary nontrivial graphs. Then

$$\begin{aligned} n_G\gamma _{k\textrm{rt}}(H) \ge \gamma _{k\textrm{rt}}(G\circ _v H) \ge {\left\{ \begin{array}{ll} n_Gk; \;\, k<n_H,\\ k+(n_G-1)(n_H-1); \;\, n_H \le k < n_H+n_G-1,\\ n_G n_H;\;\, k \ge n_H+n_G-1. \end{array}\right. } \end{aligned}$$

Moreover, the bounds are tight.

Proof

To prove the upper bound, let h be a kRTDF of H. Let $x\in V(H)$ be an arbitrary vertex, and $x_i$ the vertex in $V(H_i)\subseteq V(G\circ _v H)$ that corresponds to x. By defining f on $V(G\circ _v H)$ such that $f(x_i)=h(x)$ for every $i\in [n]$, we clearly get a kRTDF of $G\circ _v H$.

To prove the lower bound, let f denote a $\gamma _{k\textrm{rt}}$-function on $G\circ _v H$, i. e. $\gamma _{k\textrm{rt}}{(G\circ _v H)}=||f||$. First, observe that if for some i all vertices in $V(H_i)\setminus \{g_i\}$ are nonempty, then vertices of $H_i$ contribute at least $n_H-1$ to the weight of f. On the other hand, if there is $u\in V(H_i)\setminus \{g_i\}$ such that $f(u)= \emptyset$, then its neighbors, which are all contained in $H_i$, contribute at least k to ||f||. Therefore $||f||\ge mk+(n_G-m)(n_H-1)$, where m is the number of $H_i$’s containing an empty vertex in $V(H_i)\setminus \{g_i\}$. If $n_H>k$, then $n_H-1\ge k$, and therefore $||f||\ge mk+(n_G-m)k=n_Gk$.

Now suppose $k\ge n_H$. We claim that $m\ge 1$, i. e. $||f||\ge k+(n_G-1)(n_H-1)$. If there exists $H_i$ with an empty vertex in $V(H_i)\setminus \{g_i\}$, the claim clearly holds. Thus assume all vertices in $V(G\circ _v H)\setminus V(G)$ are nonempty. If there is $g_i$ with $f(g_i)=\emptyset$, then vertices in $U=\bigcup _{j\ne i} (V(H_j)\setminus \{g_j\})$ contribute at least $(n_G-1)(n_H-1)$ to ||f||, and vertices in the open neighborhood of $g_i$, which is disjoint with U, contribute at least k to ||f||, thus the claim holds also in this case. In the last case all vertices in $G\circ _v H$ are nonempty. Then $||f||\ge n_G n_H$, and since it clearly holds $\gamma _{k\textrm{rt}}{(G\circ _v H)}\le n_G n_H$, we have $||f||= n_G n_H$. If, in addition, $k<n_H+n_G-1$, we derive $0>k-n_H-n_G+1$ and further $||f||=n_G n_H>k+n_G n_H-n_G-n_H+1=k+(n_G-1)(n_H-1)$. With this we have proved that if $n_H\le k<n_H+n_G-1$, then $||f||\ge k+(n_G-1)(n_H-1)$.

Now let $k\ge n_H+n_G-1$. It is clear that $||f||=n_G n_H$ if all vertices in $G\circ _v H$ are nonempty, and if there is an empty vertex in the product, we already know that $||f||\ge k+(n_G-1)(n_H-1)$. Now we derive from $k-n_H-n_G+1\ge 0$ that $k+n_G n_H-n_G-n_H+1\ge n_G n_H$, that is $||f||\ge k+(n_G-1)(n_H-1)\ge n_G n_H$. Since clearly $||f||\le n_G n_H$, we have $\gamma _{k\textrm{rt}}{(G\circ _v H)}=n_G n_H$, as soon as $k\ge n_H+n_G-1$.

In what follows, we verify the tightness of the bounds. Let G be an arbitrary graph on at least 2 vertices and let H be a graph with $n_H>k\ge 2$ and $\gamma _{k\textrm{rt}}(H)=k$ (graphs with this property are characterized in Proposition 1). Then the theorem implies that $\gamma _{k\textrm{rt}}{G\circ _v H}=n_G k$, which means that the upper bound, as well as the lower bound in the case $n_H>k$, is attained. If G with $n_G\ge 2$ contains a universal vertex, and H is such that $\delta (H)\ge 2$, it contains a universal vertex v, and $n_H\le k \le n_H+n_G-1$, then the theorem implies $\gamma _{k\textrm{rt}}{(G\circ _v H)}\ge k+(n_G-1)(n_H-1)$. The opposite inequality is obtained by the following construction of a function f, which proves to be kRTDF: for a vertex $g_i$, which is universal in G as well as in H, let $f(g_i)=[k]$, let $f(u)=\{1\}$ for every u in $\bigcup _{j\ne i} \left( V(H_j)\setminus \{g_j\} \right)$, and $f(t)=\emptyset$ for every $t\in (V(G) \cup V(H_i))\setminus \{g_i\}$, see Fig. 1. Finally, if f is such that $f(v)=\{1\}$ for every vertex in $V(G\circ _v H)$, it is clearly a kRTDF for arbitrary graphs G and H, and the bound $n_H n_G$ is attained as soon as $k\ge n_H+n_G-1$. $\square$

Fig. 1

The rooted product graph $G\circ _v H$ satisfying $n_H\le k \le n_G+n_H-1$ with the k-rainbow total domination number equal to $k+(n_G-1)(n_H-1)$

If $k\ge n_G n_H$, by Observation 2, $\gamma _{k\textrm{rt}}{(G\circ _v H)}=n_Gn_H$. Moreover, by Theorem 6 we have the following.

Corollary 7

If $k\ge n_G+n_H-1$, then $\gamma _{k\textrm{rt}}{(G\circ _v H)}=n_G n_H$.

The lower bound in Theorem 6 in the case $n_H>k$ can be improved if H possesses a specific structure, which proves beneficial in the subsequent section. Let H be an arbitrary graph. By $H^+$ we denote a graph obtained from H by attaching a pendant vertex v to its support vertex $x\in V(H)$.

Proposition 8

Let G and H be arbitrary nontrivial graphs. Then $\gamma _{k\textrm{rt}}(G\circ _v H^+) \ge n_G\gamma _{k\textrm{rt}}(H)$, and the bound is tight.

Proof

Let f be a $\gamma _{k\textrm{rt}}$-function of $G\circ _v H^+$ and let $V(G)=\{g_1,g_2,\ldots ,g_n\}$. It suffices to show that vertices of each copy $H_i^+$ in $G\circ _v H^+$ contribute at least $\gamma _{k\textrm{rt}}(H)$ to the weight of f, i. e. $w(V(H_i^+))\ge \gamma _{k\textrm{rt}}(H)$ for each i. Let $g_i$ be an arbitrary vertex in G, and let $x_i$ be the neighbor of $g_i$ in $H^+_i$.

If $f(g_i)=\emptyset$ then $w(V(H_i^+))\ge \gamma _{k\textrm{rt}}(H)$ by Observation 5. Now assume $f(g_i)=A$ for a nonempty set $A\subseteq [k]$, and suppose to the contrary that $w(V(H_i^+))< \gamma _{k\textrm{rt}}(H)$. We distinguish the following cases in which we construct a function $g:V(H_i)\rightarrow 2^{[k]}$ such that g is a kRTDF of $H_i$.

If $|A|\ge 2$, then we define g with $g(x_i)=f(x_i)\cup A$ and $g(u)=f(u)$ for every $u\in V(H_i)\setminus \{x_i\}$. If $|A|=1$, we have three subcases. In each of them we again set $g(u)=f(u)$ for every $u\in V(H_i)\setminus \{x_i\}$. If $f(g_i)=\{j\}$ and $f(x_i)$ contains a color from [k] different than j, then we set $g(x_i)=f(g_i)\cup f(x_i)$. If $f(g_i)=f(x_i)=\{j\}$ then we set $g(x_i)=\{j,\ell \}$ where $\ell$ is an arbitrary color different than j. In the last case we have $f(g_i)=\{j\}$ and $f(x_i)=\emptyset$. Note that every color in $[k]\setminus \{j\}$ is contained in some f(u) for some neighbor $u\in V(H_i)$ of $x_i$. In this case we define $g(x_i)=\{\ell \}$ for some $\ell \in [k]\setminus \{j\}$.

In each of the above cases one can readily check that $||g||\le w(V(H_i^+))<\gamma _{k\textrm{rt}}(H)$, which leads to a contradiction, since $H_i$ is isomorphic to H and we obtained a kRTDF of H with weight strictly less than $\gamma _{k\textrm{rt}}(H)$.

By Theorem 6 we derive that $n_G\gamma _{k\textrm{rt}}(H) \le \gamma _{k\textrm{rt}}(G\circ _v H^+) \le n_G\gamma _{k\textrm{rt}}(H^+)$, therefore, if H is such that $\gamma _{k\textrm{rt}}(H^+)=\gamma _{k\textrm{rt}}(H)$, the bound is clearly attained. $\square$

Through the above proof, we have validated the following corollaries.

Corollary 9

For an arbitrary graph H it holds $\gamma _{k\textrm{rt}}(H)\le \gamma _{k\textrm{rt}}(H^+)$.

Corollary 10

If $\gamma _{k\textrm{rt}}(H^+) = \gamma _{k\textrm{rt}}(H)$, then $\gamma _{k\textrm{rt}}(G\circ _v H^+) = n_G\gamma _{k\textrm{rt}}(H)$.

The converse in Corollary 10 does not hold: using computer software we have verified our intuition that graphs H and $H^+$ in Fig. 2 have 3-rainbow total domination number 7 and 8, respectively, and $\gamma _{3\textrm{rt}}(K_2\circ _v H^+) = 14$.

Fig. 2

Graphs H, $H^+$ and $K_2\circ _v H^+$ and their $\gamma _{3\textrm{rt}}$-functions

Let G and H be graphs with $n_G$ and $n_H$ vertices, respectively. The corona product $G*H$ is a graph obtained from G and H by taking one copy of G and $n_G$ copies of H, and then joining each vertex from the i-th copy of H with the i-th vertex of G. The join graph $G_1 + G_2$ is the graph obtained from $G_1$ and $G_2$ by joining each vertex of $G_1$ to all vertices of $G_2$. One can note that the corona product $G*H$ can be seen as a rooted product graph $G\circ _v H_1$, where $H_1$ is the join graph $K_1 + H$, and v is the vertex of $K_1$.

Proposition 11

Let G and H be arbitrary graphs, and $n_H\ge k$. Then $\gamma _{k\textrm{rt}}(G*H)=kn_G$.

Proof

We let $V(G)=\{g_1,g_2,\ldots ,g_{n_G}\}$, and for any $i\in [n_G]$, $H_i$ denotes the copy of H attached to $g_i$. It is clear that $f:V(G*H)\rightarrow 2^{[k]}$ such that $f(g_i)=[k]$ for every $i\in [n_G]$, and $f(v)=\emptyset$ otherwise, is a kRTDF of $G*H$. Thus $\gamma _{k\textrm{rt}}(G*H) \le kn_G$. The opposite inequality follows by Theorem 6.

3 Complexity of 2-Rainbow Total Domination Problem

In this section we prove that the 2-rainbow total domination problem is NP-complete. The proof’s reduction will be from the dominating set problem which is a well-known NP-complete problem [8]. The dominating set problem asks whether for a given graph G and a positive integer k, the graph G contains a dominating set of cardinality at most k. The decision version of the 2-rainbow total dominating function problem is presented in Table 1.

Table 1 2-rainbow total dominating problem

First note that 2-RAINBOW TOTAL DOMINATING FUNCTION is in NP. Indeed, given a function $f:V(G)\rightarrow 2^{[2]}$ of weight k one can clearly check in polynomial time whether it is a 2-rainbow total dominating function. Namely, for each empty vertex u one has to check whether in the neighborhood of u all colors appear, and whether for each v with $|f(v)|=1$ in the neighborhood of v the color contained in f(v) appears.

Our next goal is to derive a polynomial time reduction from the dominating set problem to the 2-rainbow total domination problem. For this we use the following construction and its properties.

Let T be the graph obtained from the cycle xyzoprx by adding a vertex s and connecting it to o and x, and adding a vertex t and connecting it to p and y, see Fig. 3.

Fig. 3

The graph T

Lemma 12

For the graph T as defined above $\gamma _{2\textrm{rt}}(T) = 4$.

Proof

By Observations 3 and 4, we derive $\gamma _{2\textrm{rt}}(T) \ge 4$, and the opposite inequality holds since $f:V(T) \rightarrow 2^{[2]}$ defined with $f(x)=f(y)=\{1\}$, $f(o)=f(p)=\{2\}$ and $f(r)=f(s)=f(t)=f(z)=\emptyset$, is a 2RTDF of T. $\square$

Lemma 13

If T is a graph as defined above, and f is a 2RTDF of T with $f(x)=\{1,2\}$ then $||f||\ge 5$.

Proof

Let f be a 2RTDF of T with $f(x)=\{1,2\}$. By Lemma 12, $||f||\ge 4$. Suppose $||f||=4$. Observe that there is no vertex v in $V(T)\setminus \{x\}$ such that every vertex in $V(T)\setminus \{x,v\}$ is adjacent to x or v, so x is the only vertex in T with label $\{1,2\}$. If there exists an edge ab, where a and b are both different than x and the labels of both consist of the same color, say $f(a)=f(b)=\{1\}$, then every vertex in $V(T)\setminus \{x,a,b\}$ is empty and therefore it must be adjacent to x, which clearly contradicts the structure of T. We are left with the case when there are neighbors a and b of x with, $f(a)=\{1\}$ and $f(b)=\{2\}$, and all other vertices are empty. But this is a contradiction with f being a 2RTDF, since there exists an empty vertex such that in its open neighborhood all vertices are empty as well. Therefore $||f||\ge 5$. $\square$

Let $T^+$ be the graph obtained from T by attaching a new vertex v to x. In what follows G is an arbitrary graph with $V(G)=\{g_1,g_2,\ldots ,g_{n_G}\}$, and $G'=G\circ _v T^+$. With $T_i$ we denote the subgraph isomorphic to T in the ith copy of $T^+$ in $G'$. Also, if $i\in [n_G]$ and a is a vertex in T, we denote by $a_i$ the corresponding vertex in $T_i$.

Lemma 14

Let f be a 2RTDF of $G'$. Then $||f||>4n_G$. Moreover, the contribution of vertices in every $T_i$ to ||f|| is at least 4.

Proof

Let f be a 2RTDF of $G'$. If $f(g_i)=\emptyset$ for every i, then $f(x_i)=\{1,2\}$ for every i. By Observation 5 one can use Lemma 13 to derive that for each i vertices of $T_i$ contribute at least 5 to ||f||, therefore both claims hold in this case.

In the remaining case there is a nonempty vertex in G. Now we distinguish two types of vertices in G. If $g_i$ is empty, then by Observation 5 and Lemma 12 vertices of $T_i$ contribute at least 4 to ||f||. Now suppose $g_i$ is nonempty. If $f(x_i)=\emptyset$, then by Observation 5 vertices of $V(T_i)\setminus \{x_i\}$ contribute to ||f|| at least 2-rainbow total domination number of the graph induced by vertices of $V(T_i)\setminus \{x_i\}$, which is at least 4 by Observations 3 and 4. Now suppose that $x_i$ is nonempty. Suppose to the contrary that the contribution of $T_i$ to ||f|| is less than 4. If $f(x_i)=\{1,2\}$, then by restricting the function f on $T_i$ we obtain a 2RTDF of the graph induced by vertices of $T_i$ which is isomorphic to T. But this contradicts Lemma 13. If $|f(x_i)|=1$ then we define $g:V(T_i)\rightarrow 2^{[2]}$ by $g(x_i)=\{1,2\}$ and $g(v_i)=f(v_i)$ for $v_i \in V(T_i)\setminus \{x_i\}$. Note that this is again a 2RTDF of the graph induced by vertices of $T_i$ of weight less than 5, a contradiction with Lemma 13 again. Therefore the contribution of vertices in every $T_i$ to ||f|| is at least 4, and $||f||>4n_G$ since we have at least one $T_j^+$ contributing at least 5 to ||f||. $\square$

Now we can prove the key fact for our reduction. Recall that for an arbitrary graph G we introduced $G'=G\circ _v T^+$, where $T^+$ is obtained from the graph in Fig. 3 by attaching a leaf to x.

Proposition 15

$G'$ has a 2RTDF of weight at most $k+4n_G$ if and only if G has a dominating set D of size at most k.

Proof

$(\Leftarrow )$ Let D be a dominating set of G, and $|D|=l\le k$. Without loss of generality assume $D=\{g_1,g_2,\ldots ,g_l\}$. Then by setting

• $f(g_i)=f(x_i)=f(y_i)=\{1\}$ for every $i\in [l]$,

• $f(x_j)=f(y_j)=\{2\}$ for every $j\in \{l+1,l+2,\ldots ,n_G\}$,

• $f(o_i)=f(p_i)=\{2\}$ for every $i\in [l]$,

• $f(o_j)=f(p_j)=\{1\}$ for every $j\in \{l+1,l+2,\ldots ,n_G\}$, and

• f assigns $\emptyset$ to every other vertex in $G'$,

we get a function of weight $l+4n_G$, which is clearly a 2RTDF of $G'$.

$(\Rightarrow )$ Let f be a 2RTDF of $G'$. By Lemma 14, $||f||>4n_G$, i.e. $||f||=k+4n_G$ for some positive integer k. For $i\in \{1,2\}$ let $V_i^G$ denote vertices $g\in V(G)$ such that $f(g)=\{i\}$, let $V_{\emptyset }^G$ denote vertices $g\in V(G)$ such that $f(g)=\emptyset$ and let $V_{12}^G$ be the set of vertices in V(G) to which $\{1,2\}$ is assigned under f. Now we construct a new function $f':V(G')\rightarrow 2^{[2]}$. To do so, we distinguish different types of vertices with respect to the values of f in G:

• Type A: if $g_i\in V_1^G$ or $g_i\in V_{\emptyset }^G$ and it has a neighbor in $V_2^G$ but no neighbor in $V_1^G$, we say that $g_i$ is of Type A. If $g_i\in V_1^G$, we set $f'(g_i)=\{1\}$. If $g_i\in V_{\emptyset }^G$ is such that it has a neighbor in $V_2^G$ but no neighbor in $V_1^G$, then $f'(g_i)=\emptyset$. In both cases in the corresponding copy $T_i$ we set $f'(x_i)=f'(y_i)=\{1\}$, $f'(o_i)=f'(p_i)=\{2\}$, and $f'(z_i)=f'(t_i)=f'(s_i)=f'(r_i)=\emptyset$.

• Type B: if $g_i\in V_2^G$, then $f'(g_i)=\{2\}$, and if $g_i\in V_{\emptyset }^G$ and it has a neighbor in $V_1^G$ and no neighbor in $V_2^G$, then $f'(g_i)=\emptyset$. In both cases in the corresponding copy $T_i$ we put $f'(x_i)=f'(y_i)=\{2\}$, $f'(o_i)=f'(p_i)=\{1\}$, and $f'(z_i)=f'(t_i)=f'(s_i)=f'(r_i)=\emptyset$.

• Type C: if $g_i\in V_{12}^G$, or $g_i\in V_{\emptyset }^G$ either has a neighbor in $V_{12}^G$ or it has a neighbor in $V_1^G$ and a neighbor in $V_2^G$, then the assigned value of $f'$ to $g_i$ as well as to every vertex in $T_i$ remains the same as under f.

• Type D: $g_i\in V_{\emptyset }^G$ is such that all its neighbors in G belong to $V_{\emptyset }^G$ as well. For this type of vertices we assign $f'(g_i)=f'(x_i)=f'(y_i)=\{1\}$, $f'(o_i)=f'(p_i)=\{2\}$ and $f'(z_i)=f'(t_i)=f'(s_i)=f'(r_i)=\emptyset$.

It is a straightforward task to verify that $f'$ is a 2RTDF. Next, we claim that $||f'||\le ||f||$. If $g_i$ is either of Type A or B, then the contribution of vertices that are included in G to ||f|| and to $||f'||$ is the same, and Lemma 14 ensures that the contribution of vertices in $V(T_i)$ to the weight of $f'$ is clearly less or equal to the contribution to the weight of f. The contribution of vertices in $T_i^+$ to ||f|| and to $||f'||$ is the same if $g_i$ is of type C. If $g_i$ is of Type D it must hold $f(x_i)=\{1,2\}$. So the contribution of vertices in $V(T_i^+)$ to the weight of f is at least 5 by Lemma 13. On the other hand, the contribution of the same vertices to the weight of $f'$ is 5, thus the claim is proved.

Let D be the set of vertices in G such that $f'(v)\ne \emptyset$. Note that D is a dominating set in G. Namely, $f'$ was constructed in such a way that there is no vertex in G with label $\emptyset$ having all its neighbors in G labeled with $\emptyset$ as well.

To finish the proof we must show that $|D|\le k$. Note that vertices from copies of T contribute at least $4n_G$ to the weight of $f'$, and each vertex from D contributes at least 1 to it. Therefore $||f'||\ge 4n_G+|D|$. We derive $4n_G+|D|\le ||f'|| \le ||f||=4n_G+k$ and thus indeed $|D|\le k$. $\square$

Clarly, one can construct $G'$ from G in linear time. Furthermore, from Proposition 15 and its proof we derive the following. If D is a minimum dominating set of G, i.e. $\gamma (G)=|D|$ and $|D|=k$, then $\gamma _{2\textrm{rt}}(G')\le k+4n_G=\gamma (G)+4n_G$. On the other hand, if $f'$ is a 2RTDF on $G'$ of minimum weight with $\gamma _{2\textrm{rt}}(G')=4n_G+k$, and D a dominating set of G comprised of vertices v with property $f'(v)\ne \emptyset$, then $\gamma _{2\textrm{rt}}(G')=4n_G+k\ge 4n_G+|D|\ge 4n_G+\gamma (G)$. Thus $\gamma _{2\textrm{rt}}(G')=\gamma (G)+4n_G$. Therefore, by constructing the 2RTDF $f'$ on $G'$ from a given 2RTDF f, and then selecting all vertices from V(G) with nonempty weight under $f'$, one can construct a dominating set of G in polynomial time. With this we have arrived at the main result of this section.

Theorem 16

2-RAINBOW TOTAL DOMINATING FUNCTION is NP-complete.

It is known that dominating set problem is NP-complete for planar graphs [8]. Since the graph $G'$ from the above proof is planar if G is planar, we infer the following.

Corollary 17

2-RAINBOW TOTAL DOMINATING FUNCTION is NP-complete even when restricted to planar graphs.

4 Conclusion

In our aim to establish NP-completeness of the 2-rainbow total domination problem, we briefly touched upon the topic of of k-rainbow total domination concerning rooted and corona product graphs, which stand as interesting topics in their own right. While we have obtained the tight bounds for both (notably, the corona product can be seen as a special rooted product), there are many questions that naturally arise. One of them pertains to the converse of Corollary 10, which does not hold in general, which raises a question: can we characterize graphs H such that $\gamma _{k\textrm{rt}}(G\circ _v H^+) = n_G\gamma _{k\textrm{rt}}(H)$? Also, can we characterize graphs H with $\gamma _{k\textrm{rt}}(H^+) = \gamma _{k\textrm{rt}}(H)$? More generally, can we derive enclosed formulae, as it is the case when considering ordinary domination and total domination, [5, 16]?

Further, in Proposition 11 we have obtained the closed formula for the corona product of graphs if $n_H\ge k$. Note that if $n_H< k$, strict inequality $\gamma _{k\textrm{rt}}(G*H)<kn_G$ can be obtained, as it can be seen by the example of family of graphs depicted in Fig. 1. Therefore it would be interesting to further explore the case when $n_H< k$.

Last but not least, we wonder whether it is possible to extract properties of the graph T in Fig. 3, with the aim of generalizing these properties in such a way that would allow the proof of Theorem 16 for a general value of k (see the problem in Table 2).

Table 2 k-rainbow total dominating problem

Conjecture 18

Given a positive integer k, the k-rainbow total dominating problem is NP-complete.