Abstract
The COVID-19 (SARS-CoV-2 virus) pandemic has led to a substantial loss of human life worldwide by providing an unparalleled challenge to the public health system. The economic, psychological, and social disarray generated by the COVID-19 pandemic is devastating. Public health experts and epidemiologists worldwide are struggling to formulate policies on how to control this pandemic as there is no effective vaccine or treatment available which provide long-term immunity against different variants of COVID-19 and to eradicate this virus completely. As the new cases and fatalities are recorded daily or weekly, the responses are likely to be repeated or longitudinally correlated. Thus, studying the impact of available covariates and new cases on deaths from COVID-19 repeatedly would provide significant insights into this pandemic’s dynamics. For a better understanding of the dynamics of spread, in this paper, we study the impact of various risk factors on the new cases and deaths over time. To do that, we propose a marginal-conditional based joint modelling approach to predict trajectories, which is crucial to the health policy planners for taking necessary measures. The conditional model is a natural choice to study the underlying property of dependence in consecutive new cases and deaths. Using this model, one can examine the relationship between outcomes and predictors, and it is possible to calculate risks of the sequence of events repeatedly. The advantage of repeated measures is that one can see how individual responses change over time. The predictive accuracy of the proposed model is also compared with various machine learning techniques. The machine learning algorithms used in this paper are extended to accommodate repeated responses. The performance of the proposed model is illustrated using COVID-19 data collected from the Texas Health and Human Services.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Countries around the world are overwhelmed by the outbreak of the COVID-19 pandemic, as the SARS-CoV-2 virus (COVID-19) has been transmitted across the globe at an alarming rate. As of December 31, 2021, according to World health organization (WHO) [1], a total confirmed new cases and deaths are over 281 millions and 5.4 millions, respectively. Due to its astonishing nature of transmission, public health experts and epidemiologists are struggling to formulate policies on how to control and end this pandemic. Health policy planners from all the countries are trying to flatten the curves for both the new cases and deaths of COVID-19. However, public health and government officials are witnessing a recent new spike of cases in countries where the spread of the COVID-19 was once assumed to be under control. Thus, the initial flattened curves of COVID-19 do not mean the crisis is over. Health officials introduced various restrictions on people’s mobility and socialization to reduce the spread and hence death. Consequently, the socio-economic, psychological, and other impacts of COVID-19 on people have already started to become visible continuously [1, 2]. However, as there has been more than one wave of the virus already, there could be another increase or spike in cases after the waves of infections stabilized. Besides, this pandemic curve can have multiple severe surges or spikes in new cases before it stabilizes with more effective doses of vaccine. Lifting of existing restrictions to control this pandemic too quickly could send countries around the world ”back into confinement” once a consecutive wave hits.
To identify the COVID-19 transmission patterns, spread and development, various statistical modelling techniques were employed by health researchers around the world since the beginning of 2020 [3,4,5,6,7,8,9]. For example, to predict COVID-19-related new cases and deaths, autoregressive integrated moving average (ARIMA)-based modelling techniques were incorporated by researchers in the literature ([3,4,5,6,7]). Shastri et al [8] proposed recurrent neural network (RNN)-based deep learning techniques to forecast COVID-19 new cases and death. To predict the dynamic deportment of COVID-19, Da Silva et. al. [9] have exploited artificial intelligence (AI)-based modelling techniques such as Bayesian regression neural network, cubist regression, k-nearest neighbours, quantile random forest, and support vector regression. To predict the transmission of COVID-19, machine learning algorithm has also been employed in the literature [10].
Our research is motivated by COVID-19 data collected from the Texas Health and Human Services website (https://dshs.texas.gov/coronavirus///additionaldata.aspx). In this paper, we have considered the daily new cases and deaths for 254 counties in Texas between March 4, 2020, and July 25, 2020, along with the population size for each county. As some counties have no daily deaths for several days, we summed weekly deaths and new cases for our analysis. Thus, for modelling, we have used any death or no death during a week for a total of 20 consecutive weeks. As COVID-19 is causing excess fatalities all over the world, predicting fatality trajectories has gained compelling interest among public health researchers. In this paper, we are interested in predicting the trajectory risks of weekly death and the impact of available risk factors on the trajectory. As the repeated weekly deaths in a specific county are likely to be correlated, we propose a joint modelling-based regressive class approach to estimate the trajectory risks [11, 12].
Studying the impact of available covariates and new cases on deaths from COVID-19 longitudinally would provide significant insights into this pandemic’s dynamics. To better understand the dynamics of spread, we need to study the impact of risk factors and new cases on deaths over time, first conditionally and then jointly, which is crucial to the health policy planners for taking necessary measures. The conditional model is a natural choice to study the underlying property of dependence in consecutive weeks [13]. Using this model, one can examine the relationship between outcomes and predictors, and it is possible to calculate risks of the sequence of events longitudinally [14]. Also, we must understand how the transitions between weeks occur and how the covariates influence these transitions for better prediction. The advantage of repeated measures is that one can see how individual responses change over time [15]. Lindsey and Lamber [15] suggested that this must generally be conditioned on the previous history of a subject. Lee and Nelder [16] concluded that the conditional models are of fundamental interest, and marginal predictions can be made from conditional models. Sometimes the transition probabilities may depend on different models, each model representing a transition from one stage to another. Lindsey and Lamber [15] examined some important theoretical aspects concerning the use of marginal models (e.g. GEE) and demonstrated various limitations. Another alternative is the subject-specific models considering the random effects by allowing random effect terms in the linear predictor [17]. However, the proposed method provides a more general and flexible set up for addressing the risk prediction of repeated categorical outcomes emerging from longitudinal studies. The regressive models at the subsequent follow-ups provide the estimates of the parameters of the conditional models.
We organize the rest of the paper as follows. In Sect. 2, we present proposed joint modelling approach for the repeated measurements to predict fatality trajectories along with various machine learning techniques. Estimation techniques of the model parameters are presented in Sect. 3. The results of data analysis are presented in Sect. 4. Finally, in Sect. 5, some concluding remarks are presented.
2 Predicting Fatality Trajectories for COVID-19
In this section, we present a proposed marginal-conditional based joint modelling approach for predicting trajectories of repeated COVID-19 deaths. In addition, we also incorporate three machine learning algorithms neural network (NN), support vector machine (SVM) and random forest (RF), and compared their performance with the proposed method. The chosen machine learning algorithms have widespread use in various fields. However, these machine learning algorithms are developed for the classification of categorical outcomes measured cross-sectionally or data collected from a single time point. These models also allow the prediction of the probability of the outcome categories. But the problem at our hands is longitudinal, and we are interested in predicting trajectory risk. In other words, we want to predict the joint probability of a sequence of events that occurs longitudinally. Besides, we need to assess the covariate impact on the series of events. We extended these machine learning algorithms using the proposed marginal conditional approach to obtain the marginal and conditional probability and, ultimately, the joint probability to predict the trajectory risks. In other words, we extend these machine learning models for repeated measures data to predict the trajectory risks based on the covariates. First we present proposed joint modelling approach to predict fatalities trajectories for COVID-19 in Sect. 2.1. We then present various machine learning algorithms in Sect. 2.2.
2.1 Joint Modelling Approach
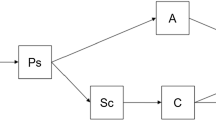
Let \({Y_{i1}},{Y_{i2}},...,{Y_{iJ_i}}\) represent the occurrence of COVID-19-related death in the i-th county of Texas, USA at j-th week \((i=1,2,...,n \text { and }j=1,2,...,J_i)\). Note that the data set we used in this paper has \(n=254\) and \(J_i = J = 20\). We also assume \(Y_{ij}=s\) follows a binomial distribution where \((s=0,1)\) with the category 0 denotes no COVID-19 related death and 1 denotes COVID-19 related death during a week for the ith county in Texas, USA. To be specific, in Fig. 1, we present the trajectory path using three consecutive weeks for the ith county.
The marginal trajectory probability of the response at the first week \(Y_{i1}\) for the ith county can be calculated using the following formula:
where \({\varvec{\beta }}_{y_1}=[\beta _0, \beta _1,...,\beta _p]^\prime \) is a \(1\times (p+1)\) regression coefficients corresponding to the covariate vector \({\varvec{z}} = [1, z_1,...,z_p]^\prime = [1, x_1,...,x_p]^\prime \). Similarly, the conditional trajectory probability of the response at the second week \(Y_{i2}\) given the first week \(Y_{i1}\) can be calculated using the first-order regressive logistic models as:
where \({\varvec{\beta }}_{y_2.y_1}=\left[ \beta _{y_20}, \beta _{y_21},...,\beta _{y_2p}, \beta _{y_2y_1}\right] ^\prime \) is \(1\times (p+2)\) vector of regression coefficients corresponding to the covariate vector \({\varvec{z}}= [1, z_1,...,z_p,z_{p+1}]^\prime =[1, x_1,...,x_p,y_1]^\prime \). Thus, the general form of the first-order regressive logistic models for j consecutive outcomes \(Y_{i1},\cdots ,Y_{ij}\) can be shown to be:
where \({\varvec{\beta _{y_j.y_{j-1}}}}=\left[ \beta _{y_j0}, \beta _{y_j1},...,\beta _{y_jp},,\beta _{y_jy_{j-1}}\right] ^\prime \) is a \(1\times (p+2)\) vector of regression coefficients corresponding to the covariate vector \({\varvec{z}}=\left[ 1,z_1,...,z_p,z_{p+1}\right] ^\prime =\left[ 1,x_1,...,x_p,y_{j-1}\right] ^\prime \).
Consequently, the joint probability mass function of \(Y_{i1},Y_{i2},...,Y_{iJ}\) with covariate vector \({\varvec{X=x}}\) can be expressed as:
where \({\varvec{X}}^\prime =[1,x_1,...,x_p]\) is vector of covariates. It should be noted that \({\varvec{X}}={\varvec{x}}\) can be time dependent.
Now using the fitted marginal and conditional models, we can estimate the trajectory risks as follows:
In the next subsection, we discuss various machine learning techniques to predict fatalities of COVID-19.
2.2 Machine Learning Approaches
In this section, we present three machine learning algorithms: neural network (NN), support vector machine (SVM) and random forest (RF), which will be used to predict trajectories. Although there are other machine learning approaches available, we considered these three commonly used techniques for illustration and comparisons. It may be noted that these machine learning algorithms are developed for cross-sectional data or data from a single time point. However, using the proposed approach, we extended these algorithms for trajectory risk prediction for longitudinal events.
2.2.1 Neural Networks (NN)
Neural networks are often used as a building block for deep learning due to the excellent predictive performance. The NN algorithm is tuned by constructing many layers and neurons, then trimming off the unnecessary neurons and layers using regularization through cross-validation. A neural network does not assess associations between predictors and the response as its objective is to predict outcome class. Also, multicollinearity does not create many problems in the neural network. More details of the theory of a neural network can be found in Ripley [18].
2.2.2 Support Vector Machine (SVM)
A popular classifier, support vector machine (SVM), was originally introduced by Boser et. al. [19]. It has been updated by Cortes and Vapnik [20]. The main idea is to separate the space of the feature variables using hyperplanes so that the response classes become as distinct as possible. Also, SVM is not affected by the presence of multicollinearity. This model often provides excellent predictive performance and becomes intuitive, visualizing the support vectors in the lower dimension. This algorithm is computationally demanding, and much attention is required to tune the model parameters.
2.2.3 Random Forests (RF)
A random forest is an aggregated collection of classifiers of classification trees (an ensemble). This prediction model is compelling and provides one of the top prediction performances. The strength of the ensemble depends on the depths of the constituent classification trees and diversity between the trees. The RF needs to tuned using the number of trees to grow in a forest. The random selection of independent variables keeps the correlation between predictors to the minimal. When the objective is to make better predictions, multicollinearity does not affect the results. However, the algorithm may appear computationally demanding for high-dimensional data.
3 Estimation of Model Parameters
In this section, we develop estimation techniques for estimating model parameters to predict trajectories using the proposed approach. To do that, we obtain the log-likelihood function of the joint mass function in (4) which can be expressed as:
From Eq. (6), it is clear that the joint mass function boils down to univariate mass function for any first-order regressive model. In other words, all the first-order regressive models are equivalent to that of the marginal model and follow the same estimation procedure. Then, the likelihood function of the first-order regressive model for sample of n independent observations can be written as:
where \({\varvec{z}}=[1,z_1,z_2,...,x_z,y_{(j-1)}]^\prime =[1,x_1,x_2,...,x_p,y_{(j-1)}]^\prime \). Differentiating the log-likelihood with respect to the parameters and equating the derivatives to zero, we obtain the equations whose solutions give the following maximum likelihood estimates for \((p+2)\) parameters.
Thus, the observed information matrix can be obtained using the second derivatives as follows:
and
\(\text{ where } q, q^\prime =0,1,...,p,(p+1)\). The observed information matrix \(I({\varvec{\beta }})\) is the \((p+2) \times (p+2)\) matrix where elements are the negative of the second derivatives. It can be shown that the asymptotic covariance matrix is \([I({\varvec{\beta }})]^{-1}\). Consequently, we can use a Newton–Raphson iterative logarithm to obtain the estimated regressive logistic coefficients. To do that, we first arrange the data into a new structure. Then, all these models can be estimated in a usual manner with an appropriate data structure and using Python, R, or other software capable of fitting logistic regression. Then, we can exploit the parallel programming to analyse all the subsets of data using multiple cores in a single computer or using several CPU in a distributed system.
3.1 Significance of the Joint Model
The significance of the joint model based on Eq. (4) can be tested using a likelihood ratio test between the joint constant only model (reduced) and joint full model (full) as follows:
which is distributed asymptotically as \(\chi ^2\) with \([(p+1)+\{(p+2)\times (j-1)\} ]-j\) degrees of freedom. It is noteworthy to point out that \({\varvec{\hat{\beta }_{Reduced}}}\) includes all the regression parameters from the constant only joint model and \({\varvec{\hat{\beta }_{Full}}}\) includes all the parameters from the full joint model.
3.2 Predictive Models and Joint Probabilities
The predicted joint probability that a subject with covariate vector \(({\varvec{X}}^*={\varvec{x}}^*)\) for a trajectory as shown in Fig. 1 can be predicted using Eq. (5) and using the predicted marginal first-order conditional probabilities from the fitted marginal and all first-order regressive logistic models. Based on Eq. (5), the predicted joint probabilities for \(Y_{i1}=y_{i1}\) and \(Y_{i2}=y_{i2}\) are:
Now, the predicted marginal probabilities \(\hat{P}(Y_{i1} = 1\mid {\varvec{X}}={\varvec{x}})\) and \(\hat{P}(Y_{i1} = 0\mid {\varvec{X}}={\varvec{x}})\) can be estimated from the fitted marginal model. The first-order conditional probabilities \(\hat{P}(Y_{i2} = s\mid Y_{i1} = y_{i1};{\varvec{X}}={\varvec{x}})\), \(s, y_1=0,1\), can be estimated from the fitted first-order regressive model using covariate vector \({\varvec{Z^\prime }}=[{\varvec{x}}^*,y_{i1}]\) and \({\varvec{X}}^*={\varvec{x}}^*\). Then, we can plug-in the predicted marginal and conditional probabilities in Eq. (5) to obtain the joint probabilities for events.
4 Analysis of Texas COVID-19 Data
Texas COVID-19 data used in this paper were downloaded from the Texas Health and Human Services website (https://dshs.texas.gov/coronavirus///additionaldata.aspx). It provides daily new cases and deaths for 254 counties in Texas. We used data from March 4, 2020, to July 25, 2020. Also, the population size for each county is considered as covariate, which ranges from 92 to 4978845 for different counties. As some counties do not have any daily fatality for many days, we summed weekly deaths and new cases for our analysis. For modelling purposes, we have converted death as binary variable with any death as 1 or no death as 0, as the goal of public health experts and scientists are to minimize the death as 0. In our analysis, we have considered death as repeated binary outcome variable which repeats over the 20 weeks and are defined as \(Y_{i1},\cdots ,Y_{i20}\), respectively. We are interested in predicting the trajectory risks of death over the weeks and the impact of available risk factors on the trajectory. Due to the small sample size, i.e. only 254 counties in Texas, we divide the data into training (90%) and test (10%) sets based on the first-week samples to determine over(under)fitting and to assess the generalization ability of the models used. We used R and parallel programming package to fit all the models simultaneously. Table 1 displays the distribution of weekly death.
The prediction accuracy of the proposed joint model along with the three machine learning techniques is presented in Table 2. In general, the weekly accuracy of all three models such as proposed regressive model, neural network (NN), random forest (RF) is relatively very high compared to support vector machine (SVM) technique. The accuracy of SVM is low for most of the weeks. The same is true for both the training and test data. Also, we observed overfitting a few models. Regarding the model performance, comparing the accuracy of all these three models, it is found that the random forest model showed the highest accuracy, followed by the proposed regressive model and neural network, respectively. The fitted coefficients for marginal and proposed regressive models are shown in Table 3. The population size is positive and significantly associated with the outcomes for all the marginal and first-order regressive models with few exceptions. A similar pattern is observed between daily new cases and death. Daily new counts of cases for all the first-order regressive models are positive and significantly associated with the outcomes except for some. While we assessed the effect of covariates using proposed statistical learning models as shown in Table 3, we could not do so using machine learning models as those have interpretation problems. But we used those as one of our objectives is to predict fatality.
The predicted trajectory of conditional probabilities for Harris county is displayed in Fig. 2. The population of this county is 4978845. We presented the predicted trajectories using all four models. Both the proposed regressive and random forest models predicted the highest risks of deaths over time and these two lines overlapped. The dashed line is from the proposed model and the dashed-dotted line from the random forest models. The neural network (dotted line) closely follows these trajectories. The trajectory (the solid bottom line) predicted using the support vector machine showed the worst performance. This county has the highest population size and observed death in all the 20 consecutive weeks. However, there were no new cases during week 11 for this county. The predicted trajectories using the proposed regressive model and random forest are similar and predicted the highest risk, which is expected. However, the support vector machine algorithm predicted much lower risks and downward trends up to the 10th week. This may be due to no new cases during the 11th week. The corresponding trajectories of joint probabilities are shown in Fig. 3. After the pre-processing, the data for two counties (Anderson and Archer) used for model fitting are shown in Table 4.
In Fig. 4, we present the trajectory of conditional probabilities for Andrewes county using all the models. The population size of this county is much smaller (22269) compared to Harris county. Also, this county did not observe death during the majority of the weeks. It is clear from the figure that the probability of death is lower than 0.50 or close to zero when no new cases are observed during a week. This flattening trend of lowering death risk is clearly visible from the trajectories of joint probabilities shown in Fig. 5. In general, the predicted paths from all the models are relatively close except for support vector machine.
5 Conclusions
This paper proposed a marginal-conditional modelling approach to predict trajectory risks of fatalities from COVID-19 longitudinally using daily new cases and other available covariates from 254 counties from Texas in the USA. We assess the impact of weekly new cases and the county population size on the trajectories. Also, we extended some commonly used machine learning algorithms that use for the classification of categorical outcomes from cross-sectional data for the trajectory risk predictions from repeated measures data. It is evident from our study that controlling the occurrence of new cases reduces the risk of death. Also, the trajectory risk of death is much higher for the densely populated county. Relevant authorities of all countries are trying hard to reduce the new cases of COVID-19 towards zero. Only by ending the pandemic everywhere, we can achieve this goal.
Governments around the world are implementing various strict restrictions, including travel bands, social distancing, and unnecessary movements, besides travel restriction and quarantine of both suspected individuals and subjects who have had close contacts with suspected cases. The aim is that reducing new infections towards zero will reduce the spread of this disease hence death. While people around the world overwhelmingly support pandemic-related restrictions, but many communities became impatient for these restrictions and want those removed. A positive association of population size with death from our studies may reiterate the need for those restrictions for highly populated places to reduce the new cases and hence an increasing number of fatalities. We believe that analysis with the availability of more detailed data along with related risk factors may provide an in-depth understanding regarding the dynamics.
References
WHO Coronavirus Disease (COVID-19) Dashboard, Map Data, 2020. Available from: https://covid19.who.int/
Carpenter, T.E., O’Brien, J.M., Hagerman, A.D., et al.: Epidemic and economic impacts ofdelayeddetectionoffoot-and-mouthdisease: acasestudyofasimulatedoutbreakinCalifornia. J. Vet. Diagn. Invest. 23, 26–33 (2010)
Sahai, A.K., Rath, N., Sood, V., Singh, M.P.: ARIMA modelling & forecasting of COVID-19 in top five affected countries. Diabetes Metab. Syndr.: Clin. Res. Rev. 14(5), 1419–1427 (2020). https://doi.org/10.1016/j.dsx.2020.07.042
Dal Molin Ribeiro, M.H., da Silva, R.G., Mariani, V.C., dos Santos Coelho, L.: Short-term forecasting COVID-19 cumulative confirmed cases: perspectives for Brazil Chaos. Solitons Fractals (2020). https://doi.org/10.1016/j.chaos.2020.109853
Vena, A., Giacobbe, D. R., Di Biagio, A., Mikulska, M., Taramasso, L., De Maria, A., et. al.: Clinical characteristics, management and in-hospital mortality of patients with coronavirus disease 2019 in Genoa, Italy, Clinical Microbiology and Infection, Available online 15 August 2020, doi: https://doi.org/10.1016/j.cmi.2020.07.049
Ceylan, Z.: Estimation of COVID-19 prevalence in Italy, Spain, and France. Sci. Total Environ. 729, 10 (2020). https://doi.org/10.1016/j.scitotenv.2020.138817
Yang, Q., Wang, J., Ma, H., Wang, X.: Research on COVID-19 based on ARIMA model\(^\Delta \)-Taking Hubei, China as an example to see the epidemic in Italy. J. Infect. Public Health 13(10), 1415–1418 (2020). https://doi.org/10.1016/j.jiph.2020.06.019
Shastri, S., Singh, K., Kumar, S., Kour, P., Mansotra, V.: Time series forecasting of Covid-19 using deep learning models: India-USA comparative case study, Chaos. Solitons Fractals (2020). https://doi.org/10.1016/j.chaos.2020.110227
da Silva, R.G., Dal Molin Ribeiro, M.H., Mariani, V.C., dos Santos Coelho, L.: Forecasting Brazilian and American COVID-19 cases based on artificial intelligence coupled with climatic exogenous variables, Chaos. Solitons Fractals (2020). https://doi.org/10.1016/j.chaos.2020.110027
Tuli, S., Shikhar, T., Rakesh, T., Rakesh, S.S.: Gill Predicting the growth and trend of COVID-19 pandemic using machine learning and cloud computing. Internet Things (2020). https://doi.org/10.1016/j.iot.2020.100222
Islam, M.A., Chowdhury, R.I.: Prediction of disease status: a regressive model approach for repeated measures. Stat. Methodol. 7, 520–540 (2010). https://doi.org/10.1016/j.stamet.2010.03.001
Chowdhury, R.I., Islam, M.A.: Regressive models for risk prediction for repeated multinomial outcomes: an illustration using Health and Retirement Study (HRS) data. Biometric. J. 62, 898–915 (2020). https://doi.org/10.1002/bimj.201800101
Islam, M.A., Chowdhury, R.I., Huda, S.: Markov Models with Covariate Dependence for Repeated Measures. Nova Science, New York (2009)
Islam, M.A., Chowdhury, R.I., Singh, K.P.: A Markov model for analyzing polytomous outcome data. Pak. J. Stat. Op. Res. 8, 593–603 (2012)
Lindsey, J.K., Lamber, P.: P, On the appropriateness of marginal models for repeated measurements in clinical trials. Stat. Med. 17, 447–469 (1998)
Lee, Y., Nelder, J.A.: Conditional and marginal models: another view. Stat. Sci. 19, 219–238 (2004)
Breslow, N.E., Clayton, D.G.: Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 88, 9–25 (1993)
Ripley, Brian D.: Pattern Recognition and Neural Networks. Cambridge University Press, Cambridge (1996)
Boser, B.E., Guyon, I.M. and Vapnik, V.N.: A training algorithm for optimal margin classifiers. 5th Annual ACM Workshop on COLT. Pittsburgh, PA, ACM Press, pp. 144-152 (1992)
Cortes, C., Vapnik, V.: Support-vector networks. Machine Learn. 20, 273–297 (1995)
Acknowledgements
This research was supported by grants from the Natural Sciences and Engineering Research Council of Canada (NSERC).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they do not have any conflict of interest to declare.
Additional information
Communicated by Shahariar Huda.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chowdhury, R.I., Hasan, M.T. & Sneddon, G. Regressive Class Modelling for Predicting Trajectories of COVID-19 Fatalities Using Statistical and Machine Learning Models. Bull. Malays. Math. Sci. Soc. 45 (Suppl 1), 235–250 (2022). https://doi.org/10.1007/s40840-022-01287-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-022-01287-z