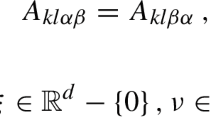Abstract
We study the following second-order differential system
which can be regarded as a second-order Hamiltonian system with a damped term. Here, the nonlinearity H(t, u) is superquadratic as \(|u|\rightarrow \infty \). We do not need any periodic conditions, and we obtain infinitely many nontrivial homoclinic orbits of this system by variational methods. Our result improves and extends the corresponding results existed.
Similar content being viewed by others
References
Ambrosetti, A., Coti Zelati, V.: Multiple homoclinic orbits for a class of conservative systems. Rend. Semin. Mat. Univ. Padova 89, 177–194 (1993)
Benci, V., Rabinowitz, P.H.: Critical point theorems for indefinite functionals. Invent. Math. 52, 241–273 (1979)
Chen, G., Ma, S.: Periodic solutions for Hamiltonian systems without Ambrosetti–Rabinowitz condition and spectrum. J. Math. Anal. Appl. 379, 842–851 (2011)
Chen, G.: Non-periodic damped vibration systems with sublinear terms at infinity: infinitely many homoclinic orbits. Nonlinear Anal. TMA 92, 168–176 (2013)
Chen, G.: Nonperiodic damped vibration systems with asymptotically quadratic terms at infinity: infinitely many homoclinic orbits. Abstr. Appl. Anal. 2013, 937128 (2013)
Costa, D.G., Magalhães, C.A.: A variational approach to subquadratic perturbations of elliptic systems. J. Differ. Equ. 111, 103–122 (1994)
Costa, D.G., Tehrani, H.: On a class of singular second-order Hamiltonian systems with infinitely many homoclinic solutions. J. Math. Anal. Appl. 412, 200–211 (2014)
Ding, Y.: Existence and multiplicity results for homoclinic solutions to a class of Hamiltonian systems. Nonlinear Anal. 25, 1095–1113 (1995)
Izydorek, M., Janczewska, J.: Homoclinic solutions for a class of second order Hamiltonian systems. J. Differ. Equ. 219, 375–389 (2005)
Kim, Y.: Existence of periodic solutions for planar Hamiltonian systems at resonance. J. Korean Math. Soc. 48, 1143–1152 (2011)
Mawhin, J., Willem, M.: Critical Point Theory and Hamiltonian Systems. Applied Mathematical Sciences, vol. 74. Springer, New York (1989)
Omana, W., Willem, M.: Homoclinic orbits for a class of Hamiltonian systems. Differ. Integral Equ. 5, 1115–1120 (1992)
Paturel, E.: Multiple homoclinic orbits for a class of Hamiltonian systems. Calc. Var. Partial Differ. Equ. 12, 117–143 (2001)
Rabinowitz, P.H.: Minimax Methods in Critical Point Theory with Applications to Differential Equations. In: CBMS Regional Conference Series in Mathematics, vol. 65. American Mathematical Society, Providence, RI (1986)
Rabinowitz, P.H.: Homoclinic orbits for a class of Hamiltonian systems. Proc. R. Soc. Edinb. Sect. A 114, 33–38 (1990)
Rabinowitz, P.H., Tanaka, K.: Some results on connecting orbits for a class of Hamiltonian systems. Math. Z. 206, 473–499 (1991)
Séré, E.: Existence of infinitely many homoclinic orbits in Hamiltonian systems. Math. Z. 209, 133–160 (1992)
Sun, J., Chen, H., Nieto, J.J.: Homoclinic solutions for a class of subquadratic second-order Hamiltonian systems. J. Math. Anal. Appl. 373, 20–29 (2011)
Sun, J., Nieto, J.J., Otero-Novoa, M.: On homoclinic orbits for a class of damped vibration systems. Adv. Differ. Equ. (2012). doi:10.1186/1687-1847-2012-102
Sun, J., Wu, T.F.: Multiplicity and concentration of homoclinic solutions for some second order Hamiltonian systems. Nonlinear Anal. 114, 105–115 (2015)
Tang, X., Xiao, L.: Homoclinic solutions for non-autonomous second-order Hamiltonian systems with a coercive potential. J. Math. Anal. Appl. 351, 586–594 (2009)
Wan, L., Tang, C.: Existence and multiplicity of homoclinic orbits for second order Hamiltonian systems without (AR) condition. Discrete Contin. Dyn. Syst. Ser. B 15, 255–271 (2011)
Wang, J., Xu, J., Zhang, F.: Homoclinic orbits for a class of Hamiltonian systems with superquadratic or asymptotically quadratic potentials. Commun. Pure Appl. Anal. 10, 269–286 (2011)
Willem, M.: Minimax Theorems. Birkhäuser, Boston (1996)
Wu, X., Zhang, W.: Existence and multiplicity of homoclinic solutions for a class of damped vibration problems. Nonlinear Anal. 74, 4392–4398 (2011)
Xiao, J., Nieto, J.J.: Variational approach to some damped Dirichlet nonlinear impulsive differential equations. J. Frank. Inst. 348, 369–377 (2011)
Zhang, Z., Yuan, R.: Homoclinic solutions for some second-order nonautonomous systems. Nonlinear Anal. 71, 5790–5798 (2009)
Zhang, P., Tang, C.: Infinitely many periodic solutions for nonautonomous sublinear second-order Hamiltonian systems. Abstr. Appl. Anal. (2010). doi:10.1155/2010/620438
Zhang, Q., Liu, C.: Infinitely many homoclinic solutions for second order Hamiltonian systems. Nonlinear Anal. 72, 894–903 (2010)
Zhu, W.: Existence of homoclinic solutions for a class of second order systems. Nonlinear Anal. 75, 2455–2463 (2012)
Zou, W.: Variant fountain theorems and their applications. Manuscr. Math. 104, 343–358 (2001)
Acknowledgments
I would like to thank the referees for their valuable comments which have led to an improvement of the presentation of this paper.
Conflict of interest
The author declares that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Rosihan M. Ali.
Research supported by National Natural Science Foundation of China (No. 11401011).
Appendix
Appendix
Here, we give an example with infinitely many nontrivial homoclinic orbits for the system (1.2) in the special case \(N=2\).
For \(N=2\), we let \(u=u(t)=(\begin{array}{c}u_1(t)\\ u_2(t)\end{array})=(\begin{array}{c}u_1\\ u_2\end{array}), L(t)=(t^4\sin ^2t+1)(\begin{array}{cc}1\quad 0\\ 0\ \quad 1\end{array}), M=(\begin{array}{cc}0\quad -1\\ 1\ \quad 0\end{array})\) and \(H_u(t,u)=\nu P(t)|u|^{\nu -2}u\) with \(P(t)=\frac{b}{\nu -2}e^{|t|}\ge \frac{b}{\nu -2} (b\) and \(\nu \) are the constants in Corollary 1.1), then (1.2) becomes to
Obviously, Theorem 1.1 and Corollary 1.1 imply the above system has infinitely many nontrivial homoclinic orbits.
Rights and permissions
About this article
Cite this article
Chen, G. Multiple Homoclinics for Nonperiodic Damped Systems with Superlinear Terms. Bull. Malays. Math. Sci. Soc. 41, 1361–1376 (2018). https://doi.org/10.1007/s40840-016-0396-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-016-0396-1