Introduction

Ti–Ni shape memory alloy (SMA) is the most studied and technologically important SMA system possessing excellent shape memory and superelastic properties. By virtue of some of its practical advantages such as good mechanical properties and corrosion resistance, technological refinements in the fabrication of Ti–Ni SMA have been well established and indeed it has been widely used for various industrial and medical applications. Meanwhile, from the scientific viewpoint, Ti–Ni and its derived SMA systems continue to engender fundamental interest in the nature of B2/B19′ martensitic transformation (MT). In the Ni-rich portion of the Ti–Ni system, it is well known that the MT start temperature (T Ms) suddenly disappears at around 51.4 at.% Ni [1]. Such a suppression of MT has only been explained so far by the concept of strain glass, which is one of the class of glassy states in transformation strain essentially similar to spin glass and relaxor [2, 3]. This concept explains the anomaly observed in the parent (P) state of high-Ni content alloys on the basis of the breaking of strain order. However, no consensus has been reached and the origin of the disappearance of MT is still under discussion.

Very recently, our group has reported superelastic behavior in the temperature region down to 40 K in a Ti–51.8Ni alloy, whose composition is in the strain glass region exhibiting no thermally induced MT [4]. This study revealed that the entropy change, \(\Delta S\), estimated by the Clausius–Clapeyron (CC) equation from critical stresses of stress-induced transformation (SIT), σ Ms (forward SIT start stress) and σ Af (reverse SIT finish stress), obtained at many different temperatures, shows a decrement curve toward zero with decreasing temperature and that the superelastic stress hysteresis, σ hys, defined by σ Ms–σ Af, dramatically increases with decreasing temperature. These findings imply that the individual considerations of temperature dependences of the equilibrium SIT stress, σ 0 (≈(σ Ms + σ Af)/2) [5] and σ hys within the frameworks of thermodynamics and kinetics of MT, respectively, are mandatory, especially in the low-temperature region.

In the present study, characteristic temperatures (T Ms, the reverse MT finish temperature, T Af, and equilibrium MT temperature, T 0) and specific heat of Ni-rich Ti–Ni alloys were precisely determined and the MT behavior was studied. Especially, clarification of the origin of the disappearance of MT was attempted by consideration of transformation entropy change, \(\Delta S\).

Experimental Procedures

Ti100−x Ni x alloy ingots, listed in Table 1, were prepared by arc melting under an argon atmosphere. The obtained buttons were homogenized at 1173 K for 30 h in a vacuum followed by water quenching. In order to confirm whether they exhibit the thermally induced MT or not, thermal analysis and electrical resistivity (ER) measurement were performed using a differential scanning calorimeter (DSC) and the physical property measurement system (PPMS), respectively. Temperature sweeping rates for these measurements were set to ±5 K/min. Latent heat of MT was measured by a high-resolution DSC (Netzsch DSC 204 F1 Phoenix) with a heating rate of 10 K/min. Isobaric specific heat (c P) was measured by the relaxation method in the temperature region below 300 K using PPMS. The chemical compositions of samples were checked by an electron probe microanalyzer (EPMA) and determined as listed in Table 1, where the error bar is in about ±0.1 at.% Ni. In this paper, prepared alloys are represented with their analytical compositions (e.g., 49.98 Ni) or mole fractions (e.g., x = 0.4998).

Table 1 Analytical compositions, characteristic temperatures, latent heat, and entropy change of the prepared alloys
Full size table

Results and Discussion

Determination of Transformation Temperatures

The results of DSC measurements for the 49.98, 50.55, and 50.92 Ni alloys are presented in Fig. 1a. They all show clear exothermal and endothermal peaks accompanied by the forward and reverse MTs, onset and offset temperatures being defined as T Ms and T Af (open and filled triangles), respectively.

Fig. 1
figure 1

a DSC curves for 49.98, 50.55, and 50.92 Ni specimens. b ER vs temperature curves for 50.55, 50.71, 50.92, 51.09, 51.23, 51.54, and 51.75 Ni specimens

Full size image

ER vs temperature curves are presented in Fig. 1b, in which the ER values are normalized by that at 350 K. In 50.55, 50.71, 50.92, and 51.09 Ni specimens, the MT is obviously detected as a drastic change of ER and thermal hystereses associated with the MT are confirmed, T Ms and T Af being indicated by open and filled triangles, respectively. It should also be noted that although the ER curves have a positive temperature dependency in the martensite (M) phase, they hardly show temperature dependence in the P phase. Such ER flow has already been observed in the system exhibiting the B2–B19′ MT [6, 7].

In contrast, the ER curves of 51.23, 51.54, and 51.75 specimens show no apparent change due to MT, whereas that of the 51.23 sample has a faint hysteresis at around 180 K. Although the origin of this small hysteresis is not clear, no MT could be detected by other techniques. These results suggest that these three specimens kept the P phase condition down to 4 K. It is seen that the ER curves started to increase at around 300 K with decreasing temperature, becoming almost constant in the temperature region below ~100 K. Such a negative temperature dependence of the ER curve has been reported in some previous papers on not only Ni-rich Ti–Ni alloys, but also Ti–Ni–Fe (more than 6 at.% Fe) alloys [6, 8, 9], which is discussed in relation to the concept of strain glass by Ren et al. [3].

All the determined characteristic temperatures, T 0, T Ms, and T Af, are listed in Table 1 and plotted in Fig. 2 as a function of x together with data from some previous reports [1, 7, 10–17], T 0 being approximated as the average of T Ms and T Af in this study. T Ms in 49.98 Ni (338 K) well accords with that in the slowly cooled stoichiometric TiNi (333 K) [16]. As x increases, T 0, T Ms, and T Af tend to decrease linearly with maintaining an almost constant T hys, and a deviation from this linearity starts to be visible at 50.92 Ni. In x > 51.09, T Ms and T Af are not detected down to ~0 K; disappearance of MT actually occurs between 51.09 and 51.23 Ni.

Fig. 2
figure 2

Critical temperatures, T 0, T Ms, and T Af, as a function of Ni content [1, 7, 10–17]

Full size image

Transformation Entropy Change

\(\Delta S_{ \exp } \left( { = S_{ \exp }^{\text{P}} - S_{ \exp }^{\text{M}} } \right)\) was evaluated as \(\Delta S_{ \exp } = Q^{{{\text{M}} \to {\text{P}}}} /T_{\text{p}}\) from latent heat, \(Q^{M \to P}\), and peak temperature, T p, in the reverse MT determined by high-resolution DSC. All the numerical data obtained by DSC examinations are listed in Table 1 and plotted as a function of T 0 in Fig. 3, together with some data reported in Ref. [18–20]. In addition to them, some data evaluated by a different method are also plotted with red filled squares in this figure. In this method, \(\Delta S_{ \exp }\) was estimated from temperature dependence of σ 0 in the superelastic 51.8 Ni specimen via the following CC equation in the σ 0–T coordinate [4]:

$$\frac{{{\text{d}}\sigma_{0} }}{{{\text{d}}T}} = - \frac{\Delta S}{{\varepsilon \cdot V_{\text{m}} }}.$$
(1)

with the ideal full transformation strain ε and the molar volume \(V_{\text{m}}\). The 51.8 Ni alloy used in that paper is the same as that in the present study, and the analyzed composition is 51.75 Ni. It should be noted that the present data plotted in Fig. 3 are almost 2/3 of those reported in Ref. [4], because in this study \(\Delta S_{ \exp }\) was re-estimated using a more relevant value of ε (=0.044), but not an incorrect value of 0.06 used in the literature, in conversion by Eq. 1, where the relevant value of ε in compressive stress was obtained by the Taylor model for a polycrystalline specimen with no texture [21]. As shown in Fig. 3, the present data are very consistent with all other data, and the fitting curve shows an S-shape.

Fig. 3
figure 3

Entropy changes, \(\Delta S_{ \exp }\), \(\Delta S_{\text{CP}}\), and \(\Delta S_{\text{D}}\), obtained from experiments [4, 18–20], specific heat measurement, and Debye model calculation, respectively, as a function of temperature

Full size image

Specific Heat Measurements

In order to examine the temperature dependence of \(\Delta S\) especially at low temperatures, specific heat measurements were carried out by PPMS. Figure 4 shows resultant c P in a c P /T–T 2 coordinate. As shown in this figure, almost complete linearity is confirmed for data obtained at temperatures lower than ~7 K (T 2 < 50) for all the specimens. As a general approach, the relationship between c P and temperature (T) can be expressed as

$$\frac{{c_{P} }}{T} \approx \beta T^{2} + \gamma ,$$
(2)

where \(\gamma\) is the electronic specific heat coefficient [22]. The coefficient \(\beta\) can be used to obtain the apparent Debye temperature, \(\varTheta_{D}\), as

$$\varTheta_{\text{D}} \approx \left( {\frac{{12\pi^{4} R}}{5\beta }} \right)^{1/3} ,$$
(3)

where R is the gas constant [22]. The values of \(\varTheta_{\text{D}}\) and \(\gamma\) derived from Eqs. 2–3 are listed in Table 2 and plotted as a function of Ni content in Fig. 5a, b together with reference data [6]. First, an anomalously small \(\varTheta_{\text{D}}\) in the P phase is observed, thought to be the result of inherent lattice instability, which is referred to as the resultant of the softening of a TA2[110] phonon branch at the position q ~ 1/3[110]2π/a [23–25]. Qualitatively, a larger \(\gamma\) suggests a larger electronic density of states (DOS) at the Fermi energy level (\(D(\varepsilon_{\text{F}} )\)). The smaller \(D(\varepsilon_{\text{F}} )\) in the M phase than in the P phase in x ≤ 51.09 seems to be consistent with the Kakeshita’s reports [6, 26], where \(D(\varepsilon_{\text{F}} )\) of the B19′ M phase has also been found to be smaller than that of the B2 P phase.

Fig. 4
figure 4

Temperature dependences of isobaric specific heat, c P, in a c P /T–T 2 coordinate determined for M (49.98, 50.55, 50.92, and 51.09 Ni) and P (51.54 and 51.75 Ni) phases

Full size image
Table 2 Debye temperature Θ D and electronic specific heat coefficient γ of the prepared alloys
Full size table
Fig. 5
figure 5

Ni content dependences of a Debye temperature, Θ D, and b electronic specific heat coefficient, γ [6], extracted from the data in Fig. 4

Full size image

If we suppose that the isovolume specific heat \(c_{V}\) can simply be broken down into the three contributions of phonon, \(c_{{{\text{V}}\;{\text{ph}} .}}\), magnon, \(c_{{{\text{V}}\,{\text{mag}} .}}\), and electron, \(c_{{{\text{V}} \,{\text{el}} .}}\), as follows:

$$c_{\text{V}} = c_{{{\text{V}}\,{\text{ph.}}}} + c_{{{\text{V}}\,{\text{mag.}}}} + c_{{{\text{V}}\,{\text{el.}}}} ,$$
(4)

then each component can be approximated as

$$c_{{{\text{V}}\,{\text{mag.}}}} = 0,$$
(5)
$$c_{{{\text{P}}\,{\text{el.}}}} \sim c_{{{\text{V}}\,{\text{el.}}}} = \gamma T,$$
(6)

and under the Debye theory,

$$c_{{{\text{P}}\,{\text{ph.}}}} \sim c_{{{\text{V}}\,{\text{ph.}}}} = 9R\left( {\frac{T}{{\varTheta_{\text{D}} }}} \right)^{3} \int\limits_{0}^{{\varTheta_{\text{D}} /T}} {\frac{{x^{4} { \exp }(x)}}{{\left[ {\exp \left( x \right) - 1} \right]^{2} }}{\text{d}}x} ,$$
(7)

with the isobaric electronic and lattice specific heat (\(c_{{{\text{P}}\,{\text{el.}}}}\) and \(c_{{{\text{P}}\,{\text{ph.}}}}\)). Equations 4–7 allow the estimation of temperature dependence of \(c_{\text{P}} ( = c_{{{\text{P}}\,{\text{ph.}}}} + c_{{{\text{P}}\,{\text{el.}}}} )\) only using \(\varTheta_{\text{D}}\) and \(\gamma\). Moreover, consequent \(c_{\text{P}}\) immediately leads to the derivations of entropy, S, and its constituting components of vibrational entropy, \(S_{{{\text{ph.}}}}\), magnetic entropy, \(S_{{{\text{mag.}}}}\), and electronic entropy, \(S_{{{\text{el.}}}}\), by the following equations:

$$S = S_{{{\text{ph.}}}} + S_{{{\text{mag.}}}} + S_{{{\text{el.}}}} ,$$
(8)
$${S_{{\rm{mag.}}}} = 0,\;{S_{{\rm{el.}}}}\sim \gamma T,\;{S_{{\rm{ph.}}}}\left( {{\Theta _{\rm{D}}},T} \right) = \int\limits_0^T {\left( {{c_{{{\text{P}}\,{\text{ph.}}}}}/T} \right)dT.}$$
(9)

Using Eqs. 8–9, S and its constituents for the M and P phases in 51.75 Ni are calculated, where \(\varTheta_{\text{D}}\) and \(\gamma\) for the P phase are raw data of 242.4 K and 4.573 mJ/(mol K2) and those for the M phase are estimated to be 270.8 K and 3.689 mJ/(mol K2), respectively, by extrapolating these x dependences in the M phase region to 51.75 Ni (broken circles in Fig. 5a, b). The difference, \(\Delta S_{\text{D}} ( = S_{\text{D}}^{\text{P}} - S_{\text{D}}^{\text{M}} )\), which subtracts entropy of the M phase from that of the P phase, is represented by a blue line as a function of temperature in Fig. 3. It is seen that this Debye model-based \(\Delta S_{\text{D}}\) curve is not in agreement with the experimental one.

To investigate the reason for such disagreement, \(c_{\text{P}}\) measurements up to 200 and 300 K were carried out for the 50.92 Ni M and 51.75 Ni P phases, resultant data (\(c_{{{\text{P}}\,{\text{exp.}}}}\)) being shown in Fig. 6a, b, respectively, together with the calculated \(c_{{{\text{P}}\, {\text{ph.}}}}\), \(c_{{{\text{P}}\,{\text{el.}}}}\), and \(c_{\text{P}} ( = c_{{{\text{P}}\,{\text{ph.}}}} + c_{{{\text{P}}\,{\text{el.}}}} )\) using their own \(\varTheta_{\text{D}}\) and \(\gamma\). Interestingly, a sharp contrast can be recognized between these specimens, that is, whereas the experimental and calculated \(c_{\text{P}}\) values in the M phase well accord with each other for all of the measured temperatures, those in the P phase remarkably differ in the temperature range 20–170 K (see the insets of Fig. 6a, b). This means that the Debye model with the experimental apparent Debye temperature fails to describe the temperature dependence of specific heat in the P phase. This may be attributed to the fact that the phonon softening exists in the Ni-rich Ti–Ni P phase [23–25]. In the same manner, experimentally obtained entropy, \(S_{\text{CP}} ( = \mathop \smallint \limits_{0}^{T} \left( {c_{{{\text{P}}\,{\text{exp.}}}} /T} \right)dT),\) is presented in Fig. 6c, d. While showing a good agreement in the M phase of 50.92 Ni, the experimental and calculated S do not agree in the P phase of 51.75 Ni, except for the data below ~20 K. Such deviation between the experimental and calculated S is observed only in the P phase of 51.75 Ni, directly resulting from the discrepancy in \(c_{\text{P}}\) as shown in Fig. 6b. Open circles in Fig. 3 are given as the difference (\(\Delta S_{\text{CP}} = S_{\text{CP}}^{\text{P}} - S_{\text{CP}}^{\text{M}}\)) between the entropies obtained from the \(c_{\text{P}}\) measurements for 51.75 Ni (\(S_{\text{CP}}^{\text{P}}\)) and 50.92 Ni (\(S_{\text{CP}}^{\text{M}}\)). Even though obtained from the difference between two alloys with different compositions, the \(\Delta S_{\text{CP}}\) gradually increases with increasing temperature, enabling a better fitting to the experimental plots than the Debye model-based \(\Delta S_{\text{D}}\).

Fig. 6
figure 6

Temperature dependences of c P exp. (experimentally obtained isobaric specific heat), c P ph., and c P el. (phonon and electron components of calculated isobaric specific heat, respectively) and their sum for a M (50.92 Ni) and b P (51.75 Ni) phases. Temperature dependences of S exp. (experimentally obtained entropy), S ph., and S el. (phonon and electron components of calculated entropy, respectively) and their sum for a M (50.92 Ni) and b P (51.75 Ni) phases

Full size image

All these results suggest that the drastic decrease of the experimental \(\Delta S_{ \exp.}\) in the temperature region below about 280 K is apparently unusual, caused by the abnormal specific heat in the P phase rather than in the M phase. It has been reported that an incommensurate–commensurate (IC-C) transition, referred to as the resultant precursor state of the above-mentioned lattice softening [27, 28], occurs at the temperature around which ER starts to increase. Another possibility is that it occurs by the strain glass phenomenon. In any case, what relatively stabilizes the P phase may occur in the temperature region below around 300 K.

Composition–Temperature Phase Diagram

The phase equilibrium condition between an external field, such as pressure, magnetic field, or uniaxial stress, and temperature is usually expressed by the CC equation. This can apparently be expanded to the relation between composition and temperature such as x 0–T phase diagram, where x 0 is the equilibrium composition at which the Gibbs energy of the P phase is equal to that of the M phase, in the present case.

When considering Gibbs energies of the P and M phases in the Ti–Ni binary system under equilibrium,

$$G^{\text{M}} = G^{\text{P}} .$$

The differentiation is

$${\text{d}}G^{\text{M}} = {\text{d}}G^{\text{P}} .$$

Since \({\text{d}}G^{\text{i}} = - S^{\text{i}} {\text{d}}T + \mu_{\text{Ti}}^{\text{i}} {\text{d}}x_{ 0}^{\text{Ti}} + \mu_{\text{Ni}}^{\text{i}} {\text{d}}x_{ 0}^{\text{Ni}}\) for the i phase in a fixed pressure,

$$- S^{\text{M}} {\text{d}}T + \mu_{\text{Ti}}^{\text{M}} {\text{d}}x_{0}^{\text{Ti}} + \mu_{\text{Ni}}^{\text{M}} {\text{d}}x_{0}^{\text{Ni}} = - S^{\text{P}} {\text{d}}T + \mu_{\text{Ti}}^{\text{P}} {\text{d}}x_{0}^{\text{Ti}} + \mu_{\text{Ni}}^{\text{P}} {\text{d}}x_{0}^{\text{Ni}}$$
$$S^{\text{M}} {\text{d}}T + \left( {\mu_{\text{Ti}}^{\text{M}} - \mu_{\text{Ni}}^{\text{M}} } \right){\text{d}}x_{0}^{\text{Ni}} = S^{\text{P}} {\text{d}}T + \left( {\mu_{\text{Ti}}^{\text{P}} - \mu_{\text{Ni}}^{\text{P}} } \right){\text{d}}x_{0}^{\text{Ni}} .$$

Then, the CC relation for x 0–T system is given by

$$\frac{{{\text{d}}T}}{{{\text{d}}x_{0}^{\text{Ni}} }} = - \frac{{\left( {\mu_{\text{Ti}}^{\text{P}} - \mu_{\text{Ni}}^{\text{P}} } \right) - \left( {\mu_{\text{Ti}}^{\text{M}} - \mu_{\text{Ni}}^{\text{M}} } \right)}}{{S^{\text{P}} - S^{\text{M}} }} = - \frac{{\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} }}{\Delta S},$$
(10)

where \(S^{\text{i}}\) is entropy, \(\mu_{\text{Ti }}^{\text{i}} {\text{and }}\mu_{\text{Ni}}^{\text{i}}\) are chemical potentials of Ti and Ni of the i phase, respectively, and \(x_{ 0}^{\text{Ni}} ( = 1 - x_{ 0}^{\text{Ti}} )\) is the equilibrium Ni fraction of alloy. \(\Delta \mu_{\text{Ti}}\) and \(\Delta \mu_{\text{Ni}}\) are the differences in the chemical potentials of the constituting elements Ti and Ni between the P and M phases, and \(\left( {\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} } \right) = - \left( {\partial G^{\text{P}} /\partial x_{0}^{\text{Ni}} - \partial G^{\text{M}} /\partial x_{0}^{\text{Ni}} } \right)\). This equation manifests \({\text{d}}T/{\text{d}}x_{0}^{\text{Ni}} \to - \infty\) as \(T \to 0,\) since \(\Delta S\) usually converges to zero as T approaches 0 K. In comparison with Eq. 1, Eq. 10 can be modified as

$$\frac{{{\text{d}}T}}{{{\text{d}}x_{0}^{\text{Ni}} }} = \frac{{{\text{d}}T}}{{{\text{d}}\sigma_{0} }} \cdot \frac{{\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} }}{{\varepsilon \cdot V_{\text{m}} }}.$$
(11)

This means that the temperature dependence of x 0 should be similar to that of σ 0, when the temperature and composition dependences of \(\left( {\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} } \right)\) and \(\varepsilon \cdot V_{\text{m}}\) are negligible.

In order to convert the σ 0–T relation to the x 0–T relation using Eq. 11, the numerical values of \(\varepsilon\), \(V_{\text{m}}\), and \(\left( {\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} } \right)\) need to be estimated. The ε and V m can be assumed to be simply constant: ε = 0.044 and V m = 8.25 × 10−6 m3/mol, independent of temperature and alloy composition. The numerical values of \(\left( {\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} } \right)\) were evaluated by Eq. 10 from the \(\Delta S\) determined for the 49.98 and 50.92 Ni alloys (see Table 1) and the slope of x–T 0 curve shown in Fig. 2. The \(\left( {\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} } \right)\) evaluated for 49.98 and 50.92 Ni are about 44 and 48 kJ/mol, respectively, being roughly independent of alloy composition. Under a simple condition that all the values of \(\varepsilon\), \(V_{\text{m}}\), and \(\left( {\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} } \right)\) are constant, the conversion between stress- and concentration-field can be given by

$$\Delta x_{0}^{\text{Ni}} \approx \frac{{\varepsilon \cdot V_{\text{m}} }}{{\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} }} \cdot \Delta \sigma_{0} = C\Delta \sigma_{0} .$$
(12)

When \(\left( {\Delta \mu_{\text{Ti}} - \Delta \mu_{\text{Ni}} } \right)\) = 48 kJ/mol for 50.92 Ni is used, the constant, C, becomes 7.6 × 10−9 m3/kJ (= 7.6 × 10−6 MPa−1), in which \(\Delta \sigma_{0} =\) 1000 MPa is equivalent to \(\Delta x_{0}^{\text{Ni}}\) = 0.0076 (=0.76 at.%). It is apparent that Eq. 12 is available for conversion not only of σ 0 → x 0, but also of σ Ms → x Ms and σ Af → x Af, because it simply converts mechanical energy to chemical energy. Figure 7a exhibits x 0, x Ms, and x Af curves obtained from σ 0, σ Ms, and σ Af curves in Fig. 7b, respectively, where the original point of the composition curves is set at 51.67 Ni, but not at 51.75 Ni. Such a shift of the original point was performed in accordance with the following experimental data on reverse transformation stress. In the case of the σ Af curve for 51.75 Ni in Fig. 7b, σ Af = 0 is obtained at about 40 K, which may correspond to T Af for this composition. It is known that T Af estimated from SIT is not always coincident with the thermal transformation temperature. In the present alloy, it has been reported that the thermal transformation temperatures are comparable to those evaluated from the critical stress of SIT [4]. The other T Af values evaluated by the same method for 51.30 and 51.59 specimens [29] are plotted by filled circles in Fig. 7(a). The original point of the x–T curves converted from the σ–T ones was determined by fitting to these T Af data.

Fig. 7
figure 7

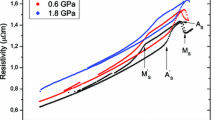
a Composition–temperature phase diagram in an Ni-rich Ti–Ni portion. In a, transformation temperatures, T 0, T Ms, and T Af, above 180 K are experimentally determined (broken lines) and critical compositions, x 0, x Ms, and x Af, below 180 K are speculated using CC equations of Eqs. 10–12 (solid lines). Closed and open red circles are T Af (118 K in 51.30 Ni, 50 K in 51.59 Ni [29], and 40 K in 51.75 Ni [4] ), which correspond to a temperature giving σ Af = 0 in the stress–temperature phase diagram as shown in b. b Stress–temperature phase diagram in 51.75 Ni [4]

Full size image

As shown in Fig. 7a, the x 0, x Ms, and x Af curves proposed at temperatures below 180 K almost perfectly connect, respectively, with T 0, T Ms, and T Af curves determined at higher temperatures. Moreover, the x Ms (namely, T Ms) curve has an inverted C-shape with a maximum at about 120 K around 51.22 Ni, which means that the T Ms suddenly disappears at this composition and that MT does not occur at temperatures below around 120 K. Thus, the reason why the T Ms suddenly disappears at around 51.4 at.% Ni [3] is explained by the temperature dependence of x Ms with an inverted C-shape, which is obviously brought about by the drastic increase of “composition hysteresis” reflecting stress hysteresis at low temperatures. Such a dramatic increase of hysteresis is explained by the existence of a thermal activation term in friction against migration of the P/M phase interface and analyzed by a phenomenological theory in Ref. [30, 31].

Conclusions

For some Ni-rich Ti–Ni alloys, B2/B19′ martensitic transformation temperatures, transformation entropy change, and specific heat were precisely determined and the following results were obtained:

  1. 1.

    With increasing Ni composition from 49.98 Ni, while gradually decreasing in the beginning, martensitic transformation temperatures acceleratedly decline toward the high-Ni content region of ~51 % and are not detected in compositions over 51.23 %.

  2. 2.

    Although the values of entropy change evaluated from DSC measurement for 49.98–50.75 Ni are roughly the same, those for 50.92 Ni are almost half of those in the lower Ni alloys. The entropy change plotted to T 0 temperature shows an S-shaped curve, which starts to drastically decrease at about 300 K.

  3. 3.

    The entropy change estimated from direct measurements of specific heat for 51.75 Ni (B2) and 50.92 Ni (B19′) is more consistent with the experimental data, rather than the calculated curve based on the Debye model for vibration specific heat, which is attributed to the lattice instability inherent in the parent phase.

  4. 4.

    The Clausius–Clapeyron equation for the x–T system was proposed, and a previously reported σ–T diagram was converted to an x–T diagram. The derived x–T phase diagram below 180 K is almost completely compatible with that above 180 K experimentally determined. Moreover, the reason for the sudden disappearance of T Ms around 51.4 Ni was successfully explained by the inverted-C-shaped behavior of x Ms (T Ms) line converted from σ Ms.