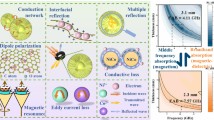
Highlights
-
A Cr5Te8@expanded graphite heterostructure is fabricated by chemical vapor deposition, exhibiting remarkable microwave absorption performance with a minimum reflection loss of up to − 57.6 dB at a thin thickness of only 1.4 mm under a low filling rate of 10%.
-
Density functional theory calculations deeply reveal the polarization loss mechanism triggered by heterogeneous interfaces.
-
The heterostructure coating displays a remarkable radar cross section reduction of 31.9 dB m2, demonstrating a great electromagnetic microwave scattering ability and radar stealth capability.
Abstract
Two-dimensional (2D) transition metal chalcogenides (TMCs) hold great promise as novel microwave absorption materials owing to their interlayer interactions and unique magnetoelectric properties. However, overcoming the impedance mismatch at the low loading is still a challenge for TMCs due to the restricted loss pathways caused by their high-density characteristic. Here, an interface engineering based on the heterostructure of 2D Cr5Te8 and graphite is in situ constructed via a one-step chemical vapor deposit to modulate impedance matching and introduce multiple attenuation mechanisms. Intriguingly, the Cr5Te8@EG (ECT) heterostructure exhibits a minimum reflection loss of up to − 57.6 dB at 15.4 GHz with a thin thickness of only 1.4 mm under a low filling rate of 10%. The density functional theory calculations confirm that the splendid performance of ECT heterostructure primarily derives from charge redistribution at the abundant intimate interfaces, thereby reinforcing interfacial polarization loss. Furthermore, the ECT coating displays a remarkable radar cross section reduction of 31.9 dB m2, demonstrating a great radar microwave scattering ability. This work sheds light on the interfacial coupled stimulus response mechanism of TMC-based heterogeneous structures and provides a feasible strategy to manipulate high-quality TMCs for excellent microwave absorbers.

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Electromagnetic microwave absorption (EMA) materials hold importance in the prevention of electromagnetic contamination produced by electronic productions [1,2,3]. Recently, 2D materials such as graphene, MXenes, and transition metal chalcogenides (TMCs) with exceptional properties have emerged as promising EMA materials, shining brightly in electromagnetic protection [4,5,6,7]. Unfortunately, pure materials exhibit poor EMA performance at a low loading due to the impedance mismatch caused by the deficiencies of interfacial polarization, dipole polarization and conductive loss [8,9,10,11].
Manipulating simultaneously chemical components and structural engineering is highly effective in achieving suitable electromagnetic parameters, leading to positive impedance matching and collaborative loss for the fabrication of advanced absorbers [12, 13]. TMCs offer a unique platform to explore novel electromagnetic protection properties benefiting from their layered structure, strong spin–orbit coupling [14], and various electronic band structures [15]. It is worth noting that the synthetic methods for high-quality TMCs are mainly based on high-temperature solid-state reactions (such as chemical vapor deposit (CVD) [16, 17] and solid-phase sintering and recrystallization [18, 19]). Indeed, high-quality TMCs crystals can bring excellent intrinsic magnetoelectric properties for an outstanding candidate of microwave attenuation components [12, 20]. For instance, Huang et al. [18] synthesized the high-quality ferromagnet Fe3GeTe2 absorber with a minimum reflection loss (RL) value of − 34.7 dB with a thickness of 5.5 mm at the loading of 70 wt%. Among other TMCs, chromium telluride (CrmTen) is one of the most representative Chromium-based chalcogenides (CrmXn, where X = S, Se, and Te) owing to its tunable energy band structure via stoichiometric variations and magnetic properties derived from the strong spin–orbit coupling of Te atoms [16], which demonstrates that pushing forward CrmTen into the novel absorber research is highly feasible and holds significant promise. However, the inherent characteristic of high density makes it challenging to easily manipulate TMCs into excellent absorbers, as it hinders overcoming the impedance mismatch due to the restricted attenuation channels at the low loading [20]. Therefore, the structural engineering design is a feasible strategy for TMCs to broaden the territory of electromagnetic attenuation abilities which is important to design the next generation of EMA materials.
Impressively, the prominent merits of heterointerface engineering inject infinite vitality into the design of high-efficiency and stimuli-responsive microwave absorbers [21, 22]. The TMCs-based heterostructures not only inherit the distinctive electromagnetic characteristics of intrinsic components but also introduce a range of compelling physicochemical properties. These properties fundamentally affect the polarization loss, conduction loss, and magnetic response due to the charge rearrangement and electron transport [21, 23]. Consequently, selecting the materials with suitable band structures to construct heterojunctions provides an opportunity for realizing the high-performance microwave absorbers at a low loading [21, 24]. However, previous reports on TMC-based heterostructures mainly focus on optimizing magnetoelectric components to enhance the EMA performance but in-depth and systematic studies are often lacking [12, 19, 25]. Thereby, designing a novel heterostructure and deeply excavating stimulus response polarization mechanism are urgent and significant for achieving the high-quality TMC-based EMA materials with excellent properties.
Herein, we ingeniously utilize the intrinsic property advantages of Cr5Te8 to establish a “face-to-face” heterostructure between 2D Cr5Te8 and graphite (EG) via a simple and efficient one-step CVD. Intriguingly, the optimal Cr5Te8@EG (ECT) shows superior EMA performance which the minimum RL can reach − 57.6 dB at 15.4 GHz with a thin thickness of 1.4 mm under a low filling rate of 10%. Density functional theory (DFT) calculations confirm the abundant interface coupling polarization between Cr5Te8 and EG owing to charge redistribution and energy band alignment. Besides, radar cross section (RCS) simulations prove that ECTs possess excellent electromagnetic loss capability under different plane microwave angles in near-practical situations, indicating the potential applications of ECTs in electronic communication devices. This work provides an efficient strategy for fabricating 2D TMC-based EMA materials and offers a valuable reference for in-depth microscopic analysis of the polarization loss mechanism.
2 Experimental Section
2.1 Materials
Te powders (99.999%), CrCl3 powders (99.9%), and primary expandable graphite (PEG) powders were purchased from Beijing InnoChem Science & Technology Co., Ltd. (China).
2.2 CVD Synthesis of 2D Cr5Te8
CrCl3 and Te powders were used as precursors, and Si/SiO2 wafer was used as the substrate. A quartz boat loaded with Te powders was placed in upstream of the hot zone, where the temperature was about 500 °C. Subsequently, a ceramic boat containing CrCl3 powders was covered by a Si/SiO2 substrate. The boat was then placed at the heating center of the one-inch-diameter quartz tube. Before the heating process, high-purity argon (Ar, 500 sccm) gas was loaded to purge the reaction chamber for 5 min. After that, a mixture of Ar and H2 (100/5 sccm) was used as the carrier gas. The growth temperature was set to 730 °C with a ramp rate of 50 °C min−1 and maintained for 15 min for the growth of Cr5Te8. Then, natural cooling was adopted when the reaction was completed.
2.3 CVD Preparation of ECT-1
40 mg CrCl3 powders and 10 mg PEG powders were well-mixed and thinly spread in a quartz boat, which PEG powers serve as the role of substrates. Then, this quartz boat was placed at the heating center of the one-inch-diameter quartz tube. A quartz boat loaded with Te powders was placed in upstream of the hot zone, where the temperature was about 500 °C. Before the heating process, high-purity argon (Ar, 500 sccm) gas was loaded to purge the reaction chamber for 5 min. After that, a mixture of Ar and H2 (100/5 sccm) was used as the carrier gas. The growth temperature was set to 730 °C with a ramp rate of 50 °C min−1 and maintained for 15 min for the growth of ECT-1. Then, natural cooling was adopted when the reaction was completed. ECT-2 and ECT-3 with different mass ratios of CrCl3 powders to PEG powers (1:1 and 1:4, respectively) were prepared by the same method.
2.4 Preparation of EG
PEG powders were put into a quartz boat and then placed at the heating center of the one-inch-diameter quartz tube. Before the heating process, high-purity argon (Ar, 500 sccm) gas was used to purge the reaction chamber for 5 min. Then, the furnace temperature was ramped to the expandable temperature of 730 °C, with a mixture gas of 100 sccm Ar and 5 sccm H2, and maintained for 15 min for the growth of EG.
2.5 Characterizations
The morphology and thickness of CVD-grown Cr5Te8 were characterized by OM (BX51, Olympus) and atomic force microscopy (AFM, Bruker ICON microscope). Scanning electron microscopy (SEM) was obtained by using Zeiss Ultra-55. Transmission electron microscopy (TEM) and high-resolution TEM (HRTEM) images were obtained by using JEOL JEM2100F operated at the accelerating voltage of 200 kV. Raman spectra was obtained on a Witec Raman spectroscope, with a 532 nm laser excitation. X-ray diffraction (XRD) patterns were obtained by using an x-ray diffractometer (Bruker D8 Advance) operated at 40 kV and 40 mA using Cu-Kα as the irradiation source (λ = 1.54060 Å). All samples were scanned at 0.8 s/step with a step size of 0.02° within the range of 5–90°. X-ray photoelectron spectroscopy (XPS) was conducted by using scanning x-ray microprobe (Thermo Scientific K-Alpha +) using Al Kα radiation and the C1s peak at 284.8 eV as internal standard. Nitrogen adsorption–desorption isotherms were measured by an accelerated surface area and pore size analyzer (ASAP, Micromeritics TriStar II 3020). The pore size distributions were measured by the Barrett–Joyner–Halenda (BJH) method. Electromagnetic parameters were measured by an Agilent PNAN5244A vector network analyzer in the 2–18 GHz range scope. The measured materials were prepared by homogeneously mixing the absorbents with the paraffin matrix by the mass fraction of 10% and compacted into a coaxial ring of 7.00 mm outer diameter and 3.04 mm inner diameter. According to the transmission line theory, EMA intensity is defined by complex permittivity (εr = ε′ − jε″) and complex permeability (µr = µ′ − jµ″) [26, 27]. The RL values can be calculated by the following equations [28, 29]:
where εr and μr represent the complex permittivity and complex permeability, respectively, d is the measured sample thickness, Zin, Z0, c, and f are the input impedance, free space impedance, speed of light, and measured frequency, respectively.
Impedance matching (Z) is used to describe the ability of electromagnetic microwaves to enter the absorbents, which can be accessed as follows [23]:
2.6 RCS Simulation
CST Studio Suite 2021 was used for simulating the radar cross-sectional of the magnetic-dielectric ECT. According to the metal back model, the simulation model of the specimens was established as a square (10 × 10 cm2) with dual layers, which consisted of an ECT absorption layer and a back plate of the perfect electric conductor (PEC). The thickness of the bottom PEC layer was 1.0 mm, and the absorber layer thickness values were set as 1.4 mm at the frequency of 15.4 GHz, respectively. The ECT-PEC model plate is placed on the X-O-Y plane and linear polarized plane electromagnetic microwaves incident from the positive direction of the Z-axis to the negative direction of the Z-axis. Meanwhile, the direction of electric polarization propagation is along the X-axis. Open boundary conditions are set in all directions with a field monitor frequency of 15.4 GHz. The RCS values can be described as follows [7]:
Here, S is the area of the target object simulation model, λ is the wavelength of the electromagnetic microwave, and Es and Ei represent the electric field intensity of the scattered microwave and the incident microwave, respectively.
2.7 Computational Methods
The static theoretical calculations were performed using spin polarized DFT as implemented in the Vienna ab initio simulation package [31]. The projected augmented wave (PAW) method was applied to treat the electron–ion interactions. The Perdew–Burke–Ernzerhof (PBE) exchange correlation functional within a generalized gradient approximation (GGA) was employed [32, 33]. Dispersion correction was applied in all calculations with the zero-damping DFT + D3 method of Grimme [34]. The valence electrons were expanded in a plane wave-cutoff basis set with a cutoff energy of 400 eV. The energy and force convergence were set to 10–5 eV and 0.02 eV Å−1 during the structure relaxation. The Brillouin zone was sampled using 3 × 3 × 1 Monkhorst–Pack k-point mesh in the geometrical optimization, while a 6 × 6 × 1 grid was used in the electronic structure calculations. Bader charge analysis was performed using the code developed by Henkelman’s group [35]. Coulomb interaction energy for Cr d orbitals was self-consistently determined to Ueff = 4.94 eV applied to Dudarev’s approach [36].
3 Results and Discussion
3.1 Synthetic Strategy and Structural Characterization
To precisely and controllably synthesize Cr5Te8 crystals, an efficient CVD was applied, and the experimental setup is schematically shown in Fig. 1a. Briefly, tellurium (Te) and chromium trichloride (CrCl3) powders were used as precursors to directly synthesize 2D Cr5Te8 nanoflakes and ECT.
Synthetic strategy and structure characterization of 2D Cr5Te8 and ECT. a Schematic representation of the CVD method for the growth of Cr5Te8 and ECT. b Optical and AFM image of Cr5Te8 nanoflakes. c Diffraction patterns of Cr5Te8 crystals. d EDS mapping and HRTEM image of Cr5Te8 crystals (orange represents Te atoms, blue represents Cr atoms), showing the high-quality Cr5Te8 crystals were successfully synthesized by CVD. e–g SEM, HRTEM, and TEM-EDS mapping images, respectively. h–j XRD patterns, Raman spectra, and XPS spectra, respectively, demonstrating the successful preparation of ECT van der Waals heterojunction. (Color figure online)
Figure 1b displays the optical image of the synthesized 2D Cr5Te8 crystals. AFM analysis indicates a flat surface with an approximate height of 22 nm. Moreover, two characteristic peaks at 124 and 141 cm−1 correspond to the out-of-plane A1g and in-plane Eg of Cr5Te8, respectively, which is consistent with the previously reported results (Fig. S1a) [16]. XRD pattern in Fig. S1b shows that the diffraction peaks are in good agreement with the standard card of PDF#50-1153, suggesting that Cr5Te8 belongs to the p-3m1 space group with a trigonal crystal structure. Subsequently, the composition and atomic structure of Cr5Te8 were further examined by selected area diffraction and HRTEM. The crystal structure of trigonal Cr5Te8 can be regarded as Cr atoms intercalated in the van der Waals interlayer of CrTe2 [16]. The intercalation of Cr atoms leads to a new periodicity with the same orientation but half the frequency of the CrTe2 lattice in reciprocal space. This effect can be distinctly observed in the diffraction pattern from the [001] zone axis of Cr5Te8 [17]. As shown in Fig. 1c, the (200) spot is derived from the CrTe2 backbones and the inner (100) supercell spot comes from the intercalated Cr atoms. Meanwhile, the lattice spacing marked by the white line in the HRTEM image is 6.66 Å, which is twice the interplanar spacing of the (200) plane (Fig. 1d). Additionally, the atomic model shown in the magnified view of the HRTEM image reveals an alternating arrangement of Te and Cr atoms, which is confirmed by the intensity line profile extracted from the rectangular region marked with dashed lines (Fig. S1c). Furthermore, the HAADF image of Cr5Te8 and the corresponding electron diffraction spectrum (EDS) elemental mapping manifest the homogeneous spatial distribution of Cr and Te. The above characterizations demonstrate the high quality of as-synthesized Cr5Te8 crystals.
Subsequently, structural analysis was performed on the Cr5Te8@EG heterostructure. Figure 1e displays that Cr5Te8 nanoflakes are randomly anchored on EG. As shown in Fig. 1f, the lattice fringe of 3.31 Å corresponds to the (200) facet of trigonal Cr5Te8. The associated EDS elemental mapping illustrates the homogeneous distribution of Cr and Te elements in the Cr5Te8 crystals, while the C element identifies interfacial coupling (Fig. 1g). Significantly, the obvious lattice mismatch and distortion in the heterointerface region of the Cr5Te8 and EG phases will be beneficial in increasing the interfacial polarization relaxation. Moreover, the XRD patterns in Fig. 1h unveil distinct (002) and (004) characteristic peaks of Cr5Te8 and EG, respectively, indicating their well-defined layered structure. Notably, the XRD and Raman peaks of Cr5Te8 and EG were both identified in the ECT, implying the successful construction of a van der Waals heterojunction. Importantly, the value of ID/IG for ECT is larger than that of EG (0.72 vs 0.65), suggesting that more defects are produced (Fig. 1i) [37]. Then, XPS pattern was further used to characterize the heterostructure (Fig. 1j). Two peaks located at a binding energy of 583.27 and 572.91 eV can be assigned to Te 3d5/2 and Te 3d3/2 [38], respectively, while the peaks at 587.02 and 576.67 eV can be attributed to Te 3d5/2 and Te 3d3/2 [39]. Intriguingly, compared with pure Cr5Te8, both peaks of Cr and Te in ECT shift to higher binding energy, affirming electron transfer from Cr5Te8 to the EG. In short, these results elaborate on the successful construction of ECT van der Waals heterojunction and the directed flow of electrons through the intimate interface, leading to changes in the electronic structure and redistribution of spatial charges.
3.2 High-Efficiency EMA Properties
The frequency dependence of the RL values of Cr5Te8 and EG was investigated with different filler loadings, as shown in Fig. S2. It can be clearly seen that both Cr5Te8 and EG exhibit poor EMA performances for the following reasons: (i) Inappropriate electromagnetic parameters lead to unmatched impedance [40, 41]. According to Eq. (3) in the Experimental Section, a better impedance match is achieved when the values of |Zin/Z0 − 1| are closer to zero [42]. Unfortunately, as shown in Fig. S3a, b, the |Zin/Z0 − 1| values of Cr5Te8 and EG are far from zero. (ii) For pure Cr5Te8 or EG, the loss mechanism is relatively single, resulting in poor EMA ability.
Notably, the construction of Van der Waals heterojunctions can indeed enhance the final EMA performance (Fig. 2) and balance the impedance matching (Fig. 3). Compared with pure Cr5Te8 and EG, the minimum RL values of ECT-1, ECT-2, and ECT-3 significantly increase to − 50.1 dB at 1.2 mm, − 57.6 dB at 1.4 mm, and − 20.4 dB at 1.2 mm, respectively (Fig. 2a-c). Besides, the effective absorption bandwidth (EAB) values of ECTs are 4.0, 4.6, and 4.4 GHz, respectively (Fig. 2d-f). Figure 2g-h provides a more intuitive comparison of EMA performances, showing that ECTs have superior RL values and EAB at different thicknesses. Intriguingly, Fig. S4 shows that the EMA performance of ECTs far exceeds that of the physical mixture of EG and Cr5Te8, manifesting that the heterojunction plays a positive role in improving the absorption performance. Moreover, the attenuation constant α is another key metric for evaluating EMA performance. It can be defined as [43]:
EMA performances of the Cr5Te8, ECT-1, ECT-2, ECT-3, and EG. a, d 3D RL values and corresponding contour maps of ECT-1, respectively. b, e 3D RL values and corresponding contour maps of ECT-2, respectively. c, f 3D RL values, and corresponding contour maps of ECT-3, respectively. All ECTs show excellent EMA performance. g RL and EAB values of ECT-1, ECT-2, and ECT-3. h RL values comparison of CT-1.4mm, ECT-1-1.2mm, ECT-2-1.4mm, ECT-3-1.2mm, and EG-1.4mm, indicating that ECTs with the heterostructure have superior EMA performance than pure EG or Cr5Te8. i The attenuation constant α curves. j Comparison of the minimum RL and corresponding thickness among different absorbers. See Refs. [S1-S15] in Table S1. k Comparison of the minimum RL and corresponding loading among different absorbers (see the references in Table S2), indicating that ECT has better absorption performance than other absorbers under low loading rate and thin thickness (wt% represents the loading rate of the absorber mixed with paraffin). (Color figure online)
Impedance matching capability of ECTs. Impedance matching curves under different thicknesses of ECT-1 (a), ECT-2 (d), and ECT-3 (e), respectively. The difference between the Z values of ECT and the value of 1 is less than 0.2, showing the good impedance matching ability of ECTs. b, c RL-f, tm − f, and |Zin/Z0|-f curves of ECT-1 and ECT-2 at different thicknesses (the filled ellipse represents the experimental matching thickness value), respectively, indicating ECT-1 and ECT-2 match well with the λ/4 matching model. (Color figure online)
As shown in Fig. 2i, the successive decrease in α values of ECT-2, ECT-1, ECT-3, EG, and Cr5Te8 indicates a decrease in attenuation ability, which is consistent with the trend of their RL curves. In addition, the comparison of the minimum RL with different thicknesses (Fig. 2j) and different filler loadings (Fig. 2k) among various EMA materials illustrate that our ECT has an excellent EMA ability at a thinner thickness and a lower filler loading.
Evidently, correspondingly to the good EMA performances of ECTs is their great impedance matching degree. As shown in Fig. 3a, d, e, the |Zin/Z0 − 1| values of ECTs are close to the value of zero, indicating the input impedance of ECTs absorbers matches well with the free space impedance. Specifically, according to the quarter wavelength (λ/4) matching model, the simulated thickness (tm) values of absorbers are estimated by the equation: tm = nc/\(\left( {4 fm\sqrt {|\mu_{r} ||\varepsilon_{r} |} } \right)\) (n = 1, 3, 5,…) [25, 44]. Figure 3b, c displays that the minimum RL values are obtained at a frequency where |Zin/Z0| is much closer to the value of 1, and the experimental matching thicknesses values exactly fall on the λ/4 curve, indicating that electromagnetic microwaves can be easily entered into the ECT absorber.
3.3 Multivariate Synergistic Loss Mechanism
Heterointerface structures and magnetic/dielectric components endow ECTs with stimulative impedance matching and efficient EMA. The detailed mechanisms can be clarified by the following four aspects.
-
i. Heterointerfaces induced interfacial polarization. To investigate the polarization loss induced by interfacial interplay, Cole–Cole plots are provided in Fig. 4a-c. The relationship between the dissipation (ε″) and storage (ε′) capacity can be established with the help of the static permittivity, εs, and permittivity at infinite high frequency, ε∞: (ε′ − εs + ε∞/2)2 + (ε′′)2 = ((εs − ε∞)/2)2 [45, 46]. Thus, the Debye semicircles in Cole–Cole curves signify the relaxation process. Apparently, compared to pure Cr5Te8 (Fig. S5a) and EG (Fig. S5b), ECTs show more Cole–Cole semicircles (Fig. 4a-c). This indicates that ECTs undergo the Debye relaxation process more prominently than pure Cr5Te8 and EG, which can be attributed to the interface polarization behaviors [47, 48]. Furthermore, the linear Cole–Cole curves are related to the conduction loss [49, 50].
Interfacial polarization mechanism of ECTs. The Cole–Cole curves of ECT-1 (a), ECT-2 (b), and ECT-3 (c). DFT calculations of heterojunction (d–h). d The atomic model and the three-dimensional charge density difference of the heterostructure interface. The blue isosurface suggests a decrease of electron density, and the yellow isosurface depicts an increase of electron density (0.0003 electrons/Å). e Z-axis charge density difference of ECT in (d). f Projected density of state of EG, Cr5Te8, and ECT heterojunction, all the energies are referred to the Fermi level. g Work function of Cr5Te8 (200) surface. h Energy band alignment of Cr5Te8 and EG heterojunction before and after Mott–Schottky contact, vacuum energy (Evac), conduction band (Ec), valence band (Ev), Fermi level (EF) and work function (Φ), showing that the contact between Cr5Te8 and EG can trigger the redistribution of interfacial charge. (Color figure online)
To deeply understand the mechanisms of the interface enhanced the EMA capability of ECT heterojunctions, we conducted static DFT calculations to further investigate charge migration and distribution at the interface. Primarily, the (200) surface of Cr5Te8 crystals observed in Fig. 1 and the (001) surface of EG were selected for modeling, and the optimized structure is shown in Fig. 4d. Specifically, the contact between Cr5Te8 and EG forms a van der Waals heterojunction rather than interfacial atomic bonding. Moreover, electron density difference isosurfaces and corresponding integration along the z-axis of the heterojunction interface are displayed in Fig. 4d, e. Although the charge transfer at the interface is bidirectional with charge accumulation and depletion, Bader charge analysis shows that there is a net charge transfer of 0.6 |e| from Cr5Te8 to EG through the interface. Further, the projected density of states (PDOS) was inspected to analyze the charge transport of the ECT heterojunction (Fig. 4f). The energy bands of Cr5Te8 crystals and ECT heterojunction significantly cross the Fermi level, indicating their metallic nature. Besides, the band structure of the ECT heterojunction exhibits higher dispersion compared to that of Cr5Te8, leading to enhanced electronic conductivity and conduction loss [51]. It’s worth noting that carbon materials can exhibit properties of either a metal or a semiconductor under specific conditions [21, 52]. Therefore, we measured the band gap of EG using a UV–vis spectrophotometer, and the value is 1.06 eV (Fig. S6a). This result manifests that the absence of the EG bandgap in PDOS stems from the PBE function containing unphysical self-Coulomb repulsion, resulting in a systematic underestimate of the bandgap [53].
Intriguingly, the Mott–Schottky heterojunction is adapted to disclose the positive effect of the interface on the EMA capacity due to the heterostructure formed between metallic Cr5Te8 and semiconducting EG. The work function (Φ) of Cr5Te8 (200) and EG was calculated by UPS to be 3.67 and 4.54 eV, respectively, as shown in Fig. 4g and Fig. S6b-c. Figure 4h shows the interface coupling between Cr5Te8 and EG. Their band alignment generates a built-in electric field and Schottky barrier, benefitting intensive interface polarization loss.
-
ii. Magnetic-dielectric synergistic effect. This combined effect of dielectric loss and magnetic loss is mainly evaluated by electromagnetic parameters and their derived loss parameters. The complex permittivity (ε′ and ε″) and the complex permeability (µ′ and µ″) with frequency-dependent fluctuations are depicted in Fig. 5a, b. The ε′ values of ECT and EG exhibit a decreasing trend as the frequency increases, which is related to the frequency dispersion behavior caused by polarization hysteresis under a high-frequency electric field [30]. The ε″ values are associated with the dissipation potential of electric field energy [54]. Compared with Cr5Te8, both ECT and EG display higher ε″ values, indicating the introduction of porous expanded graphite can enhance electron migration efficiency and further enhance electromagnetic energy dissipation. The inconspicuous variation of µ′ indicates the relaxation of magnetic moments precession rather than magnetic hysteresis, while the fluctuated µ″ values show the strong magnetic dissipation capability. Additionally, as shown in Fig. 5c1, the calculated dielectric loss tangent (tanδε = ε″/ε′, where the tanδε value is positively correlated with the dielectric loss capacity) values of all samples exhibit the same trends as ε″ values, confirming the stronger attenuation capability of ECTs to electric field energy [29, 55]. Similarly, the superior magnetic loss capacity of ECTs and Cr5Te8 is evident in the higher magnetic loss tangent (tanδμ = μ″/μ′) values in Fig. 5c2 [55], primarily due to the robust magnetic coupling interaction stemming from the spin polarization of Cr5Te8 nanoflakes [17]. When microwaves propagate into the Cr5Te8/graphite composite, the high-frequency magnetic field component induces spin precession in the Cr5Te8 nanoflakes [56]. Their stray magnetic fields can affect neighboring Cr5Te8 through corresponding dynamic variation [57]. As a result, a mutual induction process occurs between adjacent Cr5Te8 nanoflakes, achieving the interparticle coupling interaction. Therefore, these magnetic coupling interactions among Cr5Te8 nanoflakes effectively interact with microwaves to achieve electromagnetic microwave attenuation. Furthermore, magnetic loss depends significantly on eddy current loss, natural resonance, and exchange resonance. As shown in the coefficient curves (C0 = μ"(μ')−2f−1) [58, 59], the C0 values of ECTs exhibit significant fluctuations in 2–10 GHz, indicating natural resonance occurring at the low frequency (Fig. 5d) [19, 59]. The several fluctuations located at high-frequency regions (especially > 10 GHz) are attributed to exchange resonance [7, 60, 61]. Briefly, the introduction of the Cr5Te8 component can effectively induce exchange resonance loss and natural resonance loss, which are the main sources of magnetic loss resulting from magnetic coupling interaction, pinning effect, and spin wave excitation. Therefore, it can be concluded that the magnetoelectric synergistic loss mechanism of ECTs with a heterostructure plays a vital role in improving microwave absorption capacity.
-
iii. Multiple reflection and interlayer scattering. The vertical spatial distribution of ECT allows multiple reflections and scatterings to trap electromagnetic microwaves. Moreover, the porous EG microstructure is verified by the N2 adsorption–desorption isotherm curves (Fig. S7). The pore structure facilitates the reduction of absorber density and the appropriate specific surface area is conducive to improving the impedance matching and interfacial polarization, thereby promoting microwave attenuation [22].
-
iv. Conduction loss caused by conductive networks. The randomly distributed Cr5Te8 units contribute to the construction of a spatial conductive network and an increase of conductive pathways [1, 62]. When electromagnetic microwaves permeate the network, the excited electrons migrate along the axial direction or to other neighboring lamellas [22]. This process leads to the transformation of electromagnetic energy into thermal energy due to the resistance of the absorber.
a1 Imaginary part and b1 real part of permittivity. a2 imaginary part and b2 real part of permeability. ECTs have an excellent impedance matching degree due to the appropriate electromagnetic parameters. c1 dielectric and c2 magnetic loss tangents. ECTs possess excellent dielectric and magnetic loss capabilities. d Coefficient (C0) values of ECTs. The magnetic loss of ECTs primarily generates from natural resonance and exchange resonance. (Color figure online)
Figure 6 generalizes the multivariate synergistic loss mechanism of the ECT absorber, which includes the generous interface polarization loss brought about by the heterostructure. Subsequently, the abundant micro-conducting network brings the conductive loss. Additionally, the structural advantages, including the ample heterointerface, the layered structure of Cr5Te8, and the porous EG, lead to multi-level reflection and interlayer scattering of electromagnetic microwaves. Meanwhile, the strong atom spin effect of Cr5Te8 enhances the magnetic loss and optimizes impedance matching of ECT. These synergistic effects result in the powerful EMA.
3.4 Excellent RCS Reduction Ability
With the rapid development of stealth technology, more attentions have been focused on the RCS which can evaluate the anti-detection ability of the target. In general, the lower RCS corresponds to the stronger anti-detection ability [63]. Notably, EMA materials can effectively reduce RCS due to the efficient attenuation of incident electromagnetic waves [64]. Therefore, to assess the practical electromagnetic loss potential of ECTs under near-practical situations, the RCS of the as-prepared ECTs in the far-field response range was simulated using CST software, as shown in Fig. 7. This simulation provides insights into the performance of absorbing materials under more realistic conditions. The 3D radar scattering results in Fig. 7a-c reveal that EG and Cr5Te8 present the largest radar scattering signals among those tested, which is detrimental for stealth applications. In sharp contrast, ECT-2 exhibits the lowest radar scattering signals, indicating superior stealth performance. To further evaluate their performance, the simulated RCS values within a scanning angle range of –60° to 60° at 15.4 GHz (Ku band) of PEC and ECT-covered PEC are shown in Figs. 7d and S8. Obviously, the RCS peak values decrease when θ is changed from 0° to ± 60°, proving scanning angles affect the displayed RCS. Besides, the RCS values of PEC, EG, and Cr5Te8 are basically coincidental and are larger than other composite coatings, indicating that ECT-1, ECT-2, and ECT-3 coatings have a great contribution to electromagnetic microwave attenuations. In addition, when the incident angle of the electromagnetic microwave is greater than 20°, the RCS value of all coatings is less than − 10 dB, suggesting that radar reflections with large incident angles account for a smaller proportion. Therefore, it is important to develop materials that have good absorption even at small incident angles. To separately analyze the specific contribution of ECTs to RCS values, the RCS reduction values in small angles can be obtained in Fig. 7e by calculating the RCS values of ECTs, except PEC. Figure 7e reveals that the RCS contribution of ECTs is basically greater than 10 dB m2. When the incident angle is 0°, the RCS contribution of ECT-2 can reach 31.9 dB m2, which is superior than previous reports [5, 18, 65]. For electromagnetic microwaves incident at 0–60°, the RCS values of ECT-1 and ECT-2 all exceed 15 dB m2, demonstrating the excellent EMA characteristics of ECT. Moreover, the corresponding RCS value of the representative incident angle of ECT-2 at 1.4 mm is also statistically analyzed (Fig. 7f). The results show that the RCS value remains consistently below − 10 dB m2 when the incident angle exceeds 30°, highlighting the material coating has great electromagnetic attenuation characteristics. Undoubtedly, ECT-absorbing coatings can effectively reduce RCS and play an irreplaceable role in the system of protecting high-value targets.
RCS simulations. The three-dimensional radar microwave scattering signals of a Cr5Te8, b ECT-2, and c EG, respectively, showing that ECT-2 has a better radar signal scattering ability. d RCS simulated curves at different incident thetas of PEC and Cr5Te8, EG and ECT-2. e The RCS reduction values of ECTs. f Frequency dependences of ECT-2 RCS values at different incident thetas. Inset is the schematic diagram of CST simulation, showing the excellent radar signal scattering ability of ECT-2 under different incident thetas. (Color figure online)
4 Conclusions
In summary, we have successfully constructed ECTs by assembling Cr5Te8 nanoflakes and porous dielectric EG via CVD. As a result, an optimal RL of − 57.6 dB is achieved in a 1.4 mm film with a low filling rate of 10%, which is mainly attributed to the dielectric polarization induced by the charge redistribution at the interfaces. Meanwhile, the RCS reduction of ECT coating can reach 31.9 dB m2, and the RCS value is almost less than − 10 dB m2 when the incident angle is greater than 30°, demonstrating great electromagnetic microwave scattering ability and radar stealth capability. The powerful combination of magnetic-dielectric integrated compositions, strong interface polarization relaxation induced by heterogeneous interfaces, and abundant interlayer scattering, lead to the promoted impedance matching and superior EMA properties of ECTs. This work provides new perspectives for designing 2D TMC-based EMA materials to achieve essential breakthroughs in mechanistic investigations in this promising field.
References
Z. Wu, H.W. Cheng, C. Jin, B. Yang, C. Xu et al., Dimensional design and core-shell engineering of nanomaterials for electromagnetic wave absorption. Adv. Mater. 34(11), 2107538 (2022). https://doi.org/10.1002/adma.202107538
J. Cheng, H. Zhang, M. Ning, H. Raza, D. Zhang et al., Emerging materials and designs for low- and multi-band electromagnetic wave absorbers: The search for dielectric and magnetic synergy? Adv. Funct. Mater. 32(23), 2200123 (2022). https://doi.org/10.1002/adfm.202200123
Z. Tang, L. Xu, C. Xie, L. Guo, L. Zhang et al., Synthesis of CuCo2S4@expanded graphite with crystal/amorphous heterointerface and defects for electromagnetic wave absorption. Nat. Commun. 14, 5951 (2023). https://doi.org/10.1038/s41467-023-41697-6
Y. Liu, X.F. Zhou, Z.R. Jia, H.J. Wu, G.L. Wu, Oxygen vacancy-induced dielectric polarization prevails in the electromagnetic wave-absorbing mechanism for Mn-based MOFs-derived composites. Adv. Funct. Mater. 32(34), 2204499 (2022). https://doi.org/10.1002/adfm.202204499
X. Li, Z. Wu, W. You, L. Yang, R. Che, Self-assembly MXene-rGO/CoNi film with massive continuous heterointerfaces and enhanced magnetic coupling for superior microwave absorber. Nano-Micro Lett. 14, 73 (2022). https://doi.org/10.1007/s40820-022-00811-x
M. Han, D. Zhang, C.E. Shuck, B. McBride, T. Zhang et al., Electrochemically modulated interaction of MXenes with microwaves. Nat. Nanotechnol. 18(4), 373–379 (2023). https://doi.org/10.1038/s41565-022-01308-9
Y. Wu, Y. Zhao, M. Zhou, S. Tan, R. Peymanfar et al., Ultrabroad microwave absorption ability and infrared stealth property of nano-micro CuS@rGO lightweight aerogels. Nano-Micro Lett. 14, 171 (2022). https://doi.org/10.1007/s40820-022-00906-5
Z.X. Li, W. Yang, B. Jiang, C.A. Wang, C.X. Zhang et al., Engineering of the core-shell boron nitride@nitrogen-doped carbon heterogeneous interface for efficient heat dissipation and electromagnetic wave absorption. ACS Appl. Mater. Interfaces 15(5), 7578–7591 (2023). https://doi.org/10.1021/acsami.2c20766
K. Yang, Y.H. Cui, L.Y. Wan, Y.B. Wang, M.R. Tariq et al., Preparation of three-dimensional Mo2C/NC@MXene and its efficient electromagnetic absorption properties. ACS Appl. Mater. Interfaces 14(5), 7109–7120 (2022). https://doi.org/10.1021/acsami.1c19033
M.Q. Huang, L. Wang, B. Zhao, G.Y. Chen, R.C. Che, Engineering the electronic structure on MXenes via multidimensional component interlayer insertion for enhanced electromagnetic shielding. J. Mater. Sci. Technol. 138, 149–156 (2023). https://doi.org/10.1016/j.jmst.2022.07.047
G.H. Dai, R.X. Deng, X. You, T. Zhang, Y. Yu et al., Entropy-driven phase regulation of high-entropy transition metal oxide and its enhanced high-temperature microwave absorption by in-situ dual phases. J. Mater. Sci. Technol. 116, 11–21 (2022). https://doi.org/10.1016/j.jmst.2021.11.032
Z. Gao, Z. Ma, D. Lan, Z. Zhao, L. Zhang et al., Synergistic polarization loss of MoS2-based multiphase solid solution for electromagnetic wave absorption. Adv. Funct. Mater. 32(18), 2112294 (2022). https://doi.org/10.1002/adfm.202112294
P. Liu, G. Zhang, H. Xu, S. Cheng, Y. Huang et al., Synergistic dielectric-magnetic enhancement via phase-evolution engineering and dynamic magnetic resonance. Adv. Funct. Mater. 33(13), 2211298 (2023). https://doi.org/10.1002/adfm.202211298
S. Manzeli, D. Ovchinnikov, D. Pasquier, O.V. Yazyev, A. Kis, 2D transition metal dichalcogenides. Nat. Rev. Mater. 2(8), 17033 (2017). https://doi.org/10.1038/natrevmats.2017.33
T. Heine, Transition metal chalcogenides: Ultrathin inorganic materials with tunable electronic properties. Acc. Chem. Res. 48(1), 65–72 (2014). https://doi.org/10.1021/ar500277z
C. Chen, X. Chen, C. Wu, X. Wang, Y. Ping et al., Air-stable 2D Cr5Te8 nanosheets with thickness-tunable ferromagnetism. Adv. Mater. 34(2), 2107512 (2022). https://doi.org/10.1002/adma.202107512
B. Tang, X. Wang, M. Han, X. Xu, Z. Zhang et al., Phase engineering of Cr5Te8 with colossal anomalous hall effect. Nat. Electron. 5(4), 224–232 (2022). https://doi.org/10.1038/s41928-022-00754-6
G. Li, S. Ma, Z. Li, Y. Zhang, J. Diao et al., High-quality ferromagnet Fe3GeTe2 for high-efficiency electromagnetic wave absorption and shielding with wideband radar cross section reduction. ACS Nano 16(5), 7861–7879 (2022). https://doi.org/10.1021/acsnano.2c00512
G. Li, S. Ma, Z. Li, Y. Zhang, Y. Cao et al., Temperature-induced self-decomposition doping of Fe3GeTe2 to achieve ultra-high Tc of 496 K for multispectral compatible strong electromagnetic wave absorption. Adv. Funct. Mater. 33(15), 2210578 (2023). https://doi.org/10.1002/adma.202106195
H. Zhang, J. Cheng, H. Wang, Z. Huang, Q. Zheng et al., Initiating VB-group laminated NbS2 electromagnetic wave absorber toward superior absorption bandwidth as large as 6.48 GHz through phase engineering modulation. Adv. Funct. Mater. 32(6), 2108194 (2022). https://doi.org/10.1002/adfm.202108194
L. Liang, W. Gu, Y. Wu, B. Zhang, G. Wang et al., Heterointerface engineering in electromagnetic absorbers: new insights and opportunities. Adv. Mater. 34(4), 2106195 (2022). https://doi.org/10.1002/adma.202106195
Q. Liu, Q. Cao, H. Bi, C. Liang, K. Yuan et al., CoNi@SiO2@TiO2 and CoNi@air@TiO2 microspheres with strong wideband microwave absorption. Adv. Mater. 28(3), 486–490 (2016). https://doi.org/10.1002/adma.201503149
P. Liu, Y. Wang, G. Zhang, Y. Huang, R. Zhang et al., Hierarchical engineering of double-shelled nanotubes toward hetero-interfaces induced polarization and microscale magnetic interaction. Adv. Funct. Mater. 32(33), 2202588 (2022). https://doi.org/10.1002/adfm.202202588
B.J. Wang, F.Z. Huang, H. Wu, Z.J. Xu, S.P. Wang et al., Enhanced interfacial polarization of defective porous carbon confined CoP nanoparticles forming Mott-Schottky heterojunction for efficient electromagnetic wave absorption. Nano Res. 16(3), 4160–4169 (2022). https://doi.org/10.1007/s12274-022-4779-3
Z.T. Yang, T. Wang, J.F. Wang, Z.X. Luo, Q.Y. Zhang et al., Heterogeneous N-doped carbon composite NiSe2-FeSe double-shell hollow nanorods for tunable and high-efficient microwave attenuation. Carbon 201, 491–503 (2023). https://doi.org/10.1016/j.carbon.2022.09.023
T. Guo, S. Chang, Y. Akinay, Synthesis of PPy@Ba0.5Sr0.5Fe12O19/CNFs by reverse in-situ polymerization method for microwave absorption applications. Synth. Met. 266, 116387 (2020). https://doi.org/10.1016/j.synthmet.2020.116387
C. Wen, X. Li, R. Zhang, C. Xu, W. You et al., High-density anisotropy magnetism enhanced microwave absorption performance in Ti3C2Tx MXene@Ni microspheres. ACS Nano 16(1), 1150–1159 (2022). https://doi.org/10.1021/acsnano.1c08957
R.C. Che, C.Y. Zhi, C.Y. Liang, X.G. Zhou, Fabrication and microwave absorption of carbon nanotubes/CoFe2O4 spinel nanocomposite. Appl. Phys. Lett. 88(3), 033105 (2006). https://doi.org/10.1063/1.2165276
C. Li, D. Li, L. Zhang, Y. Zhang, L. Zhang et al., Boosted microwave absorption performance of transition metal doped TiN fibers at elevated temperature. Nano Res. 16(2), 3570–3579 (2022). https://doi.org/10.1007/s12274-023-5398-3
H. Sun, R. Che, X. You, Y. Jiang, Z. Yang et al., Cross-stacking aligned carbon-nanotube films to tune microwave absorption frequencies and increase absorption intensities. Adv. Mater. 26(48), 8120–8125 (2014). https://doi.org/10.1002/adma.201403735
G. Kresse, J. Furthmiiller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 6(1), 15–50 (1996). https://doi.org/10.1016/0927-0256(96)00008-0
G. Kresse, J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54(16), 11169–11186 (1996). https://doi.org/10.1103/PhysRevB.54.11169
J.P. Perdew, J.A. Chevary, S.H. Vosko, K.A. Jackson, M.R. Pederson et al., Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46(11), 6671–6687 (1992). https://doi.org/10.1103/PhysRevB.46.6671
S. Grimme, J. Antony, S. Ehrlich, H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132(15), 154104 (2010). https://doi.org/10.1063/1.3382344
G. Henkelman, A. Arnaldsson, H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density. Comp. Mater. Sci. 36(3), 354–360 (2006). https://doi.org/10.1016/j.commatsci.2005.04.010
S.L. Dudarev, G.A. Botton, S.Y. Savrasov, C.J. Humphreys, A.P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an lsda+u study. Phys. Rev. B 57(3), 1505–1509 (1998). https://doi.org/10.1103/PhysRevB.57.1505
H. Zhao, X. Xu, Y. Wang, D. Fan, D. Liu et al., Heterogeneous interface induced the formation of hierarchically hollow carbon microcubes against electromagnetic pollution. Small 16(43), 2003407 (2020). https://doi.org/10.1002/smll.202003407
M. Bian, L. Zhu, X. Wang, J. Choi, R.V. Chopdekar et al., Dative epitaxy of commensurate monocrystalline covalent Van der waals moiré supercrystal. Adv. Mater. 34(17), 2200117 (2022). https://doi.org/10.1002/adma.202200117
B. Tang, J. Zhou, P. Sun, X. Wang, L. Ba et al., Phase-controlled synthesis of monolayer ternary telluride with a random local displacement of tellurium atoms. Adv. Mater. 31(23), 1900862 (2019). https://doi.org/10.1002/adma.201900862
J.C. Shu, W.Q. Cao, M.S. Cao, Diverse metal-organic framework architectures for electromagnetic absorbers and shielding. Adv. Funct. Mater. 31(23), 2100470 (2021). https://doi.org/10.1002/adfm.202100470
X. Zhang, X.L. Tian, Y. Qin, J. Qiao, F. Pan et al., Conductive metal-organic frameworks with tunable dielectric properties for boosting electromagnetic wave absorption. ACS Nano 17(13), 12510–12518 (2023). https://doi.org/10.1021/acsnano.3c02170
J. Tao, L. Xu, H. Jin, Y. Gu, J. Zhou et al., Selective coding dielectric genes based on proton tailoring to improve microwave absorption of MOFs. Adv. Powder Mater. 2(1), 100091 (2023). https://doi.org/10.1016/j.apmate.2022.100091
Y.X. Xie, Y.Y. Guo, T.T. Cheng, L.B. Zhao, T. Wang et al., Efficient electromagnetic wave absorption performances dominated by exchanged resonance of lightweight PC/Fe3O4@PDA hybrid nanocomposite. Chem. Eng. J. 457, 141205 (2023). https://doi.org/10.1016/j.cej.2022.141205
C. Wang, Y. Liu, Z. Jia, W. Zhao, G. Wu, Multicomponent nanoparticles synergistic one-dimensional nanofibers as heterostructure absorbers for tunable and efficient microwave absorption. Nano-Micro Lett. 15, 13 (2022). https://doi.org/10.1007/s40820-022-00986-3
M.H. Li, W.J. Zhu, X. Li, H.L. Xu, X.M. Fan et al., Ti3C2Tx/MoS2 self-rolling rod-based foam boosts interfacial polarization for electromagnetic wave absorption. Adv. Sci. 9(16), 2201118 (2022). https://doi.org/10.1002/advs.202201118
F. Pan, L. Cai, Y.Y. Shi, Y.Y. Dong, X.J. Zhu et al., Phase engineering reinforced multiple loss network in apple tree-like liquid metal/Ni-Ni3P/N-doped carbon fiber composites for high-performance microwave absorption. Chem. Eng. J. 435, 135009 (2022). https://doi.org/10.1016/j.cej.2022.135009
H. Niu, P. Liu, F. Qin, X. Liu, Y. Akinay, PEDOT coated Cu-BTC metal-organic frameworks decorated with Fe3O4 nanoparticles and their enhanced electromagnetic wave absorption. Mater. Chem. Phys. 253, 123458 (2020). https://doi.org/10.1016/j.matchemphys.2020.123458
Y. Cao, A.M. Mohamed, M. Mousavi, Y. Akinay, Poly(pyrrole-co-styrene sulfonate)-encapsulated MWCNT/Fe-Ni alloy/NiFe2O4 nanocomposites for microwave absorption. Mater. Chem. Phys. 259, 124169 (2021). https://doi.org/10.1016/j.matchemphys.2020.124169
J. Cheng, H. Zhang, H. Wang, Z. Huang, H. Raza et al., Tailoring self-polarization of bimetallic organic frameworks with multiple polar units toward high-performance consecutive multi-band electromagnetic wave absorption at gigahertz. Adv. Funct. Mater. 32(24), 2201129 (2022). https://doi.org/10.1002/adfm.202201129
Y.H. Wu, G.D. Wang, X.X. Yuan, G. Fang, P. Li et al., Heterointerface engineering in hierarchical assembly of the Co/Co(OH)2@carbon nanosheets composites for wideband microwave absorption. Nano Res. 16(2), 2611–2621 (2022). https://doi.org/10.1007/s12274-022-5263-9
W.-L. Song, M.-S. Cao, Z.-L. Hou, X.-Y. Fang, X.-L. Shi et al., High dielectric loss and its monotonic dependence of conducting-dominated multiwalled carbon nanotubes/silica nanocomposite on temperature ranging from 373 to 873 K in X-band. Appl. Phys. Lett. 94(23), 233110 (2009). https://doi.org/10.1063/1.3152764
B. Zhao, Y.Q. Du, Z.K. Yan, L.J. Rao, G.Y. Chen et al., Structural defects in phase-regulated high-entropy oxides toward superior microwave absorption properties. Adv. Funct. Mater. 33(1), 2209924 (2023). https://doi.org/10.1002/adfm.202209924
J.M. Crowley, J. Tahir-Kheli, W.A. Goddard, Resolution of the band gap prediction problem for materials design. J. Phys. Chem. Lett. 7(7), 1198–1203 (2016). https://doi.org/10.1021/acs.jpclett.5b02870
J.L. Bai, S.J. Huang, X.M. Yao, X.J. Liu, Z.R. Huang, Surface engineering of nanoflower-like MoS2 decorated porous Si3N4 ceramics for electromagnetic wave absorption. J. Mater. Chem. A 11(12), 6274–6285 (2023). https://doi.org/10.1039/d3ta00122a
Y. Wang, X.C. Di, Z. Lu, R.R. Cheng, X.M. Wu et al., Controllable heterogeneous interfaces of cobalt/carbon nanosheets/rGO composite derived from metal-organic frameworks for high-efficiency microwave attenuation. Carbon 187, 404–414 (2022). https://doi.org/10.1016/j.carbon.2021.11.027
R.C. Che, L.M. Peng, X.F. Duan, Q. Chen, X.L. Liang, Microwave absorption enhancement and complex permittivity and permeability of fe encapsulated within carbon nanotubes. Adv. Mater. 16(5), 401–405 (2004). https://doi.org/10.1002/adma.200306460
Z. Wu, K. Pei, L. Xing, X. Yu, W. You et al., Enhanced microwave absorption performance from magnetic coupling of magnetic nanoparticles suspended within hierarchically tubular composite. Adv. Funct. Mater. 29(28), 1901448 (2019). https://doi.org/10.1002/adfm.201901448
W.J. Ma, P. He, J. Xu, X.Y. Liu, S.L. Lin et al., Self-assembly magnetized 3D hierarchical graphite carbon-based heterogeneous yolk-shell nanoboxes with enhanced microwave absorption. J. Mater. Chem. A 10(21), 11405–11413 (2022). https://doi.org/10.1039/d2ta01798a
Y. Liu, Z.R. Jia, Q.Q. Zhan, Y.H. Dong, Q.M. Xu et al., Magnetic manganese-based composites with multiple loss mechanisms towards broadband absorption. Nano Res. 15(6), 5590–5600 (2022). https://doi.org/10.1007/s12274-022-4287-5
L. Liang, Q. Li, X. Yan, Y. Feng, Y. Wang et al., Multifunctional magnetic Ti3C2Tx MXene/graphene aerogel with superior electromagnetic wave absorption performance. ACS Nano 15(4), 6622–6632 (2021). https://doi.org/10.1021/acsnano.0c09982
J. Liu, M.-S. Cao, Q. Luo, H.-L. Shi, W.-Z. Wang et al., Electromagnetic property and tunable microwave absorption of 3D nets from nickel chains at elevated temperature. ACS Appl. Mater. Interfaces 8(34), 22615–22622 (2016). https://doi.org/10.1021/acsami.6b05480
Y. Akinay, F. Hayat, M. Çakir, E. Akin, Magnetic and microwave absorption properties of PVB/Fe3O4 and PVB/NiFe2O4 composites. Polym. Compos. 39(10), 3418–3423 (2018). https://doi.org/10.1002/pc.24359
Y. Akinay, B. Çolak, M.E. Turan, I.N. Akkuş, H.Ç. Kazici et al., The electromagnetic wave absorption properties of woven glass fiber composites filled with Sb2O3 and SnO2 nanoparticles doped mica pigments. Polym. Compos. 43(12), 8784–8794 (2022). https://doi.org/10.1002/pc.27061
Y. Akinay, U. Gunes, B. Çolak, T. Cetin, Recent progress of electromagnetic wave absorbers: a systematic review and bibliometric approach. ChemPhysMater 2(3), 197–206 (2023). https://doi.org/10.1016/j.chphma.2022.10.002
X. Huang, J. Wei, Y. Zhang, B. Qian, Q. Jia et al., Ultralight magnetic and dielectric aerogels achieved by metal-organic framework initiated gelation of graphene oxide for enhanced microwave absorption. Nano-Micro Lett. 14, 107 (2022). https://doi.org/10.1007/s40820-022-00851-3
Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant No. 62174013, 92265111), Central Government Guides Local Funds for Science and Technology Development (No. YDZJSX2022A021), and the funding Program of BIT (grant No. 3180012212214 and 3180023012204).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no interest conflict and have no known competing financial interests or personal relationships.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qin, L., Guo, Z., Zhao, S. et al. Two-Dimensional Cr5Te8@Graphite Heterostructure for Efficient Electromagnetic Microwave Absorption. Nano-Micro Lett. 16, 60 (2024). https://doi.org/10.1007/s40820-023-01271-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40820-023-01271-7