Introduction

Korteweg–de Vries Burgers (KdV-Burgers or KdVB) is a nonlinear partial differential equation that incorporates the dispersion, nonlinearity, and dissipation effects. This only happens when using Navier–Stokes equations after following some series expansion in terms of the amplitude parameter up to the first order level. This equation has general form:

$${u}_{t}+u{u}_{x}+\delta {u}_{xxx}-\varepsilon {u}_{xx}=0$$
(1)

where \(u\) is the field variable, the subscripts \(x, t\) denote differentiation with respect to distance and time respectively, and \(\delta ,\varepsilon\) are constant variables. This equation describes physical phenomena such as weak shock waves in plasma, propagation of waves in a liquid-filled elastic tube, and the evolution of liquid–gas mixture [1].

Jeffrey and Xu [2] extracted the exact solution of KdVB equation where they proposed a transformation that reduces the equation into a quadratic form in a new dependent variable and its partial derivatives, where the equation can be solved in terms of a series exponentials. The authors found that the KdVB equation has only two solutions in contrast with the KdV equation, that has infinite number of solutions which was put into a bilinear form in terms of Hirota’s bilinear operator. A year after Jeffrey and Mohamad [3] proposed two different methods for solving the KdV-Burgers equation: the first is based on combined solution for KdV and Burgers equations, the second depends on a series extension of Hirota’s method.

Bona and Schonbek [4] proved the existence and uniqueness solution of KdVB which has limiting behaviors related to the dispersion and dissipation coefficients. The authors stated that if dispersion dominates, the limit of this solution has an oscillatory character in the form of weak undular bore, but one can get the solitary wave solution if the dispersion coefficient is positive and fixed. On the other hand, this equation will mimic the trend of Burgers equation if the fixed positive dissipation coefficient dominates. Johnson [5] discussed the integrated form of KdVB equation, he showed that the solution is (for small damping) a cnoidal wave with varying period passing through all the possible wave types and culminating in the solitary wave, such profile is exactly what has been observed in the undular bore. The integrated forms of the PDEs can help in finding exact solutions depending on the ODEs form. Kaliappan [6] for instance used the Painlevé property for the reduced form of KdVB, but he found that this condition using Painlevé property is sufficient but not necessary for the integrated form of Eq. (1). The author extracted the exact solution with deep discussion for stability and boundedness.

The numerical methods used in solving KdVB and Benjamin-Bona-Mahony (BBMB) equations are varied. Che et al. [7] proposed a convergent, unconditionally stable linear implicit finite difference scheme for the initial-boundary problem of the generalized Benjamin–Bona–Mahony-Burgers (BBM-Burgers or BBMB) equation. Omrani and Ayadi [8] used the implicit Crank Nicolson scheme to find the numerical solution of BBMB equation. The authors used Brower’s fixed-point theorem to study the existence of the solution and the discrete energy method to study the stability and uniqueness of it. The Homotopy Analysis method (HAM) is a numerical method that has many advantages like rapid convergence for the solution and it does not require large computer memory, that is why Fakhari et al. [9] used it to solve BBMB equation, and their results show that the HAM provides accurate numerical solution. The Variational Iteration and Homotopy Perturbation Methods (VIM and HPM) is applied by Tari and Ganji [10] to derive approximate explicit solutions for a special form of generalized nonlinear Benjamin–Bona–Mahony-Burgers (BBMB), the obtained solutions are compared with the exact solutions with approximate agreement with them.

Other method is used by Ganji et al. [11] which is the Exp-Function method also for solving the generalized BBMB equation. This method is a relatively new analytical technique; the authors used some numerical examples to illustrate the efficiency and reliability of the method. Mittal and Jain [12] proposed a stable collocation method by using cubic B-splines to numerically solve nonlinear parabolic partial differential equations with Neumann’s boundary conditions, including equations with damping effect. Ramos et al. [13] derived a one-step hybrid block method to solve first order initial value problems and is further applied to a system of first order differential equations obtained after applying the modified Cubic B-spline collocation method to PDE for space derivatives such as Burgers, Buckmaster and FitzHugh-Nagumo equations. Also, Kormaz and Dağ [14] used the same scheme of the cubic B-spline to discretize the nonlinear Burgers’ equation in space, the resultant ordinary equation system is integrated via Runge–Kutta method of order four in time. A matrix stability analysis is also performed by determining eigenvalues of the coefficient matrices numerically.

To avoid the discretization of differentiations, Adomain method is used by Alkhaled et al. [15]; they also applied this method to the BBMB equations. The Adomain method showed fast convergence and it avoids difficulties and massive computational work. A different team by Arora et al. [16] used quartic B-spline collocation method to solve BBMB equation, where the B-spline basis functions were used for space integration, and Crank-Nicolson formulation for time integration. The authors provided unconditional stability of the proposed method using von-Neumann method. The same quartic B-Spline interpolation functions are used by Saka and Dağ [17] who wrote an algorithm for the numerical solutions of the KdVB equation, which is a finite element approach using the Galerkin method. The Homotopy perturbation numerical method (HPM) was used by El-Tanway et al. [18] to solve the damped nonplanar Schamel Korteweg–de Vries Burgers (SKVB) for studying the characteristics of the dissipative nonplanar dust-acoustic solitary and shock waves. Also, the damped nonplanar Schamel Korteweg–de Vries (SKDV) equation is solved numerically with moving boundary method which is called the multistage HPM (MsHPM).

“Data driven symbolic regression tools can be strongly useful for inferring complex models from sensor data when underlying physicsis partially or completely unknown”. Vaddireddy et al. [19], who demonstrated that the sparse regression techniques STRidge and the evolutionary optimization algorithm GEP are effective RS tools for identifying hidden physical laws from observed data. The authors recovered many models including Burgers equation, where the key to recover the PDEs is to construct a feature library of basis functions that contains higher order derivatives of the solution field. Aviliov et al. [20] were interested in the numerical evolution of an oscillatory zone in the „step decay” when low viscosity presents. This oscillatory zone is described in a framework of the Bogolyubov–Whitham averaging method using a set of cnoidal travelling waves of the KdV equation. The low viscosity turns the solution to oscillate infinitely with a damped amplitude and tend to a soliton at the leading edge.

In the present work, three different models that incorporates the damping effects were introduced, a KdVB and two BBMB equations. The main difference between the last two BBMB equations is the scaling used in the perturbation method. The first BBMB model includes only the effect of gravity force, while the second one includes the effects of both gravity and Coriolis forces, respectively. The KdV-Burgers equation is going to be studied analytically in the phase plane. The model is going to be solved numerically using Implicit finite difference scheme. The BBMB models are going to be solved numerically using the Quartic B-Spline collocation method proposed previously by Arora et al. [16]. Those models also will be used to track the solitary single Kelvin mode and compare the effect of damping on the form of wave as propagates with time. Also, it is going to be used to study the real signal recorded from the Acoustic Doppler Velocimeter under bore and breaking bore forms appear on the surface.

The paper is organized as follows: in Experiment section a brief description of the device used in the experiemnts and the new channel model, in System of Equations section introducing the system of equations and flow assupmtions, in KdV-Burgeres Model section we introduce the new KdV-Burgers model, where the discussion of the phase solution problem is presented, then the implicit finite difference method is used numerically to solve it with time, in BBM-Burgers Models section the first and the second BBM-Burgers models are introduced and solved numerically using the Quartic B-Spline collocation method and compared with the experiment, in the final section the conclusion and summary of the results were summarized.

Experiment

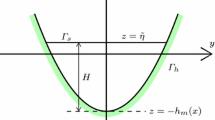
The viscous effect that is discussed in this paper is applied to the new case study about the wavy aspects in a new channel system that has cylindrical form and the motion is made by the precession effect. It consists of two concentric cylinders of Plexiglass elevated over the laboratory floor using metal cylindrical support, from which two tables are holding the cylinder, the lower one is fixed to the metal support and is rounded in shape and is able to rotate only, other circular woody table rests over it that is supported with three screws that are adjustable in their lengths. Those screws enable the change of the slope of the upper table where the cylinders rest. The cylindrical metal support is able to rotate by the help of shaft mechanism connected to an electrical motor connected to electrical battery. The three main control parameters in the problem are the angle of tilt, the volume of water in the channel, and the power provided to the system. Figure 1 shows a sketch for the channel and the whole system.

Fig. 1
figure 1

Sketch of the channel flume used in the experiments to track the wave aspects observed

Full size image

The motion is tracked using Coupled-Charged-Device Sensor type camera that is put in front of the channel on the laboratory floor to record the whole motion with time, more details can be found in Alshoufi [21]. Precession is pretty good mechanism to excite the waves inside the channel, those wavy aspects are varied from simple small sinusoidal ones, to single big amplitude waves, to bore and breaking aspects. We are concerned in this paper on studying the effect of viscousity on the single big amplitude waves noticed, those are called Kelvin waves as well, and they have features similar to the famous solitary wave in open channels far from rotation effects.

System of Equations

The lower table holds the cylinder discussed in the previous section is able to rotate with specific rotation rate characterized by the angular frequency \(\Omega\), the cylinders are able to rotate with specific precession rate characterized by the slope \(\tau\) times the angular frequency \(\tau \Omega\). The motion is tracked on the outer surface of the cylinder thus the body-fixed cylinderical coordinate system is used. The motion is assumed two-dimensional one (the azimuthal and the axial directions only) due to the fact that the channel radius does not exceed 10 cm, thus the radial direction was eliminated. The velocity components in the azimuthal and axial directions are \(u, w\) respectively.

The azimuthal velocity is assumed a function independent of the axial direction of motion \(u=u\left(\theta , t\right)\), and the additional forces resulted from rotation effect are all scaled by \(\Omega \tau\) or \({\Omega }^{2}\tau\) or \({\Omega }^{2}{\tau }^{2}\). Those effects mainly come from transforming the motion from the laboratory floor system to the body-fixed coordinates. Those forces (can be found in the previous work [21]) were added up to order \(O\left(\tau \right)\), this forces the centrifugal force to vanish, and it is assumed that the wobbling Euler force effect is relatively small and neglected. Then the equations of continuity, momentum, and the kinematic condition will be:

$${u}_{t}+\frac{u{u}_{\theta }}{r}+w{u}_{z}=g\tau \sin\left(\Omega t-\theta \right)-\frac{{P}_{\theta }}{r.\rho }-2\Omega \tau \cos\left(\Omega t-\theta \right)w+v\left[\frac{{u}_{\theta \theta }}{{r}^{2}}+{u}_{zz}-\frac{u}{{r}^{2}}\right]$$
(2)
$${w}_{t}+\frac{u{w}_{\theta }}{r}+w{w}_{z}=-g-\frac{{P}_{z}}{\rho }+2\Omega \tau \cos\left(\Omega t-\theta \right)u+v\left[\frac{{w}_{\theta \theta }}{{r}^{2}}+{w}_{zz}\right]$$
(3)
$${u}_{\theta }+r{w}_{z}=0$$
(4)
$$w={\eta }_{t}+\frac{u{\eta }_{\theta }}{r}$$
(5)

Impermeable boundary conditions are assumed at the inner and the outer radii in addition to the bottom \(w=0\) at \(z=0\), whereas periodic motion is assumed azimuthally. As stated in the previous section that we are concerned with the single Kelvin mode that has symmetrical form and moves with constant speed like the characteristics of the solitary wave in open channels, however the effect of rotation on this wave is sever when its amplitude bigger than the average depth of water. The previous work [22] presented new precessional KdV equation that includes the rotation effect in its coefficients, and the effect of tilt in a forcing term resulted from the variation of the angular velocity vector projected at the outer radius. The main difference in this work is that we do not assume potential conditions.

KdV-Burgeres Model

Equations (2), (3), (4), and (5) are going to be scaled with:

$$\begin{aligned}& z\to H\overline{z },r\to R\overline{r },\eta \to \varepsilon H\eta ,u\to \varepsilon c\overline{u },w\to \varepsilon c\delta \overline{w} \theta \to \overline{\theta },\\ & \tau \to \varepsilon \delta \overline{\tau },t\to \frac{R}{c}\overline{t },\Omega \to \frac{c}{R}\overline{\Omega },c=\sqrt{gH},\delta =\frac{H}{R},\varepsilon =\frac{A}{H},\varepsilon =O\left({\delta }^{2}\right)\end{aligned}$$
(6)

where \(\delta\) is the shallowness parameter, \(\varepsilon\) is the amplitude one and \(c\) the long wave speed. The pressure is deviated from the hydrostatic one and it is given as:

$$P\to {P}_{0}+\gamma \left(H-Z\right)+\varepsilon \rho {c}^{ 2}\overline{P },$$
(7)

where \({P}_{0}\) is the pressure on the free surface which is the atmospheric one. The final system of equations will take the form:

$${u}_{t}+\varepsilon \left(\frac{u{u}_{\theta }}{r}+w{u}_{z}\right)=\tau \sin\left(\Omega t-\theta \right)-\frac{{P}_{\theta }}{r}-{\varepsilon }^{2}\left[2\Omega \tau \cos\left(\Omega t-\theta \right)w\right]+k\left[\varepsilon \left(\frac{{u}_{\theta \theta }}{{r}^{2}}-\frac{u}{{r}^{2}}\right)+{u}_{zz}\right]$$
(8)
$$\varepsilon \left[{w}_{t}+\varepsilon \left(\frac{u{w}_{\theta }}{r}+w{w}_{z}\right)\right]=-{P}_{z}+{\varepsilon }^{2}\left[2\Omega \tau \cos\left(\Omega t-\theta \right)u\right]+k\left[{\varepsilon }^{2}\frac{{w}_{\theta \theta }}{{r}^{2}}+\varepsilon {w}_{zz}\right]$$
(9)
$${u}_{\theta }+r{w}_{z}=0$$
(10)
$$w={\eta }_{t}+\varepsilon \frac{u{\eta }_{\theta }}{r}$$
(11)

We are going to harness the unified form of the precession phase \(\left(\Omega t\right)\) and the azimuthal angle \((\theta )\) that appear in Coriolis and the gravity terms by introducing:

$$\vartheta =\theta -\Omega t$$
(12)

The motion is assumed to be slow variation one thus the time is scaled by \(t\to \frac{T}{\varepsilon }\). The final equation can be derived using the classical perturbation method, where the unknown parameters \(Q=\left(w, u, \eta , P\right)\) are going to be expanded in terms of the amplitude one \(\varepsilon\) in a series form:

$$Q={Q}^{0}+\varepsilon {Q}^{1}+{\varepsilon }^{2}{Q}^{2}+\dots$$
(13)

The final equation has the following dimensionless form:

$$\left(1+\frac{1}{{\Omega }^{2}{r}^{2}}\right){\eta }_{T}+\left(\frac{1}{\Omega {r}^{2}}-\Omega \right){\eta }_{\vartheta }+\left(\frac{2}{\Omega {r}^{2}}+\frac{1}{{\Omega }^{3}{r}^{4}}\right)\eta {\eta }_{\vartheta }+\frac{{\eta }_{\vartheta \vartheta \vartheta }}{3\Omega {r}^{4}}+\frac{\tau \sin\left(\vartheta \right)}{\Omega r}=k\left[\frac{{\eta }_{\vartheta \vartheta }}{{\Omega }^{2}{r}^{4}}-\frac{\eta }{{\Omega }^{2}{r}^{4}}\right]$$
(14)

where \(k=\frac{v}{cR{\delta }^{2}}\). We assumed \(v={10}^{-6}\) for water. This equation is going to be scaled back into the dimensional form as:

$$A{\eta }_{t}+B{\eta }_{\theta \theta \theta }+C\eta {\eta }_{\theta }+E+D{\eta }_{\theta }=F\left[{\eta }_{\theta \theta }-\eta \right]$$
(15)

where:

$$A=\frac{r}{{\varepsilon }^{2}Hc}\left(1+\frac{{c}^{2}}{{\Omega }^{2}{r}^{2}}\right),B=\frac{c}{3\Omega \varepsilon Hr},C=\left(\frac{{c}^{3}}{{\Omega }^{3}{r}^{3}}+\frac{2c}{\Omega r}\right)\frac{1}{{\varepsilon }^{2}{H}^{2}},E=\frac{\tau c}{\varepsilon \delta \Omega r}\sin\left(\theta -\Omega t\right),D=\left(\frac{c}{\Omega r}-\frac{R\Omega }{c}\right)\frac{1}{\varepsilon H},F=\frac{k{c}^{2}}{\varepsilon H{r}^{2}{\Omega }^{2}}.$$
(16)

Phase Solution

Equation (15) has the damping effect on its right-hand side. This equation can be turned into total differential equation by replacing \(\frac{\partial }{\partial t}=-\Omega \frac{\partial }{\partial \theta }\) from the fact in Eq. (12) where we assume tracking the wave in a frame reference moving with the wave itself in a steady behaviour. The forcing gravity term is computed from the experiment it turned out that it has trivial value and can be neglected in favor the direct integration for one time:

$$\frac{{d}^{2}\eta }{d{\vartheta }^{2}}+R\eta +S{\eta }^{2}=U\frac{d\eta }{d\vartheta }$$
(17)

where:

$$R=\frac{D-\Omega A}{B},S=\frac{F+C}{2B},U=\frac{F}{B}.$$
(18)

Equation (17) is similar to the one extracted by Johnson [5] and Grad and Hu [23]. Johnson [5] for instance discussed the phase problem and the viscous effect on wave formation, the author stated that eliminating the damping leads to the solitary wave formation, while including it leads to damping sinusoidal effect represented by the spiral phase diagram. In our experiments, the single Kelvin mode suffered from the breaking and turbulence behaviour on its surface and some of them were accompanied with small wobbling effect appears in the form of small waves near the wave edges or in the assumed far field 180° far from the crest. We apply this phase methodology to our system with comparison with the experiment, the main effect of the three control parameters is taken into account. To study the phase, we introduce a new variable \(w\):

$$\left\{\begin{array}{l}\frac{d\eta }{d\vartheta }=w\\ \frac{dw}{d\vartheta }+R\eta +S{\eta }^{2}=Uw\end{array}\right.$$
(19)

Two equilibrium points (singular points) appear for the first order differential equation system are:\(\left(\eta , w\right)=\left(0, 0\right)\), \(\left(\eta , w\right)=\left(-\frac{R}{S}, 0\right)\), For the first case \(\left(\eta , w\right)=\left(0, 0\right)\), we have:

  1. 1.

    If \(\sqrt{{U}^{2}-4R}<0\), stable spiral.

  2. 2.

    If \(\sqrt{{U}^{2}-4R}>0\), & \(<U\), unstable node.

  3. 3.

    If \(\sqrt{{U}^{2}-4R}>0\), & \(>U\), saddle node.

For the second case \(\left(\eta , v\right)=\left(-\frac{R}{S}, 0\right)\), we have:

  1. 1.

    If \(\sqrt{{U}^{2}+4R}<U\), unstable node.

  2. 2.

    If \(\sqrt{{U}^{2}+4R}>U\), saddle node.

The effect of damping is included in the \(U, S\) variables which are mainly connected to the damping term \({F}_{1}\) and \({C}_{1}\), which are mainly connected with the volume and power effects, experimentally we tracked three solitary Kelvin waves for different volumes, angles of tilts and powers provided to the system, the bigger those terms the more important the damping effect is. It was noticed that for volumes 10,000 ml and 14,000 ml the damping effect does not dominate the solution which after plotting the phase plane scheme reflected saddle node solution about the first singular point \(\left(\eta , w\right)=\left(0, 0\right)\), represented in the parabola form, which means a set of troughs moving in the plane \(\left(\eta , \vartheta \right)\), and for the second point the solution gives the periodic solution represented in ellipse form rotating about the signular point \(\left(\eta , v\right)=\left(-\frac{R}{S}, 0\right)\). The damping effect was bigger for the 12,000 ml case where the rotation rate was smaller, in such case the solution gives spiral so that the solution starts as solitary wave initially but then deviates to spiral about the singular point \(\left(\eta , w\right)=\left(-\frac{R}{S}, 0\right)\), depending on the volume, rotation rate, and the tilt the solutions are clear in Figs. 2, 3 and 4.

Fig. 2
figure 2

Phase diagram, \(V=\mathrm{10,000}\) ml, \(\tau =0.01667\), \(\Omega =6.84\) rad/s

Full size image
Fig. 3
figure 3

Phase plane, \(V=\mathrm{14,000}\) ml, \(\tau =0.02333\), \(\Omega =6.82\) rad/s

Full size image
Fig. 4
figure 4

Stable Spiral Phase plane, \(V=\mathrm{12,000}\) ml, \(\tau =0.0117\), \(\Omega =6.02\) rad/s

Full size image

Numerical Integration

Equation (15) is going to be solved with time, a simple implicit finite difference scheme is proposed where the derivatives are replaced with discretizations, for the first and the third order a normal Taylor Series expansion is used taking the central difference, while the second order is approximated using a polynomial of degree four fit through five points leads to a fourth-order approximation on uniform grids [24], those are given by:

$$\left\{\begin{array}{c}{\eta }_{\theta }=\frac{{\eta }_{i+1}-{\eta }_{i-1}}{2\Delta \theta }\\ {\eta }_{\theta \theta }=\frac{-{\eta }_{i+2}+16.{\eta }_{i+1}-30.{\eta }_{i}+16.{\eta }_{i-1}-{\eta }_{i-2}}{12.{\Delta \theta }^{2}}\\ {\eta }_{\theta \theta \theta }=\frac{{\eta }_{i+2}-2.{\eta }_{i+1}+2.{\eta }_{i-1}+{\eta }_{i-2}}{2.{\Delta \theta }^{3}}\end{array}\right.$$
(20)

The derivatives will be averaged between the previous and the new time using Euler forward time discretization, thus, after applying (19) into (14) we arrive at the final recurrence equation:

$${a}_{1}\cdot{\eta }_{i}^{n+1}+{a}_{2}\cdot{\eta }_{i+1}^{n+1}+{a}_{3}\cdot{\eta }_{i-1}^{n+1}+{a}_{4}\cdot{\eta }_{i-2}^{n+1}+{a}_{5}\cdot{\eta }_{i+2}^{n+1}=-\Delta t.{E}_{1}+{b}_{1}\cdot{\eta }_{i}^{n}+{b}_{2}\cdot{\eta }_{i+1}^{n}+{b}_{3}\cdot{\eta }_{i-1}^{n}+{b}_{4}\cdot{\eta }_{i-2}^{n}+{b}_{5}\cdot{\eta }_{i+2}^{n}$$
(21)

The coefficients are given in the Appendix A. We assume boundary conditions of the form:

$$\left\{\begin{array}{c}{\eta }_{\theta }\left(-\pi ,t\right)={\eta }_{\theta }\left(\pi ,t\right)=0\\ {\eta }_{\theta \theta }\left(-\pi ,t\right)={\eta }_{\theta \theta }\left(\pi ,t\right)=0\end{array}\right.$$
(22)

After applying the boundary conditions into the recurrence Eq. (21) we can arrange the matrix form of the problem as:

$$A.{\eta }_{i}^{n+1}=B{\eta }_{i}^{n}+G$$
(23)

where the coefficients matrices \(A, B\) can be found in Appendix A for more information. The general solution of the equation is plotted in Fig. 5 where the time discretization is chosen too small to ensure the stability of the problem and is given by: \(\Delta t=0.0003\) s, and the space discretization is given by: \(\Delta \theta =0.0422\). The experiment was run for volume 12,000 ml, and rotation rate \(\Omega =6.018\) rad/s, the tilt angle characterized by the slope was \(\tau =0.0117\).

Fig. 5
figure 5

KdV-Burgers Implicit solution behaviour with time

Full size image

A convergence test is carried out, as no exact solution we follow the method provided by Mittal et al. [16] and assuming that the exact solution is when the grid is refined up to \(m=200\) for instance. The absolute error is computed accordingly by \({L}_{\infty }=max\left|{\eta }_{exact}-{\eta }_{computed}\right|\), the results in Table 1.

Table 1 Absolute error \({L}_{\infty }\) and the order of convergence (OFC)
Full size table

BBM-Burgers Models

BBM-Burgers or Benjamin-Bona-Mahony equation is a partial differential equation includes the nonlinear-dispersive and damping effects. When no viscosity it turned into the BBM equation which was originally derived by Peregrine [25] to study the dispersive shocks in open channels. This equation was re-introduced by Benjamin et al. [26] (which now takes their names) where they shed the light on the main shortcomings in KdV-equation that can be tackled by using this modified version. Including the damping effect was first included by Johnson (1969) in his PhD work on the flow in a long elastic tube taking the viscous effects, it was also used to study the undular bores under shear effect in open channels by Chester [27] and Johnson [28]. The derivation of this equation in this system will be followed using the simplified work of Peregrine [25] based on Johnson [29]. There are mainly two models which precisely depend on the scaling process, the first includes only the gravity, pressure and shear forces, the second includes the Coriolis effect as well. Both equations will be solved using the Quartic B-Spline method.

The B-spline method can replace the derivatives of the main functions by piecewise polynomials. Those polynomials cover certain number of segments which depend mainly on the highest order of space derivative needed for the problem. More discussion will be added in the "Numerical Solution-Model I" section and "Numerical Solution-Model II" section when implying this method to the extracted equations.

Model I

Equations (2), (3), (4), and (5) are going to be scaled with:

$$\begin{aligned} t& \to \frac{\overline{t}}{\Omega },\Omega \to \overline{\Omega },\tau \to \sqrt{\sigma }\overline{\tau },\theta \to \overline{\theta },u\to \varepsilon R\Omega \overline{u },\\ w& \to \varepsilon H\Omega \overline{w },P\to {P}_{0}+\gamma \left(H-z\right)+\varepsilon \rho {R}^{2}{\Omega }^{2}\overline{P },{F}_{r}=\frac{H{\Omega }^{2}}{g},\\ r& \to R\overline{r },z\to H\overline{z },\sigma ={\left(\frac{H}{R}\right)}^{2},\varepsilon =\frac{A}{H},\eta \to \varepsilon H\overline{\eta}\end{aligned}$$
(24)

The continuity and kinematic conditions are going to be the same as in Eqs. (10) and (11). The only change is in the momentum:

$${u}_{t}+\varepsilon \left(\frac{u{u}_{\theta }}{r}+w{u}_{z}\right)=-\frac{{P}_{\theta }}{r}+\frac{\tau }{{F}_{r}}\sin\left(t-\theta \right)+\varepsilon \left(-2\tau \cos\left(t-\theta \right)w\right)+k\left[\varepsilon \left(\frac{{u}_{\theta \theta }}{{r}^{2}}-\frac{u}{{r}^{2}}\right)+{u}_{zz}\right]$$
(25)
$$\varepsilon \left[{w}_{t}+\varepsilon \left(\frac{u{w}_{\theta }}{r}+w{w}_{z}\right)\right]=-{P}_{z}+\varepsilon \left[2\tau \cos\left(t-\theta \right)u+k\left({w}_{zz}+\varepsilon \frac{{w}_{\theta \theta }}{{r}^{2}}\right)\right]$$
(26)

where \(k=\frac{v}{\delta \Omega {R}^{2}}\). In a similar manner to what is done in Eq. (14) at the leading order of the problem, it is assumed that if \(\varepsilon \to 0\) (which is the solution we are interested in for small wave amplitude) then \(\tau \to 0\), so that the forced term of gravity force does not appear:

$${w}_{0}={\eta }_{0t},{u}_{0\theta }+r{w}_{0z}=0,{P}_{0}={\eta }_{0},{u}_{0t}=-\frac{{\eta }_{0\theta }}{r}$$
(27)

At the first order of the problem, we have:

$$\left\{\begin{array}{l}{w}_{1}={\eta }_{1t}+\frac{{u}_{0}{\eta }_{0\theta }}{r}\\ -{P}_{1z}+2\tau \cos\left(t-\theta \right){u}_{0}={w}_{0t}\\ {u}_{1t}+\frac{{u}_{0}{u}_{0\theta }}{r}=-\frac{{P}_{1\theta }}{r}-2\tau \cos\left(t-\theta \right){w}_{0}+..\\ ..\frac{\tau }{{F}_{r}}\sin\left(t-\theta \right)+k\left[\frac{{u}_{0\theta \theta }}{{r}^{2}}-\frac{{u}_{0}}{{r}^{2}}\right]\end{array}\right.$$
(28)

When the pressure value is inserted into the momentum equation and applying Taylor series expansion about \(z=1\) for the kinematic condition, we can balance between the kinematic condition and the azimuthal momentum using the values of continuity equation and assuming that \(u\approx \eta\). The final new version of BBM-Burgers equation is:

$${u}_{t}+\frac{3u{u}_{\theta }}{2r}+\frac{{u}_{\theta }}{r}=\frac{{u}_{\theta \theta t}}{6{r}^{2}}+\tau \cos\left(t-\theta \right)\frac{{u}_{\theta }}{r}+\tau \sin\left(t-\theta \right)\frac{u}{2r}+\frac{\tau }{{2F}_{r}}\sin\left(t-\theta \right)+k\left[\frac{{u}_{\theta \theta }}{2{r}^{2}}-\frac{u}{2{r}^{2}}\right]$$
(29)

This equation has dimensional form:

$$A.{u}_{t}+Bu{u}_{\theta }+\left(C-E\right){u}_{\theta }=D.u+G+F{u}_{\theta \theta t}+H\left({u}_{\theta \theta }-u\right),$$
(30)

where the coefficients are:

$$\begin{aligned} A& =\frac{1}{\varepsilon r{\Omega }^{2}},B=\frac{3}{2{\varepsilon }^{2}{\Omega }^{2}{r}^{2}},D=\frac{\tau }{2H\varepsilon \Omega }\sin\left(\Omega t-\theta \right),\\ E& =\frac{\tau }{\varepsilon H\Omega }\cos\left(\Omega t-\theta \right),G=\frac{\tau r}{2{F}_{r}H}\sin\left(\Omega t-\theta \right),H=\frac{k}{2\varepsilon r\Omega }.\end{aligned}$$
(31)

Numerical Solution-Model I

In this part, we are going to apply the Quartic B-Spline collocation method to Eq. (30). We follow the same procedure done by Arora et al. [16]. The B-Spline method is widely used by other researchers as well. Mittal and Jain [12] used the cubic B-Spline method to solve Burgers equation; after using the finite difference discretization, they arrived at the recurrence relation in terms of the redefined version of equations so that the basis functions vanish at the boundaries where Dirichlet’s conditions are applied. The authors checked the instability using the von-Neumann scheme where they proved that the method is unconditionally stable. Other team conducted by Hidayat et al. [30] improved the stability of the global B-Spline method, by overlapping the domain decomposition of multiplicative Schwarz algorithm combined with the global method, and the results were satisfactory. In this section we apply the method to Eq. (30), the core function is the velocity \(u\) and the domain is the outer periphery of the cylinder \(\left[0, 2\pi \right]\). The domain is going to be discretized into \(N\) segment, each has length \(h={\theta }_{i+1}-{\theta }_{i}\) for \(i=0, 1, 2,\dots N\). The exact solution is a function of time and space, the B-spline method suggests separation variable method by splitting the exact solution into two parts, one is time dependent and the other one is space dependent based on B-Spline polynomials as follows:

$${U}_{i}\left(\theta ,t\right)=\sum_{j=i-2}^{i+1}{\delta }_{j}\left(t\right){Q}_{j}\left(\theta \right) i=\mathrm{0,1},\dots ,N$$
(32)

The polynomials can be written as:

$${Q}_{i}\left(\theta \right)=\frac{1}{{h}^{4}}\left\{\begin{array}{c}{\left(\theta -{\theta }_{i-2}\right)}^{4}, \theta \in \left[{\theta }_{i-2},{\theta }_{i-1}\right]\\ {\left(\theta -{\theta }_{i-2}\right)}^{4}-5{\left(\theta -{\theta }_{i-1}\right)}^{4}, \theta \in \left[{\theta }_{i-1},{\theta }_{i}\right] \\ {\left(\theta -{\theta }_{i-2}\right)}^{4}-5{\left(\theta -{\theta }_{i-1}\right)}^{4}+10{\left(\theta -{\theta }_{i}\right)}^{4}, \theta \in \left[{\theta }_{i},{\theta }_{i+1}\right] \\ {\left({\theta }_{i+3}-\theta \right)}^{4}-5{\left({\theta }_{i+2}-\theta \right)}^{4}, \theta \in \left[{\theta }_{i+1},{\theta }_{i+2}\right] \\ {\left({\theta }_{i+3}-\theta \right)}^{4}, \theta \in \left[{\theta }_{i+2},{\theta }_{i+3}\right]\\ 0\quad otherwise\end{array}\right.$$
(33)

The discretization of the derivatives and functions is being done using the finite difference approximations, where we use the averaging over time between the new and the old values, with forward Euler discretization with time:

$$\left[\frac{{\left(A.u-F{u}_{\theta \theta }\right)}^{n+1}-{\left(A.u-F{u}_{\theta \theta }\right)}^{n}}{\Delta t}\right]+J\left[\frac{{\left({u}_{\theta }\right)}^{n+1}+{\left({u}_{\theta }\right)}^{n}}{2}\right]+K\left[\frac{{u}_{i}^{n+1}+{u}_{i}^{n}}{2}\right]=H\left[\frac{{\left({u}_{\theta \theta }\right)}^{n+1}+{\left({u}_{\theta \theta }\right)}^{n}}{2}\right]+G$$
(34)

The coefficients are the same from Eq. (30) the new ones are:

$$J=B.{u}_{i}^{n}+C-E,K=H-D$$
(35)

The approximate solution and its derivatives can be given in terms of the time dependent coefficients:

$$\left\{\begin{array}{c}{U}_{i}={\delta }_{i-2}+11{\delta }_{i-1}+11{\delta }_{i}+{\delta }_{i+1}\\ {U}_{i}{\prime}=\frac{4}{h}\left(-{\delta }_{i-2}-3{\delta }_{i-1}+3{\delta }_{i}+{\delta }_{i+1}\right)\\ {U}_{i}^{{\prime}{\prime}}=\frac{12}{{h}^{2}}\left({\delta }_{i-2}-{\delta }_{i-1}-{\delta }_{i}+{\delta }_{i+1}\right)\end{array}\right.$$
(36)

The dashes represent the derivatives, those are going to be substituted into Eq. (34) to get the recurrence relation:

$${a}_{1}\cdot{\delta }_{i-2}^{n+1}+{a}_{2}\cdot{\delta }_{i-1}^{n+1}+{a}_{3}\cdot{\delta }_{i}^{n+1}+{a}_{4}\cdot{\delta }_{i+1}^{n+1}=G.\Delta t+{b}_{1}\cdot{\delta }_{i-2}^{n}+{b}_{2}\cdot{\delta }_{i-1}^{n}+{b}_{3}\cdot{\delta }_{i}^{n}+{b}_{4}\cdot{\delta }_{i+1}^{n}$$
(37)

This can be written in a matrix form as:

$${A}_{d}\cdot{\delta }_{i}^{n+1}={B}_{d}\cdot{\delta }_{i}^{n}+{C}_{d}$$
(38)

where the coefficients can be found in Appendix B. Values of \({\delta }^{n+1}\) are determined recurssively after finding the values of \({\delta }^{n}\) from the initial conditions and applying the proper boundary conditions. The boundary conditions are assumed for the initial state that both the slope and the curvatures are zeros, thus:

$$\left\{\begin{array}{c}u\left({\theta }_{L}, t\right)=u\left({\theta }_{R}, t\right)=0\\ {u}_{\theta }\left({\theta }_{L}, 0\right)=0\end{array}\right.$$
(39)

The full details of solution can be found in Arora et al. \(\left[16\right]\), where also the initial matrix is explained with details for solving simplified BBM-Burgers. To apply this method experimentally, we conducted many experimental campagins to extract velocity signals under bore and undular bore conditions, using ADV (Acoustic Doppler Velocimeter), the signal has Cnoidal form, the vectrino profiler starts to record signal from \({t}_{0}=0.02\) s, and the time difference is \(\Delta t=0.04\) s, we assume that the corresponding initial angle \({\theta }_{0}=0\), and thus at the end of the taken singal which is \({t}_{f}=5.02\) s, the final crossed angle is \({\theta }_{f}=1.6\pi\) rad, we choose some fit function of the signal that has cnoidal form as follows:

$$Q= {A}_{m}{\left[1\pm \cos(k{r}_{max}\theta - \Omega t)\right]}^{2}$$
(40)

where \({A}_{m}\) the signal amplitude, k the wave number. The grid has \(N=126\) points this means space discretization \(\Delta \theta =0.0335\), with time discretization \(\Delta t=0.01\) s. The models were tested for three cases, those depend mainly on the three control parameters of the problem which are the angle of tilt, the volume of water and the rotation rate. Figures 6, 7, and 8 show the solution:

Fig. 6
figure 6

BBM-Burgers Model I solution behaviour, \(V=\mathrm{12,000}\) ml, \(\tau =0.0433\), \(\Omega =5.05\) rad/s, \(\theta \in \left[0, 1.6\pi \right]\)

Full size image
Fig. 7
figure 7

BBM-Burgers Model I solution using the Quartic B-Spline, \(V=\mathrm{10,000}\) ml, \(\tau =0.0233\), \(\Omega =3.534\) rad/s, \(\theta \in \left[0, 1.6\pi \right]\)

Full size image
Fig. 8
figure 8

BBM-Burgers Model I solution using the Quartic B-Spline, \(V=\mathrm{14,000}\) ml, \(\tau =0.075\), \(\Omega =5.66\) rad/s, \(\theta \in \left[0, 1.6\pi \right]\)

Full size image

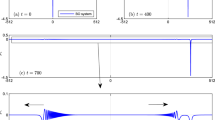
The solutions here reflect the drastic effect of Coriolis force on the solution with time, in addition to the three control parameters, the solution shows a directly proportional relationship between the stability of the solution with time and the three control parameters, the smallest the angle of tilt, the power and the volume the drastic the solution is. The wobbly effect of Coriolis force shows how the signal is swinging when time increases and in fact if we draw the signal in the early stages for very small time the signal will swing as well for the smallest angle of tilt, power and volume as clear in Fig. 9 the solution for times \({t}_{1}=0.01\) s, \({t}_{2}=0.02\) s, \({t}_{3}=0.03\) s, respectively. The effect of the angle also clear in the result with time where part of the signal increases over the original one, others show the damping effect.

Fig. 9
figure 9

Early Behaviour of the signal under damping effect. (a) \(V=\mathrm{14,000}\) ml. (b). \(V=\mathrm{12,000}\) ml. (c). \(V = \mathrm{10,000}\) ml

Full size image

Model II

Again Eqs. (1), (2), (3), and (4) are going to be scaled as follows:

$$\begin{aligned}& z\to H\overline{z },r\to \frac{H}{\delta }\overline{r },\eta \to \varepsilon H\overline{\eta },u\to \varepsilon c\overline{u },w\to {\varepsilon }^{2}\frac{c}{\delta }\overline{w },\theta \to \overline{\theta },\tau \to \varepsilon \delta \overline{\tau },t\to \frac{H}{c\delta }\overline{t },\\ & \Omega \to \frac{c\delta }{H}\overline{\Omega },c=\sqrt{gH},\lambda =2\pi {r}_{max},\delta =\frac{H}{\lambda },\varepsilon =\frac{A}{H},P\to {P}_{0}+\gamma \left(H-z\right)+\varepsilon \rho {c}^{2}\overline{P}\end{aligned}$$
(41)

The final equation has the form after doing the same process as the previous models will take the form:

$${u}_{t}+\frac{3u{u}_{\theta }}{2r}+\frac{{u}_{\theta }}{r}=\frac{{u}_{\theta \theta t}}{6{r}^{2}}+\frac{\tau }{2}\sin\left(\Omega t-\theta \right)+k\left(\frac{{u}_{\theta \theta }}{2{r}^{2}}-\frac{u}{{2r}^{2}}\right)$$
(42)

where: \(k=\frac{v}{Hc\delta }\). Equation (42) has a dimensional form:

$${A}_{1}{u}_{t}+{B}_{1}u{u}_{\theta }+{C}_{1}{u}_{\theta }={D}_{1}{u}_{\theta \theta t}+{E}_{1}+{F}_{1}\left({u}_{\theta \theta }-u\right)$$
(43)

Here the coefficients are given by:

$$\begin{aligned} & {A}_{1}=\frac{H}{{c}^{2}\delta \varepsilon },{B}_{1}=\frac{3H}{2{c}^{2}{\varepsilon }^{2}\delta r},{C}_{1}=\frac{H}{c\varepsilon \delta r},\\ & {D}_{1}=\frac{{H}^{3}}{6{\delta }^{3}{c}^{2}\varepsilon {r}^{2}},{E}_{1}=\frac{\tau }{2\varepsilon \delta }sin\left(\Omega t-\theta \right),{F}_{1}=\frac{{H}^{2}.k}{2{\delta }^{2}c\varepsilon {r}^{2}}.\end{aligned}$$
(44)

Numerical Solution-Model II

The same model proposed in the previous Numerical Solution-Model I section is going to be used here. The discretization with time is given by:

$$\left[\frac{{\left({A}_{1}.u-{D}_{1}{u}_{\theta \theta }\right)}^{n+1}-{\left({A}_{1}.u-{D}_{1}{u}_{\theta \theta }\right)}^{n}}{\Delta t}\right]+{B}_{1}\left[\frac{{\left({uu}_{\theta }\right)}^{n+1}+{\left({uu}_{\theta }\right)}^{n}}{2}\right]+{C}_{1}\left[\frac{{u}_{\theta }^{n+1}+{u}_{\theta }^{n}}{2}\right]={F}_{1}\left[\frac{{\left({u}_{\theta \theta }\right)}^{n+1}+{\left({u}_{\theta \theta }\right)}^{n}}{2}-\frac{{u}^{n+1}+{u}^{n}}{2}\right]+{E}_{1}$$
(45)

The approximate solution is assumed:

$${U}_{i}\left(\theta ,t\right)=\sum_{j=i-2}^{i+1}{\gamma }_{j}\left(t\right){q}_{j}\left(\theta \right)$$
(46)

which will lead to the new recurrence relation:

$$S{u}_{i}^{n+1}+V{u}_{\theta }^{n+1}-W{u}_{\theta \theta }^{n+1}=\Delta t.{E}_{1}+{S}_{1}{u}_{i}^{n}-{V}_{1}{u}_{\theta }^{n}+{W}_{1}{u}_{\theta \theta }^{n+1}$$
(47)

Applying the B-spline polynomials into it we get the final recurrence relation:

$${a}_{1}{\gamma }_{i-2}^{n+1}+{a}_{2}{\gamma }_{i-1}^{n+1}+{a}_{3}{\gamma }_{i}^{n+1}+{a}_{4}{\gamma }_{i+1}^{n+1}=\Delta t.{E}_{1}+{b}_{1}{\gamma }_{i-2}^{n}+{b}_{2}{\gamma }_{i-1}^{n}+{b}_{3}{\gamma }_{i}^{n}+{b}_{4}{\gamma }_{i+1}^{n}$$
(48)

which can be written in a matrix form as:

$${A}_{e}\cdot{\gamma }_{i}^{n+1}={B}_{e}\cdot{\gamma }_{i}^{n}+{C}_{e}$$
(49)

The matrices \({A}_{e}, {B}_{e}\) and the coefficients \({a}_{1}, {a}_{2}, {a}_{3}, {a}_{4}, {b}_{1}, {b}_{2}, {b}_{3}, {b}_{4}, S, W, V, {S}_{1}, {W}_{1}, {V}_{1}\), can be found in Appendix B. The model Eq. (42) is similar to the one derived by the author Alshoufi [31] but without the damping effect, it was solved analytically after direct integration and omitting the gravity forcing term, where the equation is converted into the integrated KdV equation form, we will use this analytical solution as an initial guess to track the effect on the extracted velocity signal from the experiment:

$$Q= \beta {A}_{m}{\left[1\pm \cos(k{r}_{max}\theta - \omega t)\right]}^{2}$$
(50)

where:

$$k=\sqrt{\frac{B.b}{3\Omega D{r}^{2}}},\omega =\frac{C}{A}+\frac{B\left(2a-b\right)}{3A},a=\frac{3\left(A\Omega -C\right)}{B},b=\sqrt{\frac{\left(A\Omega -C\right)}{4\Omega D{r}^{2}}}$$

Similarly, the grid is discretized so that \(N=126\), and the grid distance \(\Delta \theta =0.0335\), with time difference \(\Delta t=0.01\). The results are clear in Figs. 10, 11 and 12, The gravity effect on this signal is smaller and insensible up to time 5 that is why the results for further times are presented and the signal is not swinging, rather they are shifted to the right and damped. The control parameters affect the signal also, but opposite to the previous case of Model I, where this time increasing the power, the tilt and the volume makes the signal worse with time or increases the instability.

Fig. 10
figure 10

BBM-Burgers Model II solution behaviour, \(V=\mathrm{12,000}\) ml, \(\tau =0.0433\), \(\Omega =5.05\) rad/s, \(\theta \in \left[\mathrm{0,1.6}\pi \right]\)

Full size image
Fig. 11
figure 11

BBM-Burgers Model II solution behaviour, \(V=\mathrm{10,000}\) ml,\(\tau =0.0233\), \(\Omega =5.307\) rad/s, \(\theta \in \left[\mathrm{0,1.6}\pi \right]\)

Full size image
Fig. 12
figure 12

BBM-Burgers Model II solution behaviour, \(V=\mathrm{14,000}\) ml,\(\tau =0.075\), \(\Omega =5.66\) rad/s, \(\theta \in \left[\mathrm{0,1.6}\pi \right]\)

Full size image

BBMB for Solitary Wave Case

Those two models are also applied to the solitary wave in the channel which was discussed in the previous section for the KdVB, however we have to replace each \(u\approx \eta\) and the coefficients will be different as well, for instance for Model I the coefficients are:

$$A=\frac{1}{\varepsilon H\Omega },B=\frac{3}{2{\varepsilon }^{2}{H}^{2}},C=\frac{1}{\varepsilon H},D=\frac{\tau }{2H\varepsilon \sqrt{\delta }}\sin\left(\Omega t-\theta \right),E=\frac{\tau }{\varepsilon H\sqrt{\delta }}\cos\left(\Omega t-\theta \right),F=\frac{1}{6\varepsilon H\Omega },G=\frac{\tau }{2{F}_{r}\sqrt{\delta }}\sin\left(\Omega t-\theta \right),H=\frac{k}{2\varepsilon H}$$
(51)

And for Model II are:

$${A}_{1}=\frac{1}{c\varepsilon \delta },{B}_{1}=\frac{3}{2H{\varepsilon }^{2}\delta r},{C}_{1}=\frac{1}{\varepsilon \delta r},{D}_{1}=\frac{{H}^{2}}{6c{\delta }^{3}\varepsilon {r}^{2}},{E}_{1}=\frac{\tau }{2\varepsilon \delta },{F}_{1}=\frac{H.k}{2{\delta }^{2}\varepsilon {r}^{2}}.$$
(52)

The solutions are clear in Figs. 13 and 14, the grid for both models is discretized so that \(\Delta \theta =0.0635\), \(\Delta t=1\) s, the initial amplitude \({A}_{m}\left(t=0\right)=0.08856\) m:

Fig. 13
figure 13

The physical behaviour of the Numerical Solution of Model I, volume 12,000 ml, \(\Omega =6.018\) rad/s, \(\tau =0.0117\)

Full size image
Fig. 14
figure 14

The physical behaviour of the Numerical Solution of Model II, volume 12,000 ml, \(\Omega =6.018\) rad/s, \(\tau =0.0117\)

Full size image

In the experiment we tracked a single Kelvin mode for volume \(V=\mathrm{10,000}\) ml, and slope \(\tau =0.01667\), and power characterized by the angular frequency \(\Omega =6.84\) rad/s, up to time \(t=16.3667\) s, as clear in Fig. 15.

Fig. 15
figure 15

The real wave variation with time

Full size image

The amplitude of the single Kelvin mode is tracked using the CCD camera (Coupled-Charged-Device sensor camera), the camera captures 30 frames per second, thus with time difference between each figure \(\Delta t=0.0333\) s. The first amplitude was taken at time 0.533s, and the rest of solutions start from it, we tried to compare the crest amplitude numerically for both models I and II, and it was compared with the extracted crest experimentally, the results in Table 2.

Table 2 Numerical comparison with real experiment of the wave amplitude with time
Full size table

The detunning effect is clear experimentally, where the wave’s crest waxes and wanes but never return to the original one. The models showed first decreasing in the amplitude up to time 6.667s where after this the amplitude increased. Model II is closer to the observed results experimentally up to time 2.2667s, after this it decreased and then waxed and wanned in values close to the experiment. However, model I with Coriolis effect was worse and the results finally increased with time in unrealistic values. Of course one cannot manipulate the time difference to match the captured image experimentally. Thus, model I is not applicable, Model II is better with satisfacory match.

Conclusion

In this paper we have presented three different weakly nonlinear models to study the solitary kelvin mode noticed rotating about the outer periphery of an open cylindrical channel under conditions of precession. This case was studied previously by the author using potential KdV (Korteweg–de-Vries) model and two weakly BBM (Benjamin-Bona-Mahone) models. The new in this case study is the viscous effect where the damping effect is noticed in all models. The KdV-Burgers model is integrated once where the gravity forcing term is omitted and damping effect was studied in the phase plane problem, the decay effect was noticed in the form of decaying sinusoidal spiral model, and the case when the damping is zero led to periodic closed ellipse. To solve this equation with time an implicit finite difference model is used. The other two weakly nonlinear models are the BBM-Burgers, the first one includes the gravity and Coriolis forces, it was compared with the bore velocity signal extracted from the ADV vectrino profiler, the Coriolis effect was noticed in a wobbling in the signal, but the three control parameters affect the solution more, where it was noticed that the instability of the solution with time is directly proportional to increasing each of tilt, power, and volume of water. When applying the other version of this model for the amplitude and compare it with the solitary Kelvin mode it was damped, but the results far from the experimental observations and instability features appeared in later time. The other version of BBMB takes only the gravity force effect, it was noticed that the signal only shifted and not wobbling, and conversely to Model I, the stability was bigger when increasing the effects of tilt, power, and volume. The final bit was the solitary Kelvin mode comparison, parts of the results matched the experiments perfectly with time others diverted for Model II, and Model I was very far from real observations.