Connectivity Concepts in Intuitionistic Fuzzy Incidence Graphs with Application

Abstract

In this research article, we presented the idea of intuitionistic fuzzy incidence graphs (IFIGs) along with connectivity concepts. IFIGs are the generalization of fuzzy incidence graphs (FIGs). Specific ideas analogous to intuitionistic fuzzy cut-vertices and intuitionistic fuzzy bridges in intuitionistic fuzzy graphs, intuitionistic incidence cut-vertices, and intuitionistic incidence bridges are explored. The notion of intuitionistic incidence gain and intuitionistic incidence loss for intuitionistic incidence paths and pairs of vertices is also initiated. In the case of FIGs, we have only membership value, and we do not have non-membership value (NMSV). Therefore, we use IFIGs because they are more reliable, valuable, and helpful than FIGs. Also, we can not apply graphs, fuzzy graphs, and FIGs to the application provided in Sect. 3 due to the non-availability of NMSV. An application in selecting the best paint company for investment among different companies by using IFIG is also obtained.

Introduction and Preliminaries

Graph theory has many applications in various fields of life, including computer science, engineering, and networking. Different ideas of paths and walks in graph theory are used in different problems of real-life like resource networking and database design. This guides the expansion of innovative algorithms that can be used in many applications. In this paper, we use simple and finite graphs. Zadeh [38] first paper on fuzzy sets extremely altered the face of science and technology. Zadeh [39] presented the idea of similarity, fuzzy preordering, fuzzy ordering, and partial fuzzy ordering. After his great paper on fuzzy sets, Roselfeld [28] initiated an innovative idea of FGs. Later, Yeh and Bang [37] discussed the basic terms and notations of FGs. They also explained how FGs could be applied to clustering analysis. Bhattacharya [6] introduced center, eccentricity in FGs and attached fuzzy groups with FGs. Rashmanlou and Jun [23] explored various products in complete interval-valued FGs. Rashmanlou and Pal [24, 25] examined balanced interval-valued and antipodal interval-valued FGs. Sunitha along with Vijayakumar [36] presented the notion of the complement, self-complementary and their properties in FGs. Mordeson and Nair [15] provided several applications of FGs, including clusters, cluster analysis, cohesiveness, and slicing. Later, Pramanik et al. [22] introduced interval-valued fuzzy planar graphs and their various properties. They also defined the interval-valued fuzzy dual graph, closely associated with the interval-valued fuzzy planar graph. Raut et al. [27] brought the idea of a fuzzy permutation graph. They defined two kinds of complements of a fuzzy permutation graph, including p-complement and f-complement. They also provided a real-life application of a fuzzy permutation graph. Zadeh [40] presented the concept that the position of centrality in the nontraditional view of fuzzy logic is that of precision. Samanta [33, 34] founded the fuzzy threshold graphs and fuzzy tolerance graphs. Atanassov [5] introduced the notion of intuitionistic fuzzy sets (IFSs) due to the non-availability of NMSV in fuzzy sets. Akram and Alshehri [1] investigated intuitionistic fuzzy bridges, cycles, and trees. Akram and Davvaz [2] introduced strong intuitionistic fuzzy graphs (IFGs) and intuitionistic fuzzy line graphs. Akram and Dudek [3] gave an application of intuitionistic fuzzy hypergraphs. Akram et.al [4] explained different metric aspects of IFGs. Sahoo and Pal [29,30,31,32] have done a comprehensive research on IFGs. Borzooei and Rashmanlou [7] discussed the ring sum of two product IFGs and explored some fascinating features of isomorphism on product IFGs. Gani and Begum [11] provided the new definition of complete IFG and regular FG. They also, explained various properties of IFG. Detail work on IFGs can be seen [8, 21, 35]. FGs are unable to speak about the effect of vertices on edges. For example, if vertices represent unlike universities and edges indicate roads connecting these universities, we can have a FG demonstrating the size of traffic from one university to another. The university has the maximum number of students and will have large number of ramps in university. So, if $U_{1}$ and $U_{2}$ are two different universities and $U_{1}U_{2}$ is a road amalgamating them, then $(U_{1},U_{1}U_{2})$ could reveal the ramp system from the road $U_{1}U_{2}$ to the university $U_{1}$. In the case of an unweighted graph, $U_{1}$ and $U_{2}$ both will have an effect of 1 on $U_{1}U_{2}$. In a directed graph, the result of $U_{1}$ on $U_{1}U_{2}$ indicated by $(U_{1},U_{1}U_{2})$ is 1 whereas $(U_{2},U_{1}U_{2})$ is 0. We can generalized this concept by FIGs. Dinesh [9] proposed the idea of FIGs. After him, Malik et al. [13] apply FIGs in human trafficking. Mathew and Mordeson [14] discussed connectivity ideas and different properties in FIGs. Malik et al. [12] examined complementary FIGs. Fang et al. [10] presented the connectivity index and Wiener index in FIGs. They also defined different kinds of vertices. Later, Nazeer et al. [16, 17] presented the notion of order, size, domination, and strong pair domination in FIGs. They discussed two types of domination, including strong fuzzy incidence domination and weak fuzzy incidence domination. They also provided an application of fuzzy incidence domination to select the best medical lab among different labs for conducting tests for the coronavirus. The idea of cyclic connectivity, fuzzy incidence cycle, cyclic connectivity index, and average cyclic connectivity index was initiated by Nazeer et al. [18]. The number of operations including Cartesian product, composition, tensor product, and normal product in IFIG was presented by Nazeer et al. [19]. Later, Nazeer and Rashid [20] proposed the idea of picture fuzzy incidence graphs (PFIGs) as an extension of FIGs. They provided an application of PFIGs in controlling unlawful transit of people from India to America. The number of reasons and advantages to introducing the crucial idea of IFIGs. Firstly, in IFGs, a vertex c expresses the same impact on an edge cd and dc but in IFIGs, the impact of c on cd denoted by (c, cd) will be different from (d, cd). This motivated us to bring the concept of IFIGs. Another reason to use IFIGs is that graphs, FGs, and FIGs do not have NMSV, which becomes the fundamental reason to introduce IFIGs. We cannot use graphs, FGs, and FIGs in the application, provided in Sect. 3, due to the non-availability of NMSV. Therefore, we have used the approach of IFIGs to get the required results. IFIGs are more useful, helpful, and handy than graphs, FGs, and FIGs due to the availability of NMSV. Rashmanlou et al. [26] explored the idea of intuitionistic fuzzy cut-vertices, bridges, gain, and loss in IFGs. In this paper, we bring these ideas to IFIGs. The paper is organized as follows, Sect. 1 contains some fundamental definitions and results that are important to apprehend the remaining concepts of this paper. In Sect. 2, we introduce the notion of connectivity and its related properties in IFIGs. An application for selecting the best paint company to invest money in among various paint companies by using IFIG is provided. We provide some basic definitions and terminologies from [1, 5, 26].

A graph is an ordered pair $\breve{G}=(V,E)$, where V is the set of vertices of $\breve{G}$ and E is the set of edges of $\breve{G}$. A graph without loops and multiple edges between any two vertices is named as a simple graph. A fuzzy subset (FS) $\psi$ on a set M is a map $\psi :M\rightarrow [0,1]$. A map $\omega :M\times M\rightarrow [0,1]$ is known as a fuzzy relation on $\psi$ if $\omega (c,d)\le min\{\psi (c),\psi (d)\}$ for each $c,d \in M$. A FG is a pair $G=(\psi ,\omega )$, where $\psi$ is a FS on a set V and $\omega$ is a fuzzy relation on $\psi$. It is consider that V is finite and non empty, $\psi$ is reflexive and symmetric.

In this paper, minimum and maximum operators are expressed by $\wedge$ or min and $\vee$ or max respectively.

An IFS A on universal set M is defined as

$$\begin{aligned} A=\{\langle w,\psi _{A}(w),\omega _{A}(w)\rangle \mid w\in M\}, \end{aligned}$$

where $\psi _{A}(w)\in [0,1]$ is named as degree of membership of w in A, $\omega _{A}(w)\in [0,1]$ is named as degree of non-membership of w in A, and $\psi _{A}(w)$, $\omega _{A}(w)$ satisfies $\psi _{A}(w)+ \omega _{A}(w)\le 1$ for every $w\in M$. An intuitionistic fuzzy relation (IFR) on universal set $M\times N$ is an IFS of the form $R=\{\langle (v,w),\psi _{R}(v,w),\omega _{R}(v,w)\rangle \mid (v,w)\in M\times N\}$, where $\psi _{R}:M\times N\rightarrow [0,1]$, $\omega _{R}:M\times N\rightarrow [0,1]$ and fulfills $\psi _{R}(v,w)+\omega _{R}(v,w)\le 1$ for every $v,w\in M$. An IFR R on a universal set $M\times M$ is reflexive if $\psi _{R}(v,v)=1$ for every $v\in R$, symmetric if $\psi _{R}(v,w)=\psi _{R}(w,v)$ for any $v,w\in M$. Let $\breve{G}=(V,E)$ be a crisp graph. An IFG on $\breve{G}$ is a pair $\grave{G}=(R,S)$ in which $R=(\psi _{R},\omega _{R})$ is an IFS on V and $S=(\psi _{S},\omega _{S})$ is an IFR on E of the type $\psi _{S}(vw)\le min\{(\psi _{R}(v),\psi _{R}(w))\}$, $\omega _{S}(vw)\ge max\{(\omega _{R}(v),\omega _{R}(w))\}$ and $0\le \psi _{S}(vw)+ \omega _{S}(vw)\le 1$ for all $vw \in E$. Also, S is a symmetric IFR on R. A partial intuitionistic fuzzy subgraph (PIFS) of an IFG, $\grave{G}=(R,S)$ is an IFG $H=(R^{\prime },S^{\prime })$ such that $\psi _{R^{\prime }}(v_{i})\le \psi _{R}(v_{i})$ and $\omega _{R^{\prime }}(v_{i})\ge \omega _{R}(v_{i})$ for each $v_{i}\in V$, $\psi _{S^{\prime }}(v_{i}w_{j})\le \psi _{R}(v_{i}w_{j})$ and $\omega _{S^{\prime }}(v_{i}w_{j})\ge \omega _{R}(v_{i}w_{j})$ for every $v_{i}w_{j}\in E$. An intuitionistic fuzzy subgraph of an IFG, $\grave{G}=(R,S)$ is an IFG $H=(R^{\prime },S^{\prime })$ such that $\psi _{R^{\prime }}(v_{i})=\psi _{R}(v_{i})$ and $\omega _{R^{\prime }}(v_{i})=\omega _{R}(v_{i})$ for each $v_{i}\in V$ of H, $\psi _{S^{\prime }}(v_{i}w_{j})=\psi _{R}(v_{i}w_{j})$ and $\omega _{S^{\prime }}(v_{i}w_{j})=\omega _{R}(v_{i}w_{j})$ for every $v_{i}w_{j}\in E$ of H. An IFG is strong if $\psi (v_{i}w_{j})=\wedge \{\psi (v_{i}),\psi (w_{j})\}$ and $\omega (v_{i}w_{j})=\vee \{\omega (v_{i}),\omega (w_{j})\}$ for every $v_{i}w_{j}\in E$. An IFG is complete if $\psi (v_{i}w_{j})=\wedge \{\psi (v_{i}),\psi (w_{j})\}$ and $\omega (v_{i}w_{j})=\vee \{\omega (v_{i}),\omega (w_{j})\}$ for every $v_{i},w_{j}\in V$.

The definitions given below are taken from [10, 14].

Assume $\breve{G}=(V,E)$ is a graph with non empty vertex set V. Then, an incidence graph (IG) of $\breve{G}=(V,E)$ is indicated by $\breve{G}=(V,E,I)$ where $I\subseteq V\times E$. The members of I are called pairs or incidence pairs (IPs). Then a FIG of $\breve{G}=(V,E,I)$ is expressed by $\tilde{G}=(\psi ,\omega ,\sigma )$ where $\psi$, $\omega$ and $\sigma$ are FS of vertices, edges and IPs respectively, such that $\sigma (v,vw)\le \wedge \{\psi (v),\omega (vw)\}$ for all $v\in V, vw\in E$. If there exist such a path v, (v, vw), vw, (w, vw), w between v and w then vertices v and w are connected. v and vw are connected if there is a path from v to vw such that v, (v, vw), vw.

Intuitionistic Fuzzy Incidence Graphs

IFIGs with different kinds of examples are elaborated in this section. In the whole article we will denote an IG by $\breve{G}=(V,E,I)$ and a IFIG by $\grave{G}=(R,S,T)$.

Definition 2.1

Let $\breve{G}=(V,E,I)$ be an IG. An IFIG, $\grave{G}=(R,S,T)$ is an ordered-triplet in which

• (1) $R=(\psi _{R},\omega _{R})$ is an IFS on V.

• (2) $S=(\psi _{S},\omega _{S})$ is an IFS on $E\subseteq V\times V$.

• (3) $T=(\psi _{T},\omega _{T})$ is an IFS on $V\times E$ such that

  $\psi _{T}(v,vw)\le min(\psi _{R}(v),\psi _{S}(vw))$,

  $\omega _{T}(v,vw)\ge max(\omega _{R}(v),\omega _{S}(vw)), \forall v\in V, vw\in E$,

  and $0\le \psi _{T}(v,vw)+\omega _{T}(v,vw)\le 1$.

An example of IFIG is provided here.

Example 2.2

Here we include a daily life example of three different cities. As an illustrative case, consider a network of (IFIG) of three vertices representing the three different cities. The membership value (MSV) of the vertices indicates the percentage of people who can speak English very well, and the non-membership value (NMSV) of the vertices represents the percentage of people who can not speak English fluently. The MSV of the edges expresses the percentage of those people contacting the people of other cities to enhance their English language, and the NMSV of the edges shows the percentage of those who are taking an interest in improving their English. The MSV of the pairs represents the percentage of those people who have improved their English, and the NMSV of the pairs shows the percentage of those people who fail to improve their English.

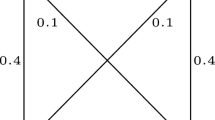
Consider an IG, $\breve{G}=(V,E,I)$ such that $V=\{p,q,r\}$, $E=\{pq, pr, qr\}$ and $I=\{(p,pq),(q,pq),(p,pr),(r,pr),(q,qr),(r,qr)\}$ as shown in Fig. 1. Let $\grave{G}=(R,S,T)$ be an IFIG associated with $\breve{G}$ provided in Fig. 2 where,

$R=\{(p,0.2,0.6), (q,0.1,0.1), (r,0.3,0.1)\}$,

$S=\{(pq,0.1,0.6), (pr,0.1,0.8), (qr,0.1,0.1)\}$,

$T=\{((p,pq),0.1,0.6), ((q,pq),0.1,0.7), ((p,pr),0.1,0.9),((r,pr),0.1,0.9), ((q,qr),0.1,0.1), ((r,qr),0.1,0.3) \}$,

Fig. 1

Incidence graph

Fig. 2

IFIG

Definition 2.3

The support of an IFIG $\grave{G}=(R,S,T)$ is defined as $G^{*}=(R^{*},S^{*},T^{*})$ where

$R^{*}=$ support of $R=\{v\in V : \psi _{R}(v)>0, \omega _{R}(v)>0 \}$

$S^{*}=$ support of $S=\{vw\in E : \psi _{S}(vw)>0, \omega _{S}(vw)>0 \}$

$T^{*}=$ support of $T=\{(v,vw)\in I : \psi _{T}(v,vw)>0, \omega _{R}(v,vw)>0 \}$

Definition 2.4

A PIFS is called a partial intuitionistic fuzzy incidence subgraph (PIFIS) $H=(R^{\prime },S^{\prime },T^{\prime })$ of an IFIG $\grave{G}=(R,S,T)$ if $\psi _{T^{\prime }}(v_{i},v_{i}w_{j})\le \psi _{T}(v_{i},v_{i}w_{j})$ and

$\omega _{T^{\prime }}(v_{i},v_{i}w_{j})\ge \omega _{T}(v_{i},v_{i}w_{j})$ for all $(v_{i},v_{i}w_{j})\in T^{*}$.

Definition 2.5

An intuitionistic fuzzy subgraph is called an intuitionistic fuzzy incidence subgraph (IFIS) $H=(R^{\prime },S^{\prime },T^{\prime })$ of an IFIG $\grave{G}=(R,S,T)$ if $\psi _{T^{\prime }}(v_{i},v_{i}w_{j})=\psi _{T}(v_{i},v_{i}w_{j})$ and

$\omega _{T^{\prime }}(v_{i},v_{i}w_{j})=\omega _{T}(v_{i},v_{i}w_{j})$ for all $(v_{i},v_{i}w_{j})$ is the set of incidence pair of H. Figs. 3 and 4 is an example of PIFIS and IFIS of IFIG given in Fig. 2.

Fig. 3

PIFIS of IFIG provided in Figure 2

Fig. 4

IFIS of IFIG given in Figure 2

Definition 2.6

A strong IFG, $\grave{G}$ is called strong IFIG if $\psi _{T}(v_{i},v_{i}w_{j})=\wedge \{\psi _{R}(v_{i}),\psi _{S}(v_{i}w_{j})\}$ and $\omega _{T}(v_{i},v_{i}w_{j})=\vee \{\omega _{R}(v_{i}),\omega _{S}(v_{i}w_{j})\}$ for each $\psi _{T}(v_{i},v_{i}w_{j})$ and $\omega _{T}(v_{i},v_{i}w_{j})$ in $T^{*}$.

Definition 2.7

A complete IFG, $\grave{G}$ is called complete IFIG if $\psi _{T}(v_{i},v_{i}w_{j})=\wedge \{\psi _{R}(v_{i}),\psi _{S}(v_{i}w_{j})\}$ and $\omega _{T}(v_{i},v_{i}w_{j})=\vee \{\omega _{R}(v_{i}),\omega _{S}(v_{i}w_{j})\}$ for each $v_{i},v_{j}\in R^{*}$.

Connectivity ideas are significant in whole graph theory. But in classical problems these ideas only tackle the disconnection of the networks. The reduction in flow is more frequent than the disconnection. Here, we are going to talk about intuitionistic incidence walk (IIW), intuitionistic incidence path (IIP), intuitionistic incidence gain path (IIGP), intuitionistic incidence loss path (IILP) intuitionistic incidence balanced path (IIBP), intuitionistic incidence optimal path (IIOP), intuitionistic incidence cut-vertices $(C_{II})$ and intuitionistic incidence bridges $(B_{II})$. These ideas will help us to deal with the reduction in the strength of connectedness between distinct pairs of vertices in an IFIGs.

Definition 2.8

If $vw\in S^{*}$ then vw is called an edge of the IFIG $\grave{G}=(R,S,T)$ and if $(v,vw),(w,vw)\in T^{*}$ then (v, vw) and (w, vw) are IPs of $\grave{G}=(R,S,T)$.

Definition 2.9

A sequence

$P: l_{0},(l_{0},l_{0}l_{1}),l_{0}l_{1},(l_{1},l_{0}l_{1}),l_{1},(l_{1},l_{1}l_{2}),l_{1}l_{2},(l_{2},l_{1}l_{2}),l_{2},...,l_{n-1},(l_{n-1},l_{n-1}l_{n}), l_{n-1}l_{n},(l_{n},l_{n-1}l_{n}),l_{n}$ in $\grave{G}$ is called IIW. If $l_{0}=l_{n}$ then an IIW is closed.

Definition 2.10

An IIP

$P:l_{0},(l_{0},l_{0}l_{1}),l_{0}l_{1},(l_{1},l_{0}l_{1}),l_{1},(l_{1},l_{1}l_{2}),l_{1}l_{2},(l_{2},l_{1}l_{2}) ,l_{2},...,l_{n-1},(l_{n-1},l_{n-1}l_{n}),l_{n-1}l_{n},(l_{n},l_{n-1}l_{n}),l_{n}$.

is a sequence of different vertices such that either one of the given below condition is satisfied:

• (1) $\psi _{T}(v_{i},v_{i}w_{j})>0$ and $\omega _{T}(v_{i},v_{i}w_{j})>0$ for some i, j,

• (2) $\psi _{T}(v_{i},v_{i}w_{j})>0$ and $\omega _{T}(v_{i},v_{i}w_{j})=0$ for some i, j,

• (3) $\psi _{T}(v_{i},v_{i}w_{j})=0$ and $\omega _{T}(v_{i},v_{i}w_{j})>0$ for some i, j.

Example 2.11

Let $\grave{G}=(R,S,T)$ be an IFIG provided in Fig. 5 where,

$R=\{(p,0.3,0.5), (q,0.6,0.2), (r,0.3,0.3), (s,0.2,0.5)\}$,

$S=\{(pq,0.3,0.7), (pr,0.2,0.5),(ps,0.2,0.6),(qr,0.3,0.3),(rs,0.2,0.8)\}$,

$T=\{((p,pq),0.2,0.8), ((q,pq),0.3,0.6), ((p,pr),0.1,0.5),((r,pr),0.2,0.8),((p,ps),0.2,0.7), ((s,ps),0.1,0.9),((q,qr),0.2,0.5),((r,qr),0.3,0.5), ((r,rs),0.1,0.8),((s,rs),0.1,0.9)\}$.

An IIW $P_{1}: p,(p,pq),pq,(q,pq),q,(q,qr),qr,(r,qr),r,(r,rp),rp,(p,rp),p$ in Fig. 5 is closed because its beginning and final vertex is identical but it is not an IIP because all vertices are not different.

The idea of loss and gain is crucial in various problems in economics, networks and computer science. We are going to connect these notions to an IFIG.

Example 2.12

Consider $\grave{G}=(R,S,T)$ is an IFIG provided in Fig. 5 where,

$R=\{(p,0.3,0.5), (q,0.6,0.2), (r,0.3,0.3), (s,0.2,0.5)\}$,

$S=\{(pq,0.3,0.7), (pr,0.2,0.5),(ps,0.2,0.6) (qr,0.3,0.3),(rs,0.2,0.8)\}$,

$T=\{((p,pq),0.2,0.8), ((q,pq),0.3,0.6), ((p,pr),0.1,0.5),((r,pr),0.2,0.8), ((p,ps),0.2,0.7)$,

$((s,ps),0.1,0.9),((q,qr),0.2,0.5),((r,qr),0.3,0.5), ((r,rs),0.1,0.8),((s,rs),0.1,0.9)\}$.

Here we include a real life example of four different university friends. As an illustrative case, consider a network (IFIG) of four different vertices representing mobile phones. The MSV of the vertices indicating the percentage of useful data in a mobile phone and the NMSV is representing the percentage of useless data. The MSV of the edges is the percentage of helpful data which they are sharing with each other and the NMSV of the edges is the percentage of harmful data which they are sharing with each other. The MSV of the pair is the percentage of effective data which one friend is sending to other friend every week and the NMSV of the pair is the percentage of worthless data which one friend is transferring to other friend each week.

Definition 2.13

Let $\grave{G}=(R,S,T)$ be an IFIG. For any $l-m$ IIP

$P: l=l_{1},(l_{1},l_{1}l_{2}),l_{1}l_{2},(l_{2},l_{1}l_{2}) ,l_{2},...,l_{n-1},(l_{n-1},l_{n-1}l_{n}), l_{n-1}l_{n},(l_{n},l_{n-1}l_{n}),l_{n}=m$ in $\grave{G}$,

we define $\wedge \{\psi _{T}(l_{1},l_{1}l_{2}),\psi _{T}(l_{2},l_{1}l_{2}),\psi _{T}(l_{2},l_{2}l_{3}) \psi _{T}(l_{3},l_{2}l_{3}),...,\psi _{T}(l_{n-1},l_{n-1}l_{n}),\psi _{T}(l_{n},l_{n-1}l_{n})\}$ as the intuitionistic incidence gain (IIG) of P. IIG of P is expressed by $G_{II}(P)$ and

$\vee \{\omega _{T}(l_{1},l_{1}l_{2}),\omega _{T}(l_{2},l_{1}l_{2}),\omega _{T}(l_{2},l_{2}l_{3}) \omega _{T}(l_{3},l_{2}l_{3}),...,\omega _{T}(l_{n-1},l_{n-1}l_{n}),\omega _{T}(l_{n},l_{n-1}l_{n})\}$ as the intuitionistic incidence loss (IIL) of P. IIL of P is denoted by $L_{II}(P)$. In Fig. 5, for an IIP, $P=psr$, $G_{II}(P)=\wedge (0.2,0.1,0.1,0.1)=0.1$ and $L_{II}(P)=\vee (0.7,0.9,0.9,0.8)=0.9$

Fig. 5

IFIG

Definition 2.14

An IIP, P is called an IIGP if $G_{II}(P)>L_{II}(P)$ and IILP if $G_{II}(P)<L_{II}(P)$.

In Fig. 5P : psr is an IILP because $G_{II}(P)=0.1<L_{II}(P)=0.9$.

Definition 2.15

An IFIG is named as connected if there exists an IIP between each pair of vertices.

Definition 2.16

Let l and m be vertices in a connected IFIG $\grave{G}$. Among all $l-m$ IIP in $\grave{G}$, an IIP whose IIG is greater than or equal to of any other $l-m$ IIP in $\grave{G}$ is called a maximum $l-m$ IIGP. It is shown by $max(l-m)_{IIGP}$. In the same way, a $l-m$ IIP whose IIL is smaller than or equal to that of any other $l-m$ IIP in $\grave{G}$ is known as minimum $l-m$ IILP. It is expressed by $min(l-m)_{IILP}$. That is an IIP, P is $max(l-m)_{IIGP}$ if $G_{II}(P)\ge G_{II}(P^{\diamond })$ and is a $min(l-m)_{IILP}$ if $L_{II}(P)\le L_{II}(P^{\diamond })$, where $P^{\diamond }$ is any $l-m$ IIP in $\grave{G}$.

Example 2.17

Table 1 shows the intuitionistic incidence max gain and intuitionistic incidence min loss between each pair of vertices of an IFIG given in Fig. 5.

Table 1 Intuitionistic incidence Max-gain and intuitionistic incidence Min-loss of vertices

Definition 2.18

In an IFIG a $l-m$ IIP, P is named as IIBP if $G_{II}(P)=L_{II}(P)$ and P is called IIOP if P is a $max(l-m)_{IIGP}$ and $min(l-m)_{IILP}$.

Example 2.19

Figure 5 does not have any IIBP because for each IIP $G_{II}(P)\ne L_{II}(P)$ but $p-s=p,(p,ps),ps,(s,ps),s$ is an IIOP.

Definition 2.20

Assume $\grave{G}=(R,S,T)$ is an IFIG and let l and m be any two vertices of $\grave{G}$. The IIG of l and m is defined as IIG of $max(l-m)_{IIGP}$. It is expressed by $G_{II}(l,m)$. Similarly, the IIL of l and m is defined as IIL of $min(l-m)_{IILP}$. It is expressed by $L_{II}(l,m)$.

Example 2.21

In Fig. 5, $G_{II}(p,s)=0.1$, $L_{II}(p,s)=0.9$, $G_{II}(q,r)=0.2$ and $L_{II}(q,r)=0.5$.

Definition 2.22

Let H ba an IFIS of $\grave{G}$, l and m be any two vertices of H then an IIG of l and m in H is the IIG of $max(l-m)_{IIGP}$ strictly belongs to H and it is shown by $G_{IIH}(l,m)$. In a similar manner, IIL of l and m in H is the IIL of $min(l-m)_{IILP}$ strictly belongs to H and it is denoted by $L_{IIH}(l,m)$. If there does not exist $max(l-m)_{IIGP}$ and $min(l-m)_{IILP}$ in H then $G_{IIH}(l,m)=0$ and $L_{IIH}(l,m)=0$.

Example 2.23

Let $\grave{G}=(R,S,T)$ be an IFIG provided in Fig. 6 which is a IFIS of IFIG provided in Fig. 5 where,

$R=\{(p,0.3,0.5), (q,0.6,0.2), (r,0.3,0.3), (s,0.2,0.5)\}$,

$S=\{(pq,0.3,0.7), (pr,0.2,0.5)\}$,

$T=\{((p,pq),0.2,0.8), ((q,pq),0.3,0.6), ((p,pr),0.1,0.5),((r,pr),0.2,0.8)\}$.

It can be seen that $G_{IIH}(p,s)=0$ and $L_{IIH}(p,s)=0$.

Fig. 6

IFIS of Figure 5

Proposition 2.24

If H is an IFIS of an IFIG, $\grave{G}=(R,S,T)$ then $G_{IIH}(l,m)\le G_{II}(l,m)$ and $L_{IIH}(l,m)\le L_{II}(l,m)$ for each pairs of vertices l and m.

Proof

Let H be an IFIS of $\grave{G}$ having same number of vertices, edges and IPs with equal membership degree and non-membership degree of vertices, edges and IPs this implies that $G_{IIH}(l,m)=G_{II\grave{G}}(l,m)$ and $G_{IIH}(l,m)=G_{II\grave{G}}(l,m)$ for every pair of vertices l and m in H. Now, if H has less number of vertices, edges and IPs then membership degree and non-membership degree of vertices,edges, and IPs will less this implies $G_{IIH}(l,m)<G_{II\grave{G}}(l,m)$ and $L_{IIH}(l,m)<L_{II\grave{G}}(l,m)$. Hence, $G_{IIH}(l,m)\le G_{II\grave{G}}(l,m)$ and $L_{IIH}(l,m)\le L_{II\grave{G}}(l,m)$. $\square$

Next, we have proposed an idea of intuitionistic incidence gain loss matrix (IIGLM) in an IFIGs.

Definition 2.25

Let $\grave{G}=(R,S,T)$ be an IFIG with n vertices, $\{l_{1},l_{2},...,l_{n}\}$. The IIGLM is defined as $M=[G_{II_{i,j}},L_{II_{i,j}}]$ where $G_{II_{i,j}}=G_{II}(l_{i},l_{j})$ and $L_{II_{i,j}}=L_{II}(l_{i},l_{j})$ for $i\ne j$ and $G_{II_{i,j}}=\psi _{R}(l_{i})$, $L_{II_{i,j}}=\omega _{R}(l_{i})$ for $i=j$.

Example 2.26

IIGLM of $\grave{G}$ shown in Fig. 5 is given below.

$$\begin{aligned} \begin{bmatrix} (0.3,0.5) &{} (0.2,0.8) &{} (0.2,0.8) &{} (0.1,0.9) \\ (0.2,0.8)&{} (0.6,0.2) &{} (0.2,0.5) &{} (0.1,0.9) \\ (0.2,0.8) &{} (0.2,0.5) &{} (0.3,0.3) &{} (0.1,0.9) \\ (0.1,0.9) &{} (0.1,0.9) &{} (0.1,0.9) &{} (0.2,0.5) \\ \end{bmatrix} \end{aligned}$$

It is clear from the matrix that IIGLM of an IFIG is a symmetric matrix.

In crisp graphs, a cut-vertex is one whose deletion results the disconnection of a graph and a bridge is an edge whose deletion results the disconnection of graph. But in IFIGs these definitions are different.

Definition 2.27

Assume $\grave{G}=(R,S,T)$ is an IFIG. A vertex $k\in R^{*}$ is named as an $C_{II}$ if there exists two vertices $l,m\in R^{*}$ of the type $k\ne l\ne m$ such that $G_{II_{\grave{G}-k}}(l,m)<G_{II_{\grave{G}}}(l,m)$ and $L_{II_{\grave{G}-k}}(l,m)>L_{II_{\grave{G}}}(l,m)$. A vertex k in an IFIG is said to be an intuitionistic incidence gain cut-vertex $(C_{IIG})$ if $G_{II_{\grave{G}-k}}(l,m)<G_{II_{\grave{G}}}(l,m)$ is satisfied and an an intuitionistic incidence loss cut-vertex $(C_{IIL})$ if $L_{II_{\grave{G}-k}}(l,m)>L_{II_{\grave{G}}}(l,m)$ is satisfied. In Fig. 7, p is an $C_{IIL}$ because $L_{II_{\grave{G}-p}}(q,r)=0.9>L_{II_{\grave{G}}}(q,r)=0.82$ and r is an $C_{IIG}$ because $G_{II_{\grave{G}-r}}(q,s)=0<G_{II_{\grave{G}}}(q,s)=0.01$ .

Fig. 7

IFIG having p as $C_{IIL}$ and r as $C_{IIG}$

Theorem 2.28

A vertex k in an IFIG $\grave{G}=(R,S,T)$ is an $C_{II}$ if and only if (iff) k is a vertex in each $max(l,m)_{IIGP}$ and in each $min(l,m)_{IILP}$, for some l and m in $R^{*}$.

Proof

Let $\grave{G}=(R,S,T)$ be an IFIG. Suppose that k is an $C_{II}$. According to the definition of $C_{II}$, there exists vertices l and m in $\grave{G}$ such that $k\ne l\ne m$ and $(i):G_{II_{\grave{G-k}}}(l,m)<G_{II_{\grave{G}}}(l,m)$ and $(ii):L_{II_{\grave{G-k}}}(l,m)>L_{II_{\grave{G}}}(l,m)$. From (i) it is clear that the deleting of k from $\grave{G}$ deletes all $max(l,m)_{IIGP}$ and from (ii) it can be seen that the deletion of k deletes every $min(l,m)_{IILP}$. Thus, k is in every $max(l,m)_{IIGP}$ and $min(l,m)_{IILP}$. Conversely, assume that k is in each $max(l,m)_{IIGP}$ and in each $min(l,m)_{IILP}$. Then the deletion of k form $\grave{G}$ results in the deletion of all $max(l,m)_{IIGPs}$ and $min(l,m)_{IILPs}$. This implies the $G_{II}$ will lessen and $L_{II}$ will enhance between l and m. So, $G_{II_{\grave{G-k}}}(l,m)<G_{II_{\grave{G}}}(l,m)$ and $L_{II_{\grave{G-k}}}(l,m)>L_{II_{\grave{G}}}(l,m)$. Hence k is an $C_{II}$. $\square$

Definition 2.29

Let $\grave{G}=(R,S,T)$ be an IFIG. An edge $e=lm$ in $\grave{G}$ is said to be an $B_{II}$ if $G_{II_{\grave{G-e}}}(\ddot{l},\ddot{m})<G_{II_{\grave{G}}}(\ddot{l},\ddot{m})$ and $L_{II_{\grave{G-e}}}(\ddot{l},\ddot{m})>L_{II_{\grave{G}}}(\ddot{l},\ddot{m})$ for some $\ddot{l},\ddot{m}\in R^{*}$. If at least one of $\ddot{l}$ or $\ddot{m}$ is distinct from l and m then $e=lm$ is called intuitionistic incidence bond and an intuitionistic incidence cutbond if both $\ddot{l}$ and $\ddot{m}$ are dissimilar from l and m.

Example 2.30

Let $\grave{G}=(R,S,T)$ be an IFIG provided in Fig. 8 where,

$R=\{(p,0.3,0.5), (q,0.4,0.4), (r,0.2,0.7), (s,0.5,0.1)\}$,

$S=\{(pq,0.05,0.75), (pr,0.08,0.72),(qr,0.2,0.8),(qs,0.2,0.4),(rs,0.1,0.7)\}$,

$T=\{((p,pq),0.03,0.75), ((q,pq),0.1,0.85),((p,pr),0.04,0.74),((r,pr),0.05,0.76),((q,qr),0.1,0.81),((r,qr),0.07,0.8),((q,qs),0.1,0.4),((s,qs),0.08,0.5), ((r,rs),0.05,0.89),((s,rs),0.03,0.82)\}$.

In Fig. 8, edges qr and qs are $B_{II}$.

Fig. 8

IFIG having $B_{II}$

Theorem 2.31

An edge $e\in S^{*}$ of an IFIG $G=(R,S,T)$ is an $B_{II}$ iff it is in each $max(l,m)_{IIGP}$ and in every $min(l,m)_{IILP}$ for some l and m $\in R^{*}$.

Proof

Let $\grave{G}=(R,S,T)$ be an IFIG. Suppose that $e=lm$ is an $B_{II}$. According to the definition of $B_{II}$, there exists vertices $\ddot{l}$ and $\ddot{m}$ in $\grave{G}$ such that $(i):G_{II_{\grave{G-e}}}(\ddot{l},\ddot{m})<G_{II_{\grave{G}}}(\ddot{l},\ddot{m})$, and $(ii):L_{II_{\grave{G-e}}}(\ddot{l},\ddot{m})>L_{II_{\grave{G}}}(\ddot{l},\ddot{m})$. From (i) it can be observe that the deleting of e from $\grave{G}$ deletes every $max(\ddot{l},\ddot{m})_{IIGP}$ and from (ii) it can be seen that the deletion of e deletes every $min(\ddot{l},\ddot{m})_{IILP}$. Thus, e is in every $max(\ddot{l},\ddot{m})_{IIGP}$ and $min(\ddot{l},\ddot{m})_{IILP}$. Conversely, assume that e is in each $max(\ddot{l},\ddot{m})_{IIGP}$ and in each $min(\ddot{l},\ddot{m})_{IILP}$. Then the deletion of e form $\grave{G}$ results in the deletion of every $max(\ddot{l},\ddot{m})_{IIGPs}$ and $min(\ddot{l},\ddot{m})_{IILPs}$. This implies the $G_{II}$ will lessen and $L_{II}$ will enhance between $\ddot{l}$ and $\ddot{m}$. So, $G_{II_{\grave{G-e}}}(\ddot{l},\ddot{m})<G_{II_{\grave{G}}}(\ddot{l},\ddot{m})$ and $L_{II_{\grave{G-e}}}(\ddot{l},\ddot{m})>L_{II_{\grave{G}}}(\ddot{l},\ddot{m})$. This proves that $e=lm$ is an $B_{II}$. $\square$

Here, we are presenting a simple theorem to examine whether a specific edge is an $B_{II}$ or not.

Theorem 2.32

An edge lm is an $B_{II}$ iff $G_{II_{\grave{G-lm}}}(l,m)<\wedge \{\psi (l,lm),\psi (m,lm)\}$ and $L_{II_{\grave{G-lm}}}(l,m)>\vee \{\omega (l,lm),\omega (m,lm)\}$ for some $l,m\in R^{*}$.

Proof

Let $\grave{G}=(R,S,T)$ be an IFIG and $e=lm$ is an edge in $\grave{G}$ of the type $G_{II_{\grave{G-lm}}}(l,m)<\wedge \{\psi (l,lm),\psi (m,lm)\}$ and $L_{II_{\grave{G-lm}}}(l,m)>\vee \{\omega (l,lm),\omega (m,lm)\}$. Since $\wedge \{\psi (l,lm),\psi (m,lm)\}\le G_{II}(l,m)$ and $\vee \{\omega (l,lm),\omega (m,lm)\}\ge L_{II}(l,m)$, we have $G_{II_{\grave{G-lm}}}(l,m)<G_{\grave{G}}(l,m)$, $L_{II_{\grave{G-lm}}}(l,m)>L_{\grave{G}}(l,m)$. This implies that lm is an $B_{II}$. Conversely, consider that lm is an $B_{II}$ then by Theorem 2.28. there will be vertices a and b in R such that lm is present on every $max(a-b)_{IIGP}$ and each $min(a-b)_{IILP}$. Assume $G_{II_{\grave{G-lm}}}(l,m)>\wedge \{\psi (l,lm),\psi (m,lm)\}$. Then, $G_{II_{\grave{G-lm}}}(l,m)=G_{II_{\grave{G}}}(l,m)$. This implies there will be a $max(l-m)_{IIGP}$ in $\grave{G}$ say, J which is dissimilar from lm. Assume K is a $max(a-b)_{IIGP}$ in $\grave{G}$. Replace lm in K by J to get an $a-b$ IIW. This IIW carries an $a-b$ IIP. The IIG of this IIP is larger than or equal to $G_{II_{\grave{G}}}(a,b)$ which is impossible. Therefore, $G_{II_{\grave{G-lm}}}(l,m)<\wedge \{\psi (l,lm),\psi (m,lm)\}$. Now, consider that $L_{II_{\grave{G-lm}}}(l,m)\le \vee \{\omega (l,lm),\omega (m,lm)\}$. Then, $L_{II_{\grave{G-lm}}}(l,m)=L_{II_{\grave{G}}}(l,m)$. This follows that there is a $min(l-m)_{IILP}$ in $\grave{G}$ call $J_{\prime }$ which is distinct from lm. Let $K^{\prime }$ be a $min(a-b)_{IILP}$. Replace lm $K^{\prime }$ by $J^{\prime }$ to get $a-b$ IIW. This IIW contains $a-b$ IIP. The IIL of this IIP is smaller than or equal to $L_{II_{\grave{G}}}(a,b)$ which is impossible. Therefore, $L_{II_{\grave{G-lm}}}(l,m)>\vee \{\omega (l,lm),\omega (m,lm)\}$.

Selection of Company or Companies to Investment by Using IFIG

Eight different paint companies $C_{1}$, $C_{2}$, $C_{3}$, $C_{4}$, $C_{5}$, $C_{6}$, $C_{7}$ and $C_{8}$ are doing their business with each other on certain $G_{II}$ and $L_{II}$. Investors are interested in investing their money in these companies to earn more. Still, before the investment, they are a bit confused about which company or companies they should invest their money in because they are unaware of the company or companies with a maximum $G_{II}$ and minimum of $L_{II}$. A mathematical model of this scenario is discussed here. Let $\grave{G}=(R,S,T)$ be an IFIG as shown in Fig. 9.

$R=\{(C_{1},0.3,0.1),(C_{2},0.2,0.7), (C_{3},0.3,0.3),(C_{4},0.1,0.8),(C_{5},0.8,0.1), (C_{6},0.7,0.2), (C_{7},0.4,0.4), (C_{8},0.5,0.5)\}$ showing the different paint companies with their $G_{II}$ and $L_{II}$ before starting their business with each other.

$S=\{((C_{1},C_{2})0.2,0.7),((C_{2},C_{3})0.15,0.75), ((C_{2},C_{4}) 0.05,0.83),((C_{2},C_{8})0.1,0.74)),((C_{3},C_{4})0.07,0.8), ((C_{4},C_{5})0.1,0.82),((C_{4},C_{6})0.07,0.87),((C_{5},C_{6})0.6,0.2), ((C_{6},C_{7})0.1,0.42),((C_{6},C_{8})0.3,0.5)\}$ representing the contract requirements of $G_{II}$ and $L_{II}$ among all companies at which they will do their business with each other.

$T=\{((C_{1},C_{1}C_{2}),0.16,0.8),(C_{2},C_{1}C_{2}),0.2,0.72)$,

$(C_{2},C_{2}C_{3}),0.11,0.76),(C_{3},C_{2}C_{3}),0.13,0.77)$,

$(C_{2},C_{2}C_{4}),0.04,0.92),(C_{4},C_{2}C_{4}),0.04,0.88)$,

$(C_{2},C_{2}C_{8}),0.1,0.81),(C_{8},C_{2}C_{8}),0.03,0.74))$,

$(C_{3},C_{3}C_{4}),0.07,0.85),(C_{4},C_{3}C_{4}),0.01,0.9)$,

$(C_{4},C_{4}C_{5}),0.08,0.84),(C_{5},C_{4}C_{5}),0.09,0.89)$,

$(C_{4},C_{4}C_{6}),0.06,0.88),(C_{6},C_{4}C_{6}),0.05,0.93)$,

$(C_{5},C_{5}C_{6}),0.6,0.21),(C_{6},C_{5}C_{6}),0.5,0.23)$,

$(C_{6},C_{6}C_{7}),0.1,0.46),(C_{7},C_{6}C_{7}),0.01,0.42)$,

$(C_{6},C_{6}C_{8}),0.27,0.65),(C_{8},C_{6}C_{8}),0.2,0.6)\}$

shows which company or companies are accomplishing and which are not achieving the said $G_{II}$ and $L_{II}$ contract requirements. After computing the $G_{II}$ and $L_{II}$ of all companies, the maximum $G_{II}=0.5$ and minimum $L_{II}=0.23$ is of company $C_{5}$ and $C_{6}$. So, investors can invest their money either in $C_{5}$ or in $C_{6}$.

Fig. 9

A mathematical model to select best company for investment

Conclusion

It is well known that graphs are among the omnipresent models for various kinds of structures. Graphs have the bulk of applications in different areas of life. However, they have failed to discover the impact of vertices on edges. This thing makes a way to introduce the idea of FIGs. FIGs can provide the effect of a vertex on edge. For example, if vertices show alike hotels and edges show the roads connecting these hotels, we can have a FG expressing the the area of traffic from one hotel to another hotel. The hotel has a large number of customers and will have maximum ramps in a hotel. So, if $H_{1}$ and $H_{2}$ are two hotels and $H_{1}H_{2}$ roads connecting them then $(H_{1},H_{1}H_{2})$ represent the ramp system from the road $H_{1}H_{2}$ to the hotel $H_{1}$. In unweighted graph, $H_{1}$ and $h_{2}$ both will have an effect of 1 on $H_{1}H_{2}$. In the case of directed graph,, the impact of $H_{1}$ on $H_{1}H_{2}$ indicated by $(H_{1},H_{1}H_{2})$ is 1 whereas $(H_{2},H_{1}H_{2})$ is 0. This concept is generalized by FIGs. FIGs are beneficial, but there is a lack of FIGs because they do not have a NMSV. Therefore, we have introduced IFIGs because IFIGs have MSV and NMSV. Also, we can not apply FIGs to the application provided in Sect. 3 due to the non-availability of NMSV. This motivates us to initiate the vital idea of IFIGs. IFIGs are more beneficial than FIGs due to the availability of MSV. Another reason to introduce IFIGs is that FIGs cannot tackle the concept of $G_{II}$ and $L_{II}$ due to the unavailability of NMSV. Still, IFIGs can handle the idea of $G_{II}$ and $L_{II}$ due to the availability of NMSV. IFIG is an extension of a FIG. In this paper, different connectivity ideas related to IFIGs are discussed. The notion of $G_{II}$ and $L_{II}$ for IIP and different pairs of vertices are examined. $C_{II}$ and $B_{II}$ are introduced with various examples. A comprehensive study on the effectiveness of IFIGs on different communication systems by using $C_{II}$ and $B_{II}$ is the main target of our forthcoming research papers. Another significant aspect of our upcoming research work is to make an application of IIGLM of IFIG in transportation problems.