Magnetohydrodynamic Radiative Simulations of Eyring–Powell Micropolar Fluid from an Isothermal Cone

Abstract

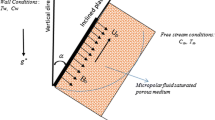
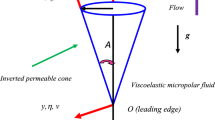
The magnetohydrodynamics thermal convection viscoelastic micropolar fluid from an isothermal cone is presented in this article. Greater temperature invokes radiation impacts that are studied by approximating Rosseland diffusion flux. To explain the non-Newtonian dynamics of the fluid, the Eyring–Powell viscoelastic model is employed that gives a great analogy for magnetic polymers. In order to simulate the polymer’s microstructural and shearing features, the Eringen’s micropolar Eyring–Powell fluid models are coupled. The Keller-Box scheme is used to solve the dimensionless couple conservation equations. Validation using previously published Newtonian solutions is also included. The fluctuations of velocity, angular velocity, temperature, concentration, skin friction, wall couple stress, heat and mass transfer rates are studied using graphical and tabulated findings. The computational modelling presented here have implications in hot polymer coating processes and industrial deposition procedures and they serve as a good reference for more generic computational fluid dynamics simulations.

Appendix A: Keller Box Numerical Details

The Keller Box Scheme comprises four stages:

• 1. Decomposition of the Nth order partial differential equation system to N first order equations.

• 2. Finite difference discretization.

• 3. Quasilinearization of non-linear Keller algebraic equations and finally.

• 4. Block-tridiagonal elimination solution of the linearized Keller algebraic equations.

The algebraic details for the present problem are provided in “Appendix A”. A typical mesh is given in Fig. 21 below.

Fig. 21

Keller box computational cell

Stage 1: Decomposition of Nth Order Partial Differential Equation System to N First Order Equations

Equations (15) to (18) subject to the boundary conditions (19) are first cast as a multiple system of first order differential equations. New dependent variables are introduced:

$$ u(x,y) = f^{\prime } ,\,\,v(x,y) = f^{\prime \prime } ,\,\,s(x,y) = \theta ,\,\,t(x,y) = \theta^{\prime } ,\,\,z(x,y) = \phi ,\,\,m(x,y) = \phi^{\prime } $$

(24)

These denote the variables for velocity, temperature and concentration respectively. Now Eqs. (15) to (18) are solved as a set of fifth order simultaneous differential equations:

$$ f^{\prime } = u $$

(25)

$$ u^{\prime } = v $$

(26)

$$ g^{\prime } = p $$

(27)

$$ s^{\prime } = t $$

(28)

$$ z^{\prime } = m $$

(29)

$$ \left( {1 + K + \varepsilon } \right)v^{\prime}\, + \frac{7}{4}fv + \xi v - \frac{1}{2}\left( u \right)^{2} - \varepsilon \delta \left( v \right)^{2} v^{\prime} + s + Nz + Kp - M\xi^{2} u = \,\frac{\xi }{4}\left( {u\frac{\partial u}{{\partial \xi }} - v\frac{\partial f}{{\partial \xi }}} \right) $$

(30)

$$ \left( {1 + \frac{K}{2}} \right)p^{\prime}\, + \frac{7}{4}fp - \frac{1}{4}ug + \xi p - BK\xi^{2} \left( {2g + v} \right) = \,\frac{\xi }{4}\left( {u\frac{\partial g}{{\partial \xi }} - p\frac{\partial f}{{\partial \xi }}} \right) $$

(31)

$$ \frac{t^{\prime}}{{{\text{Pr}}}}\left( {1 + \frac{4}{3F}} \right) + \frac{7}{4}ft + \xi t = \frac{\xi }{4}\left( {u\frac{\partial s}{{\partial \xi }} - t\frac{\partial f}{{\partial \xi }}} \right) $$

(32)

$$ \frac{m^{\prime}}{{Sc}} + \frac{7}{4}fm + \xi m = \frac{\xi }{4}\left( {u\frac{\partial \phi }{{\partial \xi }} - m\frac{\partial f}{{\partial \xi }}} \right) $$

(33)

where primes denote differentiation with respect to the variable, η. In terms of the dependent variables, the boundary conditions assume the form:

$$ \begin{aligned} & At\,\,\,\,\,\,\eta = 0,\,\,\,\,\,\,\,\,\,\,\,\,f = 0,\,\,\,\,\,\,\,\,\,v = 0,\,\,\,\,\,\,\,\,\,g = \frac{1}{2}\frac{{\partial^{2} f}}{{\partial y^{2} }},\,\,\,\,\,\,\,\,s = 1,\,\,\,\,\,\,z = 1 \\ & As\,\,\,\,\,\,\eta \to \infty ,\,\,\,\,\,\,\,v \to 0,\,\,\,\,\,\,\,g \to 0,\,\,\,\,\,\,\,\,\,s \to 0,\,\,\,\,\,\,\,\,\,\,z = 0. \\ \end{aligned} $$

(34)

Stage 2: Finite Difference Discretization

A two dimensional computational grid is imposed on the ξ–η plane as depicted in Fig. 20. The stepping process is defined by:

$$ \begin{gathered} \eta_{0} = 0,\,\,\,\,\,\eta_{i} = \eta_{i - 1} + h_{j} ,\,\,\,\,\,\,\,j = 1,2, \ldots ,J,\,\,\,\,\,\,\,\,\,\eta_{J} \equiv \eta_{\infty } \hfill \\ \xi^{0} = 0,\,\,\,\,\,\xi^{n} = \xi^{n - 1} + k_{n} ,\,\,\,\,\,n = 1,2, \ldots ,N \hfill \\ \end{gathered} $$

(35)

where k_n and h_jdenote the step distances in the ξ and η directions respectively. If $g_{j}^{n}$ denotes the value of any variable at $\left( {\eta_{j} ,\xi^{n} } \right)$, then the variables and derivatives of Eqs. (25) to (33) at $\left( {\eta_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} ,\xi^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right)$ are replaced by:

$$ g_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} = \frac{1}{4}\left[ {g_{j}^{n} + g_{j - 1}^{n} + g_{j}^{n - 1} + g_{j - 1}^{n - 1} } \right] $$

(36)

$$ \left( {\frac{\partial g}{{\partial \eta }}} \right)_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} = \frac{1}{{2h_{j} }}\left[ {g_{j}^{n} - g_{j - 1}^{n} + g_{j}^{n - 1} - g_{j - 1}^{n - 1} } \right] $$

(37)

$$ \left( {\frac{\partial g}{{\partial \xi }}} \right)_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} = \frac{1}{{2k^{n} }}\left[ {g_{j}^{n} - g_{j - 1}^{n} + g_{j}^{n - 1} - g_{j - 1}^{n - 1} } \right] $$

(38)

The resulting finite-difference approximation of Eqs. (16) to (20) for the mid-point $\left( {\eta_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} ,\xi^{n} } \right)$, take the form:

$$ h_{j}^{ - 1} \left( {f_{j}^{n} - f_{j - 1}^{n} } \right) = u_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n} $$

(39)

$$ h_{j}^{ - 1} \left( {u_{j}^{n} - u_{j - 1}^{n} } \right) = v_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n} $$

(40)

$$ h_{j}^{ - 1} \left( {g_{j}^{n} - g_{j - 1}^{n} } \right) = p_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n} $$

(41)

$$ h_{j}^{ - 1} \left( {s_{j}^{n} - s_{j - 1}^{n} } \right) = t_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n} $$

(42)

$$ h_{j}^{ - 1} \left( {z_{j}^{n} - z_{j - 1}^{n} } \right) = m_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n} $$

(43)

$$ \left( {1 + K + \varepsilon } \right)\left( {v_{j} - v_{j - 1} } \right)\, + \frac{7 + \alpha }{4}\frac{{h_{j} }}{4}\left( {f_{j} + f_{j - 1} } \right)\left( {v_{j} + v_{j - 1} } \right) + \xi \frac{{h_{j} }}{2}\left( {v_{j} + v_{j - 1} } \right) - \left( {\frac{1}{2} + \frac{\alpha }{4}} \right)\frac{{h_{j} }}{4}\left( {u_{j} + u_{j - 1} } \right)^{2} - \varepsilon \delta \left( {v_{j} + v_{j - 1} } \right)^{2} \left( {v_{j} - v_{j - 1} } \right) + \frac{{h_{j} }}{2}\left( {s_{j} + s_{j - 1} } \right) + N\frac{{h_{j} }}{2}\left( {z_{j} + z_{j - 1} } \right) + K\frac{{h_{j} }}{2}\left( {p_{j} + p_{j - 1} } \right) - M\xi^{2} \frac{{h_{j} }}{2}\left( {u_{j} + u_{j - 1} } \right) = \,\left[ {R_{1} } \right]_{j - /12}^{n - 1} $$

(44)

$$\begin{aligned} &\left( {1 + \frac{K}{2}} \right) \left( {p_{j} - p_{j - 1} } \right) + \frac{7 + \alpha }{4}\left( {f_{j} + f_{j - 1} } \right)\left( {p_{j} + p_{j - 1} } \right) + \xi \left( {p_{j} + p_{j - 1} } \right)\\ &\quad - \frac{1 + \alpha }{4}\left( {u_{j} + u_{j - 1} } \right)\left( {g_{j} + g_{j - 1} } \right) - BK\xi^{2} \left( {2\left( {g_{j} + g_{j - 1} } \right) + \left( {v_{j} + v_{j - 1} } \right)} \right) + \frac{\alpha }{4}g_{{j - 1/2}}^{n - 1} \left( {g_{j} + g_{j - 1} } \right)\\ &\quad - \frac{\alpha }{4}f_{{j - 1/2}}^{n - 1} \left( {f_{j} + f_{j - 1} } \right) = \,\,\left[ {R_{2} } \right]_{j - /12}^{n - 1}\end{aligned}$$

(45)

$$\begin{aligned} &\frac{1}{{{\text{Pr}}}}\left( {1 + \frac{4}{3F}} \right)\left( {t_{j} - t_{j - 1} } \right) + \frac{7 + \alpha }{4}\left( {f_{j} + f_{j - 1} } \right)\left( {t_{j} + t_{j - 1} } \right) + \xi \left( {t_{j} + t_{j - 1} } \right)\\ &\quad - \frac{\alpha }{4}\left( {u_{j} + u_{j - 1} } \right)\left( {s_{j} + s_{j - 1} } \right) + \frac{\alpha }{4}s_{{j - {1/2}}}^{n - 1} \left( {u_{j} + u_{j - 1} } \right)\\ &\quad - \frac{\alpha }{4}u_{{j - {1/2}}}^{n - 1} \left( {f_{j} + f_{j - 1} } \right) = \left[ {R_{3} } \right]_{j - /12}^{n - 1}\end{aligned} $$

(46)

$$\begin{aligned} &\frac{1}{Sc}\left( {m_{j} - m_{j - 1} } \right) + \frac{7 + \alpha }{4}\left( {f_{j} + f_{j - 1} } \right)\left( {m_{j} + m_{j - 1} } \right) + \xi \left( {m_{j} + m_{j - 1} } \right)\\ &\quad - \frac{\alpha }{4}\left( {u_{j} + u_{j - 1} } \right)\left( {z_{j} + z_{j - 1} } \right) + \frac{\alpha }{4}z_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n - 1} \left( {u_{j} + u_{j - 1} } \right) - \frac{\alpha }{4}u_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n - 1} \left( {z_{j} + z_{j - 1} } \right)\\ &\quad - \frac{\alpha }{4}f_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n - 1} \left( {m_{j} + m_{j - 1} } \right) + \frac{\alpha }{4}m_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n - 1} \left( {f_{j} + f_{j - 1} } \right) = \left[ {R_{4} } \right]_{j - /12}^{n - 1}\end{aligned} $$

(47)

where the following notation applies:

$$ \alpha = \frac{{\xi^{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}{{k^{n} }} $$

(48)

$$\begin{aligned} \left[ {R_{1} } \right]_{j - 1/2}^{n - 1} &= - h_{j} \Bigg[ \left( {1 + K + \varepsilon } \right)\left( {v^{\prime}} \right)_{j - 1/2}^{n - 1} + \left( {\frac{7 - \alpha }{4}} \right)\left( {fv} \right)_{j - 1/2}^{n - 1} + \xi v_{j - 1/2}^{n - 1} \\ &\quad - \left( {\frac{1}{2} - \frac{\alpha }{4}} \right)\left( {u_{j - 1/2}^{n - 1} } \right)^{2} - \varepsilon \delta \left( {v^{2} } \right)_{j - 1/2}^{n - 1} \left( {v^{\prime}} \right)_{j - 1/2}^{n - 1} + s_{j - 1/2}^{n - 1}\\ &\quad + Nz_{j - 1/2}^{n - 1} + Kp_{j - 1/2}^{n - 1} - M\xi^{2} u_{j - 1/2}^{n - 1} \Bigg] \end{aligned}$$

(49)

$$\begin{aligned} \left[ {R_{2} } \right]_{j - 1/2}^{n - 1} &= - h_{j} \Bigg[\left( {1 + \frac{K}{2}} \right)\left( {p^{\prime}} \right)_{j - 1/2}^{n - 1} + \left( {\frac{7 - \alpha }{4}} \right)\left( {fp} \right)_{j - 1/2}^{n - 1} + \xi p_{j - 1/2}^{n - 1}\\ &\quad - \left( {\frac{1 - \alpha }{4}} \right)\left( {gu} \right)_{j - 1/2}^{n - 1} - KB\xi^{2} \left( {2g_{j - 1/2}^{n - 1} + v_{j - 1/2}^{n - 1} } \right)\Bigg] \end{aligned}$$

(50)

$$ \left[ {R_{3} } \right]_{j - 1/2}^{n - 1} = - h_{j} \left[ {\frac{1}{\Pr }\left( {1 + \frac{4}{3F}} \right)\left( {t^{\prime}} \right)_{j - 1/2}^{n - 1} + \frac{{\left( {7 - \alpha } \right)}}{4}\left( {ft} \right)_{j - 1/2}^{n - 1} + \xi t_{j - 1/2}^{n - 1} + \frac{\alpha }{4}\,\left( {us} \right)_{j - 1/2}^{n - 1} } \right] $$

(51)

$$ \left[ {R_{4} } \right]_{j - 1/2}^{n - 1} = - h_{j} \left[ {\frac{1}{Sc}\left( {m^{\prime}} \right)_{j - 1/2}^{n - 1} + \frac{{\left( {7 - \alpha } \right)}}{4}\left( {fm} \right)_{j - 1/2}^{n - 1} + \xi m_{j - 1/2}^{n - 1} + \frac{\alpha }{4}\,\left( {uz} \right)_{j - 1/2}^{n - 1} } \right] $$

(52)

The boundary conditions are:

$$ f_{0}^{n} = u_{0}^{n} = 0,\,\,\,\,g_{0}^{n} = 1,\,\,\,\,s_{0}^{n} = 1,\,\,\,\,\,m_{0}^{n} = 1,\,\,\,\,u_{J}^{n} = 0,\,\,\,\,v_{J}^{n} = 0,\,\,\,\,s_{J}^{n} = 0,\,\,\,m_{J}^{n} = 0\,. $$

(53)

Step 3: Quasilinearization of Non-linear Keller Algebraic Equations

Assuming $f_{j}^{n - 1} ,u_{j}^{n - 1} ,v_{j}^{n - 1} ,s_{j}^{n - 1} ,t_{j}^{n - 1}$ to be known for 0 ≤ j ≤ J, then Eqs. (39) to (47) constitute a system of 5 J + 5 equations for the solution of 5 J + 5 unknowns $f_{j}^{n} ,u_{j}^{n} ,v_{j}^{n} ,s_{j}^{n} ,t_{j}^{n}$, j = 0, 1, 2 …, J. This non-linear system of algebraic equations is linearized by means of Newton’s method as explained in [22, 43].

Step 4: Block-Tridiagonal Elimination of Linear Keller Algebraic Equations

The linearized system is solved by the block-elimination method owing to its block-tridiagonal structure. The block-tridiagonal structure generated consists of block matrices. The complete linearized system is formulated as a block matrix system, where each element in the coefficient matrix is a matrix itself, and this system is solved using the efficient Keller-box method. The numerical results are strongly influenced by the number of mesh points in both directions. After some trials in the η-direction (radial coordinate) a larger number of mesh points are selected whereas in the ξ-direction (tangential coordinate) significantly less mesh points are necessary. η_max has been set at 16 and this constitutes an adequately large value at which the prescribed boundary conditions are satisfied. ξ_max is set at 3.0 for the simulations. Mesh independence has been comfortably attained in the simulations. The numerical algorithm is executed in MATLAB on a PC. The method demonstrates excellent stability, convergence and consistency, as elaborated by Keller [43].