Skip to main content
SpringerLink
Log in

A Hybrid Computational Scheme with Convergence Analysis for the Dependent Rosenau-Hyman Equation of Arbitrary Order Via Caputo-Fabrizio Operator

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

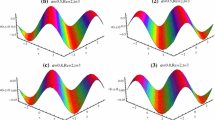
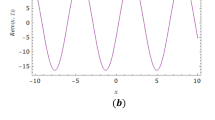
In this paper, a solution of the dependent Rosenau-Hyman (RH) equation is found by using a competent hybrid computational scheme q-homotopy analysis transform technique (q-HATT). The Liouville-Caputo fractional operator offers singularity in the kernel so fractional Caputo-Fabrizio operator with exponential non-singular kernel is chosen to describe memory effects well in analyzing solution. The q-HATT presents the solution in a convergent series at a large permissible domain. The convergence and uniqueness analysis of the time-fractional RH equation via q-HATT scheme is also presented. This scheme has an auxiliary parameter ħ which provides a fit way of handling convergence region. The given example confirms competency of q-HATT scheme. The behavior of solution by q-HATT for diverse orders of derivative is discussed by figures. The decreasing error between the successive approximations in the solution by q-HATT validates the convergence of acquired solution. The outcomes disclose that q-HATT scheme is reliable, attractive and also effective.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Availability of Data and Material

Data sharing is not applicable.

Abbreviations

\(t\) :

Time variable

\(x\) :

Space coordinate

\(\alpha \) :

Order of the fractional derivative

\(^{{CF}}\!{_{0} D }_{t}^{\alpha } f\left( t \right) \) :

Caputo Fabrizio

\(\alpha \) :

Order derivative of f(t)

\(M(\alpha )\) :

Normalization function

\(h\left(x,t\right)\) :

Source term

\({\mathbb{N}}\) :

Set of natural numbers

\(N\) :

Nonlinear operator

\(q\) :

Embedding parameter

\(n (\ge 1)\) :

Parameter

\(\psi \left( {x,t;q} \right)\) :

A real-valued function

\(\hbar \) :

Auxiliary parameter

\(H(x,t)\) :

Auxiliary function

\({\mathrm{u}}_{0}(x,t)\) :

Initial value

\(L\) :

Laplace transform operator

\(B\) :

Banach Space

\(T\) :

Nonlinear mapping from \(B\) to \(B\)

\({\mathbb{R}}\) :

Set of real numbers

References

  1. He, J.H.: Fractal Calculus and its geometrical explanation. Results Phys. 10, 272–276 (2018)

    Google Scholar 

  2. Kumar, S., Kumar, A., Momani, S., Aldhaifallah, M., Nisar, K.S.: Numerical solutions of nonlinear fractional model arising in the appearance of the strip patterns in two-dimensional systems. Adv. Differ. Equ. 2019, 413 (2019)

    Google Scholar 

  3. He, J.H.: A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 53(11), 3698–3718 (2014)

    MathSciNet  MATH  Google Scholar 

  4. Mohyud-Din, S.T., Yildirim, A.: An algorithm for solving the fractional vibration equation. Comput. Math. Model. 23, 228–237 (2012)

    MathSciNet  MATH  Google Scholar 

  5. Baskonus, H.M., Mekkaoui, T., Hammouch, Z., Bulut, H.: Active control of a chaotic fractional order economic system. Entropy 17(8), 5771–5783 (2015)

    Google Scholar 

  6. Al-Smadi, M., Freihat, A., Hammad, M.A., Momani, S., Arqub, O.A.: Analytical approximations of partial differential equations of fractional order with multistep approach. J. Comput. Theor. Nanosci. 13(11), 7793–7801 (2016)

    MATH  Google Scholar 

  7. Baskonus, H.M., Yel, G., Bulut, H.: Novel wave surfaces to the fractional Zakharov Kuznetsov-Benjamin-Bona-Mahony equation. AIP Conf. Proc. 1863(1), 560084 (2017)

    Google Scholar 

  8. Al-Smadi, M., Freihat, A., Arqub, O.A., Shawagfeh, N.: A novel multistep generalized differential transform method for solving fractional-order Lü chaotic and hyperchaotic systems. J. Comput. Anal. Appl. 19(4), 713–724 (2015)

    MathSciNet  MATH  Google Scholar 

  9. Gao, W., Yel, G., Baskonus, H.M., Cattani, C.: Complex solitons in the conformable (2+1) dimensional Ablowitz-Kaup-Newell-Segur equation. AIMS Math. 5(1), 507–521 (2019)

    MathSciNet  Google Scholar 

  10. Momani, S., Arqub, O.A., Freihat, A., Al-Smadi, M.: Analytical approximations for Fokker-Planck equations of fractional order in multistep schemes. Appl. Comput. Math. 15(3), 319–330 (2016)

    MathSciNet  MATH  Google Scholar 

  11. Prakash, A., Goyal, M., Gupta, S.: q-homotopy analysis method for fractional Bloch model arising in nuclear magnetic resonance via the Laplace transform. Ind. J. Phys. 94(4), 507–520 (2020)

    Google Scholar 

  12. Prakash, A., Goyal, M., Gupta, S.: Numerical simulation of space-fractional Helmholtz equation arising in Seismic wave propagation, imaging and inversion. Pramana 93(2), 28 (2019)

    Google Scholar 

  13. Goyal, M., Baskonus, H.M., Prakash, A.: An efficient technique for a time fractional model of lassa hemorrhagic fever spreading in pregnant women. Eur. Phys. J. Plus 134(10), 482 (2019)

    Google Scholar 

  14. Goyal, M., Baskonus, H.M., Prakash, A.: Regarding new positive, bounded and convergent numerical solution of nonlinear time fractional HIV/AIDS transmission model. Chaos Soliton. Fract. 139, 110096 (2020)

    MathSciNet  Google Scholar 

  15. Gao, W., Veeresha, P., Prakasha, D.G., Baskonus, H.M., Yel, G.: New approach for the model describing the deathly disease in pregnant women using Mittag-Leffler function. Chaos Soliton. Fract. 134, 109696 (2020)

    MathSciNet  Google Scholar 

  16. Goyal, M., Bhardwaj, V.K., Prakash, A.: Investigating new positive, bounded, and convergent numerical solution for the nonlinear time-dependent breast cancer dynamic competition model. Math. Method. Appl. Sci. 44(6), 4636–4653 (2021)

    MathSciNet  MATH  Google Scholar 

  17. Clarkson, P.A., Mansfield, E.L., Priestley, T.J.: Symmetries of a class of nonlinear third-order partial differential equations. Math. Comput. Model. 25(8–9), 195–212 (1997)

    MathSciNet  MATH  Google Scholar 

  18. Rosenau, P., Hyman, J.M.: Compactons: solitons with finite wavelength. Phys. Rev. Lett. 70(5), 564–567 (1993)

    MATH  Google Scholar 

  19. Bazeia, D., Das, A., Losano, L., Santos, M.J.: Traveling wave solutions of nonlinear partial differential equations. Appl. Math. Lett. 23(6), 681–686 (2010)

    MathSciNet  MATH  Google Scholar 

  20. Rus, F., Villatoro, F.R.: A repository of equations with cosine/sine compactons. Appl. Math. Comput. 215(5), 1838–1851 (2009)

    MathSciNet  MATH  Google Scholar 

  21. Caputo, M.: Elasticità e dissipazione. Zani-Chelli, Bologna (1969)

    Google Scholar 

  22. Ahmad, H., Akgül, A., Khan, T.A., Ahmad, I., Stanimirović, P.S., Chu, Y.-M.: New perspective on the conventional solutions of the nonlinear time-fractional partial differential equations. Complexity 2020, 8829017 (2020)

    MATH  Google Scholar 

  23. Ahmad, H., Khan, T.A., Ahmad, I., Stanimirović, P.S., Chu, Y.-M.: A new analyzing technique for nonlinear time fractional Cauchy reaction-diffusion model equations. Results Phys. 19, 103462 (2020)

    Google Scholar 

  24. Molliq, R.Y., Noorani, M.S.M.: Solving the fractional Rosenau-Hyman equation via variational iteration method and homotopy perturbation method. Int. J. Differ. Equ. 2012, 472030 (2012)

    MathSciNet  MATH  Google Scholar 

  25. Gupta, S., Goyal, M., Prakash, A.: Numerical treatment of Newell–Whitehead–Segel equation. TWMS J. App. Eng. Math. 10(2), 312–320 (2020)

    Google Scholar 

  26. Singh, J., Kumar, D., Swaroop, R., Kumar, S.: An efficient computational approach for time-fractional Rosenau-Hyman equation. Neural. Comput. Appl. 30(10), 3063–3070 (2018)

    Google Scholar 

  27. Iyiola, O.S., Ojo, G.O., Mmaduabuchi, O.: The fractional Rosenau-Hyman model and its approximate solution. Alex. Eng. J. 55(2), 1655–1659 (2016)

    Google Scholar 

  28. Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 1(2), 73–85 (2015)

    Google Scholar 

  29. Atangana, A., Alkahtani, B.S.T.: New model of groundwater flowing within a confine aquifer: application of Caputo-Fabrizio derivative. Arab. J. Geosci. 9(1), 8 (2016)

    Google Scholar 

  30. Atangana, A.: On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 273(C), 948–956 (2016)

    MathSciNet  MATH  Google Scholar 

  31. Goufo, E.F.D., Pene, M.K., Mwambakana, J.: Duplication in a model of rock fracture with fractional derivative without singular kernel. Open Math. 13(1), 839–846 (2015)

    MathSciNet  MATH  Google Scholar 

  32. Yépez-Martínez, H., Gómez-Aguilar, J.F.: Laplace variational iteration method for modified fractional derivatives with non-singular kernel. J. Appl. Comput. Mech. 6(3), 684–698 (2020)

    Google Scholar 

  33. Atangana, A., Baleanu, D.: New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Therm. Sci. 20(2), 763–769 (2016)

    Google Scholar 

  34. Abdulhameed, M., Vieru, D., Roslan, R.: Modeling electro-magnetohydrodynamic thermo-fluidic transport of biofluids with new trend of fractional derivative without singular kernel. Physica A: Stat. Mech. Appl. 484, 233–252 (2017)

    Google Scholar 

  35. Atangana, A., Koca, I.: On the new fractional derivative and application to nonlinear Baggs and Freedman model. J. Nonlinear Sci. Appl. 9(5), 2467–2480 (2016)

    MathSciNet  MATH  Google Scholar 

  36. Gómez-Aguilar, J.F.: Space–time fractional diffusion equation using a derivative with nonsingular and regular kernel. Physica A: Stat. Mech. Appl. 465, 562–572 (2017)

    MathSciNet  MATH  Google Scholar 

  37. Al-Salti, N., Karimov, E.T., Sadarangani, K.: On a differential equation with Caputo-Fabrizio fractional derivative of order 1 < β ≤ 2 and application to mass-spring-damper system. Progr. Fract. Differ. Appl. 2(4), 257–263 (2016)

    Google Scholar 

  38. Feng, G., Xiao-Jun, Y.: Fractional Maxwell fluid with fractional derivative without singular kernel. Therm. Sci. 20(3), 871–877 (2016)

    Google Scholar 

  39. Liao, S.J.: On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147(2), 499–513 (2004)

    MathSciNet  MATH  Google Scholar 

  40. El-Tawil, M.A., Huseen, S.N.: The q-homotopy analysis method (q-HAM). Int. J. Appl. Math. Mech. 8(15), 51–75 (2012)

    Google Scholar 

  41. El-Tawil, M.A., Huseen, S.N.: On convergence of the q-homotopy analysis method. Int. J. Contemp. Math. Sci. 8(10), 481–497 (2013)

    MathSciNet  Google Scholar 

  42. Prakash, A., Veeresha, P., Prakasha, D.G., Goyal, M.: A homotopy technique for a fractional order multidimensional telegraph equation via the Laplace transform. Eur. Phys. J. Plus 134(1), 19 (2019)

    Google Scholar 

  43. Prakash, A., Veeresha, P., Prakasha, D.G., Goyal, M.: A new efficient technique for solving fractional coupled Navier-Stokes equations using q-homotopy analysis transform method. Pramana 93(1), 6 (2019)

    Google Scholar 

  44. Prakash, A., Goyal, M., Baskonus, H.M., Gupta, S.: A reliable hybrid numerical method for a time dependent vibration model of arbitrary order. AIMS Math. 5(2), 979–1000 (2020)

    MathSciNet  Google Scholar 

  45. Srivastava, H.M., Kumar, D., Singh, J.: An efficient analytical technique for fractional model of vibration equation. Appl. Math. Model. 45, 192–204 (2017)

    MathSciNet  MATH  Google Scholar 

  46. Kumar, D., Agarwal, R.P., Singh, J.: A modified numerical scheme and convergence analysis for fractional model of Lienard’s equation. J. Comput. Appl. Math. 339, 405–413 (2018)

    MathSciNet  MATH  Google Scholar 

  47. Prakash, A., Goyal, M., Gupta, S.: Fractional variational iteration method for solving time fractional Newell-Whitehead-Segel equation. Nonlinear Eng. 8(1), 164–171 (2019)

    Google Scholar 

  48. Goyal, M., Prakash, A., Gupta, S.: Numerical simulation for time-fractional nonlinear coupled dynamical model of romantic and interpersonal relationships. Pramana 92(5), 82 (2019)

    Google Scholar 

  49. Wang, F., Zhang, J., Ahmad, I., Farooq, A., Ahmad, H.: A novel meshfree strategy for a viscous wave equation with variable coefficients. Front. Phys. 9, 701512 (2021)

    Google Scholar 

  50. Prakash, A., Goyal, M., Gupta, S.: A reliable algorithm for fractional Bloch model arising in magnetic resonance imaging. Pramana 92(2), 18 (2019)

    Google Scholar 

  51. Goyal, M., Baskonus, H.M.: A reliable solution of arbitrary order nonlinear Hunter-Saxton equation with time dependent derivative in Liouville-Caputo sense. Int. J. Appl. Comput. Math 7(4), 125 (2021)

    MathSciNet  Google Scholar 

  52. Goyal, M., Prakash, A., Gupta, S.: An efficient perturbation sumudu transform technique for the time-fractional vibration equation with a memory dependent fractional derivative in Liouville-Caputo Sense. Int. J. Appl. Comput. Math 7(4), 156 (2021)

    MathSciNet  Google Scholar 

  53. Prakash, A., Kaur, H.: Numerical solution for fractional model of Fokker-Planck equation by using q-HATM. Chaos Soliton. Fract. 105(C), 99–110 (2017)

    MathSciNet  MATH  Google Scholar 

  54. Kumar, D., Singh, J., Baleanu, D.: A new numerical algorithm for fractional Fitzhugh-Nagumo equation arising in transmission of nerve impulses. Nonlinear Dyn. 91(8), 307–317 (2018)

    MathSciNet  MATH  Google Scholar 

  55. Goyal, M., Prakash, A., Baleanu, D.: An efficient hybrid computational technique for the time dependent Lane-Emden equation of arbitrary order. J. Ocean Eng. Sci. (2021). https://doi.org/10.1016/j.joes.2021.07.004

    Article  Google Scholar 

  56. Veeresha, P., Prakasha, D.G., Baleanu, D.: An efficient numerical technique for the nonlinear fractional Kolmogorov–Petrovskii–Piskunov equation. Mathematics 7(3), 265 (2019)

    Google Scholar 

  57. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, pp. 1–540. Elsevier Science, New York (2006)

    MATH  Google Scholar 

  58. Argyros, I.K.: Convergence and applications of Newton type iterations. Springer Science and Business Media, Berlin (2008)

    MATH  Google Scholar 

  59. Magreñán, Á.A.: Some fourth order multipoint methods for solving equations. Appl. Math. Comput. 248, 215–224 (2014)

    MathSciNet  Google Scholar 

  60. Odibat, Z.M., Shawagfeh, N.T.: Generalized Taylor’s formula. Appl. Math. Comput. 186(1), 286–293 (2007)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

Authors are appreciative to referees for valuable comments.

Funding

No funding was granted to conduct this research work.

Author information

Authors and Affiliations

  1. Department of Mathematics, Institute of Applied Sciences and Humanities, GLA University, Mathura, India

    Shivangi Gupta & Manish Goyal

  2. Department of Mathematics, National Institute of Technology, Kurukshetra, India

    Amit Prakash

Authors
  1. Shivangi Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Manish Goyal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Amit Prakash
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

SG conceptualized and investigated the results. MG visualized the solution of Rosenau-Hyman model, supervised the methodology used and was major contributor in writing manuscript. AP validated the solution. All the authors read the final manuscript and approved.

Corresponding author

Correspondence to Manish Goyal.

Ethics declarations

Conflict of interest

The authors have no conflicts of interest/competing interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gupta, S., Goyal, M. & Prakash, A. A Hybrid Computational Scheme with Convergence Analysis for the Dependent Rosenau-Hyman Equation of Arbitrary Order Via Caputo-Fabrizio Operator. Int. J. Appl. Comput. Math 7, 259 (2021). https://doi.org/10.1007/s40819-021-01182-4

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-021-01182-4

Keywords

Search

Navigation