Skip to main content
SpringerLink
Log in

On the Convergence of Harmonic Mean Newton Method Under \(\omega \) Continuity Condition in Banach Spaces

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

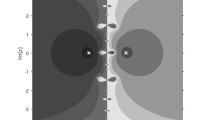
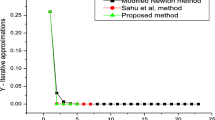
We present the local and semi-local convergence analysis of the cubically convergent harmonic mean Newton method (HNM) for obtaining solutions of Banach space valued nonlinear operator equations. The significance of this work is that the convergence study needs only the condition that the first-order Fréchet derivative obeys \(\omega \) continuity. Moreover, we avoid using higher order derivatives, which do not occur in this scheme. The dynamical properties of the scheme are also explored using basins of attraction technique for various complex polynomials. Finally, the convergence radii for benchmark numerical problems are computed applying our analytical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Agarwal, P., Agarwal, R.P., Ruzhansky, M.: Special Functions and Analysis of Differential Equations. Chapman and Hall/CRC, Boca Raton (2020). https://doi.org/10.1201/9780429320026

  2. Agarwal, P., Filali, D., Akram, M., Dilshad, M.: Convergence analysis of a three-step iterative algorithm for generalized set-valued mixed-ordered variational inclusion problem. Symmetry 13, 444 (2021). https://doi.org/10.3390/sym13030444

    Article  Google Scholar 

  3. Amat, S., Argyros, I.K., Busquier, S., Hernández-Verón, M.A., Martínez, E.: On the local convergence study for an efficient k-step iterative method. J. Comput. Appl. Math. 343, 753–761 (2018)

    Article  MathSciNet  Google Scholar 

  4. Argyros, I.K.: Convergence and Application of Newton-type Iterations. Springer, Berlin (2008)

    MATH  Google Scholar 

  5. Argyros, I.K.: On the semilocal convergence of a fast two-step Newton method. Rev. Colombiana de Mat. 42(1), 15–24 (2008)

    MathSciNet  MATH  Google Scholar 

  6. Argyros, I.K., Cho, Y.J., Hilout, S.: Numerical Methods for Equations and its Applications. Taylor and Francis, CRC Press, New York (2012)

    Book  Google Scholar 

  7. Argyros, I.K., Cho, Y.J., George, S.: Local convergence for some third order iterative methods under weak conditions. J. Korean Soc. Math. 53(4), 781–793 (2016)

    Article  MathSciNet  Google Scholar 

  8. Argyros, I.K., George, S.: Local convergence of deformed Halley method in Banach space under Hölder continuity conditions. J. Nonlinear Sci. Appl. 8, 246–254 (2015)

    Article  MathSciNet  Google Scholar 

  9. Argyros, I.K., George, S., Magreñán, Á.A.: Local convergence for multi-point-parametric Chebyshev-Halley-type methods of higher convergence order. J. Comput. Appl. Math. 282, 215–224 (2015)

    Article  MathSciNet  Google Scholar 

  10. Argyros, I.K., George, S.: Local convergence of modified Halley-like methods with less computation of inversion. Novi Sad J. Math. 45(2), 47–58 (2015)

    Article  MathSciNet  Google Scholar 

  11. Argyros, I.K., George, S.: Local convergence for an almost sixth order method for solving equations under weak conditions. SeMA J. 75(2), 163–171 (2017)

    Article  MathSciNet  Google Scholar 

  12. Argyros, I.K., George, S.: On the complexity of extending the convergence region for Traub’s method. J. Complex. 56, 101423 (2020). https://doi.org/10.1016/j.jco.2019.101423

  13. Argyros, I. K., González, D.: Local convergence for an improved Jarratt-type method in Banach space. Int. J. Interact. Multimed. Artif. Intell. 3(Special Issue on Teaching Mathematics Using New and Classic Tools), 20–25 (2015)

  14. Argyros, I.K., Hilout, S.: Computational Methods in Nonlinear Analysis. World Scientific Publishing House, New Jersey (2013)

    Book  Google Scholar 

  15. Argyros, I.K., Hilout, S.: On the local convergence of fast two-step Newton-like methods for solving nonlinear equations. J. Comput. Appl. Math. 245, 1–9 (2013)

    Article  MathSciNet  Google Scholar 

  16. Argyros, I.K., Magreñán, Á.A.: A study on the local convergence and the dynamics of Chebyshev-Halley-type methods free from second derivative. Numer. Algor. 71(1), 1–23 (2015)

    Article  MathSciNet  Google Scholar 

  17. Argyros, I.K., Sharma, D., Parhi, S.K.: On the local convergence of Weerakoon-Fernando method with \(\omega \) continuous derivative in Banach spaces. SeMA J. 77(3), 291–304 (2020). https://doi.org/10.1007/s40324-020-00217-y

    Article  MathSciNet  MATH  Google Scholar 

  18. Cordero, A., Ezquerro, J.A., Hernandez-Veron, M.A.: On the local convergence of a fifth-order iterative method in Banach spaces. Appl. Math. Comput. 251, 396–403 (2014)

    MathSciNet  MATH  Google Scholar 

  19. Cordero, A., Hueso, J.L., Martínez, E., Toregrossa, J.R.: Increasing the convergence order of an iterative method for nonlinear systems. Appl. Math. Lett. 25, 2369–2374 (2012)

    Article  MathSciNet  Google Scholar 

  20. Cordero, A., Martínez, E., Toregrossa, J.R.: Iterative methods of order four and five for systems of nonlinear equations. J. Comput. Appl. Math. 231, 541–551 (2012)

    Article  MathSciNet  Google Scholar 

  21. Hassan, S., De la Sen, M., Agarwal, P., Ali, Q., Hussain, A.: A New Faster Iterative Scheme for Numerical Fixed Points Estimation of Suzuki’s Generalized Nonexpansive Mappings. Mathematical Problems in Engineering 2020, Article ID: 3863819 (2020). https://doi.org/10.1155/2020/3863819

  22. Kanwar, M.V., Kukreja, V.K., Singh, S.: On some third-order iterative methods for solving nonlinear equations. Appl. Math. Comput. 171(1), 272–280 (2005)

    MathSciNet  MATH  Google Scholar 

  23. Kou, J., Li, Y., Wang, X.: A composite fourth-order iterative method for solving non-linear equations. Appl. Math. Comput. 184, 471–475 (2007)

    MathSciNet  MATH  Google Scholar 

  24. Martínez, E., Singh, S., Hueso, J.L., Gupta, D.K.: Enlarging the convergence domain in local convergence studies for iterative methods in Banach spaces. Appl. Math. Comput. 281, 252–265 (2016)

    MathSciNet  MATH  Google Scholar 

  25. Neta, B., Chun, C., Scott, M.: Basins of attraction for optimal eighth order methods to find simple roots of nonlinear equations. Appl. Math. Comput. 227, 567–592 (2014)

    MathSciNet  MATH  Google Scholar 

  26. Nishani, H.P.S., Weerakoon, S., Fernando, T.G.I., Liyanag, M.: Weerakoon-Fernando Method with accelerated third-order convergence for systems of nonlinear equations. Int. J. Math. Modell. Numer. Optim. 8(3), 287–304 (2018)

    Google Scholar 

  27. Özban, A.Y.: Some new variants of Newton’s method. Appl. Math. Lett. 17, 677–682 (2004)

    Article  MathSciNet  Google Scholar 

  28. Parhi, S.K., Gupta, D.K.: A sixth order method for nonlinear equations. Appl. Math. Comput. 203(1), 50–55 (2008)

    MathSciNet  MATH  Google Scholar 

  29. Parhi, S.K., Gupta, D.K.: Convergence of a third order method for fixed points in Banach spaces. Numer. Algorithm 60, 419–434 (2012)

    Article  MathSciNet  Google Scholar 

  30. Petković, M.S., Neta, B., Petković, L., D\(\tilde{{z}}\)nić, D.: Multipoint methods for solving nonlinear equations. Elsevier, Amsterdam (2013)

  31. Potra, F.A., Ptak, V.: Nondiscrete Induction and Iterative Processes. Research Notes in Mathematics, Pitman Publ, Boston (1984)

    MATH  Google Scholar 

  32. Rall, L.B.: Computational Solution of Nonlinear Operator Equations. Robert E. Krieger, New York (1979)

    MATH  Google Scholar 

  33. Ren, H., Wu, Q., Bi, W.: New variants of Jarratt method with sixth-order convergence. Numer. Algorithm 52(4), 585–603 (2009)

    Article  MathSciNet  Google Scholar 

  34. Ruzhansky, M., Cho, Y.J., Agarwal, P., Area, I.: Advances in Real and Complex Analysis with Applications (Trends in Mathematics). Birkhäuser, Basel (2017)

    Google Scholar 

  35. Shah, N.A., Agarwal, P., Chung, J.D., El-Zahar, E.R., Hamed, Y.S.: Analysis of optical solitons for nonlinear Schrödinger equation with detuning term by iterative transform method. Symmetry (2020). https://doi.org/10.3390/sym12111850

    Article  Google Scholar 

  36. Scott, M., Neta, B., Chun, C.: Basin attractors for various methods. Appl. Math. Comput. 218, 2584–2599 (2011)

    MathSciNet  MATH  Google Scholar 

  37. Sharma, D., Parhi, S.K.: Extending the Applicability of a Newton-Simpson-Like Method. Int. J. Appl. Comput. Math. 6, 79 (2020). https://doi.org/10.1007/s40819-020-00832-3

    Article  MathSciNet  MATH  Google Scholar 

  38. Sharma, J.R., Argyros, I.K.: Local convergence of a Newton-Traub composition in Banach spaces. SeMA J. 75(1), 57–68 (2017)

    Article  MathSciNet  Google Scholar 

  39. Singh, S., Gupta, D.K., Badoni, R.P., Martínez, E., Hueso, J.L.: Local convergence of a parameter based iteration with Hölder continuous derivative in Banach spaces. Calcolo 54(2), 527–539 (2017)

    Article  MathSciNet  Google Scholar 

  40. Sunarto, A., Agarwal, P., Chew, J.V.L., Aruchunan, E.: Iterative method for solving one-dimensional fractional mathematical physics model via quarter-sweep and PAOR. Adv. Differ. Equ. (2021). https://doi.org/10.1186/s13662-021-03310-2

    Article  MathSciNet  Google Scholar 

  41. Traub, J.F.: Iterative Methods for Solution of Equations. Prentice-Hal, Englewood Cliffs (1964)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Cameron University, Lawton, OK, 73505, USA

    Ioannis K. Argyros

  2. Department of Mathematics, Kalinga Institute of Industrial Technology, Bhubaneswar, Odisha, 751024, India

    Debasis Sharma

  3. Department of Computer Science, University of Oklahoma, Norman, OK, 73071, USA

    Christopher I. Argyros

  4. Department of Mathematics, Fakir Mohan University, Odisha, 756020, India

    Sanjaya Kumar Parhi

  5. Department of Mathematics, IIIT Bhubaneswar, Odisha, 751003, India

    Shanta Kumari Sunanda

Authors
  1. Ioannis K. Argyros
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Debasis Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Christopher I. Argyros
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sanjaya Kumar Parhi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shanta Kumari Sunanda
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Debasis Sharma.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Argyros, I.K., Sharma, D., Argyros, C.I. et al. On the Convergence of Harmonic Mean Newton Method Under \(\omega \) Continuity Condition in Banach Spaces. Int. J. Appl. Comput. Math 7, 219 (2021). https://doi.org/10.1007/s40819-021-01159-3

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-021-01159-3

Keywords

Mathematics Subject Classification

Search

Navigation