Shape-Preserving Rational Interpolation Scheme for Regular Surface Data

Abstract

Rational shape-preserving interpolation schemes are developed for positive and monotone regular surface data. The data points are arranged over the rectangular grid. A Bézier like bivariate rational cubic function is constructed. This Bézier like bivariate rational interpolant involves eight free parameters in each rectangular patch. Data dependent constraints are developed on four of these free parameters to preserve the positive and monotone shape of regular surface data. The rest of the parameters are used for shape refinement. The scheme is further extended to more general constraints when data is bounded below by another surface and it desired that Bézier like bivariate rational interpolant must obey the aforesaid restriction.

Introduction

Rational functions have replaced the ordinary polynomials in shape-preserving environment due to their ability to modify the shape of curves and surfaces via free parameters, without changing the data. Convexity, monotonicity and positivity are the basic shapes of data. Positivity should be maintained in graphical representation of amount of rainfall, probability distribution [4], resistance offered by an electric circuit, area, population growth, and density; the entities which are always positive. The non-negative graphical display of solution of partial differential equations arising from gas dynamics and kinetic flux splitting schemes are physically meaningless [7]. Monotone data arises in dose-response curves and surfaces in biochemistry and pharmacology [2], approximations of couples and quasi couples in statistics [2], empirical option pricing model in finance [2], approximation of potential functions in physical and chemical systems [2], in specifications of digital to analog converters (DACs) and sensors [12], erythrocyte sedimentation rate (E.S.R.) level in cancer patients [12], blood uric acid level in the patients suffering from gout [12], data generated from stress and strain of a material.

The problem of positivity and monotonicity preserving interpolation has gained attention by a number of authors in the recent past. Brodlie and Butt [3] presented a piecewise cubic interpolating scheme for positive 2D data. In a particular interval where shape of the data was lost, the author reduced the length of interval by inserting an extra knot in a manner that the shape of the data was preserved. Farouki et al. [8] introduced $G^{1}$ and $G^{2}$ PH quintic splines with tension parameters to preserve the shape of planar data. The authors in [8] found $G^{1}$ PH quintic spline scheme computationally more economical than the $G^{2}$ PH quintic splines. Goodman et al. [9] presented two schemes for the graphical display of data subject to linear constraints. The first scheme adopted the method of scaling weights and the second scheme refers to insert some extra point to preserve the shape of data. Goodman [10] provided a comprehensive review of the existing shape-preserving schemes for curve data. The authors in [13] used four parameters family of rational functions for shape-preserving positive curve and surface data. The authors in [17] used two parameters family of rational functions for positivity-preserving curve data interpolation. In [13] and [17], constraints were developed on the free parameters involved in description rational function to preserve the positive shape of data. Lamberti and Manni [14] used parametric cubic Hermite interpolant for the shape-preserving scheme. The constraints were developed on subinterval’s length for the shape preservation. The first order derivatives at the knots were estimated by a tri-diagonal system of equations which assured $C^{2}$ continuity at the knots. Wang and Tan [20] constructed a $C^{2}$ piecewise rational quartic spline with two free parameters to preserve the shape of 2D monotone data. The constraints were derived on the derivatives at the knots.

Brodlie et al. [4] addressed the problem of surface data interpolation subject to simple linear constraints. They constructed a piecewise bi-cubic function f(x, y) from data on a rectangular grid, such that f(x, y) is positive. Sufficient conditions for positivity were derived in terms of the first order partial derivatives and mixed partial derivatives at the grid points. The problem of positivity was generalized to the case of linearly constrained interpolation, where it was required that f(x, y) lie between bounds which were linear functions of x and y. Schmidt [19] provided the solution of problem of shape-preserving $C^{1}$ interpolation of data sets given on a rectangular grids. Using special rational bi-quadratic splines, criterion were derived which were sufficient for the positivity, monotonicity and convexity preservation of data.

Beatson and Ziegler [1] interpolated monotone data defined on a rectangular grid with a $C^{1}$ monotone quadratic spline. They derived necessary and sufficient conditions on functional and derivative values to preserve the monotonicity of data. Carlson and Fritsch [5] extended their result of monotone univariate interpolation to monotone bivariate interpolation for data arranged on a rectangular grid. The interpolating function was defined in terms of the first order partial derivatives and twists at all grid points. Necessary and sufficient conditions on these derivatives were derived such that the resulting bi-cubic polynomial is monotone on a single rectangular element. Delgado and Peña [6] investigated the monotonicity of rational Bézier surfaces on rectangular and triangular grids. The authors in [6] proved that rational Bézier surfaces on rectangular and triangular grids are not monotonicity-preserving. Han and Schumaker [11] first converted the given scattered data into a rectangular grid by drawing horizontal and vertical lines through data sites. The functional values at the new data sites were calculated by interpolating the original scattered data. The drawback of the method was that a system of N-scattered data points turned to $N^{2}$-rectangles and some of the rectangles were very small in one or both directions. The authors in [15] and [16] discussed the problem of positive and monotone surface data interpolation respectively.

The theory in this paper presents interpolation schemes to preserve the positive, constrained and monotone shape of regular surface data. Ordinary polynomials guarantee smoothness for high degree but do not preserve the shape characteristic of data due to undesired oscillation they produce. This phenomenon is demonstrated in Figs. 1, 12 and 17; where the bi-cubic Hermite spline although $C^{1}$ but does not preserve the positive, constrained and monotone shapes of data respectively. The solutions of these problems are the interpolation schemes proposed in this paper. A comparison of the shape-preserving schemes proposed in this research paper with the existing shape-preserving schemes is as follows:

• In [4], the constraints were derived on first order partial derivatives and mixed partial derivatives at the grid points to preserve the positive shape of 3D data. Thus the derivative values at the data sites were fixed and the positivity-preserving scheme [4] was not applicable to the data with specified values of derivatives at the data sites. The positivity-preserving scheme developed in this research paper has established constraints on parameters to preserve the positive shape of 3D data. Therefore, it can be easily used to preserve the positive shape of 3D data with specified values of derivatives at the data sites.

• In [1] and [5], the necessary and sufficient conditions were derived on derivatives values at grid points to preserve the monotone shape of the 3D data. Thus, the monotonicity-preserving schemes [1] and [5] were not applicable to data with derivatives. The monotonicity-preserving scheme proposed in this research paper can preserve the monotonicity of data comprised of functional values as well as data comprised of functional values and derivatives.

• In [3, 14], the length of the subinterval was constrained to preserve the shape of positive 2D data. The shape-preserving schemes developed in this research paper do not need data modification.

• The shape-preserving schemes [1, 4, 5] do not provide opportunity to the user to refine the shape of interpolated surface without changing the data. The shape-preserving schemes developed in this research paper provide four degrees of freedom (in the form of four free parameters) in each rectangular patch. The user can play with these parameters to achieve the desired smoothness for the given data set. However, the numerical experiments suggest that for very small value of these free parameters, tension effect will be produced. The values of these parameters should be greater than 0.5 to obtain a smooth surface.

• It has more degrees of freedom than [12].

The remainder of the paper is organized as follows. In “Bivariate Rational Cubic Function” section, a bivariate rational cubic interpolating function (extension of rational cubic function [18] with four free parameters) is developed. “Positivity-preserving interpolation by bivariate rational cubic function”, “Range Restricted Interpolation by Bivariate Rational Cubic Function” and “Monotonicity-Preserving Interpolation by Bivariate Rational Cubic Function” sections discuss the problem of positive, range restricted and monotone data interpolation respectively. “Conclusion” section concludes the paper.

Bivariate Rational Cubic Function

In this section a bivariate rational cubic interpolating scheme is developed to interpolate the data arranged over the rectangular grid.

Let $\left\{ {\left( {x_i ,y_j ,F_{i,j} } \right) : i=1,2,3,\ldots ,m; j=1,2,3,\ldots ,n} \right\}$ be the given set of data points arranged over the rectangular grid. The interpolation of boundary curves and their blending by rational cubic function [18] leads to the following bivariate rational cubic interpolating function over each rectangular patch $I_{i,j} =\left[ {x_i ,x_{i+1} } \right] \times \left[ {y_j ,y_{j+1} } \right]$.

$$\begin{aligned} S\left( {x, y} \right) =\frac{\sum \limits _{i=0}^3 {\left( {1-\phi } \right) ^{3-i}\phi ^{i}A_i}}{\hat{{q}}_{i,j} \left( \phi \right) }, \end{aligned}$$

(1)

where

$$\begin{aligned} A_0= & {} \hat{{\alpha }}_{i,j} S\left( {x,y_j } \right) , \quad A_1 =\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) S\left( {x,y_j } \right) +\hat{{\alpha }}_{i,j} \hat{{h}}_j S_y \left( {x,y_j } \right) , \nonumber \\ A_2= & {} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) S\left( {x,y_{j+1} } \right) -\hat{{\delta }}_{i,j} \hat{{h}}_j S_y \left( {x,y_{j+1} } \right) , \quad \nonumber \\ A_3= & {} \hat{{\delta }}_{i,j} S\left( {x,y_{j+1} } \right) ,\nonumber \\ \hat{{q}}_{i,j} \left( \phi \right)= & {} \hat{{\alpha }}_{i,j} \left( {1-\phi } \right) ^{2}+\hat{{\beta }}_{i,j} \left( {1-\phi } \right) ^{2}\phi +\hat{{\gamma }}_{i,j} \left( {1-\phi } \right) \phi ^{2}+\hat{{\delta }}_{i,j} \phi ^{2}.\nonumber \\&\qquad \qquad \quad S\left( {x, y_j } \right) =\frac{\sum \limits _{i=0}^3 {\left( {1-\theta } \right) ^{3-i}\theta ^{i}B_i } }{q_{i,j} \left( \theta \right) }, \end{aligned}$$

(2)

where

$$\begin{aligned} B_0= & {} \alpha _{i,j} F_{i,j} , \; B_1 =\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j} +\alpha _{i,j} h_i F_{i.j}^x , \nonumber \\ B_2= & {} \left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}-\delta _{i,j} h_i F_{i+1.j}^x , \; B_3 =\delta _{i,j} F_{i+1,j} ,\nonumber \\ q_{i,j} \left( \theta \right)= & {} \alpha _{i,j} \left( {1-\theta } \right) ^{2}+\beta _{i,j} \left( {1-\theta } \right) ^{2}\theta +\gamma _{i,j} \left( {1-\theta } \right) \theta ^{2}+\delta _{i,j} \theta ^{2}.\nonumber \\&\qquad \qquad S_y \left( {x, y_j } \right) =\frac{\sum \limits _{i=0}^3 {\left( {1-\theta } \right) ^{3-i}\theta ^{i}C_i } }{q_{i,j} \left( \theta \right) }, \end{aligned}$$

(3)

where

$$\begin{aligned} C_0= & {} \alpha _{i,j} F_{i,j}^y , \quad C_1 =\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y +\alpha _{i,j} h_i F_{i.j}^{xy} , \\ C_2= & {} \left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y-\delta _{i,j} h_i F_{i+1.j}^{xy} , \quad C_3 =\delta _{i,j} F_{i+1,j}^y . \end{aligned}$$

$S\left( {x, y_{j+1} } \right)$ and $S_y \left( {x, y_{j+1} } \right)$ are obtained by replacing j by $j+1$ in (2) and (3). Here $\theta$ and $h_i$ are normalized variable and increment along x-axis expressed mathematically as $\theta =\frac{x-x_i }{h_i }\left( {0\le \theta \le 1} \right)$, $h_i =x_{i+1} -x_i$. Similarly for y-axis, $\phi =\frac{y-y_j }{\hat{{h}}_j }$, $\hat{{h}}_j =y_{j+1} -y_j$, $0\le \phi \le 1$. $\alpha _{i,j}$,$\beta _{i,j}$, $\gamma _{i,j}$ and $\delta _{i,j}$ are the free parameters along x-axis. Similarly, $\hat{{\alpha }}_{i,j}$, $\hat{{\beta }}_{i,j}$, $\hat{{\gamma }}_{i,j}$ and $\hat{{\delta }}_{i,j}$ are the free parameters along y-axis. The elements of set $\left\{ {F_{k,l}^x , F_{k,l}^y , F_{k,l}^{xy} : k=i,i+1; l=j,j+1} \right\}$ are the partial derivatives at four corners of $\left( {i,j} \right)$ th-patch. The bivariate rational cubic function (1) has the following properties:

$$\begin{aligned} S\left( {x_i , y_j } \right) =F_{i,j} , \; S_x \left( {x_i , y_j } \right) =F_{i,j}^x , \; S_y \left( {x_i , y_j } \right) =F_{i,j}^y , \; S_{xy} \left( {x_i , y_j } \right) =F_{i,j}^{xy} . \end{aligned}$$

$S\left( {x, y} \right)$ has freedom of parameters $\alpha _{i,j}$,$\beta _{i,j}$, $\gamma _{i,j}$, $\delta _{i,j}$, $\hat{{\alpha }}_{i,j}$, $\hat{{\beta }}_{i,j}$, $\hat{{\gamma }}_{i,j}$ and $\hat{{\delta }}_{i,j}$ in each rectangular patch $I_{i,j} =\left[ {x_i ,x_{i+1} } \right] \times \left[ {y_j ,y_{j+1} } \right]$. It is interesting to mention that the following values of free parameters:

$$\begin{aligned} \hat{{\alpha }}_{i,j} =\hat{{\delta }}_{i,j} =\alpha _{i,j} =\delta _{i,j} =1\quad \hbox { and }\quad \beta _{i,j} =\gamma _{i,j} =\hat{{\beta }}_{i,j} =\hat{{\gamma }}_{i,j} =2; \end{aligned}$$

reduce the bivariate rational interpolant (1) to standard bi-cubic Hermite spline.

Positivity-Preserving Interpolation by Bivariate Rational Cubic Function

In this section simple sufficient data dependent constraints are developed on free parameters in description of bivariate rational function to interpolate the positive regular surface data as positive surface.

Let $\left\{ {\left( {x_i ,y_j ,F_{i,j} } \right) : i=1,2,3,\ldots ,m; j=1,2,3,\ldots ,n} \right\}$ be the given set of positive data arranged over the rectangular grid i.e.

$$\begin{aligned} F_{i,j} >0, \quad \forall i,j. \end{aligned}$$

(4)

The bivariate rational cubic function can be expressed in the following Bernstein-Bézier form:

$$\begin{aligned} S\left( {x, y} \right) =\sum _{k=0}^3 {\sum _{l=0}^3 {B_k^3 \left( \theta \right) B_l^3 \left( \phi \right) c_{k,l} } } , \end{aligned}$$

(5)

where the control points $c_{k,l}$, $k,l=0,1,2,3$ are:

$$\begin{aligned} c_{0,0}= & {} F_{i,j} , \; c_{0,1} \!=\!\left\{ {F_{i,j} \!+\!\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i,j}^y }{\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} }} \right\} , \quad c_{0,2} \!=\!\left\{ {F_{i,j+1} -\frac{\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i,j+1}^y }{\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} }} \right\} , \quad c_{0,3} =F_{i,j+1} ,\\ c_{1,0}= & {} \left\{ {F_{i,j} +\frac{\alpha _{i,j} h_i F_{i,j}^x }{\alpha _{i,j} +\beta _{i,j} }} \right\} , \\ c_{1,1}= & {} \left\{ {F_{i,j} +\frac{\alpha _{i,j} h_i F_{i,j}^x }{\alpha _{i,j} +\beta _{i,j} }} \right\} +\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j }{\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} }\left\{ {F_{i,j}^y +\frac{\alpha _{i,j} h_i F_{i,j}^{xy} }{\alpha _{i,j} +\beta _{i,j} }} \right\} ,\\ c_{1,2}= & {} \left\{ {F_{i,j+1} +\frac{\alpha _{i,j} h_i F_{i,j+1}^x }{\alpha _{i,j} +\beta _{i,j} }} \right\} -\frac{\hat{{\delta }}_{i,j} \hat{{h}}_j }{\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} }\left\{ {F_{i,j+1}^y +\frac{\alpha _{i,j} h_i F_{i,j+1}^{xy} }{\alpha _{i,j} +\beta _{i,j} }} \right\} ,\\ c_{1,3}= & {} \left\{ {F_{i,j+1} +\frac{\alpha _{i,j} h_i F_{i,j+1}^x }{\alpha _{i,j} +\beta _{i,j} }} \right\} ,\\ c_{2,0}= & {} \left\{ {F_{i+1,j} -\frac{\delta _{i,j} h_i F_{i+1,j}^x }{\gamma _{i,j} +\delta _{i,j} }} \right\} , \\ c_{2,1}= & {} \left\{ {F_{i+1,j} -\frac{\delta _{i,j} h_i F_{i+1,j}^x }{\gamma _{i,j} +\delta _{i,j} }} \right\} +\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j }{\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \left\{ {F_{i+1,j}^y -\frac{\delta _{i,j} h_i F_{i+1,j}^{xy} }{\gamma _{i,j} +\delta _{i,j} }} \right\} ,\\ c_{2,2}= & {} \left\{ {F_{i+1,j+1} -\frac{\delta _{i,j} h_i F_{i+1,j+1}^x }{\gamma _{i,j} +\delta _{i,j} }} \right\} -\frac{\hat{{\delta }}_{i,j} \hat{{h}}_j }{\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} }\left\{ {F_{i+1,j+1}^y -\frac{\delta _{i,j} h_i F_{i+1,j+1}^{xy} }{\gamma _{i,j} +\delta _{i,j} }} \right\} ,\\ c_{2,3}= & {} \left\{ {F_{i+1,j+1} -\frac{\delta _{i,j} h_i F_{i+1,j+1}^x }{\gamma _{i,j} +\delta _{i,j} }} \right\} , \quad c_{3,0} =F_{i+1,j} , \quad c_{3,1} =\left\{ {F_{i+1,j} +\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i+1,j}^y }{\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} }} \right\} ,\\ c_{3,2}= & {} \left\{ {F_{i+1,j+1} -\frac{\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i+1,j+1}^y }{\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} }} \right\} , \quad c_{3,3} =F_{i+1,j+1} . \end{aligned}$$

The Bernstein-Bézier like basis functions $B_k^3 \left( \theta \right)$ and $B_l^3 \left( \phi \right)$, $k,l=0,1,2,3$ are:

$$\begin{aligned} B_0^3 \left( \theta \right)= & {} \frac{\alpha _{i,j} \left( {1-\theta } \right) ^{3}}{q_{i,j} \left( \theta \right) }, \quad B_1^3 \left( \theta \right) =\frac{\left( {\alpha _{i,j} +\beta _{i,j} } \right) \left( {1-\theta } \right) ^{2}\theta }{q_{i,j} \left( \theta \right) }, \\ B_2^3 \left( \theta \right)= & {} \frac{\left( {\gamma _{i,j} +\delta _{i,j} } \right) \left( {1-\theta } \right) \theta ^{2}}{q_{i,j} \left( \theta \right) },\\ B_3^3 \left( \theta \right)= & {} \frac{\delta _{i,j} \theta ^{3}}{q_{i,j} \left( \theta \right) }, \quad B_0^3 \left( \phi \right) =\frac{\hat{{\alpha }}_{i,j} \left( {1-\phi } \right) ^{3}}{\hat{{q}}_{i,j} \left( \phi \right) }, \quad B_1^3 \left( \phi \right) =\frac{\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \left( {1-\phi } \right) ^{2}\phi }{\hat{{q}}_{i,j} \left( \phi \right) },\\ B_2^3 \left( \phi \right)= & {} \frac{\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \left( {1-\phi } \right) \phi ^{2}}{\hat{{q}}_{i,j} \left( \phi \right) }, \quad B_3^3 \left( \phi \right) =\frac{\hat{{\delta }}_{i,j} \phi ^{3}}{\hat{{q}}_{i,j} \left( \phi \right) }. \end{aligned}$$

Lemma 1

(Convex-Hull Property) The bivariate rational cubic function (5) satisfy the convex-hull property for positive values of free parameters $\alpha _{i,j}$,$\beta _{i,j}$, $\gamma _{i,j}$, $\delta _{i,j}$, $\hat{{\alpha }}_{i,j}$, $\hat{{\beta }}_{i,j}$, $\hat{{\gamma }}_{i,j}$ and $\hat{{\delta }}_{i,j}$.

Proof

It can be easily verified that

$$\begin{aligned} \sum _{k=0}^3 {\sum _{l=0}^3 {B_k^3 \left( \theta \right) B_l^3 \left( \phi \right) } } =1. \end{aligned}$$

Moreover, for positive values of free parameters $\alpha _{i,j}$,$\beta _{i,j}$, $\gamma _{i,j}$, $\delta _{i,j}$, $\hat{{\alpha }}_{i,j}$, $\hat{{\beta }}_{i,j}$, $\hat{{\gamma }}_{i,j}$, $\hat{{\delta }}_{i,j}$ and $0\le \theta ,\phi \le 1,$ we have,$B_k^3 \left( \theta \right) \ge 0$ and $B_l^3 \left( \phi \right) \ge 0$; $k,l=0,1,2,3$. $\square$

As the bivariate rational cubic function (5) satisfy the convex-hull property, therefore it can be easily deduced that bivariate rational cubic function (5) will produce a positive surface through positive data if its control points $c_{k,l}$, $k,l=0,1,2,3$ are positive.

$c_{0,0} , c_{0,3} , c_{3,0}$ and $c_{3,3}$ are positive due to necessary condition of positivity defined in (4).

$c_{0,l} , l=1,2$ if

$$\begin{aligned} \hat{{\alpha }}_{i,j}> & {} 0, \quad \hat{{\delta }}_{i,j} >0,\\ \hat{{\beta }}_{i,j}> & {} Max\left\{ {0, -\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i,j}^y }{F_{i,j} }} \right\} , \; \hat{{\gamma }}_{i,j} >Max\left\{ {0, \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i,j+1}^y }{F_{i,j+1} }} \right\} . \end{aligned}$$

$c_{1,l} ,\; l=0,1,2,3$ if

$$\begin{aligned} \hat{{\alpha }}_{i,j}> & {} 0, \; \hat{{\delta }}_{i,j} >0, \; \alpha _{i,j} >0, \; \gamma _{i,j} >0, \; \delta _{i,j} >0,\\ \beta _{i,j}> & {} Max\left\{ {0, -\frac{\alpha _{i,j} h_i F_{i,j}^x }{F_{i,j} }, -\frac{\alpha _{i,j} h_i F_{i,j+1}^x }{F_{i,j+1} }} \right\} ,\\ \hat{{\beta }}_{i,j}> & {} Max\left\{ {0, -\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y +\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} }{\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j} +\alpha _{i,j} h_i F_{i,j}^x }} \right\} ,\\ \hat{{\gamma }}_{i,j}> & {} Max\left\{ {0, \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1}^y +\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} }{\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1} +\alpha _{i,j} h_i F_{i,j+1}^x }} \right\} . \end{aligned}$$

$c_{2,l} , \; l=0,1,2,3$ if

$$\begin{aligned} \hat{{\alpha }}_{i,j}> & {} 0, \quad \hat{{\delta }}_{i,j} >0, \quad \alpha _{i,j} >0, \quad \beta _{i,j} >0, \quad \delta _{i,j} >0,\\ \gamma _{i,j}> & {} Max\left\{ {0, \frac{\delta _{i,j} h_i F_{i+1,j}^x }{F_{i+1,j} }, \frac{\delta _{i,j} h_i F_{i+1,j+1}^x }{F_{i+1,j+1} }} \right\} ,\\ \hat{{\beta }}_{i,j}> & {} Max\left\{ {0, -\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y -\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} }{\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j} -\delta _{i,j} h_i F_{i+1,j}^x }} \right\} ,\\ \hat{{\gamma }}_{i,j}> & {} Max\left\{ {0, \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} }{\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1} -\delta _{i,j} h_i F_{i+1,j+1}^x }} \right\} . \end{aligned}$$

$c_{3,l} , l=1,2$ if

$$\begin{aligned} \hat{{\alpha }}_{i,j}> & {} 0, \quad \hat{{\delta }}_{i,j} >0,\\ \hat{{\beta }}_{i,j}> & {} Max\left\{ {0, -\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i+1,j}^y }{F_{i+1,j} }} \right\} , \quad \hat{{\gamma }}_{i,j} >Max\left\{ {0, \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i+1,j+1}^y }{F_{i+1,j+1} }} \right\} . \end{aligned}$$

The above can be summarized as:

Theorem 1

The piecewise bivariate rational cubic interpolant $S\left( {x, y} \right)$, defined over the rectangular mesh $D=\left[ {x_0 , x_m } \right] \times \left[ {y_0 , y_n } \right]$, in (5), is positive if the following sufficient conditions are satisfied

$$\begin{aligned} \alpha _{i,j}> & {} 0, \quad \delta _{i,j} >0, \quad \hat{{\alpha }}_{i,j} >0, \quad \hat{{\delta }}_{i,j} >0,\\ \beta _{i,j}> & {} Max\left\{ {0, Con_k ,k=1,2} \right\} , \quad \gamma _{i,j} >Max\left\{ {0, Con_k ,k=3,4} \right\} ,\\ \hat{{\beta }}_{i,j}> & {} Max\left\{ {0, Con_k ,k=5,6,7,8} \right\} , \quad \hat{{\gamma }}_{i,j} >Max\left\{ {0, Con_k ,k=9,10,11,12} \right\} , \end{aligned}$$

where

$$\begin{aligned} Con_1= & {} -\frac{\alpha _{i,j} h_i F_{i,j}^x }{F_{i,j} }, \quad Con_2 =-\frac{\alpha _{i,j} h_i F_{i,j+1}^x }{F_{i,j+1} },\\ Con_3= & {} \frac{\delta _{i,j} h_i F_{i+1,j}^x }{F_{i+1,j} }, \quad Con_4=\frac{\delta _{i,j} h_i F_{i+1,j+1}^x }{F_{i+1,j+1} },\\ Con_5= & {} -\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i,j}^y }{F_{i,j} }, \quad Con_6 =-\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i+1,j}^y }{F_{i+1,j} },\\ Con_7= & {} -\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y +\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} }{\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j} +\alpha _{i,j} h_i F_{i,j}^x },\\ Con_8= & {} -\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y -\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} }{\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j} -\delta _{i,j} h_i F_{i+1,j}^x },\\ Con_9= & {} \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i,j+1}^y }{F_{i,j+1} }, \quad Con_{10}=\frac{\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i+1,j+1}^y }{F_{i+1,j+1} },\\ Con_{11}= & {} \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1}^y +\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} }{\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1} +\alpha _{i,j} h_i F_{i,j+1}^x },\\ Con_{12}= & {} \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} }{\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1} -\delta _{i,j} h_i F_{i+1,j+1}^x }. \end{aligned}$$

The above constraints can be rearranged as:

$$\begin{aligned} \alpha _{i,j}> & {} 0, \quad \delta _{i,j} >0, \quad \hat{{\alpha }}_{i,j} >0, \quad \hat{{\delta }}_{i,j} >0,\\ \beta _{i,j}= & {} g_1 +Max\left\{ {0, Con_k ,k=1,2} \right\} , \quad \gamma _{i,j} =g_2 +Max\left\{ {0, Con_k ,k=3,4} \right\} ,\\ \hat{{\beta }}_{i,j}= & {} g_3 +Max\left\{ {0, Con_k ,k=5,6,7,8} \right\} , \quad \hat{{\gamma }}_{i,j} =g_4 +Max\left\{ {0, Con_k ,k=9,10,11,12} \right\} ,\\ g_l> & {} 0, \; l=1,2,3,4. \end{aligned}$$

Numerical Examples

In this section, we shall apply the positivity-preserving interpolating scheme developed in “Positivity-Preserving Interpolation by Bivariate Rational Cubic Function” section over some test functions.

Example 1

The positive data in Table 1 is taken from the following function [13]:

$$\begin{aligned} F_1 \left( {x,y} \right) =\frac{4.0}{\left( {x^{2}+y^{2}} \right) ^{2}-1}, \; x,y\ne 0. \end{aligned}$$

Table 1 A positive 3D data set

Fig. 1

Bi-cubic Hermite spline

Fig. 2

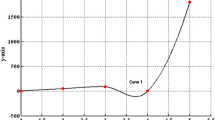
xz-view of Fig. 1

In Table 3, the numerical value of partial derivatives at the data sites are given. These values are computed for the positive data set of Table 1 by using the derivative approximation scheme [13], i.e. the arithmetic mean choice of derivatives.

Fig. 3

yz-view of Fig. 1

Fig. 4

Positive bivariate rational cubic function with $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} \; =\hat{{\delta }}_{i,j} =0.0001$

Fig. 5

Positive bivariate rational cubic function with $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} \; =\hat{{\delta }}_{i,j} =0.1$

Fig. 6

Positive bivariate rational cubic function with $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} \; =\hat{{\delta }}_{i,j} =2$

Figure 1 is produced by interpolating the positive data in Table 1 by bi-cubic Hermite spline. Figures 2 and 3 are the xz-view and yz-view of Fig. 1 respectively. Figures 1, 2 and 3 describe that bi-cubic Hermite although assures smoothness but fails to preserve the shape of positive data. Figure 4 is produced by interpolating the positive data in Table 1 using Theorem 1 with $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} =\hat{{\delta }}_{i,j} =0.0001$. It is clear from the Fig. 4 that positive shape of data is preserved but it is not smooth. The surface is further refined in Figs. 5 and 6 for the values of parameters $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} =\hat{{\delta }}_{i,j} =0.1$ and $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} =\hat{{\delta }}_{i,j} =2$. A comparison of Figs. 4, 5 and 6 easily establish that bivariate positivity-preserving scheme developed in “Positivity-Preserving Interpolation by Bivariate Rational Cubic Function” section preserves the shape of data. The values of parameters, $\beta _{i,j}$, $\gamma _{i,j}$, $\hat{{\beta }}_{i,j}$ and $\hat{{\gamma }}_{i,j}$ are obtained from Theorem 1. The rest of the free parameters can assume any positive real value. However, it is clear from the Figs. 4 and 5 that for very small values of free parameters the surface becomes tense. Thus to assure smooth surface the reasonable choice of free parameters is $\alpha _{i,j} \ge 0.5$, $\delta _{i,j} \ge 0.5$, $\hat{{\alpha }}_{i,j} \ge 0.5$, $\hat{{\delta }}_{i,j} \ge 0.5$.

The positive surface in Fig. 6 is produced by interpolating the positive data set of Table 1 using positivity-preserving scheme developed in “Positivity-Preserving Interpolation by Bivariate Rational Cubic Function” section of this research paper. The same positive data was interpolated in Fig. 7 by the positivity-preserving scheme proposed in [13]. The positivity-preserving scheme proposed in [13] also has four free parameters. By comparing the positive surfaces interpolated in Figs. 6 and 7 it is clear that the positivity-preserving scheme developed in this research paper performs better than [13].

Example 2

A positive data set is taken in Table 2.

Fig. 7

Courtesy of [13]

Table 2 A positive 3D data set

Fig. 8

Bi-cubic Hermite spline

Fig. 9

Bi-cubic Hermite spline with plane $Z=0$

This data set is produced from an exponential function: $F_2 \left( {x,y} \right) =\left( {1+2e^{r}} \right) ^{\frac{-1}{2}}+0.0001$, $r=-3\left( {\sqrt{x^{2}+y^{2}}-6.7} \right)$. In Table 4, the numerical value of partial derivatives at the data sites corresponding to positive data of Table 2 are given.

The Figs. 8 and 9 are produced by interpolating the positive data in Table 2 by bi-cubic Hermite spline. It is clear from these figures that some part of the surface is lying below the plane $Z=0$. The positive surface in Figs. 10 and 11 are produced by the positivity-preserving scheme developed in “Positivity-Preserving Interpolation by Bivariate Rational Cubic Function” section for the value of free parameters $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} =\hat{{\delta }}_{i,j} =0.01$ and $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} =\hat{{\delta }}_{i,j} =2.2$.

Fig. 10

Positive bivariate rational cubic function with $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} \; =\hat{{\delta }}_{i,j} =0.01$

Fig. 11

Positive bivariate rational cubic function with $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} \; =\hat{{\delta }}_{i,j} =2.2$

Range Restricted Interpolation by Bivariate Rational Cubic Function

In this section, a bivariate rational cubic interpolating scheme is developed to preserve the shape of data that is lying above another surface.

Let $\left\{ {\left( {x_i ,y_j ,F_{i,j} } \right) : i=1,2,3,\ldots ,m; j=1,2,3,\ldots ,n} \right\}$ be the given set of data points arranged over the rectangular grid and lying above the surface $X\left( {x, y} \right)$ i.e.

$$\begin{aligned} F_{i,j}> & {} X\left( {x_i , y_j } \right) ,\\ X\left( {x, y} \right)= & {} a_0 x^{n}+a_1 x^{n-1}y+a_2 xy^{n-1}+a_3 y^{n}+\cdots +a_{m-2} x+a_{m-1} y+a_m ,\nonumber \end{aligned}$$

(6)

where $a_i$, $i=0,1,2,\ldots ,m$ are real numbers and $n\in \left\{ {0,1,2,3} \right\} (X\left( {x, y} \right)$ can be a constant, linear, quadratic or cubic surface). It is required that the interpolating bivariate rational cubic function (5) also lies above the surface $X\left( {x, y} \right)$ i.e.

$$\begin{aligned} S\left( {x, y} \right) >X\left( {x, y} \right) , \; \forall \left( {x, y} \right) \in D, \end{aligned}$$

where $D=\left[ {x_0 , x_m } \right] \times \left[ {y_0 , y_n } \right]$.

Table 3 Numerical results of Figs. 1–7

Table 4 Numerical results of Figs. 8–11

Construct a function $H\left( {x, y} \right) =S\left( {x, y} \right) -X\left( {x, y} \right)$ such that

$$\begin{aligned} F_{i,j}^*=F_{i,j} -X_{i,j} , \end{aligned}$$

where

$$\begin{aligned} F_{i,j}^*= & {} H\left( {x_i ,y_j } \right) , \; S\left( {x_i ,y_j } \right) =F_{i,j} , \; X\left( {x_i ,y_j } \right) =X_{i,j} ,\\ H_x \left( {x_i ,y_j } \right)= & {} F_{i,j}^x -X_x \left( {x_i ,y_j } \right) , \; H_y \left( {x_i ,y_j } \right) = F_{i,j}^y -X_y \left( {x_i ,y_j } \right) , \;\\ H_{xy} \left( {x_i ,y_j } \right)= & {} F_{i,j}^{xy} -X_{xy} \left( {x_i ,y_j } \right) . \end{aligned}$$

Now the problem of interpolating the data points $\left\{ \left( {x_i ,y_j ,F_{i,j} } \right) : i=1,2,3,\ldots ,m;\right. .$ $\left. j=1,2,3,\ldots ,n \right\}$ subject to the constrained surface $X\left( {x, y} \right)$ is converted to the positivity-preserving interpolation of newly constructed positive data points $\left\{ {\left( {x_i ,y_j ,F_{i,j}^*} \right) :} \right. i=1,2,3,\ldots ,m; j=1,2,3,$ $\left. {\ldots ,n} \right\} .$ The derivatives$X_x \left( {x_i ,y_j } \right)$, $X_y \left( {x_i ,y_j } \right)$ and $X_{xy} \left( {x_i ,y_j } \right)$ are computed by the given constrained surface. The positive surface is constructed by interpolating the data points $\left\{ {\left( {x_i ,y_j ,F_{i,j}^*} \right) : i=1,2,3,\ldots ,m; j=1,2,3,\ldots ,n} \right\}$ using the positivity-preserving scheme developed in “Positivity-Preserving Interpolation by Bivariate Rational Cubic Function” section. Each rectangular patch of surface is bivariate rational cubic interpolant (5). The surface $X\left( {x, y} \right)$ is also expressed by the stitching of bivariate rational cubic function (5). The required surface $S\left( {x, y} \right)$ is computed as

$$\begin{aligned} S\left( {x, y} \right) =H\left( {x, y} \right) +X\left( {x, y} \right) , \end{aligned}$$

which is also a positive bivariate rational cubic function (5).

Numerical Examples

Example 3

The function $F_3 \left( {x,y} \right) =\sin x\cos y+0.3$, is lying above the surface $Z\left( {x,y} \right) = -0.55x^{2} -1.35x-0.2xy-0.2y-1.35.$ The domain is restricted to $\left( {x,y} \right) \!\in \! \left[ {-3,3} \right] \times \left[ {-3,3} \right]$. Forty nine data points are generated from the $F_3 \left( {x,y} \right)$ and $Z\left( {x,y} \right)$ for $h_i =\hat{{h}}_j =1$. In Table 6, the numerical values of partial derivatives at the data sites corresponding to the generated data set are given.

Table 5 Table 5

Fig. 12

Bi-cubic Hermite spline with surface Z

Fig. 13

Range restricted bivariate cubic function with $\hat{{\alpha }}_{i,j} =\hat{{\delta }}_{i,j} =1.1$

Fig. 14

Another view of, Fig. 13, the range restricted bivariate rational cubic function

Fig. 15

Bi-cubic Hermite spline

Fig. 16

Range restricted bivariate rational cubic function with $\alpha _{i,j}=\delta _{i,j}=\hat{\alpha }_{i,j}=\hat{\delta }_{i,j}=1.1$

The Fig. 12 is produced by interpolating the data taken from $F_3 \left( {x,y} \right)$ and $Z\left( {x,y} \right)$ using bi-cubic Hermite spline.Some part of the surface $F_3 \left( {x,y} \right)$is lying below the surface $Z\left( {x,y} \right)$, a contradiction to the shape of given data. Figure 13 is produced by the range restricted interpolation scheme developed in “Range Restricted Interpolation by Bivariate Rational Cubic Function” section. It is clear from the figure that surface $F_3 \left( {x,y} \right)$ is lying above $Z\left( {x,y} \right)$.

Example 4

The data set in Table 5 is lying above the plane $Z\left( {x,y} \right) =1.9999$.

Figure 15 is produced from the data set in Table 5 using bi-cubic Hermite spline where a part of the surface is lying below the plane $Z\left( {x,y} \right) =1.9999$, a contradiction to the shape of data. Surface lying above the plane $Z\left( {x,y} \right) =1.9999$ is produced in Fig. 16 by the range restricted interpolation scheme developed in “Range Restricted Interpolation by Bivariate Rational Cubic Function” section. The numerical values of partial derivatives at the data sites corresponding to the data set of Table 5 are given in Table 7.

Table 6 Numerical results of Figs. 12–14

Table 7 Numerical results of Figs. 15, 16

Monotonicity-Preserving Interpolation by Bivariate Rational Cubic Function

In this section simple sufficient data dependent constraints are developed on free parameters in description of bivariate rational cubic function (5) to interpolate monotone surface data.

Let $\left\{ {\left( {x_i , y_j , F_{i,j} } \right) , i=1,2,3,\ldots ,m; j=1,2,3,\ldots ,n} \right\}$ be the monotone data defined over the rectangular domain $D=\left[ {x_1 , x_m } \right] \times \left[ {y_1 , y_n } \right]$. The necessary conditions for monotonicity of the data $\left\{ {\left( {x_i , y_j , F_{i,j} } \right) , i=1,2,3,\ldots ,m; j=1,2,3,\ldots ,n} \right\}$ are

$$\begin{aligned} F_{i,j}< & {} F_{i+1,j} , \; \Delta _{i,j} >0, \; F_{i,j}^x >0, \hbox { whenever }\left( {x_i , y_j } \right) <\left( {x_{i+1} , y_j } \right) ,\\ F_{i,j}< & {} F_{i,j+1} , \; \hat{{\Delta }}_{i,j} >0, \; F_{i,j}^y >0,\hbox { whenever }\left( {x_i , y_j } \right) <\left( {x_i , y_{j+1} } \right) . \end{aligned}$$

The bivariate rational cubic function $S\left( {x, y} \right)$ defined in (5) preserves the shape of monotone surface data if the following conditions are satisfied:

$$\begin{aligned} S_x \left( {x, y} \right) >0, \; S_y \left( {x, y} \right) >0, \; \forall \left( {x, y} \right) \in D. \end{aligned}$$

$S_x \left( {x, y} \right)$ and $S_y \left( {x, y} \right)$ are the first order partial derivatives of bivariate rational cubic function (5) w.r.t x and y.

$$\begin{aligned} S_x \left( {x, y} \right)= & {} \frac{\sum \limits _{i=0}^5 {\left( {1-\theta } \right) ^{5-i}\theta ^{i}B_i } }{\left( {q_{i,j} \left( \theta \right) } \right) ^{2}\hat{{q}}_{i,j} \left( \phi \right) }, \end{aligned}$$

(7)

$$\begin{aligned} S_y \left( {x, y} \right)= & {} \frac{\sum \limits _{i=0}^3 {\left( {1-\theta } \right) ^{3-i}\theta ^{i}C_i } }{q_{i,j} \left( \theta \right) \left( {\hat{{q}}_{i,j} \left( \phi \right) } \right) ^{2}}, \end{aligned}$$

(8)

The complete expressions of $B_i$, $i=0,1,2,3,4,5$ and $C_i$, $i=0,1,2,3$ are written in “Appendix”.

$S_x \left( {x, y} \right) >0$ if

$$\begin{aligned} \sum _{i=0}^5 {\left( {1-\theta } \right) ^{5-i}\theta ^{i}B_i } >0 \quad \hbox { and } \quad \left( {q_{i,j} \left( \theta \right) } \right) ^{2}\hat{{q}}_{i,j} \left( \phi \right) >0. \end{aligned}$$

$\left( {q_{i,j} \left( \theta \right) } \right) ^{2}\hat{{q}}_{i,j} \left( \phi \right) >0$ if

$$\begin{aligned} \hat{{\alpha }}_{i,j} >0, \quad \hat{{\beta }}_{i,j} >0, \quad \hat{{\gamma }}_{i,j} >0 \quad \hat{{\delta }}_{i,j} >0. \end{aligned}$$

$\sum \nolimits _{i=0}^5 {\left( {1-\theta } \right) ^{5-i}\theta ^{i}B_i } >0$ if

$$\begin{aligned} B_i >0, \; i=0,1,2,3,4,5. \end{aligned}$$

$B_i >0, \; i=0,1,2,3,4,5$ if

$$\begin{aligned} \alpha _{i,j}> & {} 0, \; \delta _{i,j} >0, \; \hat{{\alpha }}_{i,j} >0, \quad \hat{{\delta }}_{i,j} >0,\\ \beta _{i,j}> & {} Max\left\{ {0, Con_k , k=13,14} \right\} , \quad \gamma _{i,j} >Max\left\{ {0, Con_k , k=15,16} \right\} ,\\ \hat{{\beta }}_{i,j}> & {} Max\left\{ {0, Con_k , k=17,18,19,20} \right\} , \quad \hat{{\gamma }}_{i,j} >Max\left\{ {0, Con_k , k=21,22,23,24} \right\} , \end{aligned}$$

where

$$\begin{aligned} Con_{13}= & {} \frac{\alpha _{i,j} F_{i,j}^x }{\Delta _{i,j} }, \quad Con_{14} =\frac{\alpha _{i,j} F_{i,j+1}^x }{\Delta _{i,j+1} }, \quad Con_{15} =\frac{\delta _{i,j} F_{i+1,j}^x }{\Delta _{i,j} },\\ Con_{16}= & {} \frac{\delta _{i,j} F_{i+1,j+1}^x }{\Delta _{i,j+1} },\quad Con_{17} =-\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i,j}^{xy} }{F_{i,j}^x },\quad Con_{18} = -\frac{\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i+1,j}^{xy} }{F_{i+1,j}^x },\\ Con_{19}= & {} \frac{-\frac{2\hat{{h}}_j \hat{{\alpha }}_{i,j} }{h_i }\left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \left( {F_{i+1,j}^y -F_{i,j}^y } \right) -\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} -\hat{{\alpha }}_{i,j} \alpha _{i,j} \hat{{h}}_j F_{i,j}^{xy} }{2\left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \Delta _{i,j} -\delta _{i,j} F_{i+1,j}^x } \right\} },\\ Con_{20}= & {} \frac{-\frac{2\hat{{h}}_j \hat{{\alpha }}_{i,j} }{h_i }\left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \left( {F_{i+1,j}^y -F_{i,j}^y } \right) -\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} -\hat{{\alpha }}_{i,j} \delta _{i,j} \hat{{h}}_j F_{i,j}^{xy} }{2\left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \Delta _{i,j} -\alpha _{i,j} F_{i+1,j}^x } \right\} },\\ Con_{21}= & {} \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i,j+1}^{xy} }{F_{i,j+1}^x },\\ Con_{22}= & {} \frac{\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i+1,j+1}^{xy} }{F_{i+1,j+1}^x },\\ Con_{23}= & {} \frac{\frac{2\hat{{h}}_j \hat{{\delta }}_{i,j} }{h_i }\left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \left( {F_{i+1,j+1}^y -F_{i,j+1}^y } \right) -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} +\hat{{\delta }}_{i,j} \alpha _{i,j} \hat{{h}}_j F_{i,j+1}^{xy} }{2\left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \Delta _{i,j+1} -\delta _{i,j} F_{i+1,j+1}^x } \right\} },\\ Con_{24}= & {} \frac{\frac{2\hat{{h}}_j \hat{{\delta }}_{i,j} }{h_i }\left\{ {\left( {\alpha _{i,j} \!+\!\beta _{i,j} } \right) \left( {F_{i+1,j+1}^y -F_{i,j+1}^y } \right) -\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} +\hat{{\delta }}_{i,j} \delta _{i,j} \hat{{h}}_j F_{i+1,j+1}^{xy} }{2\left\{ {\left( {\alpha _{i,j} \!+\!\beta _{i,j} } \right) \Delta _{i,j+1} -\alpha _{i,j} F_{i,j+1}^x } \right\} }. \end{aligned}$$

$S_y \left( {x, y} \right) >0$ if

$$\begin{aligned} \sum _{i=0}^3 {\left( {1-\theta } \right) ^{3-i}\theta ^{i}C_i } >0 \quad \hbox { and }\quad q_{i,j} \left( \theta \right) \left( {\hat{{q}}_{i,j} \left( \phi \right) } \right) ^{2}>0. \end{aligned}$$

$q_{i,j} \left( \theta \right) \left( {\hat{{q}}_{i,j} \left( \phi \right) } \right) ^{2}>0$ if

$$\begin{aligned} \alpha _{i,j} >0, \quad \beta _{i,j} >0, \quad \gamma _{i,j} >0 \; \delta _{i,j} >0, \end{aligned}$$

$\sum \limits _{i=0}^3 {\left( {1-\theta } \right) ^{3-i}\theta ^{i}C_i } >0$ if

$$\begin{aligned} C_i >0, \quad i=0,1,2,3. \end{aligned}$$

$C_i >0, \quad i=0,1,2,3$ if

$$\begin{aligned} \alpha _{i,j}> & {} 0, \quad \delta _{i,j} >0, \quad \hat{{\alpha }}_{i,j} >0, \quad \hat{{\delta }}_{i,j} >0,\\ \beta _{i,j}> & {} Max\left\{ {0, Con_k , k=25,26,27} \right\} , \; \gamma _{i,j} >Max\left\{ {0, Con_k , k=28,29,30} \right\} ,\\ \hat{{\beta }}_{i,j}> & {} Max\left\{ {0, Con_k , k=31,32,33,34} \right\} , \; \hat{{\gamma }}_{i,j} >Max\left\{ {0, Con_k , k=35,36,37,38} \right\} ,\\ Con_{25}= & {} -\frac{\alpha _{i,j} h_i F_{i,j}^{xy} }{F_{i,j}^y }, \quad Con_{26} =-\frac{\alpha _{i,j} h_i F_{i,j+1}^{xy} }{F_{i,j+1}^y }, \quad Con_{27} =\frac{-h_i \alpha _{i,j} \left( {F_{i,j+1}^x -F_{i,j}^x } \right) }{\hat{{h}}_j \hat{{\Delta }}_{i,j} },\\ Con_{28}= & {} \frac{\delta _{i,j} h_i F_{i+1,j}^{xy} }{F_{i+1,j}^y },\\ Con_{29}= & {} \frac{\delta _{i,j} h_i F_{i+1,j+1}^{xy} }{F_{i+1,j+1}^y }, \quad Con_{30} =\frac{h_i \delta _{i,j} \left( {F_{i+1,j+1}^x -F_{i+1,j}^x } \right) }{\hat{{h}}_j \hat{{\Delta }}_{i+1,j} }, \quad Con_{31} =\frac{\hat{{\alpha }}_{i,j} F_{i,j}^y }{\hat{{\Delta }}_{i,j} },\\ Con_{32}= & {} \frac{\hat{{\alpha }}_{i,j} F_{i+1,j}^y }{\Delta _{i+1,j} },\\ Con_{33}= & {} \frac{2\hat{{\alpha }}_{i,j} \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y -\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} +\delta _{i,j} \hat{{\delta }}_{i,j} h_i F_{i+1,j+1}^{xy} }{2\left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \hat{{\Delta }}_{i+1,j} -\frac{h_i \delta _{i,j} }{\hat{{h}}_j }\left( {F_{i+1,j+1}^x -F_{i+1,j}^x } \right) } \right\} },\\ Con_{34}= & {} \frac{2\hat{{\alpha }}_{i,j} \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y +\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} -\alpha _{i,j} \hat{{\delta }}_{i,j} h_i F_{i,j+1}^{xy} }{2\left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \hat{{\Delta }}_{i,j} +\frac{h_i \alpha _{i,j} }{\hat{{h}}_j }\left( {F_{i,j+1}^x -F_{i+1,j}^x } \right) } \right\} }, \; Con_{35} =\frac{\hat{{\delta }}_{i,j} F_{i,j+1}^y }{\hat{{\Delta }}_{i,j} },\\ Con_{36}= & {} \frac{\hat{{\delta }}_{i,j} F_{i+1,j+1}^y }{\Delta _{i+1,j} },\\ Con_{37}= & {} \frac{2\hat{{\delta }}_{i,j} \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} +\hat{{\alpha }}_{i,j} \delta _{i,j} h_i F_{i+1,j}^{xy} }{2\left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \hat{{\Delta }}_{i+1,j} -\frac{h_i \delta _{i,j} }{\hat{{h}}_j }\left( {F_{i+1,j+1}^x -F_{i+1,j}^x } \right) } \right\} },\\ Con_{38}= & {} \frac{2\hat{{\delta }}_{i,j} \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1}^y +\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} +\alpha _{i,j} \hat{{\alpha }}_{i,j} h_i F_{i,j}^{xy} }{2\left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \hat{{\Delta }}_{i,j} +\frac{h_i \alpha _{i,j} }{\hat{{h}}_j }\left( {F_{i,j+1}^x -F_{i+1,j}^x } \right) } \right\} }. \end{aligned}$$

The above can be summarized as:

Table 8 A monotone 3D data set

Theorem 2

The piecewise bivariate rational cubic interpolant $S\left( {x, y} \right)$, defined over the rectangular mesh $D=\left[ {x_1 , x_m } \right] \times \left[ {y_1 , y_n } \right]$, in (5), is monotone if the following sufficient conditions are satisfied

$$\begin{aligned} \alpha _{i,j}> & {} 0, \; \delta _{i,j} >0, \; \hat{{\alpha }}_{i,j} >0, \; \hat{{\delta }}_{i,j} >0,\\ \beta _{i,j}> & {} Max\left\{ {0, Con_k , k=13,14,25,26,27} \right\} ,\\ \gamma _{i,j}> & {} Max\left\{ {0, Con_k , k=15,16,28,29,30} \right\} ,\\ \hat{{\beta }}_{i,j}> & {} Max\left\{ {0, Con_k , k=17,18,19,20,31,32,33,34} \right\} ,\\ \hat{{\gamma }}_{i,j}> & {} Max\left\{ {0, Con_k , k=21,22,23,24,35,36,37,38} \right\} . \end{aligned}$$

where $Con_k$, $k=13, 14, 15,\ldots ,38$ are already defined in “Monotonicity-Preserving Interpolation by Bivariate Rational Cubic Function” section.

The above constraints can be rearranged as:

$$\begin{aligned} \alpha _{i,j}> & {} 0, \; \delta _{i,j} >0, \hat{{\alpha }}_{i,j} >0, \; \hat{{\delta }}_{i,j} >0,\\ \beta _{i,j}= & {} g_1 +Max\left\{ {0, Con_k , k=13,14,25,26,27} \right\} ,\\ \gamma _{i,j}= & {} g_2 +Max\left\{ {0, Con_k , k=15,16,28,29,30} \right\} ,\\ \hat{{\beta }}_{i,j}= & {} g_3 +Max\left\{ {0, Con_k , k=17,18,19,20,31,32,33,34} \right\} ,\\ \hat{{\gamma }}_{i,j}= & {} g_4 +Max\left\{ {0, Con_k , k=21,22,23,24,35,36,37,38} \right\} ,\\ g_l> & {} 0, \; l=1,2,3,4. \end{aligned}$$

Numerical Examples

In this section, we shall apply the monotonicity-preserving interpolating scheme developed in “Monotonicity-Preserving Interpolation by Bivariate Rational Cubic Function’ section on some test functions.

Example 5

A monotone data set is considered in Table 8. Figure 17 is produced by interpolating the monotone data in Table 8 using bi-cubic Hermite spline. Figure 18 is the yz-view of Fig. 17. Figures 17 and 18 clearly express that bi-cubic Hermite fails to preserve the monotone shape of data. The monotone surface in Fig. 19 is produced from the same data using the monotonicity-preserving scheme developed in “Monotonicity-Preserving Interpolation by Bivariate Rational Cubic Function” section with $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} = \; \hat{{\delta }}_{i,j} =0.1$. Figure 20 is another view of Fig. 19.

Example 6

The data set (four decimal places) in Table 9 is generated from the following monotone function:

$$\begin{aligned} F_4 \left( {x,y} \right) =\ln \left( {x^{2}+y^{2}} \right) +10. \end{aligned}$$

Fig. 17

Hermite rectangular surface

Fig. 18

yz-view of Fig. 17

Fig. 19

Monotone bivariate rational cubic function with $\alpha _{i,j} =\delta _{i,j} =\hat{{\alpha }}_{i,j} \; =\hat{{\delta }}_{i,j} =0.1$

Fig. 20

yz-view of Fig. 19

Figure 21 is produced from the data set in Table 9 using bi-cubic Hermite spline which loses monotonicity. Figure 22 is another view of Fig. 21. Monotone surface in Fig. 23 is produced from the same data using the monotonicity-preserving scheme developed in “Monotonicity-Preserving Interpolation by Bivariate Rational Cubic Function” section. Figure 24 is another view of Fig. 23. The values assigned to free parameters are $\alpha _{i,j} =1.1$,$\delta _{i,j} =1.2$,$\hat{{\alpha }}_{i,j} =1.3$ and $\hat{{\delta }}_{i,j} =1.1$.

Table 9 A monotone 3D data set

Fig. 21

Hermite rectangular surface

Fig. 22

Another view of Fig. 21

Fig. 23

Monotone bivariate rational cubic function with $\alpha _{i,j} =1.1, \; \delta _{i,j} =1.2, \; \hat{{\alpha }}_{i,j} =1.3,\hat{{\delta }}_{i,j} =1.1$

Fig. 24

Another view of Fig. 23

The numerical value of partial derivatives at the data sites corresponding to Tables 8 and 9 are given in Tables 10 and 11 respectively.

Table 10 Numerical results of Figs. 17–20

Table 11 Numerical results of Figs. 21–24

Remark 1

In this research paper, the arithmetic mean choice of derivatives [13] is used to estimate the values of first order partial derivatives and mixed partial derivatives at the data sites. However, any derivative estimation scheme can be used to compute the values of these derivatives at the data sites. The Tables 3, 4, 6, 7, 10 and 11, demonstrate that the values of derivatives are fixed at the data sites. Here, the shapes of the surfaces are being relaxed by altering the values of free parameters, see “Numerical Examples” sections.

Remark 2

It can be easily observed that for sufficiently small values of free parameters $\alpha _{i,j}$, $\delta _{i,j}$, $\hat{{\alpha }}_{i,j}$ and $\hat{{\delta }}_{i,j}$, the rational bivariate cubic interpolant (1) reduces to a rational bivariate linear interpolant i.e.

$$\begin{aligned} \mathop {\mathop {\lim }\limits _{\alpha _{i,j} \rightarrow 0,\delta _{i,j} \rightarrow 0}} \limits _{\hat{{\alpha }}_{i,j} \rightarrow 0,\hat{{\delta }}_{i,j} \rightarrow 0 } S\left( {x,y} \right) =\frac{\hat{{\beta }}_{i,j} \left( {1-\phi } \right) R_0 +\hat{{\gamma }}_{i,j} \phi R_1 }{\hat{{\beta }}_{i,j} \left( {1-\phi } \right) +\hat{{\gamma }}_{i,j} \phi }, \end{aligned}$$

where

$$\begin{aligned} R_0 =\frac{\beta _{i,j} \left( {1-\theta } \right) F_{i,j} +\gamma _{i,j} \theta F_{i+1,j} }{\beta _{i,j} \left( {1-\theta } \right) +\gamma _{i,j} \theta }\quad \hbox { and }\quad R_1 =\frac{\beta _{i,j} \left( {1-\theta } \right) F_{i,j+1} +\gamma _{i,j} \theta F_{i+1,j+1} }{\beta _{i,j} \left( {1-\theta } \right) +\gamma _{i,j} \theta }. \end{aligned}$$

Therefore for very small values of free parameters, the interpolated surfaces are not smooth.

The value of parameters $\beta _{i,j}$, $\gamma _{i,j}$, $\hat{{\beta }}_{i,j}$ and $\hat{{\gamma }}_{i,j}$ are dependent upon the choice of free parameters $\alpha _{i,j}$, $\delta _{i,j}$, $\hat{{\alpha }}_{i,j}$ and $\hat{{\delta }}_{i,j}$, see Theorems 1 and 2. It is also observed that for sufficiently large value of parameters, $\beta _{i,j}$, $\gamma _{i,j}$, $\hat{{\beta }}_{i,j}$ and $\hat{{\gamma }}_{i,j}$, the interpolant (1) reduces to straight lines [18]. Therefore, to obtain smooth surfaces by the rational interpolant (1), sufficiently small and large values of the free parameters should be avoided. The numerical experiments suggested that for reasonably smooth interpolation the appropriate choice of free parameters is $0.5\le \alpha _{i,j} ,\delta _{i,j} ,\hat{{\alpha }}_{i,j} ,\hat{{\delta }}_{i,j} \le 20$.

Conclusion

In this study, positive, range restricted and monotone rational interpolation schemes with eight free parameters are presented. Data dependent sufficient constraints are developed on four of the parameters to preserve the shape of data while remaining are free to refine the shape of data at user choice. The authors in [13] also developed a rational positivity-preserving interpolation scheme with eight free parameters in each rectangular patch but the visual display in [13] was less smooth than the proposed scheme of this paper. A clear difference can be seen between Figs. 6 and 7. Here, positive surface in Fig. 6 is produced by the positivity-preserving scheme proposed in this paper, whereas, Fig. 7 is produced by the positivity-preserving scheme of [13]. The positive surface in Fig. 6 obeys the smoothness, whereas, the positive surface in Fig. 7 is tense.

The proposed schemes of this paper, unlike ([1, 4, 5]) are equally applicable to both data and data with derivatives. These shape-preserving schemes do not modify the step length, whereas, [3, 14] restrict interval length. These numerical schemes have more degrees of freedom (in the form of four free parameters) in each rectangular patch than the shape-preserving scheme [12]. The derivatives are approximated by the arithmetic mean choice of derivatives [13].

Appendix

$$\begin{aligned} B_0 =\sum _{j=0}^3 {\left( {1-\phi } \right) ^{3-j}\phi ^{j}B_{0,j} } , \end{aligned}$$

with

$$\begin{aligned} B_{0,0}= & {} \alpha _{i,j}^2 \hat{{\alpha }}_{i,j} F_{i,j}^x , \quad B_{0,1} =\alpha _{i,j}^2 \left\{ {\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i,j}^x +\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i,j}^{xy} } \right\} ,\\ B_{0,2}= & {} \alpha _{i,j}^2 \left\{ {\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i,j+1}^x -\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i,j+1}^{xy} } \right\} , \quad B_{0,3} =\alpha _{i,j}^2 \hat{{\delta }}_{i,j} F_{i,j+1}^x , \end{aligned}$$

$$\begin{aligned} B_1= & {} \sum _{j=0}^3 {\left( {1-\phi } \right) ^{3-j}\phi ^{j}B_{1,j} } , \end{aligned}$$

with

$$\begin{aligned} B_{1,0}= & {} 2\alpha _{i,j} \hat{{\alpha }}_{i,j} \left( {\gamma _{i,j} +\delta _{i,j} } \right) \Delta _{i,j} -2\alpha _{i,j} \hat{{\alpha }}_{i,j} \delta _{i,j} F_{i+1,j}^x +\alpha _{i,j}^2 \hat{{\alpha }}_{i,j} F_{i,j}^x ,\\ B_{1,1}= & {} 2\alpha _{i,j} \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \Delta _{i,j} -\delta _{i,j} F_{i+1,j}^x } \right\} +\alpha _{i,j}^2 \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i,j}^x \\&+\alpha _{i,j} \hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i,j}^{xy} +\frac{2\hat{{h}}_j \alpha _{i,j} \hat{{\alpha }}_{i,j} }{h_i }\left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \left( {F_{i+1,j}^y -F_{i,j}^y } \right) -\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} ,\\ B_{1,2}= & {} 2\alpha _{i,j} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \Delta _{i,j+1} -\delta _{i,j} F_{i+1,j+1}^x } \right\} +\alpha _{i,j}^2 \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i,j+1}^x \\&-\alpha _{i,j}^2 \hat{{\delta }}_{i,j} \hat{{h}}_j F_{i,j+1}^{xy} -\frac{2\hat{{h}}_j \alpha _{i,j} \hat{{\delta }}_{i,j} }{h_i }\left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \left( {F_{i+1,j+1}^y -F_{i,j+1}^y } \right) -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} ,\\ B_{1,3}= & {} 2\alpha _{i,j} \hat{{\delta }}_{i,j} \left( {\gamma _{i,j} +\delta _{i,j} } \right) \Delta _{i,j+1} -2\alpha _{i,j} \hat{{\delta }}_{i,j} \delta _{i,j} F_{i+1,j+1}^x +\alpha _{i,j}^2 \hat{{\delta }}_{i,j} F_{i,j+1}^x , \end{aligned}$$

$$\begin{aligned} B_2= & {} \sum _{j=0}^3 {\left( {1-\phi } \right) ^{3-j}\phi ^{j}B_{2,j} } , \end{aligned}$$

with

$$\begin{aligned} B_{2,0}= & {} \left( {3\alpha _{i,j} \gamma _{i,j} +6\alpha _{i,j} \delta _{i,j} +\beta _{i,j} \gamma _{i,j} +\beta _{i,j} \delta _{i,j} } \right) \Delta _{i,j}-\delta _{i,j} \left( {3\alpha _{i,j} +\beta _{i,j} } \right) F_{i+1,j}^x \\&-\alpha _{i,j} \left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i,j}^x ,\\ B_{2,1}= & {} \left( {3\alpha _{i,j} \gamma _{i,j} +6\alpha _{i,j} \delta _{i,j} +\beta _{i,j} \gamma _{i,j} +\beta _{i,j} \delta _{i,j} } \right) \\&\quad \left\{ {\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \Delta _{i,j} +\frac{\hat{{h}}_j \hat{{\alpha }}_{i,j} }{h_i }\left( {F_{i+1,j}^y -F_{i,j}^y } \right) } \right\} \\&-\left( {3\alpha _{i,j} +\beta _{i,j} } \right) \delta _{i,j} \left\{ {\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j}} \right) F_{i+1,j}^x +\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i+1,j}^{xy} }\right\} \\&\quad -\left( {\gamma _{i,j} +\delta _{i,j} } \right) \alpha _{i,j} \left\{ {\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j}} \right) F_{i,j}^x } \right. +\left. \hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i,j}^{xy} \right\} ,\\ B_{2,2}= & {} \left( {3\alpha _{i,j} \gamma _{i,j} +6\alpha _{i,j} \delta _{i,j} +\beta _{i,j} \gamma _{i,j} +\beta _{i,j} \delta _{i,j} } \right) \left\{ \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \Delta _{i,j+1} \right. \\&\left. -\frac{\hat{{h}}_j \hat{{\delta }}_{i,j} }{h_i }\left( {F_{i+1,j+1}^y -F_{i,j+1}^y } \right) \right\} \\&-\left( {3\alpha _{i,j} +\beta _{i,j} } \right) \delta _{i,j} \left\{ {\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i+1,j+1}^x -\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i+1,j+1}^{xy} } \right\} \\&-\left( {\gamma _{i,j} +\delta _{i,j} } \right) \alpha _{i,j} \left\{ {\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i,j+1}^x } \right. -\left. \hat{{\delta }}_{i,j} \hat{{h}}_j F_{i,j+1}^{xy} \right\} ,\\ B_{2,3}= & {} \left( {3\alpha _{i,j} \gamma _{i,j} +6\alpha _{i,j} \delta _{i,j} +\beta _{i,j} \gamma _{i,j} +\beta _{i,j} \delta _{i,j} } \right) \Delta _{i,j+1} -\delta _{i,j} \left( {3\alpha _{i,j} +\beta _{i,j} } \right) F_{i+1,j+1}^x\\&-\alpha _{i,j} \left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i,j+1}^x , \end{aligned}$$

$$\begin{aligned} B_3= & {} \sum _{j=0}^3 {\left( {1-\phi } \right) ^{3-j}\phi ^{j}B_{3,j} } , \end{aligned}$$

with

$$\begin{aligned} B_{3,0}= & {} \left( {\alpha _{i,j} \gamma _{i,j} +6\alpha _{i,j} \delta _{i,j} +\beta _{i,j} \gamma _{i,j} +3\beta _{i,j} \delta _{i,j} } \right) \Delta _{i,j} -\delta _{i,j} \left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i+1,j}^x\\&-\alpha _{i,j} \left( {\gamma _{i,j} +3\delta _{i,j} } \right) F_{i,j}^x ,\\ B_{3,1}= & {} \left( {\alpha _{i,j} \gamma _{i,j} +6\alpha _{i,j} \delta _{i,j} +\beta _{i,j} \gamma _{i,j} +3\beta _{i,j} \delta _{i,j} } \right) \left\{ \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \Delta _{i,j}\right. \\&\left. +\,\frac{\hat{{h}}_j \hat{{\alpha }}_{i,j} }{h_i }\left( {F_{i+1,j}^y -F_{i,j}^y } \right) \right\} \\&-\left( {\alpha _{i,j} +\beta _{i,j} } \right) \delta _{i,j} \left\{ {\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i+1,j}^x +\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i+1,j}^{xy} } \right\} \\&-\left( {\gamma _{i,j} +3\delta _{i,j} } \right) \alpha _{i,j} \left\{ {\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i,j}^x } \right. \left. {+\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i,j}^{xy} } \right\} ,\\ B_{3,2}= & {} \left( {\alpha _{i,j} \gamma _{i,j} +6\alpha _{i,j} \delta _{i,j} +\beta _{i,j} \gamma _{i,j} +3\beta _{i,j} \delta _{i,j} } \right) \left\{ \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \Delta _{i,j+1} \right. \\&\left. -\frac{\hat{{h}}_j \hat{{\delta }}_{i,j} }{h_i }\left( {F_{i+1,j+1}^y -F_{i,j+1}^y } \right) \right\} \\&-\left( {\alpha _{i,j} +\beta _{i,j} } \right) \delta _{i,j} \left\{ {\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i+1,j+1}^x -\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i+1,j+1}^{xy} } \right\} \\&-\left( {\gamma _{i,j} +3\delta _{i,j} } \right) \alpha _{i,j} \left\{ {\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i,j+1}^x } \right. \left. {-\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i,j+1}^{xy} } \right\} ,\\ B_{3,3}= & {} \left( {\alpha _{i,j} \gamma _{i,j} +6\alpha _{i,j} \delta _{i,j} +\beta _{i,j} \gamma _{i,j} +3\beta _{i,j} \delta _{i,j} } \right) \Delta _{i,j+1} -\delta _{i,j} \left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i+1,j+1}^x\\&-\alpha _{i,j} \left( {\gamma _{i,j} +3\delta _{i,j} } \right) F_{i,j+1}^x , \end{aligned}$$

$$\begin{aligned} B_4= & {} \sum _{j=0}^3 {\left( {1-\phi } \right) ^{3-j}\phi ^{j}B_{4,j} } , \end{aligned}$$

with

$$\begin{aligned} B_{4,0}= & {} 2\hat{{\alpha }}_{i,j} \delta _{i,j} \left( {\alpha _{i,j} +\beta _{i,j} } \right) \Delta _{i,j} -2\alpha _{i,j} \hat{{\alpha }}_{i,j} \delta _{i,j} F_{i,j}^x +\delta _{i,j}^2 \hat{{\alpha }}_{i,j} F_{i+1,j}^x ,\\ B_{4,1}= & {} 2\delta _{i,j} \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \Delta _{i,j} -\alpha _{i,j} F_{i,j}^x } \right\} +\delta _{i,j}^2 \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i+1,j}^x +\delta _{i,j}^2 \\&\; \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \hat{{h}}_j F_{i+1,j}^{xy}+\frac{2\hat{{h}}_j \delta _{i,j} \hat{{\alpha }}_{i,j} }{h_i}\left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \left( {F_{i+1,j}^y -F_{i,j}^y } \right) -\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} ,\\ B_{4,2}= & {} 2\delta _{i,j} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \Delta _{i,j+1} -\alpha _{i,j} F_{i,j+1}^x } \right\} +\delta _{i,j}^2 \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i+1,j+1}^x\\&-\delta _{i,j}^2 \hat{{\delta }}_{i,j} \hat{{h}}_j F_{i+1,j+1}^{xy}-\frac{2\hat{{h}}_j \delta _{i,j} \hat{{\delta }}_{i,j} }{h_i }\left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \left( {F_{i+1,j+1}^y -F_{i,j+1}^y } \right) -\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} ,\\ B_{4,3}= & {} 2\delta _{i,j} \hat{{\delta }}_{i,j} \left( {\alpha _{i,j} +\beta _{i,j} } \right) \Delta _{i,j+1} -2\alpha _{i,j} \hat{{\delta }}_{i,j} \delta _{i,j} F_{i,j+1}^x +\delta _{i,j}^2 \hat{{\delta }}_{i,j} F_{i+1,j+1}^x , \end{aligned}$$

$$\begin{aligned} B_5= & {} \sum _{j=0}^3 {\left( {1-\phi } \right) ^{3-j}\phi ^{j}B_{5,j} } , \end{aligned}$$

with

$$\begin{aligned} B_{5,0}= & {} \delta _{i,j}^2 \hat{{\alpha }}_{i,j} F_{i+1,j}^x , \quad B_{5,1} =\delta _{i,j}^2 \left\{ {\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i+1,j}^x +\hat{{\alpha }}_{i,j} \hat{{h}}_j F_{i+1,j}^{xy} } \right\} ,\\ B_{5,2}= & {} \delta _{i,j}^2 \left\{ {\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i+1,j+1}^x -\hat{{\delta }}_{i,j} \hat{{h}}_j F_{i+1,j+1}^{xy} } \right\} , \quad B_{5,3} =\delta _{i,j}^2 \hat{{\delta }}_{i,j} F_{i+1,j+1}^x , \end{aligned}$$

$$\begin{aligned} C_0= & {} \sum _{j=0}^5 {\left( {1-\phi } \right) ^{5-j}\phi ^{j}C_{0,j} } ,\\ \end{aligned}$$

with

$$\begin{aligned} C_{0,0}= & {} \hat{{\alpha }}_{i,j}^2 \alpha _{i,j} F_{i,j}^y ,\\ C_{0,1}= & {} 2\alpha _{i,j} \hat{{\alpha }}_{i,j} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \hat{{\Delta }}_{i,j} -2\alpha _{i,j} \hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} F_{i,j+1}^y +\hat{{\alpha }}_{i,j}^2 \alpha _{i,j} F_{i,j}^y ,\\ C_{0,2} \!= & {} \!\alpha _{i,j} \left( {3\hat{{\alpha }}_{i,j} \hat{{\gamma }}_{i,j} \!+\!\hat{{\beta }}_{i,j} \hat{{\gamma }}_{i,j} \!+\!6\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\delta }}_{i,j} } \right) \hat{{\Delta }}_{i,j} -\alpha _{i,j} \hat{{\delta }}_{i,j} \left( {3\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i,j+1}^y\\&-\alpha _{i,j} \hat{{\alpha }}_{i,j} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i,j}^y ,\\ C_{0,3}= & {} \alpha _{i,j} \left( {\hat{{\alpha }}_{i,j} \hat{{\gamma }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\gamma }}_{i,j} +6\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} +3\hat{{\beta }}_{i,j} \hat{{\delta }}_{i,j} } \right) \hat{{\Delta }}_{i,j} -\alpha _{i,j} \hat{{\delta }}_{i,j} \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i,j+1}^y\\&-\alpha _{i,j} \hat{{\alpha }}_{i,j} \left( {\hat{{\gamma }}_{i,j} +3\hat{{\delta }}_{i,j} } \right) F_{i,j}^y ,\\ C_{0,4}= & {} 2\alpha _{i,j} \hat{{\delta }}_{i,j} \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \hat{{\Delta }}_{i,j} -2\alpha _{i,j} \hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} F_{i,j}^y +\alpha _{i,j} \hat{{\delta }}_{i,j}^2 F_{i,j+1}^y ,\\ C_{0,5}= & {} \hat{{\delta }}_{i,j}^2 \alpha _{i,j} F_{i,j+1}^y , \end{aligned}$$

$$\begin{aligned} C_1= & {} \sum _{j=0}^5 {\left( {1-\phi } \right) ^{5-j}\phi ^{j}C_{1,j} } , \end{aligned}$$

with

$$\begin{aligned} C_{1,0}= & {} \hat{{\alpha }}_{i,j}^2 \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y +\alpha _{i,j} F_{i,j}^{xy} } \right\} ,\\ C_{1,1}= & {} 2\hat{{\alpha }}_{i,j} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \hat{{\Delta }}_{i,j} +\frac{h_i \alpha _{i,j} }{\hat{{h}}_j }\left( {F_{i,j+1}^x -F_{i,j}^x } \right) } \right\} \qquad \qquad \qquad \qquad \\&-2\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1}^y } \right. \left. {+\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} \\&+\hat{{\alpha }}_{i,j}^2 \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y +\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} ,\\ C_{1,2}= & {} \left( {3\hat{{\alpha }}_{i,j} \hat{{\gamma }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\gamma }}_{i,j} +6\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\delta }}_{i,j} } \right) \left\{ \left( {\alpha _{i,j} +\beta _{i,j} } \right) \hat{{\Delta }}_{i,j}\right. \\&\left. +\frac{h_i \alpha _{i,j} }{\hat{{h}}_j }\left( {F_{i,j+1}^x -F_{i,j}^x } \right) \right\} \\&-\left( {3\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \hat{{\delta }}_{i,j} \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1}^y +\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} \\&-\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \hat{{\alpha }}_{i,j} \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y } \right. \left. {+\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} ,\\ C_{1,3}= & {} \left( {\hat{{\alpha }}_{i,j} \hat{{\gamma }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\gamma }}_{i,j} +6\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} +3\hat{{\beta }}_{i,j} \hat{{\delta }}_{i,j} } \right) \left\{ \left( {\alpha _{i,j} +\beta _{i,j} } \right) \hat{{\Delta }}_{i,j}\right. \\&\left. +\frac{h_i \alpha _{i,j} }{\hat{{h}}_j }\left( {F_{i,j+1}^x -F_{i,j}^x } \right) \right\} \\&-\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \hat{{\delta }}_{i,j} \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1}^y +\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} \\&-\left( {\hat{{\gamma }}_{i,j} +3\hat{{\delta }}_{i,j} } \right) \hat{{\alpha }}_{i,j} \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y } \right. \left. {+\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} ,\\ C_{1,4}= & {} 2\hat{{\delta }}_{i,j} \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) \hat{{\Delta }}_{i,j} +\frac{h_i \alpha _{i,j} }{\hat{{h}}_j }\left( {F_{i,j+1}^x -F_{i,j}^x } \right) } \right\} \\&-2\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j}^y } {+\alpha _{i,j} h_i F_{i,j}^{xy} } \right\} \\&+\,\hat{{\delta }}_{i,j}^2 \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1}^y +\alpha _{i,j} h_i F_{i,j+1}^{xy} } \right\} ,\\ C_{1,5}= & {} \hat{{\delta }}_{i,j}^2 \left\{ {\left( {\alpha _{i,j} +\beta _{i,j} } \right) F_{i,j+1}^y +\alpha _{i,j} F_{i,j+1}^{xy} } \right\} , \end{aligned}$$

$$\begin{aligned} C_2= & {} \sum _{j=0}^5 {\left( {1-\phi } \right) ^{5-j}\phi ^{j}C_{2,j} } , \end{aligned}$$

with

$$\begin{aligned} C_{2,0}= & {} \hat{{\alpha }}_{i,j}^2 \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y -\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} ,\\ C_{2,1}= & {} 2\hat{{\alpha }}_{i,j} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \hat{{\Delta }}_{i+1,j} -\frac{h_i \delta _{i,j} }{\hat{{h}}_j }\left( {F_{i+1,j+1}^x -F_{i+1,j}^x } \right) } \right\} \\&-2\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1}^y } {-\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} \\&+\,\hat{{\alpha }}_{i,j}^2 \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y -\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} ,\\ C_{2,2}= & {} \left( {3\hat{{\alpha }}_{i,j} \hat{{\gamma }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\gamma }}_{i,j} +6\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\delta }}_{i,j} } \right) \left\{ \left( {\gamma _{i,j} +\delta _{i,j} } \right) \hat{{\Delta }}_{i+1,j}\right. \\&\left. -\frac{h_i \delta _{i,j} }{\hat{{h}}_j }\left( {F_{i+1,j+1}^x -F_{i+1,j}^x } \right) \right\} \\&-\left( {3\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \hat{{\delta }}_{i,j} \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} \\&-\left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \hat{{\alpha }}_{i,j} \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y } \right. \left. {-\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} ,\\ C_{2,3}= & {} \left( {\hat{{\alpha }}_{i,j} \hat{{\gamma }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\gamma }}_{i,j} +6\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} +3\hat{{\beta }}_{i,j} \hat{{\delta }}_{i,j} } \right) \left\{ \left( {\gamma _{i,j} +\delta _{i,j} } \right) \hat{{\Delta }}_{i+1,j}\right. \\&\left. -\frac{h_i \delta _{i,j} }{\hat{{h}}_j }\left( {F_{i+1,j+1}^x -F_{i+1,j}^x } \right) \right\} \\&-\left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \hat{{\delta }}_{i,j} \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} \\&+\left( {\hat{{\gamma }}_{i,j} +3\hat{{\delta }}_{i,j} } \right) \hat{{\alpha }}_{i,j} \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y } \right. \left. {-\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} ,\\ C_{2,4}= & {} 2\hat{{\delta }}_{i,j} \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) \hat{{\Delta }}_{i+1,j} -\frac{h_i \delta _{i,j} }{\hat{{h}}_j }\left( {F_{i+1,j+1}^x -F_{i+1,j}^x } \right) } \right\} \\&-2\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j}^y } \right. \left. {-\delta _{i,j} h_i F_{i+1,j}^{xy} } \right\} \\&+\,\hat{{\delta }}_{i,j}^2 \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} ,\\ C_{2,5}= & {} \hat{{\delta }}_{i,j}^2 \left\{ {\left( {\gamma _{i,j} +\delta _{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} h_i F_{i+1,j+1}^{xy} } \right\} , \end{aligned}$$

$$\begin{aligned} C_3= & {} \sum _{j=0}^5 {\left( {1-\phi } \right) ^{5-j}\phi ^{j}C_{3,j} } , \end{aligned}$$

with

$$\begin{aligned} C_{3,0}= & {} \hat{{\alpha }}_{i,j}^2 \delta _{i,j} F_{i+1,j}^y ,\\ C_{3,1}= & {} 2\delta _{i,j} \hat{{\alpha }}_{i,j} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) \hat{{\Delta }}_{i+1,j} -2\hat{{\alpha }}_{i,j} \delta _{i,j} \hat{{\delta }}_{i,j} F_{i+1,j+1}^y +\delta _{i,j} \hat{{\delta }}_{i,j}^2 F_{i+1,j}^y ,\\ C_{3,2}= & {} \delta _{i,j} \left( {3\hat{{\alpha }}_{i,j} \hat{{\gamma }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\gamma }}_{i,j} +6\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\delta }}_{i,j} } \right) \hat{{\Delta }}_{i+1,j}\\&-\,\delta _{i,j} \hat{{\delta }}_{i,j} \left( {3\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} \hat{{\alpha }}_{i,j} \left( {\hat{{\gamma }}_{i,j} +\hat{{\delta }}_{i,j} } \right) F_{i+1,j}^y ,\\ C_{3,3}= & {} \delta _{i,j} \left( {\hat{{\alpha }}_{i,j} \hat{{\gamma }}_{i,j} +\hat{{\beta }}_{i,j} \hat{{\gamma }}_{i,j} +6\hat{{\alpha }}_{i,j} \hat{{\delta }}_{i,j} +3\hat{{\beta }}_{i,j} \hat{{\delta }}_{i,j} } \right) \hat{{\Delta }}_{i+1,j}\\&-\,\delta _{i,j} \hat{{\delta }}_{i,j} \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) F_{i+1,j+1}^y -\delta _{i,j} \hat{{\alpha }}_{i,j} \left( {\hat{{\gamma }}_{i,j} +3\hat{{\delta }}_{i,j} } \right) F_{i+1,j}^y ,\\ C_{3,4}= & {} 2\delta _{i,j} \hat{{\delta }}_{i,j} \left( {\hat{{\alpha }}_{i,j} +\hat{{\beta }}_{i,j} } \right) \hat{{\Delta }}_{i+1,j} -2\hat{{\alpha }}_{i,j} \delta _{i,j} \hat{{\delta }}_{i,j} F_{i+1,j}^y +\delta _{i,j} \hat{{\delta }}_{i,j}^2 F_{i+1,j+1}^y ,\\ C_{3,5}= & {} \hat{{\delta }}_{i,j}^2 \delta _{i,j} F_{i+1,j+1}^y . \end{aligned}$$