Some Analytical and Computational Aspects of Prime Numbers, Prime Number Theorems and Distribution of Primes with Applications

“Numbers rules the Universe.

” The Pythagoreans

“God made the integers, all the rest is the work of man.

” Leopold Kroneker

“It is India that gave us the ingenious method of expressing all numbers by ten symbols, each symbol recurring a value of position, as well as an absolute value. We shall appropriate the grandeur of the achievement when we remember that it escaped the genius of Archimedes and Applolonius.”

P. S. Laplace

“Mathematicians have tried in vain to discover some order in the sequence of prime numbers but we have every reason to believe that there are some mysteries which human minds never penetrate.

” Leonhard Euler

Abstract

This paper deal with the development of prime and composite numbers and their modern applications to mathematical and physical sciences. It contains the distribution of prime numbers, prime number theorems, Euler’s and Riemann’s zeta functions and their remarkable link with prime numbers and the celebrated unsolved Riemann Hypothesis (RH). Special attention is given to the discovery of the Fermat and the Mersenne prime numbers, and numerous modern computational results in support of the RH. Proofs of different versions of prime number theorems discovered by many greatest mathematicians of the world are mentioned. Mention is also made of one of the remarkable aspects of the distribution of prime numbers and their tendency to exhibit local irregularity and global regularity. This naturally leads to the stochastic distribution of prime numbers and the Gauss-Cramér probabilistic model to determine the stochastic prime number theorems in short intervals. It is found that the Gauss-Cramér model is consistent with the RH and the twin prime conjecture. Included are many unsolved problems and conjectures that put students, teachers, and mathematical scientists and professionals at the forefront of current advanced study and research in analytical and computational number theory.

Ancient Origins of Natural, Prime and Composite Numbers

From ancient times, the set of numbers $\mathbb {N}=\{1, 2, 3, 4, 5,\ldots \}$ is usually called natural numbers or positive integers or counting numbers. These numbers were used for measuring or counting of objects from the beginning of ancient civilizations and are still used today. In contrast to their usage, the formalization of the natural numbers as a mathematical system are relatively new. It was Guiseppe Peano (1858–1932), an Italian mathematician, who provided an mathematical foundation for the set of natural numbers in 1889 as a deductive system based on a set of axioms:

• Axiom 1 There is a first natural number, 1(one).

• Axiom 2 For each natural number, $n$, there is a next larger one, $(n+1)$ called its successor.

• Axiom 3 Given two different natural numbers, their successors are different.

• Axiom 4 If 1 is in set $S$, $n \in S$, its successor $(n+1) \in S$, then $S$ contains all natural numbers.

Although Peano did not create the natural numbers, he established the natural numbers as a deductive mathematical system, and recognized that, along with the definition of addition and multiplication, all of the fundamental properties of natural numbers can be deduced from those few basic properties.

In addition to positive integers and negative integers, zero was also discovered in ancient times. It is now well known that $\mathbb {Z}$ represents the set of all integers including zero. According to Hermann Minkowski (1864–1909), a renowned German mathematician, “The primary source (Urquell) of all mathematics are the integers”. Today integer arithmetic plays a major role in a wide spectrum of human activities and natural phenomena available to mathematics and sciences. The Pythagoras first pointed out that there was a fundamental role of integers ratios in musical scales. The occurrence of integers in biological sciences, from plant morphology to the genetic code is pervasive. In the optical spectral analysis, certain integer relations between the wavelengths of spectral lines emitted by excited atoms provided early hints for the structures of atoms which led to the creation of matrix mechanics by Werner Heisenberg (1902–1976) in 1925, an important year for the study of integer physics. In chemical physics, Antoine Lavoisier (1743–1794) discovered that chemical components are composed of fixed properties of their constituents which, when represented by proper weights, correspond to the ratios of small integers. This was one of the strongest clues for the existence of atoms that was ignored by chemical physicists for a long time. The discovery of digital computers as descendants of the abacus (suan pan) invented in China is another example of the resurrection of integers in the twentieth century. Another remarkable reason for the recent revival of integers is the convergence of congruential arithmetic with numerous applications in natural sciences and digital communications, especially in cryptography and modern public-key encryption systems. One of the most dramatic applications of congruential arithmetic is the existence of chemical elements. In 1913, Niels Bohr (1885–1962), a great Dutch mathematical physicist, postulated that certain integrals associated with electrons in orbit around the nucleus should have integer values, a requirement that became comprehensible as a wave interference phenomenon of the newly discovered matter waves in around 1925. There is an infinite sequence of energy levels that corresponds to all positive integers of the quantum number $n$. The major importance of integer physics is cited in any book on quantum mechanics including one by Schiff [1].

Historically, another basic problem of number theory was how to factor a natural number into primes which led to the Fundamental Theorem of Arithmetic which states that every natural number $n$ can be uniquely factored into primes as follows:

$$\begin{aligned} n=p^{k_1}_{1} p^{k_2}_{2} \cdots p^{k_m}_{m}=\prod _{r=1}^m p^{k_r}_{r} \end{aligned}$$

(1)

where $p_r$’s are distinct primes with exponent $k$’s. For example, $18=2^1 \times 3^2, 30=2 \times 3 \times 5=2^1 \times 3^1 \times 5^1, 300=2^2 \times 3^1 \times 5^2, 12=2^2 \times 3^1, 24=2^3 \times 3^1, 72=8 \times 9= 2^3 \times 3^2$.

There is no corresponding theorem for the additive decomposition of natural number into primes. The fundamental theorem of arithmetic (1) was found in Book IX of the celebrated 13 books of Euclid’s Elements. Although nothing is known about the great ancient Greek mathematician, Euclid’s (365–300 BC) life, he was the first professor of mathematics at the Museum of Alexandria, Egypt, and lived in Alexandria after the death of Alexander the Great (356–323 BC).

In view of the great importance of natural numbers in mathematics and natural phenomena, it is important to classify the natural numbers into two groups: such as prime numbers (or simply, primes) and composite numbers (or simply, composites), and to understand the divisibility properties of natural numbers the Greatest Common Divisor (GCD), or the Greatest Common Factor (GCF), and the Least Common Multiple (LCM) in number theory. If $m$ and $d$ are natural numbers, and if there is a natural number $n$ such that $m=d \times n$, we say that $d$ is a divisor (or factor) of $m$, or $d$ divides $m$, or $m$ is a multiple of $d$. We denote this relationship by $d|m$. For example, $6|30$ means that there exists some natural number $d=5$ such that $30=d \times 6=5 \times 6$. On the other hand, $10|3$ is false because we cannot find a natural number such that $3=10 \times n$. We write $10 \not \mid 3$ to say that $10$ does not divide $3$.

We next explain the GCD and the LCM by examples. We denote the GCD of two natural numbers $m$ and $n$ by $(m,n)$ and the LCM by $[m,n]$. For example, $m=30,~ n=24$, then by (1), $m=30=2 \times 3 \times 5=2^1 \times 3^1 \times 5^1$ , $n=24=2^3 \times 3^1 \times 5^0$. To find GCD, we select representative from the factorization with the smallest exponent. The GCD is the product of these representatives, that is, $(m,n)=2^1 \times 3^1 \times 5^0=6$. Thus, the GCD of a set of numbers is the largest number that divides each number of the set exactly. In this case, $6$ divides $24$ and $30$ exactly.

On the other hand, to find LCM of $24$ and $30$, we choose the representative of each factor with the largest exponent so that $[m,n]=[30,24]=2^3 \times 3^1 \times 5^1=120$. Thus, each member $30$ and $24$ of the set divides the LCM = 120 exactly.

It is interesting to note that the product of the GCD and the LCM is equal to the product of $m$ and $n$, that is,

$$\begin{aligned} (m,n)[m,n]=mn. \end{aligned}$$

(2)

In this case, $6 \times 120=720=30 \times 24$. The generalization of (2) for a set of three natural numbers is

$$\begin{aligned} (m,n,r)[m,n,r]=mnr. \end{aligned}$$

(3)

For example, $m=30, n=24, r=12$ so that $(30,24,12)=2 \times 4 \times 9=72, \quad [m,n,r]=8 \times 3 \times 5=120$ and hence, result (3) follows.

Natural numbers are divided into two groups as even and odd numbers. For example, $2,4,8,10,88,\ldots$ are all even, and $1,3,5,11,13,\ldots$ are all odd.

A natural number $n (>1)$ is called a prime number (or simply, a prime), if it has no factors other than $1$ and itself. A natural number $n (>1)$ is called a composite number (or simply, a composite), if it has factors more than $1$ and itself. Historically, the natural numbers $(n >1)$ are divided into two classes, prime numbers, such as $2,3,5,7,11,13,17,19,23,29,\ldots$ and composite numbers, such as $4,6,8,9,10,12,14,16,18,20,\ldots$ There were several fundamental questions in early mathematics. Whether a given natural number $n (>1)$ is prime or composite? For every natural number $n$, how to compute the number $\pi (n)$ of primes $p$ less or equal to $n$. The factoring of fairly small composite numbers is quite easy. Using electronic computers, it is possible to factorize large numbers quickly. However, the general problem of finding the factors of every large composite numbers is still a difficult problem. In general, there are no easy algorithms or methods of solutions of the above basic problem. However, for small values of $n$, it is always possible to determine whether $n$ is prime or composite, and to compute $\pi (n)$ exactly. For example, $\pi (10)=4$ and $\pi (20)=8$. But, for large $n$, it is not easy to compute $\pi (n)$.

From the table of prime numbers, ancient Greek mathematicians knew that there were infinitely many primes. About twenty-three centuries ago, Euclid recognized that there is no largest prime number, and he gave a beautiful proof by the method of contradiction (reductio ad absurdum) which verified that there are infinite number of primes so that $\pi (n) \rightarrow \infty$ as $n \rightarrow \infty$. This is known as the Euclidian prime number theorem. After the discovery of the Euclid fundamental theorem, a Greek mathematician, Eratosthenes, (266–194 BC) developed a simple method, called sieve of Eratosthenes, of finding the prime numbers and the number $\pi (n)$ of primes $p$ less or equal to a given small natural number $n$. For example, we want to find out all primes less than $20$. We write all numbers from $1$ to $20$ in a row. $1,~ 2, ~3,~ 4,~ 5,~ 6,~ 7, ~8,~ 9,~ 10,~ 11, ~12, ~13, ~14,~ 15,~ 16, ~17, ~18,~ 19,~ 20$. Cross out $1$, since it is not prime. Now $2$ is a prime, but no other even number is, since they are all divisible by $2$. So cross out all even numbers $4,6,8,\ldots$. The first number not crossed out is $3$ which is a prime. Next, cross out all subsequent multiples of $3, (6,9,12,\ldots )$. Proceeding in this way, we come to the primes $5$ and $7$ and cross out multiples of them. We look at the numbers $2,~3,~5,~7,~11,~13,~17,~19$ not crossed out. These are all primes up to $20$ and $\pi (20)=8$. This sieve method can be used to find the prime numbers less than $n$. But it does not tell us much about how many primes are there, especially when $n$ is large.

Modern Development of Prime Numbers

In the history of prime numbers, two types of prime numbers known as the Mersenne prime and the Fermat (1601–1665) prime have received considerable attention. A French Monk, Marin Mersenne (1588–1648) conjectured that there are finitely many prime numbers of the form (see Debnath [2])

$$\begin{aligned} M_p=2^p-1 \end{aligned}$$

(4)

if $p$ is a prime, These are known as the Mersenne primes. However, all primes $p$ do not generate all Mersenne primes. For example, $M_{11}=2^{11}-1=2047=23 \times 89$ which is not a prime, but a composite number. There is a fairly simple primality test for the Mersenne primes that is called the Edouard Lucas Test (Lucas [3]) which states that $M_p=2^p-1$ is a prime if and only if $M_p$ divides $S_p \quad (p>2)$, where $S_p$ is defined by the recurrence relation:

$$\begin{aligned} S_n=S^2_{n-1}-2, \qquad \text {with} \qquad S_2=4. \end{aligned}$$

(5)

This Lucas Test ensures that $M_{11}=2047$ is composite. However, this test does not determine any factors of $M_p$. There is another test that gives a factor of $M_p$ with $p=2k+3$. If $M_p$ is composite, it is divisible by $2p+1$ if and only if $M_p$ is not divisible by $\frac{1}{2} (p-1)$. For example, $M_{11}=2047$ is not divisible by $\frac{1}{2} (p-1)=5$, but it is divisible by $2p+1=23$. Similarly, $M_{23}=2^{23}-1$ is divisible by $2p+1=47$.

Euclid first discovered the Mersenne prime in 350 BC. Using the Great Internet Prime Secret (GIPS) project, as of 2014 only 48 Mersenne prime have now been discovered by several mathematicians of Europe and America including $M_p=2^{578~885~161}-1$ which was discovered in 2013. Apparently, the distribution of the Mersenne prime is very rare. It is not known whether there are infinitely many Mersenne primes. This is one of the great unsolved problems in mathematics.

It has been stated that the method of Eratosthenes gives a finite number of primes, but it is not very satisfactory to use for determining whether a given number $n$ is a prime. From ancient times, mathematicians made an attempt to find a formula that would generate every prime. In pursuit of primes, Leonhard Euler (1707–1783) developed a quadratic function in the form,

$$\begin{aligned} f(n)=n^2+n+41, \qquad n=0,1,2,\cdots \end{aligned}$$

(6)

that gives only primes. For $n=0$ to $39$, the exact values of $f(n)$ are primes. For example, $f(0)=41, f(1)=43, f(2)=47$ which are primes. Indeed, (6) produces a large number of primes, but $f(40)=1681=(41)^2$ which is not a prime.

The quadratic expression (6) generates 80 consecutive primes for $n=-40, -39,\ldots , 0$, $1, 2,\ldots , 39$. This is remarkable because it would normally take a polynomial in $n$ of degree 80 to get 80 prime for consecutive values of $n$. Moreover, there are many primes of the form $f(n)=4n^2+an+b$ which makes them lie on straight lines when $n$ is plotted along a square sprial. Thus, the upshot is that there exists no polynomials, no matter how high its degree, which give primes for all values of $n$.

Peter Gustav Dirichlet (1805–1859), a great German mathematician and Carl Friedrich Gauss’s (1777–1855) successor in Göttingen, proved a celebrated theorem that there are infinitely many primes in every linear progression

$$\begin{aligned} f(n)=an+b, \qquad n=1,2,3,\ldots , \end{aligned}$$

(7)

provided constants $a$ and $b$ are coprimes, that is, $(a,b)=1$. For example, if $a=10,~b=1,3,7~ \text{ or }~9$, there exists infinitely many primes whose last digit is $1, 3, 7 ~\text{ or }~ 9$.

In early 1982, the largest sequence known for which $an+b$ gives primes for consecutive $n$ is the progression in the form,

$$\begin{aligned} 233~ 092~ 870~n+ 233~ 613 ~ 3941 \end{aligned}$$

(8)

which are primes for sixteen successive values for $n=0,1,2,\ldots ,15$.

The first seven even numbers after $2$ are $4,6,8,10,12,14$, and $16$. Each of them can be expressed as the sum of two prime numbers as follows: $4=2+2, \quad 6=3+3, \quad 8=3+5, \quad 10=5+5, \quad 12=5+7, 14=7+7$ and $16=5+11$. The question is whether every even number can be so expressed. It seems that it can be done, but this fact has never been proved nor disproved. Consequently, it is another unsolved problem in mathematics, called the Goldbach conjecture after the famous German mathematician Christian Goldbach (1690–1764), who first made this conjecture in his letters to Euler in 1742. Euler was unable to prove or disprove this famous Goldbach conjecture. However, it has been numerically confirmed that it is true for very large numbers up to $4 \times 10^4$. Some progress has also been made on related weaker assertions. In 1937, a famous Russian mathematician, Ivan M Vinogradov (1891-1983) proved that any sufficiently large odd natural number can be written as the sum of at most three prime numbers.

There are immediate characterizations of prime numbers, that is, $p$ is prime, if and only if $\sigma (p)=p-1$. More generally, if $p$ and $q$ are different primes then

$$\begin{aligned} \sigma (pq)=\sigma (p)\sigma (q). \end{aligned}$$

(9)

For example, $\sigma (21)=\sigma (3\times 7)=\sigma (3)\sigma (7)=4 \times 8 = 32$. Euler proved a more general result, that is, the multiplicative result (9) holds not just for different prime numbers, but for any whole number whose greatest common divisor is $1$. More explicitly, Euler proved the following theorem: If $gcd (a,b)=1$, then

$$\begin{aligned} \sigma (a,b)=\sigma (a)\sigma (b). \end{aligned}$$

(10)

For example, to determine the sum of all divisor of $585$, we write into relatively prime factors, and use the above theorem. Thus,

$$\begin{aligned} \sigma (585)=\sigma (5 \times 9 \times 14)=\sigma (5)\sigma (9)\sigma (13)=6 \times 13 \times 14=1092. \end{aligned}$$

(11)

Euler used his sigma function to reformulate the definition of amicable number pairs by noting that the sum of the proper divisor of a whole number of $n$ is $\sigma (n)-n$. Consequently, $m$ and $n$ are amicable pairs if and only if $\sigma (m)-m=n$ and $\sigma (n)-n=m$. This leads to Euler’s famous definition that $m$ and $n$ are amicable if and only if

$$\begin{aligned} \sigma (m)=m+n=\sigma (n). \end{aligned}$$

(12)

Euler used this elegant characterization as his method of testing in the world of amicable numbers.

Another great discovery of Fermat are the so-called Fermat numbers consisting of the Fermat primes and the Fermat composites. The Fermat numbers are defined by

$$\begin{aligned} F_n=2^{2^n}+1, \qquad n=0,1,2,3,4,5,\ldots . \end{aligned}$$

(13)

In 1640, Fermat also conjectured that $F_n$ are all primes for $n \ge 0$, the first five $F_0=3, F_1=5, F_2=17, F_3=257$, and $F_4=65537$ are primes, but

$$\begin{aligned} F_5=2^{2^5}+1=4292~967~297=641\times 6700~417, \end{aligned}$$

(14)

is not a prime. This remarkable result was found by Euler in 1732 (about a hundred year later). Fermat numbers $F_6, F_7, F_8$ are all composite and some of their factors are known. At least two hundred Fermat’s numbers are known to be composite including, $F_n$ for $n=2478782$ which was discovered by John Cosgrave and his associates at the St. Patrick College, Dublin in 2003. In 1880, Landry had shown that $F_6$ is composite with a prime factor, $274~177$. On the other hand, Morehead and Western found $F_7$ is composite without factors in 1905, it was until 1971 where Brillhart and Morrison used an IBM 360-91 computer to find the factors of 39-digit composite $F_7$ as

$$\begin{aligned} F_7=(596~495~891~274~972~17) \times (5704~689~200~6851~290~54721) \end{aligned}$$

(15)

Morehead and Western also showed that $F_8$ is composite in 1909 without factors. Subsequently, Brent and Pollard found the factors of $F_8$ in 1981. It is evident that computational ingenuity helped factorize Fermat large composite numbers. However, as of today, it is not known whether 4933-digit Fermat number is prime or composite. On the other hand, it is amazing that $F_{3310}$ is found to be extremely large composite Fermat number with $10^{990}$ digits, and $5 \times 2^{3313}+1$ as a factor. However, it is known today that $F_n$ is composite for $5 \le n \le 32$. All these have been possible due to large and powerful super computers with modern factoring algorithms.

It is noted that $2^{m}+1$ would be a prime provided $m$ is a power of $2$. In fact, $a^m+1$ would be a prime if $a$ is even and $m=2^n$ (Fig. 1).

There are some simple properties of Fermat primes. First, they satisfy a simple recursion relation

$$\begin{aligned} F_{n+1}=(F_n-1)^2+1. \end{aligned}$$

(16)

Or, equivalently,

$$\begin{aligned} F_{n+1}-2=F_n(F_n-2)=F_nF_{n-1}(F_{n-1}-2). \end{aligned}$$

(17)

This leads to the product formula for $(F_n-2)$ as

$$\begin{aligned} F_{n}-2=F_0 F_1 \ldots F_{n-1}. \end{aligned}$$

(18)

This means that all lower Fermat primes are factors of $(F_n-2)$. In other words, $(F_n-2)$ is divisible by all lower Fermat primes:

$$\begin{aligned} F_{n-r} | (F_{n}-2), \qquad 1<r \le n. \end{aligned}$$

(19)

Fig. 1

Equilateral triangle and regular pentagon

This also leads to another interesting property that all Fermat numbers are co-prime to each other. In other words, if $m$ and $n$ are distinct primes, then

$$\begin{aligned} \left( F_m,F_n\right) =1. \end{aligned}$$

(20)

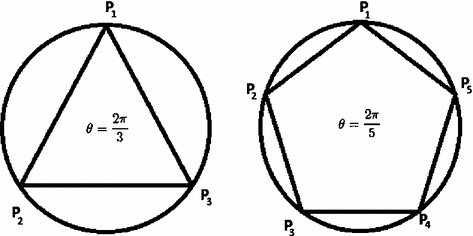
The Greek mathematicians knew how to construct n-sided regular polygons (with all of its sides are equal and all of its internal angles are equal) for $n=3, 4, 5, 6, 8, 10, 12, 15$ and $16$. This is a general problem of dividing a circle into $n$ equal parts which is equivalent to constructing a regular $n$-gon with $n$ vertices inscribed in the circle. Mathematically, the $n$ equidistant points on the unit circle are given by

$$\begin{aligned} z_m=\exp \left( \frac{2 \pi i m}{n}\right) , \qquad m=0, 1, 2,\ldots , n-1. \end{aligned}$$

(21)

This points divide the unit circle into $n$ equal parts and represent the vertices of a regular n-gon inscribed in the circle. Finding the $z_m$ in (17) is the same as solving the roots of the cyclotomic polynomial equation

$$\begin{aligned} z^n-1=(z-1)(z^{n-1}+z^{n-2}+ \cdots +z+1)=0. \end{aligned}$$

(22)

Thus, we converted the classical geometrical problem into a modern algebraic problem.

Another interesting fact is that the first Fermat prime, $F_0=3$ which corresponds to an equilateral triangle which is easy to construct. The second Fermat prime $F_1=5$ which corresponds to a regular pentagon that can easily be constructed by a ruler and a compass. The next Fermat prime $F_2=17$ which corresponds to the 17-sided regular polygon. The 19-year old Gauss first made a remarkable observation by establishing a link between the Greek geometry and Fermat numbers. The more remarkable fact is that he surprised the whole world by his ingenius construction of 17-sided polygon using a ruler and a compass. He completed the construction of 17-sided polygon based on the solution of cyclotomic polynomial equation of degree $p=17$

$$\begin{aligned} z^{17}-1=(z-1)(z^{16}+z^{15}+ \cdots +z+1)=(z-1) C_{17}(z)=0, \end{aligned}$$

(23)

where $C_{17}(z)$ cannot be further factored into polynomial with rational coefficients Fig. 2. Gauss observed that $C_{17}(z)$ can be decomposed into a set of nested quadratic equations, each solvable by geometrical method so that a regular 17-sided polygon of side length $l$ can be constructed by a ruler and a compass, where

$$\begin{aligned} l&= \frac{1}{8} \left[ (\sqrt{17}-1)+\sqrt{34-2\sqrt{17}}\right. \nonumber \\&\left. +\,\sqrt{68+12\sqrt{17}-16\sqrt{34+2\sqrt{17}} +2(\sqrt{17}-1)\sqrt{34-2\sqrt{17}}}\right] . \end{aligned}$$

(24)

This seems to be a complicated but splendid expression which contains only square roots and no other irrational quantities. Gauss was so proud of his discovery that he left an instruction before his death to engrave a regular 17-sided polygon on his grave. Although his wish was never fulfilled, such a polygon was, indeed, inscribed on the sides of the monument erected in his birthplace in Brunswick, Germany.

Fig. 2

Gauss’s 17-sided polygon

In fact, Gauss developed a spectacular method of solution of cyclotomic equation with prime $p$ in the form

$$\begin{aligned} z^p-1=0 \end{aligned}$$

(25)

in terms of roots of a sequence of equations whose degree are the prime factors of $(p-1)$. So, if $p=2^n+1$, all such equations lead to quadratic equations, and hence, the corresponding geometrical problem is solvable by Euclidean methods.

His method confirmed that a Euclidean solution of Eq. (25) is possible if and only if $p$ is a Fermat prime. More remarkable fact is that Gauss’ method had numerous modern applications including the design of highly effective error-correcting codes, fast computational algorithms in making precise measurements of exceedingly weak relativistic effects, and even the design of unique phase gratings for scattering sound in concert halls to achieve better acoustic quality. Often, some example of applications in mathematics is more spectacular than the mathematical discovery itself!

The classical problems about prime and composite numbers are closely related to Gauss’ prophetic quotation of 1801:

“The problem of distinguishing prime numbers from composite numbers, and of resolving the latter into their prime factors, is known to be one of the most important and useful in arithmetic. It has engaged the industry and wisdom of ancient and modern geometers to such an extent that it would be superfluous to discuss the problem at length. Nevertheless, we must confess that all methods that have been proposed thus far are either restricted to very special cases or are so laborious and difficult that even for numbers that do not exceed the limits of tables constructed by estimable men, they try the patience of even the practiced calculator. And these methods do not apply at all to larger numbers... . Further, the dignity of the science itself seems to require that every possible means be explored for the solution of a problem so elegant and so celebrated.”

Evidently, primality and factorization into primes have become the basic computational problems in number theory. Indeed, all branches of number theory deal with proofs, heuristic reasonings, conjectures and computations. So, there are some questions regarding elementary properties of primes or composites involved in Fermat’s Little Theorem (FLT), Euler’s phi function, and Wilson’s theorem which will be discussed below with examples.

Fermat Little Theorem. If $p$ is prime and $a$ is any integer prime to $p$, that is, $(a,p)=1$, then $a^{p-1}-1$ is divisible by $p$. In other words,

$$\begin{aligned} a^{p-1} \equiv 1 ~(\text{ mod }~p),~~\text{ or },~~a^p \equiv a ~(\text{ mod }~p). \end{aligned}$$

(26)

For example, if $p=5$ and $a=1,2,3,4$. then $a^5 \equiv a~(\text{ mod }~5)$. It seems that computing a large power modulo $p$ is a difficult computational problem. It is noted here that FLT is also true when $p$ is not a prime. If $n=341=31 \times 11$ is composite, and $a=2$, then $a^{n-1}-1=2^{340}-1$ is divisible by 341.

In 1760, Euler made a remarkable generalization of the FLT(26) by introducing a new function $\phi (n)$, known as the Euler phi (or totient) function which is defined as the number of positive integers $\phi (n)=r<n$ and relatively prime to $n$, that is, $1 \le r<n$ and $(r,n)=1$.

Euler Theorem. If $a$ is an integer and $(a,n)=1$, then $a^{\phi (n)}-1$ is divisible by $n$, that is,

$$\begin{aligned} a^{\phi (n)} \equiv 1 \qquad (\text{ mod }~n). \end{aligned}$$

(27)

For example, if $n=9$, then $\phi (n)=6$ because integers less than 9 and co prime to 9 are 1,2,3,4,5,7 and 8. If $a=5$, and $n=9$, then $5^{\phi (n)}=5^6 \equiv 1~~(\text{ mod }~9)$. In fact, $5^6=15625$ and the sum of all integers in 15625 is $1+5+6+2+5=19 \equiv 1~(\text{ mod }~9)$.

If $p$ is a prime, and $k$ is a positive integer, then $\phi (p^k)=p^k-p^{k-1}=p^k \left( 1-\frac{1}{p}\right)$, so, in general, if $n$ is of the form (1), then

$$\begin{aligned} \phi (n)=n\left( 1-\frac{1}{p_1}\right) \left( 1-\frac{1}{p_2}\right) \cdots \left( 1-\frac{1}{p_m}\right) . \end{aligned}$$

(28)

This is a general formula for the Euler phi function in terms of prime factors. For example, $\phi (30)=30\left( 1-\frac{1}{2}\right) \left( 1-\frac{1}{3}\right) \left( 1-\frac{1}{5}\right)$ and $\phi (72)=\phi (2^3 \times 3^2)=72\left( 1-\frac{1}{2}\right) \left( 1-\frac{1}{3}\right) =24$. Using prime factorization of $n$, it is possible to find another formula for $\phi (n)$, which follows directly from (28) in the form

$$\begin{aligned} \phi (n)=p_1^{k_1-1}(p_1-1)p_2^{k_2-1}(p_2-1) \cdots p_m^{k_m-1}(p_m-1). \end{aligned}$$

(29)

For example, $\phi (72)=(2^3 \times 3^2)=2^{3-1}(2-1)3^{2-1}(3-1)=24$.

On the other hand, for $a$ composite number $n$, we obtain totally new and often unexpected results. For example, $n=10,~\phi (n=10)=4$ as $r=1,3,7,9$. Then $a^4-1$ is divisible by 10. In other words, the fourth power of any number not containing the factors 2 or 5 has 1 as the last digit so that $3^4=81,~7^4=2401,~9^4=6561,~13^4=28~561$ and so on.

There is another result originally guessed by John Wilson (1741–1793) (a senior Wrangler of Cambridge University) who obtained the result based on empirical evidence. In 1770, the British mathematician Edward Waring (1736–1798) published his student Wilson’s result in Meditationes Algeraicae without a proof. This result is known as Wilson’s theorem as follows: If integer $p$ is prime, then $p$ divides $(p-1)!+1$. In other words,

$$\begin{aligned} (p-1)!+1 \equiv 0 \qquad (\text{ mod }~p). \end{aligned}$$

(30)

For example, if $p=5$, then $(5-1)!+1 \equiv 25 \equiv 0~(\text{ mod }~5)$. The Wilson primes include 5, 13, and 563.

The proof of Wilson’s theorem follows from Fermat’s theorem (26) in the form

$$\begin{aligned} a^{p-1}-1 \equiv 0 \qquad (\text{ mod }~p), \end{aligned}$$

(31)

which holds for $a=1,2,\ldots ,p-1$. According to the fundamental theorem of algebra, these $(p-1)$ roots must be all roots of Eq. (31). Thus, we can write

$$\begin{aligned} a^{p-1}-1 \equiv (a-1)(a-2)\cdots (a-p+1) \qquad (\text{ mod }~p), \end{aligned}$$

(32)

Putting $a=p$ gives

$$\begin{aligned} p^{p-1}-1 \equiv (p-1)(p-2)\cdots 1=(p-1)! \qquad (\text{ mod }~p), \end{aligned}$$

(33)

Since $p^{p-1} \equiv 0~(\text{ mod }~p)$, (33) is the Wilson theorem. In 1771, Joseph Louis Lagrange (1736-1813) gave another proof of Wilson’s theorem. This theorem initially seems to be very promising, but it is not easy to compute a large factorial. So, from a computational point of view, it is not a useful result.

A direct consequence of Wilson’s theorem is another new function $f(n)$ given by

$$\begin{aligned} f(n)=\sin \left[ \frac{\pi }{n}\{(n-1)!+1\}\right] ={\left\{ \begin{array}{ll} 1, &{} \quad n \equiv 1~ \text{ or } \text{ prime } \\ 0, &{} \quad \text {otherwise } \end{array}\right. } \end{aligned}$$

(34)

A prime $p$ is called a Sophie Germain (1776–1831) prime if $(2p+1)$ is also a prime which is often known as safe prime. For example, 23 is a Sophie Germain prime and $2 \times 23+1=47$ is the safe prime. The Sophie Germain primes include $2,~3,~5,~11,~23,~29,~41,~53,~83,~89,~131,~173,\ldots$. Sophie Germain is a famous French mathematician who first discovered the above primes in the number theory. In August 2013, the largest Sophie Germain prime was discovered. Both Sophie primes and associated safe primes have applications in public key cryptography and primality testing. It has been conjectured that there are infinitely many Sophie Germain primes which was not yet proved or disproved.

Before the late twentieth century, it was impossible for a woman to get education in schools and colleges, and to receive recognition in the academic world. Sophie Germain was not given any opportunity to study mathematics or science at French colleges and universities. She was, indeed, a self-educated research mathematician and become one of the prominent mathematicians in the world for her outstanding contributions to number theory, mathematical theory of elasticity, the curvature of surfaces and differential equations. Her research work had received relatively less attention by a galaxy of celebrated French mathematicians including Augustin Cauchy (1789–1857), S.D. Poisson (1781–1840), J.L. Lagrange (1736–1813), Joseph Fourier (1768-1830) and others. Without revealing her identity as woman, Sophie Germain began corresponding with A.M. Legendre (1752–1833) on problems of number theory, and then with Gauss regularly on problems of mathematics. It was only Gauss, Legendre and Neil Abel (1802–1829) who recognized her extraordinary talents and mathematical ability, and praised her research contributions to mathematics and mechanics.

Another prime $p$, somewhat related to Fermat prime, is called Wieferich prime if

$$\begin{aligned} 2^{p-1}-1 \equiv 0 \qquad (\text{ mod }~p^2). \end{aligned}$$

(35)

This prime was introduced by the German mathematician, Arthur Wieferich (1884-1954). The only known Wieferich primes until 2013 are 1093 and 3511.

We close this section by adding a property of an odd composite number that every composite number can be factored as the difference of two squares. If $n$ is composite with nontrivial factors $a$ and $b$ so that $n=ab$, then, we find $n=u^2-v^2=(u+v)(u-v)$, where $u=\frac{1}{2}(a+b)$ and $v=\frac{1}{2}(a-b)$. This method works very well if $n$ has a divisor very close to $\sqrt{n}$. For example, $n=8051=90^2-7^2=(90+7)(90-7)=(97)(83)$ as $\sqrt{n}=\sqrt{8051} \approx 89.73$.

Distributions of Primes and Prime Number Theorems

Although the existence of primes goes back to antiquity, some elementary properties of prime numbers were known to Greeks. As it has been mentioned, the standard modern notation $\pi (x)$ was adopted for the prime counting function which represents the number of primes less than or equal to $x$. It follows from numerous examples that $\pi (x)$ is an increasing step function of $x$. This leads to the equivalent statement of the Euclid theorem that

$$\begin{aligned} \lim _{x \rightarrow \infty } \pi (x)=\infty . \end{aligned}$$

(36)

Subsequently, this function had been a new fertile idea of advanced study and intensive research by many great mathematicians over the next three hundred years.

Using a totally different argument than Euclid, in 1737 Euler proved that the number of primes is infinite by showing that the sum of their reciprocals is divergent, that is,

$$\begin{aligned} \sum _{n=p=\text{ prime }} \frac{1}{n}=\infty . \end{aligned}$$

(37)

During the third century BC, a method of the sieve of Eratosthenes was developed for finding the number $\pi (x)$ of primes from $1$ to $x$. Thus, the analytical formula of the sieve was given by

$$\begin{aligned} \pi (x)-\pi (\sqrt{x})+1=\sum _{d} (-1)^{w(d)}\left[ \frac{x}{d}\right] , \end{aligned}$$

(38)

where $d$ takes the values of the divisors of the product of all prime numbers $\le \sqrt{x}, w(d)$ is the number of prime divisors of $d$ and $[x]$ is the integral part of $x$. However, this formula was not very suitable for finding $\pi (x)$ as $x \rightarrow \infty$.

In around 1730, Euler first introduced the zeta function defined by the convergent infinite series for real $s>1$ in the form

$$\begin{aligned} \zeta (s)=\sum _{s=1}^{\infty } \frac{1}{n^s}=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\cdots +\frac{1}{n^s}+\cdots \infty . \end{aligned}$$

(39)

When $s=1$, the series (39) becomes the celebrated harmonic series which diverges to infinity very slowly. When $s=2$. $\zeta (2)=\frac{{\pi }^2}{6}$ which is the exact sum of the squares of the reciprocals of the integers. This is known as the celebrated Basel problem. When $s=1$, the harmonic series

$$\begin{aligned} 1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \infty . \end{aligned}$$

(40)

strongly motivated Euler to discover a new mathematical constant, now known as the Euler universal constant, $\gamma$ defined by ( see Debnath [2])

$$\begin{aligned} \gamma =\lim _{n \rightarrow \infty } (1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}-\log n). \end{aligned}$$

(41)

It has not yet proved whether $\gamma$ is rational or irrational. Euler had shown from numerical computation that $\gamma =0.577218\cdots$.

Using his neat and elegant analytic proof (see Debnath [2]), Euler proved his celebrated result

$$\begin{aligned} \zeta (s)= \prod _p \left( 1-\frac{1}{p^s}\right) ^{-1}, \qquad Re(s)>1, \end{aligned}$$

(42)

where the product is taken for all primes $p$. Or, equivalently,

$$\begin{aligned} \frac{1}{\zeta (s)}= \prod _p \left( 1-\frac{1}{p^s}\right) , \end{aligned}$$

(43)

Thus, Euler result (42) or (43) expresses the zeta function as an infinite product extended over prime numbers only. This remarkable discovery of Euler was the starting point of the study Riemann’s zeta function for complex $s$, and the Riemann Hypothesis. Evidently, the zeta function is closely related to the distribution of prime numbers and plays a fundamental role in number theory and analysis. The remarkable result (42) leads to the unique factorization property of natural numbers. When $s=1$, it follows from (42) that,

$$\begin{aligned} \zeta (1)= \sum _{n=1}^{\infty } \frac{1}{n}=\prod _p \left( 1-\frac{1}{p}\right) ^{-1}. \end{aligned}$$

(44)

Or, equivalently,

$$\begin{aligned} \prod _p \left( 1-\frac{1}{p}\right) =0, \end{aligned}$$

(45)

where the product is taken over all primes. Based on his imprecise argument, Euler proved that

$$\begin{aligned} \sum _{p} \frac{1}{p}=\infty , \quad \text{ and } \quad \pi (x)>\log \left( \frac{x}{e}\right) , \end{aligned}$$

(46)

where the sum is taken over all primes $p$, and arrived at the correct conclusion that the number of primes is infinite. Of course, if there were finite number of primes, the above series (46) would converge automatically. He originally believed that prime numbers are distributed totally irregularly. The Euclid’s Elements contained the solution of the problem in a simple and elegant manner. However, Euler’s easy proof of the product formula (42) laid the foundation of the analytic number theory and stimulated considerable research on the prime number theory and analysis in the nineteenth and twentieth centuries.

As a natural generalization of his great work that there are infinitely many primes, Euler conjectured that any arithmetic progression of the form

$$\begin{aligned} a,a+h,a+2h,\ldots ,a+nh,\ldots , \end{aligned}$$

(47)

where $a$ and $h$ are relatively prime, contained infinitely many primes. It remained an unsolved problem for almost hundred years. Euler’s product formula and the conjecture inspired Dirichlet, a student of Friedrich Gauss to formulate the general problem of primes in arithmetic progression and to generalize the Euler product formula. Using Euler’s remarkable insight and imagination, Dirichlet proved that there are infinitely many primes in the arithmetic progressions

$$\begin{aligned} 1,5,9,13,\ldots ,(4k+1),\ldots \quad \text{ and } \quad 3,7,11,15,\ldots ,(4k-1),\ldots . \end{aligned}$$

(48)

In order to prove this result (48), Dirichlet first introduced what is now known as the Dirichlet character $\chi (n)=(-1)^k~~\text{ if }~~n$ is odd and $\chi (n)=0~~\text{ if }~~n=\text{ even }$, along with the celebrated Dirichlet series given below in (49). His work first brought number theory and the mathematical analysis together in a new subject now known as analytic number theory.

More remarkable was the Dirichlet’s generalization of Euler zeta function by first introducing Dirichlet L-function defined by

$$\begin{aligned} L(s,\chi )=\sum _{n=1}^{\infty } \frac{\chi (n)}{n^s} \quad \text{ for } \quad s>1 \end{aligned}$$

(49)

Clearly, $\chi (n)$ is a multiplicative function, that is, $\chi (n) \chi (m)= \chi (mn)$ for all $m,n \in \mathbb {Z}$. In particular, the function $L(s)$ is defined by

$$\begin{aligned} L(s)=1-\frac{1}{3^s}+\frac{1}{5^s}-\frac{1}{7^s}+\cdots = \sum _{n=1}^{\infty } \frac{(-1)^{n-1}}{(2n-1)^s}, \end{aligned}$$

(50)

so that

$$\begin{aligned} L(1)=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots =\frac{\pi }{4}. \end{aligned}$$

(51)

Historically, series (51) is probably the most simplest representation for $\frac{\pi }{4}$ published in 1670 by a famous British mathematician, James Gregory (1638–1675). The sum of the Gregory series was also rediscovered by the 28-year old Gottfried Wilhelm Leibniz (1646–1716) in 1674 using geometric arguments. The sum of the Gregory series can easily be calculated as the limit of a definite integral

$$\begin{aligned} \lim _{x \rightarrow 1} \int _0^{x} (1+t^2)^{-1} dt= \lim _{x \rightarrow 1} \left( x-\frac{x^3}{3}+\frac{x^5}{5}- \cdots \right) , 0<x<1. \end{aligned}$$

(52)

Or, equivalently, in the limit as $x \rightarrow 1$,

$$\begin{aligned}{}[\tan ^{-1} t]_0^1=\frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}- \cdots \infty =L(1,\chi ). \end{aligned}$$

(53)

Since the Dirichlet character function $\chi (n)$ is multiplicative, In 1837 Dirichlet generalized the Euler product formula, in the form

$$\begin{aligned} L(s,\chi )=\sum _{n=1}^{\infty } \frac{\chi (n)}{n^s}= \prod _p \left( 1-\frac{\chi (p)}{p^s}\right) ^{-1} \quad \text{ for } \quad s>1, \end{aligned}$$

(54)

where the product is over all prime numbers $p$. Based on Euler’s ingenious work, Dirichlet product theorem is another remarkable discovery.

Taking logarithm of both sides of (54) yields

$$\begin{aligned} \log L(s,\chi ) \approx \sum _p \frac{\chi (p)}{p^s}+O(1). \end{aligned}$$

(55)

In the limit as $s \rightarrow 1$ with the fact that $L(1,\chi )=\frac{\pi }{4} \ne 0$ shows that $\sum _p \chi (p)/p^s$ remains bounded. In view of the result that $\sum _p \frac{1}{p}$ diverges, it turns out that there are infinitely many primes of the form $(4k+1)$.

In 1792, 15-year old Gauss constructed a table of logarithms and a supplement which contained the first table of primes up to one million, and then, an expanded table of primes up to three millions as follows:

It follows from the above discussion that every natural number $n(>1)$ is either a prime, or can be written as a product of primes. In other words, primes are, in general, building blocks of natural numbers which can be created by multiplication of primes. It also follows from Table 1 that prime numbers are found to occur more frequently at first, but less frequently later on. Table 1 shows $40~\%$ of the natural number up to $x=10$ are primes, $25~\%$ of $x=10^2$ are primes, $16.8~\%$ of $x=10^3$ are primes, $12.29~\%$ of $x=10^4$,..., $7.9~\%$ of $x={10}^{6}$ are primes and so on. The obvious question is whether the list of primes comes to stop, or it goes on for ever. The answer to this question was discovered by Euclid long ago that there are infinitely many primes.

Table 1 Gauss’ table of $\pi (x)$

Based on his Table 1, Gauss predicted the fundamental Prime Number Theorem which states that, for large number $x$, the asymptotic formula for $\pi (x)$ is

$$\begin{aligned} \pi (x) \sim \left( \frac{x}{\ln x}\right) =Li~(x) ~~ \text{ as } ~~ x\rightarrow \infty . \end{aligned}$$

(56)

In 1798, Legendre proved the following limiting result

$$\begin{aligned} \lim _{x \rightarrow \infty } \frac{\pi (x)}{x}=0. \end{aligned}$$

(57)

This implies that there are considerably fewer prime numbers than natural numbers. The more striking fact is that the asymptotic distribution of prime numbers is closely associated with the singularities of the zeta function. Using the product formula (43), Gauss shown that, for large $x$, the asymptotic distribution of prime numbers is given by

$$\begin{aligned} \pi (x) \sim \int _2^x \frac{dt}{\ln t} = Li(x). \end{aligned}$$

(58)

Although (56) and (57) are equivalent, the logarithmic integral (58) provides a more accurate numerical approximation to $\pi (x)$ than does $(x/ \ln x)$. Both Legendre in 1785 and then Gauss in 1792 independently investigated the asymptotic distribution of $\pi (x)$ for large $x$ through an extensive study of tables of logarithms. In 1791, Gauss first conjectured result (58) which was finally proved independently by Jacques Hadamard and Charles de la Valleé Poussin (1866–1962) in 1896. However, in 1914, a great British mathematician, J.E. Littlewood (1885–1977) proved that the difference $Li(x)-\pi (x)$ assumes positive and negative values infinitely often. Although the asymptotic result (58) can numerically be verified for a very large number of cases, it may not be true for all large $x$. In 1948, Paul Erdös (1913–1996) and Atle Selberg (1917–2006) discovered an elementary proof [4] of the prime number theorem without any knowledge of complex function theory. But their proof is still long and complicated. It was Norbert Wiener (1894–1964) who proved the prime number theorem from Wiener-Ikehara Tauberian theorem. This is perhaps a more transparent proof from the analytical point of view.

It has been indicated earlier that there was no general formula discovered for determining the $n$th prime $p_n$, or even finding a polynomial whose values are all primes. If $y= \pi (x)$, it follows from (56) that

$$\begin{aligned} \frac{y \ln x}{x} \rightarrow 1 \qquad x \rightarrow \infty , \end{aligned}$$

(59)

which is, taking logarithm both sides, $\ln y +\ln (\ln x) -\ln x \rightarrow 0 ~ \text{ as } ~ x \rightarrow \infty$ so that

$$\begin{aligned} \frac{ \ln y}{\ln x}+ \frac{\ln (\ln x)}{\ln x} \rightarrow 1 \qquad x \rightarrow \infty , \end{aligned}$$

By L’Hospital rule, the second term goes to zero, and hence,

$$\begin{aligned} \frac{\ln y}{\ln x} \rightarrow 1 \qquad x \rightarrow \infty \end{aligned}$$

Combining with (56) gives

$$\begin{aligned} \frac{y \ln y}{x} \rightarrow 1 \quad \text{ as } \quad x \rightarrow \infty . \end{aligned}$$

(60)

For the $n$th prime $p_n$, that is $\pi (p_n)=n$. Putting $x=p_n$ in (60) gives the result for $p_n$ with $y=\pi (p_n)=n$ as

$$\begin{aligned} p_n \sim n \ln n \quad \text{ as } \quad n \rightarrow \infty . \end{aligned}$$

(61)

However, Legendre’s (1752–1833) great contribution to estimate the number of primes less than or equal to $x$ was published in 1808 in his second edition of Théorie des nombres. His asymptotic formula for $\pi (x)$ given by

$$\begin{aligned} \pi (x)=L(x) \approx \frac{x}{\ln x-A(x)}=\left( \frac{x}{\ln x}\right) \left[ 1+\frac{A(x)}{\ln x}+\frac{A^2(x)}{(\ln x)^2}+\cdots \right] , \end{aligned}$$

(62)

where $A(x) \approx 1.08366$, was a major step forward. In the 1849 letter to his former student, Johann Encke (1791–1865), Gauss mentioned about his curious interest in the mysterious numerical value for $A(x)$, and admitted that his original logarithmic integral formula (58) for $\pi (x)$ is less accurate than Legendre’s formula (62). Gauss extensive contributions to prime number theorem during 1791–1794 were published posthumously in his Werke in 1863. He also used the value of $x$ from $10^3$ to $10^{10}$, Gauss provided extensive computations for $\pi (x), li(x), Li(x)$ and $L(x)$ with Table 2 of comparisons with $\ln 10=2\times 30 \cdots$. It follows from the computations and other computational works that the best value of the Legendre constant $A(x)$ is one. One of the notable comments made by the Norwegian genius and celebrated mathematician, Neils Abel (1802–1829) was that Legendre’s formula (62) is the “most remarkable in the whole of mathematics”.

Table 2 A table of comparisons for large $x$

Another remarkable fact is that Euler universal constant gamma, $\gamma =0.57712$ was also involved in the prime number theorem. This was found in Franz Mertens (1840–1927) product formula

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{1}{(\ln n)} \prod _{p \le n} \left( 1-\frac{1}{p}\right) ^{-1}=e^{\gamma }. \end{aligned}$$

(63)

Without using limit notation, we can write (63) as

$$\begin{aligned} \prod _{p \le n} \left( 1-\frac{1}{p}\right) =\frac{e^{-\gamma }}{(\ln n)}. \end{aligned}$$

(64)

with $n=\sqrt{x}$, (64) has the form

$$\begin{aligned} \pi (x) \approx e^{-\gamma } \left( \frac{x}{\ln \sqrt{x}}\right) =2 e^{-\gamma } \left( \frac{x}{\ln x}\right) . \end{aligned}$$

(65)

This formula provides an interesting link between $\pi (x)$ and $\displaystyle \left( \frac{x}{\ln x}\right)$ through the Euler constant $\gamma$.

Another estimate for $\pi (x)$ can be obtained from the harmonic mean of first $x$ integers given by

$$\begin{aligned} H=\frac{x}{(\frac{1}{1}+\frac{1}{2}+\cdots +\frac{1}{x})} \approx \frac{x}{\ln x-\gamma } ~~ \text{ for } \text{ large }~~ x. \end{aligned}$$

(66)

in which the result (41) was used.

Using the standard elementary inequality, $H<G$, where $G$ is the geometric mean $(1.2.3\cdots x)^{\frac{1}{x}}$ of the first $x$ integers so that

$$\begin{aligned} H=\frac{x}{(\frac{1}{1}+\frac{1}{2}+\cdots +\frac{1}{x})} < (1.2.3\cdots x)^{\frac{1}{x}}=(x!)^{\frac{1}{x}} \end{aligned}$$

(67)

Using Sterling approximation of the factorial $(x!)$, we deduce the upper bound for $\pi (x)$ from (67), for large $x$,

$$\begin{aligned} \pi (x)=\frac{x}{(\ln x-\gamma )} \approx H<\left( \sqrt{2 \pi x}~ x^x e^{-x}\right) ^{1/x}= \frac{1}{e} (2 \pi )^{\frac{1}{x}} x^{1+\frac{1}{2x}}. \end{aligned}$$

(68)

It follows from the above discussion that these are several equivalent statements of the prime number theorem given by (56), (57), (58), (62), (65) and (68) and (62) with $A=1$. However, in 1896, Hadamard and Vallée Poussin independently proved that the value of $\frac{x}{\ln x}$ becomes closer and closer to $\pi (x)$ as $x$ gets larger and larger. In fact, $Li(x)$ is also becomes close to $\pi (x)$ as $x \rightarrow \infty$. This celebrated result shows that there is a definite mathematical pattern to the way the distribution of large prime number behaves.

In 1749, Euler presented a paper at the Berlin Academy of Sciences and reported a new function related to the zeta function defined by

$$\begin{aligned} \phi (s)= \sum _{n=1}^{\infty } (-1)^{n+1} \frac{1}{n^s}. \end{aligned}$$

(69)

He preferred to work with this alternating series for the phi function rather that the zeta function for better convergence and more accurate numerical calculation. He also discovered the following relation between $\phi (s)$ and $\zeta (s)$, and the famous functional equation for $\phi (s)$:

$$\begin{aligned} \phi (s)=(1-2^{1-s}) \zeta (s) \end{aligned}$$

(70)

$$\begin{aligned} \pi ^s (2^{s-1}-1) \phi (1-s)+(2^s-1) \cos \left( \frac{\pi s}{2}\right) \Gamma (s) \phi (s)=0. \end{aligned}$$

(71)

Euler was not successful in verifying (70) for all $s$. For $s=1$, it follows from (69) that

$$\begin{aligned} \phi (1)=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+ \cdots =\log 2. \end{aligned}$$

(72)

These identities (70) and (71) can be combined to obtain another famous functional equation for real $s$ in the form

$$\begin{aligned} \zeta (1-s)=\pi ^{-s} 2^{1-s} \Gamma (s) \zeta (s) \cos \left( \frac{\pi s}{2}\right) . \end{aligned}$$

(73)

One hundred years later, Riemann gave a rigorous proof of this equation in 1859 for complex $s=x+iy$.

After solving the famous Basel problem in 1735, Euler introduced that zeta function, $\zeta (s)$ by the infinite series (39) in around 1737. He then continued his research for finding the value of $\zeta (2n)$ for any natural number $n \ge 1$. Almost 10 years before Riemann’s discovery of $\zeta (s)$ for complex $s=z=x+iy$ in 1859, Euler used the summation of divergent series and mathematical induction to discover a remarkable functional equation for the zeta function in 1749 in the form

$$\begin{aligned} \pi ^{-\frac{s}{2}} \Gamma \left( \frac{s}{2}\right) \zeta (s)= \pi ^{-\frac{1-s}{2}} \Gamma \left( \frac{1-s}{2}\right) \zeta (1-s). \end{aligned}$$

(74)

where $\Gamma (s)$ is the Euler gamma function. Or, equivalently, the functional equation (74) takes the form $\Lambda (s)=\Lambda (1-s)$, where $\Lambda (s)$ is equal to the left hand side of (74).

In spite of progress made on different forms of prime number theorem, the real rigorous proof of this theorem was almost a formidable task. The first major progress towards a proof of the prime number theorem after Dirichlet was made by a Russian mathematician P.L.Chebyshev (1821–1894) in 1852 and 1854 based on the Euler zeta function $\zeta (x)$ for real $x$. He introduced two functions of real variables as follows:

$$\begin{aligned} \theta (x)=\sum _{p \le x} \ln p, \ \ \ \ \ \psi (x)=\sum _{p^m \le x} \ln p, \end{aligned}$$

(75)

with the relationship between them in the form

$$\begin{aligned} \psi (x)=\theta (x)+\theta (x^{1/2})+\theta (x^{1/3})+\theta (x^{1/4})+\cdots \end{aligned}$$

(76)

where $\theta (x)$ is zero for $x<2$. He also provided a numerical table for $\psi (x)$ for $x=100, 200, 300,\ldots , 1000$ with primes less than or equal to $x$. Chebyshev also proved that each of the following

$$\begin{aligned} \frac{\pi (x)}{\left( x/\ln x\right) } ,~ \frac{\theta (x)}{x} ,~ \frac{\psi (x)}{x} \end{aligned}$$

(77)

has the same asymptotic limit as $x \rightarrow \infty$, and found that

$$\begin{aligned} 0.92129 \le \lim _{x \rightarrow \infty } \text{ inf } ~Li(x) \le 1 \le \lim _{x \rightarrow \infty } \text{ sup } ~Li(x) \le 1.10555. \end{aligned}$$

(78)

For detailed information about the proof of above results, the reader is referred to Ingham’s [5] excellent treatise, The Distribution of Prime Numbers.

It is important to point out that in 1851, Chebychev also proved that for arbitrarily large $x$

$$\begin{aligned} \int _2^x \frac{dt}{\ln t}-\frac{\alpha x}{\ln ^n x} < \pi (x) < \int _2^x \frac{dt}{\ln t}+\frac{\alpha x}{\ln ^n x}, \end{aligned}$$

(79)

for arbitrarily small $\alpha >0$, and any positive integer $n$. In particular, when $n=1$, (79) becomes

$$\begin{aligned} \frac{\int _2^x \frac{dt}{\ln t}}{\left( x/\ln x\right) }-\alpha < \frac{\pi (x)}{\left( x/\ln x\right) } < \frac{\int _2^x \frac{dt}{\ln t}}{\left( x/\ln x\right) }+\alpha , \end{aligned}$$

(80)

In the limit as $x \rightarrow \infty$ combined with (56)–(58), it turns out that

$$\begin{aligned} 1-\alpha < \lim _{x \rightarrow \infty }\frac{\pi (x)}{\left( x/\ln x\right) } < 1+\alpha , \end{aligned}$$

(81)

which means that if

$$\begin{aligned} \lim _{x \rightarrow \infty }\frac{\pi (x)}{\left( x/\ln x\right) } \end{aligned}$$

(82)

exists, then it must be equal to 1, that is, $\pi (x) \sim \left( x/\ln x\right)$, but it is desirable to find out if there is a constant $A$ such that

$$\begin{aligned} \pi (x)=\frac{Ax}{\ln x}+ \varepsilon _x \end{aligned}$$

(83)

where $\varepsilon$ is an absolute error term. Chebyshev’s estimate shows that $A=1$, and consequently, Legendre’s approximation cannot be valid beyond the first term. In 1899, Valle’e Poussin proved that

$$\begin{aligned} \pi (x)=\int _2^x \frac{dt}{\ln t}+ \varepsilon _x, \end{aligned}$$

(84)

where the error term $\varepsilon _x$ is bounded by a multiple of $x\exp (-\alpha \sqrt{\ln x})$ for some positive $\alpha$. This means that

$$\begin{aligned} \pi (x)=Li(x)+O(x\exp (-\alpha \sqrt{\ln x})). \end{aligned}$$

(85)

However, Chebyshev’s function $\psi (x)$ proved to be more suitable for investigating the distribution of prime numbers than $\pi (x)$, since the best approximation for it is the very argument $x$. Thus, $\psi (x)$ is usually considered first and then the corresponding result for $\pi (x)$ is found by partial summation. Indeed, Chebyshev proved in (80) that

$$\begin{aligned} \psi (x) \sim (\log x) \pi (x) \quad \text{ as } \quad x \rightarrow \infty . \end{aligned}$$

(86)

In 1909, Edmund Landau (1877–1938) [6] established an important connection between the value of the Mobins function $\mu$ and the Chebyshev function $\psi (x)$ and $\pi (x)$ as follows:

$$\begin{aligned} \psi (x) \sim x, \qquad \sum _{n \le x} \mu (x)=o(x), \end{aligned}$$

(87)

and

$$\begin{aligned} \sum _{n=1}^{\infty } \frac{1}{n} \mu (n)=0. \end{aligned}$$

(88)

Subsequently, Landau [6] extended some results on the distribution of prime numbers to aljebraic number fields $K$ of degree $n$. If $\pi (x,K)$ is the number of prime ideals in $K$ with norm $\le x$, then

$$\begin{aligned} \pi (x,K)=Li(x)+O\left[ x \exp \left( -\frac{c}{\sqrt{n}}\sqrt{\log x}\right) \right] , \end{aligned}$$

(89)

where $c$ is an absolute positive constant, and

$$\begin{aligned} \pi (x)-Li(x)=\pm \Omega \left( \frac{\sqrt{x}}{\log x}\right) \log \log \log x, \end{aligned}$$

(90)

where $\Omega$ is the negation of the symbol o (small).

We close this section by adding another unsolved problem dealing with Twin Prime Conjecture. A pair of primes $p$ and $p+2$ is called a twin prime. For example, the first eight pairs of twin primes are $(3,5), (5,7), (11,13), (17,19), (29,31), (41,43), (59,61), (71,73)$ which are obtained from $2$ to $100$. It is generally believed that such pairs $(p,p+2)$ of prime occur infrequently. However, the major question is whether there are infinitely many twin primes. This is called celebrated Twin Prime Conjecture which has not yet proved or disproved. Using the sieve method, around 1920, Viggo Brun (1885–1978), a famous Norwegian mathematician, showed that there cannot be too many twin primes. Although the sum of the reciprocals of primes diverges, the sum of the reciprocals of twin primes converges, that is,

$$\begin{aligned} \left( \frac{1}{3}+\frac{1}{5}\right) +\left( \frac{1}{5}+\frac{1}{7}\right) +\left( \frac{1}{11}+\frac{1}{13}\right) +\cdots =1.902160 \cdots . \end{aligned}$$

(91)

Brun proved the convergence of the infinite series in (91) in around 1976 and the sum is called Brun’s constant.

On the other hand, G.H. Hardy (1877–1947) and J.E. Littlewood (1885–1977) used their celebrated circle method to prove unsuccessfully Goldback’s Conjecture that every even number ($>2$) is the sum of two primes. They also provided strong heuristic evidence for the Twin Primes Conjecture that the number of primes $p \le x$ such that $p+2$ is also a prime has the asymptotic value

$$\begin{aligned} c \int _2^x \frac{1}{(\ln u)^2} du, \end{aligned}$$

(92)

for a positive constant $c$.

Thus, an unprecedented quest to unravel the mysteries of primes and distribution of primes by many greatest mathematicians of the world has never been totally successful for the last several centuries. Therefore, it is very appropriate to include the celebrated quote of Euler:“ Mathematicians have tried in vain to discover some order in the sequence of prime numbers but we have every reason to believe that there are some mysteries which human mind never penetrate”. This quote was true in Euler’s time, but it is no longer true completely at this time.

In 1941, Yuri. V. Linnik (1915–1972) [7] discovered the method of large sieve to prove several theorems concerning the arithmetic progression $a+nh$, where $1 \le a \le h$ and $(a,h)=1$ and to describe the behavior of $\pi (x,a,h)$ and $\psi (x,a,h)$. In 1944, he [8] also proved the existence of a constant $c$ such that any arithmetic progression $a+nh$, where $1 \le a \le h$ and $(a,h)=1$ contains a prime number less than $h^c$ where the Linnik constant $c=17$. Very recently a significant breakthrough in prime number by Green and Tao [9] by proving many new results including that there are infinitely many $k$-term arithmetic progression of primes, that is, for pairs of integers $a$ and $b$ such that $a, a+d, a+2d,\ldots , a+(k-1)d$ all primes.

Riemann’s Zeta Function, Distribution of Primes and the Celebrated Riemann Hypothesis

In this study of the distribution of the primes, a renowned German mathematician, Bernhard Riemann (1826–1866) in 1859 published a remarkable eight-page paper “On the number of primes less than a given magnitude”. In this study, he extended the Euler zeta function $\zeta (s)$ for real $s>1$ to complex $s=x+iy$ in the form

$$\begin{aligned} \zeta (s)=\sum _{n=1}^{\infty } \frac{1}{n^s}. \end{aligned}$$

(93)

This is universally known as the Riemann zeta function and this function is found to be extremely important for the study of the distribution of prime numbers. Riemann also obtained an expression for the difference of $\pi (x)-Li(x)$ in terms of $x$ and those zeros of $\zeta (s)$ which belong to the strip $0 \le \text{ Re }(s) \le 1$; they are called the non-trivial zeros of $\zeta (s)$. A remarkable fact about the Riemann work is that he proved the following formula, known as Riemann explicit formula

$$\begin{aligned} \psi (x)=x-\sum _{\rho } \frac{x^{\rho }}{\rho }-\frac{\zeta '(0)}{\zeta (0)}-\frac{1}{2} \log \left( 1-\frac{1}{x^2}\right) , \end{aligned}$$

(94)

where $\rho$ is taken over all non-trivial zeros of the Riemann zeta function $\zeta (s)$. The more remarkable feature of (94) is that it has provided the link between the distribution of primes and the zeros of $\zeta (s)$. Based on his work, Riemann made the most celebrated conjecture, the so-called Riemann Hypothesis, which states that all non-trivial zeros of $\zeta (s)$ lie on the line $Re(s)=\frac{1}{2}$ which is the line of symmetry of the functional Eq. (76).

Using Euler’s argument, Riemann proved that, for complex $s$ with $Re(s)>1$,

$$\begin{aligned} \zeta (s)=\prod _p \left( 1-\frac{1}{p^s}\right) ^{-1}, \end{aligned}$$

(95)

where the product taken for all primes $p$. He also proved that $\zeta (s)$ is analytic function for $\text{ Re }(s)>1$ and has only singularities at $s=1$, and hence, the Laurent expansion about $s=1$ is of the form

$$\begin{aligned} \zeta (s)=\frac{1}{s-1}+a_0+a_1 s+\cdots \end{aligned}$$

(96)

It has been stated that Riemann proved the functional Eq. (74) for complex number $s$. Riemann also demonstrated in his 1859 paper that there is a very close relationship between the zeros of the zeta function and the properties of $\pi (x)$. It was this connection which led both Hadamard and Vallée Poussin in their respective conclusive proofs of the prime number theorem. The more important fact about the proofs of the prime number theorem is that the better estimates for the distribution of primes depend on the use of the theory of functions of a complex variables, and the celebrated Riemann Hypothesis which was a conjecture Riemann made in his paper about the complex zeros of the Riemann zeta function. Before describing the considerable work that has been done on the Riemann Hypothesis since it was first put forward in 1859, it is perhaps worth while to quote just one more specific approximation to $\pi (x)$ which involves the Riemann zeta function explicitly. This approximating function $R(x)$ is given by

$$\begin{aligned} R(x)=1+ \sum _{k=1}^{\infty } \frac{1}{k \zeta (k+1)} \frac{(\ln x)^k}{k!}. \end{aligned}$$

(97)

A tabular representation of $x$, $\pi (x)$ and $R(x)$ shows that an astonishingly good approximation to $\pi (x)$ is the function $R(x)$.

The most remarkable fact is that the behavior of $\zeta (s)$ for $s=1$ is connected with the distribution of primes. In fact, the presence of the pole of $\zeta (s)$ at $s=1$ implies that there are infinitely many primes.

On the other hand, Riemann made much more contributions than simply determining the asymptotic distribution of prime numbers based on the formula (95). Taking logarithm of (95), he obtained

$$\begin{aligned} \log \zeta (s)=\sum _{p} \frac{1}{p^s}+\frac{1}{2} \sum _{p} \frac{1}{p^{2s}}+\frac{1}{3} \sum _{p} \frac{1}{p^{3s}}+\cdots \end{aligned}$$

(98)

and then replaced $p^{-ns}$ by

$$\begin{aligned} s \int _{p^n}^{\infty } x^{-(s+1)} dx \end{aligned}$$

so that

$$\begin{aligned} \frac{1}{s} \log \zeta (s)= \int _{1}^{\infty } x^{-(s+1)} \Pi (x) dx, \end{aligned}$$

(99)

where

$$\begin{aligned} \Pi (x) \approx \pi (x)+\frac{1}{2} \pi (x^{1/2})+\frac{1}{3} \pi (x^{1/3})+ \cdots \infty . \end{aligned}$$

(100)

Riemann then expressed $\Pi (x)$ as the Fourier complex inversion integral in the form

$$\begin{aligned} \Pi (x)= \int _{c-i \infty }^{c+i \infty } \frac{\log \zeta (s)}{s} x^s ds, \qquad c>1 \end{aligned}$$

(101)

and evaluated it by the residues of the singularities of $\log \zeta (s)$ at $s=1$ and at the zeros of $\zeta (s)$. It then follows from the inversion (100) that

$$\begin{aligned} \pi (x) = \sum _{m=1}^{\infty } \frac{(-1)^{\mu }}{m} \Pi (x^{1/m}), \end{aligned}$$

(102)

where $m$ consists of all natural numbers not divisible by any square other than one, and $\mu$ is the prime factors of $m$. Thus, the distribution of the prime numbers is closely associated with the zeros of $\zeta (s)$.

Like Euler, Riemann also recognized that the zeta function and its zeros played a fundamental role in the distribution and analysis of primes in number theory. The only zeros outside the critical strip defined by the inequality

$0< Re(s) \le 1$ are at the even negative integers $(s=-2n, \quad n=1,2,3\ldots )$ known as the trivial zeros. He also proved that $\zeta (s)$ is an analytic function in the whole complex $s$-plane except for a simple pole at $s=1$ with residue one, and it has no other singularities. In 1859, Riemann formulated his celebrated Riemann Hypothesis (RH) which states that all non-trivial complex zeros of $\zeta (s)$ lie on the critical line $Re(s)=\frac{1}{2}$ in the complex $s$ plane as shown in Fig. 3. In other words, the complex zeros are at $s=\frac{1}{2} \pm i y$ which are symmetrically located on the critical line. The first few complex zeros are at $y=14 \times 134,21,25,30 \times 5,33,\ldots$. This is thought of as the most famous unsolved problem in mathematics by many. In 1918, G.H. Hardy [10] proved that there are infinitely many zeros of the Riemann zeta function on the Riemann critical line $Re(s)=\frac{1}{2}$. Many extensive numerical experiments with supercomputers have given no indication as of yet whether the Riemann hypothesis is true or false. Many recent computations reveal that fifty billion complex zeros lie on the critical line. Furthermore, precise asymptotic estimates show that at least one-third of the zeros of $\zeta (s)$ must lie on the critical line.

Fig. 3

The zeros of the Riemann zeta function

The truth of the Riemann Hypothesis implies that the deviation of the prime numbers from the asymptotic limit $Li(x)$ is

$$\begin{aligned} \pi (x)=Li(x)+O(\sqrt{x}\ln x) \end{aligned}$$

(103)

and a single zero off the line $s=\frac{1}{2}+iy$ would change the distribution of primes in a significant way.

It follows from (93) and (95) that

$$\begin{aligned} \zeta (s)= \sum _{n=1}^{\infty } \frac{1}{n^s}= \prod _p \frac{1}{(1-p^{-s})}, \qquad \text{ Re }~s>1. \end{aligned}$$

(104)

Taking logarithms of (104) and expanding gives

$$\begin{aligned} \log \zeta (s)= \sum _p \sum _{m=1}^{\infty } \frac{1}{m p^{ms}}=- \sum _p \frac{1}{(1-p^{-s})}. \end{aligned}$$

(105)

Differentiating (105) with respect to $s$ yields

$$\begin{aligned} -\frac{\zeta '(s)}{\zeta (s)}= \sum _p \sum _{m=1}^{\infty } \frac{\log p}{p^{ms}}= \sum _p \frac{p^{-s} \log p}{(1-p^{-s})}. \end{aligned}$$

(106)

The first equality of (106) gives

$$\begin{aligned} -\frac{\zeta '(s)}{\zeta (s)}= \sum _{n=1}^{\infty } \frac{\Lambda (n)}{n^s}, \end{aligned}$$

(107)

where

$$\begin{aligned} \Lambda (n) = {\left\{ \begin{array}{ll} \log p, &{}\text{ if } n=p^m \\ 0, &{} \text{ otherwise } \end{array}\right. }, \end{aligned}$$

(108)

Using (75), we obtain

$$\begin{aligned} \psi (x)=\sum _{p^m \le x} \log p= \sum _{n \le x} \Lambda (n), \end{aligned}$$

(109)

so that (107) and (108) can be written as

$$\begin{aligned} -\frac{\zeta '(s)}{\zeta (s)}= s \int _{1}^{\infty } \frac{\psi (x)}{x^{s+1}} ~dx \qquad (s>1) \end{aligned}$$

(110)

This further confirms the close connection between the functions $\zeta (s)$ and $\psi (x)$ which was investigated by Riemann in 1860.

Since the Riemann hypothesis is involved with the size of the error in approximating $\psi (x)$ by $x$., it is then involved with the error in approximating $\pi (x)$ by $Li(x)$. In 1901, Helge von Koch (1870–1924) proved that if the Riemann Hypothesis is true, the precise estimate of $\pi (x)$ is given by (103). The 1976 Fields prize winner, Enrico Bombieri has said that it is very difficult to significantly improve the result (103) because of the remarkable result of Littlewood that the degree of oscillation of $\pi (x)-Li(x)$ is asymptotically of the order $Li(\sqrt{x})\ln \ln \ln x$. Another celebrated quotation of Bombieri is “The failure of the Riemann Hypothesis would create havoc in the distribution of prime numbers”.

We close this section by adding some more recent computational evidence in support of the Riemann Hypothesis which states that if $\zeta (s)=0$ for a complex $s$, then $s$ must be form $s=\frac{1}{2}+iy$. Although Hardy was able to prove that there are infinitely many zeros whose real part is $\frac{1}{2}$, but it does not preclude that these are infinitely many more which have real part not equal to $\frac{1}{2}$. To disprove the Riemann Hypothesis computationally, it would be sufficient to find just one zero whose real part is not equal to $\frac{1}{2}$.

During the last one hundred years, there have been a number of numerical techniques for computing the values of $y$ for which the complex number $\frac{1}{2} \pm iy$ are zeros of the Riemann zeta function. In 1903, J.P. Gram was the first mathematician who used a computational approach to the Riemann Hypothesis. Using the standard numerical technique called the Euler-Maclaurin summation formula to compute the zeros of $\zeta (s)$, Gram found the first 15 values of $y$ for which $\zeta (\frac{1}{2} + iy)=0$ and first ten were computed to six decimal places so that first one was $y=14.134725$ and the tenth $y=49.773832$. The remaining five were computed to one decimal place or, the eleventh was $y=52.8$ and the fifteenth was $y=65.0$. With the complex zeros whose real parts are between 0 and 1, he further proved that there are exactly ten zeros whose imaginary part lie between 0 and 50. In other words, Gram’s computational results have strong evidence in support of the Riemann Hypothesis.

Using somewhat improved technique similar to Gram, R. Backkend in 1918 verified the RH for all zeros in range $0<y<200$. In 1925, J.J. Hutchinson made some improvements of Gram’s method to compute the zeros of $\zeta (s)$ raising the upper limit for $y$ to 300. On the other hand, in 1936, E.C. Titchmarsh (1899–1963) and L. Comrie (1893–1950) employed an improved computational method to compute 1041 zeros of $\zeta (s)$. All zeros lie on the line $Re(s)=\frac{1}{2}$ so that they support the RH.

After the Second World War, many electronic computers were available for complex computation. Several mathematicians including Carl Siegal (1896–1981), Alan Turing (1912–1954) and D.H. Lehmer (1905–1991) computed many zeros of $\zeta (s)$ of the form $s=\frac{1}{2}+iy$ in a given range, and found that they support the RH.

In 1966, R.S. Lehman computed zero to 250000, and within a few years of that J.B. Rosser and his colleagues computed zeros to 3500000. By 1983, J. van de Lune and H.J.J. de Riele computationally discovered 300000001 zeros in the range $0 \le y \le 119590809.28$ and all these zeros support the RH. In 1985, they computed about one and a half billion zeros of the type Riemann predicted. So all of the numerical evidence are in exact agreement with the RH. After so much of mathematical and computational research over the last several centuries, still all wonderful mysteries of prime number theorems, leading to the RH and has not yet completely resolved.

As far as we can tell that now it is known that 539 974 310 000 zeros lie on the critical line $Re(s)=\frac{1}{2}$, and so far none have found off the line. Despite all the work and all the computational evidence, no one really knows whether the Riemann Hypothesis is true or not. This is still one of the celebrated unsolved problems in mathematics. A new prize has been announced by the Clay Institute of Mathematics at Harvard University by offering one million dollars each for the solution of seven problems, one of which is the Riemann Hypothesis.

In 1897, F. Mertens produced a 50-page table of the Möbius function $\mu (n)$ and the Mertens function $M(n)=\sum _{1 \le k \le n} \mu (n)$ for all $n$ upto 10,000. Based on his table, he concluded that, for all $n>1$,

$$\begin{aligned} M(n)<\sqrt{n} \end{aligned}$$

(111)

This is known as the Mertens conjecture.

In 1885, in his letter to a famous French mathematician, Charles Hermite (1822–1894), T.J. Stieltger (1856–1894) a celebrated Dutch mathematician stated that the Mertens conjecture is true for large $n$. He further asserted that the Riemann Hypothesis(RH) is true which follows from the existence of any constant $A$ such that

$$\begin{aligned} |M(n)| < A \sqrt{n} \end{aligned}$$

(112)

holds for all $n$. It is easy to verify that the Mertens function is related to the RH by

$$\begin{aligned} M(x)=\frac{1}{2 \pi i} \int _{\sigma -i \infty }^{\sigma +i \infty } \frac{x^s}{s \zeta (s)} ds \end{aligned}$$

(113)

which is valid for $1<\sigma <2$ and $\frac{1}{2}<\sigma <2$ on the RH, where

$$\begin{aligned} \frac{1}{\zeta (s)}= \sum _{n=1}^{\infty } \frac{\mu (n)}{n^s}, \qquad Re(s)>1 \end{aligned}$$

(114)

During the period 1897 to 1985, many mathematicians became involved in the numerical computation of the values of $M(n)$, and suggested that the Mertens conjecture is true. In 1985, Odlyzko and te Riele proved that the Mertens conjecture is false based on mathematical methods with a result of Ingham in 1942 and combined with computational evidence. This conjecture is a remarkable example of a mathematical proof contradicting a large amount of computational evidence in favor of the conjecture. Although the Mertens function $M(x)$ is closely related to the location of the zeros of the Riemann zeta function, the Mertens conjecture is false, but the status of RH remains unchanged. However, the falsity of the Mertens conjecture seems to provide a warning to all mathematicians who believe and claim that the RH has to be true.

Stochastic Distribution of Primes

Until, 1920, all studies have been made of the deterministic distribution of prime numbers.One of the remarkable aspects of the primes is their tendency to exhibit local irregularity and global regularity. This led to the study of stochastic distribution of prime numbers from 1930s. Harold Cramér(1893–1985), a great Swedish mathematician, first gave a probabilistic interpretation of Gauss’s conjecture then a sequence of prime numbers behaves like a random sequence with the same growth constraint. This conjecture then became known as the on Gauss-Cramér probabilistic model of primes (see Elliot [11]). Although there was no precises proof of this model, but it provided a remarkable way of describing the stochastic distribution of primes.With the help of central limit theorems in probability and statistics, the Gauss-Cramér model describing primes as a sequence of 0 and 1 satisfies the prime number theorem. (see Tenenbaum and France [12]):

$$\begin{aligned} \pi (x)=Li(x)+O(\sqrt{x} \log x) \end{aligned}$$

(115)

According to the prime number theorem, the probability that an integer $n$ is a prime is asymptotic to $(\log n)^{-1}$. If $\{X_n\}_{n=2}^{\infty }$ is a sequence of independent random variables with values 0 and 1, then the probability of $X_n=1$ is given by

$$\begin{aligned} P(X_n=1)=\frac{1}{\log n}, \qquad n \ge 3 \end{aligned}$$

(116)

Then the random sequence represents, according to Cramér’s [13] , a stochastic model for the sequence of prime numbers. If $\pi _s(x)$ denote the random variable equal to the number of integer $n$ not exceeding $x$ such that $X_n=1$ then it is easy to prove that almost surely (that is, with probability 1)

$$\begin{aligned} \pi _s(x)= Li(x)+ I_s(x) \sqrt{2x \frac{x}{\log x}}, \end{aligned}$$

(117)

where $I_s(x)$ oscillates asymptotically between $-1$ and $1$.

These are several striking features of the Cramér model. First, it is consistent with Littlehood’s oscillation theorem. Second, it is also consistent with the Riemann Hypothesis. Third, if $d_n=p_{n+1}-p_n$, where $p_n$ is the $n$th prime, then it follows from the prime number theorem that

$$\begin{aligned} \sum _{n \le N} d_n=p_n-2 \approx N \log N \quad \text{ as } \quad N \rightarrow \infty \end{aligned}$$

(118)

Thus, the random prime number of Cramér’s model satisfy

$$\begin{aligned} \displaystyle \lim _{n \rightarrow \infty } \sup ~\frac{d_n}{(\log p_n)^2}=1, \end{aligned}$$

(119)

whereas slightly weaker version is

$$\begin{aligned} d_n \ll (\log p_n)^2. \end{aligned}$$

(120)

This is known as Cramér’s conjecture.

Further, Cramér’s model can be used to determine the behavior of the function $\pi (x)$ in short intervals. Finally, Cramér model is also consistent with the twin prime conjecture. It also predicts that $p$ and $p+2$ are simultaneously primes with probability $(\log x)^{-2}$. It can be shown that a random sequence is almost surely uniformly distributed in $[0,1]$, the law of logarithm in probability theory provides the almost sure estimates

$$\begin{aligned} \displaystyle \lim _{N \rightarrow \infty } \frac{\mid \sum _{n<N} \exp (2 \pi i \nu X_n)\mid }{\sqrt{2 N \log N}}=1 \end{aligned}$$

(121)

where $\nu \ne 0$. This leads to the behavior of exponential sums over prime numbers, in particular that of

$$\begin{aligned} S_N(\alpha )= \sum _{n \le N} \exp (2 \pi i \alpha p_n), \end{aligned}$$

(122)

seems to contain important information about the stochastic behavior of the distribution of primes. It is known that for every $\nu \ne 0$, the estimate $S_{N}(\nu \alpha )=O(N)$ is equivalent to the uniform distribution of $\left\{ \alpha p_{n}\right\} _{n=1}$ modulo one. This allows us to clarify whether this uniform distribution can be interpreted as the deterministic regularity or the stochastic irregularity for the sequence $\left\{ p_{n}\right\} _{n=1}$. The uniform distribution of the sequence $\left\{ \alpha p_{n}\right\} _{n=1}$ provided in 1937 by a renowned Russian mathematician, I.M. Vinogradov(1891–1983) in his proof [14] that every sufficiently large odd integer is the sum of at most three primes. This result is regarded as the most significant progress towards the Goldback conjecture. With regard to irregular distribution of primes, it is appropriate to mention Chebyshev’s conjecture which states that there are more primes of the form $4n+3$ than of the form $4n+1$, as supported by tables of primes. It is also important to point out that it is not known even today whether or not there are infinitely many primes of the form $n^{2}+1$.

It has already been mentioned earlier that there are infinitely many Mersenne primes. However, a probabilistic argument suggests that there are infinitely many twin primes and Brun’s upper bound for $\Pi _{2}(n)$ is optimal. The probability that an integer $n$ chosen at random is $\left( \log n\right) ^{-1}$. There is another conjecture, similar to that of Hardy and Littlewood, which states that the number $\pi _{2}\left( n\right)$ of pairs of twin primes not exceeding $n$ satisfies

$$\begin{aligned} \frac{\pi _2(n)}{n} \sim \left( \frac{1}{2} e^{\gamma }\right) ^2 \frac{1}{2} \prod _{2<p \le \sqrt{n}} \left( 1-\frac{2}{p}\right) \sim \frac{C}{(\log n)^2}, \end{aligned}$$

(123)

where

$$\begin{aligned} C=2 \prod _{p>2} \left[ 1-\frac{1}{(p-1)^2}\right] \approx 1.320323. \end{aligned}$$

(124)

is known as the twin prime constant. In 1990, Jie Wu used the sieve method to prove that the upper bound for $\pi _2(n)$ in the form

$$\begin{aligned} \pi _2(n) \le (3.418) C \frac{n}{(\log n)^2}, \end{aligned}$$

(125)

for sufficiently large $n$.

In 1923, Hardy and Littlewood proposed the generalized twin prime conjecture as follows: For all $k$-tuples of non-negative integers $\{a_i\}_{i=1}^{k}$ and $\{b_i\}_{i=1}^{k}$ with the properly that the polynomial

$$\begin{aligned} p(x)= \prod _{i=1}^{k} (a_i x+b_i), \end{aligned}$$

(126)

vanishes identically modules $p$, for no prime $p$, there are infinitely many integers $n$ such that $a_{i}n+b_{i}$ $\left( 1\le i\le k\right)$ are simultaneously prime. The heuristic computation can be used to obtain an asymptotic formula with the main term of the form $c_{x}\left( \log x\right) ^{-k}$ for the number of primes not exceeding $x$. Thus ,the above conjecture contains both Dirichlet theorem on arithmetic progressions and the twin prime conjecture. Finally we conclude this section by adding an old conjecture about the distribution of primes which states $\pi \left( x\right)$ is sub-addictive, that is,

$$\begin{aligned} \pi (x+y) \le \pi (x)+\pi (y) \end{aligned}$$

(127)

where, $x \ge 2$ and $y \ge 2$. This inequality is asymptotically consistent with the prime number theorem. The best result to date is due to Baker and Harman [15], who proved that.

$$\begin{aligned} \pi (x+y)-\pi (x) \ge \frac{y}{20(\log x)},\qquad (x> x_0) \end{aligned}$$

(128)

for $y=x^{0.535}$.

An arithmetic function is defined as a complex valued sequence $f:\mathbb {N} \rightarrow \mathbb {C}$. The convolution of arithmetic functions $f$ and $g$ is denoted by $(f*g)(n)$ and defined by

$$\begin{aligned} (f*g)(n)= \sum _{d|n} f(d) g\left( \frac{n}{d}\right) \end{aligned}$$

(129)

This convolution product corrosponds to the ordinary product of the Dirichlet series so that

$$\begin{aligned} \sum _{n=1}^{\infty } \frac{(f*g)(n)}{n^s}=\sum _{n=1}^{\infty } \frac{f(n)}{n^s} \sum _{n=1}^{\infty } \frac{g(n)}{n^s} \end{aligned}$$

(130)

provided all three infinite series are absolutely convergent.

It is easy to check that the function

$$\begin{aligned} \delta (n) = {\left\{ \begin{array}{ll} 1, &{}\qquad n=1 \\ 0, &{} \qquad n>1 \end{array}\right. } \end{aligned}$$

(131)

is an identity element for the convolution and that the set of arithmetic functions with ordinary addition and convolution product forms an integral commutative ring with unity.

From ancient times, the sieve of Eratosthenes represents a method for counting the number $N_m(x)$ of positive integers $n~(\le x)$ that are relatively prime to a fixed number $m$. This then led to celebrated Legendre formula for the sieve of Eratosthenes in the form

$$\begin{aligned} N_m(x)=\sum _{d|m} \mu (d) \left[ \frac{x}{d}\right] , \end{aligned}$$

(132)

where $\mu (d)$ is the standard Möbius function defined by

$$\begin{aligned} \mu (d) = {\left\{ \begin{array}{ll} (-1)^{w(d)}, &{}\text{ if } d \text{ has } \text{ no } \text{ square } \text{ factor } \text{>1 },\\ 0, &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

(133)

with $w(d)$ denotes the number of distinct prime factors of $d$, with $w(1)=0$. And $[x]$ is the integral part of a real number $x$. For example, $\left[ \frac{7}{5}\right] =1$. It can be shown that the Möbius function $\mu$ and the prime number $\pi (x)$ are closely related by the formula

$$\begin{aligned} \pi (x)= \pi (\sqrt{x})-1+ \sum _{P^{+}(d) \le \sqrt{x}} \mu (d) \left[ \frac{x}{d}\right] , \end{aligned}$$

(134)

where $P^{+}(d)$ represents the greatest prime factor of $d$ with $P^{+}(1)=1$.

The Möbius function $\mu$ can be defined as the convolution inverse of the function $\mathbf 1$ so that

$$\begin{aligned} \mathbf 1 *\mu = \delta ~~~~ \text{ or }~~~~\sum _{d|n} \mu (d)=\delta (n). \end{aligned}$$

(135)

It follows from the definition of the convolution product in terms of the ordinary product of Dirichlet series (130) that

$$\begin{aligned} \sum _{n=1}^{\infty } \frac{\mu (n)}{n^s}=\frac{1}{\zeta (s)} \qquad \text{ Re }~s=\sigma >1. \end{aligned}$$

(136)

When $s=2$,

$$\begin{aligned} \sum _{n=1}^{\infty } \frac{\mu (n)}{n^2}=\frac{1}{\zeta (2)}=\frac{6}{\pi ^2} \end{aligned}$$

(137)

The following theorem provides an interpretation of the number $\frac{6}{\pi ^2}$ as the probability that two integers selected at random be co prime (see Tenenbaum and France [12]):

Theorem 5.1

If $G(x,y)$ represents the number of integer pairs $(m,n)$ such that $1 \le m \le x$, $1 \le n \le y$ with $(m,n)=1$, then the asymptotic formula

$$\begin{aligned} G(x,y) \approx \left( \frac{6}{\pi ^2}\right) xy \end{aligned}$$

(138)

holds for $x \rightarrow \infty$ and $y \rightarrow \infty$. More precisely,

$$\begin{aligned} G(x,y)= xy \left[ \left( \frac{6}{\pi ^2}\right) +O\left( \frac{\log z}{z}\right) \right] \end{aligned}$$

(139)

where $x \ge 2$, $y \ge 2$ and $z=min(x,y)$.

Concluding Remarks

This short article describes some analytical and computational aspects of primes numbers, primes number theorems, the distribution of primes and the Riemann Hypothesis which are truely fascinating areas of mathematical sciences. Considerable attention had been given to these areas during the last century, many problems and conjectures have been formulated that have so far remained unsolved for a long time. For example, Is the set of Fermat or Mersenne prime numbers finite or infinite? Is the set of twin primes finite or infinite? Is the set of prime numbers of the form $(n^2+1)$ finite or not? Is it true that there is atleast one prime number between the squares of two consecutive natural numbers?

Each new breakthrough seems to require brilliant ideas and extraordinary analytical or computational knowledge and skills in mathematics.