Abstract
We consider the derivation of the defocusing cubic nonlinear Schrödinger equation (NLS) on \({\mathbb {R}}^{3}\) from quantum N-body dynamics. We reformat the hierarchy approach with Klainerman-Machedon theory and prove a bi-scattering theorem for the NLS to obtain convergence rate estimates under \(H^{1}\) regularity. The \(H^{1}\) convergence rate estimate we obtain is almost optimal for \(H^{1}\) datum, and immediately improves if we have any extra regularity on the limiting initial one-particle state.
Similar content being viewed by others
Notes
As usual, in the notation, we do not distinguish the kernel and the operator it defines.
The gap could be less severe in 1D and 2D as the corresponding critical regularity drops.
See [67] for some locally half-circle shaped or paralleled-tube shaped examples.
Condition (c) implies \(\Gamma _{\infty }(0)\in H_{E_{0}}^{1}\) which implies \( d\mu _{0}\) is supported in the subset of
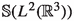 in which \(\left\| \phi \right\| _{H^{1}({\mathbb {R}}^{3})}\leqslant E_{0} \). Hence \(S_{t}\phi \) is well-defined inside the \(d\mu _{0}\) integral.
in which \(\left\| \phi \right\| _{H^{1}({\mathbb {R}}^{3})}\leqslant E_{0} \). Hence \(S_{t}\phi \) is well-defined inside the \(d\mu _{0}\) integral.The method does yield the optimal \(N^{-1}\) rate when \(\beta =0\) but one needs to change (1.1).
See also [1] for the 1D defocusing cubic case around the same time.
Private communication in 2011.
This is certainly only a fraction of all possible references as the Fock space approach is also such a vast and sophisticated subject now. Please also see the references within them and the newer ones online.
Obtaining the optimal \(N^{-\beta }\) rate using the Fock space approach assuming \(H^{4}\) has been done in the much harder \(\beta =1\) case. See [7].
Intereseted readers can see [29] for a detailed handling of this error term.
The proof shows that \(\delta \lesssim \langle C_1 \rangle ^{-1/3}\) suffices
References
Adami, R., Golse, F., Teta, A.: Rigorous derivation of the cubic NLS in dimension one. J. Stat. Phys. 127, 1194–1220 (2007)
Anderson, M.H., Ensher, J.R., Matthews, M.R., Wieman, C.E., Cornell, E.A.: Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 269, 198–201 (1995)
Bourgain, J.: Scattering in the energy space and below for 3D NLS. J. Anal. Math. 75, 267–297 (1998)
Bourgain, J.: New Global Well-posedness Results for Non-linear Schrödinger Equations, AMS Publications, (1999)
Benedikter, N., Oliveira, G., Schlein, B.: Quantitative Derivation of the Gross-Pitaevskii Equation. Comm. Pure. Appl. Math. 68, 1399–1482 (2015)
Boccato, C., Cenatiempo, S., Schlein, B.: Quantum Many-body Fluctuations around Nonlinear Schrödinger Dynamics. Ann. Henri Poincaré 18, 113–191 (2017)
Brennecke, C., Schlein, B.: Gross-Pitaevskii Dynamics for Bose-Einstein Condensates. Analysis & PDE 12, 1513–1596 (2019)
Chen, T., Hainzl, C., Pavlović, N., Seiringer, R.: Unconditional Uniqueness for the Cubic Gross-Pitaevskii Hierarchy via Quantum de Finetti. Commun. Pure Appl. Math. 68, 1845–1884 (2015)
Chen, T., Pavlović, N.: On the Cauchy Problem for Focusing and Defocusing Gross-Pitaevskii Hierarchies. Discrete Contin. Dyn. Syst. 27, 715–739 (2010)
Chen, T., Pavlović, N.: The Quintic NLS as the Mean Field Limit of a Boson Gas with Three-Body Interactions. J. Funct. Anal. 260, 959–997 (2011)
Chen, T., Pavlović, N.: A new proof of existence of solutions for focusing and defocusing Gross-Pitaevskii hierarchies. Proc. Amer. Math. Soc. 141, 279–293 (2013)
Chen, T., Pavlović, N.: Higher order energy conservation and global wellposedness of solutions for Gross-Pitaevskii hierarchies. Commun. PDE 39, 1597–1634 (2014)
Chen, T., Pavlović, N.: Derivation of the cubic NLS and Gross-Pitaevskii hierarchy from manybody dynamics in \(d=3\) based on spacetime norms. Ann. H. Poincare 15, 543–588 (2014)
Chen, T., Taliaferro, K.: Derivation in Strong Topology and Global Well-posedness of Solutions to the Gross-Pitaevskii Hierarchy. Commun. PDE 39, 1658–1693 (2014)
Chen, T., Pavlović, N., Tzirakis, N.: Energy Conservation and Blowup of Solutions for Focusing Gross-Pitaevskii Hierarchies. Ann. I. H. Poincaré 27, 1271–1290 (2010)
Chen, X.: Classical Proofs Of Kato Type Smoothing Estimates for The Schrödinger Equation with Quadratic Potential in \( R^{n+1}\) with Application. Differential and Integral Equations 24, 209–230 (2011)
Chen, X.: Second Order Corrections to Mean Field Evolution for Weakly Interacting Bosons in the Case of Three-body Interactions. Arch. Rational Mech. Anal. 203, 455–497 (2012)
Chen, X.: Collapsing Estimates and the Rigorous Derivation of the 2d Cubic Nonlinear Schrödinger Equation with Anisotropic Switchable Quadratic Traps. J. Math. Pures Appl. 98, 450–478 (2012)
Chen, X.: On the Rigorous Derivation of the 3D Cubic Nonlinear Schrödinger Equation with A Quadratic Trap. Arch. Rational Mech. Anal. 210, 365–408 (2013)
Chen, X., Holmer, J.: On the Rigorous Derivation of the 2D Cubic Nonlinear Schrödinger Equation from 3D Quantum Many-Body Dynamics. Arch. Rational Mech. Anal. 210, 909–954 (2013)
Chen, X., Holmer, J.: On the Klainerman-Machedon Conjecture of the Quantum BBGKY Hierarchy with Self-interaction. J. Eur. Math. Soc. (JEMS) 18, 1161–1200 (2016)
Chen, X., Holmer, J.: Focusing Quantum Many-body Dynamics: The Rigorous Derivation of the 1D Focusing Cubic Nonlinear Schrödinger Equation. Arch. Rational Mech. Anal. 221, 631–676 (2016)
Chen, X., Holmer, J.: Focusing Quantum Many-body Dynamics II: The Rigorous Derivation of the 1D Focusing Cubic Nonlinear Schrödinger Equation from 3D. Analysis & PDE 10, 589–633 (2017)
Chen, X., Holmer, J.: Correlation structures, Many-body Scattering Processes and the Derivation of the Gross-Pitaevskii Hierarchy, Int. Math. Res. Notices 2016, 3051-3110
Chen, X., Holmer, J.: The Rigorous Derivation of the 2D Cubic Focusing NLS from Quantum Many-body Evolution, Int. Math. Res. Notices 2017, 4173–4216
Chen, X., Holmer, J.: The Derivation of the Energy-critical NLS from Quantum Many-body Dynamics. Invent. Math. 217, 433–547 (2019)
Chen, X., Holmer, J.: The Unconditional Uniqueness for the Energy-critical Nonlinear Schrödinger Equation on \({\mathbb{T}}^{4}\). Forum Math. Pi 10(e3), 1–49 (2022)
Chen, X., Shen, S., Zhang, Z.: The Unconditonal Uniqueness for \(H^{1}\) -Supercritical NLS, to appear in Annals of PDE. (arXiv:2104.06592)
Chen, X., Shen, S., Wu, J., Zhang, Z.: The Derivation of the Compressible Euler Equation from Quantum Many-body Dynamics, arXiv:2112.14897, 48pp
Chen, X., Smith, P.: On the Unconditional Uniqueness of Solutions to the Infinite Radial Chern-Simons-Schrödinger Hierarchy. Analysis & PDE 7, 1683–1712 (2014)
Chong, J.: Dynamics of Large Boson Systems with Attractive Interaction and a Derivation of the Cubic Focusing NLS in \( {\mathbb{R}}^{3}\). J. Math. Phys. 62, 042106 (2021)
Colliander, J., Keel, M., Staffilani, G., Takaoka, H., Tao, T.: Global existence and scattering for rough solutions of a nonlinear Schrödinger equation on \({\mathbb{R}}^{3}\). Comm. Pure Appl. Math. 57, 987–1014 (2004)
Davis, K.B., Mewes, M.-O., Andrews, M.R., van Druten, N.J., Durfee, D.S., Kurn, D.M., Ketterle, W.: Bose-Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 75, 3969–3973 (1995)
Duyckaerts, T., Holmer, J., Roudenko, S.: Scattering for the non-radial 3D cubic nonlinear Schrödinger equation. Math. Res. Lett. 15, 1233–1250 (2008)
Erdös, L., Schlein, B., Yau, H.T.: Derivation of the Cubic non-linear Schrödinger Equation from Quantum Dynamics of Many-body Systems. Invent. Math. 167, 515–614 (2007)
Erdös, L., Schlein, B., Yau, H.T.: Rigorous Derivation of the Gross-Pitaevskii Equation with a Large Interaction Potential. J. Amer. Math. Soc. 22, 1099–1156 (2009)
Erdös, L., Schlein, B., Yau, H.T.: Derivation of the Gross-Pitaevskii Equation for the Dynamics of Bose-Einstein Condensate. Annals Math. 172, 291–370 (2010)
Ginibre, J., Velo, G.: Scattering theory in the energy space for a class of nonlinear Schrödinger equations, J. Math. Pures Appl. (9) 64 (1985), pp. 363–401
Gressman, P., Sohinger, V., Staffilani, G.: On the Uniqueness of Solutions to the Periodic 3D Gross-Pitaevskii Hierarchy. J. Funct. Anal. 266, 4705–4764 (2014)
Grillakis, M.G., Margetis, D.: A Priori Estimates for Many-Body Hamiltonian Evolution of Interacting Boson System. J. Hyperb. Diff. Eqs. 5, 857–883 (2008)
Grillakis, M.G., Machedon, M.: Pair excitations and the mean field approximation of interacting Bosons, I. Comm. Math. Phys. 324, 601–636 (2013)
Grillakis, M.G., Machedon, M.: Pair excitations and the mean field approximation of interacting Bosons, II. Commun. PDE 42, 24–67 (2017)
Grillakis, M.G., Machedon, M., Margetis, D.: Second Order Corrections to Mean Field Evolution for Weakly Interacting Bosons. I. Commun. Math. Phys. 294, 273–301 (2010)
Grillakis, M.G., Machedon, M., Margetis, D.: Second Order Corrections to Mean Field Evolution for Weakly Interacting Bosons. II. Adv. Math. 228, 1788–1815 (2011)
Hadac, M., Herr, S., Koch, H.: Well-posedness and scattering for the KP-II equation in a critical space, Ann. Inst. H. Poincar é Anal. Non Linéaire 26 (2009), 917-941. See also M. Hadac, S. Herr, H. Koch, Erratum to “Well-posedness and scattering for the KP-II equation in a critical space,” Ann. Inst. H. Poincaré Anal. Non Linéaire 27 (2010), 971–972
Herr, S., Sohinger, V.: The Gross-Pitaevskii Hierarchy on General Rectangular Tori. Arch. Rational Mech. Anal. 220, 1119–1158 (2016)
Herr, S., Sohinger, V.: Unconditional Uniqueness Results for the Nonlinear Schrödinger Equation. Commun. Contemp. Math. 21, 1850058 (2019)
Hong, Y., Taliaferro, K., Xie, Z.: Unconditional Uniqueness of the cubic Gross-Pitaevskii Hierarchy with Low Regularity. SIAM J. Math. Anal. 47, 3314–3341 (2015)
Hong, Y., Taliaferro, K., Xie, Z.: Uniqueness of solutions to the 3D quintic Gross-Pitaevskii hierarchy. J. Functional Analysis 270(1), 34–67 (2016)
Kenig, C., Merle, F.: Global well-posedness, scattering and blow-up for the energy-critical, focusing, non-linear Schr ödinger equation in the radial case. Invent. Math. 166(3), 645–675 (2006)
Killip, R., Vişan, M.: Scale invariant Strichartz estimates on tori and applications. Math. Res. Lett. 23, 445–472 (2016)
Kirkpatrick, K., Schlein, B., Staffilani, G.: Derivation of the Two Dimensional Nonlinear Schrödinger Equation from Many Body Quantum Dynamics. Amer. J. Math. 133, 91–130 (2011)
Klainerman, S., Machedon, M.: Space-time estimates for null forms and the local existence theorem. Comm. Pure Appl. Math. 46, 1221–1268 (1993)
Klainerman, S., Machedon, M.: On the Uniqueness of Solutions to the Gross-Pitaevskii Hierarchy. Commun. Math. Phys. 279, 169–185 (2008)
Koch, H., Tataru, D.: Dispersive estimates for principally normal pseudodifferential operators. Comm. Pure Appl. Math. 58, 217–284 (2005)
Koch, H., Tataru, D.: A priori bounds for the 1D cubic NLS in negative Sobolev spaces, Int. Math. Res. Not. IMRN (2007), no. 16, Art. ID rnm053, 36 pp
Koch, H., Tataru, D., Vişan, M.: Dispersive Equations and Nonlinear Waves, Oberwolfach Seminars 45 (2014), Birkhäuser
Knowles, A., Pickl, P.: Mean-field Dynamics: Singular Potentials and Rate of Convergence. Comm. Math. Phys. 298, 101–138 (2010)
Kuz, E.: Exact Evolution versus Mean Field with Second-order Correction for Bosons Interacting via Short-range Two-body Potential. Differential and Integral Equations 30, 587–630 (2017)
Lewin, M., Nam, P.T., Rougerie, N.: Derivation of H artree’s theory for generic mean-field Bose systems. Adv. Math. 254, 570–621 (2014)
Lin, J.E., Strauss, W.A.: Decay and scattering of solutions of a nonlinear Schrödinger equation. J. Funct. Anal. 30, 245–263 (1978)
Mendelson, D., Nahmod, A., Pavlović, N., Staffilani, G.: An infinite sequence of conserved quantities for the cubic Gross-Pitaevskii hierarchy on \({\mathbb{R}}\). Trans. Amer. Math. Soc 371, 5179–5202 (2019)
Mendelson, D., Nahmod, A., Pavlović, N., Rosenzweig, M., Staffilani, G.: A Rigorous Derivation of the Hamiltonian Structure for the Nonlinear Schrödinger Equation. Adv. Math. 365, 107054 (2020)
Mendelson, D., Nahmod, A., Pavlović, N., Rosenzweig, M., Staffilani, G.: Poisson Commuting Energies for a System of Infinitely Many Bosons, 97pp, arXiv:1910.06959
Miao, C., Xu, G., Zhao, L.: Global well-posedness and scattering for the defocusing \(H^{1/2}\)-subcritical Hartree equation in \( {\mathbb{R}}^{d}\). Ann. Inst. H. Poincaré Anal. Non Linéaire 26, 1831–1852 (2009)
Nam, P.T., Salzmann, R.: Derivation of 3D energy-critical nonlinear Schrödinger equation and Bogoliubov excitations for Bose gases. Commun. Math. Phys. 375, 495–571 (2020)
Nugent, E.: Novel Traps for Bose-Einstein Condensates, PhD thesis, University of Oxford, (2009)
Savard, T.A., O’Hara, K.M., Thomas, J.E.: Laser-noise-induced heating in far-off resonance optical traps. PRA 56, R1098 (1997)
Shen, S.: The Rigorous Derivation of the \({\mathbb{T}}^{2}\) Focusing Cubic NLS from 3D. J. Funct. Anal. 280, 108934 (2021)
Sohinger, V.: Local Existence of Solutions to Randomized Gross-Pitaevskii Hierarchies. Trans. Amer. Math. Soc. 368, 1759–1835 (2016)
Sohinger, V.: A Rigorous Derivation of the Defocusing Cubic Nonlinear Schrödinger Equation on \({\mathbb{T}}\)\(^{3}\) from the Dynamics of Many-body Quantum Systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 32, 1337–1365 (2015)
Sohinger, V., Staffilani, G.: Randomization and the Gross-Pitaevskii hierarchy. Arch. Rational Mech. Anal. 218, 417–485 (2015)
Stamper-Kurn, D.M., Andrews, M.R., Chikkatur, A.P., Inouye, S., Miesner, H.-J., Stenger, J., Ketterle, W.: Optical Confinement of a Bose-Einstein Condensate. Phys. Rev. Lett. 80, 2027–2030 (1998)
Wiener, N.: The Quadratic Variation of a Function and its Fourier Coefficients. Journal of Mathematics and Physics 3, 72–94 (1924)
Xie, Z.: Derivation of a Nonlinear Schrödinger Equation with a General Power-type Nonlinearity in \(d=1,2\). Differ. Integral Equ. 28, 455–504 (2015)
Acknowledgements
The authors would like to thank Shunlin Shen and the referees for their careful reading and checking of the paper. X.C. was partially supported by the NSF grant DMS-2005469 and by a Simons Fellowship. J.H. was supported in part by the NSF grant DMS-2055072.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Misc. Estimates
Appendix A. Misc. Estimates
1.1 A.1 Collapsing Estimates and Strichartz Estimates
We use the original Klainerman-Machedon collapsing estimate as our iterating estimate in this paper.
Lemma A.1
([13, 19, 54]) Footnote 14There is a C independent of V, j, k, and N such that, (for \(f^{(k+1)}({\mathbf {x}}_{k+1},{\mathbf {x}}_{k+1}^{\prime })\) independent of t)
To explore the time derivative gain by Duhamel type terms, we also need the \( X_{s,b}\) version of Lemma A.1. As we are using \( S^{(k)}\) to denote the space derivatives, we surpress the s notation in definition of the \(X_{s,b}\) space and define the norm \(X_{b}^{(k)}\) by
which is essentially a \(X_{0,b}\) norm. We then have the Duhamel time-derivative gain property and the \(X_{s,b}\) version of Lemma A.1.
Claim A.2
([21]) Let \(\frac{1}{2}<b<1\) and \(\theta (t)\) be a smooth cutoff. Then
Lemma A.3
([21]) There is a C independent of j, k, and N such that (for \(\alpha ^{(k+1)}(t,{\mathbf {x}}_{k+1},{\mathbf {x}}_{k+1})\) dependent on t)
In the above notation, the dual Strichartz estimates we need in this paper are the following:
Lemma A.4
([21]) Let
Then for \(N\ge 1\), we have
and
1.2 A.2. Convolution Estimates
Lemma A.5
Let \(W_{N}(x)=N^{3\beta }V(N^{\beta }x)-b_{0}\delta (x) \), where \(b_{0}=\int V(x)\,dx\). For any \(0\le s\le 1\),
for any \(1<p<\infty \). The implicit constant depends only on \(\Vert \langle x\rangle V(x)\Vert _{L^{1}}\).
Proof
The case \(s=0\) is just Young’s inequality, since \(\Vert V_{N}\Vert _{L^{1}}=\Vert V\Vert _{L^{1}}<\infty \), independent of N. We next establish the estimate for \(s=1\). Since \({\hat{V}}(0)=b_{0}\),
and thus
Let \(Y(x)=xV(x)\) so that \({\hat{Y}}(\xi )=\nabla {\hat{V}}(\xi )\). It follows that
By Minkowski’s inequality and Young’s inequality,
The cases \(0<s<1\) follow by interpolation, as follows. Let \(P_{M}\) be the Littlewood-Paley projector for frequency \(0<M<\infty \). Then by the \(s=0\) and \(s=1\) cases,
Divide the sum into the case \(M\le N^{\beta }\), for which we use \(\min (1,N^{-\beta }M)=N^{-\beta }M\), and the case \(M\ge N^{\beta }\), for which we use \(\min (1,N^{-\beta }M)=1\).
\(\square \)
Lemma A.6
Let \(W_{N}(x)=N^{3\beta }V(N^{\beta }x)-b_{0}\delta (x)\), where \(b_{0}=\int V(x)\,dx\).
Also, if \(f_{j}\) is replaced by \(P_{M_{j}}f_{j}\), then the same estimate holds but in addition we must have \(M_{1}\sim M_{2}\) (or otherwise the left side is zero).
Proof
By Plancherel
As in the proof of Lemma A.5,
Since
we can just complete the proof by Cauchy-Schwarz in (A.4) \(\square \)
Rights and permissions
About this article
Cite this article
Chen, X., Holmer, J. Quantitative Derivation and Scattering of the 3D Cubic NLS in the Energy Space. Ann. PDE 8, 11 (2022). https://doi.org/10.1007/s40818-022-00126-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40818-022-00126-5
Keywords
- N-body quantum BBGKY hierarchy
- Convergence rate
- Klainerman-Machedon theory
- Nonlinear scattering
- Koch-Tataru U-V spaces



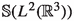 in which
in which