Numerical simulation of flow over a coastal embankment and validation of the nappe flow impinging jet

Abstract

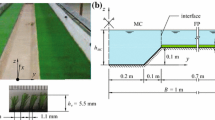
A computational fluid dynamics simulation was conducted to reproduce the overtopped tsunami from a coastal embankment model (EM) with six different crest geometric conditions, thereby decreasing the downstream surface slope angle to validate the existing experiment flow structures of nappe flow formation conditions. Crest geometries included horizontal crest (EM-N_HC), (+) 4% ascending crest slope case (EM-N_AC), (−)4% descending crest slope case (EM-N_DC), and horizontal crest with sparse (EM-VM_S), intermediate (EM-VM_I), and dense (EM-VM_D) vegetation model, respectively. For the simulation, the open-source algorithm called OpenFOAM was used with a volume of fluid (VOF) method and with the $k-\omega$ Shear Stress Transport (SST) turbulence model. Multizone meshing and the mesh refinement regions were adopted to capture the nappe flow free surface profile with minimum numerical diffusion at the free surface boundary between the section of 0.6 m and 1.7 m in the numerical domain. The mesh refinement region accurately captures the nappe flow regime from the upstream brink edge to the embankment’s downstream plunge pool. An adjustable time-step technique was used in the numerical simulation, which kept the Courant number ($Co$) less than one to avoid numerical diffusion. The experimental approach, based on the overtopping depth, determined the downstream brink depth (${h}_{d}$), upstream brink depth (${h}_{u}$), water depth of the middle section ($h$) above the crest of the embankment model for the particular setups considered, drop length (${L}_{d}$) of the nappe impinging jet, head loss downstream (${H}_{L}$) and pool water depth (${h}_{p})$ then validated with numerical results. The percentage error of the numerically predicted streamwise velocity varied between 0.6 and 5.7% concerning the selected turbulence models. Moreover, the percentage error in the nappe flow predictability for the horizontal (EM-N_HC), (+) 4% ascending (EM-N_AC), and (−)4% descending EM-N_DC crest cases were ranged between 0.9–2.2%, 0.6–2.0%, and 3.4–5.7%, respectively. The percentage error of the numerically predicted head loss varied between − 3.8 and 1.5% concerning the experiment results. The study’s numerical findings are essential in designing a coastal embankment and its scour protection mechanisms.

Appendices

Appendix 1

The conventional $k-\varepsilon$ model’s transport equations are as follows (Launder and Spalding 1972):

$$\frac{\partial k}{\partial t}+\frac{\partial {ku}_{i}}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{i}}\left[\left(\upsilon +\frac{{\upsilon }_{T}}{{\sigma }_{k}}\right)\frac{\partial k}{\partial {x}_{i}}\right]+{G}_{k}-\varepsilon$$

(1A)

$$\frac{\partial \varepsilon }{\partial t}+\frac{\partial \varepsilon {u}_{i}}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{i}}\left[\left(\upsilon +\frac{{\upsilon }_{T}}{{\sigma }_{\varepsilon }}\right)\frac{\partial \varepsilon }{\partial {x}_{i}}\right]+{C}_{1\varepsilon }\frac{\varepsilon }{k}{G}_{k}-{C}_{2\varepsilon }\frac{{\varepsilon }^{2}}{k}$$

(2A)

$${\upsilon }_{T}={C}_{\mu }\frac{{k}^{2}}{\varepsilon }$$

(3A)

where $k$ is the turbulent kinetic energy, $\varepsilon$ is the dissipation rate of the turbulence kinetic energy, $\upsilon$ is the kinematic viscosity, ${\upsilon }_{T}$ is the turbulence kinematic viscosity, ${G}_{k}$ is the generation of turbulence kinetic energy due to the mean velocity gradients, and ${\sigma }_{k}$, ${\sigma }_{\varepsilon }$, ${C}_{1\varepsilon }$, ${C}_{2\varepsilon }$, ${C}_{\mu }$ are constants.

The RNG $k-\varepsilon$ model is in the family of the $k-\varepsilon$ model, which uses the adjusted version of the transport equation of the turbulent kinetic energy dissipation rate ($\varepsilon$) to calculate the eddy viscosity terms as follows (Imanian and Mohammadian 2019):

$$\frac{\partial \varepsilon }{\partial t}+\frac{\partial \varepsilon {x}_{i}}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{i}}\left[\left(\upsilon +\frac{{\upsilon }_{T}}{{\sigma }_{\varepsilon }}\right)\frac{\partial \varepsilon }{\partial {x}_{i}}\right]+{C}_{1\varepsilon }\frac{\varepsilon }{k}{G}_{k}-\left[{C}_{2\varepsilon }+\frac{{C}_{\mu }{\eta }^{3}\left(1-\eta /{\eta }_{o}\right)}{1+\beta {\eta }^{3}}\right]\frac{{\varepsilon }^{2}}{k}$$

(4A)

Appendix 2

Statistical indicators are used to analyze the performance of the numerical prediction concerning the experimentally observed data (Imanian and Mohammadian 2019).

Root mean square error:

$$RMSE= \sqrt{\frac{1}{n}{\sum }_{i=0}^{n}{\left({u}_{exp.}-{u}_{Num.}\right)}^{2}}$$

(5A)

Normalized root mean square error:

$$NRMSE= \frac{RMSE}{\mathrm{max}\left({u}_{exp.}\right)-\mathrm{min}\left({u}_{Num.}\right)}$$

(6A)

Normalized mean square error:

$$NMSE= \frac{{RMSE}^{2}}{\left[\mathrm{max}\left({u}_{exp.}\right)-\mathrm{min}\left({u}_{exp.}\right)\right].\left[\mathrm{max}\left({u}_{Num.}\right)-\mathrm{min}\left({u}_{Num.}\right)\right]}$$

(7A)

Mean absolute percentage error:

$$MAPE= \frac{1}{n}\sum _{i=0}^{n}\left|\frac{{u}_{exp.}-{u}_{Num.}}{{u}_{exp.}}\right|$$

(8A)

Mean absolute error:

$$MAE= \frac{1}{n}\sum _{i=0}^{n}\left|{u}_{exp.}-{u}_{Num.}\right|$$

(9A)

Determination Coefficient:

$${R}^{2}={\left\{\frac{{\sum }_{i=0}^{n}\left[{u}_{exp.}-\overline{{u }_{exp.}}\right]}{\sqrt{{\sum }_{i=0}^{n}{\left[{u}_{exp.}-\overline{{u }_{exp.}}\right]}^{2}}}-\frac{\left[{u}_{Num.}-\overline{{u }_{Num.}}\right]}{\overline{{\sum }_{i=0}^{n}{\left({u}_{Num.}-\overline{{u }_{Num.}}\right)}^{2}}}\right\}}^{2}$$

(10A)

where ${u}_{exp.}$ is the experimental velocity and ${u}_{Num.}$ is the numerical velocity, respectively.