Experimental Investigation of Shot Peening on Case Hardened SS2506 Gear Steel

Abstract

Shot peening is a manufacturing process commonly used to increase fatigue life in components for the automotive and aircraft industry. In this paper the effect of shot peening is described for a case hardened gear steel. For gears there are three main factors from shot peening that influence fatigue life: residual stresses, microstructure and surface roughness. The paper describes an experimental series where these parameters were measured for common industrial shot peening settings. The aim was to show how several different measurement techniques and results correspond to each other for certain shot peening parameters. The aim was also to gather experimental results that can be used for verification of shot peening simulations. To simplify measurements and decrease variation, flat steel plates were used as targets. Residual stress, full width at half maximum (FWHM), retained austenite, surface roughness/topology, hardness and Barkhausen noise were measured and related to microstructural changes. The mean indentation diameter was measured for individual shots at low coverage of each intensity which was used to determine the average velocity of the media. The mean diameter and hardness of the shot peening media was also determined.

Introduction

Shot peening is a manufacturing process where cold working of the surface is achieved by a propelled stream of spherical shots, often called media. The process is mainly used to improve fatigue properties in mechanical parts by introducing compressive stresses in the surface layer. The fatigue performance of gears can be drastically improved by the shot peening operation which is used in several industrial sectors [1]. In the aircraft industry it is also used to form metal panels, called peen forming [2]. In the medical implant industry it is not only used to increase fatigue and fretting fatigue resistance but also to increase the physiological acceptance by adjusting the surface roughness [3, 4]. Other areas are inhibiting stress corrosion cracking; close pores in castings to prevent leaking; create surface roughness that improve adhesion of paint; adjust surface profile for enhanced oil retention of seals [5]; creating surface topologies that improve fatigue life of tools, gears and cams [6]. There are three important properties influenced by shot peening when fatigue is considered: residual stresses, work hardening and surface topography [7, 8]. Schulze [9] gives a comprehensive overview of the properties that shot peening influences and how different manufacturing parameters affect the result.

There are three main parameters that specify the shot peening: intensity, coverage and media size. The media size is a measure of the diameter of the shots, coverage is the ratio of indented area to the total area of the target and intensity is a measure of the media’s ability to create indentations [10]. Intensity is quantified by using standardized Almen strips. The procedure is explained in detail by Kirk [10] and in SAE J443 [11].

Kobayashi et al. [12] did some original investigations on shot peening by dropping large bearing balls onto steel plates and measuring the residual stresses in the plate surface. They compared the results with static indentations by loads that created the same indentation diameter as the drop tests did. The dynamic impacts resulted in a tensile residual surface stress while the static indent had zero stress at the centre of the indent. However, by creating more dynamic indentations around the first indent the tensile surface stress changed to a compressive stress.

Wohlfahrt [13] compares a collection of shot peening experiments from different authors from 1956 up to 1983 and discusses the dependence of the residual stress profiles on the relation between media and target hardness. Wohlfahrt divided the creation of residual stresses in two processes: direct plastic elongation of the surface layer and plastic deformation at the maximum shear stress depth due to the Hertzian pressure. He found that target hardness that is much lower than the media hardness tends to deform the surface layer. This gives high surface roughness and the maximum compressive residual stress occurs at or near the surface. Medium target hardness which is about the same as the media hardness gives lower surface roughness and a distinct maximum compressive stress under the surface. If the target is harder than the media, then there will be small amounts of direct surface plastic deformation and low surface roughness. The maximum compressive stress that can be attained beneath the surface can be large, both absolutely and relatively compared to the residual stress in the surface.

Residual stresses are mostly measured with X-ray diffraction or hole drilling techniques but there exist other methods, like relaxation procedures [14]. Wang et al. [15] shot peened several different steels and aluminium alloys with cast steel shots of 44–48 HRC hardness. They found linear relations between the maximum achievable compressive residual stresses and the materials yield and ultimate tensile strengths. They also quantified the depth of the compressive residual stress maximum as a function of the peening intensity and the materials yield and tensile strength. Ahmad and Crouch [16] shot peened a case carburized gear steel, SAE 8620, and concluded that a higher shot hardness typically produces higher compressive residual stresses, dual peening increases the magnitude of the stresses and by removing the oxidized upper surface layer the surface compressive residual stress is increased. Harada et al. [17] measured compressive residual stresses up to 2000 MPa in a case carburized steel SCM420 target when cemented carbide shots of hardness 1405 HV were used. If regular cast steel shots with 490 HV hardness were used then compressive residual stresses of about 1000 MPa were measured. The Vickers hardness of the workpiece was also increased to about 880 HV for the cast steel shots and to 1050 HV for cemented carbide shots. Very high hardness shots do however have the drawback that they easily fracture. To increase the service life of the media the workpiece can be heated to decrease its flow stress. Harada et al. [17] found an optimum working temperature at 300 ^∘C; above 300 ^∘C the maximum residual stress decreased.

The compressive stresses near the surface are balanced by tensile stresses deeper inside the material. Menig et al. [18] used neutron diffraction to experimentally show that the tensile stresses were evenly distributed inside a sample which had been shot peened on both sides.

The measure full width at half maximum (FWHM) is the width of the X-ray diffraction peak at half of its maximum value. It is obtained simultaneous to the residual stress measurements when using X-ray diffraction. Larger diffraction peak widths generally indicate larger amounts of cold work [19,20,21]. Zinn and Scholtes [22] noticed such behaviour for annealed 42CrMo4 steel. However, when the steel was quenched and tempered to a hardness of 500–520 HV a decrease in FWHM occurred from shot peening. Schulze [9] explains this decrease by hard materials having very high dislocation densities and that the shot peening led to dislocation rearrangements with energetically more favourable structures.

Hasegawa et al. [23] studied the temperature change of the surface of the shot peened target. The temperature was measured with an infra-red thermograph. A case hardened steel with hardness 700 HV showed no practical temperature change when shot peened while an annealed steel with hardness 220 HV displayed a 40 ^∘C rise. A much higher abrasive wear of the soft steel was suggested as the cause of the temperature change.

Prevey and Cammett [24] investigated the effect of coverage on AISI 4340 and conclude that both the residual stress profile and cold work were saturated at only 20% coverage. The bending fatigue life with R = 0.1 was also highest for the 20% coverage and was lower for higher coverages. This is in conflict with recommendations to have at least 100% coverage. Prevey et al. explain this by suggesting that previous investigations of fatigue life usually used fully reversed bending which can cause reversed yielding with loss of compressive residual stresses and the fatigue improvement seen is mostly due to work hardening. Torres and Voorwald [25] also investigated AISI 4340. They varied the intensity while keeping the coverage constant at 200%. An optimum fatigue life for rotating bending was achieved for a medium intensity.

Ando et al. [26] investigated how retained austenite content and peening under pre-stress influences the induced compressive residual stresses. They concluded that strain-induced martensite that is transformed from retained austenite during shot peening does not influence the surface and maximum residual compressive stress. Ishikura et al. [27] studied the case carburizing steel SCM420H with different hardnesses and microstructures. Shot media with hardness 950 HV was used. The results indicated that the amount of retained austenite does not greatly influence the maximum residual stress. The maximum achievable compressive residual stress is linearly dependent on target hardness as long as the media hardness is higher than the target hardness. Tsuji et al. [28] reached the conclusion that the achievable compressive residual stress is about 60% of the yield stress. The increased compressive residual stress when retained austenite was transformed was attributed to the increased yield stress. On the other hand, Van Wijk et al. [29] studied a shot peened carbonitrided steel and noted that when the shot media was softer than the target, 100% of the residual stress can be explained by retained austenite transformation. When the shot was harder than the target the contribution from plasticity and phase transformation to the resulting compressive residual stress was about 50% each.

Barkhausen noise is a phenomenon that occurs when a ferromagnetic material is subjected to a varying external magnetic field. The magnetic moments of atoms organize into magnetic domains with constant magnetic field. If the magnetic field is varied, each separate magnetic domain will change its field suddenly. This creates a stepwise increase in the magnetic response of the material which is called the Barkhausen effect. The stepwise magnetic change is influenced by the microstructural state of the material [30]. Suominen and Tiitto [31] investigated three different types of steels that were shot peened. The results show that the change of Barkhausen noise and the FWHM does not only depend on the hardness before shot peening but also on the specific types of steel. A martensitic precipitation hardening stainless steel, 15-5PH, with 45.3 HRC hardness and 2.27 ^∘ FWHM before shot peening, showed a decrease in Barkhausen noise and an increase in FWHM, both indicating work hardening. AISI 4330M with a hardness of 43 HRC and 3.05 ^∘ FWHM had small changes in FWHM and an increasing Barkhausen noise. AISI 4340M with hardness of 57.5 HRC and 5.45 ^∘ FWHM showed a decrease in FWHM and an increase in Barkhausen noise which indicated work softening. Moorthy et al. [32] investigated surface and subsurface stresses in a case carburized steel with Barkhausen noise. For elastic applied stresses the Barkhausen noise increased for tensile stresses and decreased for compressive stresses. If the applied stress plastically deformed the specimens and the Barkhausen noise was measured after unloading, then a more complex behaviour was found. The material just beneath the case might plastically deform while the case, with its higher yield stress, might still be elastically deformed. With different frequency ranges the behaviour at different depths could in theory be detected but such an analysis may require further research. Marconi et al. [33] used Barkhausen noise to monitor shot peening on Pelton wheels. The shot peened specimens showed an increased Barkhausen noise although compressive residual stresses were introduced by the shot peening. The shot peening also decreased the amount of retained austenite from 10% to less than 1%. Marconi remarks that the phase transformation of retained austenite, which is non-magnetic, to the magnetic martensite will increase the Barkhausen noise amplitude, thus counteracting the decrease the compressive stress should give.

A relatively new method of shot peening is called ”severe shot peening”. The aim is to produce a very fine grained (nanocrystallized) surface material. The shot peening is done with high coverage and/or high intensity. Bagherifard et al. [34] used an intensity of 0.18 mm Almen C and a coverage of 1500%. The average grain size was measured to 50 nm and the fatigue life improved with 246%. Hassani-Gangaraj et al. [35] used high coverage to create a fine grained structure that more easily diffuse nitrogen, decreasing the cost of gas nitriding.

Zhang et al. [36] compares traditional shot peening and micro-shot peening with respect to the scuffing resistance. They conclude that shot peening increases the scuffing capacity and micro-shot peening can improve the scuffing load up to 3 times. Micro-shot peening can also decrease the surface roughness compared to traditional shot peening.

The purpose of this study was to experimentally determine the effects of shot peening at industrial conditions on parameters important for rolling contact fatigue in a common case hardened gear steel. Apart from the parameters that influence fatigue, parameters that are important for the simulation of shot peening were included in the investigation. In particular coverage, intensity and media size were varied within normal process specifications: coverage was 100% – 400%, intensity was 0.2 – 0.5 mm Almen A and the media was cut wire of 0.7 and 0.35 mm nominal diameters. Double shot peening was also investigated. The specimens were then first shot peened with the larger media and in a second operation shot peened with the smaller media. The investigated parameters include: residual stress profile, retained austenite content, work hardening, surface roughness and Barkhausen noise. By measuring the parameters on the same or identically shot peened specimens the goal was to produce a unique set of data for relating, comparing and verifying different properties against each other. Series with low coverage were included in the work for later verification of shot peening models and to determine the media velocity.

Experimental Set-Up

Test Specimen

The test specimens used in this work are shown in Fig. 1. They are 30 × 30 mm square plates with a thickness of 10 mm. They were manufactured from gear blanks made of the Swedish standard SS 92506 steel, see Table 1 for the material specification. This steel is approximately equal to DIN 21NiCrMo2 or SAE 8620 [37]. The surface intended to be shot peened was ground in soft state to a surface roughness of about Ra = 0.5 µm. The plates were then heat treated in a pusher furnace. The process time was 702 minutes for carburizing and 117 minutes for the diffusion step. The temperature and carbon potential was 925 ^∘C and 0.80 wt.% for the carburizing step and 850 ^∘C and 0.98 wt.% for the diffusion step. The plates were then oil quenched for 5 minutes in 130 ^∘C and after that in 60 ^∘C for 5 minutes. Finally they were tempered in 200 ^∘C for 72 minutes. The tempering gave a near surface hardness of 716 HV1 and the case depth, defined as the depth where the hardness is 550 HV1, became 1.7 mm. Figure 2 shows a cross section view below the surface of the microstructure in the shot peened case. The surface is located to the left in the figure. The martensite plates are light coloured and 0.5–3 µm wide, this corresponds well with the results by de Diego-Calderón et al. [38]. The retained austenite inclusions are visible as relatively round, dark structures with less than 1 µm width. The fatigue properties for this material are reported by Preston [39] for rotating bending and supplemented with pulsating torsion results by Alfredsson and Olsson [40]. The monotonic tensile properties of the case and core can be found in Alfredsson and Olsson [41]. One hundred plates were manufactured and all were measured with a Barkhausen probe after hardening. Five of the plates showed a larger variation in Barkhausen noise over the plate width compared to the rest of the plates. These were discarded to minimize the influence of non-shot peening effects and so that all plates would have a uniform condition before the shot peening. This allowed the analysis to focus on the shot peening effect on the measured properties.

Fig. 1

Drawing of the test specimen (a) and photo of a plate after case hardening (b)

Table 1 Chemical composition of SS 92506

Fig. 2

Cross section view of microstructure close to the surface after heat treatment and medium shot peening: light areas are martensite plates and dark smooth rounded spots are inclusions of retained austenite. Scale is 2 µm

Shot Peening

The compressed air shot peening equipment is shown in Fig. 3. It was a dual pressure pot machine which means that the compressed air and shot peening media was mixed in a pressurized tank and flowed together in hoses to the nozzles. The shot flow was controlled by a magnetic shot flow control [7]. The nozzles were venturi bore type with a throat diameter of 7.9 mm, an exit diameter of 12 mm and approximately 80 mm distance between throat and exit. The nozzles were positioned 15 cm above the test specimens and with an impact angle of 90^∘. This gave a shot peened area of about 20 – 25 mm in diameter at the test specimens. To effectively cover the 30 mm wide specimens, two nozzles with a slight offset were used, see Fig. 3. Six test specimens and two Almen strip holders were mounted on a round disc with radius 19 cm. During shot peening the disc rotated with 10 rpm. Note that each plate was only under the shot blast a certain amount during the rotation of the disc. The shot peening times reported in this paper were the times the machine was operating. The effective time each plate was shot peened was much shorter, approximately 1/30 of the total time the machine was running. For the specification of the shot peening this is however not important since it is the coverage that is the controlling parameter.

Fig. 3

Test specimens in the compressed air shot peening machine

The media was cut wire, spherical conditioned to grade G3 and hardness 58 – 63 HRC, according to AMS 2431/8 [42]. Two nominal sizes were used, 0.7 mm and 0.35 mm. Figure 4 shows the 0.7 mm media. As can be seen, size, shape and roundness differed between each shot. The 0.7 mm media had been used in the machine for a long time while the 0.35 mm was a fresh refill. More than 30 shots of the media were measured with a calliper giving a mean diameter of 0.84 mm and a standard deviation of 0.1 mm for the 0.7 mm media. For the 0.35 mm media the mean diameter was 0.36 mm and the standard deviation 0.02 mm. According to [43], S280 has a mean diameter of 0.84 mm. Fitting a normal distribution to the allowed cumulative percentage for S280 [44], gives a mean of 0.81 mm and a standard deviation of 0.12 mm. It is therefore likely that the difference in mean and the relatively large standard deviation of the 0.7 mm media compared to the 0.35 mm media is due to the fact that the 0.7 mm media has been circulated, sieved and had fresh media added for a long time in the shot peening machine.

Fig. 4

Cut wire shot peening media with nominal diameter 0.7 mm. This media had been used in the shot peening machine for a long time

The hardness of the 0.7 mm media was measured by embedding the shots in a mounting holder. A flat cross section surface was then ground and polished to approximately half the shots diameter. Vickers hardness was measured in the middle of 50 shots giving a mean hardness of 742 HV1 and a standard deviation of 50 HV1. Compared to the specification 58 – 63 HRC, which can be translated to 653 – 775 HV, the measured mean was in the upper area and the lower specification limit was reached with 2 standard deviations.

Shot peening machine parameters and the intensity measurements are shown in Table 2. Media is the nominal diameter of the shot peening balls, Pressure is the air pressure used to propel the shots, Mass flow is the total mass of the balls leaving the nozzle, Duration is the total machine time each shot peening of an Almen strip took and Arc height is the corresponding measured bending height of the Almen strip. The arc heights was measured on an Almen Gage TSP-3 [45] and a 2PF curve [46] was fitted to the Duration and Arc height values. The intensity for the specific media, pressure and mass flow is defined as the saturation point which is the point on the curve when a 100% increase in duration gives a 10% increase in arc height [11]. An example from the second row in Table 2 is shown in Fig. 5.

Table 2 Shot peening intensity measurements

Fig. 5

Calculating the intensity for the second row in Table 2

Coverage was checked for the 0.35 media by painting plates with a fluorescent marker pen, PeenScan Pen [47], which shines bright in ultra-violet light. When the shot peening balls hit the surface the paint is worn off and a visual indication of the coverage can be seen. Figure 6 shows plates shot peened with six different times (the brightness and contrast has been increased from the original picture to better show in print). The plate with the shortest shot peening time, 15 s, has a lot of fluorescent paint left. As the shot peening time increase more and more of the paint is worn of. From these tests a rough estimate of the time to 98% (full) coverage was found at 55 s. For the 0.7 mm media the time to reach 98% coverage was known by experience of the operator of the shot peening machine to be 165 s. It was therefore not measured in the same way as the iD media. Even though intensity will influence the coverage the estimate of full coverage was so rough that the same time was used for all three intensities. It can here be noted that since the mass flow of both media sizes were the same, 7.5 kg/min, the number of shots per minute for the 0.35 mm size was much larger than of the 0.7 mm size. Even though the indentation diameter of the 0.35 mm media was smaller than of the 0.7 mm media this meant that the time to reach full coverage was expected to be shorter for the smaller media size.

Fig. 6

Measurement of coverage for the 0.35 mm media with PeenScan pen. The number beneath each plate is the number of seconds each plate had been shot peened

In practise the time to reach 98% is called full coverage (called 100% here after) and multiples of that time is denoted as 200%, 300% and so on. In total there were 12 shot peening variants, also counting plates that were not shot peened, denoted case hardened (CH). Table 3 lists all the shot peening variants. Note in particular that series i1, i2 and i3 were 3 different series with increasing shot peening intensity. The last three variants were double shot peened, meaning that they were first shot peened with 200% coverage of the 0.7 mm media with intensities i1, i2 or i3 and then shot peened with 100% coverage with the 0.35 mm media with intensity iD.

Table 3 Shot peening variants

Residual Stress and Retained Austenite

The residual stress and retained austenite measurements were made with an Xstress 3000 G3 X-ray diffractometer [48]. Stresses were measured in three directions on the plates with 45^∘ between each direction. Since the plates and the shot peening had no preferred direction all directions gave similar values and an average was made. A collimator with 2 mm diameter was used for all measurements. Electropolishing was used to remove material from the shot peened surface so that measurements could be made at different depths. Only a circular area with a diameter of approximately 8–9 mm was removed. The residual stresses were not corrected for relaxation because of this. Each depth removed by the electropolishing was measured by a digital dial indicator. There is no precise way to electropolish to an exact depth. Therefore, the depth was determined individually for each residual stress measurement. At the same time as the residual stress was measured the width of the diffraction peaks was also recorded, which is called full width at half maximum (FWHM). The X-ray diffraction measurement was made using Cr-K α radiation and the lattice plane {211} (2Θ 156.4^∘). The tube had a voltage of 30 kV and the current were 7 mA. Stresses were determined using $\sin ^{2}{\Psi }$ method, 9 tilt angles (Ψ) from − 40^∘ to + 40^∘ with tilt oscillation of ± 5^∘ and cross correlation technique. The exposure time at each position was 20 seconds. The elastic constants used were E = 211 GPa and ν = 0.3. In materials with dual phases that have different yield strength the microstresses can differ [49]. The residual stresses measured on one lattice plane are therefore not macroscopic but they are usually assumed to be close. Although it can be considered industry standard to measure residual stresses with X-ray diffraction on shot peened specimens some caution should be considered when comparing with other sources.

The retained austenite was measured using Cr-K α radiation with a tube voltage of 30 kV and current of 7 mA. The ferrite phase was measured on planes {211} (156.4^∘) and {200} (106.1^∘) with an exposure time of 20 seconds. The austenite phase was measured on planes {220} (130^∘) and {200} (80^∘) with an exposure time of 40 seconds. The peak for the ferrite phase was fitted with Split Pearson VII and the background with a linear fit. The peak for the austenite phase was fitted with a Gauss function and the background with a parabolic function.

X-ray diffraction measurement uncertainty

The measurement of residual stresses included several complex experimental and analytical sources of uncertainties. These can broadly be categorized into instrument, specimen, operator and elastic constants related. The elastic constants E and ν are preferable determined by measurement but if that is not done the operator has to decide what values to use. In this case 211 GPa and 0.3 was used for Young’s modulus and Poisson’s ratio. The uncertainty in the calculated stress due to uncertainty in elastic constants was assumed to be 5%. The instrument related uncertainties were estimated during the analysis as the goodness of fit of the $\sin ^{2}{\Psi }$ plot. The methodology to estimate the combined uncertainty was performed according to [50]. The uncertainty in depth depends on the repeatability of the experimental set up, the accuracy of the indicator, the flatness of the etching and the location of the diffraction beam. The accuracy of the digital indicator used for the depth measurement was 3 µm. The repeatability of the carriage used to hold the specimen was 5 µm. The flatness of the etching was evaluated within an circle with 2 mm diameter which corresponds to the size of the X-ray diffraction beam. The height difference due to the etching process was assumed to increase with increasing etch depth and level out to a constant value of 35 µm at depths deeper than 0.3 mm. The combined standard uncertainty was then expanded to correspond to 95% confidence using a multiplication factor of 2. To improve the visibility of the curves individual error bars were not plotted for the depth. A depth legend in each figure shows the max estimated uncertainty range for the depth measurements.

Surface Measurements

Surface roughness was measured with a Mitutoyo SJ-301 surface roughness tester. The instrument is a mobile, stylus type, roughness tester with a separate probe that uses a lateral skid type pick-up. Using an adjustable arm on a magnetic base the probe can be positioned for stable and aligned measurements. The measurements were made transverse to the grinding marks. Each variant of shot peening was measured on 5 individual plates and an average was calculated.

The surface topography was measured with confocal microscope PLu 2300 from Sensofar [51]. An area of 665 × 659 µm was measured with 2 µm spacing between points. In height direction, planes were scanned with 0.2 µm apart. The measured areas were then evaluated and plotted in the analysis software SensoMap 4.1 [51].

Hardness

Vickers hardness was measured with a Matsuzawa MXT 30 hardness tester equipped with a digital camera and the Buehler Omnimet MHT analysing software. Measurements were done on polished cross-sections of the plates to obtain the hardness as function of depth below the shot peened surface. A force of 100 g _f was used which gave an indent size around 15 µm. This is considerable larger than the typical size of the martensite and the retained austenite structures which are less than 1 µm in the current microstructure, see Fig. 2. Each micro-hardness indent will cover a number of martensite grains and in most cases a retained austenite inclusion. Therefore, the micro-hardness measurements can be seen as good averages of the local hardness and the values will be comparable to macro-hardness values. Also, according to Parrish [52] the austenitic grain size does not influence the hardness value to any great extent.

For the Vickers hardness measurement the scatter was estimated based on the non-shot peened plate and a repetition measurement on plate i2-200%. The estimated scatter was ± 15 HV0.1 and it was assumed equal for all indents. The scatter in depth measurement was estimated to 0.01 mm based on the position accuracy of the equipment and measurement procedure.

Barkhausen Noise Analysis

Barkhausen noise measurements were made with a camshaft probe and a MicroScan 500-2 unit from StressTech [48], using the Rollscan mode. The gain for the channel used was set to 50, the magnitude to 50 and the mode to RH 125 Hz. The magnetization frequency of 125 Hz reaches a couple of mm down into the material. The pick-up frequency was 2.5 MHz which records signals around 40–100 µm deep [48]. These settings were chosen based on experience to give measurement values in an appropriate range for the plates. The Barkhausen noise probe was moved over the plates at a certain rate while recording the signal. The mean value was recorded for each plate. Each variant was measured on 5 individual plates and the mean value of these was used as the result for each shot peened variant. The actual numerical values have no physical meaning. It is only the changes between different variants that are interesting. The Barkhausen noise value for the non-shot peened plates was therefore used as a reference value and the percent of change from this value was calculated for each shot peened variant.

EBSD Characterization of the Microstructure

Electron backscatter diffraction (EBSD) was used to characterize the microstructure on a cross section of a case hardened plate and a plate which had been hardened and shot peened with intensity i2 and 200% coverage. The samples were analyzed using a JEOL 7800F SEM fitted with a Bruker e-FlashHD EBSD detector. The software used for the measurements and the post-processing of the data was Bruker Quantax. The measurements were done with a tilt angle of 70^∘, a working distance around 20 mm and an acceleration voltage of 15 kV. The step size was 80 nm in Fig. 2 and 250 nm in Fig. 7.

Fig. 7

EBSD result of case carburized and hardened plate in (a) and (b). Case hardened and shot peened with intensity i2 and 200% coverage in (c) and (d). Length bar is 20 µm

Figure 7(a), (b) shows the EBSD measurement on a cross section of a case hardened plate as a phase map in (a) and as an inverse pole figure in (b). In the phase map BCC-structures are coloured blue and FCC-structures coloured red. In this case it means that martensite is blue and retained austenite is red. The colour scheme for the inverse pole figure is red, green and blue for Miller indices [001], [101] and [111], respectively. It can be seen that the micro structure consist mainly of martensite. The retained austenite is homogeneously dispersed between the martensite. The pole figure in Fig. 7(b) show a relatively wide spread through all Miller indices, which suggest a random distribution of material grain orientation after case hardening. Figure 7(c), (d) shows the corresponding phase map and inverse pole figure for a plate shot peened with intensity i2 and 200% coverage after heat treatment. The inverse pole figure shows a more even or limited coloured distribution of grain orientations from the surface and down to a depth of around 40 µm compared to the plate in Fig. 7(b) that had not been shot peened. The phase map shows fewer fcc-structures from the surface and down to a depth of about 80 μ m.

Results

Residual Stresses

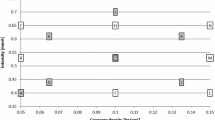
Figure 8 shows the residual stresses for the non-shot peened specimens (CH) and the four different intensities i1, i2, i3 and iD, all with 200% coverage. It is clear from Fig. 8 that the maximum compressive stress around − 1200 MPa was independent of intensity and media size. When the three different intensities i1, i2 and i3 from Table 3 are compared in Fig. 8 it was concluded that the compressive stresses penetrate deeper with higher intensity. The intensity iD, for the media with small shot diameter, and i1, for the large diameter, were almost the same. Therefore, it was also noted that a larger shot diameter create deeper compressive stress profiles for the same Almen intensity than a smaller shot.

Fig. 8

Comparison of residual stresses for case hardened (CH) and case hardened followed by shot peening with the four different intensities and 200% coverage, see Table 3

The non-shot peened (CH) residual stresses around –100 MPa are slightly lower than other researchers have reported, e.g. Epp and Zoch [53] or Dengo et al. [54]. The reason for this is partly that the case depth of 1.7 mm comprise about a 1/3 of the plates thickness of total 10 mm and partly that the quenching rate is more even due to the lower mass and different geometry than on a gear tooth.

Figure 9 shows the residual stresses for the i2 and iD intensities with 100, 200 and 400% coverage. The natural scatter in the residual stress measurements and in the depth of material removal for the measurements was larger than the difference between different coverages. This indicates that the shot peening could already have saturated the residual stresses for the present definition of 100% coverage.

Fig. 9

Effect on residual stresses from different amount of coverage for i2 and iD

Figure 10 shows the residual stress results for double shot peening according to Table 3. Compared to the single shot peened results for i1, i2 and i3 in Fig. 8 it was seen that the maximum stresses had moved closer to the surface, which was expected from a contact mechanics view. The compressive stresses at depth deeper than the maximum stress decrease slightly due to equilibrium.

Fig. 10

Residual stresses created by the double shot peening. The different intensities i1, i2 and i3 had 200% coverage and iD had 100% coverage

A comment should also be made on the estimated scatter bar in Figs. 8, 9, 10, 11, 12, 13, 14 and 15 for the depth position of individual measurements made with X-ray. The scatter bar is valid for residual stresses, FWHM and retained austenite content. This relatively wide scatter bar was estimated for positions from the peak values at 0.05–0.1 mm and below the surface. Closer to the surface the scatter decreased from the bar value and was zero at the surface. The scatter band should also be interpreted as a worst case scenario for individual data points. The most probably scenario for each data point is however that its position is relatively correctly measured, i.e. close to the centre in the scatter bar, which is confirmed by the reasonably smooth profiles found for each series in Figs. 8–15. Thus, there is an uncertainty in the depth positions that should be remembered but the actual positions in the figures are probably fairly correct.

Fig. 11

Comparison of FWHM for case hardened (CH) and the four different intensities and media sizes in Table 3 for 200% coverage

Fig. 12

FWHM created by the double shot peening. The different intensities i1, i2 and i3 had 200% coverage and iD had 100% coverage

Fig. 13

Effect of coverage on FWHM for i2 and iD

Fig. 14

Retained austenite for the four different intensities and 200% coverage, the non shot peened specimen CH (as case hardened) and double shot peening

Fig. 15

Retained austenite for different amount of coverage for intensities i2 and iD

Full Width at Half Maximum (FWHM)

Figure 11 shows FWHM measurement for the non-shot peened specimen (CH) and the four different intensities. The non-shot peened specimen has a constant peak width of about 6.3^∘, except at the surface where the peak width drops to 5.2^∘. A cause for this deviation can be seen in Fig. 7(a). The top 5 µm surface layer contains a higher ratio of red FCC-structures than the bulk material. The red structures display a banded texture from the surface indicative of grain boundary oxides. The typical procedure is that oxygen has diffused into the grain boundaries and created oxides with alloys elements such as Si, Mn or Cr. This reduces the amount of alloy elements in the surrounding bulk material and lowers its martensitic start temperature. The top surface layer will therefore have a more bainitic structure which will have a different FWHM response than martensite.

For the differently shot peened series the affected FWHM depth was consistent with the residual stress depth in Fig. 8 and the phase transformed depth in Fig. 7(c). The inverse pole Figure 7(d) shows a more even distribution of grain orientation to a depth of around 40 µm compared to the plate in Fig. 7(b) that had not been shot peened. Less variation in grain orientation should give more homogeneous residual stresses at a micro scale between different grains. The reduced variation can explain the decrease in FWHM value in the shot peened affected depth below the surface in Fig. 11. Also, since the retained austenite has mostly transformed to martensite in this area this will also reduce the variation in residual stresses at micro scale, again suggesting the reduced FWHM value.

A noticeable difference between the larger media with intensities i1, i2 and i3 and the small media iD is that the larger media has resulted in a sharp drop of the peak width at the surface while the smaller media, iD, did not. The higher peak width for the small media at the surface is repeated for the double shot peened specimens in Fig. 12. A possible cause for this behaviour can be that iD has a relatively high intensity compared to i1, i2 and i3. This means the iD–serie will give more plastic deformation at and near to the surface.

Figure 13 shows FWHM values for the different amounts of coverage for the intensities i2 and iD. The FWHM values for the iD intensity is not dependent on the coverage but for the i2 intensity there is a notable change between 100 % and 200% coverage. From 200% to 400% coverage the surface FWHM value for intensity i2 change but not below the surface. This is in agreement with the previous remark that iD have a greater relative plastic deformation and thus the curves suggest saturated change in micro-stresses and retained austenite transformation. The i2 intensity need a higher coverage to reach a similar saturation.

Retained Austenite

The retained austenite content was measured with X-ray diffraction. Figure 14 shows the retained austenite in the four series that had been single shot peened with different intensities and 200% coverage. The figure includes some individual measurements on double shot peened specimens. The influence of coverage on iD and i2 is illustrated in Fig. 15. The 200% coverage series includes all depths whereas the 100 and 400% series is recorded with some individual measurements. Table 3 summarizes the shot peening details of the different series.

Overall, the retained austenite measurements agree with the residual stress and FWHM measurements. They also confirm the EBSD pictures of retained austenite islands before and after shot peening. At the surface almost full phase transformation has been attained, which is noteworthy since full stress and strain induced phase transformation is much harder to attain in compression than in tension [55]. The 0.7 mm media was effective to a larger depth than the 0.35 mm media, see Figs. 14 and 15 which is in agreement with residual stresses in Fig. 13 and FWHM in Fig. 13. However, in contrast to those results there is no significant phase transformation difference between the series with different intensities i1, i2 and i3 in Fig. 14. This indicates that the transformation of retained austenite occurs even at low intensities. The EBSD phase map pictures in Fig. 7 can only give a qualitative illustration but it can confirm that retained austenite has transformed to a depth of about 0.1 mm. The double shot peening points in Fig. 14 show some further phase transformation close to the surface, which agree with the increased residual stress results close to the surface in Fig. 10. Thus, the second shot peening stage does give a small effect on the near surface results for retained austenite and residual stresses. In the same way as for residual stresses and FWHM, the different coverages in Fig. 15 did not significantly affect the remaining amount of retained austenite.

Hardness

Figure 16 compares Vickers hardness profiles for a non-shot peened plate (CH) and the four intensities (i1, i2, i3 and iD), all with 200% coverage. There are some deviations in the individual micro-hardness measurements, as is illustrated in the error legend, but the trends are clear both within each series and between the series for the different intensities. Close to the surface the three different intensities i1, i2 and i3 and large media resulted in relatively comparable hardness values at 870 HV. Beneath the surface and down to about 0.2 mm, a higher intensity increased the hardness more than a lower intensity. The small 0.35 mm media differed by displaying the highest surface hardness but lower hardness increase below the surface. All these relative differences in hardness changes are quite reasonable given the trends in phase transformations to the harder martensite phase, increased compressive residual stresses and work hardening by plastic deformation that the shot peening indents introduced into the plates.

Fig. 16

Vickers hardness for the four intensities in Table 3 with 200% coverage

Figure 17 shows the effect of different coverages for the i2 and iD intensities. The i2 intensity seems not to be influenced by the coverage at the surface but shows an increasing hardness for increasing coverage at about 0.1 mm beneath the surface. The iD intensity on the other hand shows a large increase in surface hardness between 100 and 200% coverage but no practical change for 400%. These results indicate that the surface hardness had saturated at 100% coverage for the i2 intensity but had not saturated for 100% coverage for iD, i.e. the small media. Since the FWHM results in Fig. 13 and the retained austenite results in Fig. 15 both shows a saturation at 100% coverage it is concluded that plastic deformation hardening causes the increased hardness from 100% to 200% coverage. This is supported by the much higher velocity of the media for the iD intensity (76 m/s) compared to the velocity for the i2 intensity (34 m/s), see Table 5.

Fig. 17

Vickers hardness for iD and i2 intensities and different coverage

Figure 18 shows the HV0.1 measurements for the double shot peened specimens. Compared to the single shot peened specimens in Fig. 16 there might be a slight increase in hardness at the surface. As with residual stresses, FWHM and retained austenite content the effect of double shot peening is limited to near surface changes.

Fig. 18

Vickers hardness for the double shot peened specimens

Surface Roughness

When surface roughness was measured several different parameters like maximum height of profile Rz, total height of profile Rt, skewness of profile Rsk or the kurtosis of the profile Rku were evaluated but the arithmetic mean deviation Ra showed the clearest trends. Figure 19 shows the surface roughness in the form of the Ra parameter for the different intensities. The unpeened plates had an Ra around 0.5 µm. When increasing the intensity for the 0.7 mm media from i1 to i2 and i3 the surface roughness also increased. This was because a higher intensity means a higher ball velocity and therefore deeper impacts. The smaller media 0.35 mm had an intensity iD close to i1 but because the balls were so small they must have a much higher velocity to reach the same intensity. The balls therefore made deeper impacts and gave the largest surface roughness among the tested variants. The last three rightmost columns in Fig. 19 show results for double shot peened plates. The plates were first shot peened with i1, i2 or i3 at 200% and then shot peened with iD at 100%. Compared to the single shot peened plates Ra increase slightly but not as much as to reach the roughness of single shot peened iD. This was likely caused by the deformation hardening of the surface and residual stresses introduced in the surface by the first stage of shot peening.

Fig. 19

Mean Ra for plates shot peened with different intensities

Figure 20 shows Ra as the coverage was increased. For the i2 intensity, Ra decreased slightly with increasing coverage. This seemed reasonable since the first balls would create deeper impacts. As the surface hardened and the residual stress increased with more impacts, the later impacts would not go as deep and should therefore flatten earlier peaks. This argument does, not quite seem to hold for the small media, iD, where the surface roughness increases from 100% coverage while it shows a slight decrease from 200% to 400% coverage. The small media size compared to the grinding marks might be one cause for this result.

Fig. 20

Mean Ra for different amounts of coverage

Surface Topography

Figures 21 and 22 present images of the surface topography. Figure 21 focuses on the effects of varied intensity whereas Fig. 22 illustrates how coverage adjusts the topography. Figure 21(a) shows a sample of the ground plate surface before shot peening. Observe that the scales in height and width direction are different. Compared to the shot peened surfaces of i1 with 200% coverage in Fig. 21(c) or i3 at 200% coverage in Fig. 21(e) it was noted that the shot peening completely removed the grinding marks. The height of the surface roughness is however of the same order. Figure 21(b), (d) and (f) show the surface after double shot peening. As a reminder, the i1, i2 and i3 intensities were with 200% coverage and then 100% coverage of intensity iD was added to the surfaces. Compared to the plates without the added double shot peening in Figs. 21(c), (e) and 22(c), the double shot peening added the same higher frequency of peaks as in Fig. 22(b).

Fig. 21

Surface topography of a ground plate before shot peening in (a). Double shot peening topography is shown in (b), (d) and (f). Topography for i1 and i3, 200%, is shown in (c) and (e)

Fig. 22

Comparison of different coverage for intensity i2 and iD

Comparison of different coverages is shown in Fig. 22 for intensities i2 and iD. The figures show the same tendencies that surface roughness decreases with increasing coverage for i2 and that iD has a maximum at 200% coverage, see also Ra in Fig. 20.

Mean Indentation Diameter, Depth and Volume

Figure 23 shows indentations in the surfaces for a very low coverage, around 20%. More than 30 indentation diameters and volumes were measured for each intensity in Table 3 and the mean and standard deviation were estimated. The diameter was estimated by fitting a circle to the most distinct edges. However, since the indents were seldom perfectly round the circle edge would often cover a larger or smaller local radius than the real indent area. The volume of each indentation was measured by extracting each indent in the SensoMap software and evaluating the volume from the top of the indent down to the bottom. Because of the relatively high peaks and valleys in the surface roughness of the plates the mean void volume of the unpeened surface was subtracted from the indent volume to give the material volume that had been displaced by the impacts. The depth was evaluated as the deepest value found in the extracted volume for each indent. Table 4 summarizes the results. It was interesting to note that the standard deviations of the mean diameters and indentation depth, for the three different intensities with media size 0.7 mm, are about the same.

Fig. 23

Surface topography of the ground plates with low coverage, around 20%, but with the different intensities in Table 3

Table 4 Measured indentation diameters, indentation depth, indentation volume and displaced material volume for each intensity

Media Velocity

The media velocity was not measured in the shot peening machine and this is not usually done or needed for production purposes. However, for simulating shot peening in an FEM program the velocities are needed. One way to determine the media velocity is to compare the indents in Fig. 23 from shot peening at low coverage with indents made at known velocities. The determination procedure for media velocity is described by Nordin and Alfredsson [56]. Single particles were shot against a plate (same manufacturing batch and 0.7 mm media as in this work) and the velocity was measured with photodiodes. Confocal microscope measurements were made of each single indent which could then be compared to the low coverage plates, illustrated in Fig. 23. Table 5 shows the Almen A intensity, the corresponding mean indent area and estimated velocity for the present shot peening.

Table 5 Measured intensity, indentation area and corresponding velocity

Barkhausen Noise

Table 6 summarises the Barkhausen noise results for each intensity and coverage. The values increase both with increasing intensity and increasing coverage for the single shot peened specimens. The double shot peened variants on the other hand show quite stable results, with around 240% noise increase from the non-shot peened specimens. Figure 24 shows the evolution of relative Barkhausen noise with increased shot peening time. The measurements were from the coverage check presented in Fig. 6 and the iD values in Table 6. The iD values are at 55, 110 and 220 s and were the averages over 5 specimens. The other points were only measured on one specimen. The scatter was estimated from the standard deviation of the 5 repeated coverages.

Table 6 Change of Barkhausen noise amplitude in percent relative to non-shot peened specimens

Fig. 24

Change in Barkhausen noise amplitude for the 0.35 mm media for increasing shot peening time

Discussion

The residual stresses measured in the plates have a maximum around −1200 MPa. Ahmad and Crouch [16] used a very similar steel, SAE 8620, and reached about −1400 MPa for a similar media hardness. The hardness of those targets was about 61 HRC which corresponds to 722 HV, quite close to the hardness on the plates in this paper (716 HV1). Adding double shot peening Ahmad and Crouch [16] reached even higher maximum compressive stress, around –1500 MPa, something that was not seen in this work. Ishikura et al. [27] reached around –1600 MPa for a case hardened steel of 718 HV but with a much harder media (950 HV). Hasegawa et al. [23] reached around –1500 MPa in a target plate of 700 HV and with 820 HV media. Thus, the residual stresses measured in this investigation were slightly lower than what can be attained and there is a potential to reach higher compressive stresses with a harder media.

Vickers hardness at about 40 µm depth changed from around 730 HV0.1 to around 870 HV0.1 by the shot peening, an increase of about 140 HV0.1. This was very similar to the results by Hasegawa et al. [23] even though they used a harder shot media of 820 HV. It should however be noted that the measured hardness will depend on both the plastic deformation induced by the shot peening, causing either work hardening or work softening, and on the transformation of retained austenite into martensite. In review articles, Altenberger [57] and Vöhringer [58] mention that the hardness measured on shot peened specimens is increased by compressive residual stresses. The work hardening of the specimen is therefore misinterpreted to be greater than what it is. As a more reliable assessment of the work hardening Altenberger [57] and Vöhringer [58] recommend the FWHM value. However, Carlsson and Larsson [59] refer to several earlier sources and also show by numerical simulations that residual stresses only have a small effect on hardness values from a sharp indenter. The decrease of the FWHM values can be explained by the more homogeneous orientation of the martensite as shown in Fig. 7(d). It is therefore concluded that the hardness has increased due to both work hardening and transformation of retained austenite.

The profiles of hardness, retained austenite and FWHM suggested a shot peening penetration depth; a depth where material properties were changed due to work hardening and phase transformation. The FWHM curves in Figs. 11 and 13 and retained austenite curves in Figs. 14 and 15 give penetration depths at about 0.1–0.15 mm for the 0.35 mm media and 0.15–0.20 mm for the 0.7 mm media. The hardness profiles in Figs. 16 and 17 for shot peened specimens display changes from the case hardened specimen at slightly deeper positions, down to 0.15 mm for the 0.35 mm media and 0.20–0.25 mm for the 0.7 mm media. Figures 8 and 9 display increases in compressive residual stress to depths of about 0.1 mm for the 0.35 mm media and to 0.15–0.20 mm for the 0.7 mm media. Based on the same penetration depth for residual stress increase, FWHM change and retained austenite transformation it was concluded that the shot peening penetration depth was 100–150 µm for the 0.35 mm media and intensity iD. For the 0.7 mm media with intensities i1, i2 and i3 it was 150–200 µm. The conclusion was supported by the hardness measurements which showed a slightly deeper depth with increased hardness. However, in this respect it should be noted that the hardness is a more direct and straight forward measurement of the mechanical properties. It is more sensitive to changes and therefore showed a slightly deeper affected depth.

The surface roughness values showed similar results as reported by other researchers [57]. Ogawa et al. [60] reached Rmax (peak to peak) surface roughness of 8 µm for target hardness around 750 HV and shot hardness of 700 HV. Hashimoto and Hoyashita [61] observed a smoothing of the roughness peaks but the Rmax value was almost unchanged when shot peening a ground surface of 3 µm Rmax. A shot ball of 600 HV hardness was however used on a target with 720–750 HV hardness which may have been the cause as explained by Wohlfahrt [13]. Figure 22 shows that the grinding marks in Fig. 21(a) were practically removed by shot peening. From a fatigue point of view this should be advantageous by decreasing the number of positions that can initiate fatigue due to notch factor sensitivity.

Barkhausen noise results in this work showed similar behaviour as results in the literature [31, 32, 62] when hard steels were plastically deformed. The Barkhausen signal increased for increasing intensity and coverage. Just as the decrease in FWHM values can be explained by the increased homogeneity of grain orientations the Barkhausen signal should increase with the larger magnetic domains. Figure 24 suggests that changes in Barkhausen noise amplitude could be an alternative method to measure coverage than by optical or fluorescent paint methods. There was a marked knee in Barkhausen noise at the point that was judged as 100% coverage by the PeenScan method. This can be useful where optical inspection is difficult, for example inside holes. However, more experiments with different kinds of materials must be evaluated to confirm this behaviour.

Conclusions

Shot peening a case hardened SS2506 gear steel with the current machines, methods and best practise gave the following conclusions. The conclusions assume that full coverage has been reached and is valid for the current media and intensity range.

• The maximum compressive stress was independent of intensity.

• The depth of the maximum compressive stress increased with increasing intensity but was independent of coverage.

• Adding a double shot peening operation with the smaller media onto a surface that had already been peened with a larger media increased the residual stresses by approximately 10% from the surface and down to 25 µm below the surface.

• Shot peening effectively changed the topography and removed the grinding marks.

• The surface roughness increased with increasing intensity for a given coverage.

• For a given intensity shot peening initially increase the surface roughness. After a certain coverage had been reached, the roughness decreased with increasing coverage.

• At low coverage, individual indents could be identified and measured. The size of the individual indentations increased with increasing intensity but the standard deviation of the indentation size remained the same.

• Low coverage indents are useful to save the shot peening impact on the target. The media velocity of the production equipment can be estimated if a correlation function exist or can the attained between velocity and single impacts for the media and target combination at hand.

• Vickers hardness showed the largest hardness increase at the surface of the target.

• Residual stress, FWHM and retained austenite are all affected to the same depth and hardness to a slightly deeper depth.

• The Barkhausen noise relation against peening time showed a knee at the estimated full coverage time.

• The more homogeneous grain orientation after shot peening can explain both the decrease in FWHM values and the increase in Barkhausen signal.