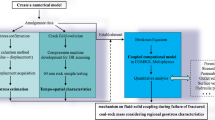
Abstract
To rationalize the setting of joint parameters, model size, and initial value of vertical stress in simulation of mining of steeply inclined coal seams, a fault tree analysis method of discrete element numerical simulation was used and a mathematical model was proposed. A method of eliminating the influences of size-effect errors on the parameters of coal and rock samples was obtained based on previous work. Furthermore, the constitutive equation and eigenvalue determination formula of a joint discontinuity surface were established, and a method of determination of the joint parameters was proposed, forming the complete “coupling chain” between parameters for numerical simulation. In addition, a formula for the initial value of vertical stress was constructed by way of the compression and shear model of the element body. Also, the minimum dimension was determined by means of strength factor analysis of fracture mechanics. Taking the research literature as an example, the model size and initial value of vertical stress were calculated. On this basis, the physical parameters of coal samples, the physical parameters of coal rocks considering the influence of the size effect and the calculated coal rock joint parameters considering the influence of size effect were directly used to comparatively analyze the displacement and stress fields, thus verifying the reasonability and correctness of the mathematical model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Discrete element numerical simulation method focuses on the evolution of throttle fissures (Jobmann and Billaux 2010), length expansion of fractures (Suner and Tulu 2022; Zhang et al. 2017, 2016), or a change in the permeability of the rock mass (Lak et al. 2017; Poulsen et al. 2018). Between the aforementioned conditions, the method is more widely used in application of safe mining technology, including research into the height of overlying rock in “three zones” of the working face, the evolution of water and gas conducting channels, the failure depth of the floor under the influence of mining, selection of dominant channels for coalbed methane migration, etc.
Discrete element numerical simulation method using UDEC, 3DEC, PFC, and other packages has been adopted to construct the model and assign parameters for calculation according to the primary and secondary differences of the research problem. The parameters involved in the numerical calculation include the model size, the initial vertical stress on the top of the model, the physical–mechanical parameters of the model, and the mechanical parameters of joints. The setting of parameters plays a vital role in the final result: their improper selection can lead to calculation errors, non-convergence of calculations, and large differences between the calculated results and the actual on-site behavior.
Taking the numerical calculation in UDEC software as an example, the mechanical parameters pertaining to the rock mass, including density, bulk modulus, shear modulus, elastic modulus, cohesion, internal friction angle, and tensile strength, mechanical parameters of the joints including normal stiffness, shear stiffness, internal friction angle, cohesion, and tensile strength were analyzed.
Due to the complexity of geological conditions in underground coal mining and the limitations of hardware and software facilities, the mechanical parameters of the rock mass and joint were set according to the in-situ sampling of the rock mass, so the influence of any size effect was ignored (Cerato and Lutenegger 2006; Liu et al. 2021; Xu et al. 2012). The initial vertical stress on the top of the model is usually determined jointly by the burial depth of the coal seam and the vertical distance between the coal seam and the top of the model. However, for steeply inclined coal seams, it is difficult to assign an accurate initial vertical stress due to the fluctuation of the burial depth. Besides, the size of the model is set based on the mining area and the reserved mining boundary, thus lacks any theoretical basis for quantitative calculation.
To solve these problems, the present research focuses on the assignment of mechanical parameters, and deduces a universal formula for the initial vertical stress to be assigned on the top of the model through mechanical analysis, and obtains the minimum solution of model size considering the influence of model boundaries. The results provide a complete and scientific theoretical support for the parameter setting of the discrete element numerical calculation.
2 Common errors in discrete element numerical simulation
Taking the discrete element numerical simulation of overlaying strata breaking in a steeply inclined working face as an example, an error analysis was conducted.
In the mining stage of near-horizontal, gently inclined and inclined coal seam working faces, the classical theories of overlying strata included masonry beam (Xu 2016; Qian et al. 2003), transfer rock beam (Song 1988; Lu et al. 2010) and thin-plate structure models (Chen et al. 2018; Dufva and Shabana 2005), etc. According to the key layer theory of rock stratal control (Qian et al. 2010), the overall self-weight of the upper strata structure of key strata acted uniformly on the lower coal body, and the nephogram of vertical stress shows symmetrically. When the overlying strata of steeply inclined coal seams were mined at the working face, the vertical stress on the goaf formed an arch (Fig. 1). Also, the goaf was asymmetrically distributed as evinced by the cloud map of mining stress (Qin et al. 2022).
As shown in Fig. 2, a fault tree analysis method was displayed (Bobbio et al. 2001; Khakzad et al. 2011; Cepin and Mavko 2002). Unreasonable mechanical parameter settings resulted in the overlying rock layer not collapsing, crack propagation being inconsistent with theory, grid destruction occurring in the non-anomalous zone, and the instability of the model making it impossible to calculate by its failure to reach equilibrium. At the same time, incorrect assignment of the initial vertical stress leads to the evolution of the stress field, displacement field, velocity field, and energy field being inconsistent with theory. Besides, choice of an inappropriate model size causes boundary failure.
Taking one example, the collapse of overburden strata was not obvious, and the situation shown in Fig. 3 is often attributed to the large value of the normal strength of the roof.
Taking the grid embedding error as a second example, when the working face was affected by mining, there was a large amount of flexural movement of the rock block (Li et al. 2015). Due to the insufficient robustness of the numerical calculation parameters of the lower rock mass, the force characteristic line field and the velocity line of the surrounding joints were inconsistent and readily caused mesh embedding. As shown in Fig. 4, once the stability of the model joints was insufficient, it would inevitably affect the normal slippage of the remaining rock formations, making it difficult for the model to balance the stress transfer, which renders subsequent numerical simulation impossible.
In summary, the assignment of joint parameters, model size, and initial value of vertical stress was of great significance for discrete element numerical simulation.
3 How to determine the mechanical parameters?
In mining, sampling of coal and rock strata remains the most common method for obtaining the mechanical parameters. Before discrete element numerical simulation of the stress field, displacement field, velocity field, and energy field when working face is mining, it was necessary to take coal and rock samples for measurement of laboratory mechanical parameters. However, the different locations of coal and rock sampling points lead to large differences in the measured test results of physical parameters.
On one hand, the sample acquisition should avoid the influence of mining stress. In addition, the sampling should avoid mining influence and geological structure areas (such as faults, folds, collapse columns, etc.), as shown in Fig. 5.
After physical experiments, taking the average value at multiple sampling points is often the most effective way to eliminate errors. However, the physical parameters of the sample were used to replace the model parameters that ignore the influence of size effect, in other words, the sample could only represent the local physical characteristics of the model.
At present, it was stated that the parameter values pertaining to the coal and rock mass in the numerical model were inconsistent with the measured values of coal and rock specimens in the laboratory, and parameters for the numerical model of coal and rock were obtained by quantitative equivalent calculation while considering size effects. It was suggested that the elastic modulus, cohesion, and tensile strength were generally 0.1 to 0.25 times the measured values, and Poisson’s ratio was generally 1.2 to 1.4 times the measured values of coal and rock specimens (Cai et al. 2013). Also, the stiffness and uniaxial compressive strength in the numerical model should be 0.469 and 0.284 times the measured values of laboratory coal and rock specimens, respectively (Mohammad et al. 1997). Besides, a comparative analysis of numerical simulation and laboratory test data was undertaken, suggesting that there was no significant difference between the internal friction angle values of rock mass and specimen, which was within the allowable range of error (Chen et al. 2015; Le et al. 2016).
Therefore, on the basis of considering the size effect, in the present research, a constant ratio calculation was implemented for each mechanical parameter (verifying the result in Sect. 7).
In summary, considering the size effect, and heterogeneity of materials and stress, a method for recovering samples and converting the measured parameters of coal and rock samples in the laboratory into parameters of the numerical model was proposed to avoid errors in numerical simulation.
4 Mathematical model for mechanical parameter setting of the joint
The previous part focused on how to eliminate the size effect error caused by the size parameters of coal samples, however, this section focuses on how to construct a mathematical model for calculation of coal rock joint parameters when the mechanical parameters of the joints in the coal rock are unknown.
In the study of mining operations, the reasonable transfer stress of joints in the model is important, and the reasonable assignment of normal stiffness Kn and shear stiffness Ks is key to the research. Nevertheless, due to the rigor of the experimental conditions in its application to the hardware and software facilities, discrete element numerical mechanical parameters of joints are difficult to obtain, therefore, more scholars have a reference for similar mines facilitating subsequent research; the correctness of this method is probabilistic, because the joint surface is a material surface, there are differences in roughness.
Here, to analyze the mechanics of the discontinuous surface between the layers, the constitutive theory of the discontinuous surface of the non-associated plastic material was proposed, as shown in Fig. 6, the X and Y-axes of the coordinate system were in the discontinuous plane, while the Z-axis lay normal to the section. At the same time, the size of the material plane was a × b × H, and the X, Y, and Z-axes formed a right-handed coordinate system. Taking any point A in the discontinuous plane, assuming that point A has been displaced and deformed, at this time, the displacement discontinuity vector of point A* was determined using Eq. (1):
In the formula: < DIS > is the displacement increment of point A along the Z-direction, m. H denotes the thickness of the discontinuity model, m. h represents the actual thickness of the rock discontinuity, m. γxy, γyz, γxz, and εz respectively, represent the shear strain in the XOY-direction, the shear strain in the YOZ-direction, the shear strain in the XOZ-direction, and the normal strain in the Z-direction.
According to the modified hyperbolic yield criterion f and plastic potential function g (Wang et al. 2018), the calculation formulae are given in Eqs. (2) and (3):
where, τyz and τxz respectively, represent the shear stress in the YOZ direction, and the shear stress in the XOZ direction, MPa; μ is the coefficient of internal friction of the layer; C denotes the cohesion of the layer, MPa; θ represents the flow coefficient of the layer, such that 0 ≤ θ ≤ 1; σT is the tensile strength of the discontinuous surface, MPa; σZ represents the normal stress on the discontinuous surface along the Z-direction, MPa.
Furthermore, a constitutive model matrix of non-correlated layered materials based on a hyperbolic correction criterion as given by Eq. (4) is adopted (Yin 2011):
where, Dep and De respectively, represent the constitutive matrix and elastic matrix of non-correlated layered materials; μ' represents the derivative of the internal friction coefficient function of the layer; C' denotes the derivative of the cohesive force function of the layer, MPa; φ and Ψ respectively, represent constant matrices; τ is the shear stress in the Z-direction of the discontinuous surface, MPa; K denotes the bulk modulus of the discontinuous surface, MPa; G represents the shear modulus of discontinuous surface, MPa.
To simplify the calculation, it is usually considered that µ and C are constants, then C' = 0 and μ' = 0, as a result, the matrix expression of Dep was solved according to Eqs. (5) to (9) as Eqs. (10) and (11):
To facilitate the establishment of the corresponding relationship with the < DIS > variable, a conjugate stress array was established as given in Eq. (12):
Simultaneous solution of Eqs. (1), (10), (11), and (12) yields the constitutive relationship given in Eq.(13):
Regarding the normal and tangential stiffness Kn and Ks at the contact points of the model joints, the relational expressions were set as follows (Yin 2011):
According to the simultaneous Eqs. (1), (12), (13), (14), and (15), Eq. (16) could be obtained:
where, Kn, and Ks respectively, represent the normal and tangential stiffness of the material plane model. However, if the mine lacks corresponding hardware facilities, following Eq. (14), Eq. (15) provides suitable estimates.
According to the characteristics of the discontinuous surface of the material, the stability of the discontinuous surface of the joint should be maintained during the initial assignment of the model, so the matrix must have positive definiteness, i.e. \(\left|\overline{Dep}\right|>0\), furthermore, according to Eq. (16), the characteristic value of the matrix is determined:
To ensure the stability of the joints of the material discontinuities, the parameters μ, θ, C, KS, Kn, σT, τxz, and τyz were required to satisfy X1 > 0, X2 > 0, and X3 > 0 at the same time, also X2 > 0 and X3 > 0 were established as being applicable at any time, therefore, only the parameters μ, θ, C, KS, Kn, σT, τxz, and τyz were required to satisfy X1 > 0 to ensure the stability of the material forming such discontinuous surface joints.
Therefore, Eqs. (14), (15), and (17) constituted the “coupling chain” relationship for the parameters μ, θ, C, KS, Kn, σT, τxz, and τyz. When undertaking numerical calculations, whether the parameter settings are correct can be verified according to the “coupling chain” relationship.
5 Assignment of initial vertical stress σ
In the numerical simulation of a coal face, the initial vertical stress σ at the top was determined by the burial depth of the coal seam and the distance between it and the top of the model. However, it was difficult to assign an initial vertical stress σ at the top of a fully mechanized mining face in an inclined coal seam due to the significant variation in burial depth, so a universally applicable calculation method for initial vertical stress σ at the top of the model was derived based on the analysis of fracture slip energy extremum.
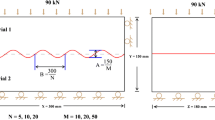
As shown in Fig. 7, the upper AOFC region was subjected to uniform initial vertical stress σ (unit: N/m2), and the area of region was n × L. Then, the element body of the whole rock layer was taken as the analysis object (Fig. 8). The cross-sectional area of the element body A was n1 × L1, thus, the stress structure shown in Fig. 9 was established.
Under the action of stress σ, the axial displacement was U (Fig. 9). At the same time, the upper part of the element body slipped along the direction of the fracture line which was at an angle β to the horizontal, through distance V (Fig. 10). Thus, the external potential energy of the element body was:
Similarly, the unit body deformed internally under compression, and the accumulated strain energy was:
Shear dissipation energy of interface shear slip agglomeration occurred thus:
where, μ is internal friction coefficient of rock mass; C0 represents the initial cohesion. When the rock mass is an ideal plastic material, the cohesion of the element remains unchanged, that is, C=C0; H' denotes strengthening modulus of rock mass material. If the material is a deformation strengthening model, H' > 0. If the material is a deformation softening model, H' < 0.
Finally, the total energy of broken shear slip of unit body was obtained by combing Eqs. (20), (21), and (22):
According to the extremum theorem of total energy of shear slip for element body, Wt is the partial derivative of U and V respectively:
The expression for σ is obtained by solving Eqs. (24) and (25):
In summary, through the establishment of a mechanical analysis model for the compression-shear slip of the unit body, a quantitative solution for the initial vertical stress σ was obtained according to the total energy extreme value theorem, which involves the initial cohesive force C0 of the rock mass, the fracture line angle β, strengthening modulus H', slip distance V, and internal friction coefficient of rock mass μ.
6 Minimum solution of model size
According to the fracture mechanics model of the unit body (Fig. 9), unit body sliding along the cutting-plane line is shown in Fig. 10. In the picture, the top stress parameter of the model is σ, and the equivalent uniform load on the side is λσ, where λ is the lateral pressure coefficient.
Referring to the basic theory of fracture mechanics, the model in Fig. 11 is equivalent to the stress intensity factor caused by the initial vertical uniform load σ and the horizontal.
lateral pressure λσ in the numerical simulation. The following is a step-by-step solution thereto:
① Stress intensity factors K1λσ, K2λσ, and dimensionless parameters Fσ1(a/h) and Fσ2(a/h) were caused by horizontal pressure λσ under shear (Chen et al. 2007; Lazzarin and Zambardi 2001; Yang et al. 2016; Yu et al. 1991), as shown in Eqs. (27) to (30):
In the formula: a is the vertical component length of the broken line along the gravity line in the model, m; h demotes the vertical height of the model or the actual thickness of the model, m.
② Stress intensity factor caused by uniformly distributed vertical load σ compression shear.
The horizontal section of the overall model measured n × L, the vertical pressure on the upper part of the model was \(nL\sigma\) and the supporting force on the bottom supported by the lower coal strata was N (Li et al. 2020; Ning et al. 2020). These forces only cause type-II stress, and the solution is as follows:
Dimensionless parameter FN(a/h) is given by Eq. (30)( Chen et al. 2007;):
According to the conditions for determination of rock mass compression-shear fracture (Yang et al. 2016; Chen et al. 2007; Yu et al. 1991):
where B refers to the pressure-shear ratio and Kc is fracture toughness coefficient of rock.
Simultaneous Eqs. (27) to (32) were incorporated into Eq. (33) to give:
Through the analysis of fracture mechanics strength factors, the minimum size of the model (34) was obtained, which was also the minimum size of the model considering boundary influences. Further, the final model size was determined by the reality of the prevailing mining situation at the coal seam working face.
7 Numerical simulation results and analysis
7.1 Numerical simulation calculation scheme
To prove the rationality of the mathematical model size, joint stiffness parameter selection, and the calculation formula for initial vertical stress σ at the top of the model, literature with sufficient coal and rock sample parameters and difficult initial vertical stress parameter assignment was selected as examples (Xie 2016), and the working face was set at 70 m for analysis of three model parameters: ① According to Eq. (34), the size of the calculated model was compared with that of the numerical model in the literature, and a rational calculation model was selected. ② Layout of measuring points for mining at the working face. ③ Taking 70 m of working face mining as an example, simulation according to the parameters of coal and rock samples in the literature was conducted. ④ Considering the size effect, the parameters of coal and rock samples in the literature were processed according to the method provided in Sect. 3 and introduced to the model. ⑤ Stiffness parameters of joints were obtained according to Eqs. (14) and (15), and the size effects of all numerical calculation parameters were calculated (Sect. 3). The initial vertical stress parameter σ in Eq. (26) was derived, and numerical calculation was then performed. ⑥ In the case of the same model size and the same number of mining steps on the mining face, the changes in vertical stress in the Y-direction named as SYY, the displacement along the Y-direction named as Ydisp, horizontal stress in the Y-direction named as SXX, the displacement along the X-direction named as Xdisp, and the normal stress in a plane named as Nstress at the same point in steps ③ to ⑤ were compared and analyzed.
7.2 Model size parameter setting
Solving the stress parameter σ according to Eq. (26), where the variables: β = 41° (Xie 2016), μ = 0.466 (Xie 2016), H' = 0, C0 = 0.035 MPa (Xie 2016; Zhang et al. 2021), giving σ = 0.200 MPa.
Solving (nL)min according to Eq. (34), where the variables: a/h = 0.366 (Xie 2016), Fσ1(a/h) = 0.083, Fσ2(a/h) = 1.185, FN(a/h) = 1.415, Kc = 1.84 MPa m1/2 (Chen et al. 2007; Li et al. 2020; Zhang et al. 2000), N = 10.3 MN (Li et al. 2020), λ = 0.6 (Li et al. 2012) and B = 1(Li et al. 2020; Yang et al. 2016), the solution is: (nL)min = 67.81 m2. When the calculation model is a two-dimensional plane, L = 1 m or n = 1 m.
According to the literature, the size of the plane calculation model was 160 m× 215 m (Xie 2016), which met the requirements of Eq. (14) in the case of a mining face with a length of 70 m.
7.3 Mechanical parameter setting
Selection of three model parameters proceeded as follows:
-
(1)
Parameter 1: physical parameters of rock strata and mechanical parameters of joints were obtained according to the parameters of coal and rock samples (Xie 2016), as shown in Tables 1 and 2.
-
(2)
Parameter 2: considering the influence of size effect for model parameter selection (Cai et al. 2013; Mohammad et al. 1997; Chen et al. 2015; Le et al. 2016), the initial vertical stress σ = 2.01 MPa (Xie 2016), as shown in Tables 3 and 4.
-
(3)
Parameter 3: according to Eqs. (14), (15), and (17), the joint parameters were solved and the size effect was considered (Cai et al. 2 013; Mohammad et al. 1997; Chen et al. 2015; Le et al. 2016), and the initial vertical stress parameter σ = 0.2 MPa was found from Eq. (26) (Tables 5 and 6).
Incorporating the parameters in Tables 5 and 6 into Eq. (17): X1 = 0.426, proving that the parameters (as thus set) could ensure stability of the material plane.
7.4 Numerical model establishment and calculation
The size of the numerical model was set to 160 m × 215 m, and the No. 2 coal seam grid was generated (Fig. 12). Measuring points were arranged at a distance of 5 m from the main roof to the coal seam, and the distance between measuring points was 20 m. At the same time, from bottom to top, measuring points 1 to 8 were arranged (Fig. 13). In addition, choosing measuring point 2, Nstress Xdis distributions from the three different parametric models were compared; measuring point 4 was employed to compare Ydis, and measuring point 8 was used to compare SYY (Figs. 14, 15, 16 and 17).
Through this comparison, the following results could be obtained: (1) The trend of curves obtained by three different parameters was similar, which could explain the trend in stress and displacement during mining of the working face; (2) The curves of stress and displacement obtained by numerical simulation using coal and rock sample parameters were less than the results of considering the size effect. (3) Considering the size effect, the proposed joint parameter calculation model matched the numerical simulation results of coal and rock samples considering the size effect, which further verified the correctness of the model.
8 Conclusions
-
(1)
A relatively simple and feasible method for parameter selection of discrete element numerical simulation considering the size effect was proposed, especially in the case of missing joint parameters, including model size parameter calculation, stress parameter σ, joint parameter calculation, and subjective engineering judgement
-
(2)
To ensure the logicality of lithologic parameters in numerical simulation, the “coupling chain” relationships of parameters μ, θ, C, KS, Kn, σT, τxz, and τyz were formed by means of the constitutive theory of non-correlated plastic materials at discontinuity surfaces.
-
(3)
For a given model size and consistent mesh division, the same number of mining steps could be guaranteed to obtain the feasibility and rationality of the proposed parametric mathematical model.
References
Bobbio A, Portinale L, Minichino M, Ciancamerla E (2001) Improving the analysis of dependable systems by mapping fault trees into Bayesian networks. Reliab Eng Syst Saf 71(3):249–260. https://doi.org/10.1016/s0951-8320(00)00077-6
Cai MF, He MC, Liu DY (2013) Rock mechanics and engineering. Science Press, Bei Jing
Cepin M, Mavko B (2002) A dynamic fault tree. Reliab Eng Syst Saf 75(1):83–91. https://doi.org/10.1016/s0951-8320(01)00121-1
Cerato AB, Lutenegger AJ (2006) Specimen size and scale effects of direct shear box tests of sands. Geotech Test J 29(6):507–516
Chen ZH, Feng JJ, Xiao CC, Li RH (2007) Fracture mechanical model of key roof for fully-mechanized top-coal caving in shallow thick coal seam. J China Coal Soc 32(5):449–452
Chen LF, Zhu JG, Yin JH (2015) Numerical simulations of mechanical characteristics of coarse grained soil with different aspect ratios of tri-axial test. J Cent South Univ Sci Technol 46(7):2643–2649. https://doi.org/10.11817/j.issn.1672-7207.2015.07.035
Dufva K, Shabana AA (2005) Analysis of thin plate structures using the absolute nodal coordinate formulation. Proc Inst Mech Eng Part K-J Multi-Body Dyn 219(4):345–355. https://doi.org/10.1243/146441905x50678
Jobmann M, Billaux D (2010) Fractal model for permeability calculation from porosity and pore radius information and application to excavation damaged zones surrounding waste emplacement boreholes in opalinus clay. Int J Rock Mech Min Sci 47(4):583–589. https://doi.org/10.1016/j.ijrmms.2010.04.005
Khakzad N, Khan F, Amyotte P (2011) Safety analysis in process facilities: comparison of fault tree and Bayesian network approaches. Reliab Eng Syst Saf 96(8):925–932. https://doi.org/10.1016/j.ress.2011.03.012
Lak M, Baghbanan A, Hashemolhoseini H (2017) Effect of seismic waves on the hydro-mechanical properties of fractured rock masses. Earthq Eng Eng Vib 16(3):525–536. https://doi.org/10.1007/s11803-017-0406-9
Lazzarin P, Zambardi R (2001) A finite-volume-energy based approach to predict the static and fatigue behavior of components with sharp V-shaped notches. Int J Fract 112(3):275–298. https://doi.org/10.1023/a:1013595930617
Le HL, Wu JM, Gao XB, Shi W, Song JL (2016) Influence of size effect on shearing strength of zig-zag structure plane. J Liaoning Tech Univ Nat Sci 35(6):745–750
Li XP, Wang B, Zhou GL (2012) Research on distribution rule of geostress in deep stratum in Chinese Mainland. Chin J Rock Mech Eng 31(S1):2875–2880
Li Z, Wang JA, Li L, Wang LX, Liang RY (2015) A case study integrating numerical simulation and GB-InSAR monitoring to analyze flexural toppling of an anti-dip slope in Fushun open pit. Eng Geol 197:20–32. https://doi.org/10.1016/j.enggeo.2015.08.012
Li JH, Chen WX, Su PL, Duan D, Song YJ (2020) Research on the fracture mechanics model of deep hole pre-splitting. Coal Geol Explor 48(6):217–223
Liu D, Huang M, Hong CJ, Chen XN, Du SG (2021) Experimental study on size effect of compressive strength of jointed rock mass based on representative sampling. Chin J Rock Mech Eng 40(4):766–776
Lu GZ, Tang JQ, Song ZQ (2010) Difference between cyclic fracturing and cyclic weighting interval of transferring rock beams. Chin J Geotech Eng 32(4):538–541
Mohammad N, Reddish DJ, Stace LR (1997) The relation between in situ and laboratory rock properties used in numerical modelling. Int J Rock Mech Min Sci 34(2):289–297. https://doi.org/10.1016/S0148-9062(96)00060-5
Ning J, Xu G, Zhang CH, Sun ML (2020) Mechanical model and fracturing characteristics of multi-area supporting roof in fully mechanized mining working face. J China Coal Soc 45(10):3418–3426
Poulsen BA, Adhikary D, Guo H (2018) Simulating mining-induced strata permeability changes. Eng Geol 237:208–216. https://doi.org/10.1016/j.enggeo.2018.03.001
Qian MG, Miao XX, Xu JL, Mao XB (2003) Key layer theory of rock strata control. China University of Mining and Technology Press, Xu Zhou
Qian MG, Shi PW, Xu JL (2010) Mine pressure and rock formation control. China University of Mining and Technology Press, Xu Zhou
Qin S, Lin HF, Wei ZY, Shen W (2022) Study on instability discriminating condition and permeability variation of triangle articulated structure in highly inclined goaf. Energy Explor Exploit 40(4):1197–1216. https://doi.org/10.1177/01445987221077364
Song ZQ (1998) Practical ground pressure and control. China University of Mining and Technology Press, Beijing
Suner MC, Tulu IB (2022) Examining the effect of natural fractures on stone mine pillar strength through synthetic rock mass approach. Min Metall Expl 39(5):1863–1871. https://doi.org/10.1007/s42461-022-00649-2
Xie DY (2016) Research on the overlying strata movement and regulations of top coal drawing in steeply inclined three-soft coal seam with longwall top-coal caving mining. Dissertation, China University of Mining Science and Technology
Xu JL (2016) Evolution of mining-induced fracture and its application. China University of Mining and Technology Press, Xu Zhou
Xu DP, Feng XT, Cui YJ, Jiang YL, Huang K (2012) A comparative study on the shear behavior of an interlayer material based on laboratory and in situ shear tests. Geotech Test J 35(3):375–386
Yang DF, Zhang LF, Chai M, Li B, Bai YF (2016) Study of roof breaking law of fully mechanized top coal caving mining in ultra-thick coal seam based on fracture mechanics. Rock Soil Mech 37(7):2033–2039
Yin YQ (2011) Rock mechanics and stability of rock engineering. Peking University Press, Bei Jing
Yu XZ, Qiao CX, Zhou QL (1991) Fracture mechanics of rock and concrete. Central South University of Technology Press, Chang Sha
Zhang YC, Yang SQ, Chen M, Zang CW, Long JK (2017) Deformation and failure mechanism of entity coal side and its control technology for roadway driving along next goaf in fully mechanized top coal caving face of deep mines. Rock Soil Mech 38(4):1103–1113
Zhang JH, Yao ZH, Feng SQ, Huang LH, Yang D, Zhao J, Ding L (2021) Strength characteristics of undisturbed loess based on field and laboratory shear tests. W Resour Hydropower Eng 52(6):188–197
Zhang BP, Tian GR, Shen WB, Shan WW (2000) The study of fracture toughness under different stress conditions. In: 6th national conference of rock mechanics and engineering 436–439
Zhang X, Qiao W, Lei LJ, Zeng FS, Zhang H, Wang YZ (2016) Formation mechanism of overburden bed separation in fully mechanized top-coal caving. J Chin Coal Soc 41(S2):342–349. https://doi.org/10.13225/j.cnki.jccs.2015.1992
Acknowledgements
We gratefully acknowledge the financial support for this work provided by the National Natural Science Foundation of China (52174207, 51874236), and Shaanxi Outstanding Youth Fund Project (2020JC-48).
Funding
National Natural Science Foundation of China (52174207).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qin, S., Lin, H., Yang, S. et al. A mathematical model for parameter setting in discrete element numerical simulation. Int J Coal Sci Technol 10, 87 (2023). https://doi.org/10.1007/s40789-023-00644-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40789-023-00644-y