1 Introduction

Multi-seam mining is widely practiced in several mining areas in China, including Datong, Yanzhou, Pingdingshan, Huainan, Shanxi, Xinwen, and others (Huang et al. 2021; Mou 2021; Yu et al. 2014; Liu et al. 2023). While this mining system yields large volumes of coal, it also leaves behind residual coal pillars that can potentially lead to instability as they degrade. Continuous creep fracture and individual pillar failures can result in overloading and chain pillar failure (Feng et al. 2021; Guy et al. 2017; Kang et al. 2017; Ma et al. 2022a, b, c; Zhang et al. 2018). Therefore, it is crucial to investigate this mechanism of failure and define the conditions under which it can occur.

Four primary approaches have been employed to characterize the modes of unstable failure: First, the residual coal pillar and rock strata are idealized as a composite coal-rock system, and various characteristics such as instantaneous and creep mechanical energy, acoustic emission (AE), electromagnetic radiation, ultrasonic wave velocity variation, and other properties of coal-rock composites are studied through theoretical analysis, laboratory rock mechanics tests, and numerical simulation (Gao and Yang 2021; Li et al. 2022; Ma et al. 2021; Song et al. 2021; Tan et al. 2022; Xu et al. 2023; Zhao et al. 2008, 2020, 2021). Studies have also analyzed the effects of coal-rock proportion, height ratio, interface dip, contact surface parameters, loading conditions, and water content to define mechanisms of instability for the composite coal-rock system (Chen et al. 2019, 2021; Liu et al. 2016; Ma et al. 2020, 2022a, b, c; Zhao et al. 2021). Second, residual coal pillar size, strength, and yield conditions can also be used to determine the cause of coal pillar instability (Liu et al. 2008; Xie 2014). Third, the limiting condition for the breadth of the yield area and the abrupt instability of the residual coal pillar can be determined using catastrophe theory (Cao et al. 2014; Wang et al. 2012). Additionally, renormalization group theory can be used to evaluate the transfer of stresses among neighboring coal pillars and define the resulting stability (Zhang et al. 2016). Finally, rotation and sliding can result in instability, and destress blasting of the coal pillar, shortening of the working face, and increasing the advance rate have all been proposed as mitigation strategies (Fu et al. 2016).

However, the mechanical evolution process of the linkage collapse of the upper rock stratum caused by the failure and instability of the coal pillar is very complex. The research on the mechanism of failure and instability is still superficial. Especially from the view of surrounding rock stiffness (LMS) and coal pillar post-peak stiffness, there are few reports on the linkage instability mechanism of residual coal pillar and rock stratum in multi coal seam mining. However, the lithology of the roof and floor of the residual coal pillar varies during multi seam mining. When other conditions are the same, different lithology can be considered as different stiffness (Guy et al. 2017; Gao and Yang 2021). At present, there is little research on the effect of stiffness on the instability mechanism of residual coal pillar. According to the existing research, the harder the roof rock is, the easier the rock burst will occur, and the more destructive the rock burst will be. However, when mining under the conditions of medium stability or even weak roof, destructive rock burst often occurs (Tan et al. 2019; Du et al. 2021; Wang and Kaunda 2019a, b). At the same time, the mining of the lower coal seam will also cause the spalling of the overlying remaining coal pillars, and the stiffness of surrounding rock and coal pillars will also continuously change. Further in-depth investigation is needed to explore the relationship between the mechanism of coal pillar instability-induced roof failure and the rigidity of the overlying strata.

Therefore, in this paper, considering the amount of spalling of coal pillar, the influence of lower coal seam mining on the stability of overlying residual coal pillar is studied through theoretical and experimental analysis. Through the calculation and analysis of the safety factor fs of coal pillar, the surrounding rock stiffness LMS and the post-peak stiffness kc of coal pillar, we have established the linkage failure instability mechanism of residual coal pillar and rock stratum. We also analyzed the influence of caving zone height, coal pillar width and coal pillar height. The research is expected to provide a theoretical reference for the study of the linkage failure and instability mechanism of residual coal pillar and rock stratum in multi seam mining under similar mining and geological conditions.

2 Case study

2.1 Geological setting

Taking the Datong mining area as an example, the seams in the mining district are mainly of Jurassic and Carboniferous age. Preliminary exploration identifies the reserves as covering 1827 square kilometers and amounting to 37.6 billion tons.

The upper coal seams in the Datong mining area access the #7, #8, #11, #12, #14 and other seams. Seam thickness is ~ 0.8–9.0 m at a buried depth of ~ 100–300 m and with a small seam spacing of ~ 6–20 m with a dip angle of 3° ~ 7°. Proctor coefficient of the roof and floor f = 7 ~ 10, representing hard roof and floor. By definition of the Mine Safety Regulations, the Jurassic coal seams in the Datong area are “close to each” other and thus exert significant influence during mining. The thickness of the lower Carboniferous seam is ~ 15–20 m and the separation to the overlaying Jurassic coal seam is ~ 130–200 m. A stratigraphic column for the Datong area is shown in Fig. 1 (Yu et al. 2014; Mou 2021).

Fig. 1
figure 1

Stratigraphy from boreholes for dual-system coal seam group in Datong (Yu et al. 2014; Mou 2021)

Full size image

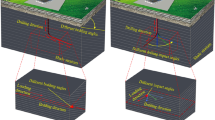
During multi seam mining, a large number of coal pillars are retained to avoid undue loading on the underlaying seam and impact on mining (Gao and Yang 2021; Tan et al. 2022; Song et al. 2021; Li et al. 2022). The residual coal pillars in the Datong mining area mainly include: knife pillars, room pillars, strip pillars, short wall pillars, roadway pillars, warehouse pillars and skip mining pillars (Feng et al. 2021). The safety of the rock strata-pillar composite system, comprising the pillar and overburden rock strata, controls the stability at the mining workface and in the overburden strata potentially to the ground surface (Ma et al. 2020, 2021; Chen et al. 2019). Instability of the coal pillars during production may result in dynamic instabilities such as hydraulic support failure and rock bursts (Fig. 2) (Yu et al. 2014; Mou 2021). Finally, instability of pillars in the gob during mine closure may result in large mine earthquakes and failure reaching the surface and manifest as surface subsidence (Fig. 3) (Lokhande et al. 2015; Bai 2019; Huang 2020).

Fig. 2
figure 2

Overstress failures in mine workings in the Datong mining area (Yu et al. 2014; Mou 2021)

Full size image
Fig. 3
figure 3

Consequences of surface subsidence in coal mines (Lokhande et al. 2015; Bai 2019; Huang 2020)

Full size image

The oldest residual coal pillars within the Jurassic strata in the Datong mining area are approximately 70 years old (Feng et al. 2021). Due to changes in surface loads from new construction, mining disturbances in the lower coal seams, gob water accumulation, and air oxidation, the stability of the Jurassic coal pillars is significantly impacted. As a result, further investigation into the stability of these coal pillars is crucial to ensure mining safety and minimize mine accidents. This has resulted in local and large-scale instability and failure (Guy et al. 2017; Ma et al. 2022a, b, c; Kang et al. 2017). To mitigate against the effects of overlying abandoned workings on the mining of the lower seams—it is necessary to understand the linkage between them.

2.2 Pillar failure—safety factor

The main theories for assessing the safety of pillars include consideration of both ultimate strength and progressive failure (Feng et al. 2021; Guy et al. 2017; Ma et al. 2022a, b, c) with finite element models capable of accommodating the reduction in strength based on progressive failure theory. The factor of safety of the residual coal pillar is characterized by fs and requires the strength of, and load on, the pillar. The specific calculation process is:

  1. (1)

    Pillar load.

When the stratum in the goaf is fully collapsed, the loading of the overburden and the weight of the overhanging stratum in the goaf (on one or both sides) are jointly borne by the coal pillar and gangue, as shown in Fig. 4.

Fig. 4
figure 4

Schematic showing the weight borne by the residual coal pillars (Zhang 2015)

Full size image

When the two edges of the remaining pillar are recovered, the average stress on the remaining coal pillars is (Zhang 2015):

$$\upsigma_{q} = \frac{q}{w} = \frac{{\left[ {wH + 2m\left( {H - m} \right)\text{tan}\updelta + m^{2} \text{tan}\updelta } \right]\upgamma }}{w}$$
(1)

where, q is load borne by the residual coal pillar, MPa; w is the breadth of pillar, m; L is the breadth of goaf, m; H is the buried depth of coal seam, m; m is the height of failing strata in goaf, m; \(\delta\) is the residual angle of collapse of the overburden strata in the goaf, °; \(\gamma\) is the average weight of overburden strata, kN/m3.

  1. (2)

    Pillar strength.

Pillar strength is the basic factor required to evaluate the stability of coal pillars. Different countries have developed a range of formulae for different geological conditions. For the Jinhuagong Mine, in the Datong area, the residual coal pillar strength is calculated by the Logie and Matheson (Zhang 2015) equation:

$$\sigma_{\text{p}} = \sigma_{\text{m}} \left[ {0.64 + 0.36\left( \frac{w}{h} \right)} \right]^{n}$$
(2)

where: \(\sigma_{\text{p}}\) is the pillar strength, MPa; \(\sigma_{\text{m}}\) is the unconfined compressive strength (UCS) of the pillar, MPa; h is the pillar height, m.

Other repeating parameters are the same as above. When w/h > 5, n is taken as 1.4. When w/h < 5, n is taken as 1. The breadth of the residual coal pillars in the multi seam mining of the Jinhuagong Mine is 24 m, and the ratio of breadth to height is greater than 5. Therefore, n is taken as 1.4.

The proportion of the strength of the pillar to load it is subjected to is known as the fs of the coal pillar (Zhang 2015):

$$f_{\text{s}} = \frac{{\sigma_{\text{p}} }}{{\sigma_{q} }}$$
(3)

In a stable coal pillar with fs > 1.5, the maximum stress is predominantly concentrated in the core of the pillar. As the safety factor decreases, the maximum stress is further focused on the core of the pillar, and the failure of the pillar will occur from the outside to the inside. This ultimately leads to the complete failure and instability of the entire pillar. When the safety factor drops below 1.5, the pillar can no longer maintain long-term stability and is at risk of collapsing under the impact of mining-induced stress.

3 Influence of under-mining on upper coal pillars and intervening strata

3.1 Stability of residual coal pillar-rock stratum

To the side of the gob, roof failure above the pillar forms a structure comprising key blocks A, B and C as shown in Fig. 5. When this system (blocks A, B, C) is stable, the roof will be in equilibrium. When key block B is unstable it will transfer stresses to the residual coal pillar below. This will lead to greater stress concentration within these pillars. The interlayer rock stratum will bear the weight transmitted by the upper rock stratum through the residual coal pillar–potential causing shear failure through the intervening stratum. Once the shear failure occurs in the interlayer rock, it may cause failure of the hydraulic support at the lower working face. Therefore, as a key rock block, the free body defined by block B must meet certain stability conditions if it is to remain stable (Wu 2014).

Fig. 5
figure 5

Structural stability analysis of the overburden strata when the working face advances through the tributary area of the residual coal pillars (Wu 2014)

Full size image
  1. (1)

    Sliding instability condition (Wu 2014).

If the frictional strength between block A and B is greater than the shear force between them, B will not slip and thus remain stable. That is to say:

$$T_{\text{AB}} \tan \left( {\varphi - \beta } \right) > f_{\text{AB}}$$
(4)

where, TAB is horizontal force of A to B, kN; φ is friction angle between A and B, °; β is fracture angle of the roof rock, °; fAB is shear force acting on key block B, kN.

  1. (2)

    Rotational instability condition (Wu 2014).

If the force between blocks A and B is greater than UCS strength the contact will be crushed. This will result in rotational instability of B. For stable B is avoided:

$$T_{\text{AB}} < L_{\text{E}} \alpha \psi \sigma_{\text{c}}$$
(5)

where, LE is along strike length of rock block, m; α is location parameters between rock blocks with fracture structure; ψ is contact coefficient between rock blocks; σc is compressive strength of roof rock, MPa.

In addition, the coal pillars in the overburden coal seam will render the overlying rock stratum laterally discontinuous (as shown in Fig. 6a) while the rock stratum above the coal pillars remains relatively continuous. A similar bridging hinged-structure is formed on the two sides of the pillar and this articulated structure bears the load of the overburden stratum and the stratum above the stratum. With mining of the working face in the underlying seam, the articulated structure will be further broken due to the mining disturbance (as shown in Fig. 6b). This will cause failure of the pillar in the overburden seam. The fractured rock blocks will rotate and the large force generated by this rotation will further lead to the sliding of the roof of the lower coal seam. Finally, this may result in dynamic displacement such as damage to the hydraulic support or rock bursting in the underlying seam.

Fig. 6
figure 6

Change in overburden structure during mining of the #11 coal seam

Full size image

The following will analyze the mechanistic linkage in instability of strata induced by this residual coal pillar instability and the geometric mechanisms elucidated above.

3.2 Influence of mining of the underlaying coal seam on stability of the coal pillar-rock stratum

Under the action of tributary stress from the overlying strata, the plastic zone at the pillar boundary will spall under the influence of under-mining (as shown in Fig. 7). The effective load area of the pillar will decrease and the stress borne by the pillar will concomitantly increase. Then the outer sheath of the coal pillar will spall. A continuous increase in the pillar stress will form a new plastic zone that expands to the middle of the pillar. This will continue to reduce the effective support area of the pillar (Ma et al. 2022a, b, c; Salamon and Madden 1998; Merwe 2003).

Fig. 7
figure 7

Deformation and failure processes in pillars (Ma et al. 2022a, b, c; Salamon and Madden 1998; Merwe 2003)

Full size image

Salamon and Madden (1998) first noted the influence of spalling behavior of pillars, and established a model for this spalling. Many field observations have also observed this progressive behavior (as is shown in Fig. 8). The effective coal pillar dimension calculated from current theory may not maintain long-term stability. Thus, a pillar size calculated from current theory (without considering spalling) may not be able to maintain long-term stability. For example, when some mines are closed, coal pillar instability will also occur, leading to surface subsidence, building damage and other disasters and accidents. In multi-seam coal mining, cumulative mining disturbances have an increased impact on the coal pillar spalling behavior. Van der Merwe (2003) noted that, the crux to determine the safety of pillars by using the safety factor fs is whether spalling of the coal pillar is properly accommodated.

Fig. 8
figure 8

Spalling behavior of mine pillars (Merwe 2003; Wu 2017; Esterhuizen et al. 2011)

Full size image

Van de Merwe (2003) proposed the concept of coal pillar spalling rate R on the basis of field investigations and in situ test analysis, considering time, coal pillar breadth to height ratio and other factors. R is calculated as follows:

$$R = 0.1624\left[ \frac{h}{T} \right]^{0.8135}$$
(6)

where, h is mining height, m; T is time after terminating mining of coal in the seam, year.

The spalling breadth of the coal pillar is obtained by the following formula:

$$d_{\text{p}} = RT$$
(7)

Substituting Eq. (6) into (7), the spalling breadth of the coal pillar can be defined as:

$$d_{\text{p}} = 0.1624h^{0.8135} T^{0.1865}$$
(8)

The longer the time the greater the spalling and the more unstable the pillar. It should be noted here that the amount of wall spalling of the pillar is different from the plastic area of the pillar. Extension of the plastic area of the pillar and spalling in the outer wall will reduce the capacity of the pillar. But it is essentially different from the reduction of load-bearing capacity in the plastic zone. The plastic area is the edge of yield deformation of the residual coal pillar caused by the additional stress of mining. The plastic zone coal either completely or partially loses its bearing capacity. However, the remaining pillar remains intact.

However, the spalling of the pillar is the separation of the unrestrained wall under the influence of multiple factors such as overburden stress, goaf water accumulation, natural oxidation, mining disturbance and other factors. The cross-section of the pillar is gradually decreased. The residual coal pillar after wall spalling may still have a plastic zone. As the dimensions of the pillar decreases, the plastic area of the pillar may further develop after the spalling of the pillar and expand to the core area of the remaining coal pillar. As a consequence, the breadth of the core and the effective bearing breadth of the pillar are further reduced. During under-mining of the lower seam, the pillar in the overlying strata will gradually spall and the effective breadth of pillar will be gradually reduced. The stress distribution of the pillar will also appear in the following three situations as shown in Fig. 9. When the stress within a coal pillar reaches its strength, the coal pillar will undergo plastic deformation or failure, forming a plastic yielding zone on both sides of the pillar. However, the coal within the plastic yielding zone has not yet separated from the coal pillar. The portion of the coal pillar in which the stress within the plastic yielding zone transitions back to the original rock stress is called the elastic zone. The spalling zone is the part of the coal body that has separated from the coal pillar due to the stress exceeding the strength of the coal pillar.

Fig. 9
figure 9

Key parameters used to calculate of the breadth of the plastic area for pillar #l considering the various severities of spalling behavior

Full size image

4 Linkage mechanism for instability of the residual pillar-stratum

Residual coal pillars in goafs are subjected to various factors such as overburden rock pressure, mining-induced disturbances in the underlying coal seam, goaf water accumulation, and natural oxidation, leading to their deformation and destruction. This process typically results in the formation of a central elastic core zone, plastic zone, and spalling zone. The main load is mainly carried by the elastic core, while the coal within the plastic zone has a reduced bearing capacity, which is not easily defined. However, the spalling zone will gradually peel off and be removed from the coal pillar, as illustrated in Fig. 10. Consequently, coal within the spalling area will no longer provide significant load-bearing capacity. Therefore, when investigating the linkage between failure and instability of residual coal pillars and rock strata, the influence of spalling should be taken into consideration.

Fig. 10
figure 10

Schematic diagram showing residual coal pillar after spalling

Full size image

4.1 Mechanism of coal pillar-rock stratum instability during progressive failure of coal pillar

Without taking into account the spalling behavior of the pillars, limit equilibrium theory, defines the breadth of the plastic area (Liu et al. 2008; Xie 2014; Cao et al. 2014):

$$l = \frac{h}{2gf}\ln \frac{q + c\cot \varphi }{{g\left( {p_{1} + c\cot \varphi } \right)}}$$
(9)
$$l = l_{1} + l_{2}$$
(10)
$$w = 2l_{1} + 2l_{2} + l_{3}$$
(11)

where, h is coal seam mining thickness, m; g is triaxial stress factor, \(g = {{\left( {1 + \sin \varphi } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \sin \varphi } \right)} {\left( {1 - \sin \varphi } \right)}}} \right. \kern-0pt} {\left( {1 - \sin \varphi } \right)}}\); f is Friction coefficient, \(f = \tan \varphi\); q is concentrated stress on coal pillars, MPa; c is cohesion, MPa; φ is internal friction angle, °; p1 is binding force of falling gangue on coal pillar, MPa.

According to Eqs. (7) and (8), the spalling breadth of the coal pillar is:

$$l_{1} = 0.1624h^{0.8135} T^{0.1865}$$
(12)

When considering the spalling behavior of the coal, the breadth of the plastic zone can be obtained according to Eqs. (10), (11) and (12):

$$l_{2} = l - l_{1} = \frac{h}{2gf}\ln \frac{q + c\cot \varphi }{{g\left( {p_{1} + c\cot \varphi } \right)}} - 0.1624h^{0.8135} T^{0.1865}$$
(13)

Then the effective bearing breadth d of the residual coal pillar changes accordingly, namely:

$$d = w - 2l_{1}$$
(14)

Therefore, when considering the spalling behavior of the coal pillars, the safety factor fs becomes.

$$f_{\text{s}} = \frac{{\sigma_{\text{p}} }}{{\sigma_{q} }} = \frac{{\sigma_{\text{m}} \left[ {0.64 + 0.36\left( \frac{d}{h} \right)} \right]^{n} d}}{{\left[ {dH + 2m\left( {H - m} \right)\tan \delta + m^{2} \tan \delta } \right] \cdot \gamma }}$$
(15)

Taking the coal pillar of the #8 coal seam in Panel 307 of the Jinhuagong mine as an example, the fs of the pillar may be calculated. The mining height of the #8 seam is h = 2.5 m, the breadth of coal pillar is w = 24 m, the buried depth is H = 312 m, caving high of the strata in the goaf is m = 62 m, the residual angle is 33°, and the mean specific weight is 25.5 kN/m3.

When the spalling of the coal pillar is not considered, the above data can be substituted into Eq. (3) to obtain a safety factor fs = 2.11 of the coal pillar left over from the #8 coal seam in Panel 307 of the Jinhuagong coal mine. That is to say, fs > 1.5 for the safety factor of the pillar from the #8 seam that should guarantee the long-term safety of the pillar without considering the spalling of the pillar. When considering spalling, the above data can be substituted into Eq. (15) to obtain the fs = 1.71 for the pillar stability. That is to say, when considering the spalling of the coal pillars, the safety factor fs of the residual coal pillar is greater than 1.5, which can still ensure the safety of the pillars. However, the safety factor of pillars when considering the spalling of coal pillar is clearly smaller than that when not considering spalling.

In addition, according to the relevant parameters of panel 307 above, the curves of fs for the pillars varying with the high of caving and the valid load breadth d of pillar are obtained, as shown in Fig. 11a and b respectively. As can be seen from Fig. 11a, the safety factor fs of the pillar in the seam decreases correspondingly, regardless of whether the spalling of the coal pillar is considered or not. When fs is less than 1.5, the pillar will be destroyed and unstable. As can be seen from Fig. 11b, as the effective bearing breadth of the pillar decreases due to the mining disturbance of the underlying seam, fs of the pillar with or without spalling also decreases.

Fig. 11
figure 11

Safety factor for pillar stability with the caving zone and effective bearing breadth of pillar

Full size image

4.2 Mechanism of coal pillar-rock stratum instability during unstable failure of pillar

From Sect. 4.1, the fs of the pillar in the #8 coal seam is still greater than 1.5, regardless of whether spalling of thel pillar is considered or not—representing a theoretically safe and stable state. However, when the underlying #11 seam is removed, the residual pillar in the overlying seam is still damaged due to ethis disturbance, causing overall collapse of the overburden strata. Elevated stresses are produced in the #11 coal seam. In fact, in both underground hard rock mines and coal mines, when a certain volume of brittle material is loaded by a relatively soft loading system and exceeds its strength, unstable failure will occur (Manouchehrian and Cai 2016; Wang 2019). According to the analogy between laboratory samples and coal pillars, Salamon (Wang 2019) proposed a criterion for stable and unstable failure. That is, if the local mine stiffness (LMS) is less than the maximum stiffness kc of the pillar, as shown in Fig. 12, the pillar will fail in an unstable (impact) or dynamic manner. It should be noted that when comparing the magnitudes of the LSS or λ, their absolute values should be compared. This will be manifest as a rock burst (Wang 2019; Salamon 1970; Hudson et al. 1972).

Fig. 12
figure 12

Criterion for transition from stable to unstable failure (Wang 2019; Salamon 1970; Hudson et al. 1972)

Full size image

With the effect of the disturbance of the lower seam, the pillar will continuously spall. The effective bearing breadth of pillar will continuously decrease. The proportion of breadth to height of pillar also changes accordingly. The influence of the proportion of pillar breadth to height on pillar strength and post peak behavior is known. With a change in the proportion of breadth to height, kc will also change (Zipf 1999). Through the back analysis of the field pillar tests, an empirical equation for the stiffness kc of the pillar and the proportion of breadth to height of the pillar have been defined. Zipf (Zipf 1999) proposed the following expression to calculate kc, as:

$$k_{\text{c}} = - 1750 + 437\frac{w}{h}$$
(16)

where, w is breadth of pillar; h is height of pillar.

The LMS can be calculated according to the criterion for the threshold for the transition from stable and unstable failure of the coal pillar (Jaiswal and Shrivastva 2012; Gao et al. 2019). We use numerical modeling to define this stiffness (LMS) where the residual coal pillar has not been excavated or has been excavated, respectively. The steps to determine the surrounding rock stiffness (LMS) through numerical simulation are shown in Fig. 13. The specific calculation method for the surrounding rock stiffness (LMS) is as follows (Jaiswal and Shrivastva 2012):

$$\text{LMS} = \frac{{f_{1} }}{{C_{\text{e}} - C_{\text{p}} }}$$
(17)
$$f_{1} = \sigma_{Z} A$$
(18)

where, σZ is vertical stress on coal pillar; A is area of pillar; Cp is the amount of floor and roof stratum movement before the removal of pillar; Ce the amount of floor and roof stratum movement after removal of coal pillar.

Fig. 13
figure 13

Steps in determining the geometric stiffness of the surrounding strata (LMS) through numerical simulation (Jaiswal and Shrivastva 2012)

Full size image

However, excavation within the underlying seam during multi-seam mining will affect the valid bearing breadth. As a result, the breadth to height ratio of the pillar decreases, and its post peak stiffness is also decreased. We use the empirical expression of Zipf (1999) as modified for spalling of the coal pillar as:

$$k_{{\text{c}}1} = - 1750 + 437\frac{{w - 2l_{1} }}{h}$$
(19)

The stiffness calculation for the surrounding rock changes correspondingly when considering the influence of pillar spalling. Assuming the reserved breadth of the pillar is w and the length is a, its bearing area is A = w × a. When considering the spalling of coal pillar caused by mining disturbance, the valid bearing breadth of the pillar becomes w − 2l1. The effective bearing area is correspondingly changed to (w − 2l1) × a. Then the evaluation of the surrounding rock stiffness considering the disturbance due to multi-seam mining becomes:

$${\text{LMS}}_{1} = \frac{{\sigma_{Z} A}}{{C_{\text{e}} - C_{\text{p}} }} = \frac{{\sigma_{Z} \left( {w - 2l_{1} } \right)a}}{{C_{\text{e}} - C_{\text{p}} }}$$
(20)

Hence, to determine the stable and unstable failure of coal pillars, the criterion proposed by Salamon (Salamon 1970; Wang and Kaunda 2019a, b; Guy et al. 2017) may be used. Specifically, even when the safety factor of the coal pillar exceeds 1.5, it may be subject to unstable failure due to the disturbance caused by lower seam mining. Thus, the criterion for the unstable failure of a coal pillar can be expressed as:

$$LMS_{1} < k_{{\text{c}}1}$$
(21)

Similarly, we may again consider the pillar of the #8 coal seam in Panel 307 of the Jinhuagong mine for comparison. The breadth is w = 24 m, the length is a = 500 m, the height is h = 2.5 m, and the vertical stress is σz = 13.5 MPa. The floor and roof displacement before pillar removal is Cp = 0.12 m, and the roof and floor displacement after coal pillar removal Ce = 0.35 m. This allows us to evaluate both kc and LMS. The kc of the pillar and the LMS of the rock are obtained, as shown in Fig. 14a and b respectively. Both the kc and the LMS are smaller than those when the spalling of the pillar is not considered. In addition, increasing the breadth results in an increase in kc and LMS.

Fig. 14
figure 14

Change in post peak stiffness and surrounding rock stiffness of the pillar as a function of pillar width (breadth)

Full size image

In summary, the linkage between progressive and dynamic failure of pillars and adjacent strata is as follows: After the upper seam is extracted, the roof rock may remain stable for an extended period of collapse and adjustment. During this period, the residual coal pillar in the goaf will continue to support the weight of the overlying strata, leading to the generation of concentrated tributary stress that is transferred to the coal seam below through the floor rock. When mining of the lower seam causes further disturbance and deformation in the roof, the fracture height of the roof will impact the safety of the pillar when it reaches the affected area of the upper pillar, as illustrated in Fig. 15. Therefore, the fracture height of the roof should be taken into consideration when evaluating the stability of residual coal pillars in multi-seam mining.

Fig. 15
figure 15

Schematic diagram showing interaction of the mining disturbance in the upper seams on the recovery of the lower seam and its linkage to instability

Full size image

There are two separate conditions defining coal pillar instability. (1) LMS > kc. Although the pillar will not be subject to unstable damage, the effective bearing breadth of the pillar in the overlying seam will continue to decrease due to the action of the lower seam. The height of the strata caving zone increases, and fs decreases. When fs < 1.5, the pillar is damaged. The instability of the pillar leads to instability and failure of the stable stratum in the overlying coal pillar bearing zone. The instability of the stable rock stratum further causes instability of the pillar in the overburden seam and the strata in the bearing area. As a result, the entire stratum fractures and collapses with the destruction of the pillar, leading to elevated ground pressure/stresses on the lower mined seam. Recovery of the lower seam results in an overburden caving zone and the stress concentration zone of the pillar and rock are superposed. This will cause a stiffness mismatch between rock and coal pillar. (2) LMS < kc. The pillar will be unstable. The instability of the stable stratum in the upper seam bearing area will result in instability of the coal pillar. Instability in the stable rock stratum in the upper bearing area will further cause the instability of the coal pillar and roof stratum in the overlying seam. It will also result in fracture and collapse of the entire rock stratum with the destruction of the coal pillar and causing elevated ground pressures and potentially further collapse.

However, it should be noted that the mechanism of residual coal pillar-rock strata instability obtained from either progressive coal pillar failure or unstable failure does not take into account the influence of water, goaf environment, and other factors. In addition, further research is needed to investigate the impact of coal pillar stripping caused by multi-seam mining, taking into account the applicability to different mines. Thus, considering different geological conditions and different mining engineering conditions, will better explain the mechanism as a result of the failure of coal pillars.

5 Conclusions

  1. (1)

    A large percentage of pillars should be retained in the mining area during multi-seam coal mining. Pillar instability may result in dynamic failure such as rock bursting and mining-induced seismicity with instability potentially manifest at the surface as subsidence.

  2. (2)

    Coal pillar-rock stratum instability during progressive failure of the coal pillar. Under the effect of the mining disturbance of the underlying seam, the effective bearing breadth of the pillar in the overlying seam will gradually decrease. The height of the overlying strata caving zone will increase and the fs of the pillar will decrease. When fs is less than 1.5, the pillar may be considered as “damaged” and susceptible to progressive failure. Failure of that pillar will lead to instability of the stable stratum in the overlying pillar bearing area. Any instability of the stable stratum will further cause instability in the overburden pillar and the stratum present in the pressure bearing area. Eventually, the entire stratum will break and collapse with the destruction of the coal pillar, resulting in high transferred stresses on the underlying coal seam.

  3. (3)

    Coal pillar-rock stratum instability during unstable failure of the coal pillar. The superposed influence of the overburden collapse zone and concentration of stresses in the coal pillar floor from mining disturbance of the underlying seam, will change the stiffness of the surrounding rock and coal pillar. When the LMS is less than kc, the pillar will be unstable. Instability of the stable rock stratum in the upper bearing area will result from instability of the coal pillar. The instability of the rock strata in the overlying bearing area further causes instability in the pillars and roof strata of the overlying seams. It also causes the entire stratum to fracture and collapse with the failure of the pillar, and finally causes the appearance of strong ground pressure in the lower coal seam.

Although the previous provides some valuable conclusions, more study is needed. First of all, the influence of water, weathering and the goaf environment on the coal pillar stiffness remain ill defined. Second, evaluation of the amount of spalling of the coal pillar as a result of multi-seam mining needs further constraint. Third, this paper only gives a linkage mechanism for the instability of pillars and strata under specific geological conditions. Thus, considering different geological conditions and different mining engineering conditions, will better explain the mechanism as a result of the failure of coal pillars.