1 Introduction

An airlift is a dynamic pump with non-movable components that can be used for the vertical conveyance of all kinds of fluids and slurry. The driving force of this non-electric pump is provided by injecting compressed air near the end of a riser pipe. After the air is injected, the specific gravity of the liquid-solid mixture decreases, and the buoyancy force along with the shear force between the air bubble and the liquid phase causes the fluid to move upward and when the air-water velocity reaches a suitable value, the solid parts start vertical motion (Mahrous 2012).

The use of this pump outside of mines has been most often documented in the literature for wastewater treatment facilities (Zejda et al. 2020), pumping liquid hydrocarbons (Ganat and Hrairi 2018), and for fish farms (Barrut et al. 2012). This pump has also seen a great deal of use in deep-sea mining and seafloor dredging because of sufficient availability of water and little maintenance requirements. Sadatomi et al. (2013) considered an airlift pump equipped with bubble-jet-generator for sand dredging from riverbeds.

Although it is very easy to install this pump at low initial cost, the literature does not address the transfer of minerals extracted from underground mines and even the centimetric dimension ranges. Many researchers (Weber and Dedegil 1976; Halde and Esvenson 1981; Yoshinaga and Saito 1996; Fujimoto et al. 2003; Deendarliantoa et al. 2018) analyzed the airlift in the three-phase flow with small solid particles that rarely exceeded one centimeter in size. Such dimensions are generally not common for all elements in the mining extraction as well as the pumping process. Zhao et al. (2023) carried out the experiments using two kinds of footpieces for conveying river sand with a diameter of 2.5 mm and density of 2534 kg/m3. Monitoring particle transportation with a three-axis motion control system showed that uniform holes on the footpiece has a better result compared to a non-uniform pattern. To carry larger particles, a riser tube with a larger inner diameter is usually required in addition to more compressed air.

What increases the presence of the airlift pump in the transportation of minerals is the efficiency in transporting larger particles, which requires larger diameter pipes compared to the diameter of conventional pipes that are used to study and verify the theories of multiphase flows in the lab. Regarding the diameter of the pipe, Arens et al. (2007) proposed that the average internal diameter of the suction pipe should be 2–3 times larger than the diameters of the particles in order to prevent the clogging of the suction zone with solid particles.

Among the various advantages, the only weak point of this pump is its low efficiency (Maliky 2014). As a result, in recent decades there has been an increased interest in making water delivery as efficient as possible. However, due to the difficulty of analyzing vertical three-phase flows, there are few sources for pumping solids. To the best of the authors’ knowledge, the effects of some positive ideas in a two-phase flow have not yet been investigated in the mineral transportation mode (three-phase flow). Ahmed et al. (2016) used a novel design of the air jacket to enhance the pumping rate of the water, which allowed different amounts of air to be injected simultaneously in the vertical and horizontal directions into the riser pipe. Moreover, Kumar et al. (2003) used a tapered pipe whose diameter increased from the bottom to the top and discovered that the pump efficiency had increased due to the delay in subsequent agglomeration of air bubbles.

Unlike conventional pumps for solid transmission, the airlift pump has a large independent variation that can influence pumping efficiency. In the studies performed to determine the efficiency of the airlift pump in carrying solid particles (Wang et al. 2020; Kassab et al. 2007; Fujimoto et al. 2003; Yoon et al. 2000; Hatta et al. 1999; Kandil and Elmiligui 1998; Yoshinaga and Saito 1996; Kato et al. 1975), a certain rate has been used to supply solid materials at the inlet of the suction pipe which does not correspond to the actual particle suction possibility. Therefore, the obtained results will be overestimated.

One of the aspects that has not been sufficiently studied is the effect of solid particles on a different types of vertical flow regimes. Muria et al. (2022) considered the local transient dynamics of the multiphase fluid (two-phase and three-phase flow) by changing the gas flow rate and mass loading of solid particles. Measuring of void fraction and liquid flow rate in the slug flow regime by an ultrasound Doppler method revealed that particles destabilized long slug bubbles, which reduces the ratio between the liquid flow rate and the void fraction.

The above researches explored the working characteristics of the airlift pump based on experimental tests on small spherical particles and rarely involve examining centimetric size particles, which are beneficial to utilize this pump for river sand extraction or deep-sea mining. However, most of these studies focus on the transport performance of the airlift pump under different air inflow and submergence levels, and less attention on optimization of the solid transport from the first stage of motion, which leads to decreased air consumption. Basically, if it is possible to move the particle in an optimal way from the state of zero velocity, then conveying it to a higher level does not require much energy.

According to the literature, Fujimoto et al. (2003) conducted a study on the start of particle movement in air-water mixture and compared it with the conditions at water ambient. The accuracy of their proposed model has not been examined to date. Their derived model is flawed due to the incorrect selection of correlation for annular flow conditions to calculate air void fraction, as well as considering superficial water velocity as input data. Therefore, this paper takes the optimization of the theoretical model as the research object, and intends to assess the accuracy of it with not only spherical particles but also irregular shaped coal particles in the centimetric size dimension. Since the Fujimoto model only predicts the conditions of single particle movement, an interest was felt to put forward some criteria with respect to superficial water and air velocity not only for the onset of one particle, but also for the group of particles.

2 Materials and methods

2.1 Experimental apparatus

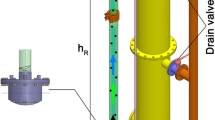
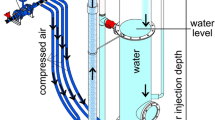
To evaluate the performance of an airlift pump in shallow coal transportation, a HydroCoal-Plus project supported by the Research Fund for Coal and Steel (European Commission) was defined. The pump was then installed in one experimental mine (Reiche Zeche, Germany) at the ambient temperature of 17.0 °C and the static pressure of 97.8 kPa. Figure 1 demonstrated the schematic view of the pump. The experimental pump consists of a transparent vertical tube with one air jacket, attached to its lower part to evenly distribute compressed air and produce of small bubbles. Supplemental Fig. S1 depicts the schematic structure and technical information of the tested air jacket.

Fig. 1
figure 1

A schematic diagram of the airlift pump setup

Full size image

To simplify the description of each part, the pipe below the air jacket is called the suction pipe, which includes a mixture of water and solid flows. The other part is a riser pipe in which the three-phase mixture flows (liquid-solid-gas). the transmission pipe has an internal diameter of 10.2 cm with a total height of 5.64 m. In order to separate the air and reuse the water, a separator tank was installed at the upper ends of the riser pipe. The separator tank is responsible for releasing the air into the atmosphere and directing water to the storage tank (downcomer), which is a steel pipe with a diameter of 41 cm. The advantage of this design is that the water flows in a closed cycle, moreover, the submergence ratio (Sr = hr/hw) does not change during the test. The air source was a rotary screw compressor (Kaeser CS121) with the maximum outflow of 11.6 m3/min and a pressure of 6 to 6.5 bars. Two electrical sensors made by IFM company were installed before the on/off valve to measure the properties of the compressed air such as pressure, temperature, and volume flow rate before it entered the manifold.

One rate-controlling parameter for vertical movement of solid particles was water flow (Qw) below the air jacket. To measure it in this level, a magnetic inductor sensor from Optifux with a precision of ≈ 0.5% was employed. Another variable controlled was the submergence ratio (Sr). Since the airlift performance in two- and three-phase flows is highly dependent on the submergence ratio, and due to limited water resources in underground mines, six submergence ratios were used to evaluate airlift performance in three-phase mode: 0.31, 0.4, 0.5, 0.6, 0.7 and 0.8.

2.2 Test particles

The experiments were performed at first with a single particle, and then with the maximum of 1.5 kg of uniform and also non-uniform ones, whose characteristics are listed in Table 1. The spherical particles, made up glass with a diameter of 1.4 and 1.6 cm, were thus utilized to calibrate the results. The non-uniform particles were also of coal with two sizes and same density (ρs). In order to have almost the same particles in terms of average diameters and weight, the coal types with three standard sieves (25, 31.5, 45 mm) were first separated, and then selected with a scale, so that their weight difference was in the range of ± 3 gr. To better identify each particle, one symbol was given to them, denoted by its materials, shapes, and main dimensions. For example, GS1 stands for glass with spherical shape and smaller diameter.

Table 1 Parameters of test particles
Full size table

For the real use of an airlift pump, there should be no obstruction inside the conveying pipes. A total of two iron meshes with 1 cm2 square holes were employed to restrain the solid particles between points A and B, where their position is shown in Fig. 1. The position of the lowest mesh had no negative impacts on the effective dimensions of the air bubbles, and the highest mesh prevented the possible escape of particles from the riser pipe. The passage of bubbles through the upper mesh may cause them to split or shrink, which does not impact the pump operation because the bubbles have reached the end of their vertical path. According to the results, the two meshes reduced the water flow by 0.2% on average. This effect was taken into account in the final results of this study.

2.3 Experimental procedure

First of all, one of the four types of test particles was selected, and one particle was placed inside the riser pipe (between point A and B). Then the desired amount of submergence ratio was satisfied by adding pure water. The compressed air flow rate was then increased slowly by adjusting the on/off valve so as not to cause a fast upward particle transmission. When air flow exceeded a certain value, the particle started to move upward and the critical flux for air and water could be determined. Supplying irregular-shape particles in a completely heterogeneous set will not be free from error, but in order to provide accurate experimental data that can be represented with the same rule for the group of particles, exclusively for coal particles, the first series of experiment were carried out on three different particles. We did not test them at the same time, and all tests were done separately to find arithmetic average data. To avoid ambiguity in the following sections, mention of three coal particles was avoided and all results will be presented as a single particle in the text.

In general, with the same fluid flow conditions, the rule of single particle motion due to possible collisions with others, when placed among the group of particles, has differences. To consider the role of particle mass, the second series of experiments were performed using three different solid masses of 0.5, 1.0 and 1.5 kg. In the first step, the compressed air inflow was adjusted to a sufficient value to start vertical conveying of one particle, and at this point, the water flow rate was recorded. Then, the inlet air flow rate was increased so that most of the particles were placed in the predefined observatory area along the vertical pipe. Fig. S2 in the supplementary materials better illustrates this issue. The placement of particles in this control area is checked with typical visual observations from the naked eye. Therefore, for each submergence ratio, six measurements were carried out in each test series to ensure superficial velocity data with a relative error of less than 5%, and the arithmetic mean values were used as a final result.

2.4 Experimental uncertainty

The uncertainty sources related to repeatability measurements together with readability (one half of the least count), and error limits are considered in calculation base on correct data distribution. Since the measurements are obtained under acceptable environmental conditions, as specified by both manufacturers, the environmental factors are not considered. The reported standard uncertainty for measured variables are listed in Table 2. It should be emphasized that the specification of the pressure and temperature uncertainties are used only in the theoretical part and have no influence on the experimental measurements. Moreover, Oueslati and Megriche (2017) considered the role of temperature on an airlift pump’s efficiency. As they raised the temperature up to 70 °C, the minor improvement in pump efficiency became apparent.

Table 2 Instrument details and the associated uncertainties
Full size table

3 Results and discussion

We know that the Taylor bubble is among the shapes of air bubbles present when moving vertically in a column of water. The ability of this bubble to carry very fine particles has been delineated in related literature. However, it was not considered in this study because a slight increase in the compressed air injection, the bubble flow regime begins where the Taylor bubble is no longer stable, and transported particle comes back to the level of the first mesh (A). Nevertheless, an interesting observation at the beginning of the first series of experiments showed that the weak region behind the Taylor bubble could lift a coal particle with a few centimeters in size to more than four meters, but the next bubble could not carry it (see supplementary video S1). Therefore, the Taylor bubble is able to carry a particle with an initial velocity close to zero, and if the particle has a velocity in the opposite direction of its motion, it cannot hinder it from falling and move it upward again.

3.1 Effects of submergence ratio

In the initial phase of particle movement, the drag force between water and solid particles plays a decisive role (Fujimoto et al. 2003). It is quite reasonable that the prerequisite for the motion of the solid particle is the motion of the water phase, i.e. the solid particle will not initiate moving until the transferred water reaches a certain velocity. Therefore, the amount of air required to pump water is less than the amount of compressed air to move a particle vertically. In addition, recent studies in the two-phase mode (air-water) and also the three-phase mode (air-water-solid) point to the same consensus among researchers that with an increase in the submergence ratio, there is an increase in the flow rate of pumped water (Enany et al. 2021; Ramdhani et al. 2020; Kassab et al. 2007; Hatta et al. 1999), so this factor must be accurately evaluated for the onset of solid phase motion. To this end, we performed experiments on the air-water-solid flow on six submergence ratios: 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8. This parameter was arranged by the three drainage valves connected to the downcomer pipe (Fig. 1).

Figures 2a–d demonstrates the correlations between the amount of water lifted and the air consumed to initiate the tested particles on six different submergence ratios (Sr). A first look at the Figures shows that, with the same trend in all cases, as the submergence ratio increases, the amount of air required for the onset of particle holdup decreases. It can be due to the fact that air bubbles have more travel distance when Sr increases. So, air bubbles have enough time to transfer their energy to a mixture of water and solids, which can result in less amounts of compressed air inflow to start vertical solid motions.

Fig. 2
figure 2

Effect of submergence ratio on superficial fluid velocity for particle initiation

Full size image

It also appeared from Figs. 2a–d that, as the submergence ratio decreases from 0.6 to 0.3, the difference in the superficial air velocity and water velocity required to start a motion of a single particle with the group of particles increases, so that this difference peaks at 0.3. One explanation for that is, owing to the unstable bubbly two-phase flow effects, with low air inflow at Sr less than 0.6, it is normal to see pulsations (discontinues flow) in the upward motion of the air-water mixture, which phenomenon could also be found in most researches (Enany et al. 2021; Kalenik (2015); Maliky (2014); Fujimoto et al. (2003). Such a situation changes as the amount of air inflow increases and leads to the slug flow regime. This phenomenon for group of particles caused the erratic fall behavior of the particles after a short distance from the vertical path. Due to the fact that at low submergence ratio, the volume fraction of air (αg) is higher than the water phase and the settling velocity of particles in air is higher than that of water, particle collision is completely unavoidable in these conditions. Moreover, changing constant particle orientation, especially for irregular-shape particle, makes it difficult to determine the effective area of particles in the holdup process and allocate a single drag coefficient for it. On the other hand, the collision of particles causes a loss of upward kinetic energy of the particles. In total, the presented results prove that the compressed air consumption can be saved up to eight times by raising the Sr from 0.3 to 0.8 on average. This is the evidence for the use of airlift pumps at submergence ratios closer to or greater than 0.7.

3.2 Effects of particles specification

3.2.1 Particle size

In this section, the effects of one of the most important geometrical parameters of a particle, i.e. particle size, on the onset of vertical motion in a three-phase flow was investigated. In practice, a very small number of particles for transferring are spherical, so to better analyze this issue, in addition to spherical particles, non-geometric shape particles are used as well. Since a similar trend of data was obtained for other submergence ratios, the outcomes for onset of a particle motion in the three-phase flow at Sr equal to 0.7 are showed in Fig. 3.

Fig. 3
figure 3

Effect of particle size on the onset of vertical motion at different submergence ratios (CI2 > CI1, GS2 > GS1).

Full size image

We know, as the average particle size increases, owing to the lower buoyancy force and the higher drag force between the bubble and the particle, the net lifting force on the particle decreases (Ahmadi and Zhang 2005). On the other hand, with a constant density, the increase in particle size increases the force of gravity on it, which requires more vertical force to pick-up the particle (Mahrous 2012). Although the diameter of the glass particle GS2 is only 0.2 mm larger than that of the GS1, it can be clearly seen in Fig. 3 that more compressed air is needed for the particle GS2 to initiate vertical motion. A similar result is also obtained for the coal particles CI1 and CI2. In terms of size, although the coal particles are about two times larger than spherical particles, but the earlier beginning of their motion indicates that a circular particle with a higher density requires higher velocities for the air and water phases in order to force it to move vertically. The shear stress between particle with uneven surface and with water and air phases are much higher than that between spherical particle, moreover, lower density increases the drag force for the ascent of such particle. In contradiction with our results, in their research on two types of asymmetric particles, Kandil et al. (1998) concluded that the role of particle size is more effective than the role of density in the transfer of solid particles. Therefore, for optimal performance of the airlift pump, the use of non-spherical particles with lower density is recommended.

3.2.2 Particle mass

As described above, to evaluate the effects of solid mass on the onset of solid motion, three values of 0.5, 1.0, and 1.5 kg for each of the tested particles were provided and each time a certain weight of them was placed in the riser pipe. Figures 4a–d shows the relationship between compressed air velocity and water velocity for different mass of particles GS1 and CI2 at various submergence ratios. At a glance, it can be seen that the data for all three types of mass show the same trend by single particle motion. The only obvious difference is in the superficial velocity of the fluid phases, which is related to the fact that more mass of the solid phase is introduced into the riser. Thus, group of particles require a higher velocity of the air phase to overcome this increase in weight of the solid-water mixture.

Fig. 4
figure 4

Influence of particle mass along with submergence ratio on onset of particle motion for smaller size glass particle (GS1), and larger size coal particle (CI2).

Full size image

Reducing the water phase velocity by increasing the mass of particles is another issue that has been tested separately for each amount of particle mass. As explained in Sect. 2.3, based on the data obtained from the motion of one particle, to have the same criteria, the inlet air velocity was set equal to the value required for the condition in which the one particle initiates moving. The experimental data for particle CI2 can be found in Fig. S3 of Supplementary Materials. Fig. S3 illustrates that at constant submergence ratio, for every half kilogram increase in the tested particles, the superficial water velocity decreases by ≈ 1%.

So far, few studies have been conducted on the effects of air bubbles passing through the group of particles, and in the meantime, the role of non-spherical particles with dimensions of about a few centimeters is not well understood. Hence, the effects of solid mass on the flow regime cannot be determined with certainty. For example, conducting an experiment on spherical particles with a diameter of 2 mm, Miller and Cain (1986) showed that the solid mass has no effect on the transition of the flow regime from the slug to the churn, but it accelerates the change of the flow regime from the bubble to the slug. We know that as the weight is constant, the increased size of the particles leads to a decrease in their number. For example, in this study, half a kilogram of coal is equivalent to 19 and 7 pieces CI1 and CI2 particles, respectively. The outcomes of practical study indicate that the number of particles inside the riser pipe does not have a significant effect on the motion of the group particles, and in practice it is the size of the particle that plays a more significant role.

It can be seen from Figs. 4a–d, irrespective of the kind of particle shape, at Sr equal to 0.8, the amount of injected air required to hold up the solid particle to the control area is the same in different cases: 0.5, 1.0, and 1.5 kg. In this condition, a decrease in the superficial water velocity due to the increase in weight of the water-solid mixture in the riser pipe is quite evident. For each half kilogram increase in the tested particles at submergence ratio equal to 0.7, a slight increase in compressed air flow is required to move the particles vertically, which compensates for the decrease in water velocity. Therefore, in Figs. 4b and d, no decrease in water velocity is observed. Without loss of generality, for Sr between 0.7 and 0.8, it seems that with the same superficial velocity of the air phase, higher mass of solid particles can be forced to move upward. Thus, the input rates of solids should be designed in order to obtain maximum efficiency and use the whole compressed air energy.

3.3 Comparison with the theoretical formulas

In this part, we intend to evaluate the results of our applied research with the reference to the equation presented by Fujimoto et al. )2003) to estimate the initiation of the single-particle motion in three-phase flow. This equation was accordingly derived based on a one-dimensional mixture model, using a momentum equation, for a single spherical solid particle in the mixture of air and liquid.

$${j}_{\text{w, min}}= \frac{1}{{\rho }_{\text{w}}} (\sqrt{\frac{4 . {\rho }_{\text{m}} . {d}_{\text{s}} . g . \left({\rho }_{\text{s}}-{\rho }_{\text{m}}\right)}{3 . {C}_{\text{D}} . {\rho }_{\text{w}}}} - {\rho }_{\text{g}} . {j}_{\text{g}})$$
(1)

in which jw,min, ρw, ρm, ds, g, ρs, CD, ρg, and jg are the minimum volumetric water flux (the rate of volume flow across a unit area), water density, air-water mixture density, solid diameter, gravitational acceleration, solid density, drag coefficient, air density and volumetric air flux, respectively. By applying the ideal gas law, the density of air can be calculated as a function of temperature (T) and static pressure (P) at the level of air jacket.

$${\rho }_{\text{g}} =\frac{P}{R T\text{ }}$$
(2)

due to the small volume of one solid particle compared with that of air and water, the solid part was negligible in calculating the air-water mixture density.

$${\rho }_{\text{m}}= {\alpha }_{\text{w} }{\rho }_{\text{w}} + {\alpha }_{\text{g}} {\rho }_{\text{g}}$$
(3)

here, αw and αg denote the volumetric fraction of water and air in the riser pipe, respectively. The sum of the volumetric fractions for the gas and water also approaches unity, from which the following relation can be easily derived:

$${\alpha }_{\text{w}} = 1- {\alpha }_{\text{g}}$$
(4)

of note, Fujimoto et al.’s (2003) model has a deficit for predicting the minimum superficial water velocity to initiate one solid particle in three-phase flow, because air velocity, particle specification, and water velocity must be given as input data to determine the minimum superficial water velocity. On the other hand, it is necessary to know the value of jw in advance to calculate the void fraction. The key point to deal with this deficit is to use the iterative method between Eq. (1) and the suitable model for computation of air volumetric fraction until jw converges.

The effect of air intake on pump performance depends on the type of vertical flow regime. Most of the literature agrees that water discharge increases as air inflow increases until a maximum discharge flow rate in annular flow reaches, which further air injection is insignificant. Another point that can be mentioned is that Fujimoto et al. (2003) used the model presented by Smith (1969) to determine the gas volumetric fraction (αg), which is basically consistent with the annular flow regime. According to the data presented by the original research (Fig. 4), they never conducted any experiments under the annular flow regime conditions. It is worth noting that the incorrect use of Smith’s equation is also seen in some studies (Wang et al. 2020; Kassab et al. (2007); Yoshinaga and Saito (1996). From a practical viewpoint, it is rather inconceivable that a small particle with a low or middle density needs a large amount of compressed air to start vertical motions. Basically, such a particle onset transition occurs in the slug flow regimes or maximizes in the churn flow regime if the submergence ratio is low. Hence, to raise the accuracy of the void fraction calculations, the models offered by Nicklin et al. (1962) for the slug flow range (Eq. (5)) and Hasan (1988) for churn flow regimes (Eq. (6)) were used.

$${\alpha }_{\text{g}}=\frac{{j}_{\text{g}}}{1.2 {(j}_{\text{g}}+ {j}_{\text{w}}) + 0.35 \sqrt{g D} }$$
(5)
$${\alpha }_{g}=\frac{{j}_{g} }{1.15\text{ }{(j}_{g}+\text{ }{j}_{w}) + 0.345\text{ }\sqrt{\frac{ g . D .\left({\rho }_{w}-\text{ }{\rho }_{g}\right)}{{ \rho }_{w}}} }$$
(6)

where D denotes the dimeter of the riser pipe.

The drag coefficient for a spherical particle in this study is considered to be 0.42. To increase the accuracy of CD for coal particles, the settling time in still water was measured experimentally. The length of the tube was enough for a particle to reach 63% of its terminal velocity. To maximally reduce the artificial measured error, this test was performed 50 times in a tube with a diameter of 40 cm. An average drag coefficient was estimated to be 0.472 and 0.498 for CI1 and CI2 particles, respectively. It should be emphasized that the particle volume was measured using the pycnometric method and the effective area was calculated employing the method provided by Dellino et al. (2005) for irregular-shape particles.

The values predicted by Eq. (1), together with the experimental points for different submergence ratios, are plotted in Figs. 5a–c. Based on the values obtained using the uncertainty analyses in Table 2, and considering relevant sensitivity coefficient, by substituting air density and particle dimension uncertainties estimates in minimum water velocity in calculating onset of particle motion, the total standard uncertainty can be considered as ± 0.081 m/s. Although the measured data are not well close to the predictions in some cases. It can be accepted from these figures that the computation results on the basis of the present theoretical model give the best fit to the experimental data for both types of tested particles. The minor deviation in results between calculations and experiments in all three graphs does not follow a particular pattern. Perhaps this slight difference for the coal particle is related to the effective area and drag coefficient.

Fig. 5
figure 5

Comparison between present modified model and experimental results: a Smaller coal particle (CI1) b Smaller glass particle (GS1) and c Bigger glass particle (GS2)

Full size image

The term Fujimoto-Nicklin in Figs. 5a–c refers to the fact that the equation presented by Nicklin et al. (1962) for slug flow regimes was exploited to calculate the volume fraction of air in Eq. (1). Although there is no apparent difference between the results of the computation with Fujimoto-Nicklin and Fujimoto-Hasan, estimation with Fujimoto-Nicklin is closer most of the time to the experimental values.

In a vertical tube filled with water (suction pipe), irrespective of the amount of Sr, the particle often begins the vertical motion at a certain superficial velocity of water. To facilitate the next analysis, the water velocity range required to start pick-up of a particle in water ambient is also marked with two horizontal lines in Figs. 5a–c. For instance, if superficial water velocity stands in the range of 0.50 to 0.52 m/s, then the spherical glass particle (GS1) starts a vertical motion in the suction pipe. A video of this additional test, which has been done just to build more confidence, can be seen in video S2 of supplementary materials.

Fujimoto et al. (2003), theoretically claimed that the jw,min to initiate the motion of a particle in the main water flow was bigger than that in a two-phase air-water state. They came to this conclusion by examinations on two spherical particles made up of glass and alumina with diameters of 2, 3 and 5 mm. Unfortunately, it was not specified exactly for which range of the submergence ratio this could be applied. Considering Figs. 5a–c, this idea holds true just for spherical particles under the present experimental conditions. It can be clearly seen that water velocity for the onset the motion of a single coal particle in water ambient is bigger than the air-water mixture flow only for Sr < 0.8. According to these results, more compressed air must be injected to exceed the water velocity, in order to suck the coal particle (CI1) into the suction pipe, when Sr is lower than 0.8, which means that the pump efficiency is reduced. As demonstrated in an our previous study (Enany et al. 2022), spherical particles have the lowest transfer velocity compared to half-sphere and irregular-shape ones. Therefore, such particles are not suitable for transfer by an airlift pump. Furthermore, the results in Figs. 5b-c also confirme in another way that the pumping of the spherical particles diminishes the efficiency of the airlift pump due to the difference in water velocity to move the particle in water and air-water conditions. In general, the suction pipe should be considered as short as possible to raise the efficiency of the pump for transporting solids, which can slightly moderate the difference in the onset of particle motion in two-phase and three-phase flows by decreasing frictional velocity drop between water and the pipe wall.

It should be noted that the excessive reduction in the suction pipe length, and at the same time, the presence of a large number of solid particles in the pump causes the compressed air travel to have a path with less resistance and exits from the suction pipe inlet. From the observation in Figs. 5a–c, it is also evident that the solid particle does not always start moving at a certain superficial velocity of water, and this value increases with increasing Sr. In general, considering the role of just one character such as water is an imperfect indicator for explanation of the onset particle holdup in vertical three-phase flow. Therefore, it is necessary to consider the role of another fluid, such as air together with submergence ratio on the mechanism of particle motion. For this purpose, a new dimensionless parameter called the SS is presented, as it represents the role of both superficial fluid velocity and submergence ratio, which is obtained by dividing the minimum superficial air velocity to water velocity at initiation of vertical motion of the particles (SS = jg/jw).

The values of the SS parameter ​​according to the results obtained from the data of the practical experiments for three tested particles are presented in Table 3. The data in Table 3 clearly illustrate that the SS parameter is almost unique for each submergence ratio and does not depend on the shape, dimensions, and density of the particle. It was previously explained that the larger the particle, the higher the air velocity it needs to initiate vertical motion, which also increases the water phase velocity, but overall there is a certain ratio between air velocity and water velocity to occur the particle motion. We emphasize that the equation presented by Fujimoto et al. (2003) for the group of particles is not applicable due to the lack of two parameters associated with the collision of the particles with each other and the friction parameter. However, the SS parameter can also be used to estimate the motion of group of particles with a good approximation. The values of this parameter for mass of 1 kg are presented in Table 4. The slight difference in the value of the SS parameter for one particle to initiate its motion compared to a group of particles can be due to three reasons: (1) Particles collide with each other immediately after vertical motion; (2) Particles collide with the pipe wall; and (3) Changes in the dimensions of the air bubbles when passing through the particles.

Table 3 The values of the parameter SS to start the vertical motion of one particle in air-water flow
Full size table
Table 4 The values of the parameter SS to start the vertical motion of 1 kg particle in air-water flow
Full size table

It should be noted that all of these three items are uncontrollable parameters, especially the last one, which can behave differently in each pump due to multiple options for air-jacket design and hole dimension size. According to above and simultaneously considering the results of Tables 3 and 4, to find optimum operating condition of airlift pump for solid particle holdup, the ratio of gas volumetric flux to water volumetric flux has to be less than 1. It means that to have a cost-effective pumping process, working with submergence ration greater than 0.7 is highly recommended.

4 Conclusions

In the present study, the main conditions at which solid particles can start the vertical motion easier with an airlift pump were theoretically and experimentally explored.

From the performed tests, it appeared that the role of parameters related to particle characteristics is significant. The very slight increase in the particle size, the GS2 particle is only 0.2 mm larger in diameter than the GS1, clearly indicates that intake air injection must be increased to reach the critical point of solid particle movement. Moreover, the spherical shape particles have a poor vertical flowability with the airlift pump compared to non-geometrical particles because the difference in the velocity of the fluid required to initiate its movement in water ambient is greater than in an air-water mixture. Without loss of generality, the results under the raising mass of particle condition did not show particular change compared to the tests with a single particle. The only difference was the increase in air consumption due to the increase in the weight of the water-solid mixture in the riser tube. It should be noted that although a single particle could travel the entire vertical path after the onset of motion without increasing the air supply rate at Sr greater than 0.6, this ability was maintained with increasing mass of particles to 1.5 kg only at Sr equal to 0.8.

Contrary to the start of particle movement in the suction tube (water ambient), the same superficial velocity is not observed for the initiation of particle motion in the riser tube (air-water mixture). The amount of velocity required for both water and air tends to increase with decreasing submergence level. In total, in accordance with the main influencing parameters of the experiment, a strong effect on onset of particle movement appeared according to the submergence ratio, so that by increasing its level from 0.3 to 0.8, the compressed air consumption can be reduced on average by a factor of eight.

In the analysis, Fujimoto et al.’s model for predicting the moment of vertical particle motion is modified by incorporating an appropriate correlation of air void fraction in air-water mixtures. Moreover, the weakness of the model regarding to superficial water velocity as input data is solved by using an iterative solution. The computation results with our recommendations are not too far off from the experimental values for both types of tested particles; hence, the agreement between the experimental data and theoretical estimation is good.

As discussed in detail above, considering only the jw,min index to assess the onset of particle transmission in vertical three-phase flow is flawed and requires the role of air and submergence ratio to be taken into account. Therefore, we offered new criteria based on the superficial velocity ratio of main fluids for each submergence ratio. With respect to the experimental data, this criterion showed very good accuracy for conditions where only one particle starts moving and can also be used with a suitable approximation for the group of particles. In general, the ratio of gas volume to water volume flux should be less than 1 to achieve the optimal operation of the airlift pump to move solid particles upwards. Further work can be performed in that matter, in particular for assessing the impact of other parameters such as riser pipe diameter and air bubble size.