1 Introduction

Stop-and-go waves frequently occur at a signalized intersection due to a full stop, abrupt acceleration, and deceleration. And this can compromise traffic mobility, increase safety hazards, and cause serious environmental effects. With the development of connected vehicles (CVs) and connected autonomous vehicles (CAVs), it is possible to obtain traffic information (e.g., traffic signal timing, vehicle speed, acceleration), and communicate between vehicle and vehicle/infrastructure, then help/control vehicles to drive smoothly through advisory speed limit. Numerous speed control studies have been conducted to improve traffic efficiency, safety, and fuel economy, such as Optimal Speed Advisory (OSA) (Mahler and Vahidi 2012; Wan et al. 2016), Green Light Optimal Speed Advisory (GLOSA) (Nguyen et al. 2016), Eco-driving (De Nunzio et al. 2016; Jiang et al. 2017; Huang et al. 2018; Guo et al. 2021), Eco-Cooperative Adaptive Cruise Control (ECACC) (Kamalanathsharma et al. 2013; Yang et al. 2017), Variable Speed Limit (VSL) (Yang et al. 2013; Ubiergo and Jin 2016; Lyu et al. 2017; Yao et al. 2018) and trajectory smoothing (Zhou et al. 2017; Guo et al. 2019; Soleimaniamiri et al. 2020; Yao and Li 2021).

CAV technologies (Yang et al. 2017; Jiang et al. 2017; Shi and Li 2021a, b; Li et al. 2021), however, can control detailed vehicle trajectories in high resolution. They are relatively future technologies and may not be implemented in the near future. Therefore, this paper focuses on connected manned vehicles. In other words, vehicles in this study are controlled by human drivers, though with assistance from individual vehicle-based information provided by the connectivity technology. Most studies on speed control strategies have focused on the algorithms for generating optimized speed profiles or vehicular trajectories. However, in practice, the driver’s behavior is stochastic, and it is difficult to predict the vehicle arriving patterns (i.e., arriving headway), and it is hard for a driver to exactly follow the optimal speed profiles or trajectories. To make these speed control strategies more realistic, some research focused on driver's behavior based on eco-driving. Jamson et al. (2015) proposed in-vehicle eco-driving assistance aiming to investigate the most effective and acceptable in-vehicle system for the provision of guidance on fuel-efficient accelerator usage. Then, Pampel et al. (2015)studied the mental models of eco-driving that regular drivers have, and verified that in-vehicle guidance could increase driving safety compared to practicing eco-driving without them. Xiang et al. (2015) developed a speed advisory model with driver’s behavior adaptability for eco-driving, and it showed the proposed model could improve fuel economy. Li et al. (2016) proposed a modified stochastic model predicting a control-based energy management strategy considering driver's behavior to improve fuel economy. Numerous researchers focused on the queue effect at a signalized intersection. He et al. (2015) presented a multi-stage optimal control formulation to obtain the fuel-optimal vehicle trajectory on signalized arterial accounting for vehicle queue and traffic light status. Yang et al. (2017) developed an Eco-CACC algorithm considering queue effects to compute the fuel-optimum vehicle trajectory at a signalized intersection. Others studied the stochastic problems at a signalized intersection. Tong et al. (2015) utilized a stochastic programming model for oversaturated intersection signal timing, considering the uncertainty in traffic demand to minimize the vehicle delay. Sun and Liu (2015) developed a stochastic eco-routing algorithm in a signalized traffic network, incorporating the stochastic traffic light condition into the Markov decision process (MDP). Further, in our previous work (Yao et al. 2018), we proposed a trajectory smoothing method based on Individual Variable Speed Limits (IVSL) with location optimization at a signalized intersection. Results show that the proposed IVSL strategy can greatly increase traffic efficiency and reduce fuel consumption.

In the above studies, car-following models were adopted to reproduce longitudinal human-driven vehicle behaviors, including the Newell’s model (Newell 2002), Gipps’ model (Gipps 1981), and IDM model (Treiber et al. 2000). However, the impacts of different car-following models on IVSL have not been investigated. Also, limited efforts have been made to consider stochastic vehicle arriving patterns. Without considering realistic stochastic traffic patterns, the resulting speed control strategies might not be feasible in the real world. This study is motivated to address the two limitations. First, we compare three car-following models with the deterministic IVSL model. Then, we develop a two-stage stochastic IVSL optimization model considering the stochastic vehicle arriving patterns. The Monte-Carlo method (Metropolis and Ulam 1949) and the DIRECT algorithm (Jones et al. 1993) are adopted to solve the stochastic IVSL model.

The rest of this paper is organized as follows. Section 2 introduces the Individual Variable Speed Limit (IVSL) trajectory planning problem. Section 3 first presents three different car-following models in the IVSL control strategy. Next, a deterministic IVSL model is formulated, as well as a two-stage stochastic IVSL model, which is integrated into the Monte-Carlo framework. Section 4 conducts numerical studies to test the model results. Section 5 concludes this paper and briefly discusses future research directions.

2 Problem statement

This section introduces the IVSL trajectory planning problem.

2.1 Road

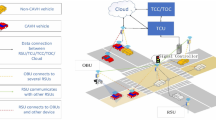
As is shown in Fig. 1, a single-lane segment leading to a signalized intersection has a length of \(L\). The traffic signal is installed at the segment exit at location \(L\), and the traffic moves from location 0 to location \(L\).

Fig. 1
figure 1

Illustration of the IVSL system

Full size image

2.2 Traffic signal

A fixed signal timing with an effective green time length of \(G\), an effective red time of \(R\), and a signal cycle length of \(C \, \text {which equals to} \, G + R\) are considered. Without loss of generality, the system is started from the beginning of a green phase at time 0.

2.3 Vehicles

Let \({\mathbf{N}}: = \left\{ {1,2, \cdots ,N} \right\}\) denote the set of all \(N\) vehicles. We assume that all vehicles have the same kinetic characteristics and do not move back. Let \({x}_{n}\left(t\right)\) denote the trajectory of vehicle \(n\) (\(n\in \mathbf{N}\)) at time \(t\) (\(t\in \left[0,\right.\left.+\infty \right)\)). Thus vehicle \(n\)’s trajectory is \({x}_{n}\), and the set of all vehicle trajectories is denoted as\(\mathbf{x}={\left\{{x}_{n}\right\}}_{n\in N}\). The first-order differential \({\dot{{\rm of} \, x}}_{n}\left(t\right)\) is the speed of vehicle \(n\) at time \(t\). We require \({\dot{x}}_{n}\left(t\right)\in \left[0,{v}_{\text{max}}\right]\) where \({v}_{\text{max}}\) is the maximum allowed speed on this segment. And the second-order differential of \({\ddot{x}}_{n}\left(t\right)\) is the acceleration of vehicle \(n\) at time \(t\). With slight abuse of the math, define the inverse function \(x_{n}^{ - 1} \left( l \right): = argmin_{t} x_{n} \left( t \right) = l\),\(\forall l\in \left[0,L\right]\). A subset of vehicles, denoted by \({\mathbf{N}}^{\mathrm{C}}\subset \mathbf{N}\), are assumed to be equipped with an onboard unit that can receive real-time speed limits from the IVSLs while passing them.

2.4 Trajectory planning measures

Two IVSLs, i.e., IVSL1 and IVSL2, are set along the segment at locations \({L}_{1}\) and \({L}_{2}\), respectively, where\(0\le {L}_{1}\le {L}_{2}\le L\). Each vehicle \(n\) proceeds in the following way before considering signals. Dynamic speed limits \(\overline{v}_{n}\) are provided to CVs when passing these two locations. It can be calculated by solving \(x_{n}^{ - 1} \left( L \right) - x_{n}^{ - 1} \left( {L_{1} } \right) = \left( {\frac{{\overline{v}_{n} - v_{n}^{{L_{1} }} }}{d}} \right) + \left( {\frac{{L_{2} - L_{1} }}{{\overline{v}_{n} }} - \frac{{\overline{v}_{n}^{2} - \left( {v_{n}^{{L_{1} }} } \right)^{2} }}{{2d \times \overline{v}_{n} }}} \right) + \left( {\frac{{v_{n}^{ + } - \overline{v}_{n} }}{a}} \right)\), where \(L\), \(a\), \(d\), \(v_{\text{max}}\), \({ }v_{n}^{{L_{1} }}\), \(v_{n}^{ + }\), \(x_{n}^{ - 1} \left( 0 \right)\), \(x_{n}^{ - 1} \left( {L_{1} } \right)\) and \(x_{n}^{ - 1} \left( L \right)\) are all known parameters and locations \(L_{1}\) and \(L_{2}\) are the variables to be optimized. Note that once \(L_{1}\) and \(L_{2}\) are given, \(\overline{v}_{n}\) can be easily solved.

Three car-following models are compared to show their impacts on IVSL strategies, such as the Gipps' model, modified Newell's model (M-Newell's model), and Intelligent Driver Model (IDM).

This paper is an extension based on the previous work of IVSL (Yao et al. 2018). IVSL utilizes onboard devices with V2I communications to smooth vehicle trajectories and eliminate full stops at a signalized intersection. It allows dynamic adjustment of speed limits for an individual vehicle in response to real-time traffic states using in-vehicle displays. Figure 1 is the operations of the IVSL system. With the IVSL system, a trajectory smoothing method is proposed to improve traffic efficiency and decrease vehicle fuel consumption and emissions. This method uses two individual IVSLs to guide vehicles on this highway segment (which would otherwise be held stopped at the current or following red light phase) to drive smoothly without a full stop (if possible) and just hit the beginning of the next green light. Note that the IVSL essentially only needs to control some identified Target Control Vehicles (TCV) as lead vehicles of these platoons and the rest can be smoothed accordingly by just following the TCVs with their regular car-following behavior. In addition, noted that the queue effects of conventional vehicles and incompliant CV vehicles (i.e., compliance rate) are considered. Further, the locations of these two IVSLs, i.e., IVSL1 and IVSL2, affect the smoothed trajectory shapes and need to be carefully selected to optimize the overall traffic performance. Differ from the previous work, vehicle arriving patterns (i.e., arriving headway) are varied with different traffic conditions in a whole day, e.g., sparse traffic, intermediate traffic, and dense traffic. Thus, stochastic arriving patterns are considered in IVSLs optimization is a two-stage problem called the Individual Variable Speed Limit with Stochastic Optimization (IVSL-SO). Before installing the IVSL system, we can use historical data to estimate the vehicle trajectories with the IVSL-SO and pre-set the IVSLs.

For convenience, Table 1 presents all parameters used in this paper.

Table 1 Descriptions of parameters
Full size table

3 Methodology

This section first introduces three popular car-following models used in the IVSL. Next, IVSL models with a deterministic vehicle arriving pattern and a stochastic arriving pattern are formulated, respectively.

3.1 Car-following models in the IVSL

3.1.1 Gipps’ model

A simplified Gipps’ car-following model (Treiber and Kesting 2013) is formulated as follows:

$$\dot{x}_{n} \left( {t + \Delta t} \right) = F^{Gipp} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right): = \text{min}\left[ {\dot{x}_{n} \left( t \right) + a \times \Delta t,v_{\text{max}} ,v_{n}^{\text{safe}} \left( {s_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right)} \right)} \right],$$
(1)

where, \(a\) is the maximum acceleration; \(\Delta t\) is the constant time gap; and \({v}_{n}^{\text{safe}}\left({s}_{n}\left(t\right),{\dot{x}}_{n-1}\left(t\right)\right)\) defines the “safe speed” (the highest possible speed for a vehicle \(n\)),

$$v_{n}^{\text{safe}} \left( {s_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right)} \right) = d \times \Delta t + \sqrt {d^{2} \times \Delta t^{2} + \dot{x}_{n - 1} \left( t \right)^{2} - 2d \times \left( {s_{n} \left( t \right) - s_{j} } \right)} ,$$
(2)

where, \(d\) is the maximum deceleration, it’s negative; \({s}_{n}\left(t\right)={x}_{n-1}\left(t\right)-{x}_{n}\left(t\right)\) is the gap between vehicle \(n\) and \(n-1\); and \({s}_{j}\) is the minimum gap. To make the above car following law applicable to vehicle 1, we can simply set \({\dot{x}}_{0}\left(t\right)={v}_{\text{max}}\), \({s}_{1}\left(t\right)=\infty\), \(\forall t\). And we use a set of limitations defined by (Gipps 1981) to govern the acceleration of vehicles except for the TCV:

$$a_{n}^{\text{free}} \left( t \right) = 2.5 \times a \times \left( {1 - \frac{{\dot{x}_{n} \left( t \right)}}{{v_{\text{max}} }}} \right) \times \sqrt {0.025 + \frac{{\dot{x}_{n} \left( t \right)}}{{v_{\text{max}} }}} ,$$
(3)
$$a_{n}^{\text{cong}} \left( t \right) = \frac{1}{\tau } \times \left[ {\frac{1}{\Delta t} \times \left( {s_{n} \left( t \right) - s_{j} + \frac{{\dot{x}_{n - 1} \left( t \right)^{2} - \dot{x}_{n} \left( t \right)^{2} }}{2 \times d}} \right) - \dot{x}_{n} \left( t \right)} \right],$$
(4)
$$\ddot{x}_{n} \left( t \right) = \text{max}\left\{ {d,\text{min}\left\{ {a_{n}^{\text{free}} \left( t \right),a_{n}^{\text{cong}} \left( t \right)} \right\}} \right\},$$
(5)

where, \(a_{n}^{\text{free}} \left( t \right)\) is the acceleration of free-flow traffic, \(a_{n}^{\text{cong}} \left( t \right)\) is the acceleration of congested traffic, and \(\tau\) is the sensitivity coefficient (1.2 s).

Once the vehicle \(n\) arrives at location 0, if it is a compliant vehicle (\(n \in {\mathbf{N}}^{{\text{C}}}\)), we can identify whether it is a TCV through the following hypothesis test. The hypothesis is that vehicle \(n\) is not a lead vehicle, and thus its trajectory can be predicted according to the Gipps’ car-following law up to the stop-line. If the exit time of vehicle \(n\) is in the middle of a green phase, i.e., \(iC < x_{n}^{ - 1} \left( L \right) \le G + iC\), \(\exists i \in \left\{ {0,1, \ldots } \right\}\), then the hypothesis holds and vehicle \(n\) is not a TCV. In this case, vehicle \(n\) will proceed according to the Gipps’ car-following law without activating the IVSL. Otherwise, vehicle \(n\) would hit a green light if it just follows the preceding vehicle, and it thus shall be labeled as a TCV whose trajectory needs to be smoothed by the IVSL to pass the intersection at the beginning of the next green phase. If vehicle \(n\) is a TCV, in addition to being constrained by the car-following law, it receives a variable speed limit \(\overline{v}_{n}\) at location \(L_{1}\) and will decelerate to \(\overline{v}_{n}\) from location \(L_{1}\) if its speed is greater than \(\overline{v}_{n}\). At location \(L_{2}\), speed limit \(\overline{v}_{n}\) is lifted, and vehicle \(n\) proceeds only according to the Gipps’ car-following law.

If vehicle \(n\) is a non-compliant vehicle, in addition to the Gipps’ car-following law, we check whether it needs to stop at a red light. First, we let vehicle \(n\) just follow Gipps’ car-following law. If its exit time \(x_{n}^{ - 1} \left( L \right)\) is in a red phase, then we have \(x_{n}^{ - 1} \left( L \right) \in \left( {i_{n} C + G,\left( {i_{n} + 1} \right)C} \right]\) where \(i_{n} \in \left\{ {0,1, \cdots } \right\}\) denotes the cycle index for this red light violation. In this case, we set \(\dot{x}_{n} \left( t \right) = \min \left\{ {F^{{{\text{Gipp}}}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right),F^{{{\text{Gipp}}}} \left( {\dot{x}_{n} \left( t \right),0,L - x_{n} \left( t \right)} \right)} \right\}\) when \(t \le \left( {i_{n} + 1} \right)C\) and \(\dot{x}_{n} \left( t \right) = F^{{{\text{Gipp}}}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right)\) when \(t > \left( {i_{n} + 1} \right)C\). Otherwise, if \(x_{n}^{ - 1} \left( L \right)\) is green, then vehicle \(n\) only follows the Gipps’ car-following law. This case can be incorporated into the previous formulations by setting \({i}_{n}=-1\).

With all these operation rules, the system dynamics are described as follows:

$$\dot{x}_{n} \left( {t + \Delta t} \right) = \left\{ {\begin{array}{*{20}c} {{\text{min}}\left\{ {F^{\text{Gipp}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right), {\text{max}}\left\{ {\overline{v}_{n} ,\dot{x}_{n} \left( t \right) + d \times \Delta t} \right\}} \right\}, {\text{if }}x_{n} \left( t \right) \in \left[ {L_{1} ,L_{2} } \right];} \\ {F^{\text{Gipp}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right),{\text{ otherwise,}}} \\ \end{array} } \right.{\text{if }}n\space \;{\text{is a TCV}}{.}$$
(6)
$$\dot{x}_{n} \left( {t + \Delta t} \right) = \left\{ {\begin{array}{*{20}c} {{\text{min}}\left\{ {F^{\text{Gipp}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right),F^{\text{Gipp}} \left( {\dot{x}_{n} \left( t \right),0,L - x_{n} \left( t \right)} \right)} \right\}, {\text{if }}t \le \left( {i_{n} + 1} \right)C;} \\ {F^{\text{Gipp}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right),{\text{ otherwise,}}} \\ \end{array} } \right.{\text{if }}n\space \;{\text{is not a TCV}}{.}$$
(7)
$$x_{n} \left( {t + \Delta t} \right) = x_{n} \left( t \right) + \dot{x}_{n} \left( {t + \Delta t} \right) \times \Delta t.$$
(8)

3.1.2 Modified Newell’s model

A simplified Newell’s car-following model is proposed by (Newell 2002) as follows:

$$x_{n} \left( {t + \Delta t} \right) = F^{\text{Newell}} \left( {x_{n} \left( t \right),x_{n - 1} \left( t \right)} \right){\text{: = min}}\left\{ {x_{n - 1} \left( t \right) - s_{j} ,x_{n} \left( t \right) + v_{\text{max}} \times \Delta t} \right\}$$
(9)

where \({s}_{j}\) is the minimum safe distance, \(v_{\text{max}}\) is the maximum allowed speed, and \(\Delta t\) is the time gap.

For a specific vehicle, if it can run in a state with the maximum allowed speed \({v}_{\text{max}}\), we say it is in a free-flow state, while if it has to run by following its tightly previous vehicle, it is defined to be in the following state. As shown in Fig. 2, according to the simplified Newell’s car-following model, if vehicle \(n\) runs in the following state when it enters the control area, we can derive its trajectory in the cyan solid curve by simply translating the trajectory of vehicle \(n-1\). However, if vehicle \(n\) runs in the free-flow state when it enters, its trajectory can be depicted in the solid yellow curve. After running in the free flow state for a while, vehicle \(n\) will switch into the following state. As illustrated in Fig. 2, this state transition at the merging point between the solid yellow curve and cyan solid curve forms a "speed jump" rather than a smooth change, which is highlighted by a red circle. This phenomenon is not consistent with real-world situations.

Fig. 2
figure 2

Time–space trajectory diagram of “speed jump”

Full size image

Here, referring to the processing method of Liu et al. (2012), we utilize two quadratic functions to smooth the state transition by approximating the original function at the merging point. The time–space trajectory diagram after processing is shown in Fig. 3.

Fig. 3
figure 3

Time–space trajectory diagram after processing

Full size image

As is shown in Fig. 3, for vehicle \(n\), \({t}_{n}^{ms}\) and \({t}_{n}^{me}\) are the starting and ending timestamps of the merging process separately. Then, we can modify the simplified Newell’s model, called the M-Newell’s model,

$$\begin{aligned} x_{n} \left( {t + \Delta t} \right) = & F^{\text{M - Newell}} \left( {x_{n} \left( t \right),x_{n - 1} \left( t \right),t_{n}^{ms} ,t_{n}^{me} } \right) \\ = & \left\{ {\begin{array}{*{20}c} {\dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) \times \left( {t - x_{n}^{ - 1} \left( 0 \right)} \right) + 0.5 \times d \times \left( {t - x_{n}^{ - 1} \left( 0 \right)} \right)^{2} , if \; t \in \left[ {t_{n}^{ms} ,t_{n}^{me} } \right],} \\ {\text{min}\left\{ {x_{n - 1} \left( t \right) - s_{j} ,x_{n} \left( t \right) + v_{\text{max}} \times \Delta t} \right\}, \text{otherwise}.} \\ \end{array} } \right. \\ \end{aligned}$$
(10)

So, at the timestamp \({t}_{n}^{me}\), the speed and location of vehicle \(n\) should be equal to those derived by transferring the trajectory of vehicle \(n-1\),

$$\left\{ {\begin{array}{*{20}c} {\dot{x}_{n} \left( {t_{n}^{ms} } \right) + d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right) = \dot{x}_{n} \left( {t_{n}^{me} - \Delta t} \right),} \\ {\dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) \times \left( {t_{n}^{me} - x_{n}^{ - 1} \left( 0 \right)} \right) + 0.5 \times d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right)^{2} = x_{n - 1} \left( {t_{n}^{me} - \Delta t} \right) - s_{j} } \\ \end{array} } \right..$$
(11)

According to the simplified Newell’s rule, the \(n-1\) vehicle’s trajectory can be translated from the LEAD vehicle’s trajectory (the first vehicle in the platoon) when the \(n-1\) vehicle is at the following state, thus Eq. (11) can be rewritten as:

$$\left\{ {\begin{array}{*{20}c} {\dot{x}_{n} \left( {t_{n}^{ms} } \right) + d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right) = \dot{x}_{LEAD} \left( {t_{n}^{me} - n \times \Delta t} \right),} \\ {\dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) \times \left( {t_{n}^{me} - x_{n}^{ - 1} \left( 0 \right)} \right) + 0.5 \times d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right)^{2} = x_{\text{LEAD}} \left( {t_{n}^{me} - n \times \Delta t} \right) - n \times s_{j} } \\ \end{array} } \right..$$
(12)

To solve \(t_{n}^{ms}\) and \(t_{n}^{me}\) from Eq. (12), three possible situations are considered:

  1. (1)

    If \(t_{n}^{me} - n \times \Delta t \in t_{\text{LEAD1}}\), where \(t_{\text{LEAD1}}\) is the time interval of deceleration for the LEAD vehicle. Equation (12) can be rewritten as:

    $$\left\{ \begin{gathered} \dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) + d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right) = \dot{x}_{\text{LEAD}} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) + d \times \left( {t_{n}^{me} - n \times \Delta t - t_{\text{LEAD1}}^{ - } } \right) \hfill \\ \dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) \times \left( {t_{n}^{me} - x_{n}^{ - 1} \left( 0 \right)} \right) + 0.5 \times d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right)^{2} \hfill \\ = L_{1} + \dot{x}_{\text{LEAD}} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) \times \left( {t_{n}^{me} - n \times \Delta t - t_{\text{LEAD1}}^{ - } } \right) \hfill \\ + 0.5 \times d \times \left( {t_{n}^{me} - n \times \Delta t - t_{\text{LEAD1}}^{ - } } \right)^{2} - n \times s_{j} . \hfill \\ \end{gathered} \right.$$
    (13)

Here \({t}_{\text{LEAD1}}^{-}\) is the timestamp starting deceleration of the LEAD vehicle.

  1. (2)

    If \(t_{n}^{me} - n \times \Delta t \in t_{\text{LEAD2}}\), where \(t_{\text{LEAD2}}\) is the time interval of LEAD vehicle moving at the speed limit \(\overline{v}_{\text{LEAD}}\) before hitting location \(L_{2}\). Equation (12) can be rewritten as:

    $$\left\{ {\begin{array}{*{20}c} {\dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) + d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right) = \overline{v}_{\text{LEAD}} ,} \\ {\dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) \times \left( {t_{n}^{me} - x_{n}^{ - 1} \left( 0 \right)} \right) + 0.5 \times d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right)^{2} = L_{1} + \dot{x}_{\text{LEAD}} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) \times t_{\text{LEAD}1} } \\ { + 0.5 \times d \times t_{\text{LEAD}1}^{2} + \overline{v}_{\text{LEAD}} \times \left( {t_{n}^{me} - n \times \Delta t - t_{\text{LEAD}2}^{ - } } \right) - n \times s_{j} .} \\ \end{array} } \right.$$
    (14)

    Here \({t}_{\text{LEAD2}}^{-}\) is the timestamp starting cruising during \({t}_{\text{LEAD2}}\).

  1. (3)

    If \(t_{n}^{me} - n \times \Delta t \in t_{\text{LEAD3}}\), where \({t}_{\text{LEAD3}}\) is the time interval of acceleration for the LEAD vehicle. Equation (12) can be rewritten as:

    $$\left\{ {\begin{array}{*{20}c} {\dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) + d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right) = \overline{v}_{\text{LEAD}} + a \times \left( {t_{n}^{me} - n \times \Delta t - t_{\text{LEAD3}}^{ - } } \right),} \\ {\dot{x}_{n} \left( {x_{n}^{ - 1} \left( 0 \right)} \right) \times \left( {t_{n}^{me} - x_{n}^{ - 1} \left( 0 \right)} \right) + 0.5 \times d \times \left( {t_{n}^{me} - t_{n}^{ms} } \right)^{2} = } \\ {L_{1} + L_{2} + \overline{v}_{\text{LEAD}} \times \left( {t_{n}^{me} - n \times \Delta t - t_{\text{LEAD3}}^{ - } } \right) + 0.5 \times \left( {t_{n}^{me} - n \times \Delta t - t_{\text{LEAD3}}^{ - } } \right)^{2} - n \times s_{j} .} \\ \end{array} } \right.$$
    (15)

    Here \(t_{\text{LEAD}3}^{ - }\) is the timestamp starting acceleration of the LEAD vehicle.

In Eqs. (13)–(15), only \(t_{n}^{ms}\) and \(t_{n}^{me}\) are variables, so by solving Eqs. (13)–(15), we can get three combinations of \(t_{n}^{ms}\) and \(t_{n}^{me}\). However, in practice, only one situation among the three can actually happen, so only one of the three solutions makes sense (i.e., only one solved \(t_{n}^{me}\) is consistent with its assumption condition). Once get the starting timestamp \(t_{n}^{ms}\) and ending timestamp \(t_{n}^{me}\) of merging, we can derive the vehicle’s trajectory with no “speed jump”.

Thus, the system dynamics can be described with the M-Newell’s model as follows:

$$x_{n} \left( {t + \Delta t} \right) = \left\{ {\begin{array}{*{20}c} {{\text{min}}\left\{ {\begin{array}{*{20}c} {F^{\text{M - Newell}} \left( {x_{n} \left( t \right),x_{n - 1} \left( t \right),t_{n}^{ms} ,t_{n}^{me} } \right),} \\ {{\text{max}}\left\{ {x_{n} \left( t \right) + \overline{v}_{n} \times \Delta t,x_{n} \left( t \right) + \dot{x}_{n} \left( t \right) \times \Delta t + 0.5 \times d \times \Delta t^{2} } \right\}} \\ \end{array} } \right\}, {\text{if }}x_{n} \left( t \right) \in \left[ {L_{1} ,L_{2} } \right];} \\ {F^{\text{M - Newell}} \left( {x_{n} \left( t \right),x_{n - 1} \left( t \right),t_{n}^{ms} ,t_{n}^{me} } \right), {\text{ otherwise,}}} \\ \end{array} } \right.$$
$${\text{if }}n {\text{ is a TCV}}{.}$$
(16)
$$x_{n} \left( {t + \Delta t} \right) = \left\{ {\begin{array}{*{20}c} {{\text{min}}\left\{ {\begin{array}{*{20}c} {F^{\text{M - Newell}} \left( {x_{n} \left( t \right),x_{n - 1} \left( t \right),t_{n}^{ms} ,t_{n}^{me} } \right),} \\ {{\text{max}}\left\{ {x_{n} \left( t \right) + \overline{v}_{n} \times \Delta t,x_{n} \left( t \right) + \dot{x}_{n} \left( t \right) \times \Delta t + 0.5 \times d \times \Delta t^{2} } \right\}} \\ \end{array} } \right\}, {\text{if }}t \le \left( {i_{n} + 1} \right)C;} \\ {F^{\text{M - Newell}} \left( {x_{n} \left( t \right),x_{n - 1} \left( t \right),t_{n}^{ms} ,t_{n}^{me} } \right), {\text{ otherwise,}}} \\ \end{array} } \right.$$
$${\text{if }}n {\text{ is not a TCV}}{.}$$
(17)
$$\dot{x}_{n} \left( {t + \Delta t} \right) = {\text{max}}(0,\left( {x_{n} \left( {t + \Delta t} \right) - x_{n} \left( t \right)} \right)/\Delta t).$$
(18)
$$\ddot{x}_{n} \left( {t + \Delta t} \right) = \left( {\dot{x}_{n} \left( {t + \Delta t} \right) - \dot{x}_{n} \left( t \right)} \right)/\Delta t$$
(19)

3.1.3 IDM

The IDM (Treiber et al. 2000) is presented in the following equations:

$$\ddot{x}_{n} \left( t \right) = F^{\text{IDM}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right): = \text{max}\left\{ {d,a \cdot \left[ {1 - \left( {\frac{{\dot{x}_{n} \left( t \right)}}{{v_{\text{d}} }}} \right)^{\delta } - \left( {\frac{{s_{n}^{*} \left( t \right)}}{{s_{n} \left( t \right)}}} \right)^{2} } \right]} \right\},$$
(20)
$$s_{n}^{*} \left( t \right) = s_{j} + \text{max}\left\{ {0,\dot{x}_{n} \left( t \right) \cdot T + \frac{{\dot{x}_{n} \left( t \right) \cdot \left[ {\dot{x}_{n} \left( t \right) - \dot{x}_{n - 1} \left( t \right)} \right]}}{{2 \cdot \sqrt {a \cdot \left| b \right|} }}} \right\}$$
(21)

here \({v}_{\text{d}}\) is the desired speed, \(T\) is thse safe time headway (1.6 s), \(\delta\) is the acceleration exponent (4, dimensionless), \(b\) is the comfortable deceleration.

The model is divided into a “desired” acceleration on a free road, and a braking acceleration induced by the preceding vehicle. The acceleration on a free road decreases from the initial maximum acceleration \(a\) to zero while the vehicle’s speed approaches the specified speed limit, \(\ddot{x}_{n} \left( t \right) = a \cdot \left[ {1 - \left( {\dot{x}_{n} \left( t \right)/v_{\text{d}} } \right)^{\delta } } \right]\) is utilized to express the tendency of acceleration. The braking term is based on a comparison between the “desired dynamical distance” \({s}_{n}^{*}\), and the actual distance to the front vehicle. If the spacing is approximately equal to \({s}_{n}^{*}\), then the breaking acceleration part of the model essentially compensates for the free acceleration part, so the resulting acceleration is nearly zero.

And the system dynamics can be presented in the following equations:

$$\ddot{x}_{n} \left( t \right) = \left\{ {\begin{array}{*{20}c} {{\text{min}}\left\{ {F^{\text{IDM}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right), {\text{max}}\left\{ {0,d} \right\}} \right\}, {\text{if }}x_{n} \left( t \right) \in \left[ {L_{1} ,L_{2} } \right];} \\ {F^{\text{IDM}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right),{\text{ otherwise,}}} \\ \end{array} } \right.$$
$${\text{if }}n {\text{ is a TCV}}{.}$$
(22)
$$\ddot{x}_{n} \left( t \right) = \left\{ {\begin{array}{*{20}c} {{\text{min}}\left\{ {F^{\text{IDM}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right),F^{\text{IDM}} \left( {\dot{x}_{n} \left( t \right),0,L - x_{n} \left( t \right)} \right)} \right\}, {\text{if }}t \le \left( {i_{n} + 1} \right)C;} \\ {F^{\text{IDM}} \left( {\dot{x}_{n} \left( t \right),\dot{x}_{n - 1} \left( t \right),s_{n} \left( t \right)} \right),{\text{ otherwise,}}} \\ \end{array} } \right.$$
$${\text{if }}n {\text{ is not a TCV}}{.}$$
(23)
$$\dot{x}_{n} \left( {t + \Delta t} \right) = {\text{max}}(0,x_{n} \left( t \right) + \ddot{x}_{n} \left( t \right) \times \Delta t).$$
(24)
$$x_{n} \left( {t + \Delta t} \right) = x_{n} \left( t \right) + \dot{x}_{n} \left( {t + \Delta t} \right) \times \Delta t.$$
(25)

3.2 Deterministic IVSL optimization

Once the set of all trajectories \(\mathbf{x}={\left\{{x}_{n}\right\}}_{n\in N}\) is solved with car-following models, we use the following measures to evaluate the system's performance. Essentially, all trajectories \(\mathbf{x}={\left\{{x}_{n}\right\}}_{n\in N}\) can be uniquely solved once locations \({L}_{1}\) and \({L}_{2}\) are given, and we thus denote these trajectories as functionals \(\mathbf{x}\left({L}_{1},{L}_{2}\right)\). More details of the deterministic model can be found in Yao et al. (Yao et al. 2018). Therefore, all measures defined later depending on \(\mathbf{x}\) can be equivalently denoted as functions of these two locations.

Measure 1: Travel Time (\(\text{TT}\)). For \(N\) vehicles, their total travel time, which indicates the traffic efficiency, is computed as follows:

$$\text{TT}\left( {L_{1} ,L_{2} } \right) = \mathop \sum \limits_{n = 1}^{N} \left( {x_{n}^{ - 1} \left( L \right) - x_{n}^{ - 1} \left( 0 \right)} \right).$$
(26)

Measure 2: Fuel Consumption (\(\text{FC}\)). Based on the VT-micro vehicle fuel consumption and emission model (Ahn et al. 1999), we can measure total fuel consumption as follows:

$$\text{FC}\left( {L_{1} ,L_{2} } \right) = \mathop \sum \limits_{n = 1}^{N} \mathop \smallint \limits_{{x_{n}^{ - 1} \left( 0 \right)}}^{{x_{n}^{ - 1} \left( L \right)}} \text{exp}\left\{ {\mathop \sum \limits_{i = 0}^{3} \mathop \sum \limits_{j = 0}^{3} K_{ij} \left( {\dot{x}_{n} \left( t \right)} \right)^{i} \left( {\ddot{x}_{n} \left( t \right)} \right)^{j} } \right\}\text{d}t,$$
(27)

where \(i\) and \(j\) are the power indexes, \({K}_{ij}\) is a constant coefficient (Zegeye et al. 2013), \({\dot{x}}_{n}\left(t\right)\) means the first-order derivative of \({x}_{n}\left(t\right)\) (or velocity), and \({\ddot{x}}_{n}\left(t\right)\) means the second-order derivative of \({x}_{n}\left(t\right)\) (or acceleration). The coefficients matrix for \(\left\{{K}_{ij}\right\}\) is shown in Table 2.

Table 2 Coefficients for fuel consumption (the unit of fuel consumption, speed, and acceleration are in \(\mathbf{l}/\mathbf{s}\), \(\mathbf{m}/\mathbf{s}\), and \(\mathbf{m}/{\mathbf{s}}^{2}\), respectively)
Full size table

For a given vehicle arriving pattern, locations of two IVSLs should be optimized with total travel time (\(\text{TT}\)) and total fuel consumption (\(\text{FC}\)) measures of the proposed IVSL method. The overall performance objective \(\text{SC}\left({L}_{1},{L}_{2}\right)\) can be formulated as one of, a weighted summation of, or a vector of measures (26) and (27):

$$\text{SC}\left( {L_{1} ,L_{2} } \right) = \varphi_{\text{T}} \text{TT}\left( {L_{1} ,L_{2} } \right) + \varphi_{\text{F}} \text{FC}\left( {L_{1} ,L_{2} } \right)$$
(28)

Weights \({\varphi }_{\text{T}}\) and \({\varphi }_{\text{F}}\) can be simply obtained as the dollar value of unit travel time and unit fuel consumption. Then, the IVSL location optimization problem can be formulated as follows:

$${\text{min}}_{{L_{1} ,L_{2} }} \text{SC}\left( {L_{1} ,L_{2} } \right),$$
(29)

s.t.

$$L - \frac{{v_{\text{max}}^{2} }}{2a} \le L_{2} \le L$$
(30)
$$0 \le L_{1} \le L_{2} - \frac{{v_{\text{max}}^{2} }}{2d}.$$
(31)
$${\text{and}} \; {\space\mathbf{x}}\left( {L_{1} ,L_{2} } \right) = \left\{ {\begin{array}{*{20}c} {\left\{ {x_{n} } \right\}_{n \in \text{N, Gipps}} , \text{if subject to Equations} \left( 1 \right) - \left( 8 \right);} \\ {\left\{ {x_{n} } \right\}_{n \in \text{N, M - Newell}} , \text{if subject to Equations} \left( 9 \right) - \left( {19} \right);} \\ {\left\{ {x_{n} } \right\}_{n \in \text{N, IDM}} , \text{if subject to Equations} \left( {20} \right) - \left( {25} \right).} \\ \end{array} } \right.$$
(32)

Constraint (30) confines the location of IVSL2 to this effective range. Although a feasible \(L_{2}\) could be less than \(L - v_{\text{max}}^{2} /2a\), the oscillation of vehicle trajectory is dependent on the deceleration/acceleration. The influence of acceleration is the same (i.e., \(L_{2} \le L - v_{\text{max}}^{2} /2a\) and \(L_{2} = L - v_{\text{max}}^{2} /2a\) yield the same optimal objective value) when \(L_{2} \le L - v_{\text{max}}^{2} /2a\), and the performance of the objective is independent of location \(L_{2}\) whenever \(L_{2} \le L - v_{\text{max}}^{2} /2a\). Therefore, we just consider \({ }L_{2} \ge L - v_{\text{max}}^{2} /2a\) to simplify the formulation and improve optimization efficiency. Constraint (31) ensures there is enough spacing for a vehicle decelerating from \(v_{\text{max}}\) to any speed limit \(\overline{v}_{n}\) imposed by IVSL1 before hitting IVSL2, and IVSL1 is set along the segment \(L\). Constraint (32) means that the set of all the vehicles' trajectories \({\mathbf{x}}\left( {L_{1} ,L_{2} } \right) = \left\{ {x_{n} } \right\}_{n \in \text{N}}\) are generated by the simulation described above with different car-following models (i.e., Eqs. (1)–(8) for the Gipps’ model, Eqs. (9)–(19) for the M-Newell’s model, and Eqs. (20)–(25) for the IDM).

Since this optimization problem is not necessarily monotone or convex, we must numerically search for the optimal solution. To improve the search efficiency and solution quality, we apply the DIRECT method to search the global optimum instead of a linear search. A typical iteration of the DIRECT algorithm integrating the IVSL based simulation is illustrated in Fig. 4. For each candidate location of \({L}_{1}\) and \({L}_{2}\), the simulation is called to output the system performance measures. Then based on the evaluation of system performance, the DIRECT decides the next candidate \({L}_{1}\) and \({L}_{2}\) values by dividing Hyper-Rectangles. This iteration will be repeated until the near-optimal solution of \({L}_{1}\) and \({L}_{2}\) is found. Please refer to Jones (1993) for the detail of this algorithm.

Fig. 4
figure 4

A typical iteration of the DIRECT algorithm

Full size image

3.3 Two-stage stochastic IVSL optimization

However, the vehicle arriving pattern (i.e., \(\mathbf{h}={\left\{{h}_{n}\right\}}_{n=\mathrm{2,3},\dots ,\text{N}}\), arriving headway set) is uncertain in practice, we need to develop a two-stage stochastic IVSL optimization (IVSL-SO) model considering the uncertain fluctuation in \(\mathbf{h}\).

To better describe the uncertain vehicle arriving pattern, we assume \(\mathbf{h}\) as a random variable vector whose probability distribution is known based on previous work. And it should be pointed out that an intersection experiences different demand levels at different times (e.g., a simple classification can include sparse traffic, intermediate traffic, and dense traffic) during a whole day. To be simplified, the set of three traffic demand levels in a whole day can be denoted as \(\Omega =\left\{ST,IT,DT\right\}\) with a simple distribution: \(\text{Volume/Capacity}=0.32\) (sparse traffic) with probability \({p}_{ST}\), 0.68 (intermediate traffic) with probability \({p}_{IT}\) and 0.84 (dense traffic) with probability \({p}_{DT}\), where \(\text{Volume}\) is the traffic flow on a given road which can be described by \(\mathbf{h}\), \(\text{Capacity}\) is the maximum traffic flow on a given road, and \({p}_{ST}\), \({p}_{IT}\), \({p}_{DT}\) is the probability of sparse, intermediate, and dense traffic, respectively. And we also set \({p}_{ST}+{p}_{IT}+{p}_{DT}=1\).

According to May (1990), it is assumed that \(\mathbf{h}\) follows: 1) negative exponential distribution for sparse traffic; 2) Pearson Type III distribution for intermediate traffic; and 3) normal distribution for dense traffic. To compact the three different random distribution functions, the Weibull distribution (Weibull 1951) with different parameters is employed here. The probability density function of the Weibull distribution is given below:

$$f^{\text{weibull}} \left( {h;\lambda ,k} \right) = \left\{ {\begin{array}{*{20}c} {\frac{k}{\lambda }\left( {\frac{h}{\lambda }} \right)^{k - 1} e^{{ - \left( {h/\lambda } \right)^{k} }} , { }h \ge {0;}} \\ {0, { }h{ < 0}{\text{.}}} \\ \end{array} } \right.$$
(33)

Here \(h\) is the continuous headway, and we can discrete it to \(h_{n} = x_{n} \left( 0 \right) - x_{n - 1} \left( 0 \right), n = 2,3, \ldots ,N\), i.e., the arriving headway between vehicle \(n\) and \(n - 1\), \(k > 0\) is the shape parameter and \(\lambda > 0\) is the scale parameter of the distribution. According to Weibull, the mean value is \(\lambda {\Gamma }\left( {1 + 1/k} \right)\) where \({\Gamma }\left( \cdot \right)\) is the Gama function. Thus, when \(k = 0.5\) and \(\lambda = 2.125\), it is a negative exponential distribution (i.e., sparse traffic); when \(k = 1.5\) and \(\lambda = 1.0423\), it has a similar shape to the Pearson Type III distribution (i.e., intermediate traffic); and when \(k = 3\) and \(\lambda = 0.4267\), it is the same shape as the normal distribution (i.e., dense traffic).

Since stochastic vehicle arriving headway is incorporated, we assume \({\mathbf{h}}\) as the random vector with known distribution subjected to Eq. (33), and \({\mathbf{h}}^{\omega }\) as its realization under scenario \(\omega\).

Then, we extend the deterministic optimization model (29) into a two-stage stochastic optimization model. In the first stage master problem, we determine the location of \(L_{1}\) and \(L_{2}\), subject to the deterministic constraints on the allowable location setting range. In the second stage sub-problem, we evaluate the total travel time (\(\text{TT}\)) and the total fuel consumption (\(\text{FC}\)) measures of \(L_{1}\) and \(L_{2}\) under scenario \(\omega\).

The first stage of the stochastic optimization model considers the expected location of \({\text{EL}}_{1}\) and \({\text{EL}}_{2}\) is formulated as follows:

$${\text{min}}_{{\text{EL}_{1} ,\text{EL}_{2} }} E\left[ {Q\left( {L_{1}^{\omega } ,L_{2}^{\omega } ,{\mathbf{h}}^{\omega } } \right)} \right],$$
(34)

s.t.

$$L - \frac{{v_{\text{max}}^{2} }}{2a} \le \text{EL}_{2} \le L,$$
(35)
$$0 \le \text{EL}_{1} \le \text{EL}_{2} - \frac{{v_{\text{max}}^{2} }}{2d},$$
(36)

where \(\omega\) is a scenario that is included in \({\Omega }\) with three states, each state determines a distribution of \({\mathbf{h}}^{\omega }\); \(Q\left( {L_{1}^{\omega } ,L_{2}^{\omega } ,{\mathbf{h}}^{\omega } } \right)\) is the optimal objection function value of the second stage problem under the first stage solution (E \(\text{L}_{1}\),\(\text{EL}_{2}\)) and vehicle arriving headway set \({\mathbf{h}}\) under scenario \(\omega\); \(E\left[ {Q\left( {L_{1}^{\omega } ,L_{2}^{\omega } ,{\mathbf{h}}^{\omega } } \right)} \right]\) is the expectation value.

According to Eq. (33), the second stage scenario sub-problem can be formulated as follows:

$$Q\left( {L_{1}^{\omega } ,L_{2}^{\omega } ,{\mathbf{h}}^{\omega } } \right) = \text{min}_{{L_{1}^{\omega } ,L_{2}^{\omega } }} \text{SC}\left( {{\mathbf{x}}^{\omega } ,{\mathbf{h}}^{\omega } } \right),$$
(37)

s.t.

$$L - \frac{{v_{\text{max}}^{2} }}{2a} \le L_{2}^{\omega } \le L.$$
(38)
$$0 \le L_{1}^{\omega } \le L_{2}^{\omega } - \frac{{v_{\text{max}}^{2} }}{2d}.$$
(39)
$${\mathbf{x}}^{{\varvec{\omega}}} \left( {L_{1}^{\omega } ,L_{2}^{\omega } } \right) = \left\{ {x_{n}^{\omega } } \right\}_{n \in \text{N}, \text{M - Newell}} ,{ } {\text{subject to Equations }}\left( 9 \right) - \left( {19} \right).$$
(40)
$${\mathbf{h}}^{\omega } = \left\{ {h_{n}^{\omega } } \right\}_{n = 2,3, \ldots ,\text{N}} = \rho_{ST} \times f^{\text{weibull}} \left( {h;2.125,0.5} \right) + { }\rho_{IT} \times f^{\text{weibull}} \left( {h;1.0423,1.5} \right){ } + \rho_{DT} \times f^{\text{weibull}} \left( {h;0.4267,3} \right).$$
(41)
$$\rho_{ST} = \left\{ {\begin{array}{*{20}c} {1, \text{if}\; \omega \in ST;} \\ {0, \text{else}.} \\ \end{array} } \right.$$
(42)
$$\rho_{IT} = \left\{ {\begin{array}{*{20}c} {1, \text{if}\; \omega \in IT;} \\ {0, \text{else}.} \\ \end{array} } \right.$$
(43)
$$\rho_{DT} = \left\{ {\begin{array}{*{20}c} {1, \text{if}\; \omega \in DT;} \\ {0, \text{else}.} \\ \end{array} } \right.$$
(44)
$$ST = p_{ST} \times {\Omega }.$$
(45)
$$IT = p_{IT} \times {\Omega }.$$
(46)
$$DT = p_{DT} \times {\Omega }.$$
(47)
$${\Omega } = \left\{ {ST,IT,DT} \right\}.$$
(48)
$$p_{ST} + p_{IT} + p_{DT} = 1.$$
(49)

Here \(\left({L}_{1}^{\omega },{L}_{2}^{\omega }\right)\) is decision variables under scenario \(\omega\), and they must follow constraints (38) and (39). Constraint (40) depicts the set of all the vehicles' trajectories \({\mathbf{x}}^{{\varvec{\omega}}}\ge {\left\{{x}_{n}^{\omega }\right\}}_{n\in \text{N, M-Newell}}\) under scenario \(\omega ,\) which are generated by the simulation with the M-Newell’s model described in Sect. 3 (i.e., Equations \((9)-(19)\)). Constraints (41)-(49) describe the headway is generated by the Weibull distribution function with different parameters according to three different traffic states, i.e., sparse traffic, intermediate traffic, and dense traffic.

One solution method of the two-stage stochastic optimization is to replace the expectation in the master problem with a sample mean estimator with a smaller size than the original sample space. And a common approach to reducing the scenario set to manageable sample size is using the Monte Carlo simulation. In this paper, we generate a random sample and use the sample mean estimator to approximate the expectation in the original scenario space. Thus, the first stage master problem is approximated by the sample average,

$${\text{min}}_{{\overline{{L_{1} }} ,\overline{{L_{2} }} }} \frac{1}{M}\mathop \sum \limits_{j = 1}^{M} Q\left( {L_{1}^{{\varvec{j}}} ,L_{2}^{{\varvec{j}}} ,{\mathbf{h}}^{{\varvec{j}}} } \right),$$
(50)

s.t.,

$$L - \frac{{v_{\text{max}}^{2} }}{2a} \le \overline{{L_{2} }} \le L,$$
(51)
$$0 \le \overline{{L_{1} }} \le \overline{{L_{2} }} - \frac{{v_{\text{max}}^{2} }}{2d},$$
(52)

where \(M\) is the number of samples, \(\overline{{L_{1} }} = \frac{1}{M}\mathop \sum \limits_{j = 1}^{M} L_{1}^{{\varvec{j}}}\) and \(\overline{{L_{2} }} = \frac{1}{M}\mathop \sum \limits_{j = 1}^{M} L_{2}^{{\varvec{j}}}\) are approximated to the expected locations \(\text{EL}_{1}\) and \(\text{EL}_{2}\), respectively.

This is also known as the Sample Average Approximation method. A typical framework of the Monte-Carlo method with the DIRECT algorithm integrating the IVSL is illustrated in Fig. 5. And IVSL-SO is built on this framework to find the optimal sample average.

Fig. 5
figure 5

Framework of the IVSL-SO system

Full size image

4 Numerical experiments

In this section, we use numerical experiments to test the performance of the proposed IVSL models.

4.1 Deterministic optimization results

In this subsection, we use numerical experiments to test the performance of the deterministic IVSL with different car-following models. The parameters are set to the following values at default: \(L = 800\,{\text{m}}\), \(N = 60\), \(s_{j} = 10\,{\text{m}}\), \(\Delta t = 1 \, {\text{ sec}}\), \(v_{\text{max}} = 16\,{\text{m}}/{\text{s}}\), \(\dot{x}_{1} \left( {x_{1}^{ - 1} \left( 0 \right)} \right) = v_{\text{max}}\), \(a = 2\,{\text{m}}/{\text{s}}^{{2}}\), \(d = - 3\,{\text{m}}/{\text{s}}^{{2}}\), \(G = 50{\text{ sec}}\), \(C = 100{\text{ sec}}\), \(\varphi_{\text{T}} = 20\$ /{\text{hour}}\), \(\varphi_{\text{F}} = 1\$ /{\text{liter}}\),\({ }\tau = 1.2\,{\text{sec}}\), \(v_{\text{d}} = 16\,\text{m/s}\), \(T = 0.85\,\text{s}\), \(b = - 3\,{\text{m}}/{\text{s}}^{{2}}\), \(\delta = 4\) and the saturation time headway is 2 s (Yao et al. 2018).

Table 3 shows the comparison results for the IVSL with three different car-following models depending on the traffic levels. And the measurements include the system travel time (min), the system fuel consumption (liter), the system cost ($), and solution time (sec). In Table 3, IVSL-Gipps, IVSL-M-Newell, and IVSL-IDM represent the IVSL with the Gipps' model, the modified Newell's model, and the IDM, respectively. All three models are used in the joint optimization to optimize the system cost, combined with travel time and fuel consumption. Table 3 shows the results under control and without control (i.e., benchmark, shown after the slash symbol). And Fig. 6 presents the increment rate of the IVSL with three car-following models compared to the benchmark, respectively.

Table 3 Result comparison for three different car-following models
Full size table
Fig. 6
figure 6

The performance results of 4955 samples

Full size image

As shown in Table 3, with all three car-following models, the IVSL strategy can significantly improve both mobility and the environment as the traffic level increases. The effect of the IVSL-Gipps model is the most remarkable. This is probably because that the Gipps’ model has more parameters than the IDM and M-Newell’s model to reflect the vehicular dynamic, thus it can be more accurate to present the effect of the IVSL strategy. And the tendencies of the IVSL-Gipps model and IVSL-M-Newell model are approximately the same, but the IVSL-IDM is totally different. The results of the IVSL-IDM are a little higher than the IVSL-Gipps and IVSL-M-Newell in Table 3. This is probably due to the instability of the IDM, i.e., the oscillation of speed occurs in the free-flow state. Then we assume traffic level in a whole day follows a specific distribution (i.e., the probability of intermediate traffic, sparse traffic, and dense traffic are 1/2, 1/4, and 1/4, respectively). And we can calculate the average increment rate of the system cost per day, which is 10.96% for the IVSL-Gipps model, 8.59% for the IVSL-M-Newell model, and 8.05% for the IVSL-IDM. That means the IVSL-Gipps model has the best performance, and the IVSL-M-Newell model is a little worse than the IVSL-Gipps model. On the other hand, the IVSL-Gipps model and IVSL-IDM cost more solution time than the IVSL-M-Newell model (2–4 times). As explained above, models with more parameters may cost higher solution time.

4.2 Stochastic optimization results

This subsection conducts numerical experiments to test the performance of the stochastic IVSL (i.e., IVSL-SO). The parameters are set to the following values at default: \(L=800\mathrm{m}\), \(N=60\), \({s}_{j}=10\,\mathrm{m}\), \(\Delta t=1\mathrm{ sec}\), \({v}_{\text{max}}=16\,{\text{m}}/{\text{s}}\), \({\dot{x}}_{1}\left({x}_{1}^{-1}\left(0\right)\right)={v}_{\text{max}}\), \(a=2\,{\text{m}}/{\text{s}}^{2}\), \(d=-3\,{\text{m}}/{\text{s}}^{2}\), \(G=50\,\mathrm{sec}\), \(C=100\,\mathrm{sec}\), \({\varphi }_{\text{T}}=20\$/\mathrm{hour}\), \({\varphi }_{\text{F}}=1\$/\mathrm{liter}\), \({p}_{ST}=0.25\), \({p}_{IT}=0.5\), \({p}_{DT}=0.25\). In Sect. 4.2.1, we vary the sample number \(M\) from 100 to 5000 to test the performance of the Monte-Carlo method. And in Sect. 4.2.2, according to the analysis in Sect. 4.2.1, we set a suitable sample number to investigate the performance of the IVSL-SO.

4.2.1 Monte-Carlo sample test

This section investigates the performance of the Monte-Carlo method with the DIRECT algorithm integrating the IVSL for selecting a suitable sample range. Here, we firstly use the Monte-Carlo method to generate 5000 samples, and then the Pauta criterion (Xiao et al. 2021) is presented to remove the worse samples (the final sample number is 4955). The performance results of 4955 samples are shown in Fig. 6. It illustrates that IVSL1 is located between 0 and 100 m, IVSL2 is set in the range between 730 and 790 m, and the optimal value oscillates from 26 to 45$ after the proposed optimization. And the color probability distribution follows the probability distribution of the traffic demand level in a whole day, i.e., the hotter one denotes the dense traffic, the colder one represents the sparse traffic, and the more part shows the probability of the intermediate traffic. These results demonstrate that the sample average can present a credible value due to a short fluctuation range. Thus, we can select the IVSLs according to this value.

Next, Table 4 and Fig. 7 present the performance of the Monte-Carlo method with varied sample numbers (i.e., 100, 500, 1000, 4955). \(\overline{\text{TT} }\) is the sample average of the system travel time, \(\overline{\text{FC} }\) is the sample average of the system fuel consumption, \(\overline{\text{SC} }\) is the sample average of the system cost, \(\overline{{L }_{1}}\) is the sample average of the IVSL1’s location, and \(\overline{{L }_{2}}\) is the sample average of the IVSL2’s location. And SD_ \(\overline{\text{TT} }\), SD_ \(\overline{\text{FC} }\), SD_ \(\overline{\text{SC} }\), SD_ \(\overline{{L }_{1}}\), and SD_ \(\overline{{L }_{2}}\) denote the standard deviation of \(\overline{\text{TT} }\), \(\overline{\text{FC} }\), \(\overline{\text{SC} }\), \(\overline{{L }_{1}}\), and \(\overline{{L }_{2}}\), respectively. In the Monte-Carlo method, the sample average approximates the expected value.

Table 4 Performance of the Monte-Carlo method with various sample numbers
Full size table
Fig. 7
figure 7

Performance of the Monte-Carlo method with various sample numbers

Full size image

As shown in Table 4 and Fig. 7, the expected measurements (including travel time, fuel consumption, and joint system cost) and the expected locations (including IVSL1 and IVSL2) become stable as the sample number increases. And \(\overline{\text{TT} }\) is more susceptible than \(\overline{\text{FC} }\) and \(\overline{\text{SC} }\) to the varied sample number. In Fig. 7 b, \(\overline{{L }_{1}}\) is almost stable below 500 samples, and \(\overline{{L }_{2}}\) is obviously fluctuant when the sample number is under 500. This is probably because that \(\overline{{L }_{1}}\) is set to apply a speed limit value to the vehicle for deceleration, \(\overline{{L }_{2}}\) is set to remove the speed limit value for acceleration, and the acceleration operation has a more obvious effect on system measurements (especially travel time), and this makes sense why \(\overline{\text{TT} }\) is more susceptible. From the above analyses, the sample number is set as 500 in the following part.

4.2.2 Performance of the IVSL-SO

In this section, we set the sample number equal to 500 to investigate the performance of the IVSL-SO. According to subsection 4.2.1, we can obtain the sample average through the Monte-Carlo method. Then, we can apply random sampling (\(M\)=500) from the total sample set (the total sample number is 4955), which follows the distribution of \(\Omega =\left\{ST,IT,DT\right\}\). After a random sampling, a sample average is obtained. Subsequently, we set the sampling frequency as 50,000 to get the optimal sample average through the Monte-Carlo method.

The stochastic optimization of IVSL’s location requires a fast computation speed. As a result, IVSL-M-Newell model is chosen to be embedded in the Monte-Carlo simulation because it is the most computationally efficient without significant loss of system cost compared to the IVSL-Gipps model and IVSL-IDM.

Figure 8 shows the convergence result of the IVSL-SO. We can find that the convergence result is excellent. And after 50,000 sampling frequencies, the optimal expected system cost converges to stable as \({\overline{\text{SC}} }^{*}=\) 36.00$, and the optimal expected locations are \({\overline{{L }_{1}}}^{*}=\) 12.73 m and \({\overline{{L }_{2}}}^{*}=\) 762.51 m.

Fig. 8
figure 8

Convergence result of the IVSL-SO

Full size image

Table 5 shows the comparison results between the IVSL-SO and Benchmark (i.e., without control). After 10,000 sampling frequencies, the performance of the Benchmark is \({\overline{\text{SC}} }^{B}\)=40.62$, \({\overline{\text{FC}} }^{B}\)=9.67L and \({\overline{\text{TT}} }^{B}\)=80.15 min. Thus, the improvement in travel time, fuel consumption, and system cost is 8.95%, 19.11%, and 11.37%, respectively.

Table 5 Comparison result between the IVSL-SO and Benchmark
Full size table

Figure 9 shows the time–space trajectories with/without control under specific scenarios, i.e., sparse traffic, intermediate traffic, and dense traffic. Overall, we can see that the IVSL-SO can eliminate full stops as expected no matter which demand level is loaded. Vehicles inevitably suffer from full stops when no extra control is imposed on the vehicle platoon except for the regular signal control (i.e., Benchmark). Figure 9 a, b, and cshow that increasing the demand level will incur more full stops, which is intuitive since longer waiting in front of the red signal results from a higher demand level. Especially in Fig. 9 c, stop times increase to 2 or 3. Whereas, we see that the IVSL-SO can well balance trajectory smoothing and queuing adjustment such that all vehicles can drive smoothly to the extent of not having full stops. This verifies the efficiency of the IVSL-SO system.

Fig. 9
figure 9

Time–space trajectories with/without control under different scenarios

Full size image

5 Conclusions

This paper first investigates the impacts of different car-following models with the deterministic IVSL strategy in a CV environment at a signalized intersection. Then, we propose a stochastic IVSL model as a two-stage optimization problem considering the stochastic vehicle arriving patterns. We apply the Monte Carlo framework with the DIRECT algorithm to solve this problem. A set of numerical experiments is conducted to test the model performance. Regarding different car-following models (i.e., the Gipps’ model, modified Newell’s model, and IDM), results show that the Gipps’ model yields better results than the other models. This is probably because the safety features are considered in the Gipp’s model, which is more realistic. Further, the stochastic IVSL model is verified to improve 8.95% travel time, 19.11% fuel consumption, and 11.37% system cost compared to the benchmark without speed control.

In real-world applications, the proposed IVSL system requires a CV environment where V2X communications (e.g., dedicated short-range communication [DSRC] and cellular vehicle-to-everything [C-V2X]) are enabled. Two virtual control points are set with the proposed stochastic optimization model and historical vehicle arriving patterns. Once a CV reaches the control point, it would send an advisory speed to the CV, and thus the CV can smooth its trajectory. Therefore, the IVSL system can be easily implemented with existing technologies and configurated per requirements (e.g., different geometry and traffic conditions).

Although the proposed model yields valuable benefits regarding travel time, fuel consumption, and system cost, several research directions can be extended from this work. First, this paper only considers the longitudinal motions in a single-lane road. The lateral motions (e.g., lane changing behaviors) should be considered in the future. Second, this paper only considers a small-scale problem with an isolated signalized intersection. It is valuable to investigate the speed control strategy on a larger scale (e.g., corridors and networks). Third, with the development of new energy vehicles (e.g., electrical vehicles), the energy performance might change and is not accurate with traditional fuel consumption models. It would be interesting to investigate the IVSL performance in new energy vehicles with new models and field data.