1 Introduction

Rockburst as a result of induced seismic activity of the rock mass are commonly encountered phenomena in the world mining operations. They are recorded wherever specific geomechanical conditions occur with high-level stresses and considerable strength of rocks. Therefore, rockburst and seismic tremors induced by mining activity are observed in five continents, in countries where deep underground mining is performed. It should be noted that in many mining basins, in which the mining works have been performed for a long period of time, rockburst and mining tremors appeared when the certain depth of operation typical of specific region was exceeded. This includes mainly Coeur d’Alene basin in the US, South African gold-bearing basins, Kolar Gold Fields in India, Ostrava-Karviná coal basin in the Czech Republic as well as the Upper Silesian Coal Basin in Poland. The high-energy tremors occur also in the Legnica-Glogow Copper Mining District (LGOM – Poland), where the copper sources are located within strong roof rocks deposits (Kidybiński 2003).

Over the years, certain regularities in the appearance of phenomena such as rockburst and mining tremors have been established. Many studies have been conducted in order to look for temporal or spatial patterns of mining-induced seismic event occurrences (Trifu et al. 1993; Gibowicz 1997; Kijko 1997). Due to the complexity of the problem, however, the physical mechanism of interactions has not yet been established. The occurrence of rockburst and mining tremors results from changes in the stress field in the rock mass in proximity of mine excavations (Orlecka-Sikora 2009). Even a small stress anomaly can cause seismic events under high pre-stressed conditions (Gibowicz and Kijko 1994). The influence of a stress diffusion mechanism on the stronger events occurrence was also identified in the Creighton Mine in Canada (Marsan et al. 1999). Studies on mining-related tremors in deep South African gold mines revealed that their incidence is often affected by stress, strain rate, and the proximity of specific mining and geological features (Kgarume et al. 2010). The research conducted on seismic hazard in Borynia-Zofiowka-Jastrzebie Ruch Zofiowka colliery in Poland exposed that the tremors were caused by displacement of roof layers over a selected goaf space as well as natural stresses in the rock mass originated from the fault zones in the vicinity of considered longwall (Stec 2015).

Today, with advances in technology and knowledge on seismic, a number of approaches and techniques are used in order to eliminate the tremors and limit their consequences. In the face of a great hazard resulting from the rock mass behaviour, adequate tremor prevention is crucial in the actions against dynamic manifestation of rock pressure. The conclusion is that the identification of conditions in the rock mass influencing the occurrence of seismic hazard is extremely important as it would allow to appropriate manipulation of parameters of mining systems and ensure the safest variant of mining method.

2 Seismic activity in LGOM

The copper ore deposit exploited by KGHM Polish Copper Ltd. is located in Fore-Sudetic Monocline within the LGOM of south-western part of Poland. Copper ore extraction in Poland is concentrated in three underground mines: Lubin, Rudna and Polkowice-Sieroszowice. The depth of deposits in LGOM ranges from 600 m in Lubin mine, to more than 1100 m in Rudna mine. Copper minerals are hosted by three main lithological Zechstein rock types: sandstone, shale and dolomite. Generally, the rock mass in the area of copper mines in LGOM is characterized by a layered structure. In a majority of the area, the thick dolomite layer occurs directly above the excavations roof. The dolomite rocks are characterized by a relatively high strength and small deformability. In the floor instead the weaker sandstone rocks are deposited. The copper ore exploitation is conducted by the room-and-pillar mining system with adopting the technique using the phenomenon of natural roof settlement. The principle of this solution is to eliminate the extracted voids by the deflection of the roof and prop it on the residual technological pillars as well as by self-acting roof fall (Butra et al. 1996).

Fifty years of copper ore exploitation in Fore-Sudetic Monocline and the extraction of large areas of the deposits make mining operations increasingly difficult to conduct due to the constraint mining conditions. In addition, adopted structure of the mines where the excavations are carried on in the deposit layer as well as the applied technological rock bump prevention, which consists in a roof deflection of the transport excavations, lead to more frequent cases of separation of the deposit remnants surrounded by goaf and yielded zones. Moreover, in mining panels difficult geological and mining conditions often occur disturbing the continuous advance of mining faces.

Generally, it can be assumed that there are two basic groups of measurable factors influencing the deformation and stress state in the rock mass constituting the vicinity of operated deposit:

  1. (1)

    Mining parameters including the length and width of the pillars, the geometry of the excavations, the height and the length of the mining face, the technology of excavation liquidation, etc.,

  2. (2)

    Rock mass properties associated with the spatial configuration of individual rock layers, their thickness, strength, deformability, discontinuities characteristics, the depth of the mining operations, etc.

A major natural hazard associated with LGOM mining is occurrence of dynamic phenomena, physically observed as seismic tremors. Some of them generate effects in the form of relaxations or bumps. The number of events with the adverse consequences has not been successfully reduced radically so far, mainly due to the constantly insufficient knowledge about the nature of the phenomenon and the relatively limited capacity of computing devices to handle with the extended rock mass calculation models.

The primary objective of this study is to answer the question, which of the factors considered as “influencing” the dynamic phenomena occurrence in copper mines have a statistically significant effect on seismic activity and to what extent. Using the general linear regression model procedure, an attempt has been made to quantify the impact of different parameters on seismic activity based on historical data from 2000 to 2010 concerned with the dynamic phenomena recorded in different mining panels in Rudna mine.

3 Introduction to general linear model

The linear regression model was developed in the late 19th century, and the correlational methods shortly thereafter. They both were derived from the theory of algebraic invariants which are quantities remaining unchanged under algebraic transformations. Regression and correlation methods constitute the basis for the general linear model (GLM). The general linear model, in detail, may be treated as an extension of linear multiple regression for a single dependent variable. The difference between them comprises the number of analyzed dependent variables and unknown regression coefficients which have to be evaluated. This can be presented in matrix notation as:

$$\left[ {\begin{array}{*{20}c} {y_{1,1} } & {y_{1,2} } & {\begin{array}{*{20}c} \cdots & {y_{1,k} } \\ \end{array} } \\ {y_{2,1} } & {y_{2,2} } & {\begin{array}{*{20}c} \cdots & {y_{2,k} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {y_{n,1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {y_{n,2} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \cdots & {y_{n,k} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & {x_{1,1} } & {\begin{array}{*{20}c} \cdots & {x_{1,p - 1} } \\ \end{array} } \\ 1 & {x_{2,1} } & {\begin{array}{*{20}c} \cdots & {x_{2,p - 1} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ 1 \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {x_{n,1} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \cdots & {x_{n,p - 1} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \quad \times \left[ {\begin{array}{*{20}c} {\beta_{0,1} } & {\beta_{0,2} } & {\begin{array}{*{20}c} \cdots & {\beta_{0,k} } \\ \end{array} } \\ {\beta_{1,1} } & {\beta_{1,2} } & {\begin{array}{*{20}c} \cdots & {\beta_{1,k} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\beta_{p - 1,1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\beta_{p - 1,2} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \cdots & {x\beta_{p - 1,k} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \quad + \left[ {\begin{array}{*{20}c} {\varepsilon_{1,1} } & {\varepsilon_{1,2} } & {\begin{array}{*{20}c} \cdots & {\varepsilon_{1,k} } \\ \end{array} } \\ {\varepsilon_{2,1} } & {\varepsilon_{2,2} } & {\begin{array}{*{20}c} \cdots & {\varepsilon_{2,k} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\varepsilon_{n,1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\varepsilon_{n,2} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \cdots & {\varepsilon_{n,k} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(1)

Indeed, the Y vector of n observations of a single Y variable in linear multiple regression is replaced by a Y-matrix of n observations of k different Y variables, and, similarly, the β vector of regression coefficients is transformed. These changes yield the so-called multivariate regression model (StatSoft 2013).

Generally, there are some assumptions making that the general linear model goes a step further than the multivariate regression model as well as the multiple regression model, since it is able to consider:

  1. (1)

    The existence of linear relationships between independent variables X,

  2. (2)

    The existence of linear transformations or combinations of many dependent variables Y,

  3. (3)

    The qualitative predictors in the model.

A one-way analysis of variance (ANOVA) allows identifying the differences between the means of two or more groups. Therefore, the one-way ANOVA verifies the impact of one factor (divided on many levels) on the values of examined dependent variable. The analysis of variance is subjected to the assumptions of normality of distributions as well as homogeneity of variance for all groups of the considered factor. In the case of failure to meet the ANOVA requirements, the non-parametric tests should be applied (Scheffé 1959).

GLM is a kind of ANOVA procedure. The null hypothesis is verified concerning the effect of different independent variables on the group means of a dependent variable. Therefore, the calculations are performed using a least squares regression approach to describe the statistical relationship between one or more predictors and a response variable. A correct general linear model operates under general assumptions concerning the population of error values ε (residuals). They must have an expected value of zero and constant variance. Moreover, there is an assumption on uncorrelated and normally distributed error values (Draper and Smith 1998).

4 Background of the analysis

Based on historical data from 2000 to 2010 on the dynamic phenomena recorded in different mining panels in Rudna mine, an attempt has been made to verify the common impact of factors (further called predictors or independent variables), including the depth of deposit (H), the thickness of a dolomite-limestone layer in the roof (Ca1), the presence of goaf in the vicinity of operating mining panels (G) and the direction of mining face advance (A), on seismic activity using a general linear model procedure. In practice, the seismic activity has been examined in terms of logarithms of the average annual energy of tremors ln(E tA ), number of tremors ln(N t ) and total energy of tremors ln(E tT ), which will be called the dependent variables.

Some of the factors considered as “influencing” the dynamic phenomena occurrence in copper mines were represented as the quantitative discrete predictors, including the presence of goaf in the vicinity of operating mining panels (G) and the direction of mining face advance (A). The different classes have been identified for them. In the other hand, the predictors of the depth of deposit (H) and the thickness of a dolomite-limestone layer in the roof (Ca1) were taken as the quantitative continuous variables.

The mining situation in the adjacent vicinity has been described by numbers, depending on the mined-areas location, as follows.:

  1. (1)

    G = 1, when the mining panel has only one border with goaf (Fig. 1a),

    Fig. 1
    figure 1

    The goaf situation in selected mining panels in Rudna mine. a Back border with goaf (G = 1), b Back and right border with goaf (G = 2), c Back, left and right border with goaf (G = 3)

    Full size image
  2. (2)

    G = 2, when the mining panel has two borders with goaf (Fig. 1b),

  3. (3)

    G = 3, when the mining panel has three borders with goaf (Fig. 1c).

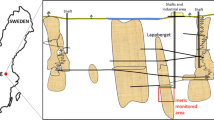
Similarly, the direction of mining face advance (Fig. 2) may be represented by numbers providing the angle ranges as:

Fig. 2
figure 2

The method of determination of the azimuth angle α of the direction of the mining face advance against the backdrop of the orthogonal direction system of development excavations in Rudna mine

Full size image
  1. (1)

    A = 0, when the azimuth α of face advance is in the range of 0°–90°,

  2. (2)

    A = 1, when the azimuth α of face advance is in the range of 91°–180°,

  3. (3)

    A = 2, when the azimuth α of face advance is in the range of 181°–270°,

  4. (4)

    A = 3, when the azimuth of face advance is in the range of 271°–360°.

The results of primary stress measurements conducted in Rudna mine (Fabich and Pytel 2003–2004; Butra et al. 2013) indicate that the vector of dominant component of normal stress acts in the 300°–340° azimuth. It is thought-provoking that this range of azimuth values and the advance direction of the majority of mining faces in Rudna mine are coincident (Fig. 2). This can be explained by the geological structure of the copper deposit as well as by its dip direction. Moreover, the adverse consequence of the orthogonal direction system of development excavations (Fig. 2) may be high level of seismic activity in this region which could be much lower if the in situ stress distribution was taken into account at the design stage of Rudna mine 40 years ago.

5 Results of the analysis

For the purpose of the analysis, three linear regression models have been considered (Eqs. (2)–(4)). In each case, the impact of the same set of predictors on different dependent variables was analysed, as follows:

$$ln\left( {E_{tA} } \right) = \beta_{01} + \beta_{11} A + \beta_{21} G + \beta_{31} Ca1 + \beta_{41} H + \varepsilon$$
(2)
$$ln\left( {N_{t} } \right) = \beta_{02} + \beta_{12} A + \beta_{22} G + \beta_{32} Ca1 + \beta_{42} H + \varepsilon$$
(3)
$$ln\left( {E_{tT} } \right) = \beta_{03} + \beta_{13} A + \beta_{23} G + \beta_{33} Ca1 + \beta_{43} H + \varepsilon$$
(4)

Where, \(ln\left( {E_{tA} } \right),\) ln(N t ), ln(E tT ) are dependent variables: logarithms of the average energy of tremors, number of tremors and total energy of tremors, respectively; β 01, β 02, β 03 are intercept; β 11, β 12, β 13, β 21, β 22, β 23, β 31, β 32, β 33, β 41, β 42, β 43 are parameters; \(A, G, Ca1, H\) are predictors: the direction of mining face advance, the goaf situation, thickness of a dolomite-limestone layer in the roof and depth of deposit, respectively; ɛ is error term (difference between the observation and the model).

The solution of equations above is the vector of parameter estimates β 0, β 1, β 2, β 3, β 4 called regression coefficients b 0, b 1, b 2, b 3, b 4. They are estimated by commonly used the least squares method (Table 3). It allows to determine the regression coefficients by minimizing the sum of squared residuals (deviations). Their values enable to draw conclusions regarding the impact of the independent variable (for which the coefficient was estimated) on the dependent one. The regression coefficient indicates about how many units of dependent variable change when the independent continuous variable changes by one unit. When considering variable is discrete, the regression coefficient estimated for it is then the average difference in the dependent variable between the category of the independent variable representing the reference group and the other categories. In the present case there are two discrete variables: A and G, wherein the reference groups for them are A = 3 and G = 3.

In order to determine which predictors in the considered models are statistically significant a stepwise regression analysis with backward elimination was performed. In this method, the consecutive predictors are removed from the model which includes all variables taken for analysis. In each step, the significance of remaining predictors is assessed and only of them, with the least impact on the dependent variable, is removed from the model. In this way, the objective is to obtain the best model.

Quality of the built linear regression model can be assessed by estimating the significance of all the variables in the model by analysis of variance (F-test). This test verifies three equivalent hypotheses:

$${\mathcal{H}}_{0} : all \beta_{i} = 0, {\mathcal{H}}_{1} : \beta_{i} \ne 0$$
$${\mathcal{H}}_{0} : R^{2} = 0, {\mathcal{H}}_{1} : R^{2} \ne 0$$
$${\mathcal{H}}_{0} :linearity of the relationship = 0, {\mathcal{H}}_{1} : lack of linearity$$

A test statistic in the F-test is as follows (Fisher 1924):

$$F = \frac{{E_{MS} }}{{R_{MS} }}$$
(5)

where, \(E_{MS} = \frac{{E_{SS} }}{{df_{E} }}\) is mean squares explained by the model; \(R_{MS} = \frac{{R_{SS} }}{{df_{R} }}\) is the residual mean squares; df E  = k, df R  = n − (k + 1) is degrees of freedom.

The statistic has the Snedecor’s F-distribution with df E and df R degrees of freedom. A p-value determined on the basis of the test statistic is compared with a significance level α:

$${\text{if}}\,p \le \alpha \text{ } \to {\mathcal{H}}_{0}\, {\text{is rejected in favour of}}\, {\mathcal{H}}_{1}$$
$${\text{if}}\,p > \alpha \to {\text{there is no basis to reject}}\,{ \mathcal{H}}_{0} .$$

Traditionally, the significance level α, also called the type I error rate, is set to 0.05 (5 %), meaning that it is acceptable to have a 5 % probability of rejecting the null hypothesis given that it is true (Fisher 1925).

6 Discussion and results

Only two models (Eqs. (3) and (4)) comply with the requirement on statistical significance of a linear relationship based on the results of an F-test (Table 1). The F-statistic values greater than 1 and, at the same time, p-values less than the adopted significance level p = 0.05 confirm the significant linear relationships of models with logarithm of the number of tremors and total energy of tremors as the dependent variables. The model of logarithm of the average annual energy of tremors is not statistically significant so it will not be further considered. Adjusted R-squared values equal to 0.27 and 0.23 indicate that only 27 % and 23 % of variation of the dependent variables as the number of tremors and total energy of tremors, respectively, can be explained by the considered predictors (Table 1).

Table 1 The significance test for models
Full size table

In order to know which of the selected independent variables have the most influence on the results of the dependent variables, the partial eta-squared values have been evaluated (Table 2). It is appropriate measure in the case of a multivariate analysis. In the model of ln(N t ) the partial eta-squared is the greatest for the goaf (G) factor (12 %) and for azimuth (A) factor (10 %). This indicates that they have the most influence on the number of tremors. However, the azimuth factor is not statistically significant since the probability value of an F-test is greater than the adopted significance level p = 0.05. The statistically significant main effect of Ca1 factor means that examined thickness values of a dolomite and limestone layer in the roof differ with respect to the average number of tremors. The results indicate that only the G and Ca1 factors affect the observed number of tremors in examined region. The Ca1 factor is also able to explain 8 % of the results of the dependent variable on the basis of the partial eta-squared value.

Table 2 Univariate significance tests and size of effects for significant models of ln(N t ) and ln(E tT )
Full size table

In the model of ln(E tT ) the statistical significance was confirmed for the azimuth (A) and goaf (G) factors (Table 2). These predictors are able to explain 16 % and 13 % of the results of the dependent variable, respectively. To sum up, the direction of mining face advance as well as the goaf situation in the vicinity of the mining panel have the most influence on the total energy of tremors.

The detailed assessment of discrete significant parameters in the model of number of tremors indicates that statistics significant at the 0.05 level was achieved for the azimuth (A) factor at the first-level (range between 91°–180°), for the goaf (G) factor at the first-level (the mining panel has one border with goaf) as well as for the Ca1 factor (Table 3). In the model of total energy of tremors the statistically significant are the A factor at the first-level and the G factor at the first-level (Table 3). The means in these groups differ significantly from at least one mean in other groups.

Table 3 Assessment of parameters in the models
Full size table

It is widely known (Draper and Smith 1998; Kutner et al. 2005) that the general linear model should operate under general requirements concerning the population of residuals. The assumption of the equality of residual variances is called homoscedasticity. It is verified using, inter alia, the plot of residuals versus corresponding predicted values (Fig. 3). The distribution of points scattered randomly (constant spread) about 0 (constant mean) is indicative of homoscedasticity of residuals (Faraway 2005). The verification of normality assumption is based on the normal probability plot of residuals (Fig. 4) as well as the results of Shapiro–Wilk test (Table 4). The residuals are plotted as a function of the corresponding normal order statistic medians, defined as (Chambers et al. 1983):

Fig. 3
figure 3

Residuals versus predicted plots—both shows that the residuals and the fitted values are uncorrelated (mean and spread of points are approximately constant)

Full size image
Fig. 4
figure 4

Normality plots of residuals—on both the points form a nearly linear pattern which indicates a good fit to the normal distribution

Full size image
Table 4 Verification of GLM assumptions
Full size table
$$N_{i} = G(U_{i} )$$
(6)

where, U i is the uniform order statistic medians; G is the percent point function of the normal distribution (inverse of the cumulative distribution function).

A straight line is added as a reference line. The more observations deviate from the straight line the more their distribution differs from normality.

Based on the location of points on the plots in relation to the fitted straight line, one can conclude that the distribution of residuals does not differ significantly from the normal distribution. The p-values from the Shapiro–Wilk test greater than the chosen alpha level have confirmed that there is no reason to reject the hypothesis of normally distributed residuals of significant models of ln(N t ) and ln(E tT ).

7 Summary and conclusions

On the basis of the above analyses, it is concluded that, the variance within each group of the dependent variables is the same based on the residuals versus predicted plots. The normality assumption implies that the dependent variables are normally distributed within each group as well. Actually it reveals the fulfilment of the GLM assumptions. Due to this, the obtained models of number of tremors and total energy of tremors are considered to be correct.

They predictive power (ability to generate credible predictions) of ln(N t ) and ln(E tT ) models is low based on the adjusted coefficient of determination. The adjusted R-squared values indicate that only 27 % and 23 % of variation of the dependent variables as the number of tremors and total energy of tremors, respectively, can be explained by the considered predictors.

The results show that the goaf (G) and Ca1 factors are the most influencing in terms of the observed number of tremors in examined region. The azimuth of mining face advance in the range of 91°–180°, the one-side vicinity of goaf as well as the thickness of a dolomite-limestone layer in the roof determine the number of tremors. However, the azimuth (A) factor is not statistically significant in this case.

The azimuth (A) and goaf (G) factors have the most influence on the total energy of tremors. It is affected by azimuth of mining face advance in the range of 91°–180° as well as the one-side vicinity of goaf in the examined region.

To sum up, the direction of mining face advance as well as the goaf situation in the vicinity of the mining panel are of the greatest interest in the case of the seismic activity. It can be assumed that the appropriate manipulation of parameters of mining systems should ensure the safest variant of mining method under specific geological and mining conditions.