1 Introduction

Methane emission is a primary cause of disasters in Chinese coal mines. According to statistics (Zhou and Lin 1999), gas accidents in general are the most likely among all accident types to take place, as well as cause most damages. However, with advancements in science and technology, methane can now be turned into a clean resource if it is utilized well, e.g. by purification, and thus both economic and environmental benefits can be achieved. Presently, methane drainage is mainly used to control the concentration in goafs, so as to secure the safety of the workface and achieve methane recycling. In recent years, with mining depth increasing and the implementation of more complex and fully-mechanized caving mining processes, the methane emission problem in goafs has become increasingly serious because of the substantial fracturing of rock strata that develops around stopes. In closed-range mines, except for self-regulated coal seams, methane always concentrates in neighboring coal seams because methane there can flow to stopes along the fracture between coal seam groups. In caving regions, methane flow is very complex because of the air leakage and methane sources. This problem demands an appropriate design of methane drainage in goafs.

In academic circles at present, for goaf closure, researchers mainly perform a theoretical analysis of the fissure development of overlying rock strata based on the “three belts” assumption. Furthermore, by identifying drill-hole locations, or through numerical simulation, they directly remake the gas mitigation law and predict drainage effects under the design scheme. Several studies have summarized the continuous “O” circle characteristics of goaf roofs and the variation features in the junction of two adjacent “O” circles. Consequently, the rational design of the height and spacing of drill-hole sites, as well as the length of drill holes, has been discussed (Zhou and Lin 1999; Zhang and Hou 2008). Li et al. (2004) calculated the goaf flow parameters under tailgate methane drainage conditions to determine a reasonable drainage flux with a 2D model. Hu et al. (2007) and Jin and Yao (2010) numerically solved the 3D methane migration law in goafs, which is in better agreement with that of the 2D assumption. Wang (2011) carried out a theoretical study on methane flow laws when stereoscopic methane drainage between short distance coal seam groups was applied; however, how the methane distribution after drainage changed was not examined. Yao et al. (2010) exploited a 3D numerical simulation of goaf methane distribution under high-level drill-hole conditions, but the configuration of the drill hole in the model was too simple to reflect the true situation.

On the basis of the above research outcomes, the present study concentrates on drainage results of a high-level drill hole in a goaf using a numerical method. A physical model is established according to the site conditions, which includes a sector drill-hole arrangement at different heights. Hence, the simulation results that reflect the methane distribution are used to validate a rational drill arrangement. Thus, the theoretical conclusions can be verified by site-measured data and serve in practical applications.

2 Methane migration features and their mathematical description

Overlying rock strata fracture and bend along the face advancement, so abundant cracks are produced around stope wall rock. The primitive coal seam can release methane to adjacent coal seams along the release fracture because of the relatively small range between short-distance coal seam groups. Owing to ventilation and relatively low pressure at the workface, a proportion of the methane spreads to goafs under the methane pressure in the coal seam and mixes with the methane released by the leftover coal in the goaf, thus entering the workface via carriage by air leakage. The methane seepage velocity in this process is so low that most studies on methane migration are established on the basis of the Darcy and Fick law. Then, because of its low velocity, the convection effect can be ignored. The steady seepage model can be simplified in the form below after considering gravity in the vertical direction (Liu 2006):

$$\Delta p + \rho g = - \mu \frac{v}{k}$$
(1)

where the first term on the left represents the dynamics produced by the pressure difference, the second term is gravity, and the term on the right-hand side is viscosity loss. Specifically, \(\Delta p\) is the air leakage pressure determined by the air leakage velocity and resistance; \(\rho\) is the gas density (kg/m3); \(k\) is the permeability of the coal rock, which can be calculated by the Carmen–Kozeny relationship (Yang et al. 2009a, b), \(k = \frac{{D_{P}^{2} \varepsilon^{3} }}{{150(1 - \varepsilon )^{2} }}\), where \(\varepsilon\) is porosity and \(D_{P}\) is the particle size in the goaf (mm); \(\mu\) is the dynamic viscosity of air (\(1.7894\; \times \;10^{ - 5} \;{\text{Pa}}/{\text{s}}\)); and \(v\) is the gas seepage velocity (m/s).

Apart from the above model, the control equation system should also add a continuous equation and diffuse-seepage equation reflecting the change in methane regulation in the simulation process:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0$$
(2)
$$\frac{{\partial C_{a} u}}{\partial x} + \frac{{\partial C_{a} v}}{\partial y} + \frac{{\partial C_{a} w}}{\partial z} - D_\alpha\left(\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}\right) = S$$
(3)

where \(u\), \(v\) and \(w\) are the gas seepage velocities in three directions (m/s), \(C_{a}\) is the mass fraction of methane, \(D_{a}\) is the diffuse coefficient of methane (m2/s), and \(S\) is the methane emission intensity (kg/(m3·s)). The model should include a two-equation model of κ and ε if the analysis object is expanded to the whole stope containing the face, goaf, and the intake or return airway. The coupled equations must be simultaneously solved and their specific expression is not discussed further.

3 Experiment site description and physical model establishment

The calculation example is taken from the prototype of a protective layer mining face of one coal mine that has a 2 m high low-methane coal seam. This face uses a “U” type ventilation at about 2,100 m3/min with 320 m length and 160 m width. Because the protected seam at high methane pressure exits over 28 m from the floor of the mining face, abundant methane from the protected seam flows towards the goaf along the cracking roof rock in the mine’s coal seam. For the control of methane emission from the goaf, a high-level drill hole is used to drain the high concentration of methane gushing from the goaf and the protected layer. The main aim of this study is to determine the drill-hole position to ensure it can drain enough methane in steady fashion and decrease the discharge value of methane by ventilation.

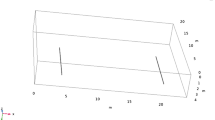
Figure 1 is a schematic representation of the physical model. The model includes a 65-m-high space above the face floor and a set of 6-m-high coal seam as the complementary methane source. The fracture surface of the intake has a width of 3.5 m and a height of 4 m, so the air from the intake will seep into the goaf, except when leaving towards the return way. In Fig. 2, three kinds of 110 mm drill holes, representing low, middle and high positioned holes, are set in the roof of the return way in a sector pattern to investigate the drainage effect of different drill-hole heights. For these drill holes, the low hole is only set at 20 m above the roof of the face; the middle hole is set in the inner region of the protected layer, which is greater than 30 m from the floor; and the high hole passes through the protected layer. This configuration can estimate the impact of each kind of drill hole in the drainage process according to the scope of change in methane concentration around the hole and the redistribution of methane concentration in the goaf. Thus, the model can provide a reference for engineering design.

Fig. 1
figure 1

Schematic diagram of the physical model (Y is the dip direction, X is the length direction, and Z the vertical direction.)

Full size image
Fig. 2
figure 2

Schematic diagram of the high-level drill-hole position

Full size image

4 Numerical simulation of the high-level drainage drill effect

4.1 Resistance coefficient arrangement in the model space

Cracked coal rock is compacted gradually from both ends to the middle part in the goaf. Furthermore, the permeability will feature some kinds of change trend. The resistance coefficient is considered as the reciprocal of permeability in FLUENT software (m−2). The porosity in caving regions can be chosen by the relationship between rock features, mining height, and the position of the goaf, as proposed by Liang et al. (2009). If the particle size is assumed to be 20 mm, the resistance needing input can be calculated by the Carmen–Kozeny formula, which is shown in Fig. 3a and b. Furthermore, the resistance coefficient in the fracture region and bend sink region is assumed to be 1 × 109 and 1 × 1013 m2, respectively (Hao et al. 2011). Above this altitude, the resistance coefficient is assumed to be 1 × 1019 m2.

Fig. 3
figure 3

Distribution of the seepage parameter in the model

Full size image

4.2 Explanation of the boundary conditions and simulation program

The intake and return airway are set as a pressure inlet and outlet at 107,531 and 107,487 Pa, respectively. Each drill hole is also set as a pressure outlet at about 20 kPa, and the rest of the boundary is set as a wall. The methane emission intensity is adopted at 0.05 m3/s. Because the protected coal seam exists in the caving zone, the release of methane pressure is lower than the original pressure. It is difficult to detect the dynamic decay process of the methane pressure in this sector, and hence this study only sets the situation that the protected layer is full at 100 % volume fraction methane in the initial conditions. Thus, a finite amount of methane in this region can seep towards the surrounding area and decay for the setting of permeability. Therefore, an unsteady calculation in the short term can also obtain a similar situation regarding the methane complementary source from the protected layer. This assumption does not reflect the methane emission intensity of the protected layer precisely, but the main aim is not to accurately describe the methane migration law, but to compare the drainage effect of different drill holes. Hence, the research aim is met under this configuration.

First, the above physical model should be brought into the FLUENT software. Then, the resistance coefficient discussed in Sect. 4.1 is input into FLUENT, solved by the UDF function, and the upper boundary condition is set as described above. The intensity difference effect is also considered by opening the gravity tab for −9.81 m/s2 in the vertical direction. The convection and diffusion terms are dispersed with the second-order upwind and central difference scheme. The coupled relation between velocity and pressure is calculated using the SIMPLE method. The calculation result is supposed to converge when the residual is smaller than 10 × e−5. The research aim can be reached by observing the change of methane concentration in the limited time when each kind of drill hole is opened and estimating the drainage effect by the scope of influence of the methane distribution around each drill hole.

4.3 Calculation results and discussion

The spatial distribution of methane and oxygen in the model (Fig. 4) is first obtained from the FLUENT calculation results of mass, momentum, and component conservation. It can be seen from Figs. 4a and b that oxygen and methane have a dual distribution for the dilution effect of air. The methane concentration distribution increases from the face to the depth of the caving region and from the intake airway to the return airway, which is in accordance with the conclusions based on 2D model analysis (Li et al. 2008; Yang et al. 2009a, b). In Fig. 4c, the methane concentration in the high position is higher than in the low position in the vertical direction due to the relatively smaller intensity of methane than air. On account of the dual distribution of methane and air by the reciprocal dilution effect, the seepage characteristics can also be analyzed from the methane concentration distribution in each vertical slice. Additionally, the air can seep along the vertical direction. In the intake airway, the relatively high air leakage pressure can drive the air into the deep part of the caving region, and then this part of the air will form an upward air mass to dilute the methane dramatically when the pressure decreases. From the methane distribution of four slices in Fig. 4c, the above air seepage influence decreases toward the return airway side because of the upward air mass disappears gradually and air accumulates at the air leakage boundary near the workface, and the vertical seepage in the slice near the upper corner decreases to the weakest level. Therefore, there has the highest concentration methane to be drained by drill hole theoretically. The small scope area near the upper corner induces the methane from the vertical and horizontal direction when the methane drainage is not applied. It can also be seen that the large ventilation flux discharging methane and leading the seepage scope of air is very wide. Furthermore, an oxygen concentration of more than 10 % can reach 140 m from the face, which is unfavorable to guard against spontaneous combustion in the goaf, and in such way methane drainage must be carried out to decrease the methane emission and ventilation flux of the face.

Fig. 4
figure 4

Three-dimensional methane distribution in the high-level drill hole without drainage

Full size image

Next, the drill hole is opened to simulate the methane distribution when methane drainage is applied. The calculation results in Fig. 5 reflect the fact that the methane concentration, especially at the nose part near the upper corner, moves back towards the deep part of goaf in the horizontal direction when every drill hole is opened to drain methane. In the vertical direction, the methane near the drill hole decreases dramatically. For the single hole drainage effect, the methane drainage flux of the low hole is worse than the others because, owing to the fact that the low hole is not in the high methane concentration region, the methane near the hole does not change obviously. However, because of its relatively close position to the face, it can provide a protective effect for shallow methane emission. Conversely, the drainage effect of the high-level hole is the best among all the holes for the reason that the methane near the high-level hole decreases dramatically and the average drainage concentration reaches 62 % in the outlet of the hole, due to its position being in the high methane concentration region. Additionally, the high-level hole has the longest scope of influence in the vertical and horizontal direction, and an arched region of influence forms at the end of the hole because it has the longest length. Thus, the drainage effect of the middle hole lies between the high- and low-level hole. Therefore, the high-level drainage hole crossing the protective coal seam should be set as often as possible to drain the high concentration of methane, and only 1 or 2 low level holes should be set near the face at every drill site.

Fig. 5
figure 5

Three-dimensional methane concentration distribution in the high-level drill hole after 15 days

Full size image

According to the conclusion drawn from the simulation, in our experiment field, the drill site, which has four high-level holes and only one low-level hole to drain methane from the goaf and protective coal seam, were arranged along the roof of the return airway. The example is depicted in Fig. 6. This drainage pattern achieved a satisfactory effect and the methane concentration in the upper corner decreased substantially. Beyond that, the quantity of ventilation at the face fell to a certain degree due to the decreasing methane emission. Hence, the risk of spontaneous combustion in the goaf also declined.

Fig. 6
figure 6

a Arrangement of the high-position drill hole in the roof, and b a cross section through A–A in (a)

Full size image

5 Conclusions

  1. (1)

    This research used an unstructured mesh to establish a physical model that included drill holes and the whole stope. The oxygen or methane distribution in a 3D space is obtained by solving the mass, momentum and component equations. The methane had a floating effect and the dilution influence of air on methane decreased from the intake airway and return airway in the vertical direction, except for the dual distribution of methane and oxygen in the horizontal direction.

  2. (2)

    From the simulation results, the high-level drill crossing hole had a wider influence and higher drainage concentration than the low hole. The latter only played an assisting role because the main methane source was the short-range coal seam above, which also exited in the fracture region. So, the high drill hole should be set as far as possible.

  3. (3)

    On-site applications showed that the drainage pattern with high and low drill holes not only obtained methane with high purity for recycling, but also controlled the methane concentration in the upper corner. Because of the “U” type ventilation, methane in the caving region streams down towards upper corner easily following air leakage, and hence the low drill is an essential part of the drainage pattern.

  4. (4)

    This paper only analyzed the methane distribution under high-level drill drainage qualitatively. In 3D space, the key factor for calculating methane distribution regulation is the position and intensity of the methane source. The methane pressure of the protected coal seam undergoes a dynamic decreasing process because it exits in the fracture region. This research has simplified this problem by an steady solving and definite volume of the methane source. More precise basal parameters must be investigated in future work to analyze this problem accurately.