An adaptive trimming approach to Bayesian additive regression trees

Abstract

A machine learning technique merging Bayesian method called Bayesian Additive Regression Trees (BART) provides a nonparametric Bayesian approach that further needs improved forecasting accuracy in the presence of outliers, especially when dealing with potential nonlinear relationships and complex interactions among the response and explanatory variables, which poses a major challenge in forecasting. This study proposes an adaptive trimmed regression method using BART, dubbed BART(Atr) to improve forecasting accuracy by identifying suspected outliers effectively and removing these outliers in the analysis. Through extensive simulations across various scenarios, the effectiveness of BART(Atr) is evaluated against three alternative methods: default BART, robust linear modeling with Huber’s loss function, and data-driven robust regression with Huber’s loss function. The simulation results consistently show BART(Atr) outperforming the other three methods. To demonstrate its practical application, BART(Atr) is applied to the well-known Boston Housing Price dataset, a standard regression analysis example. Furthermore, random attack templates are introduced on the dataset to assess BART(Atr)’s performance under such conditions.

Introduction

Bayesian Additive Regression Trees (BART), introduced by Chipman et al. [1], has gained significant attention due to its ability to effectively capture nonlinear relationships even in complex scenarios [2,3,4,5,6]. It combines the precision of likelihood-based inference with the flexibility of machine learning algorithms. BART is a non-parametric Bayesian regression approach that models the response variable as a sum of many small trees, each contributing a small portion to the overall prediction. This ensemble of trees allows for capturing intricate patterns and interactions in the data, while the Bayesian framework provides a principled way to quantify uncertainty and prevent overfitting. Theoretical investigations explore the concentration of posterior distributions, providing empirical evidence of BART’s effectiveness [2]. Furthermore, BART’s Bayesian nature allows for the incorporation of prior information and the quantification of uncertainty in the predictions, making it a valuable tool for decision-making under uncertainty. BART models have been successfully applied to a wide range of problems, including predicting solar radiation [7], forecasting sales [8], and identifying accident hot spot [9].

Despite the advancements made by the BART, it still faces several fundamental challenges when handling outliers. Firstly, BART employs a sum of regression trees as its base learners. Outliers in the responses can lead to splits that overfit those outlier points. Secondly, unlike other robust regression techniques like M-estimators, BART lacks an explicit mechanism to downweight or remove the influence of outliers during model fitting. It relies solely on the tree ensemble structure and regularization to provide robustness. Thirdly, BART models the mean response as a sum of trees, and outliers can increase the residual error, which is then modeled by a separate residual error term. If there are many outliers, say, more than 25%, modeling this complex residual error becomes more challenging [3]. Lastly, BART uses Bayesian posterior averaging over many trees. While this provides robustness against overfitting, it may also cause the influence of outliers to persist across multiple trees in the ensemble [10]. Hence, it is apparent that achieving improved forecasting accuracy in the presence of outliers using BART remains a challenging task. Therefore, in this work, we aim to enhance the reliability and trustworthiness of BART-based forecasting models, enabling their deployment in real-world applications where data is contaminated with outliers.

In statistics, traditional regression analysis relies on least squares procedures, which are potent tools. However, the presence of outliers in the data poses a significant challenge for accurate analysis within these traditional regression models. Hence, there is a pressing need to devise more suitable methods capable of handling outliers effectively. The pioneering work in robust statistics, including Tukey, Huber, and Hampel, are recognized for their seminal contributions [11,12,13]. Their work laid the foundation for robust statistical techniques. Recently, a review of robust statistics has been elaborated upon [14], where the M-estimation method, the most important class for the field of data rectification, is the main focus of these papers [14,15,16,17]. In robust linear regression, emphasis is placed on considering only residuals that do not deviate excessively when estimating regression parameters. This approach is encapsulated by the least trimmed squares estimator. Additionally, an adaptive least trimmed squares method has been devised to robustly estimate both the proportion of affected data and the coefficients in a multiple linear regression model [18,19,20], where the adaptive least trimmed squares method is a data-driven method which adaptively estimates the proportion of unaffected data p according to the data. Recently, such techniques have been successfully applied to address challenges in electricity demand forecasting against cyberattacks, leveraging an adaptive trimmed regression method [18].

As mentioned before, the presence of outliers in data poses a significant challenge for accurate analysis using the traditional BART computational algorithm. Therefore, our motivation is to construct a robust version of BART to enhance prediction performance by introducing the trimmed regression approach. Outliers can lead to splits that overfit the affected branches. We propose a trimmed approach so that the suspected outliers are trimmed, and their bad effects can therefore be alleviated. A key and challenging issue is what proportion we should trim—over-trimming will lose useful data necessarily while under-trimming will cause some outliers to be treated as “normal” data and hence have more detrimental effects on prediction.

Following our motivation, we introduce an adaptive trimmed regression approach based on BART, BART(Atr), which extends the robust approach by incorporating data-driven tuning parameters, as described in VandenHeuvel et al. [18], where it was originally applied to linear regression. More precisely, we extend the adaptive trimmed method to BART, which is a nonparametric regression model involving nonlinear regression, employing an inclusive framework that incorporates the estimation of the scale parameter, the proportion, and the weight function. Specifically, a suitable weight function for each data point, only residuals that do not exceed a certain threshold are utilized to estimate the true regression function. We explore the performance of our proposed method through simulation studies featuring varying attack rates and diverse distributions, as well as real data analysis involving random attacks, under the guidance of Lemma and Theorem. To demonstrate the effectiveness of BART(Atr), we perform a comparative analysis with three alternative methods: BART(Def), RLM, and RLMD. BART(Def), as mentioned in Chipman et al. [1], is a simpler and more efficient version of BART. RLM utilizes robust regression with Huber’s loss function [12], while RLMD applies data-driven robust regression with the same loss function [21]. It is worth noting that Huber’s loss function is widely used in robust regression, particularly in the M-estimation method [14]. Both RLM and RLMD are recognized as powerful tools for robust regression. So, we compare BART(Atr) against these three methods: BART(Def), RLM, and RLMD.

Therefore, the main contributions in this paper can be summarized as follows.

• a. We present an extended robust regression technique based on BART, incorporating data-driven tuning parameters. This approach builds upon the original application of the method in linear regression, as described in VandenHeuvel et al. [18].

• b. We propose an iterative procedure that robustly trains a comprehensive framework, encompassing the estimation of the scale parameter $\sigma$, the proportion of outliers to be trimmed, $1-p$, and the weight function $\psi (\cdot )$ under the guidance of Lemma and Theorem. The weight function $\psi (\cdot )$ is carefully selected for each data point.

• c. To establish the efficacy of our training procedure, we conduct simulation studies and evaluate its performance. Furthermore, we analyze a real-world scenario involving random attacks. The experimental results unequivocally demonstrate the superior performance and forecasting capabilities of our proposed method compared to three alternative methods.

The paper is organized as follows: In “An adaptive trimmed BART” Section outlines the proposed method, followed by “Simulation studies” Section, which presents simulation studies evaluating its performance. In “Real data analysis” Section illustrates the application of the proposed method to real data subjected to random attacks. Finally, “Conclusions” Section provides conclusions and outlines avenues for future research.

An adaptive trimmed BART

BART

BART consists of three primary components: a sum-of-trees model, a regularization prior to the parameters of this model, and a Bayesian backfitting MCMC algorithm. Each of these components will be briefly described below.

Sum-of-trees model

Suppose that observations $D=\{(\varvec{x_{i}},y_{i}),x_{i} \in R^{c},y_{i} \in R, i=1,2,\ldots ,n\}$ are independent identical distribution(i.i.d.) from a population, where $\varvec{x_{i}}$ and $y_{i}$ represent c dimensional vector and variable, respectively. A BART model by Chipman et al. [1] assumes the observations D follow:

$$\begin{aligned} y_{i} = f(\varvec{x_{i}}) + \epsilon _{i}, \quad i=1, \ldots , n, \end{aligned}$$

(1)

where $f(\varvec{x_{i}})$ is represented as the regression function by the following expression:

$$\begin{aligned} f(\varvec{x_{i}}) = g(\varvec{x_{i}},\mathcal {T}_{1}, \mathcal {M}_{1})+\ldots +g(\varvec{x_{i}},\mathcal {T}_{m}, \mathcal {M}_{m}). \end{aligned}$$

(2)

The error terms $\epsilon _{1},\ldots ,\epsilon _{n}$ in Eq. (1) are i.i.d. from a normal distribution, denoted as $\epsilon _{i} \sim N(0,\sigma ^{2})$. In Eq. (2), $\mathcal {T}_{j}$ represents the jth regression tree, where j ranges from 1 to m. Each of the trees is a binary regression tree consisting of a set of interior node splitting rules and a set of terminal nodes. $\mathcal {M}_{j}=\{\mu _{j1},\ldots ,\mu _{jb_{j}}\}$ represents the collection of parameters for the $b_{j}$ leaves of the jth tree. Given the jth tree $\mathcal {T}_{j}$, the function $g(\varvec{x_{i}}, \mathcal {T}_{j}, \mathcal {M}_{j})$ assigns a value in $\mathcal {M}_{j}$ to $\varvec{x_{i}}$ based solely on which terminal node $\varvec{x_{i}}$ belongs to.

Regularization prior

The entities $\mathcal {T}_{1},\ldots ,\mathcal {T}_{m}$, $\mathcal {M}_{1},\ldots ,\mathcal {M}_{m}$, and $\sigma$ correspond to the structures of the trees, the parameters of the terminal nodes, and the standard deviation of the model described in Eq. (1), respectively. To account for a regularization prior applied to these parameters, the following prior distribution is considered:

$$\begin{aligned}&P((\mathcal {T}_{1},\mathcal {M}_{1}),\ldots ,(\mathcal {T}_{m}, \mathcal {M}_{m}),\sigma )\nonumber \\&\quad =\left\{ \prod _{j=1}^{m}\left( \prod _{k=1}^{b_{j}} P\left( \mu _{j k} \mid \mathcal {T}_{j}\right) \right) P\left( \mathcal {T}_{j}\right) \right\} P(\sigma ). \end{aligned}$$

(3)

This prior distribution is determined based on a set of independence and symmetry assumptions. As a result, the priors for $\mathcal {T}_{j}$, $\mu _{j k} \mid \mathcal {T}_{j}$, and $\sigma$ as depicted in Eq. (3) can be expressed by introducing hyperparameters such as $\alpha$, $\beta$, k, m, $\nu$, and q, along with the application of conjugate prior distributions. The default settings for hyperparameters are recommended in this study (as described in “Simulation studies” Section). For more comprehensive details, refer to Chipman et al. [1].

Backfitting MCMC algorithm

A Bayesian backfitting MCMC algorithm can be used to sample, and Bayesian setup induces a posterior distribution $P\left( \left( \mathcal {T}_{1}, \mathcal {M}_{1}\right) , \ldots ,\left( \mathcal {T}_{m}, \mathcal {M}_{m}\right) , \sigma \mid D \right)$ given observations D. Specifically, the sample $\mathcal {T}_{j}$ can be obtained using the Metropolis-Hastings algorithm of CGM98 in Chipman et al. [22]; the draw of $\mathcal {M}_{j}$ conditionally on $\mathcal {T}_{j}$, $\mathcal {M}_{j}=\{\mu _{j1},\ldots ,\mu _{jb_{j}}\}$, is implemented by independently draws from a normal distribution; to sample $\sigma ^{2}$, conditional on the updated tree structures $\{\mathcal {T}_{1},\ldots ,\mathcal {T}_{m}\}$ and the terminal node parameters $\{\mathcal {M}_{1},\ldots ,\mathcal {M}_{m}\}$, is implemented from an inverse $\chi ^{2}$ distribution. Thus, generating a sequence of draws of $(\mathcal {T}_{1},\mathcal {M}_{1}),\ldots ,(\mathcal {T}_{m}, \mathcal {M}_{m}),\sigma$, it is converging (in distribution) to the posterior $P\left( \left( \mathcal {T}_{1}, \mathcal {M}_{1}\right) , \ldots ,\left( \mathcal {T}_{m}, \mathcal {M}_{m}\right) , \sigma \mid D \right)$. $\hat{f}(\varvec{x_{i}}) = \frac{1}{\kappa }\sum _{\iota =1}^{\kappa }f^{*}_{\iota } (\varvec{x_{i}})$ is a natural choice [1], where $1,\ldots ,\kappa$ denotes the index of sequence after burn-in period, and $f^{*}_{\iota }(\varvec{x_{i}})= \sum _{j=1}^{m} g(\varvec{x_{i}},\mathcal {T}_{j},\mathcal {M}_{j})$. It may be of interest to note that $\hat{f}(\varvec{x_{i}})$ approximates the posterior mean. Thereby, $\hat{\epsilon }_{i}=y_{i}-\hat{f}(\varvec{x_{i}}),i=1, \ldots , n$.

For clarity, Algorithm 1 presents the outline of BART as referenced in Wang et al. [23].

Algorithm 1

BART Algorithm

An adaptive trimmed BART

In this subsection, we will examine the statistical properties of the residuals, $\hat{\epsilon }_{i}=y_{i}-\hat{f}(\varvec{x_{i}})$, which can be approximated with a mean of $E(\hat{\epsilon }_{i})=0$ and a variance of $Var(\hat{\epsilon }_{i})=\sigma ^{2}$. This approximation is justified based on the following reasoning.

Firstly, let’s consider the mean:

$$\begin{aligned} E(\hat{\epsilon }_{i})&=E(y_{i})-E(\hat{f}(\varvec{x_{i}})) = f(\varvec{x_{i}}) \\&\quad - E\left( \frac{1}{\kappa } \sum _{\iota =1}^{\kappa }f^{*}_{\iota }(\varvec{x_{i}})\right) \approx f(\varvec{x_{i}}) - f(\varvec{x_{i}}) = 0, \end{aligned}$$

where $f^{*}_{\iota }$ refers to the function induced by the $\iota$th posterior draw, and converges to the posterior distribution on the true function f, as mentioned in Chipman et al. [1].

Secondly, let’s consider the variance:

$$\begin{aligned} Var(\hat{\epsilon }_{i})= & {} Var(y_{i}-\hat{f}(\varvec{x_{i}})) = Var(f(\varvec{x_{i}}) + \epsilon _{i} - \hat{f}(\varvec{x_{i}}))\\= & {} Var(\epsilon _{i}-\hat{f}(\varvec{x_{i}})) \approx \sigma ^{2}; \end{aligned}$$

this approximation relies on the delta method and a condition. More precisely, it is Taylor’s formula to the first order, $g(x) \approx g(x_{0})+g^{'}(x_{0})(x-x_{0})$, and next, calculate the expected value conditionally on $E(\epsilon _{i}\hat{f}(\varvec{x_{i}})) =E((\hat{f}(\varvec{x_{i}})-f(\varvec{x_{i})})\hat{f} (\varvec{x_{i}}))$.

Considering $y_{i}$ follows a normal distribution from the assumption of Eq. (1), as well as the same distribution for $\hat{f}(\varvec{x_{i}})$ according to central limit theorem [24], we assume $\hat{\epsilon }_{i}=y_{i}-\hat{f}(\varvec{x_{i}})$ follows a normal distribution with mean 0 and variance $\sigma ^{2}$, and these $\hat{\epsilon }_{i}$’s are i.i.d.. With this assumption, the distribution of the absolute residuals ${|\hat{\epsilon }_{1}|,\ldots , |\hat{\epsilon }_{n}|}$ follows the folded normal distribution, denoted as $FN(0,\sigma ^{2})$, with location 0 and scale $\sigma ^{2}$.

For the sake of simplification in notation, let’s use $\varphi , \Phi , \Phi ^{-1}$ to represent the density function, cumulative distribution function, and quantile function of the standard normal distribution, respectively. Furthermore, we’ll employ $f(\delta )=2\varphi (\delta /\sigma )/\sigma , F(\delta )=2\Phi (\delta /\sigma )-1, F^{-1}(\delta )=\sigma \Phi ^{-1}((1+\delta )/2)$ to characterize the density function, cumulative distribution function, and quantile function of the folded normal distribution, $FN(0,\sigma ^{2})$. Now, considering $|\hat{\epsilon }|_{(i)}$ as the i-th smallest value in the set of absolute residuals ${|\hat{\epsilon }_{1}|,\ldots , |\hat{\epsilon }_{n}|}$, ordered in ascending order, i.e., $|\hat{\epsilon }|_{(1)} \le |\hat{\epsilon }|_{(2)} \le \cdots \le |\hat{\epsilon }|_{(n)}$, we can express the following relationships:

$$\begin{aligned} \tilde{p}_{j}=\frac{j}{n+1}, \quad \xi _{j}=F^{-1}(\tilde{p}_{j}), \quad j=1, \ldots , n. \end{aligned}$$

(4)

Define $s_{i}^{2}$ as follows

$$\begin{aligned} s_{i}^{2}=\sum _{j=1}^{i}|\hat{\epsilon }|_{(j)}^{2}/i. \end{aligned}$$

(5)

To find the distribution of $s_{i}^{2}$, the following theorem is given as follows.

Lemma

Suppose $i \in \{ 1,2,\ldots ,n\}$ and consider $|\hat{\epsilon } |_{(1)}, |\hat{\epsilon }|_{(2)} , \ldots , |\hat{\epsilon } |_{(n)}$. Then, the asymptotic joint distribution of $\sqrt{n} (|\hat{\epsilon }|_{(1)} - \xi _{1}),\ldots , \sqrt{n} (|\hat{\epsilon }|_{(i)} - \xi _{i})$ is i-dimensional normal with zero mean vector and covariance matrix $\sum _{(i)}$, defined such that its (j, k) entry $\sigma _{(i),jk}$ as $\sigma _{(i),jk}=\frac{\tilde{p}_{j}(1-\tilde{p}_{k})}{f(\xi _{j})f(\xi _{k})}, 1\le j \le k \le i$.

Proof

This lemma could be regarded as a modification of the more general result introduced by David and Nagaraja ([25], Theorem 10.3) [25], which is the asymptotics of a joint distribution of order statistics. We need to verify the hypotheses of the theorem. More precisely,

• 1. The first hypothesis is that $0<\tilde{p}_{1}<\tilde{p}_{2}<\cdots<\tilde{p}_{i}<1$, it holds, due to $\tilde{p}_{j}$ in (4), naturally, $0<\frac{1}{n+1}<\frac{2}{n+1}<\cdots<\frac{i}{n+1}<1$.

• 2. The second hypothesis is that $r_{j}/n-\tilde{p}_{j}=o(n^{-\frac{1}{2}})$, here $r_{j}=j$. Considering $\sqrt{n}[r_{j}/n -\tilde{p}_{j}]=j/[\sqrt{n}(n+1)]$, $j=1,\ldots ,i$, $\sqrt{n}[r_{j}/n- \tilde{p}_{j}]$ is infinitesimal of higher order for $n^{-\frac{1}{2}}$. This condition is true.

• 3. The third hypothesis is that $0< f(\xi _{j}) < \infty , j=1,\ldots ,i$. Considering the density f is defined in terms of $\varphi$, according to the property of $\varphi$, $0< f(\xi _{j}) < \infty , j=1,\ldots ,i$, it holds.

• 4. The final hypothesis is that F for these absolute residuals is differentiable at each $\xi _{j}$. Considering $F(\delta )=2\Phi (\delta /\sigma )-1$ and $\Phi$ is differentiable, so too is F.

Thus, all hypotheses given by David and Nagaraja (2003, Theorem 10.3) [25] are satisfied, and the lemma is proved. $\square$

Theorem

Suppose the residuals $\hat{\epsilon }_{1},\hat{\epsilon }_{2},\ldots ,\hat{\epsilon }_{n}$ be i.i.d., each following the distribution $N(0,\sigma ^{2})$, $\sigma > 0$. Then, provided that $|\hat{\epsilon }|_{(1)} > 0$,

$$\begin{aligned}{} & {} \sqrt{n}\left\{ s_{i}^{2}-\frac{1}{i}\sum _{j=1}^{i}\xi _{j}^{2} \right\} \bigg / \left( \frac{2}{i}\sqrt{\zeta _{i}^{T}\Sigma _{(i)}\zeta _{i}}\right) \\{} & {} \quad {\mathop {\longrightarrow }\limits ^{d}}N(0,1),i=1, \ldots , n, \end{aligned}$$

as $n \rightarrow \infty$, where ${\mathop {\longrightarrow }\limits ^{d}}$ denotes convergence in distribution.

Proof

Define $|\hat{\varepsilon } |_{(i)}=(|\hat{\epsilon } |_{(1)},\ldots ,|\hat{\epsilon } |_{(i)})^{T}$, $\zeta _{i}=(\xi _{1}, \ldots , \xi _{i})^{T}$. Lemma shows that $\sqrt{n} (|\hat{\varepsilon } |_{(i)}-\zeta _{i}) {\mathop {\longrightarrow }\limits ^{d}}N_{i}({\textbf {0}}_{(i)},\Sigma _{(i)})$, where ${\textbf {0}}_{(i)}$ is an i-dimensional zero vector. Furthermore, note that $s_{i}^{2}=g(|\hat{\varepsilon } |_{(i)})=\sum _{j=1}^{i}|\hat{\epsilon }|_{(j)}^{2}/i$, according to the multivariate delta method (Wasserman, 2004, Theorem 5.15) [26] we considered the following

$$\begin{aligned} \sqrt{n}\left\{ s_{i}^{2}-\frac{1}{i}\sum _{j=1}^{i}\xi _{j}^{2} \right\} \bigg / \left( \frac{2}{i}\sqrt{\zeta _{i}^{T}\Sigma _{(i)}\zeta _{i}}\right) {\mathop {\longrightarrow }\limits ^{d}}N(0,1) \end{aligned}$$

conditional on $|\hat{\epsilon }|_{(1)} > 0$ and the gradient of $g(|\hat{\varepsilon } |_{(i)}) > 0$. For continuous $y_{i}$, $|\hat{\epsilon }|_{(1)} = 0$ is a probability zero event, the gradient function of $g(|\hat{\varepsilon } |_{(i)})$ is equal to $\frac{2}{i}|\hat{\varepsilon } |_{(i)}$.

Thus, all conditions given by Wasserman ([26], Theorem 5.15) [26] satisfied, the theorem is proved. $\square$

From the theorem, we have the following modified MAD estimator for $\sigma ^{2}$

$$\begin{aligned} \hat{\sigma }^{2}=\sum _{i=1}^{\lfloor np \rfloor } |\hat{\epsilon }|_{(i)}^{2} \bigg / \sum _{i=1}^{\lfloor np \rfloor }\left[ \Phi ^{-1}\left( \frac{1+\tilde{p}_{i}}{2}\right) \right] ^{2}, \end{aligned}$$

(6)

where $\lfloor np \rfloor$ denotes the value of np rounded down. The upper index in the sums in (6) are set to $\lfloor n/4 \rfloor$, which ensures that only $25\%$ clean data are used for estimating $\sigma ^{2}$.

Thus, the asymptotic mean of $s_{i}^{2}$ is given by $E(s_{i}^{2})=\frac{1}{i}\sum _{j=1}^{i}\xi _{j}^{2}$. Define the set $S = \{i \in \{1, \ldots , n \}: s_{i}^{2}/E(s_{i}^{2}) \le Q \}$ and set

$$\begin{aligned} \hat{p}^{(\text{ Iter})}=|S |/n, \text{ Iter }=1,2,\ldots ,\text{ Iter}_{\max }, \end{aligned}$$

(7)

where $\text{ Iter }, |S |, \text{ Iter}_{\max }$ and Q denote the iteration number, the number of indices in S, the maximum number of iterations and the tuning parameter, respectively.

Next, the weight function is defined by

$$\begin{aligned} \psi (\hat{\epsilon }_{i})=\left\{ \begin{aligned} 0&,&|\hat{\epsilon }_{i}|> |\hat{\epsilon } |_{(\lfloor np \rfloor )},\\ 1&,&|\hat{\epsilon }_{i}|\le |\hat{\epsilon } |_{(\lfloor np \rfloor )}, \end{aligned}\right. \end{aligned}$$

(8)

where $\psi (\hat{\epsilon }_{i})$ assigns a weight of 1 to nonoutliers and 0 to outliers.

Run BART model using the sample with $\psi (\hat{\epsilon }_{i})=1$. Afterwards, update $\hat{\epsilon }_{i}$ with the new model and calculate the revised estimations for $\sigma ^{2}$, p, and the weights $\psi (\hat{\epsilon }_{1}),\ldots ,\psi (\hat{\epsilon }_{n})$. Continue this process iteratively until the absolute difference between $\hat{p}^{(\text{ Iter})}$ and $\hat{p}^{(\text{ Iter }-1)}$ divided by $\hat{p}^{(\text{ Iter})}$ is less than a specified tolerance $\tau$, where $\tau$ is a predefined value, or a maximum number of iterations, $\text{ Iter}_{\max }$, is met. It’s important to note that this iterative process converges within a finite number of steps [19], and in this context, $\tau$ is set to be $10^{-4}$ as referenced in VandenHeuvel et al. [18].

Fig. 1

The training procedure for the proposed adaptive trimmed Bayesian additive regression trees

We now outline the procedure of our BART(Atr) as follows:

• Step 1: Start by obtaining the initial estimate of $\epsilon _{i}$ using the BART model for the observations ${(x_{i1},x_{i2},\ldots ,x_{ic},y_{i}),i=1, \ldots , n}$, denoted as $\hat{\epsilon }_{i}^{(\text{ Iter})}$.

• Step 2: Next, compute the estimate of $\sigma ^{2}$ using (6) for the order statistics of $\hat{\epsilon }_{i}^{(\text{ Iter})}$, and use (4) to obtain values for $\tilde{p}_{i}$ as well as set $\lfloor np \rfloor =\lfloor n/4 \rfloor$.

• Step 3: Calculate the estimate of p using (7) and Theorem for $s_{i}^{2}$ and $E(s_{i}^{2})$, then update the value of $\hat{p}^{(\text{ Iter})}$; Noted that with the initial value $\hat{p}^{(\text{0 })}=0.5$.

• Step 4: Compute the weights $w_{i}=\psi (\hat{\epsilon }_{i})$ using (8). Fit the BART model to the samples with weights $w_{i}$ and update $\hat{\epsilon }_{i}^{(\text{ Iter }+1)}$.

• Step 5: Repeat Steps 2 to 4 iteratively until the condition $|\hat{p}^{(\text{ Iter})}-\hat{p}^{(\text{ Iter }-1)} |/\hat{p}^{(\text{ Iter})}<\tau$ or a maximum number of iterations, $\text{ Iter}_{\max }$, is met, where $\tau =10^{-4}$, $\text{ Iter}_{\max }=20$.

In addition, the training flowchart for the proposed adaptive trimmed Bayesian additive regression trees is presented in Fig. 1.

Remark

The BART(Atr) procedure begins by obtaining an initial estimate of the residuals $\epsilon _{i}$ using the BART model on the observations. Steps 2 to 4 then calculate estimates for the residual variance $\sigma ^{2}$, the trimming proportion p, and the weights $w_{i}=\psi (\hat{\epsilon }_{i})$, guided by the provided Lemma and Theorem. The residual estimate $\epsilon _{i}$ is then updated. Step 5 iterates Steps 2 to 4 until one of the specified conditions is met. Notably, the estimation of $\sigma ^{2}$ and p in Steps 2 and 3 follows the guidance of the Lemma and Theorem. It is important to highlight that the primary objective is to improve forecasting accuracy in the presence of outliers by employing BART(Atr).

Simulation studies

In this section, we delve into a nonlinear model found in the BART literature [1, 24], originally introduced by Friedman [27]. We aim to employ this model to show the capabilities of BART(Atr) and compare it with the three methods (BART(Def), RLM, and RLMD), as stated in “Introduction” Section, where BART(Def) is vastly easier and faster to use in Chipman et al. [1], RLM is the linear model by robust regression with the Huber’s loss function, and RLMD is the data-driven robust regression with the Huber’s loss function, respectively. All experiments are conducted using R’s ‘bartMachine’ [28], ‘rlmDataDriven’ [29], and ‘MASS’ [30] packages. To facilitate the easy implementation of the four methods, the default setting considered in this paper is shown in Table 1.

Table 1 Methods, packages, and default settings

Experimental settings

We examine the nonlinear model given by:

$$\begin{aligned} y_{i}&=10 \sin (\pi x_{i1} x_{i2})+20 (x_{i3}-0.5)^{2}\nonumber \\&\quad +10 x_{i4}+5 x_{i5}+\epsilon _{i},\quad i=1, \ldots , n. \end{aligned}$$

(9)

In this model, the variables $x_{i1}, x_{i2}, \ldots , x_{i5}$ are i.i.d. from Uniform(0,1). The error term $\epsilon _{i}$ follows a mixture distribution, represented as $p N(0,0.1^{2})+(1-p) F$. Here, p, $1-p$, and n denote the proportion of unattacked data, attacked data, and the sample size, respectively. We consider three different distributions for F as follows:

• Case 1. Normal distribution, where the errors are attacked by a normal distribution, $N(0,1.5^{2})$, with the proportion of attacked $1-p$. Different $1-p$ are considered, that is, $1-p=0\%, 5\%, 10\%, 15\%, 20\%, 25\%, 30\%, 35\%, 40\%, 45\%$, and $50\%$.

• Case 2. Student’s t distribution, where the errors are attacked by t(3) with three degrees of freedom, with the proportion of attacked $1-p$. Different $1-p$ are considered, that is, $1-p=0\%, 5\%, 10\%, 15\%, 20\%, 25\%, 30\%, 35\%, 40\%, 45\%$, and $50\%$.

• Case 3. Exponential distribution, where the errors are attacked by an exponential distribution, $Exp(0.5)-2$, with the proportion of attacked $1-p$. Different $1-p$ are considered, that is, $1-p=0\%, 5\%, 10\%, 15\%, 20\%, 25\%, 30\%, 35\%, 40\%, 45\%$, and $50\%$.

Cases 1–3 are the normal errors, attacked via three distributions: $N(0,1.5^{2})$, t(3), and $Exp(0.5)-2$ with the proportion of attacked $1-p$. We simulate i.i.d. datasets with $n = 1000$ and fit the model using the proposed method, BART(Atr), for $p \in \{0.5, 0.55, \ldots , 0.95, 1.0\}$. Considering $Q \in \{1.0, 1.07, \ldots ,1.49\}$, at the cost of increased computation time, $Q = 1.28$ is selected in this work based on fitting the model (9), according to the majority of the minimal MAE and MAPE values in Case 1. Thus, we use $Q = 1.28$ for all cases in BART(Atr). All are implemented 100 times in all cases for the four methods, BART(Atr), BART(Def), RLM, and RLMD.

Evaluation criterion

We assess the performance of the four methods using three key metrics: the estimates $\hat{p}$ for p, mean absolute error (MAE), and mean absolute percentage error (MAPE). In the case of $\hat{p}$ estimates, we collect 100 simulation results and then calculate the average and median for each p. The last two metrics are defined as follows:

$$\begin{aligned} \text {MAE}=\frac{1}{n}\sum _{i=1}^{n}|\mu _{i}-\hat{y}_{i}|, \end{aligned}$$

and

$$\begin{aligned} \text {MAPE}=\frac{100}{n}\sum _{i=1}^{n}\frac{|\mu _{i} -\hat{y}_{i} |}{|\mu _{i} |}, \end{aligned}$$

where $\hat{y}_{i}$ and $\mu _{i}$ represent the predicted value for $y_{i}$ and the expected value in the model (9), respectively. Notably, the expected value $\mu _{i}$ corresponds to the observed value without the additional noise.

Results and discussion

The simulation results are presented in Tables 2, 3, and 4. Table 2 provides the results in Case 1 for the estimates of p, $\hat{p}$, and the MAE and MAPE values. Our method, BART(Atr), performs better than the other three methods in terms of all the metrics. For instance, at $p=0.75$, firstly, the estimate $\hat{p}$ for p lies within (0.701, 0.754), where the interval is given by the mean and median from BART(Atr), while it is not provided in BART(Def), RLM and RLMD. Moreover, the MAE of 0.309 (mean) and 0.306 (median) are given by BART(Atr), whereas 0.383 (mean) and 0.381 (median) are given by BART(Def); 1.770 and 1.763 are given by RLM and RLMD, respectively. Here 1.770 and 1.763 largely outweigh 0.309 and 0.383, so, the following focus on the two methods, BART(Atr) and BART(Def). An obvious decline from 0.383 (or 0.381) to 0.309 (or 0.306), a difference of about $24\%$ times. Similarly, we have a MAPE of $2.6\%$ with BART(Atr), whereas $3.2\%$, $15\%$, and $14.9\%$ are provided in BART(Def), RLM, and RLMD, respectively. In the same way, BART(Atr) and BART(Def) are focused on, for BART(Atr), a difference of about $23\%$. At the same time, it should be noted that there is no difference between the two methods, BART(Atr) and BART(Def) when $p=1$. To summarise, BART(Atr) provides better estimates of $\hat{p}$ in Case 1 and provides greater forecasting accuracy in the four methods.

Table 2 Simulation study results in Case 1

Table 3 Simulation study results in Case 2

Table 4 Simulation study results in Case 3

Table 3 presents the findings for Case 2, including estimates of p represented as $\hat{p}$, as well as the accompanying MAE and MAPE values. Just as in the previous case, BART(Atr) outperforms the other three methods across all metrics. For example, at $p=0.85$, the estimated value $\hat{p}$ falls within the interval of (0.848, 0.898), as defined by the mean and median values from BART(Atr). However, BART(Def), RLM, and RLMD do not provide such an interval. Furthermore, BART(Atr) reports an MAE of 0.267 (mean) and 0.261 (median), while BART(Def) yields an MAE of 0.342 (mean) and 0.340 (median), 1.769 and 1.763 are given in RLM and RLMD, respectively. Here 1.769, and 1.763 largely outweigh 0.267 and 0.342, as in the previous case, the following focus on the two methods, BART(Atr) and BART(Def). This results in a significant reduction, approximately 28%, when transitioning from BART(Def) to BART(Atr). Similarly, in terms of MAPE, BART(Atr) records a value of 2.2%, while BART(Def) provides a MAPE of 2.8%, leading to a difference of about 27%. It’s important to note that there is no difference between the two methods, BART(Atr) and BART(Def) when $p=1$. Therefore, BART(Atr) delivers improved estimates of $\hat{p}$ that consistently overestimate the true p values, particularly when $p=0.65,0.6$, and it significantly outperforms BART(Def) as well as RLM and RLMD in the context of Case 2.

Table 4 displays the outcomes for Case 3, encompassing the estimates of p denoted as $\hat{p}$, and the associated MAE and MAPE values. Much like in the previous cases, BART(Atr) outperforms the other three methods across all metrics. For example, when $p=0.95$, the estimate $\hat{p}$ falls within the range of (0.884, 0.956), as defined by the mean and median values from BART(Atr). However, BART(Def), RLM, and RLMD do not provide such an interval. Furthermore, BART(Atr) produces an MAE of 0.247 (mean) and 0.241 (median), whereas BART(Def) yields an MAE of 0.288 (mean) and 0.286 (median), 1.770 and 1.763 are given in RLM and RLMD. Here 1.770, and 1.763 largely outweigh 0.247 and 0.288, as in the previous cases, the following focus on the two methods, BART(Atr) and BART(Def). This indicates a noticeable reduction, approximately 17% when transitioning from BART(Def) to BART(Atr). Similarly, in terms of MAPE, BART(Atr) reports a value of 2%, while BART(Def) provides a MAPE of 2.4%, resulting in a difference of about 20%. It’s important to note that there is no difference between the two methods, BART(Atr) and BART(Def) when $p=1$. In summary, BART(Atr) offers estimates of $\hat{p}$ that consistently underestimate the true p values, particularly when $p=0.8,0.75,0.7,0.65,0.6$, and it significantly outperforms the other three methods in the context of Case 3.

Tables 2, 3, and 4 demonstrate that BART(Atr) consistently outperforms the other three methods across all cases, as viewed from three different metrics, the estimates of p, $\hat{p}$, MAE and MAPE values. It’s important to highlight that both the mean and median values of MAE and MAPE increase as the parameter p decreases from 1 to 0.5 in both BART(Atr) and BART(Def). This trend appears reasonable given that the proportion of attacked data, represented by $1-p$, increases from 0 to 0.5. Furthermore, it’s worth noting that BART(Atr) delivers the best performance among all cases, especially when it comes to estimating the parameter p, while the other three methods cannot provide estimates for the parameter p.

Fig. 2

Estimates $\hat{p}$ for p in all Cases. Here $*$,$\circ$, and $\triangle$ refer to true values of p, estimates of p using the new method by the median and mean for 100 simulations, respectively. Namely, $*$,$\circ$ and $\triangle$ denote True, Esti (median), Esti (mean)

As depicted in Fig. 2, it is evident that for Case 1, the true values of p are almost consistently found within the intervals represented by Esti (Mean) and Esti (Median). In other words, these intervals tend to encompass the true values of p. Similarly, for Case 2 and Case 3, the true values of p are also well-contained within such intervals. The novel method, BART(Atr), performs exceptionally well and consistently yields similar results for Cases 1, 2, and 3. It’s worth noting that in Case 2, two intervals overestimate p. For instance, when the true value is $p=0.6$, the estimated value falls within the range of $\hat{p} \in [0.629,0.642]$. On the other hand, in Case 3, five intervals underestimate p. For instance, when the true value is $p=0.7$, the estimated value falls within the range of $\hat{p} \in [0.645,0.662]$. As previously described in VandenHeuvel et al. [18], it is preferable to have a method that underestimates p, which means potentially removing clean data points during the regression function estimation. BART(Atr) contributes to greater forecasting accuracy, in contrast to the other three methods, especially for BART(Def).

Real data analysis

In this section, we demonstrate the application of the BART(Atr) model using the Boston Housing Price dataset, a well-known example commonly used for regression analysis [31, 32]. This dataset is accessible via the R package MASS and comprises 506 entries with 14 variables. The response variable is “medv” (median value of owner-occupied homes), and the dataset includes the following covariates: “crim” (per capita crime rate by town), “zn” (proportion of residential land zoned for lots over 25,000 square feet), “indus” (proportion of non-retail business acres per town), “chas” (Charles River, equal to one if the tract borders the river, zero otherwise), “nox” (nitrogen oxides concentration), “rm” (average number of rooms per dwelling), “age” (proportion of owner-occupied units built before 1940), “dis” (weighted mean of distances to five Boston employment centers), “rad” (index of accessibility to radial highways), “tax” (full-value property-tax rate), “ptratio” (pupil-teacher ratio by town), “black” ($1000(B - 0.63)^{2}$, where B represents the proportion of black residents by town), and “lstat” (lower status of the population). Descriptive statistics for the Boston Housing Price dataset can be found in Table 5.

Table 5 Descriptive statistics in the Boston housing price dataset

Table 5 provides statistics for the variables under consideration, which include minimum and maximum values, as well as mean and median values. It’s worth noting that, due to the discrete nature of the “chas” variable (taking values 0 or 1), mean statistics are not computed for it. Notably, the “black” and “zn” variables display a substantial difference between their maximum and minimum values, indicating higher volatility compared to the other variables. Additionally, the response variable “medv” exhibits nearly identical mean and median values, suggesting a symmetric distribution for “medv”. In the subsequent analysis, we use $\mu _{0}=23$, which is consistent with the mean of “medv”.

Random attacks

We consider random attacks, defined by

$$\begin{aligned} y_{i,a}=\left( 1+\frac{s}{100}\right) y_{i}, \end{aligned}$$

where $y_{i}$ is the unattacked data, $y_{i,a}$ is the attacked data, and $s \sim N(\mu ,\sigma ^{2})$. The $1 + s\%$ factor denotes randomly scales the data in the random attack. Here considering rand-attack 1 and 2:

• 1) rand-attack 1: $\mu =\mu _{0}$, $\sigma =50, 80, 150$; and

• 2) rand-attack 2: $\mu =2 \mu _{0}$, $\sigma =50, 80, 150$.

Generate a training dataset by randomly choosing 70% of the entries, while reserving the remaining 30% for the test dataset. Ensure a fair comparison by subjecting the training set to a random attack 100 times, and subsequently assess the outcomes, which encompass MAE and MAPE values, on the test set.

Results

Table 6 Forecasting results of the Boston housing price data under rand-attack 1

Tables 6 and 7 display the results for “rand-attack 1” and “rand-attack 2”. In “rand-attack 1”, Table 6 presents the MAE and MAPE values, as well as the running time, where MAE and MAPE are derived from 100 independent realizations, and the running time is the mean value of time in 100 realizations. Notably, when comparing BART(Atr) to the other three methods, BART(Atr) consistently yields significantly lower MAE and MAPE values. For instance, at a given parameter setting of $1-p=0.1$ and $\sigma =50$, BART(Atr) achieves a mean MAE of 2.634, while 2.888, 3.319 and 3.292 are provided in BART(Def), RLM and RLMD, respectively. This represents a substantial decrease, approximately 10%, 26%, 25%, in MAE from BART(Def), RLM, and RLMD to BART(Atr). At the same time, BART(Atr) achieves a median MAE of 2.616, while 2.850, 3.326, and 3.302 are provided in BART(Def), RLM, and RLMD, respectively. This represents a substantial decrease, approximately 9%, 27%, 26%, in MAE from BART(Def), RLM, and RLMD to BART(Atr). Similarly, the mean MAPE for BART(Atr) is 12.8%, whereas 14.2%, 16.5%, and 16.2% are provided in BART(Def), RLM, and RLMD, respectively. For BART(Def), RLM, and RLMD, they resulted in a roughly 11%, 29%, and 27% improvement with BART(Atr). At the same time, the median MAPE for BART(Atr) is 13%, whereas 14%, 16.6%, and 16.2% are provided in BART(Def), RLM, and RLMD, respectively. For BART(Def), RLM, and RLMD, they resulted in a roughly 8%, 28%, and 25% improvement with BART(Atr). Therefore, BART(Atr) exhibits superior performance to the three methods across MAE and MAPE metrics, offering significantly higher accuracy in the context of “rand-attack 1”. However, it should be noted that BART(Atr) needs more computational costs. More computational costs are required to find a proper value of p, where p signifies the proportion of unaffected data as stated in “Introduction” Section.

Table 7 Forecasting results of the Boston housing price data under rand-attack 2

Table 7 displays the results for “rand-attack 2”, presenting the MAE and MAPE values, as well as the running time. In the context of “rand-attack 2”, BART(Atr) almost consistently outperforms BART(Def) by yielding notably lower MAE and MAPE values. For instance, under the specified parameter settings of $1-p=0.1$ and $\sigma =50$, BART(Atr) achieves a mean MAE of 2.725, in contrast, BART(Def), RLM, and RLMD produce mean MAE of 2.930, 3.341 and 3.275. These result in a significant reduction, approximately 8%, 23%, and 20% in mean MAE when transitioning from BART(Def), RLM, and RLMD to BART(Atr). At the same time BART(Atr) achieves a median MAE of 2.694, in contrast, BART(Def), RLM, and RLMD produce mean MAE of 2.900, 3.342, and 3.265. These result in a significant reduction, approximately 8%, 24%, and 21% in median MAE when transitioning from BART(Def), RLM, and RLMD to BART(Atr). Similarly, the mean MAPE for BART(Atr) is 13.7%, whereas BART(Def), RLM, and RLMD yield the MAPE of 15%, 17.3%, and 16.7% indicating a substantial improvement of approximately 9.5%, 26.3% and 21.9% with BART(Atr). At the same time, the median MAPE for BART(Atr) is 13.6%, whereas BART(Def), RLM, and RLMD yield the MAPE of 14.9%, 17.1%, and 16.7% indicating a substantial improvement of approximately 9.6%, 25.7% and 22.8% with BART(Atr). In summary, BART(Atr) almost consistently demonstrates superior performance to the three methods across the MAE and MAPE values metrics within the context of “rand-attack 2”, showcasing a considerable increase in accuracy.

It’s important to note that BART(Atr) isn’t the best in the specified parameter settings of $1-p=0.4,0.5$ and $\sigma =150$, RLMD is the best in four methods. It shows that RLMD is a good choice under “rand-attack 2” with $1-p=0.4,0.5$ and $\sigma =150$. Just as in the previous “rand-attack 1” BART(Atr) gets the maximum value in four methods from a running time standpoint. It is noted that more computational costs in BART(Atr) are required to find a proper value of p, as stated in “Introduction” Section, where p signifies the proportion of unaffected data.

Fig. 3

Boxplots of results under rand-attack 1 with $\mu =\mu _{0}$, $\sigma =50$

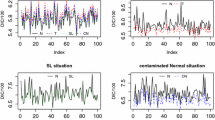
Figure 3 indicates boxplots in “rand-attack 1” with $\mu =\mu _{0}$, $\sigma =50$. According to the reviewer’s opinion, considering six boxplots as Fig. 3 for “rand-attack 1” and “rand-attack 2” with different $1-p=0.1,0.2,0.3,0.4,0.5$ and different $\sigma =50,80,150$, here only Fig. 3 as an example. Each boxplot in Fig. 3 represents 100 MAE and MAPE values in the test set based on 100 independent realizations. BART(Atr) is the best, which coincides with Table 6. Note also that Fig. 3 shows the MAE and MAPE values increase with a growth of $1-p$ in the methods.

To demonstrate the significance of our proposed BART(Atr) method in forecasting, we conducted a Wilcoxon signed-rank test using MAE and MAPE indexes. These indexes were obtained from 100 repeated experiments on the test set, specifically under rand-attack 1, as mentioned in Wu and Wang [33]. The results of the statistical tests are documented in Table 8. Based on the tests, it was determined that BART(Atr) outperformed three other methods in terms of prediction accuracy. However, it is important to note that BART(Atr) incurred higher computational costs, as indicated in Tables 6 and 7. Regarding MAE with $1-p=0.4,0.5$ and $\sigma =150$, neither BART(Atr) nor the RLMD methods exhibited statistical significance when considering $p \le 0.05$.

Table 8 Results of the Boston housing price data under rand-attack 1 with four different methods

Conclusions

In this study, we have introduced an extension to the robust regression method originally developed by Vandenheuvel et al. [18]. Our extension involves adaptive robust regression based on BART, which is tailored for nonlinear regression models. This novel approach referred to as BART(Atr), was employed to conduct analyses akin to those in the model presented in Chipman et al. [1], Cao and Zhang [24]. Specifically, we focused on forecasting in the presence of outliers. We further compared the performance of BART(Atr), as well as RLM, RLMD and BART(Def) in terms of forecasting metrics, including estimates of p, $\hat{p}$, and MAE and MAPE values. Our new method expands upon the concept of an asymptotic distribution for the order statistics of the residuals, utilizing BART to handle outliers in a regression context. We conducted a real data analysis involving random attacks, similar to the approach used in VandenHeuvel et al. [18], to assess the performance of our new method. The evaluation was based on metrics such as MAE and MAPE, and we measured these values across 100 independent realizations. Our findings consistently showed that the forecasts generated by the new method outperformed those of BART(Def), RLM, and RLMD in both simulation studies and real data analysis.

The findings presented in this study come with several significant limitations. Firstly, we restricted our analysis to random attack templates. For a more comprehensive understanding, especially in the context of forecasting electricity loads, it would be valuable to investigate the performance of BART(Atr) with different attack templates, such as ramp attacks. Future work should explore how the method performs under varying attack scenarios. Secondly, this study was primarily focused on the nonlinear regression model with i.i.d. errors. It might be beneficial to extend this framework to include models with non-i.i.d. errors, as contemplated in Sela and Simonof [34]. Furthermore, we specifically concentrated on the weight function $\psi (\cdot )$ mentioned in (8), following the recommendation in VandenHeuvel et al. [18]. We acknowledge that there exist various alternative weight functions, as extensively discussed in papers such as Wang et al. [21, 32], Wu and Wang [33], and Pratola et al. [35]. Among these alternatives, the two most commonly utilized functions are Huber’s weight function and the bisquare weight function shown in Wang et al. [21], Jiao et al. [36]. Future research endeavors should delve into exploring additional weight functions, expanding the scope of investigation in this area. Lastly, we limited our investigation to the default settings in the BART model, including parameters like $\alpha =0.95$ and $\beta =2$, as recommended in Chipman et al. [1]. We can consider $\alpha$ as an example; it represents the probability associated with a splitting node given $\beta =0$. In future research, it would be advantageous to explore data-driven approaches and examine how they compare to fixed-tuning parameter settings, as they tend to yield superior performance.