Two-stage many-objective evolutionary algorithm: enhanced dominance relations and control mechanisms for separated balance

Abstract

Although the multiobjective evolutionary algorithms (MOEAs) have been proved to bring promising prospects for solving multiobjective optimization problems (MOPs), the performance of the algorithm deteriorates sharply in high-dimensional objective space due to the weak selection pressure and the unregulated balance, which is caused by the increase of objective space dimension. Some current MOEAs with two-stage strategy (TS) strive to address above issues by dividing the evolutionary process into two independent stages, in which convergence and diversity are handled separately within successive generations of different stages. However, TS-MOEAs have some weaknesses, such as sensitivity to stage division, and incomplete separation of convergence and diversity. In this paper, TS/KW-MaOEA is proposed for solving many-objective optimization problems (MaOPs), which keeps TS as the central and equips a perfect control mechanism for separated balance. More specifically, TS/KW-MaOEA can automatically adjust the balance trend and provide appropriate selection pressure for MaOPs according to the Kondratiev wave (KW) search model and the objective space dimension. To verify the effectiveness of the proposed algorithm, a series of experiments are carried out against seven state-of-the-art many-objective optimization algorithms on 15 benchmark problems with up to 30 objectives. Experimental results indicate that the proposed algorithm is highly competitive against peer competitors.

Introduction

In recent years, multiobjective optimization problems have attracted a considerable interest of researchers due to their widespread appearance in the real world. A multiobjective optimization problem (MOP) [1] that involves two or more conflicting objectives to be optimized simultaneously is briefly stated as

$$\begin{array}{c}\underset{\mathbf{x}}{\text{min}}F\left(\mathbf{x}\right)=\left({f}_{1}\left(\mathbf{x}\right),{f}_{2}\left(\mathbf{x}\right),\dots ,{f}_{m}\left(\mathbf{x}\right)\right)\\ s.t. x\in \Pi \end{array}$$

(1)

where m is the number of objective functions, Π is the decision space with $\mathbf{x}=\left({x}_{1},{x}_{2},\dots ,{x}_{n}\right)$ being a decision vector of n decision variables. For a vector x in the decision space, there exists a corresponding objective vector, denoted by f(x), in the objective space. Multiobjective optimization problems (MOPs) with more than three objectives are often referred to as many-objective optimization problems (MaOPs) [2]. Without loss of generality, the MaOPs discussed in this paper are all minimization problems.

Since evolutionary algorithms (EAs) can obtain a set of solutions in a single run due to the population-based heuristic, multiobjective EAs (MOEAs) have developed quickly over the last 2 decades [3]. For many real-world engineering applications, any optimization of one objective often leads to a deterioration in at least one other objective due to the conflicting nature between objectives. Since the consideration of conflicting objectives is the key to deal with optimization problems, many MOEAs tend to a compromise search. Classical MOEAs can be roughly classified into three categories: Pareto-dominance-based MOEAs, decomposition- and indicator-based MOEAs.

The basic idea of Pareto-dominance-based MOEAs is to distinguish and select candidate solutions according to dominance relation, that is, the dominant solution dominates the inferior solution. Specifically, the solutions are sorted according to the Pareto dominance relation. Then, auxiliary strategies are applied to select the nondominated solutions, and finally a set of optimal solutions are obtained, which are distributed uniformly on the Pareto front (PF). An example of these algorithms is NSGA-II [4], designed by Deb et al., which is an elitist nondominated sorting genetic algorithm. Pareto-dominance-based MOEAs show significant effect in dealing with MOPs, however, the performance of these algorithms deteriorate severely when the number of objectives increases. With the increase of dimension and the mushrooming of nondominated solutions [5], MOEAs tend to search randomly. Since Pareto dominance is employed as a major selection criteria, the weakening of selection pressure will bring down the convergence ability of the solution toward the Pareto front.

The decomposition-based MOEAs decompose the MOP into a number of single objective optimization problems (SOPs) and optimize them simultaneously. An example of classical algorithms is MOEA/D proposed by Zhang and Li [6]. Compared with Pareto-dominance-based MOEAs, decomposition-based MOEAs are more efficient in dealing with MaOPs since they do not need to consider the conflict between objectives. However, decomposition-based MOEAs relies too much on the decomposition method and relevant mathematical methods. Whereas the weight aggregation method is not effective for the minimization problems with non-convex PF.

The indicator-based algorithms aim to enhance the environmental selection pressure to improve the undesirable effect of Pareto dominance relation in solving complex problems. The indicator-based MOEAs employ certain performance indicators, such as hypervolume (HV) indicator, R2 indicator and ∆p indicator [7,8,9] to measure the quality of solutions. A representative example of classical algorithms is IBEA [10], proposed by Zitzler et al., which uses fitness values based on scaled values to select individuals, regardless of Pareto-based ranking of the individuals. However, the computational complexity of most of the indicators is quite expensive, and there is no indicator preference for evaluating all problems.

Based on the above analysis, there still some challenges for MOEAs to deal with MaOPs. First, Pareto dominance lacks selection pressure in high-dimensional objective space [11]. Since most solutions of the population for next generation always come from nondominated solutions on the first PF, it is difficult to distinguish superior solutions and inferior solutions. Consequently, the performance of algorithms may worsen since their search ability are noticeably deteriorated. Second, it is difficult to make a good balance between convergence and diversity with the increase of spatial dimensions [12]. Third, how to reasonably allocate resources and reduce computational cost to improve algorithm performance becomes a challenge task as the number of objectives increases.

To solve the above problems, MaOEAs are proposed for MaOPs, most of which are the extension and improvement of traditional mainstream MOEAs. The main improvement methods can be summarized as follows.

1) Pareto-dominance-based MOEAs is extended to further balance the convergence and diversity in the evolutionary process. Three kinds of improvements can be observed, that is, evolution strategies, elite selection mechanism and diversity maintenance mechanism. For the first case, Lin et al. [13] proposed multiple search strategies to accelerate convergence and maintain population diversity. For the second case, the Pareto dominance relationship definition and the ranking methods of solutions are modified to solve MaOPs, such as g-dominance [14] and r-dominance [15] based on reference point, $\epsilon$-dominance [16] based on grid system design and fuzzy dominance with fuzzy logic [17, 18]. The dominance relations mentioned above are the relaxed form of Pareto dominance relation, which can more easily dominate solutions in a high-dimensional objective space. For the last case, Deb and Jain [19] proposed a reference-point-based many-objective NSGA-II, namely NSGA-III. NSGA-III uses a set of evenly distributed reference vectors to maintain diversity and modifies niche strategies simultaneously. Although the loss of selection pressure caused by Pareto dominance cannot be solved directly, a set of well-spread reference vectors is beneficial for balancing the convergence and diversity. Grid-based evolutionary algorithm (GrEA) [20] employs the grid adaptive strategy to enhance the selection pressure while ensuring uniform distribution among solutions. Knee point-driven evolution algorithm (KnEA) [21] employs knee points as a secondary selection criteria to strengthen the selection pressure. As the representative of the compromise solution, the knee points can accelerate convergence but have the tendency to prefer local optimum.

(2) The decomposition- and indicator-based MOEAs are improved to reduce the dimension and complexity of MaOPs. Three kinds of improvements are proposed, that is, decomposition strategies, reduction of redundant objectives and preference space, specific indicator-based MaOEAs. For the first case, the mainstream methods that decompose MaOP into SOPs include weighted sum approach, Tchebycheff approach and penalty-based boundary intersection approach, which have been fully discussed in [6]. Similarly, there are good prospects to explore the way in which MaOP is decomposed into MOPs. For the second case, Pal et al. [22] proposed a differential evolution using clustering based objective reduction algorithm (DECOR), which employs clustering method to eliminate minor objectives. However, it is difficult to reduce objectives in the real-world applications, since objective reduction methods only rely upon a relative order importance between the objectives [17]. For more problems, even if the number of objectives is fully reduced, it is also difficult to use PF in the low-dimensional objective space to portray the true PF in the original high-dimensional objective space. MaOEA based on objective space reduction and diversity improvement (MaOEA-RD) algorithm [23] incorporated the decomposition approach to reduce the objective space, which is more effective for specific PF. For the last case, the specific indicator-based EAs are developed for solving MaOPs, such as hypervolume-based MaOEA [7], pure diversity indicator (PD) [24] and IGD indicator-based MaOEA [25].

(3) Hybrid methods that combine several methods, such as Pareto dominance and performance indicators, are developed to pursue the promising convergence and diversity instead of a compromise between them. A representative example is a two-stage strategy (TS). TS divides the evolution into two stages, the convergence is considered in the former stage, while the diversity is addressed in the latter stage. In other words, there is no longer any compromise search tendency during the two-stage evolution, since the balance that is oriented toward which one will be adjusted by the separation control mechanism. Although this method is conducive to adjusting the trend of balance to satisfy the requirements of different MaOPs, most TSs cannot guarantee that the separated properties do not affect each other. Typical algorithms such as MaOEA-IT [26] should not only address the balance between convergence and diversity, but also reduce the complexity of MaOPs.

The above two-stage evolution studies provide an effective way to address MaOPs and bring a promising prospect to the domain. Nevertheless, as highlighted in [26], further research is still needed since the proposed methods cannot be effective in solving some MaOPs. In addition, the change of a single property in two sequential stages may influence the balance between convergence and diversity due to their conflicting nature. This observation greatly motivates us to exploit more effective control strategies for separated balance. Inspired by the theory of Kondratiev waves [27], a novel MaOEA with two-stage framework, termed TS/KW-MaOEA, is proposed in this paper. In the proposed TS/KW-MaOEA, the appropriate enhancement Pareto method is used to guide the search direction in each stage, which improves one feature of convergence and diversity without deteriorating the other. Furthermore, inspired by Kondratiev waves, the proposed algorithm can effectively deal with the problems caused by the lack of selection pressure in the high-dimension objective space and significantly alleviate the conflict between convergence and diversity in two stages. In conclusion, the contributions of TS/KW-MaOEA are highlighted as follows.

(1) A novel two-stage strategy model for dealing with MaOPs is proposed, which has dynamic periodicity similar to Kondratiev waves. The originally independent two stages alternate with each other according to the evolution process and the number of objectives. TS/KW model can promote the information transfer between different stages and weaken the negative effect on balance caused by the change of a single property.

(2) Two enhancement dominance methods that match the stage features are proposed, where the combination of decomposition approach and Pareto dominance is conducive to separation control. In the first stage, the hybrid dominance method is used to maintain population diversity without deterioration in convergence-dominated circumstances, which propels the obtained solutions to effectively approximate the true PF. In the second stage, the grid dominance method is employed to provide dynamic selection pressure.

(3) Two environmental selection components that match the dominance relation are proposed, which aims to maintain population diversity in the first stage, explicitly improves population diversity in the second stage, and reduces the computational complexity of the algorithm.

(4) This paper discusses the influence of different components in TS on algorithm performance, especially the importance of the first stage in TS. In addition, this paper studies the parameter settings of related components and search behavior, and gives rational explanations on advantages and deficiencies of TS/KW model.

The remaining of this paper is organized as follows. Section “Related works” reviews the related works and introduces the motivation of the proposed TS/KW-MaOEA. Section “Proposed algorithm” discusses TS/KW-MaOEA in detail. To evaluate the performance of TS/KW-MaOEA, a series of experiments is carried out and discussed in Section “Experimental results and discussion”. Finally, the conclusion and future works are given in Section “Conclusion”.

Related works

In this section, we briefly introduce some basic components related to our work, as well as their advantages and deficiencies.

Hybrid dominance

Pareto-dominance- and decomposition-based MOEAs have shown significant effects in dealing with simple MOPs. However, the former can hardly provide sufficient selection pressure for solutions to converge to the true PF due to its compromise nature, while the latter can hardly maintain the distribution of solutions due to its diversity characteristics. The two methods interact violently due to their failure to be effectively separated during the search, hence, they cannot work effectively for solving complex MOPs or MaOPs. Meanwhile, Pareto-dominance- or decomposition-based MOEAs usually employ distance metric or angle metric. However, with the increase of dimensions, the distribution of solutions becomes more complex and tends to be orthogonal, which significantly reduces the effectiveness of the methods. Therefore, many improvement strategies have been developed to make up for deficiencies. Zhang et al. [28] employed the information feedback model, which uses the information in the previous iteration to update the current individual. Yi et al. [29] proposed an array of improved crossover operators to improve the performance of the NSGA-III algorithm. Sun et al. [30] proposed an improved memetic algorithm (IMOMA-II), which uses the increment of the hypervolume to develop an activation strategy for every local search procedure.

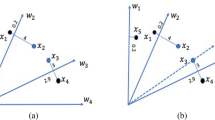
The dominance relation that combines Pareto dominance and decomposition-based approach is termed as hybrid dominance. The hybrid dominance method decomposes the complex problem into a number of simple subproblems to reduce its computational complexity. In addition, the hybrid dominance method can guarantee the effectiveness of the combination metric of distance and angle, which is conductive to separated balance control. Research shows [19] that hybrid dominance method has a promising potential for higher-dimensional problems. Some examples are MOEA/D-D [31] and RP-dominance-based (NSGA-II-RPD) [32]. In the NSGA-II-RPD, the reference-point dominance (RPD) is designed. First, a set of uniformly distributed reference vectors is defined in the objective space [19, 33]. Then, the projection distance and vertical distance of the solution with respect to the reference vector are calculated by formulas (2) and (3). Each solution is associated with the reference vector with the minimum vertical distance.

$${d}_{1}\left(\mathbf{x}\right)=\frac{\Vert f{\left(\mathbf{x}\right)}^{T}w\Vert }{\Vert w\Vert }$$

(2)

$${d}_{2}\left(\mathbf{x}\right)=\Vert f\left(\mathbf{x}\right)-{d}_{1}\left(\mathbf{x}\right)\frac{w}{\Vert w\Vert }\Vert $$

(3)

where f(x) is an objective vector of a solution x, and w is a reference vector. d₁(x) and d₂(x) represent the projection distance and vertical distance of the solution x with respect to the reference vector w, respectively, as shown in Fig. 1.

Fig. 1

Distance measures d₁ and d₂ with respect to the reference vector w

The RP-dominance relation (RPD) is defined as follows.

Definition 1 (RPD):

For two solutions u and v, u is said to dominate v, denoted by $u{\prec }_{RP}v$ if one of the following conditions holds true.

• (1) $u\prec v$ or.

• (2) $u$ and v are equivalent in terms of Pareto.

  • (a) u and v are associated with the same reference vector, and ${d}_{1}\left(u\right)<{d}_{1}\left(v\right)$ or.

  • (b) u and v are associated with the different reference vector, ${d}_{1}\left(u\right)<{d}_{1}\left(v\right)$ and $SD\left(u\right)<SD\left(v\right)$.

where SD(u) represents the density of the subregion u belongs to, that is, the number of solutions associated with the reference vector of u.

RPD uses a set of uniformly distributed reference points to construct a strict partial order on a set of nondominated solutions [32]. However, the adverse effects caused by standardization operation are not considered. In addition, the dominance rule based regional density only considers the convergence measure d₁ and ignores the diversity measure d₂, which easily leads to the sparse distribution of the solution set.

Grid dominance

The grid-based Pareto-dominance relation is termed as grid-domination relation (GRD). A grid has the characteristics of reflecting the distribution of solutions based on coordinates [20]. The convergence of solutions can be estimated by the coordinate difference of solutions. The grid-domination system has taken shape in ϵ-MOEA and expanded in GrEA. GRD divides the objective space into a group of hyperboxes with the same size and assigns coordinates to each solution by formulas (4)–(7).

$${lb}_{k}={fmin}_{k}-\left({fmax}_{k}-{fmin}_{k}\right)/\left(2\times div\right)$$

(4)

$${ub}_{k}={fmax}_{k}+\left({fmax}_{k}-{fmin}_{k}\right)/\left(2\times div\right)$$

(5)

$${d}_{k}=\left({ub}_{k}-{lb}_{k}\right)/div$$

(6)

$$ G_{k} \left( {\mathbf{x}} \right) = \left\lfloor {\left( {f_{k} \left( {\mathbf{x}} \right) lb_{k} } \right)/d_{k} } \right\rfloor $$

(7)

where ub_k and lb_k represent the upper and lower bounds of the grid in the kth objective, respectively. fmax_k and fmin_k represent the maximum and minimum values of the solution in the kth objective, respectively. div represents the number of divisions of each objective dimension, while d_k represents the width of the hyperbox in the kth objective. G_k(x) and f_k(x) denote the coordinate and the function value of the solution x in the kth objective, respectively. Figure 2 shows an example of a grid setting in the kth objective.

Fig. 2

An example of a grid setting in the kth objective

RGD is defined as follows.

Definition 2 (RGD):

For two solutions u and v, u is said to dominate v, denoted by $u{\prec }_{GP}v$ if one of the following conditions holds true.

• (1) $u\prec v$ or.

• (2) $u$ and v are equivalent in terms of Pareto. For $\forall i\in \left(\text{1,2},\dots ,m\right)$ such that ${G}_{i}\left(u\right)\le {G}_{i}\left(v\right)$, and there is $j\in \left(\text{1,2},\dots ,m\right)$ such that ${G}_{j}\left(u\right)<{G}_{j}\left(v\right)$.

In addition, the coordinate difference is converted into grid difference (GD) by formula (8). The larger the div, the smaller the size of a unit hyperbox and the greater the difference between solutions.

$$GD\left(u,v\right)=\sum_{k=1}^{M}\left|{G}_{k}\left(u\right)-{G}_{k}\left(v\right)\right|$$

(8)

Although the grid-dominance relation achieves better results in dealing with MaOPs, the method based on hyperbox relies on data structure with exponential growth. In addition, since the grid system increases extra computation to deal with the solutions in the hyperbox, the computational cost is high.

Kondratiev wave

The statistical research concludes that Kondratiev wave is the pattern of long run fluctuations in economic growth [27]. As shown in Fig. 3, the cycle marked by T₁ includes four periods from t₁ to t₄, namely the recovery, prosperity, recession and depression of economic development, and the economic law follows this cycle.

Fig. 3

Illustration of Kondratiev wave

Kondratiev waves are driven by technological innovations. The dividend brought by the new technology triggered the economic balance from depression to recovery, however, the saturation of dividends and the stagnation of technology have broken the balance, making the economy turn from prosperity to recession [34]. The Economics of Keynes advocates macro-control in the period of economic downturn. In short, the waves with opposite influence caused by discontinuous superposition can counteract or moderate the extent of recession.

In MaOEAs, convergence and diversity conflict with each other during the evolution [10, 35], and thus the solution with good convergence usually has poor diversity. In the second stage of TS, the adjustment method focusing on diversity often deteriorates the convergence. Similar to the Kondratiev waves cycle, TS-MaOEAs involve parameters that control resource allocation during the evolution. The parameters determine when the search enters the second stage, and then affect the balance of convergence and diversity. However, it is difficult to determine the computational resources required at each stage, and improper allocation will lead to performance degradation. Thus it can be seen that there are great commonalities between TS-MaOEAs evolution process and Kondratiev waves. It is feasible to study the evolution behavior of TS-MaOEAs with the assistance of Kondratiev waves.

Proposed algorithm

In this section, the TS/KW-MaOEA framework and its components are introduced, where the control mechanisms for separated balance are described in detail. To ensure the compatibility and robustness of TS/KW-MaOEA, the control mechanisms for separated balance can be summarized into the following three levels. In the first level, the equilibrium state of the solution set is separated into the convergence state and the distribution state, and the corresponding compromise search tendency is separated into convergence first and diversity first. Stages with different search tendencies are carried out alternately through TS/KW model. In the second level, the stages with different search tendencies employ appropriate dominance rules, selection criteria and maintenance strategies, which are designed in the dominance relation, mating selection components and environmental selection components. In the third level, the measurement values that correspond to the stage characteristics are used to represent the convergence state and distribution state at different stages.

The framework of TS/KW-MaOEA is outlined in Section “Framework of TS/KW-MaOEA.” Section Enhanced dominance relations describes the two enhanced dominance relations in detail. Finally, mating selection component, environmental selection component and Pareto-optimal subspace learning strategy are discussed in Sections 3.3 to 3.6.

Framework of TS/KW-MaOEA

Similar to NSGA-II, the framework of the proposed TS/KW-MaOEA is outlined in Algorithm 1, which consists of the following three steps. First, the Das and Dennis’s method is used to generate a set of reference vectors $W=\left\{{w}_{1},{w}_{2},\dots ,{w}_{N}\right\}$ with the same size as the population P. Meanwhile, an archive A is initialized for storing the nondominated solution obtained in the first phase (lines 1–4). Second, the current stage S is calculated with the TS/KW model (line 6). The construction of the TS/KW model will be described in the experiment in Section IV-E. Subsequently, the binary tournament selection, simulated binary crossover [36] and the polynomial mutation [37] operators are employed to generate the offspring U’ (lines 7–8). In the first and second stages, the mating selection component employs d₂ metric and SD metric, which are mentioned in Section Hybrid dominance, as the secondary criteria for selection, respectively. Finally, the solutions that are propagated to the next generation are selected from the union of the parent population and the offspring. The final solution set is obtained through continuous iteration (lines 9–12). In the first and second stages, the environmental selection component uses the truncation method and the allocation method as the elimination strategy, respectively. In addition, the archive A is used to learn the Pareto-optimal subspace in the second stage. An efficient nondominated sorting (ENS) approach [38] is used in the proposed TS/KW-MaOEA.

Algorithm 1: Framework of TS/KW MaOEA

Enhanced dominance relations

(1) Subregion hybrid Dominance relation

Since the penalty-based boundary intersection (PBI) approach can obtain a set of Pareto optimal solutions that approximate the PF very well, the PBI-based subregion hybrid dominance relation (PHD) is introduced to control the convergence independently in the first stage of TS. Mathematically, PBI approach is in the form

$$PBI\left(\mathbf{x}\right)={d}_{1}\left(\mathbf{x}\right)+\theta {d}_{2}\left(\mathbf{x}\right)$$

(9)

where d₁(x) and d₂(x) are defined in Eqs. (2)–(3). θ is a penalty parameter, which can control the search direction and affect the convergence process [39]. When the θ is small, the search emphasizes the convergence, otherwise the diversity is emphasized. However, most MaOEAs usually set the parameter θ to 5 to maintain a compromise search tendency. In view of the balance tendency in the first stage, θ is set to 1 in this paper. PHD is described as follows, where $\left(\overline{\cdot}\right)$ denotes the normalization.

Definition 3 (PHD):

: For two solutions u and v, u is said to dominate v, denoted by $u{\prec }_{PH}v$ if one of the following conditions holds true.

(1) $u\prec v$ or.

(2) $u$ and v are equivalent in terms of Pareto.

a) u and v are associated with the same reference vector in the case of normalization.

• $\overline{PBI }\left(u\right)<\overline{PBI }\left(v\right)$

• $\overline{PBI }\left(u\right)>\overline{PBI }\left(v\right)$, u and v are associated with the same reference vector in the case of standardization; $PBI\left(u\right)<PBI\left(v\right)$, ${d}_{1}\left(u\right)<{d}_{1}\left(v\right)$ and $\overline{{d }_{1}}\left(u\right)<\overline{{d }_{1}}\left(v\right)$.

b) u and v are associated with the different reference vector in the case of normalization. However, u and v are associated with the same reference vector in the case of standardization; $\overline{PBI }\left(u\right)<\overline{PBI }\left(v\right)$ and $PBI\left(u\right)<PBI\left(v\right)$; $\overline{{d }_{1}}\left(u\right)<\overline{{d }_{1}}\left(v\right)$, ${d}_{1}\left(u\right)<{d}_{1}\left(v\right)$ and $\overline{SD }\left(u\right)<\overline{SD }\left(v\right)$.

As shown in Fig. 4, since the scale of each objective is different, the distribution of the solution and reference vector has changed in the case of standardization and normalization. In the Fig. 4a, the reference vectors with standardization are uniformly distributed in the entire objective space, while they are not necessarily uniformly distributed on the entire PF. As shown in Fig. 4b, the normalized solution set has the same span for each objective. However, the reference vectors are not uniformly distributed in the entire objective space, which is more likely to lead to the non-uniform distribution of solutions on the PF. Therefore, d₁ and SD are different in the case of standardization and normalization, and the dominance relation between solutions are also different [39, 40].

Fig. 4

Distribution of standardized or normalized reference vectors in the objective space, and distribution of standardized or normalized solutions on PF

PHD follows the dominance rules of normalization first and standardization second. For two normalized solutions u and v that are associated with the same reference vector, the solution with smaller $\overline{PBI }$ is superior in comparison. To ensure the accuracy of the results, it is necessary to judge whether they are associated with the same reference vector in the case of standardization. If so, PBI values are further compared. To ensure better convergence, the inferior solution in the above cases should meet the requirements of the smaller PBI, d₁ and $\overline{{d }_{1}}$ are used to reverse its disadvantage position. Similarly, for two normalized solutions u and v that are associated with different reference vectors, strong selection pressure is required to distinguish them. The superior solution should meet the requirements of the smaller $\overline{PBI }$, PBI, $\overline{{d }_{1}}$, d₁ and $\overline{SD }$, which can avoid the deterioration of the diversity of the superior solution.

(2) Dual grid dominance relation

Since the grid can explicitly depict the distribution of solutions, the second stage of TS uses a dual grid dominance (DGD) relation to conduct separated control on diversity. DGD eliminates the comparison between the solutions inside the hyperbox to reduce the computational cost. Coordinate parameters of solution x, $GP\left(x\right)=\left\{{G}_{1}\left(x\right),{G}_{2}\left(x\right),..{G}_{m}\left(x\right)\right\}$, are obtained from formulas (4)–(7). A solution is assigned a level according to the coordinate parameters, and the second level grid consists of the hyperboxes with the same level.

Figure 5 shows an example of two-dimensional objective space. The first level distinguishes a pair of Pareto equivalent solutions in a similar way to GRD. For instance, the solution in hyperbox C can dominate the region marked by the dotted line. The sum of coordinate parameters of hyperbox is calculated by $GS\left(x\right)={G}_{1}\left(x\right)+{G}_{2}\left(x\right)+\dots +{G}_{m}\left(x\right)$. The solutions in the same hyperbox share the GS value. For example, for any solution x in hyperbox A, $GS\left(x\right)=7$. The hyperboxes at the same level in the second grid are labeled as connected regions with the same color and share the Level value. For instance, for any solution x in hyperbox D and E, $Level\left(x\right)=4$.

Fig. 5

Illustration of DGD in the objective space with M = 2 and div = 5

In view of the above-mentioned description, DGD is defined as follows.

Definition 4 (DGD):

For two solutions u and v, u is said to dominate v, denoted by $u{\prec }_{DG}v$ if one of the following conditions holds true.

(1) $u\prec v$ or.

(2) $u$ and v are equivalent in terms of Pareto.

(a) In the first level grid, $u{\prec }_{GR}v$.

(b) u and v are equivalent in terms of the first level grid; $GS\left(u\right)<GS\left(v\right)$ and $Level\left(u\right)<Level\left(v\right)$.

As shown in Fig. 5, any couple of solutions from hyperboxes A and C are equivalent in terms of Pareto, and the advantages and disadvantages of the two are hard to distinguish with GRD. Here, the square of distance metric δ² is used to indicate the convergence state of the solution, where δ is the Euclidean distance from the ideal point to the hyperbox. core_δ² denotes the convergence of the central solution of the hyperbox. max_δ² and min_δ² represent the maximum and minimum convergence of the solution inside the hyperbox, respectively. Then, the convergence of hyperboxes A and C is calculated respectively, that is, $coer\_{\delta }^{2}\left(A\right)=22.5$ and $coer\_{\delta }^{2}\left(C\right)=12.5$. Hyperbox C is significantly better than hyperbox A. From a solution perspective, ${min\_\delta }^{2}\left(a\right)=17$ and $max\_{\delta }^{2}\left(c\right)=18$, where a and c are the solutions in the hyperboxes A and C, respectively. Since the worst case of the solution in hyperbox C is almost the same as the best case of the solution in hyperbox A, there is a high probability that the solution from hyperbox C has better convergence than the solution from hyperbox A. In the case of sufficiently small hyperbox, each hyperbox can hold one solution at most, then hyperbox C has faster convergence than hyperbox A. For simplicity, the GS value is used to represent the convergence of the solution in the hyperbox. For instance, $GS\left(C\right)=6$ and $GS\left(A\right)=7$. Therefore, hyperbox C is better than hyperbox A in terms of convergence. It is worth noting that GS implicitly protects the hyperbox along the border while representing the convergence state. For example, the convergence of hyperboxes C and E is $core\_{\delta }^{2}(C)=core\_{\delta }^{2}(E)=12.5$, and $max\_{\delta }^{2}\left(c\right)=18$, $max\_{\delta }^{2}\left(e\right)=17$, $min\_{\delta }^{2}\left(c\right)=9$, $min\_{\delta }^{2}\left(e\right)=8$. It can be seen from the results that the convergence of hyperboxes C and E is almost the same. However, $GS\left(E\right)=5$ and $GS\left(C\right)=6$, due to the grid characteristics, the hyperbox E along the boundary wins the comparison, which is inconsistent with the result that the solution in hyperbox C is equivalent to the solution in hyperbox E in a large probability.

When comparing a couple of approximate Pareto equivalent solutions, since the GS metric overestimates the solution in the hyperbox along the boundary, the Level metric is used in the second level grid to complement the GS metric. The second level grid layers the hyperbox horizontally according to δ². The closer the hyperbox is to the ideal point, the smaller its Level value is, and the better the hyperbox convergence at this level is. In the comparison of a couple of approximate Pareto equivalent solutions, the Level metric may highly evaluate the hyperbox in the inner layer, which can guarantee the convergence and implicit loose diversity representation. Therefore, according to the DGD relation, hyperbox C can dominate hyperbox A and is equivalent to hyperbox E. For other simple cases, for example, hyperbox B can dominate hyperbox A.

Compared with GRD, DGD has simple structure and less computation, but it does not compare Pareto equivalent solutions within the same hyperbox. If the hyperbox is sufficiently small, each hyperbox can hold one solution at most. Accordingly, there are no two Pareto equivalent solutions in the same hyperbox. The number of hyperbox can be formed as

$$div=\alpha \cdot \left(1+\frac{\Vert {PF}_{1}\Vert }{\Vert {P}_{t}\Vert }\right)$$

(10)

where $\Vert \cdot \Vert$ denotes the number of vectors. α is the threshold factor related to the objective number m. PF₁ denotes nondominated solutions on the first PF, and P_t is the population at generation t. Considering the number of reference points with m objectives ($m\in [\text{3,15}]$) generated by the Das and Dennis method, α is set to $2m(m-2)$ in this paper. Clearly, formula (10) indicates that the number of hyperboxes can be controlled within the range [$\alpha ,2\alpha$]. After the above operations, Pareto equivalent solutions still exist in the same hyperbox, so the environmental selection components based on the decomposition method and allocation principle are used to select these solutions. The details are presented in Section III-D.

Mating selection

In TS/KW-MaOEA, the mating selection component uses the binary tournament, which follows convergence measure (CM) first and diversity measure (DM) second. The steps of mating selection is shown in Algorithm 2, which is composed of three steps: (1) initialize mating pool (line 1) and (2) different nondominated sorting methods are selected according to the evolution state (lines 3–9). For the first stage that focuses on convergence, the efficient nondominated sorting with PBI-subregion hybrid dominance (PHD-ENS) is used, where the nondominated rank representing convergence is stored in CM (line 4), and the d₂ metric representing diversity is stored in DM (line 5). For the second stage that focuses on diversity, the efficient nondominated sorting with dual grid dominance (DGD-ENS) is used, in which the nondominated rank representing convergence is stored in CM (line 7), and the SD metric representing diversity is stored in DM (line 8). $DM\left(x\right)$ represents the metric value obtained by normalizing the solution x and the associated reference vector. 3) Solution a and solution b are randomly selected from the current set P for comparison, and the solution with small CM value wins in comparison (lines 12–15). If the CM values of a and b are the same, the solution with smaller DM value wins in comparison (lines 17–20). Otherwise, one of the two is randomly selected as the winner (lines 22–26). The winner is put into the mating pool, and the comparison operation is repeated until the mating pool is saturated.

Algorithm 1: Mating Selection

The mating selection component continues to consider diversity on the premise of ensuring convergence, and selects the appropriate dominant method for the search operation at each stage. The PHD method is conducive to selecting solutions that can effectively promote population convergence without deteriorating its distribution state, while the DGD method can select solutions with good diversity from approximate Pareto equivalent solutions. In addition, the d₂ metric and SD metric utilized in the components can be reused, which can replace the crowding-distance to reduce the consumption of computational resources.

Environmental selection

The environmental selection component in TS/KW-MaOEA uses the diversity maintenance strategy including truncation mode and allocation mode, and the diversity metric is used to replace the crowding-distance. The steps of environmental selection operation are shown in Algorithm 3. First, different nondominated sorting methods are selected according to the evolution state (lines 3–10). In the first stage that focuses on convergence, PHD-ENS is used as a nondominated sorting method. The nondominated rank representing convergence is stored in $CM^{\prime}$ (line 4), and the d₂ metric representing diversity is stored in $DM^{\prime}$ (line 5). In the second stage that focuses on diversity, DGD-ENS is used as a nondominated sorting method. The nondominated rank representing convergence is stored in $CM^{\prime}$ (line 8), and the cosine similarity value representing diversity is stored in $DM^{\prime}$ (line 9). $DM^{\prime}(x)$ represents the metric value of solution x and the associated reference vector in the case of normalization, and $DM^{\prime}\left(x,{w}_{j}\right)$ represents the metric value of solution x and the specified reference vector w_j in the case of normalization. Third, the solutions in each PF are added into the solution set P in the order of their rankings until no more solutions can be accommodated (lines 11–14). Finally, in the first stage, if the size of solution set P is larger than N, P is truncated in the ascending order of d₂ metric (lines 15–19). The nondominated solutions in the first PF are copied into the archive A (line 20). In the second stage, the cosine similarity of each solution and its specified reference vector w_j is calculated, and each reference vector is assigned a solution with the maximum cosine similarity.

Algorithm 3: Environmental Selection

In the second stage, the environmental selection component in TS/KW-MaOEA employs the allocation method based on cosine similarity metric to maintain diversity, that is, each reference vector is assigned a solution closest to it. Since the reference vector is the same size as the solution set, the closer the assigned solution is to the reference vector, the more the solution can maintain a similar uniform distribution with the reference vector. Figure 6 shows an example of solution selection based on cosine similarity metric.

Fig. 6

An example of solution selection based on cosine similarity metric

In Fig. 6, solutions a and b with the same d₂ metric are on the right side of the reference vector w₁, while solutions c and d with the same d₂ metric are on the left side of the reference vector w₂. If d₂ metric and the truncation method are used, solutions b and d in the inner PF will be reserved. In the above cases, due to the small distance between the reserved solutions on the opposite side and the large distance between the solutions on the same side, it is easy to cause dense regions and sparse regions, which is not conductive to diversity maintenance. If the allocation method based on cosine similarity metric is employed, solutions a and c will be reserved, which can significantly improve the distribution state of solution set. However, the solutions with better convergence in the inner PF are eliminated, which will deteriorate the convergence of solutions.

Figure 7 shows an example of environmental selection process at different stages. As shown in Fig. 7a, in the first stage of focusing on convergence, since the environmental selection component focuses on preventing the deterioration of diversity, the traditional truncation method is used. In the second stage of focusing on diversity, since the environmental selection component aims to improve the distribution of solutions, the allocation method is used. As shown in Fig. 7b, the allocation method can provide opportunities for eliminated solutions that use the truncation method to enter the next generation. However, some solutions may far away from the true PF. To address this problem, a Pareto optimal subspace learning strategy is used before the nondominated sorting, which aims to find subregions that approximate the true PF and reduce the regions outside the subregions to compensate for the loss of convergence. In addition, the alternate execution of the two stages used in TS/KW-MaOEA can effectively alleviate the adverse effects on convergence caused by environmental selection in the second stage.

Fig. 7

Example of environmental selection process at different stages. a Stage 1; b Stage 2

Pareto-optimal subspace learning

The principal component analysis approach (PCA) used in TS/KW-MaOEA aims to learn the Pareto optimal subspace. The execution process can be roughly divided into the following three steps, as shown in Algorithm 4. First, the archive A is used to construct the sample matrix K of PCA, and the threshold value ϵ is initialized. Each row of matrix K represents a solution x, and each column represents a component of the solution set. The second step is to conduct principal component analysis (lines 4–9). Specifically, the eigenvalue $V=\left\{{v}_{1},{v}_{2},\dots ,{v}_{M}\right\}$ of $K{\prime}$ is calculated, and then the principal component is determined based on the subscript and the threshold ϵ. Finally, the mean value is used to replace the upper and lower bounds of non-principal components. The space bounded by the new upper and lower bounds is called the Pareto optimal subspace (lines 10–14).

Algorithm 4: Pareto optimal Subspace Learning

The Pareto optimal subspace learning strategy can locate the region where the true PF exists and reduce the region outside the located region. On the one hand, computational resources are concentrated on potential regions. On the other hand, it compensates for the convergence loss caused by the environmental selection component in the second stage. In addition, since both DGD and allocation strategies require more computational resources, the Pareto optimal subspace learning strategy uses the PCA dimensionality reduction method with low computational complexity to reduce the computational cost in the second stage.

Experimental results and discussion

To evaluate the performance of the proposed algorithm TS/KW-MaOEA in solving MaOPs, a series of experiments is performed against six state-of-the-art MaOEAs.

Experimental setting

(1) Benchmark Test Problems: Two popular test problems, DTLZ test suite [41] and WFG test suite [42], are used in the experiments. The DTLZ test suite is widely used as a benchmark for testing MOEA performance. The WFG test suite consists of a set of difficult benchmark test problems that involve deceptive problems. Compared with DTLZ test suite with separable variables, WFG test suite is more complex and difficult to deal with. The parameter settings for DTLZ1-DTLZ7 and WFG1-WFG8 are shown in Tables 1, 2, respectively.

Table 1 Settings of test problems DTLZ1-DTLZ7

Table 2 Settings of test problems WFG1-WFG8

(2) Population Size: The population size depends on the number of reference vectors generated by Das and Dennis method, which is a binomial coefficient [19]. To avoid excessive number of reference vectors, the Das and Dennis method uses a two-level segmentation method. For fair comparison, the population size is set to a binomial coefficient that is closest to 200. The detailed parameter settings are shown in Table 3.

Table 3 Population size settings for different objective numbers

(3) Crossover and Mutation: SBX [36] and polynomial mutation [37] are used to generate offspring. The distribution index of crossover ${n}_{c}=20$, the probabilities of crossover ${p}_{c}=1.0$; The distribution index of mutation ${n}_{m}=20$, the probabilities of mutation ${p}_{m}=1/D$.

4) Performance Metric: Four widely used metrics are selected for evaluation, including comprehensive metrics IGD [10] and HV [43], convergence metric GD [44], and diversity metric PD [24]. The smaller the GD and IGD values, the better the result. The larger the PD and HV values, the better the result. In addition, the reference point for HV value is set to (1, 1,…,1), and the number of sampling points is set to 1,000,000.

(5) Termination Criterion and Number of Runs: The maximum number of iterations ${G}_{max}$ is used as the termination criterion. Each algorithm runs 20 times for each test function. According to the general settings, ${G}_{max}=100$ when $M<10$ and ${G}_{max}=1000$ otherwise.

(6) Comparison Algorithms: Seven state-of-the-art algorithms are selected as the peer competitors, including MaOEA-IT [26], NSGA-II-RPD [32], MOEA/D-D [31], MOEA/D-PBI [6], I-DBEA [33], MaOEA-RD [23] and NSGA-III [19]. NSGA-II-RPD and MOEA/D-D are characterized by the use of hybrid dominance. MOEA/D-PBI is a variant MOEA/D base on PBI strategy. I-DBEA is a decomposition-based EA, in which two independent distance measures are used to maintain a balance between convergence and diversity. MaOEA-RD is a novel many-objective evolutionary algorithm that uses a two-stage strategy to reduce objective space and improve diversity. NSGA-III is an extension of NSGA-II, which is usually used as a benchmark algorithm to verify the performance of MaOEA.

(7) Statistical method: In view of statistics significance of the results, the Mann–Whitney-Wilcoxon rank-sum test [45] at the 5% significance level is used to compare TS/KW-MaOEA with other algorithms. The symbols “ + ”, “−” and “ = ” are employed to indicate that the performance of the compared algorithm is better than ( +), worse than (–), and similar to ( =) that of TS/KW-MaOEA, respectively. The best results are marked in bold face.

(8) Experimental environment: Experiments are conducted via PlatEMO [46] with MATLAB R2018a on Intel Core i5-4460 (3.20 GHz, RAM 8 GB).

Influence of PBI parameter on equilibrium

In this section, we investigate the influence of parameter θ used in PBI on the performance of TS/KW-MaOEA. Tables 4, 5 show the results obtained by TS/KW-MaOEA with different θ at the first stage for solving DTLZ1 to DTLZ7. Tables 6, 7 show the results obtained by TS/KW-MaOEA with different θ at the first stage for solving WFG1 to WFG8. For a more convenient description, SG1/KW-RPD/1 is the abbreviation of TS/KW-MaOEA in the first stage, where the reference-point dominance (RPD) relation is employed and θ is set to 1. Similarly, SG1/KW-RPD/5 denotes that θ is set to 5. Experimental results show that SG1/KW-RPD/1 significantly outperformed SG1/KW-RPD/5 on nearly half of test problems. The detained analysis is as follows.

Table 4 GD and PD values obtained by TS/KW-MaOEA with different θ at the first stage on DTLZ1-DTLZ7

Table 5 IGD and HV values obtained by TS/KW-MaOEA with different θ at the first stage on DTLZ1-DTLZ7

Table 6 GD and PD values obtained by TS/KW-MaOEA with different θ at the first stage on WFG1-WFG8

Table 7 IGD and HV values obtained by TS/KW-MaOEA with different θ at the first stage on WFG1-WFG8

(1) Convergence: For DTLZ test suite, compared with SG1/KW-RPD/5, SG1/KW-RPD/1 achieves the best value on almost all problems except DTLZ1, and shows significantly advantages on nearly half of the problems. This indicates that a smaller θ can guide the search toward the true PF direction, which significantly improves the convergence of the solutions. However, since there are $\left({11}^{k}-1\right)$ local optima on the PF of DTLZ1, the search is easily fall into local optima due to strong convergence ability. Consequently, SG1/KW-RPD/1 performs poor on DTLZ1. Similarly, with regard to DTLZ3 with $\left({3}^{k}-1\right)$ local optima on PF and DTLZ6 with discontinuous PF, SG1/KW-RPD/1 failed to achieve significant results. For WFG test suit, if the parameter θ is set to 1, SG1/KW-RPD/1 achieves the best values in almost all problems except for WFG2, and exhibits advantages in nearly half of the problems. SG1/KW-RPD/1 performs poorly on WFG2. The main reason is that the algorithm focuses on the search tendency of convergence while ignoring the distribution of solutions, which leads to the loss of solutions within the subregion where the true PF is located.

(2) Diversity: For DTLZ test suite, SG1/KW-RPD/1 obtains the best value on all objectives of DTLZ1 and DTLZ3, which indicates that the algorithm has certain advantages. Since convergence and diversity are complementary, the diversity of solutions can compensate for the convergence loss of solutions on DTLZ1 and DTLZ3. However, the diversity of solutions obtained by SG1/KW-RPD/1 are lost on 15-objective test problems, such as DTLZ2, DTLZ4 and DTLZ7. The reasons are as follows. On the one hand, as the dimension of the problem increases, it becomes more difficult to maintain a better balance between convergence and diversity. On the other hand, the non-uniformly distributed solutions depend more on diversity. In addition, SG1/KW-RPD/1 fails to achieve satisfactory results on DTLZ5 and DTLZ6 problems with different objectives, and even suffers a serious loss of diversity. The reason is that the PF of DTLZ5 and DTLZ6 are both degenerated curves, which requires adjusting the balance between convergence and diversity to obtain better results. Similarly, for WFG test suit, SG1/KW-RPD/1 slightly loses diversity to compensate for convergence on the WFG1 and WFG2 problems, but performs slightly worse on WFG3 problem with degenerate curve. For WFG1-WFG3 with the objective number less than 30, it is worth noting that the diversity of the algorithm has not been degraded, and even improved in some problems.

(3) Equilibrium State: SG1/KW-RPD/1 can obtain the best value on almost all problems, and demonstrates advantages on nearly half of the problems. It can be seen from Tables 4, 5, 6, and 7 that a smaller parameter θ can increase the convergence tendency in equilibrium. Since the convergence improvement of the solution set is much higher than the loss caused by diversity, it can significantly improve the algorithm performance on most problems. In addition, for problems with objective numbers less than 30, SG1/KW-RPD/1 almost always achieves better balance.

In summary, if the parameter θ is set to 1, it can guide TS/KW-MaOEA to search in the direction of convergence in the first stage. Moreover, the convergence of the solution set can be significantly improved without seriously deteriorating diversity, which can conduct an effective control on separated balance.

Influence of normalized correction strategy on distribution

In this section, we investigate the influence of RPD relation and the PBI-based subregion hybrid dominance relation (PHD) on the performance of TS/KW-MaOEA. For a more convenient description, SG1/KW-RPD/1 NC is the abbreviation of algorithm SG1/KW-RPD/1 with a normalized correction (NC) strategy. Table 8 shows the results obtained by TS/KW-MaOEA with different strategies at the first stage for solving DTLZ1 – DTLZ4. Table 9 shows the results obtained by TS/KW-MaOEA with different strategies at the first stage for solving WFG1 – WFG4. Experimental results show that SG1/KW-RPD/1 NC can obtain the best GD and IGD values on almost all problems, which demonstrates that the normalized correction strategy can significantly improve algorithm performance. Since both ${z}^{*}$ and ${z}^{nad}$ used in the normalization operation are obtained by estimating current solution set, and the stability and accuracy of the solution set in previous generations are at a low level, the normalized solution set does not correspond to the distribution of the true PF, subsequently, the dominance rule based on region density does not work.

Table 8 GD and PD values obtained by SG1/KW-RPD/1 and SG1/KW-RPD/1 NC on DTLZ1-DTLZ4

Table 9 GD and PD values obtained by SG1/KW-RPD/1 and SG1/KW-RPD/1 NC on WFG1-WFG4

Figure 8 visualizes the results obtained by SG1/KW-RPD/1 and SG1/KW-RPD/1 NC of the 3-objective DTLZ1-DTLZ4 and WFG1-WFG4 problems. To clearly show the contrast with the true PF, the sparse parts in the solution set are marked with dark colors. Compare Fig. 8a with Fig. 8b, the results on DTLZ2 and DTLZ4 clearly demonstrate that the normalized correction strategy can reduce the number and size of the sparse parts. It can be concluded that the dominance rule based on region density tends to result in sparse distribution. The normalized correction strategy can alleviate this problem and improve the distribution of the solution set. Compare Fig. 8c with Fig. 8d, the results on WFG4 also indicate that the strategy is effective. It is worth noting that for WFG4 with objective numbers greater than 10, the GD index performance of SG1/KW-RPD/1NC decreases while its IGD index performance is significantly improved. This indicates that the normalization correction strategy can compensate for excessive convergence to some extent, which is caused by the small parameter θ. Compare Fig. 8c with Fig. 8d, the results obtained from solving the WFG3 problem indicate that although the normalization correction strategy can improve the distribution of solutions obtained by the algorithm for solving the problem with degenerate curve to a certain extent, it still cannot guarantee that all solutions converge to the true PF.

Fig. 8

Solutions obtained by different algorithms on the 3-objective DTLZ1-DTLZ4 and WFG1-WFG4 problems. (a) SG1/KW-RPD/1 (without normalized correction strategy) on DTLZ1-DTLZ4; (b) SG1/KW-RPD/1 NC (with normalized correction strategy) on DTLZ1-DTLZ4; (c) SG1/KW-RPD/1 (without normalized correction strategy) on WFG1-WFG4; (d) SG1/KW-RPD/1 (with normalized correction strategy) on WFG1-WFG4

Comparison of the stage one in TS

The experimental results on DTLZ1-DTLZ7 obtained by TS/KW-MaOEA and two state–of-the–art TS-MaOEAs in the first stage are shown in Tables 10, 11. The experimental results on WFG1-WFG8 obtained by TS/KW-MaOEA and two state–of-the–art TS-MaOEAs in the first stage are shown in Tables 12, 13. In the first stage, both MaOEA-IT and MaOEA-RD use the decomposition method to transform the MaOP into a group SOPs. Subsequently, MaOEA-IT uses a periodic dynamic weight aggregation method to obtain an approximate Pareto optimal solution, while MaOEA-RD uses d₁ and d₂ measures to obtain an approximate Pareto optimal solution. Tables 10, 11, 12, 13 show that the overall quality of the approximate Pareto optimal solutions obtained by TS/KW-MaOEA significantly outperforms the other two competitors. In addition, TS/KW-MaOEA achieves the best value on almost all problems.

Table 10 GD values obtained by different algorithms in the first stage on DTLZ1-DTLZ7

Table 11 IGD values obtained by different algorithms in the first stage on DTLZ1-DTLZ7

Table 12 GD values obtained by different algorithms in the first stage on WFG1-WFG8

Table 13 IGD values obtained by different algorithms in the first stage on WFG1-WFG8

In terms of GD metric, MaOEA-RD significantly outperforms the other two peer competitors on DTLZ4 and DTLZ5 problems with different objectives, while performs worse on DTLZ6 and DTLZ7. TS/KW-MaOEA significantly outperforms the other two peer competitors on DTLZ6, DTLZ7, WFG2, WFG4, WFG5, WFG6, WFG7, and WFG8 problems with different objectives, while performs slightly worse on DTLZ4 and DTLZ5. In addition, for DTLZ1 and DTLZ3 problems, TS/KW-MaOEA performs better in low-dimensional objective space, while MaOEA-RD performs better in high-dimensional objective space. For WFG1, MaOEA-IT performs better on low-dimensional problems; TS/KW-MaOEA performs better on high-dimensional problems, and MaOEA-RD performs better on 30-objective problems. For WFG3, MaOEA-IT performs better on high-dimensional problems, and TS/KW-MaOEA performs better on low-dimensional problems.

The results obtained by different algorithms on the 3-objective DTLZ4, DTLZ6, and WFG3 problems are visualized in Fig. 9. Compare Fig. 9a with Fig. 9b, although MaOEA-RD can achieve better GD values on DTLZ4, the approximate Pareto optimal solutions are concentrated near the extreme points. As shown in Fig. 9a and Fig. 9b, the approximate Pareto optimal solution obtained by MaOEA-IT on DTLZ4 is easy to converge to the PF boundary. Therefore, MaOEA-IT performs better on DTLZ6 with a curved front. Although the GD values obtained by TS/KW-MaOEA on DTLZ4 are relatively poor, the diversity of solutions is still maintained, which ensures that the obtained approximate PF optimal solutions are closer to the distribution of the true PF. Since TS/KW-MaOEA uses the variant PBI operators in the dominance method at the first stage, it is difficult for it to generate equivalent individuals. Therefore, TS/KW-MaOEA exhibits significant advantages in high-dimensional problems. For WFG3, MaOEA-IT exhibits strong convergence to the boundary in the first stage, thus the algorithm has an advantage in dealing with high-dimensional degradation problems.

Fig. 9

Approximate optimal solutions obtained by different algorithms in the first stage on the 3-objective DTLZ4 and DTLZ6 problems. a DTLZ4; b DTLZ6; c WFG3

In conclusion, TS/KW-MaOEA in the first stage can effectively approximate the true PF and ensure the convergence without excessive loss of diversity simultaneously, which helps to improve the performance of TS/KW-MaOEA in the second stage and enhance the effectiveness of the Pareto optimal subspace learning strategy. In addition, both TS/KW-MaOEA and MaOEA-IT use the cumulative archive to store the obtained approximate Pareto optimal solutions, thereby determining the region where the true PF is located. The difference between TS/KW-MaOEA and MaOEA-IT is as follows. In the second stage, the environmental selection component in the TS/KW-MaOEA uses the Pareto optimal subspace learning strategy. Moreover, TS/KW-MaOEA alternately performs two stages with TS/KW model, which ensures that inaccurate judgments, namely, the location of the Pareto optimal subspace region, can be immediately corrected in the next stage. MaOEA-IT does not work in the second stage until the Pareto optimal subspace is obtained. Due to the lack of a Pareto optimal subspace correction mechanism, the entire search process of MaOEA-IT will be affected by inaccurate Pareto optimal subspace locations.

Construction of the TS/KW Model

Figure 10 shows the average IGD values obtained by TS-MaOEA/μ over DTLZ1, DTLZ3, DTLZ5, DTLZ6 and DTLZ7 problems with 3-, 5-, 8-, 10- and 15-objective. TS-MaOEA/μ is the abbreviation of the proposed algorithm with the traditional two-stage instead of the TS/KW model. In TS-MaOEA/μ, the first stage and the second stage are executed once each. The radio of the number of iterations in the first stage to the maximum number of iterations, denoted as μ, is used to control the search balance. The horizontal axis represents the value of μ, $\mu \in [\text{0.5,0.9}]$. The vertical axis represents the average IGD values of m objectives obtained by the algorithm on all difficult problems. The statistical results show that the search balance of the proposed algorithm is characterized by dynamic periodicity.

Fig. 10

Average IGD values obtained by TS-MaOEA/μ over DTLZ1, DTLZ3, DTLZ5, DTLZ6 and DTLZ7 problems with m objectives

The statistical results show that as the number of objective increases, the corresponding PF becomes more complex. Since the solution set is difficult to approximate the true PF, the proportion of the first stage in TS should be increased. Inspired by Kondratiev waves, the TS/KW model utilizes the idea of macro-control and above statistical results to automatically control parameter μ, which can effectively adjust the separation control of the balance. The selection of different stages (I) is formulated by

$$ \begin{aligned} I=\left\{\begin{array}{l}2, if \frac{{G}_{done}}{{G}_{max}}>\left(0.75+0.25\bullet \frac{M-{M}_{min}}{{M}_{max}-{M}_{min}}\right) and \\ rand\left(1\right) >\frac{M-{M}_{min}}{{M}_{max}-{M}_{min}} \\ \qquad\qquad\qquad 1, otherwise\end{array}\right. \end{aligned}$$

(11)

where ${G}_{done}$ is the current iteration number, and ${G}_{max}$ is the maximum number of iterations. ${M}_{max}$ and ${M}_{min}$ represent the maximum and minimum objectives, respectively. When μ is set to 0.75, the algorithm can obtain better IGD values on optimization problem with m objectives, therefore, 0.75 is used as the benchmark in formula (11). As can be seen in formula (11), the first 75% of the search process is performed in the first stage, which not only ensures convergence, but also helps to determine the Pareto optimal subspace to reduce computational cost. In the last 25% of the search process, the two stages are randomly performed alternately based on the objective number of MaOPs. For optimization problems with many objectives, the proposed scheme can allocate more computational resources for the first stage to accelerate the rate of convergence, and compensate for the loss of diversity in the first stage while quickly correcting the Pareto optimal subspace location.

Results on the DTLZ and WFG Suite

Tables 14, 15 show the results obtained by TS/KW-MaOEA and six state-of-the-art MaOEAs on DTLZ1-DTLZ7 and WFG1-WFG8, respectively. As can be seen in Table 14, the proposed TS/KW-MaOEA is competitive in the DTLZ test suite. More specifically, for DTLZ1-DTLZ4 and DTLZ7, TS/KW-MaOEA obtained the best IGD on 13 test instances out of 30 test instances. For DTLZ5 and DTLZ6, TS/KW-MaOEA ranks second on almost all objective problems. Similarly, it can be seen from Table 15 that TS/KW-MaOEA shows significant advantages in the WFG test suite. For WFG2, and WFG4 -WFG8, TS/KW-MaOEA obtained the best IGD on 34 test instances out of 36 test instances. For WFG1 and WFG3, TS/KW-MaOEA ranks first on 4 test instances out of 12 test instances and second on the other 8 test instances. The detailed analysis of the experimental results is as follows.

Table 14 IGD values obtained by different algorithms on DTLZ1-DTLZ7

Table 15 IGD values obtained by different algorithms on WFG1-WFG8

(1) DTLZ1 and DTLZ3: For DTLZ1 and DTLZ3, TS/KW-MaOEA obtains the best results on the 3- and 5-objective test problems, while MOEA/D and MOEA/D-D win on the 8-, 10- and 15- objective test problems. DTLZ1 and DTLZ3 are characterized by multiple local optima on the PF, therefore, the performance obtained by the algorithm on these problems depends largely on its global optimization ability. Since decomposition methods focus on convergence and can explicitly improve diversity to enhance global optimization ability, TS/KW-MaOEA, MOEA/D and MOEA/D-D all have considerable global optimization abilities. However, in order to ensure the distribution of solutions which are closely approximating the Pareto optimal solutions, TS/KW-MaOEA is relatively inferior to MOEA/D and MOEA/D-D in terms of the convergence. Consequently, as the objective number increases, the advantages of TS/KW-MaOEA gradually decrease. Although I-DBEA and MaOEA-RD have certain global search abilities, I-DBEA follows the principle of the diversity metric d₂ first and the convergence metric d₁ second, while the approximate Pareto optimal solution obtained by MaOEA-RD in the first stage is not accurate enough. Therefore, I-DBEA and MaOEA-RD perform worse on DTLZ1 and DTLZ3. For 30-objective problems, it is worth noting that the performance of NSGA-II-RPD on DTLZ3 deteriorates sharply, which may be caused by RPD losing selection pressure in high-dimensional objective space.

(2) DTLZ2 and DTLZ4: For DTLZ2, TS/KW-MaOEA obtains the best results, while MOEA/D ranks second. For DTLZ4, MOEA/D-D achieves the best results, while TS/KW-MaOEA ranks second. Since decomposition methods are more suitable for dealing with many-objective optimization problems than traditional Pareto dominance methods, algorithms that use decomposition methods or hybrid dominance methods demonstrate advantages on DTLZ2 and DTLZ4. However, the diversity maintenance method that uses the uniformly distributed reference vectors is not appropriate for dealing with DTLZ4 that the Pareto optimal solution are not uniformly distributed on PF. Therefore, the performance achieved by MOEA/D and TS/KW-MaOEA on DTLZ4 is inferior to that of MOEA/D-D. However, MOEA/D and TS/KW-MaOEA showed slower performance degradation as the objective gradually increased to 30, and the trend of change was basically consistent with MOEA/D-D. The reason is that all three algorithms are fully exploited and use the PBI operator during the evolution process. Due to the fact that PBI operator is not prone to generating equivalent individuals, the problem of loss of selection pressure has been alleviated to some extent. Similarly, NSGA-II-RPD and NSGA-III achieve worse performance on DTLZ4. The PBI operator used in NSGA-II-RPD is insufficient. The strategies used in I-DBEA depend much on d₂ and d₁ metrics, which cannot ensure the solutions with good distribution. Accordingly, I-DBEA performs worse on DTLZ2 and DTLZ4.

(3) DTLZ5 and DTLZ6: For DTLZ5 and DTLZ6, MOEA/D achieves the best results on most problems, while TS/KW-MaOEA ranks second and NSGA-II-RPD ranks third. Experimental results show that MOEA/D has significant advantages in dealing with an optimization problem with degenerated front due to its strong convergence ability. Since such problems have a relatively low sensitivity to regional density, NSGA-II-RPD can achieve better performance in low dimensional problems. However, the performance of NSGA-II-RPD deteriorates sharply on 30-objective problems. For DTLZ6, MOEA/D-D shows significant advantages. Compared with MOEA/D, MOEA/D-D is more suitable for dealing with an optimization problem with discontinuous front. In addition, NSGA-III can achieve the best values on optimization problems with fewer objectives.

(4) DTLZ7: NSGA-III and TS/KW-MaOEA show advantages on DTLZ7 with complex front. The niche mechanism used in NSGA-III strives to select a number of well-spread reference vectors during the search to adjust the distribution of solutions, which helps to deal with the optimization problem with disconnected regions on the front. Although NSGA-III has a robust diversity maintenance mechanism, due to the lack of effective balance separation mechanism, the algorithm suffers from severe loss of convergence when dealing with the problems that have many objectives. Therefore, for 8-, 10-, 15- and 30-objective optimization problems, the performance of NSGA-III becomes worse. For 30-objective DTLZ7, it is worth noting that the performance degradation of I-DBEA even exceeds that of NSGA-II-RPD. This indicates that I-DBEA is weak in handling hybrid frontiers with a large number of objectives.

(5) WFG1: For WFG1, TS/KW-MaOEA shows the best results on 10-, 15- and 30-objective test problems, and MOEA/D achieves the best performance on 3-, 5- and 8-objective test problems. Experimental results show that TS/KW-MaOEA and MOEA/D can effectively deal with problems with mixed shape Pareto front. Furthermore, TS/KW-MaOEA is able to solve the problems with a large number of objectives.

(6) WFG2 and WFG4: For WFG2 and WFG4, TS/KW-MaOEA performs very well and achieves the best results on the problems with almost all considered numbers of objectives. NSGA-III ranks second. The experimental results show that TS/KW-MaOEA can effectively deal with multimodal problems. The Pareto optimal subspace learning strategy used in the second stage of TS/KW-MaOEA can find the subregions where the true PF exists, which helps to search multiple sets of Pareto optimal solutions in the subspace. Due to the lack of effective mechanisms for dealing with multimodal problems, MOEA/D performs worse on WFG2 and WFG4. Similarly, NSGA-II-RPD, MOEA/D-D, I-DBEA and MaOEA-RD perform worse on multimodal problems.

(7) WFG3 and WFG6: For WFG3, NSGA-III obtains the best results on the problems with almost all considered numbers of objectives and followed by TS/KW-MaOEA. For WFG6, TS/KW-MaOEA shows significant advantages on all the problems and obtains the best results. Experimental results show that the niche preservation used in NSGA-III can work well on nonseparable degradation problems. Based on the results of DTLZ5 and DTLZ6, TS/KW-MaOEA can effectively deal with nonseparable problems. However, TS/KW-MaOEA cannot obtain the outstanding results on nonseparable problems with degeneration curve. In addition, MOEA/D and I-DBEA perform worse on nonseparable problems, such as WFG2, WFG3, WFG6 and WFG8, which demonstrates their insufficient abilities on nonseparable problems. For 30-objective WFG3, it is worth noting that MaOEA-RD achieves the best value and significantly outperforms other algorithms. This indicates that algorithms with strong convergence can effectively handle problems with degenerate curve in high-dimensional objective spaces. In addition, whether the problem is separated also has an impact on algorithm performance.

(8) WFG5 and WFG8: For WFG5 and WFG8, TS/KW-MaOEA shows significant advantages and obtains the best results on the problems with almost all considered numbers of objectives. NSGA-III ranks second. TS/KW-MaOEA employs the allocation mechanism to maintain population diversity in the second stage, as discussed in Section III-E, and the allocation mechanism can compensate for diversity by driving some solutions slightly away from the approximate PF in some cases. Therefore, this mechanism helps the algorithm jump out of the local optima, which can effectively handle deceptive problems. Since the corner-sort strategy is used to construct the hyperplane, I-DBEA performs better on WFG5 than on other problems. In addition, I-DBEA employs an encounter replacement strategy instead of a restricted neighborhood model, which helps to deal with deceptive problems. However, I-DBEA performs worse on WFG8, which is characterized by nonseparability and deception. Since great emphasis is placed on convergence, MOEA/D and MaOEA-RD perform worse on deceptive problems. For the same reason, due to the strong convergence characteristics, the performance of MOEA/D and MaOEA-RD deteriorate slowly in solving 15- and 30-objective problems. Consequently, even for deceptive problems, if the objective number of the problem reaches 30 or more, the demand for convergence will always exceed the demand for maintaining diversity. There is still a long way to go to solve dimensional disasters and loss of selection pressure.

Conclusion

In this paper, we propose a novel MaOEA with two-stage, termed TS/KW-MaOEA, which aims to conduct a separate control on convergence and diversity in balance during the search process. In TS/KW-MaOEA, two enhanced dominate relations, namely PHD and DGD, are proposed. PHD can reduce diversity loss while significantly improving the convergence. DGD can strengthen the selection pressure in the diversity direction while promoting the convergence, i.e., solutions with better diversity can be selected from Pareto equivalent solutions. To further guide the two stages toward a promising search direction, this paper proposes a mating selection component based on the convergence metric CM and the diversity metric DM. The CM metric used in the two stages stores the PHD nondominated sorting ranking and the DGD nondominated sorting ranking, while the DM metric stores the d₂ metric and the SD metric, respectively. Finally, an environmental selection component with two selection strategies is developed. In the first stage, the truncation method is used for diversity maintenance to avoid deterioration of diversity. In the second stage, the cumulative archive is used to learn the Pareto optimal subspace. Subsequently, an allocation method is employed to maintain the diversity. More specifically, for the uniformly distributed reference vectors with the same size as the solution set, each reference vector is assigned a closest solution based on cosine similarity to compensate for the loss of convergence.

Systematic experiments are carried out on 15 test problems to compare TS/KW-MaOEA with a series of state-of-the-art MaOEAs. The results demonstrate that TS/KW-MaOEA is very competitive in handling MaOPs. In addition, we investigated the parameters used in TS/KW-MaOEA, including the influence of the PBI parameter used in PHD on search directions, and studied the automatic configuration of the TS/KW model. Finally, visualization figures of some experimental results are displayed to further illustrate the influence of normalization operations on the distribution of solution sets, as well as the distribution of approximate Pareto optimal solutions obtained by the three TS-MaOEAs in the first stage.

Experimental results and analysis show that the proposed TS/KW-MaOEA still has some shortcomings. In the future, we will investigate more effective mechanisms to deal with front degeneration problems, such as DTLZ5 and DTLZ6. In addition, since the normalization correction strategy is relatively complicated, it would be interesting to study the update mechanism for reference vectors. Finally, TS/KW-MaOEA will be extended to solve real-world problems.