Automatic algorithm design of distributed hybrid flowshop scheduling with consistent sublots

Abstract

The present-day globalized economy and diverse market demands have compelled an increasing number of manufacturing enterprises to move toward the distributed manufacturing pattern and the model of multi-variety and small-lot. Taking these two factors into account, this study investigates an extension of the distributed hybrid flowshop scheduling problem (DHFSP), called the distributed hybrid flowshop scheduling problem with consistent sublots (DHFSP_CS). To tackle this problem, a mixed integer linear programming (MILP) model is developed as a preliminary step. The NP-hard nature of the problem necessitates the use of the iterated F-Race (I/F-Race) as the automated algorithm design (AAD) to compose a metaheuristic that requires minimal user intervention. The I/F-Race enables identifying the ideal values of numerical and categorical parameters within a promising algorithm framework. An extension of the collaborative variable neighborhood descent algorithm (ECVND) is utilized as the algorithm framework, which is modified by intensifying efforts on the critical factories. In consideration of the problem-specific characteristics and the solution encoding, the configurable solution initializations, configurable solution decoding strategies, and configurable collaborative operators are designed. Additionally, several neighborhood structures are specially designed. Extensive computational results on simulation instances and a real-world instance demonstrate that the automated algorithm conceived by the AAD outperforms the CPLEX and other state-of-the-art metaheuristics in addressing the DHFSP_CS.

Introduction

In recent years, the distributed manufacturing pattern has seen a sharp rise in popularity among manufacturing enterprises, owing to the highly globalized economy and diverse market demands. This pattern provides manufacturers with the flexibility to distribute processing tasks to different factories, resulting in increased customization, shorter lead times, and reduced costs compared to single factory pattern. Moreover, distributed manufacturing is more environmentally sustainable [1, 2]. Under the distributed environment, this paper investigates a hybrid flowshop configuration in each factory, which appears in various flexible processing systems, such as the electronics, furniture, textile, petrochemical, and pharmaceutical industries [3]. Production scheduling is of paramount importance for manufacturing systems, as efficient scheduling decisions lead to improved profitability and customer satisfaction [4]. The distributed hybrid flowshop scheduling problem (DHFSP) addressed in this paper is a multi-plant extension of the regular hybrid flowshop scheduling problem (HFSP) [5, 6]. The DHFSP involves scheduling a set of jobs in multiple factories, each with a hybrid flowshop configuration formed by multiple stages consisting of several parallel and identical machines. Therefore, solving the DHFSP requires addressing three problems, namely, the assignment of jobs to factories, the sequence of jobs in each factory, and the assignment of jobs to machines at each stage. Over the past few years, the DHFSP has captured growing interest and attention from researchers, with some advanced scheduling technologies and approaches being proposed [5, 6].

To our knowledge, in the previous studies addressing the DHFSP, it has not been possible to split the job, that is, the job must be completed at a given stage before it can be moved to the downstream stage. However, this can negatively impact production efficiency in scenarios adhering to the model of the multi-variety and small-lot, wherein a job (referred to as a lot) comprises a series of identical items. The technology of lot streaming has a wide range of applications across different industries, such as automotive industry, semiconductor manufacturing, food and beverage industry, and pharmaceutical industry. Using this technology, a lot is divided into smaller sublot, and each sublot can be processed and transferred separately. In this paper, the technique of consistent sublots [7], a type of lot streaming, is introduced into the DHFSP, thereby resulting in a novel problem, i.e., the distributed hybrid flowshop scheduling problem with consistent sublots (DHFSP_CS). By employing the consistent sublots, a lot is divided into several smaller sublots, whose sizes may vary but remain consistent across different stages. Considering the consistent sublots, two important features must be addressed: the transfer of sublots between consecutive stages and the machine setup prior to lot processing.

The work has drawn inspiration from a real-world scheduling problem encountered in a mechanical processing workshop at an automobile production company, which is detailed in "Case study" and can be reduced to the DHFSP_CS addressed in the paper. The DHFSP_CS represents an extension of the DHFSP. Recall that the DHFSP needs to solve the allocation of jobs to factories, the allocation of jobs to machines, and the job sequence at each stage. In addition to the three problems, the DHFSP_CS needs to solve the lot split, thereby considerably expanding the solution space. Thus, the DHFSP_CS is more complex than the DHFSP. Given that the DHFSP is a known NP-hard problem [6], it follows that the DHFSP_CS is also NP-hard. To solve the DHFSP_CS, in this paper, a mixed integer linear programming (MILP) model is first developed, which can solve the small-scale instances to optimality. Due to the NP-hard nature of the problem, metaheuristics are suggested to solve the problem, which show superior performance for solving various optimization problems. As is well established, the setting of parameters, both numerical and categorical, can significantly impact metaheuristic performance, with no single optimal setting for parameters across all problems [8, 9]. Hence, the parameters can be assumed to be configurable and should be set appropriately using suitable methodologies. Among them, the I/F-Race (Iterated F-Race) [9], a competitive automatic algorithm design (AAD), has the ability to construct a metaheuristic automatically with little user intervention, and has been successfully applied in various fields [10]. Its goal is to automatically create an automated algorithm within an algorithm framework that performs well for the given problem by testing a range of instances to determine the ideal combination of parameter values. Regarding the algorithm framework, an extension of the collaborative variable neighborhood descent (ECVND) algorithm is introduced by conducting more efforts on the critical factory of the best solution, rendering it an ideal choice for the DHFSP_CS.

The remainder of this paper is organized as follows. In "Literature review", we present a brief literature review. "Problem statement" describes the DHFSP_CS, and the MILP model is presented. The algorithm configuration is defined in "Algorithm configuration". "Experimental study" and "Case study" discuss the experimental study and case study, respectively. The conclusions and future studies are presented in "Conclusion".

Literature review

To our knowledge, the DHFSP_CS has not been previously investigated, and thus, we will provide a comprehensive review of related works. First, this section provides the literature review of the HFSP and HFSP with consistent sublots. Then, a summary of the literature review of the DHFSP is presented. Finally, an analysis of the review and the research questions are outlined.

Related work

The HFSP is a mixture of two classical scheduling problems: parallel machine scheduling and flowshop scheduling. It is a well-known and hot research area. There are many studies addressing the HFSP with different constraints, objective functions, and solution algorithms. Several review papers [11, 12] can be found in the literature to give comprehensive guides for the readers with respect to the research work on HFSP. Specifically, considering the technique of consistent sublots, Zhang et al. [13] first formulated an MILP model with the minimization of makespan, and proposed a collaborative variable neighborhood descent (CVND) algorithm. Then, based on the above research, Zhang et al. [14] studied a multi-objective optimization problem with simultaneously minimizing the makespan and the number of sublots. And they employed the I/F-Race to conceive the algorithm automatically. Yilmaz and Yilmaz [15] extended the above problems by considering the machine capability and limited waiting time constraint, and employed the genetic algorithms to solve the problem. The proposed strategies dealing with the lot split in the above studies can have an important promoting effect on the study in this paper.

In the research area of DHFSP, Ying and Lin [6] first successfully studied the HFSP in the distributed environment. To solve the problem, they proposed an MILP model and developed a self-tuning iterated greedy algorithm (SIG). The computational results showed that the SIG is extremely efficient and effective. Since then, the DHFSP has attracted much attention from researchers. A number of studies on the DHFSP with various constraints and objectives inspired by real-world scenarios have been published. For example, considering heterogeneous factories instead of the same factories, Wang and Wang [16] presented an MILP model for the addressed problem, and proposed a bi-population cooperative memetic algorithm to solve the problem. Considering the sequence-dependent setup times, Li et al. [17] designed a machine position-based mathematical model and proposed an improved artificial bee colony algorithm.

Shao et al. [18] studied the DHFSP with heterogeneous factories and differentiated production resources, and they proposed a network memetic algorithm to solve the problem. They also considered the blocking constraint in the DHFSP with heterogeneous factories [19], and proposed a learning-based selection hyper-heuristic framework for solving it. Lu et al. [20] formulated a multi-objective optimization for the DHFSP with considering energy consumption and production efficiency simultaneously. Considering the sequence-dependent setup times, Meng et al. [21] developed three MILP models and a constraint programming model for the same-factory and different-factory environments. Tao et al. [22] introduced the resource constraint into the DHFSP, and proposed a self-adaptive artificial bee colony algorithm. Cai et al. [23] introduced the assembly processing constraint into the DHFSP, and proposed a novel shuffled frog-leaping algorithm incorporating the Q-learning, which is used to dynamically select the search strategy for memeplex search. To the best of our knowledge, the technique of consistent sublots has not been introduced into the DHFSP.

Review analysis and research questions

This study aims to solve the DHFSP_CS, which entails integrating the consistent sublots into the DHFSP. In addition. The transfer of the sublots and the setup operations for the lots are considered. It is important to note that, to the best of our knowledge, no paper has studied this problem. Given its significant practical implications, it is imperative to devise effective and efficient algorithms for solving the DHFSP_CS. To tackle the problem, this paper endeavors to answer two key research questions.

• How can the problem be formulated in a mathematical model to obtain a deep understanding of the problem and to help develop the solution algorithm?

• How can the solution algorithm be constructed for the addressed problem more efficiently by considering the existing methods and experience?

Problem statement

Problem formulation

This subsection answers the first question raised in "Literature review". The DHFSP_CS under consideration involves multiple factories, each of which operates on a hybrid flowshop configuration. In this configuration, there exist a series of consecutive stages, with each stage comprising several machines. A series of lots must be processed through the shop, with each lot consisting of a large number of identical units that can be split into several sublots, each comprising a small number of identical units. By minimizing the makespan, the DHFSP_CS aims to determine the factory assignment, lot split, lot sequence, and machine assignment. Factory assignment pertains to the allocation of lots to factories, while lot splitting involves determining the quantity and size of the sublots that will be accommodated in each lot. Lot sequencing involves the arrangement of lots assigned to each factory, and machine assignment involves the allocation of lots to the machines at each stage. It is essential to recognize that the scheduling problem at hand is based on several assumptions.

• Each lot can only be assigned to exactly one factory.

• Each lot is processed through the stages one by one, and at a specific stage, each lot is assigned to exactly one machine.

• All items from all lots are released at the initial time.

• Preemption and interruption are not considered.

• Machine idle time is allowed, and buffer capacity is infinite between stages.

• Each lot is split into a number of sublots but limited to a maximum value, and different sublots might contain different number of units.

• A sublot is transported to the downstream stage immediately after it has been processed completely at a specific stage.

• The sublots can be started after it has been transported to this stage and its preceding sublot has been processed completely.

• Sublots from a same lot take turns to be processed on one machine at each stage.

• The machine setup time is required when a lot starts to be processed on a machine, while the setup time among the sublots from a same lot is neglected.

• At any time, one machine can at most process one item, and the items from the same sublot are continuously processed.

Sets and indices:

$I$:

Set of stages.

$J$:

Set of lots.

$K$:

Set of factories.

$M_{i}$:

Set of machines.

$i$:

Stage index, and $i \in I = \{ 1, \ldots ,M\}$.

$j$:

Lot index, and $j \in J = \{ 1, \ldots ,N\}$.

$f$:

Factory index, and $f \in K = \{ 1, \ldots ,F\}$.

$k$:

Machine index, and $k \in M_{i} = \left\{ {1, \ldots ,\sigma_{i} } \right\}$.

$e$:

Index for the sublots, and $e \in \left\{ {1, \ldots ,L} \right\}.$

Parameters:

F:

Number of factories.

N:

Number of lots.

M:

Number of stages.

$\sigma_{i}$:

Number of machines at stage i.

$T_{j}$:

Number of units of lot j.

$l_{j}$:

Number of sublots of lot j.

$L$:

Maximum number of sublots of each lot.

$p_{i,j}$:

Unit processing time of lot j at stage i.

$t_{i,j}$:

Setup time of lot j at stage i.

$f_{i,j}$:

Transportation time of lot j from stage i to stage $i + 1$.

$G$:

A positive large number.

Decision variables:

$B_{i,j,e}$:

Beginning time of sublot e of lot j at stage i.

$E_{i,j,e}$:

Ending time of sublot e of lot j at stage i.

$S_{j,e}$:

Size of sublot e of lot j.

$Z_{j,f}$:

Binary variable that takes the value of 1 when lot j is assigned to factory f.

$W_{j,e}$:

Binary variable that takes the value of 1 when sublot e of lot j is larger than 0 and 0 otherwise.

$D_{i,j,f,k}$:

Binary variable that takes the value of 1 when lot j is assigned to machine k at stage i in factory f and 0 otherwise.

$Y_{i,j,j^{\prime},f,k}$:

Binary variable that takes the value of 1 when lot j assigned to factory f is scheduled immediately before lot j’ assigned to factory f on machine k at stage i.

With the notations listed above, an MILP model for the DHFSP_CS is formulated as follows.

Objective:

$$ {\text{Minimize}}\quad z = C_{\max } . $$

(1)

Constraints:

$$ C_{\max } \ge E_{M,j,L} \quad \forall j \in J $$

(2)

$$ \sum\limits_{f = 1}^{F} {Z_{j,f} = 1\quad \forall j \in J} $$

(3)

$$ \sum\limits_{k = 1}^{{\sigma_{i} }} {D_{i,j,f,k} } \le 1\quad \forall i \in I,j \in J,f \in K $$

(4)

$$ Z_{j,f} = \sum\limits_{k = 1}^{{\sigma_{i} }} {D_{i,j,f,k} } \quad \forall i \in I,j \in J,f \in K $$

(5)

$$ \sum\limits_{e = 1}^{L} {S_{j,e} = T_{j} } \quad \forall j \in J $$

(6)

$$ B_{1,j,1} \ge t_{1,j} \quad \forall j \in J $$

(7)

$$ E_{i,j,e} - B_{i,j,e} = p_{k,j} \times S_{i,j,e} \;\;\;\forall i \in I,j \in J,e \in [1, \ldots ,L] $$

(8)

$$ B_{i,j,e + 1} - E_{i,j,e} \ge 0\quad \forall i \in I,j \in J,e \in [1, \ldots ,L - 1] $$

(9)

$$ B_{i,j,1} - E_{i,j^{\prime},L} - t_{i,j} + G \times \left( {3 - Y_{i,j^{\prime},j,f,k} - D_{i,j,f,k} - D_{i,j^{\prime},f,k} } \right) \ge 0\quad \forall i \in I,j,j^{\prime} \in J,f \in K,k \in M_{i} $$

(10)

$$ B_{i + 1,j,e} - E_{i,j,e} - f_{i,j} * W_{j,e} \ge 0\quad \forall i \in \left\{ {1,2, \ldots ,M - 1} \right\},j \in J,e \in \left[ {1,...,L} \right] $$

(11)

$$ {{S_{j,e} } \mathord{\left/ {\vphantom {{S_{j,e} } G}} \right. \kern-0pt} G} \le W_{j,e} \le S_{j,e} \quad \forall j \in J,e \in [1,...,L] $$

(12)

$$ W_{j,e} \ge W_{j,e + 1} \quad \forall j \in J,e \in \left[ {1, \ldots ,L - 1} \right] $$

(13)

$$ Y_{i,j,j^{\prime},f,k} + Y_{i,j^{\prime},j,f,k} \le 1\quad \forall i \in I,j,j^{\prime} \in J,f \in K,k \in M_{i} $$

(14)

$$ Y_{i,j,j^{\prime},f,k} + Y_{i,j^{\prime},j,f,k} \le D_{i,j,f,k} + D_{i,j^{\prime},f,k} \quad \forall i \in I,j,j^{\prime} \in J,f \in K,k \in M_{i} $$

(15)

$$ D_{i,j,f,k} + D_{i,j^{\prime},f,k} - 1 \le Y_{i,j,j^{\prime},f,k} + Y_{i,j^{\prime},j,f,k} \;\forall i \in I,j,j^{\prime} \in J,f \in K,k \in M_{i} $$

(16)

$$ D_{i,j,f,k} \in \{ 0,1\} \quad \forall i \in I,j \in J,f \in K,k \in M_{i} $$

(17)

$$ Y_{i,j,j^{\prime},f,k} \in \{ 0,1\} \quad \forall i \in I,j,j^{\prime} \in J,f \in K,k \in M_{i} . $$

(18)

Equation (1) defines the objective, namely makespan, of the MILP model. Equation (2) illustrates that the makespan must be larger than the completion of the last sublot of each lot. Equation (3) establishes a constraint for the decision variable $Z_{j,f}$, and represents that for each lot, it can be only assigned to exactly one factory. Equation (3) establishes a constraint for the decision variable $D_{i,j,f,k}$, and represents that for each lot, it can be assigned to at most one machine in a factory. Equation (5) defines the relationship between $Z_{j,f}$ and $D_{i,j,f,k}$, and illustrates two cases, i.e., whether the given lot is assigned to the given factory or not. Equation (6) establishes a constraint for the decision variable $S_{j,e}$, and guarantees that for a given lot, the lot size is equal to the sum of the sizes of its sublots. Equation (7) guarantees that for each lot, its first sublot at the first stage can be started after the corresponding setup. Equation (8) guarantees that the processing of the sublots of each lot is consecutive. Equation (9) illustrates that for each lot, the following sublot can be started only after its previous sublot is completed. Equation (10) guarantees that if two lots are assigned to the same machine at a given stage, the first sublot of the following lot can be started only after the last sublot of the previous lot is completed. Equation (11) represents that for each lot, its sublots can be started at a given stage and can be started only after they have been completed at the previous stage and transferred to the given stage. Equation (12) establishes the relationship between two decision variables, i.e., $S_{j,e}$ and $W_{j,e}$. Equation (13) represents that for each lot, its previous sublots are given higher priority to accommodate the units. Equations (14)–(16) together establish the relationships between the two decision variables, i.e., $D_{i,j,f,k}$ and $Y_{i,j,j^{\prime},f,k}$. Equations (17) and (18) define the value ranges for $D_{i,j,f,k}$ and $Y_{i,j,j^{\prime},f,k}$.

Problem illustration

To elucidate the problem, we consider an example featuring two factories and six lots. Each factory comprises two stages, each containing two machines. The relevant processing data are presented in Table 1. Let us suppose that the maximum sublot quantity is 3. The example is then run on the CPLEX solver, and the optimal solution is obtained. To display the solution in an intuitive manner, the obtained optimal schedule is portrayed in Fig. 1. Figure 1a, b depicts the schedules in factory 1 and factory 2, respectively. It is evident from Fig. 1 that the four problems, i.e., factory assignment, lot split, lot sequence, and machine assignment, are all determined. For the factory assignment, lot 2 and lot 4 are allocated to factory 1, while lot 1, lot 3, lot 5, and lot 6 are assigned to factory 2. For the lot sequence in factory 1, the lot sequence at stage 1 is 2 and 4, whereas at stage 2 it is 4 and 2. For the lot sequence in factory 2, the lot sequences at both stages are all 3, 5, 6, and 1. For the machine assignment, it can be observed directly from the figure. For the lot split, the decision variable $S_{j,e}$ shows the split information. For instance, the sublot sizes for the three sublots derived from lot 1 are 37, 19, and 10, respectively.

$$ S_{6,3} = \left[ {\begin{array}{c@{\quad}c@{\quad}c} {37} & {19} & {10} \\ {46} & {23} & {11} \\ 9 & {12} & {29} \\ {13} & {19} & {28} \\ {30} & {30} & {30} \\ {18} & {14} & {18} \\ \end{array} } \right]. $$

Table 1 The relevant processing data

Fig. 1

Gantt chart of the schedule for example

Algorithm configuration

In this section, the second question raised in "Literature review" is answered. To configure an automated algorithm using the I/F-Race, the problem of algorithm configuration is defined, tailored to the problem-specific characteristics. First, the employed algorithm framework with configurable parameters, including the numerical and categorical parameters, is introduced. Then, to facilitate global search, a solution encoding scheme is designed. Considering the solution encoding and the characteristics of the consistent sublots, configurable solution decoding strategies are introduced. Finally, the potential values of the parameters and neighborhood structures are designed.

Algorithm framework

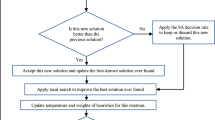
The algorithm framework ECVND, as shown in Fig. 2, is an extension of the collaborative variable neighborhood descent (CVND) algorithm. The CVND was proposed in [13] for solving the HFSP with consistent sublots. When compared to the CVND, the ECVND conducts more efforts on the critical factory of the best solution, thereby making it more suitable for handling distributed scheduling problems. To successfully solve the DHFSP_CS, four problems, as illustrated in "Problem statement", must be addressed, which are coupled and correspond to different solution spaces. Consequently, the coevolution of the four problems should be conducted to acquire a global solution. Given the above, it makes sense to employ the variable neighborhood descent (VND) strategy, which involves exploring the whole solution space by systematically switching the different neighborhood structures associated with different solution spaces. In addition to the VND strategy, the ECVND also employs a collaborative process to store historical information to cater to the global search ability.

Fig. 2

The framework of the ECVND

Algorithm 1

The procedure of the VND-based local search

The ECVND encompasses five main phases, including primary solution and archive set initializations, VND-based local search, collaborative process, primary solution and archive set restart, and a loop of classical VND process on the best solution found so far. In the primary solution and archive set initializations, a primary solution and an archive set containing a number of solutions are initialized based on the heuristics. In the VND-based local search, the primary solution is sufficiently exploited on the defined neighborhoods, and the promising solutions found are accommodated in the archive set. Algorithm 1 shows the procedure of the VND-based local search.$Neighborhood({\mathbf{X}}^{P} ,N_{k} )$ means conducting the neighborhood $N_{k}$ on ${\mathbf{X}}^{P}$, and $UpdateArchiveSet{(}{\mathbf{X}}^{P} {)}$ means updating the worst solution in the archive set with ${\mathbf{X}}^{P}$. The collaborative process is displayed in Algorithm 2, and its role lies in exploring more collaborative information on promising solutions. In Algorithm 2, $CollaborativeOperator({\mathbf{X}}^{a} ,{\mathbf{X}}^{b} )$ means conducting a collaborative method on ${\mathbf{X}}^{a}$ and ${\mathbf{X}}^{b}$ to yield a child solution that inherits information from the two parent solutions. The primary solution and archive set restart process are displayed in Algorithm 3, which aims to help the algorithm jump out of the local optima. Algorithm 4 outlines the procedure of carrying out a loop of the classical VND process on the best solution, focusing only on the neighborhoods on the critical factories.

Algorithm 2

The procedure of the collaborative process

Algorithm 3

The procedure of the primary solution and archive set restart

Algorithm 4

The procedure of a loop of classical VND process on the best solution

In ECVND, there are four numerical parameters that need to be set: the number of solutions in the archive set (P), the maximum consecutive failings (C) of updating the primary solution in the VND process, the maximum consecutive failings (Q) of updating the archive set in the collaborative process, and the overall maximum consecutive failings (R) of updating the archive set. Categorical parameters are strongly associated with the specific characteristics of the addressed problem. Considering the problem-specific characteristics, the solution encoding is first designed, and then, the initialization method is considered to be a configurable categorical parameter. Moreover, in line with the ECVND, the collaborative methods in the collaborative process and the primary solution restart are also considered to be categorical parameters, which are detailed in the following.

Solution encoding

Recall that the DHFSP_CS requires determining four problems simultaneously, i.e., factory assignment, lot split, lot sequence, and machine assignment. Using metaheuristics to solve optimization problems, solution encoding needs to contain the relevant information that can be interpreted by well-designed decoding rules. The solution encoding is composed of two parts. One part, namely the sequencing part, is a set of F-dimensional vectors $\prod_{F} = \left\{ {{{\varvec{\uppi}}}_{1} , \ldots ,{{\varvec{\uppi}}}_{f} , \ldots ,{{\varvec{\uppi}}}_{F} } \right\}$, where $F$ is the number of factories and ${{\varvec{\uppi}}}_{f}$ is the sequence vector accommodating the lots in factory f. The sequence information reflected in the vectors represents the processing sequence of the lots in each factory. Another part, namely the split part, is a set of N-dimensional vectors ${{\varvec{\Delta}}}_{N} = \left\{ {\psi_{1} , \ldots ,\psi_{j} , \ldots ,\psi_{N} } \right\}$, where N is the number of lots and $\psi_{j}$ is the split vector for lot j. Figure 3 illustrates a solution encoding of the example shown in "Problem statement".

Fig. 3

An example solution encoding

Configurable solution decoding strategies

The solution decoding is utilized to decode a solution representation into a feasible schedule. Recall that the DHFSP_CS involves solving four problems: the allocation of lots to factories, the allocation of lots to machines at each stage, the lot sequence at each stage, and the lot split. As outlined in "Solution encoding", the solution encoding enables the direct representation of the allocation of lots to factories and the lot split. For solving the lot sequence and allocation of lots to machines at each stage, two heuristic rules are introduced, which have shown superior performance in addressing the time-based objectives while using the permutation encoding mechanism.

Regarding the allocation of lots to machines, the “first idle” rule is used, which has excellent performance when addressing the time-based objectives. This rule assigns priority to the machine that has the earlier available time. For the lot sequence at the first stage, it can be directly reflected in the solution representation. While at the following stages, the lot sequence is determined by the “first-come-first-served” rule. That is, the lot completed earlier at the previous stage is given priority to be scheduled at the following stage. In case of the consistent sublots, two methods are raised when using the “first-come-first-serve” rule in the previous study [13]. One method, namely the sublot preemption (SP), gives a lot a higher priority at a given stage when its first sublot is completed earlier at the previous stage. Another method, namely the lot preemption (LP), gives a lot a higher priority at a given stage when its last sublot is completed earlier at the previous stage. Our preliminary experiments have revealed that the suitability of the two methods varies across different instances. In this study, we therefore present a novel method called the hybrid preemption (HP) by combining the two methods. To be specific, during the solution decoding process, the LP and SP are randomly executed with a 50% probability.

In view of the above description, the decoding process is configurable according to the three alternative methods, i.e., LP, SP, and HP. The detailed decoding process is as below.

Step 1. Take ${{\varvec{\uppi}}}_{f}$ from $\Pi_{F}$ in sequence, i.e., from $f = 1$ to $f = F$, and conduct the following steps.

Step 2. Schedule the lots assigned to factory f from the first stage to the last stage, i.e., from $i = 1$ to $i = M$, in the following two cases.

Case 1. If $i = 1$, take the lot j from ${{\varvec{\uppi}}}_{f}$ in sequence. For lot j, find the earliest available machine, and assign it to this machine.

Case 2. If $i \ne 1$, obtain a new lot sequence according to the three alternative methods, i.e., “lot preemption”, “sublot preemption”, and “hybrid preemption”.

Step 2.1. At the stage i, calculate the processing time of the sublots of the lot j according to the split vector $\psi_{j}$.

Step 2.2. At the stage i, schedule the sublots of the lot j consecutively according to the production constraints.

Step 2.3. Once all the sublots of the lot j is scheduled completely, update the available time of the selected machine.

Step 3. Check whether the lots assigned to factory f are scheduled. If yes, go to Step 4. Otherwise, return to Step 2.

Step 4. Check whether all the factories are scheduled. If yes, terminate the decoding process. Otherwise, return to Step 1.

Configurable solution initializations

Good initial solutions are beneficial for enhancing the efficiency and effectiveness of the metaheuristics [24]. To initialize the primary solution and the solutions in the archive set, configurable initialization methods are employed. According to the solution representation, there are two parts, i.e., the sequencing part $\Pi_{F}$ and the split part $\Delta_{N}$. With respect to the characteristics of the problem, once the split part is constructed, the processing time of the sublots can be determined, and this enables the determination of the sequencing part through the use of heuristics that consider the processing time data. Thus, in this study, we first determine the split part, and subsequently construct the sequencing part.

To initialize the split part of a solution, three methods are employed, including the uniform initialization (UI), random initialization (RI), and mixed initialization (MI). Detailed information can be found in reference [14]. To ensure the diversity of solutions in the archive set, the sequencing part of a solution is initialized through a designed process as follows. First, a whole permutation accommodating all the lots is randomly generated. Second, this permutation is randomly split into the sequencing parts in all the factories. Finally, the heuristic rule is applied to initialize the lot sequence in each factory. In this study, six types of heuristic rules from the literature are introduced, which have demonstrated superior performance in determining the permutation. They are the shortest processing time (SPT) [25], variant of SPT (VSPT) [26], Nawaz, Enscore, and Ham (NEH) [27], greedy randomized adaptive search procedure (GRASP) [28], combination of GRASP and NEH (GRASP_NEH) [14], and random initialization (RI) [14]. In summary, the solution initialization for DHFSP_CS is configurable and hierarchical. To initialize the split part, three methods are adopted, whereas for initializing the sequencing part, six methods are employed. Thus, a total of 18 combinations can be obtained for initializing the solution.

Configurable collaborative operators

In the collaborative process and primary solution restart, the collaborative operator is utilized to generate a candidate solution by performing an operation between two solutions. For the scheduling problem, the crossover operators have been proven to be effective [29, 30], as they can maintain genetic information and possess global search capabilities. For the permutation-based sequencing part, the widely used crossover operators include the partial mapped crossover (PMX), order crossover (OX), position-based crossover (PBX), order-based crossover (OBX), cycle crossover (CX) and subtour exchange crossover (SEX). In addition, the collaborative operator based on the memory consideration (MC) [13] is also adopted. However, conducting the crossover operator on the two corresponding sequence vectors may result in infeasible solutions. Thus, the following process is executed to generate the sequencing part of the candidate solution.

Step 1. For each solution in the two parent solutions, a lot sequence containing all the lots is constructed by combining the lot sequence ${{\varvec{\uppi}}}_{f}$ in turn, i.e., from $f = 1$ to $f = F$.

Step 2. Conduct the specific collaborative operator on the two lot sequences, and obtain a novel lot sequence.

Step 3. Distribute the obtained lot sequence into F sequence vectors randomly.

For the split part of the candidate solution, the crossover operators and the memory consideration are not available. Thus, the matrix selection [13] is employed. To be specific, when determining the split information for one lot, it is selected from one parent solution with a 50% probability.

In summary, the collaborative process and the primary solution restart are configurable, and there are seven methods in total.

Designed neighborhood structures

The ECVND adopts two VND-based processes, which aim to perform the local exploitation in the neighborhood of the solution, including the VND-based local search for the primary solution and the classical VND process for the best solution. Therefore, we need to design the neighborhood structures according to the solution encoding. To cover the solution space fully, four kinds of neighborhood structures are designed.

The first kind, as depicted in Fig. 4(1) and Fig. 4(3), is called the intra-factory neighborhoods, which is used to make small perturbation for the sequencing part without changing the lots within the selected factory. This kind has two specific structures: intra-factory lot insertion and intra-factory lot swap. In the intra-factory lot insertion, a factory containing more than two lots is first selected, and then, a lot in a position is randomly inserted into another position. In the intra-factory lot swap, a factory containing more than two lots is first selected, and then, the positions of two lots are swapped. The second kind, as shown in Fig. 4(5) and Fig. 4(6), is called the inter-factory neighborhoods for the sequencing part, which aims to make small perturbation for the sequencing part while changing the lots within the two selected factories. Two specific structures are contained in this kind: inter-factory lot insertion and inter-factory lot swap. In the inter-factory lot insertion, a factory containing more than one lot is first randomly selected. Then, a lot at a position is selected and deleted from this factory. Finally, the selected lot is inserted into a position of another factory selected randomly. In the inter-factory swap, two factories containing more than one lot are first randomly selected. Then, in each factory, a lot is randomly selected. Finally, the positions of two lots are swapped. The third kind, as illustrated in Fig. 4(2) and Fig. 4(4), is called the critical-factory neighborhood for the sequencing part, which is used to make small perturbation for the sequencing part without changing the lots contained within the critical factory. This kind has two specific structures: critical-factory lot insertion and critical-factory lot swap. The processes of the two structures are similar to those of the intra-factory structures, but the difference is that the selected factory is unique and is the factory with the maximum completion time. The fourth kind, as illustrated in Fig. 4(7), is named the split mutation for the split part, which is used to make small perturbation for the split part. This kind has only one method. In this method, from the lot split matrix, a lot with two or more sublots is first randomly selected, and two sublots are then randomly selected. A random number in distribution U[1, 5] is subtracted from the size of one sublot, and the same number is added to the size of the other sublot.

Fig. 4

Illustrations of neighborhood structures

Regarding the set of neighborhood structures in the classical VND process for the best solution, only the above neighborhoods changing the sequences and split matrices of lots assigned to the critical factories are included.

Algorithm configuration

In summary, there are a total of eight parameters that are configurable, i.e.,$X_{d}$, $d = 1, \ldots ,8.$ These parameters have different distributions and can be sampled from different parameter spaces. Table 2 summarizes the configurable parameters and their relevant information. When using the I/F-Race to conceive an automated algorithm, a set of instances must be tested. Let $\theta = \{ x_{1} , \ldots ,x_{d} , \ldots ,x_{8} \}$ denote an algorithm configuration where $x_{d}$ is a unique value sampled from the relevant parameter space, and let $c(\theta )$ denote the expected cost value of the algorithm configuration $\theta$ over the set of instances. The I/F-Race aims to find the best configuration $\theta *$ that has a minimum $c(\theta^{*} )$, which is to be implemented by the iterated racing procedure described below.

Table 2 Configurable parameters and their value spaces

The iterated racing procedure is composed of multiple races, and its procedure is given in Algorithm 5. It starts with a finite set $\Theta^{k}$ of candidate configurations, which are uniformly sampled from the parameter space ${\mathbf{X}}$. These configurations will be tuned on a set $I$ of instances with a total budget $B$. The core idea of the iterated racing procedure is to update the sampling distribution continuously to bias the sampling toward the best configurations. $Race(\Theta_{j} ,B_{j} )$ is used to choose the elite configurations, which are employed to update the sampling distribution. The process of a race is designed as follows.

Algorithm 5

Iterated racing procedure

A race consists of a number of iterated steps. At each step, the candidate configurations are evaluated on a single instance. After evaluation, the candidate configurations that are statistically worse than at least one other are discarded, leaving only the surviving configurations to proceed to the next step. For a detailed outline of the procedure for a race, the reader can refer to the literature [14].

Experimental study

This section provides a systematic evaluation of the automated algorithm conceived by the AAD, in comparison with the state-of-the-art metaheuristics and MILP model. For the metaheuristics, the maximum CPU elapsed time is used as the stopping criterion, as the ability to obtain satisfactory solutions within a reasonable time is of practical significance. In this study, for solving the instance with F factories, N lots, and M stages, the termination is set as $t \times F \times N \times M$ milliseconds. t is set as 40 in this paper. This termination allows more computational time for instances with a larger scale. All of the metaheuristics being compared are coded in C++, and the experiments are executed on a 3.60 GHz Intel Core i7 CPU processor.

Two sets of instances have been collected. One set accommodates the large-scale instances. The number of factories F comes from $\left\{ {2,3,4,5,6} \right\}$, the number of lots N comes from $\left\{ {20,40,60,80,100} \right\}$ and the number of stages M comes from $\left\{ {3,5,8,10} \right\}$. This will lead to 100 different combinations of $F \times N \times M$. For each combination, 5 instances are randomly generated, leading to 500 instances in total. Another set accommodates the small-scale instances. To be specific, F comes from $\left\{ {2,3,4} \right\}$, N comes from $\left\{ {5,6,7,8} \right\}$, and M comes from $\left\{ {2,3,4} \right\}$. This will lead to 36 different combinations of $F$, N and M. For each combination, only one instance is randomly generated. For both small and large instances, the number of machines at each stage is generated from a uniform distribution U[5, 10], and the maximum quantity of the sublots from a lot is set to 5.

Regarding the production data generation, we consider the following reasonable ranges according to the relevant literature [13, 14]. The number of units for each lot is taken from a uniform distribution $U[50,100]$. The unit time is randomly generated using a uniform distribution U[1, 10]. The fixed setup and transportation time are drawn from uniform distributions U[50, 100] and U[10, 20], respectively. The instances can be found at the website.¹ In this study, the relative percentage increase (RPI) over the best result is selected as the performance metric

$$ {\text{RPI}} = \frac{{c - c_{{{\text{Best}}}} }}{{c_{{{\text{Best}}}} }} * 100, $$

(19)

where $c$ is the result obtained by the given algorithm, and $c_{{{\text{best}}}}$ is the best result obtained by all the compared algorithms.

Automated algorithm tuning phase

To make a comprehensive tuning phase to identify the promising algorithm configuration, a series of 100 instances with varying problem scales are randomly selected from the large-scale instances. These 100 instances constitute the set of instances in Algorithm 5, and their rank indices are randomly scrambled. We set the computational budget as a number of experiments, where an experiment is the application of a configuration to an instance. The total budget is fixed at 2000, and both the number of minimum survivals and the selected elite configurations are set to 10. The settings of the other parameters can be found in the literature [14]. Algorithm 5 is conducted following the initialization of these parameters, and Table 3 provides some important data in the decision-making process.

Table 3 Data in the I/F-Race process

From Table 3, we can discern that there are five iterated races in total. After testing 24 instances, the AAD outputs the best ten elite configurations, as shown in Table 4. It is evident from Table 4 that each configuration varies from the others, underscoring the notion that a promising algorithm can be achieved by configuring different values of the parameters. The numerical parameter $X_{1}$, in all of the elite configurations, exceeds a value of 1, evincing that swarm-based algorithms outperform single-based algorithms. We observe the same trend with the numerical parameter $X_{2}$, verifying the effectiveness of taking full advantage of the current neighborhood in VND-based local search. For the numerical parameter $X_{3}$, the majority of configurations possess values greater than 1, indicating that the interactions between solutions can have a positive impact on improving the algorithm performance. With respect to the categorical parameter $X_{5}$, all of the configurations opt for UI as the heuristic rule for initializing the split matrix. This suggests that UI is much better than the other heuristic rules. In terms of initializing the lot sequences in different factories, VSPT and RI both appear in the configurations. As for the categorical parameter $X_{6}$, all configurations select SP. The reason behind this can be illustrated as the sublot preemption in the decoding process can get more benefits from the technique of lot streaming. Considering the categorical parameters $X_{7}$ and $X_{8}$, we can deduce that SEX is more appropriate in the collaborative process and primary solution restart. In the forthcoming algorithm testing phase, the top-ranked configuration in Table 4 will configure the automated algorithm to tackle the addressed problem.

Table 4 The best ten elite configurations

Automated algorithm testing phase

This subsection aims to evaluate the performance of the automated algorithm, denoted as AAD, by comparing it with five neighborhood-based metaheuristics in the literature. They are OCVND [13], MSVND [31], IABC [17], MDABC [32], and SABC [22], which have been recently presented in the literature to solve scheduling problems in distributed flowshop or hybrid flowshop configurations and have been proven to have outstanding performance. For the compared algorithms, if the AAD methodology is also used, novel algorithm configuration problems should be developed, and these might be new studies. Therefore, to ensure a fair comparison, the following adaptions are made in the following two aspects. One aspect concerns the numerical parameters. The numerical parameters in the compared algorithms are set appropriately according to the design of experiment suggested in [13, 33], which leverages the problem-specific characteristics of the addressed problem. Another aspect is about the algorithm operators. They all adopt the solution encoding strategy proposed in this paper and the decoding strategy with SP, because they have been verified to have the best performance. Regarding the initialization methods, all algorithms adopt UI_VSPT, which has been proven to have the best performance. For the neighborhood structures, all the compared algorithms are neighborhood-based algorithms and adopt the multiple neighborhood structures. Thus, the neighborhood structures designed for the DHFSP_CS can be directly incorporated in the compared algorithms. For the other operators that are not related to the addressed problem, they are reproduced in strict accordance with the original process in the literature.

Comparisons between CPLEX and metaheuristics on small-scale instances

This subsection presents a comparison of metaheuristics and CPLEX in solving the small-scale instances. Each instance is run on IBM ILOG CPLEX 12.7.1, and the time limit for CPLEX is set in two ways. One is fixed at 600 s, while the other is set to the same value as the metaheuristics, i.e., $40 \times F \times N \times M$ ms. The computational results are collected in Table 5, where for CPLEX, two objective values under the two limits are given, while for the metaheuristics the best (Best) and average (Avg) objective values, standard deviations (Std), and the number of times reaching the best values (Ntb) gathered through 20 independent runs are given. It can be seen from Table 5 that for $2 \times 8 \times 4$ and the instances with 2 stages, the CPLEX can solve them to optimality within 600 s. However, as the problem scale increases, the CPLEX fails to obtain optimal solutions. The metaheuristic also has the ability to acquire optimal solutions, which can be observed from the instances $2 \times 8 \times 2$, $3 \times 8 \times 2$, $3 \times 10 \times 2$, and $4 \times 10 \times 2$. When the instances involve four factories, it can be seen that the AAD can get lower objective values for most instances. In comparison to other metaheuristics, the Best and Avg values obtained by the AAD are superior for all instances. Furthermore, regarding the Std values, the values obtained by the AAD are observed to be the smallest for most of the instances. Combined with the Ntb values, which show that the AAD can obtain the largest values for most instances, it can be concluded that the robustness of the AAD is highly competitive. In conclusion, metaheuristics offer high solving accuracy and efficiency for solving the addressed problem, with the AAD being the most suitable among the compared algorithms.

Table 5 Comparison results for the small-scale instances

Comparisons among metaheuristics on large-scale instances

This subsection summarizes the computational results obtained by the metaheuristics for solving the large-scale instances. For each instance, the average RPI value (Avg) and standard deviations (Sd) are obtained based on 20 independent runs. Subsequently, for each algorithm, the average RPI values and standard deviations of the five instances under the same problem scale are averaged again. Tables 6, 7, 8, 9 and 10 display the computational results for instances with 2, 3, 4, 5, and 6 factories, respectively. Note that the results of CPLEX are not presented for large-scale instances, since they are not competitive. Moreover, to conduct significance analysis of the results, one-factor analysis of variance (ANOVA) [13, 33] is conducted, where the algorithm type is considered as a single factor. Figure 5 displays the box plots, and mean plots of the average RPI values collected from the tables with Tukey HSD (honestly significant difference) intervals at the 95% confidence level. Note that if the confidence intervals of any two algorithms overlap, there is no statistically significant difference between them. Furthermore, to show the performance of the metaheuristics as the problem scale changes, Figs. 6, 7 and 8 show the interaction plots between the metaheuristics and the number of factories, lots, and stages, respectively.

Table 6 Comparison results for the large-scale instance with 2 factories

Table 7 Comparison results for the large-scale instance with 3 factories

Table 8 Comparison results for the large-scale instance with 4 factories

Table 9 Comparison results for the large-scale instance with 5 factories

Table 10 Comparison results for the large-scale instance with 6 factories

Fig. 5

The 95% confidence intervals and box plots for the results

Fig. 6

Interaction plot between algorithms and the number of factories

Fig. 7

Interaction plot between algorithms and the number of lots

Fig. 8

Interaction plot between algorithms and the number of stages

Tables 6 and 7 demonstrate that the AAD consistently achieved the lowest average RPI values for all the problems with 2 and 3 factories, resulting in much smaller overall values of 0.119 and 0.237. This indicates that the AAD has a better ability of obtaining the objective values with higher accuracy. The ANOVA results shown in Fig. 5A1 for solving the problems with 2 factories reveal that the AAD performs statistically better than the OCVND and MSCNVD, but there are no significant differences among the AAD, IABC, MDABC, and SABC. For solving the problems with 3 factories, Fig. 5B1 shows that the AAD outperforms the OCVND, MSVND, and MDABC, and there are no significant differences among AAD, IABC, and SABC. As the problem scale increases to 4 factories, it can be obtained from the average RPI values that the AAD also yields a much smaller overall value of 0.364 when compared to the OCVND (2.967), MSVND (3.387), IABC (1.116), MDABC (2.197), and SABC (1.274). Additionally, Fig. 5C1 indicates that the AAD outperforms all other algorithms except for the IABC. However, when the problem scales come to 5 and 6 factories, as can be seen from Fig. 5D1, E1, the AAD performs significantly better than all other compared metaheuristics. The above observations indicate that the advantage of the AAD in solving accuracy becomes increasingly evident with the increase of the problem scale. Moreover, Figs. 6, 7 and 8 illustrate that the average RPI (ARPI) values yielded by the algorithms have a trend of gradual increase as the number of factories, lots, and stages increases. This finding confirms that the complexity of the problem increases as the problem scale increases. The reason behind this is that the increasing scale of factories increases the complexity of determining the factory to be assigned, and that more lots and stages mean more computational complexity. Meanwhile, it can be seen that the ARPI values obtained by the AAD remain relatively stable as the problem scale increases, and they are all closest to 0. In conclusion, the AAD exhibits promising performance in terms of solving accuracy, and as the problem scale increases, its advantage becomes increasingly evident. From Tables 6, 7, 8, 9 and 10, it can be observed that the AAD can achieve the smallest standard deviations for most of the instances. Moreover, the box plots shown in Fig. 5 illustrate that the distribution intervals obtained by the AAD are the shortest, and the median values are closest to zero. Therefore, the robustness of the AAD can be guaranteed. Given the above, we can obtain the following conclusions.

• The AAD has the best solving accuracy for solving the problems with different scales.

• As the problem complexity increases, the advantage of the AAD becomes increasingly obvious.

• The robustness of the AAD can be guaranteed.

Case study

This section focuses on the practical application of the MILP model and methodology proposed in this study to a mechanical processing workshop at an automobile production company in China. Based on the actual situation and circumstances in the workshop, the scheduling problem can be reduced to the DHFSP_CS, as discussed in this paper.

The real-world case

The cylinder block serves as a vital core component of the engine, possessing a complex structure consisting of various assembled parts, such as holes, plane grooves, screw holes, and deep holes. The dimensional and position accuracy requirements for cylinder block parts are higher than those for other engine parts. To meet the demands of the diverse range of engines and real-time orders, the workshop adopts the model of multi-variety and small-lot, and has set up three hybrid flowshop lines. In a practical scenario, the workshop processes eight distinct products, including naturally ventilated engine cylinder blocks of 1.6, 1.8, 2.4, and 3.6 L, as well as turbocharged engine cylinder blocks of 1.2, 1.5, 1.8, and 2.0 T. The comprehensive process flow diagram, detailing the complete processing journey from the initial blank to the end, is depicted in Fig. 9.

Fig. 9

The flowchart of cylinder block processing

As depicted in Fig. 9, the process of converting a blank into a final product entails a series of 16 distinct operations, with some operations carried out at the same station. To streamline the production process, these operations are consolidated into 8 stages: positioning reference (including Operation 1), rough machining (including Operation 2 to Operation 5), intermediate cleaning (including Operation 6), pressure inspection (including Operation 7), press assembly (including Operation 8), finishing (including Operation 9 to Operation 14), cleaning (including Operation 15), and final inspection (including Operation 16). Each of these stages employs identical parallel machines, with 4 machines, 2 machines, 1 machine, 3 machines, 1 machine, 2 machines, 1 machine, and 1 machine being utilized across the 8 stages, respectively. All the lots undergo these stages in a sequential manner. According to the actual production situation, the machine has the replacement time of fixture, and the replacement time is fixed. Table 11 summarizes the production requirements of cylinder block on a given day, including lot size, unit processing time, setup time, and transfer time at each stage. In cases where using the consistent sublots is used, the maximum sublot quantality is set at 5.

Table 11 The production task of the workshop on a given day

Case solving and verification

The aforementioned scenario is addressed using the CPLEX, AAD and compared metaheuristics. The CPLEX struggles to attain the optimal solution within 600 s. Ultimately, the schedule depicted in Fig. 10 is generated, with a makespan of 1506.3 min. To ensure a fair comparison, the time limit for the CPLEX is also set to 5.12 s, identical to that of the metaheuristics. The resulting schedule has a makespan of 1716.4 min that is much larger than that obtained by the metaheuristics. With the termination time set as 5.12 s ($40 \times 2 \times 8 \times 8$ milliseconds), the makespan values obtained in the 20 independent runs of the compared metaheuristics are listed in Table 12, where the average values and standard deviations are also given. It can be seen from Table 12 that the AAD and MDABC can get the best schedule with a makespan of 1497.6 min, which is better than that obtained by the CPLEX within 600 s. The best schedule obtained by the AAD is presented in Fig. 11. In terms of the average values, it is clear that the AAD achieves a much lower value. To give the significance analysis of the results, the Wilcoxon rank sum test is conducted, and the corresponding p and h values are shown in Table 13. Based on the results presented in Tables 12 and 13, it can be concluded that the AAD statistically outperformed the other algorithms. Therefore, the efficiency and effectiveness of the AAD has been successfully demonstrated in the real-world scenario.

Fig. 10

Gant chart of the schedule obtained by CPLEX

Table 12 The objective values in 20 independent runs

Fig. 11

Gant chart of the schedule obtained by AAD

Table 13 The results of Wilcoxon rank sum test

Conclusion

This study delved into the DHFSP_CS with the objective of minimizing the makespan, which, to our knowledge, has not been addressed previously. To solve the problem, the MILP model was initially developed to handle small-scale instances with precision. Due to its NP-hard nature, to solve the large-scale instances, the I/F-Race was implemented as the AAD methodology to construct an automated algorithm within the ECVND framework. ECVND, an extension of the previously proposed CVND, considered the characteristics of distributed scheduling. Additionally, regarding the problem-specific characteristics, a novel solution encoding was developed. The configurable values for the categorical parameters, i.e., solution decoding, solution initialization, and collaborative operator, were designed. Moreover, the neighborhood structures were specially designed. From the extensive experiments conducted, the following conclusions were drawn: (1) The automated algorithm has the highest solving accuracy for solving the problems with different scales when compared with the other metaheuristics and CPLEX. (2) The advantage of the automated algorithm becomes increasingly apparent as the problem complexity increases. (3) The stability of the automated algorithm can be guaranteed.

In relation to the DHFSP_CS, our forthcoming research will entail the development of more efficient encoding and decoding strategies, along with problem-specific characteristics, to improve the results. Furthermore, given the potential for complex and unpredictable events, it is imperative to derive useful properties, such as dynamic and rescheduling strategies. In this case, it is also crucial to establish suitable indicators of system stability. Regarding the AAD methodology, we will endeavor to develop technologies that optimize computational costs.