Introduction

In recent years, there has been a significant increase in the popularity of graph embedding, which involves encoding nodes and edges into low-dimensional vectors so that the graph’s structural information can be optimally preserved. Graph embedding technology has demonstrated excellent results in various applications, such as node classification [1], link and community detection [2,3,4], social recommendation systems [5], and traffic detection [6]. Although these new embedding methods typically offer more significant qualitative advantages than traditional methods, many of them are not scalable for large-scale datasets, such as graphs with more than 10,000 nodes, and their computation is expensive, and they require a considerable amount of memory. For example, Deepwalk [7] generates the node’s neighbor sequence points via random walk, while the Skip-gram idea is employed to train the nodes’ feature vector. Node2vec [8] is a sequence of information that incorporates random breadth walk, following Deepwalk’s random depth walk. The original graph is transformed into a multi-layer graph structure, and this is followed by a context sequence of random walks with offset information. The vector representation of nodes is ultimately acquired through Skip-gram training. These methods aim to embed a graph based on its topology while not including node attribute knowledge. This factor decreases their embedding capability and imposes a substantial amount of CPU time to acquire an adequate number of walks to train the embedding model.

Due to the high computational cost and memory use of graph embedding in large-scale graphs [9, 10], several approaches have been proposed to embed scalable graphs using a multi-level framework. The process involves three steps: first, a hybrid matching strategy is implemented to repeatedly shrink the original graph into smaller graphs; second, existing embedding techniques are utilized to generate the embedding on the coarse graph, which is computationally inexpensive, occupies relatively minimal memory, and captures the global structure of the original graph; and finally, a graph convolution network-based learning refinement model is proposed [11]. This model uses a nonlinear activation function to identify linear transformation of all nodes’ neighbors. This model improves the quality of embedding from the coarse graph to the original. The process of learning refinement in the graph convolution network is dependent on the embedment method, structure, and the selection of the relation graph.

Multi-level frameworks have significantly improved the embedding speed of some large-scale graphs. Previous research has been carried out toward coarsening, particularly focused on preserving diverse attributes. Typically, this method involves the spectra of both the original and the coarse graphs [9, 10, 12]. A more advanced coarsening algorithm [13] that could efficiently manage the first few eigenvectors of the graph Laplacian matrix was subsequently discovered. These eigenvectors are particularly crucial for preserving the critical structure of the graph. Nonetheless, experimental outcomes demonstrate that graph embedding is not effective for nodes with several features and complicated structures. It becomes inappropriate to evaluate the two graphs solely based on the difference in their eigenvalues since the spectral distance between the coarse and the original graph is not clearly defined. The Graph Convolutional Network (GCN) model is restricted in its ability to obtain information from high-order neighbors since it has little refinement capacity. However, adding more layers and increasing nonlinearity can hinder the performance of these models, leading to oversmoothing. This implies that as the number of layers goes up, the GCN’s nodes representation tends to specific values, making them indistinguishable.

This paper introduces a novel multi-level graph embedding refinement framework, MERIT, designed to enhance the efficiency of large-scale graph embeddings. Specifically, MERIT contains three key components: graph coarsening, graph embedding, and embedding refinement. First, the graph is coarsened by assessing the similarity between the original and coarsened graphs based on the shift in spectral distance [14] and capturing structural adjustments in the graph coarsening process. The paper proposes a novel coarsening algorithm that locally clusters nodes with a high spectral affinity to create a graph with fewer nodes (adjacency matrix). The previously mentioned process is repeatedly performed to optimize the termination criterion for coarsening. Second, any existing unsupervised graph embedding technique can be employed for node embedding of the global graph in the base graph embedding stage. Finally, this paper proposes a new refinement model that employs learning-based graph convolutional networks to improve the embedding from the coarsest graph to the original graph. This graph convolutional network utilizes the inherent dependencies of the graph structure and the selected embedding technique to achieve a refinement process.

This paper evaluates the proposed MERIT framework on three benchmark datasets: the bioinformatics dataset PPI, the reviews dataset Reddit, and the social reviews dataset Flickr. Furthermore, this paper evaluate the progress of MERIT on the literature citation network public dataset CORA and the bibliographic network dataset DBLP. The experimental results demonstrate that MERIT significantly reduces runtime while improving classification accuracy and prediction precision.

The main technical contributions of this article are summarized as follows:

  • MERIT is a powerful tool for generating high-quality embeddings for large-scale graphs. This paper introduces a new coarsening algorithm that significantly reduces graph size. As part of the refinement process, the GCN model is tweaked to prevent over-smoothing and to continuously improve network performance as its depth increases. As a result, embedding accuracy is improved by 11% compared to existing embedding technologies (Fig. 1).

  • The MERIT approach is highly scalable, greatly enhancing the scalability of embedding methods by a factor of up to 40, both in terms of runtime and memory usage.

  • MERIT offers high flexibility. The framework is independent of the underlying graph embedding technology and can be combined with any unsupervised graph embedding method.

Fig. 1
figure 1

The MERIT embedding method consists of three stages: graph coarsening, base embedding, and GCN refinement

Full size image

Related work

There is a large and active body of research on both multi-level graph embedding and graph convolutional networks that inspire MERIT to improve the performance and speed of unsupervised embedding methods. This paper provides a summary of recent research in these areas, with a focus on the latest developments.

Graph embedding

In recent years, numerous network embedding and graph embedding approaches have been proposed. LINE [15], which preserves first-order and second-order proximities, and SDNE [16], which captures the non-linear structure through deep neural networks, are two notable graph embedding algorithms. Matrix decomposition technique has also been utilized in graph embedding [17, 18]. As a result, more network embedding methods were developed for information-rich graphs and heterogeneous networks [19,20,21,22]. Efforts to improve the scalability of graph embedding are relatively minimal [23]. Current methods are constrained to moderate-sized datasets. The aim of multi-level graph embedding is to simplify an original graph by breaking it down into smaller graphs of decreasing sizes. These smaller graphs are then fragmented into clusters, which are used to reconstruct partitions recursively from the coarse-grained graph. The final step involves connecting the resulting embedding vectors to generate a hierarchically built multilevel graph that provides the final node embedding for the original graph [24]. Although prior research has concentrated on improving embedding quality, scalability was not always a priority. However, embedding frameworks based on the coarsest graph are more scalable [12]. Unfortunately, many of these techniques lack the necessary refinement processes required to generate high-quality embeddings. It is important to note that improving the accuracy and scalability of graph embedding techniques are seen as separate issues. This study aims to address the need for faster large-scale graph embedding while simultaneously enhancing the quality of the embedding.

Multi-level graph embedding

Previous efforts attempted to enhance embedding quality by training the coarsest graph for coarse embedding, and later refining with GCN [9, 10]. However, the drawback with this approach is that the article necessitates training a time-intensive GCN model for large-scale graphs, which is problematic when stacking multiple layers. To address this issue, the multi-level graph embedding in GraphZoom [13] utilizes a GCN model for filtering, which eliminates high-frequency noise in the node characteristic matrix. This approach demonstrated the fundamental relationship between graph embedding and filtering. A filtering neural network (gfNN) is proposed to yield a more robust graph filter, which enhances embedding quality. Additionally, two generalized graph filters are derived and incorporated into the graph embedding model for various classification tasks, further improving the embedding quality. It is worth noting that the neural network produced by training graphs captures not only the features of the graphs themselves but also their relative relationships [25, 26].

In the refinement process, a graph filter is employed in the iterative thinning step to smooth the intermediate embeddings. This step plays a pivotal role in enhancing the quality of the final embedding. However, datasets such as PPI [27] contain multiple node types, and the contextual and sequential amino acid information must be filtered and aggregated efficiently. When these datasets are extended to deep neural structures, the learning process becomes inefficient, and developing an effective GCN model becomes challenging due to the vanishing gradient problem.

Over-smoothing

The problem of over-smoothing in GCN has received significant attention in recent work. JKNet [28] addresses this issue by utilizing dense hop connections to maintain the locality of node representation. DropEdge [29] proposes to randomly delete some edges in the input graph to alleviate the effects of over-smoothing. These methods demonstrate a slower decline in performance when increasing network depth. However, for semi-supervised tasks, shallow models still provide the most advanced results, casting doubt on the benefits of increasing network depth. In order to address this challenge, MERIT proposed in this paper extends the depth model through a simple yet effective modification. In addition, it introduces a graph convolutional network based on the proportion of initial values and identity mapping, which constructs jump connections at each layer of the training model. In this model, each layer adds a certain percentage of the initial values, and the identity mapping adds the unit matrix to the weight matrix, as described in detail in the method section.

Problem formulation

Let \({\mathcal {G}}=({\mathcal {V}}, {E}, {W})\) represent the input graph with \({\mathcal {V}}\) and E as the node-set and edge-set, respectively. \({W} \in {\mathbb {R}}^{N \times N}\) is the adjacency matrix, and \(w(i) \in {\mathbb {R}}^{N}\) represents the weight of all possible edge vectors. The purpose of each node in \({\mathcal {G}}\) is to best preserve the attributes of the graph. To improve the speed of existing graph embedding methods without compromising on quality, this paper extend the embedding method to accommodate large-scale datasets.

This paper is to address the following problem: given a graph \({\mathcal {G}}=({\mathcal {V}}, {\mathcal {E}}, {W})\) and a graph embedding method \(f(*)\), the aim is to present a mechanism that can improve the scalability of the graph embedding while maintaining or enhancing the quality of output equal to, or even better than, that of \(f(*)\).

Graph coarsening

The coarse graph \({\mathcal {G}}_{m}=\left( {\mathcal {V}}_{m}, {E}_{m}, {W}_{m}\right) \) with \(n=|v_{m}|\) is coarsened from the original graph \({\mathcal {G}}\) with respect to a set of non-overlapping graph partitions \(P=\left\{ {\mathcal {S}}_{1}, {\mathcal {S}}_{2}... {\mathcal {S}}_{n}\right\} \subset {\mathcal {V}}\), \({\mathcal {V}}\) covers all nodes. Each partition \({\mathcal {S}}_{i}\) corresponds to a "supernode" denoted by \({\mathcal {S}}_{p}\) and the "superedge" connecting the supernodes \(W_{m}(p, q)\) has the edge weight as the accumulative edge weights between nodes in the corresponding graph partitions \({\mathcal {S}}_{p}\) and \({\mathcal {S}}_{q}\):

$$\begin{aligned} W_{m}(p, q)=w\left( {\mathcal {S}}_{p}, {\mathcal {S}}_{q}\right) :=\sum _{v_{i} \in {\mathcal {S}}_{p}, v_{j} \in {\mathcal {S}}_{q}} W(i, j) \end{aligned}$$
(1)

Let \(P \in {\mathbb {R}}^{n \times N}\) be the matrix whose columns are partition indicator vectors,

$$\begin{aligned} P(p, i)= {\left\{ \begin{array}{ll}1, &{} \text{ if } v_{i} \in {\mathcal {S}}_{p} \\ 0, &{} \text{ othewise } \end{array}\right. } \end{aligned}$$
(2)

An established fact is that the weight matrix W m of the coarse graph \({\mathcal {G}}{m}\) satisfies \(W_{m}=P W P^{\top }\). Using this relationship, the coarsened Laplacian matrices can be directly defined as:

$$\begin{aligned} L_{m}=D_{m}-W_{m} \text{ and } L_{m}=I_{n}-D_{m}^{-1 / 2} W_{m} D_{m}^{-1 / 2} \end{aligned}$$
(3)

The spectral graph partitioning algorithm, first proposed by Fiedler, was initially interpreted as a clustering algorithm because graph partitioning is often analogous to clustering. In this paper, a set P of graph partitions \(\left\{ {\mathcal {S}}{1}, {\mathcal {S}}{2}, \ldots , {\mathcal {S}}_{n}\right\} \subset {\mathcal {V}}\) is referred to as a "cut" of a graph because it creates a partition of \({\mathcal {V}}\) into P and \({\bar{P}}\).

Definition 1

The definition of the volume of a vertex is as follows:

$$\begin{aligned} {\text {vol}} v=\sum _{u} W_{v, u} \end{aligned}$$
(4)

Likewise, the volume of a set is

$$\begin{aligned} {\text {vol}} P=\sum _{v \in P} {\text {vol}} v \end{aligned}$$
(5)

Finally, the volume of a cut is

$$\begin{aligned} {\text {vol}} \partial P=\sum _{u \in P, v \in {\bar{P}}} W_{u, v} \end{aligned}$$
(6)

One important property of the \({\text {vol}} \partial P\) is that

$$\begin{aligned} {\text {vol}} \partial P={\text {vol}} \partial {\bar{P}} \end{aligned}$$
(7)

By definition, the partitioning algorithm follows a simple set of steps. First, the normalized cut of a partition P in a graph \({\mathcal {G}}\) is calculated in this paper.

$$\begin{aligned} {\text {ncut}}(P)={\text {vol}} \partial P\left( \frac{1}{{\text {vol}} P}+\frac{1}{{\text {vol}} {\bar{P}}}\right) \end{aligned}$$
(8)

The normalized cut of a graph is the minimum value over all possible subsets P. Additionally, the expansion of a partition P of a graph \({\mathcal {G}}\) is defined as:

$$\begin{aligned} \rho (P)=\frac{{\text {vol}} \partial P}{\min (\mid P\mid ,\mid {\bar{P}}\mid )} \end{aligned}$$
(9)

It should be noted that this paper implements the graphical partitioning algorithm for coarsening with the constraint outlined in Eq. (1). The set of nodes that form "supernodes" following the partitioning of the original graph is known as the matching. By utilizing advanced matching techniques that adhere to spectral distance constraints, the graph can be effectively coarsened while still preserving its global structure.

This paper proposes a new spectral distance SD, which is based on the coarsening relationship between spectral distance and graph coarsening as described in [30,31,32]. The spectral distance SD is defined as the eigenvalues of the normalized Laplacian matrices represented by \(\lambda \), which are used during the matching process. Specifically, the spectral distance is used to measure the distance between graph \({\mathcal {G}}\) and \({\mathcal {G}}{m}\), where \({\mathcal {G}}{m}\) is the coarsened version of \({\mathcal {G}}\).

$$\begin{aligned} S D\left( {\mathcal {G}}, {\mathcal {G}}_{m}\right) =\left\| \varvec{\lambda }-\varvec{\lambda }_{l}\right\| _{1}=\sum _{i=1}^{N}\mid \varvec{\lambda }(i)-\varvec{\lambda }_{l}(i)\mid \end{aligned}$$
(10)

The vectors \(\lambda \) and \(\lambda _{l}\) contain the eigenvalues of the original and coarsened layer graphs, respectively. In the ideal scenario, the merged nodes possess the same normalized edge weight.

  • Proposition 1: Let \({\mathcal {G}}_{m}\) be the graph obtained by coarsening \({\mathcal {G}}\) according to a specific set of partitions.

    $$\begin{aligned} P=\left\{ {\mathcal {S}}_{1}, {\mathcal {S}}_{2},,, {\mathcal {S}}_{n}\right\} \subset {\mathcal {V}} \end{aligned}$$
    (11)

    If the selection of P is such that all nodes in a given partition possess the same normalized edge weights,

    $$\begin{aligned} \frac{{\varvec{w}}(i)}{d(i)}=\frac{{\varvec{w}}(j)}{d(j)} \quad \text{ for } \text{ all } v_{i}, v_{j} \in {\mathcal {S}} \text{ and } {\mathcal {S}} \in \ P \end{aligned}$$
    (12)

    Since \(SD({\mathcal {G}}, {\mathcal {G}}_{m})\) is equal to 0, the coarsening process of ideal graphs yields a minimum (both complete and partial) spectral distance. This paper presents a general result that illustrates how the graph coarsening framework of spectral structure changes can be captured by spectral distance. Specifically, the rough graph is a basic graph formed by merging a group of nodes (i.e., \(n=N-1\)). The paper establishes a proof for the following result:

  • Proposition 2: Suppose that graph \({\mathcal {G}}_{m}\) is obtained by merging a pair of nodes \({\mathcal {V}}_{a}\) and \({\mathcal {V}}_{b}\) from \({\mathcal {G}}\). If the normalized edge weights of the merged nodes meet:

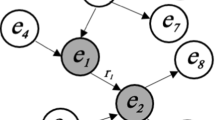
    $$\begin{aligned} \left\| \frac{w(a)}{d(a)}-\frac{w(b)}{d(b)}\right\| _{1} \le \epsilon \end{aligned}$$
    (13)

    The spectral distance between the original and coarse graphs is bounded by \(S D\left( G, G_{m}\right) \le N \epsilon \). The two propositions above illustrate that the spectral distance is limited by the edge weight of merging nodes that have been normalized. In other words, minimizing the edge weight division of nodes within the same region results in boundary and leads to the bounded spectral disturbance. In this paper, the Multi-level Spectral Graph Coarsening (MSGC) algorithm is employed to iteratively merge node pairs that share similar data (Fig. 2).

Fig. 2
figure 2

The graph coarsening process involved a random graph sampled from a stochastic block model with a total of 130 nodes across 13 predefined blocks. The coarse graph was derived from the predefined partitions

Full size image

The Multi-level Spectral Graph Coarsening (MSGC) algorithm is an iterative process that merges node pairs having similar characteristics. During each iteration, MSGC seeks normalized edge weights with the most similarity to merge, and creates supernodes. A restriction is applied to the candidate graph’s nodes to limit them to a 2-hop distance, and \(N_i\) represents the node-set of a 2-hop distance from node \({\mathcal {V}}_{i}\). The MSGC pseudo-code is provided in Algorithm 1. The spectral distance of the MSGC algorithm is analyzed as follows: It is assumed that node pairs \({\mathcal {V}}_{a_i}\) and \({\mathcal {V}}_{b_i}\) (i ranging from n to \(N+1\)) are merged iteratively from graph \({\mathcal {G}}\) coarsening to graph \({\mathcal {G}}_{m}\). If the normalized edge weight of the merged node satisfies Eq. (13) formula, it follows from Proposition 2 that the boundary of the spectral distance between the original graph and the coarse graph is:

$$\begin{aligned} SD\left( G, G_{m}\right) \le N \sum _{i=N}^{n+1} \epsilon _{i} \end{aligned}$$
(14)

The hybrid matching under the spectral distance constraint is achieved by constructing \({\mathcal {G}}_{i+1}\) from \({\mathcal {G}}_{i}\) to obtain the initial mapping \({\mathcal {M}}\), followed by collapsing the nodes in each match into supernodes in \({\mathcal {G}}_{i+1}\). When \({\mathcal {S}}_{p}={\mathcal {S}}_{q}={\mathcal {S}}\), the weight \({\varvec{W}}_{m}(i, j)\) is equivalent to the weight of all edges in the subgraph induced by \({\mathcal {S}}\). Thus, if \({\varvec{W}}_{m}(i, j)\) is the same for all \(v_{i}, v_{j} \in {\mathcal {S}}\), then \({\varvec{W}}_{m}(i, j)={\varvec{W}}(i, j)\), and in-partition weights are precisely preserved by successive coarsening. In this paper, the Laplacian adjacency matrix \(A_{i+1}\) for \({\mathcal {G}}_{i}\) is established by matrix operations, while the matching matrix, which contains the matching information from \({\mathcal {G}}_{i}\) to \({\mathcal {G}}_{i+1}\) as a binary matrix \(M_{i, i+1} \in \{0,1\}^{\mid V_{i}\mid \times \mid V_{i+1}\mid }\), is created. The row and column of \(M_{i, i+1}\) is set to 1 if the node in \({\mathcal {G}}_{i}\) is collapsed into super-node \({\mathcal {S}}\) in \({\mathcal {G}}_{i+1}\), and is set to 0 if it is not. Each column of \(M_{i, i+1}\) represents a matching, while each unmatched vertex appears as an individual column in \(M_{i, i+1}\) with merely one entry set to 1. In this paper, the adjacency matrix of \({\mathcal {G}}_{i+1}\) is constructed using the following method:

$$\begin{aligned} A_{i+1}=M_{i, i+1}^{T} A_{i} M_{i, i+1} \end{aligned}$$
(15)

The initial mapping \({\mathcal {M}}\) inevitably contains some mismatches between node pairs. For the mapping \({\mathcal {M}}\) between graphs \({\mathcal {G}}_{i}\) and \({\mathcal {G}}_{i+1}\) in this paper, the consistent degree of a mapped pair \((u, v) \in {\mathcal {M}}\) is defined as the number of consistent edges connected to u (or v) in \({\mathcal {G}}_{i}\) (or \({\mathcal {G}}_{i+1}\)), and the consistent degree is calculated for each matched pair in the mapping. Korula et al. [33] demonstrated that if a node pair has at least three correctly mapped neighbors, the node pair has a high probability of being correctly mapped. Therefore, this paper sets the minimum confidence level for a subset to three. If the consistency of the sub-mapping is greater than three, the mapping pair gets added to the sub-mapping. Otherwise, the two graphs are copied directly to \({\mathcal {G}}_{i+1}\) because they do not match.

Algorithm 1
figure a

Multi-level Spectral Graph Coarsening

Full size image

Algorithm 1 employs the spectral distance to enhance graph matching fusion by coarsening the graph while maintaining the global structure and improving speed. The spectral distance coarsening algorithm has three steps in the calculation process: first, the graph is partitioned and the adjacency information is compiled in the partition, then the weight-sum of all adjacent nodes is counted, and adjacent similar nodes are combined into "supernodes." Finally, spectral distance restrictions update the neighboring points and edges to trigger the next iteration of neighboring nodes. The entire process is parallelized to allow for high-dimensional points. The choice of coarsening level is dependent on the application domain and graph properties, although this study found that a small number of coarsening levels (2 to 4) typically resulted in the best quality embedding and at a relatively rapid pace.

Base embedding on coarsened graph

The graph size decreases significantly after each coarsening iteration, with the graph size halving in the best-case scenario. m iterations of coarsening are carried out, with the coarsest graph \({\mathcal {G}}_{m}\) designated as the embedding method \(f({\mathcal {G}}_{m})\), leading to \({\mathcal {E}}_{m}=f({\mathcal {G}}_{m})\). In the MERIT framework, any graph embedding algorithm may be employed as the fundamental embedding because the adopted graph embedding method is unknown.

Refinement of embeddings

In the final step of MERIT, the focus shifts to embedding refinement, given a series of coarsened graphs represented by \({\mathcal {G}}_{0},{\mathcal {G}}_{1},{\mathcal {G}}_{2},\ldots ,{\mathcal {G}}_{m}\), along with their corresponding matching matrices denoted by \({M}_{0,1},{M}_{1,2},\ldots ,{M}_{m-1,m}\), and the node embeddings \({\mathcal {E}}_{m}\) generated on \({\mathcal {G}}_{m}\). This study aims to develop a method for inferring the node embedding of \({\mathcal {G}}_{0}\) from \({\mathcal {G}}_{m}\). Specifically, the study begins by addressing a relatively straightforward subtask. The subtask aims to infer the embeddings \({\mathcal {E}}_{i}\) on graph \({\mathcal {G}}_{i}\) while given the graph \({\mathcal {G}}_{i}\), its coarsened form \({\mathcal {G}}_{i+1}\), the matching matrix \({M}_{i,i+1}\), and the node embeddings \({\mathcal {E}}_{i+1}\) obtained from \({\mathcal {G}}_{i+1}\). After solving the subtask mentioned above, it can then be applied sequentially to each pair of continuous graphs from \({\mathcal {G}}_{m}\) to \({\mathcal {G}}_{0}\) resulting in the node embedding of \({\mathcal {G}}_{0}\). To perform the embedding refinement, a graph-based neural network model is employed in this study.

The study introduces the Graph Convolution Network for Refinement Learning, where the node embedding is projected from the coarse-grained graph \({\mathcal {G}}_{i+1}\) to the fine-grained graph \({\mathcal {G}}_{i}\) using the matching information between \({\mathcal {G}}_{i}\) and \({\mathcal {G}}_{i+1}\), which is available. The following equation is utilized for the projection:

$$\begin{aligned} \varepsilon _{i}^{p}=M_{i, i+1} \varepsilon _{i+1} \end{aligned}$$
(16)

In order to solve the problem of sharing the same embedding among super nodes, a graph-based neural network model is proposed in this paper, which leverages \(\varepsilon _{i}^{p}\) and adjacency matrix \(A_{i}\) to obtain refined embedding \({\mathcal {E}}_{i}\) through the model RF (refinement model), i.e., \({\mathcal {E}}_{i}={\text {RF}}\left( {\mathcal {E}}_{i}^{p}, A_{i}\right) \), as the simple projection method that copies the embedding directly has the obvious limitation of the same embedding among super nodes. This limitation will exacerbate in the iterative refinement of graph embedding from \({\mathcal {G}}_{m},{\mathcal {G}}_{m-1},\ldots ,{\mathcal {G}}_{0}\). The adjacency matrix A of a graph \({\mathcal {G}}\) can be used to derive a fast approximation to the convolution of the graph with the adjacency matrix, which is required to compute the l-th layer of the neural network model [11]. The neural network’s \(l^{th}\) layer is a crucial component of the model.

$$\begin{aligned} H^{(\ell )}(X, A)=\sigma \left( {\widetilde{D}}^{-\frac{1}{2}} {\tilde{A}} {\widetilde{D}}^{-\frac{1}{2}} H^{(\ell -1)}(X, A) W^{(\ell )} \Theta ^{(l)}\right) \end{aligned}$$
(17)

The activation function \(\sigma (*)\), trainable weight matrix \(\Theta ^{(l)}\), and representation degree matrix \({\widetilde{D}}\), which includes self-connected edges, are all essential components of the neural network model. Specifically, \({\tilde{A}}=A+I_{n}\) is the adjacency matrix representation of the graph neural network.

$$\begin{aligned} {\mathcal {E}}_{i}={\text {RF}}\left( \varepsilon _{i}^{p}, A_{i}\right) =H^{(\ell )}\left( \varepsilon _{i}^{p}, A_{i}\right) \end{aligned}$$
(18)

The refinement model’s learning process involves learning \(\Theta ^{(l)}\) for each \(k \in [1, l]\) using Eq. (17). The graph convolution model \(H^{(l)}(\cdot )\) predicts embeddings \({\mathcal {E}}_{i}\) on graph \({\mathcal {G}}_{i}\) by replicating \({\mathcal {G}}_{m}\) and building a virtual coarsening graph to learn E on the coarsest graph. Refinement embeddings are inferred by repeatedly applying the same set of parameters \(\Theta ^{(l)}\). Parameter sharing between levels using the same set of parameters \(\Theta ^{(l)}\) is a trade-off between efficiency and effectiveness. In summary, the refinement model integrates the structural information of the current graph \({\mathcal {G}}\) into the projected embedding \({\mathcal {E}}_{i}^{p}\) by repeatedly performing spectral graph convolution. This procedure involves the propagation of embeddings in the embedding refinement process defined as Eq. (17). Each layer of graph convolution satisfies Eq. (13) normalized edge weight. The final node embedding on \({\mathcal {G}}_{0}\) is derived by sharing \(\Theta ^{(l)}\) values and applying the technique to each consecutive pair of graphs from \({\mathcal {G}}_{m}\) to \({\mathcal {G}}_{0}\).

Optimized GCN model

The classification of nodes using GCN is limited to 2–3 layers. Attempting to increase the number of layers in a GCN model leads to two problems.

Question 1: Smoothing occurs when all nodes eventually tend to the same value.

Question 2: As the number of layers increases, so does the number of parameters exponentially. Additionally, expanding the size of the neighborhood used becomes increasingly difficult.

Therefore, choosing the correct depth model is crucial. Recent works, such as [29, 34], have produced graph convolutional networks that aim to address this issue. This paper presents a new model for graph convolutional networks. The proposed model involves adding a certain proportion of the initial value to \(H^{(0)}\) for each layer while maintaining a balance of identity mapping \(I_n\) to ensure that the sum of the harmony with the current layer is 1. The GCN model’s layers are then redefined as follows:

$$\begin{aligned} H^{(\ell +\!1)}= & {} \sigma \!\left( \left( (1-\!\alpha )\!{\tilde{P}}\! H^{(\ell )}+\!\alpha H^{(0)}\right) \left( \left( 1\!-\!\frac{\beta }{\ell }\!\right) I_{n}+\!\frac{\beta }{\ell } W^{(\ell )}\!\right) \right) \nonumber \\ \end{aligned}$$
(19)

In comparison to the ordinary GCN model, the following improvements have been made by discussing and comparing the two super parameters, \(\alpha \) and \(\beta \):

  • The initial value of the first layer, \(H^{(0)}\), is combined proportionally with the smooth representation \({\tilde{P}} H^{(\ell )}\).

  • The weight matrix, \(W^{(\ell )}\), should have an added identity map, \(I_n\).

The approach in this paper includes ensuring that even when multiple layers are used in training, the final representation of each node retains at least the \(\alpha \) part of the input layer. Typically, \(\alpha =\) 0.1 or 0.2 are used to contain at least a portion of the input features. Notably, \(H^{(0)}\) may not be equivalent to the characteristic matrix X. If the typical dimension d is large, an initial representation \(H^{(0)}\) can be obtained with lower dimensions using a fully connected neural network applied on X before forward propagation. However, only adding a certain proportion of the initial value \(H^{(0)}\) would not be sufficient to extend GCN into a depth model.

To overcome the limitation of extending GCN to a depth model, a self-identity mapping matrix, \(I_n\), is included in the weight matrix. The identity mapping guarantees that the deep GCN model produces performance equivalent to its shallow-layer counterpart. Additionally, as the number of layers increases, the attenuation of the weight matrix increases adaptively. At some point, the depth model ignores \(W^{(\ell )}\) and reduces to a simulation:

$$\begin{aligned} H^{(\ell +1)}=(1-\alpha ) {\tilde{P}} H^{(\ell )}+\alpha H^{(0)} \end{aligned}$$
(20)

The selection of GCN layers has been improved by considering the graph convolution model as a message-passing operator. Each layer l is associated with the aggregation of structural information from the neighbors jumped by each node l. While it is necessary for the number of layers to be greater than 1 to reflect the connected structure outside a node’s nearest neighbors, too many layers can make the node embeddings homogeneous and difficult to distinguish. Since the problem of smooth transition is addressed, the layer selection is better than that of the original GCN. Experimental results presented in this paper indicate that the best results are obtained when \(l=3\).

The principle of embedding refinement involves refining from a coarse graph to a fine-grained graph in two steps—

step 1: Through matrix multiplication (Eq. (16)), nodes based on response matching are embedded and projected onto the fine-grained graph.

step 2: The optimized GCN model (Eq. (19)) is applied to propagate the localization of the node embedding.

This paper presents a pseudo-coarsening graph which is created by copying \({\mathcal {G}}_{m}\). This approach not only reduces one graph coarsening iteration, but also avoids the base embedding of \({\mathcal {G}}_{m}\), since \({\mathcal {E}}_{i+1}={\mathcal {E}}_{i}\). Compared to a partitioning strategy with edge slicing, a coarsening-based strategy reduces the maintenance of copies of edges and conserves more memory space. Additionally, parallelizing high-dimensional points using the coarsening algorithm makes the base embedding save calculation time significantly as the coarsening level m increases. The training of the refinement model can be done effectively on the coarsest graph by minimizing the difference between the generated embeddings and the embeddings generated by the refinement model (GCN). The learning refinement model can then be used to generate embeddings for other coarsening levels. Finally, the embedding refinement process is affordable and involves only sparse matrix multiplications, using Eq. (18).

Algorithm 2
figure b

Multi-level embedding refinement(MERIT)

Full size image

Experiments and results

In this section, a series of experiments and comparisons are conducted on large-scale datasets and basic embedding methods to validate the effectiveness of the MERIT method.

Databases

The multi-level graph embedding refinement framework proposed in this paper is evaluated together with several unsupervised graph embedding techniques [17, 35]. Table 1 reports the statistical data of the datasets used in the experiments, including the CORA citation network public dataset, pre-processed biological information dataset PPI, and pre-processed social commentary datasets Flickr and Reddit. Moreover, it includes the computer science bibliography network dataset DBLP, which collects information from four research areas: database, data mining, machine learning, and information retrieval.

Table 1 The statistics of databases
Full size table

Base embedding methods

Three popular graph embedding approaches are explored in this paper to demonstrate that MERIT is compatible with different methods.

  • Random-walk based methods: Specifically Deepwalk [7] and Node2vec [8, 36]. To compare with traditional multi-level graph embedding frameworks, the number of random length walks is set to 80, the number of walks per node is set to 10, and the size of the context window is set to 10. In Node2Vec, p is set to 4.0 and q is set to 1.0, which have been found empirically to generate better results across all datasets.

  • Matrix-factorization-based methods: NMF-AP [37] is a link prediction method that uses non-negative matrix decomposition, while NETMF [17] is a more popular approach. To evaluate and compare their performance, the window size is set to 10 and the level of factorization is set to \(h = 1024\).

This paper utilizes the TensorFlow software package to implement the fine-grained embedding learning section, taking advantage of the available parallelism in various methods (e.g., generating random walks in DeepWalk and Node2Vec, refining models in MERIT, etc.).

MERIT framework performance

This paper investigates the effectiveness of the MERIT framework when applied to different graph embedding methods. Figures 3 and 4 depict the performance of varying MERIT datasets with different basic embedding methods at diverse coarsening stages of node classification [8] and link prediction [38], respectively.

Evaluation Metrics: This paper employs multi-label node classification and link prediction. The embeddings are utilized as 10-fold cross-validated features for node classification, and the average Micro-F1 and Macro-F1 are recorded for analysis. The performance of link prediction is evaluated via 5-fold cross-validation for AUROC and the average score is presented.

  • CORA (Suitable for node classification and link prediction tasks): CORA is a citation network dataset used for academic paper classification and citation relationships. It contains papers from multiple academic fields, with each node representing a paper and edges representing citation relationships. The node classification task aims to classify each paper into its corresponding academic discipline, while the link prediction task aims to predict the citation relationships between papers. Due to the rich paper features and label information provided by the CORA dataset, such as titles, abstracts, keywords, and references, it is highly suitable for node classification and link prediction tasks.

  • PPI (Suitable for link prediction and node classification tasks): PPI is a preprocessed biological information dataset representing protein-protein interaction relationships. Nodes represent proteins, and edges represent interactions between proteins. The link prediction task aims to predict unknown protein-protein interactions, while the node classification task aims to classify various protein characteristics. The PPI dataset provides rich protein features and known interaction information, making it suitable for performing link prediction and node classification tasks.

  • Flickr and Reddit (Suitable for node classification tasks): Flickr and Reddit are two preprocessed social comment datasets used for social media comment analysis. Each node in the dataset represents a user or comment, while edges represent relationships between users. The node classification task involves categorizing each user or comment into different classes, such as sentiment classification or topic classification. These datasets provide text features and category labels for users or comments, making them suitable for node classification tasks.

  • DBLP (Suitable for link prediction tasks): DBLP is a computer science bibliography network dataset that collects information from four research fields: databases, data mining, machine learning, and information retrieval. Nodes represent papers, and edges represent citation relationships. The link prediction task can involve predicting citation relationships between papers in the DBLP dataset or predicting other papers related to a given paper. Due to the availability of paper metadata and citation relationships in the DBLP dataset, it is suitable for link prediction tasks.

Running time: This paper presents an end-to-end clock time for scalability analysis, where the time scale is selected as hours for large-scale graph embedding and minutes for small-scale graph embedding. Moreover, the runtime of the proposed graph embedding method based on the MERIT framework includes the execution time of all stages, as well as the training time of the refinement model.

Impact of MERIT on embedding quality: This paper evaluates node classification and link prediction performance using various underlying embedding methods and coarsening levels on the PPI dataset through the MERIT framework. Figure 3 illustrates how node classification performance changes with increasing coarsening levels in the MERIT framework (Note that \(m=0\) indicates the original method without MERIT). When the coarsening level reaches 1 (\(m=1\)), this paper achieve a large-scale graph (PPI) of \(2.3\times \) to \(4.7\times \) acceleration while enhancing the qualitative aspect. At a coarsening level of 2 (\(m=2\)), the acceleration ratio further increases (up to \(16.3\times \)), with the same level of embedding quality as the original method reflected in Micro-F1 scores. In the case of link prediction, depicted in Fig. 4, performance improves with increasing coarsening levels through the MERIT framework, which leads to a reduction in the running time of the embedding method and an improvement in link prediction results.

MERIT effectively improves the quality and acceleration of embedding for large-scale graphs. Figure 3 illustrates that there is a significant increase in Micro-F1 scores on all datasets when the coarsening level moves from \(m=0\) to \(m=1\) compared to basic embedding methods. With further increases in the coarsening level m within the MERIT framework, the running time decreases sharply, while the embedding quality decreases only slightly. In the coarsening process, the spectral distance eliminates superfluous information from the source graph and retains essential spectral attributes for embedding. Moreover, MERIT incorporates a defined percentage of initial values and identity mapping matrices in the embedding refinement process, addressing the over-smoothing problem and enhancing the overall embedding quality.

Fig. 3
figure 3

The performance and the run time of node classification vary with increasing coarsening levels in MERIT. Micro-F1 scores and running time are presented on the left and right, respectively, with time measured in minutes. Note that \(m=0\) indicates usage of the original embedding method (best viewed in color)

Full size image
Fig. 4
figure 4

The performance and run time of link prediction vary with the increase of the number of coarsening levels in MERIT. AUROC scores and running time are presented on the left and right, respectively, with time measured in minutes. Note that \(m=0\) indicates the use of the original embedding method

Full size image

Large graph embedding

The paper aims to demonstrate the scalability of the MERIT framework for graph embedding on large-scale Reddit datasets. The three fundamental embedding methods researched by the paper took over twenty-four hours to complete, and even with improved computer performance, Deepwalk struggled to complete. Notably, the MERIT framework simplifies graph embedding on large-scale datasets. Figure 5 depicts how the MERIT framework significantly reduces execution time and enhances the Micro-F1 score in node classification. For instance, when using the MERIT framework with a coarsening level of 5, the scores of DeepWalk, Node2Vec, and NetMF are improved by 2.3\(\times \), 2\(\times \), and 1.8\(\times \), respectively, and their scores increase from 0.441 to 0.453, from 0.451 to 0.465, and from 0.459 to 0.461. Furthermore, when using the MERIT framework with a coarsening level of 25, the execution time of all tested methods decreases from over 24 h to 1 h, while the Micro-F1 score only decreases by 1.5% from 0.453 to 0.438. The experiment showed that increasing the coarsening level from 5 to 10 did not significantly influence the Micro-F1 score, but resulted in a two-fold increase in execution time. Thus, the results confirm that the MERIT framework can generate high-quality embeddings and improve the graph embedding algorithms.

The proposed method achieves excellent performance in the link prediction task and greatly reduces the execution time. As shown in Table 2, on the Flickr dataset, an increase in coarsening level using the MERIT framework corresponds to an increase in AUROC score. When the coarsening level is 6, the AUROC scores of DeepWalk, Node2Vec, and NetMF increase from 0.652 to 0.681, from 0.801 to 0.902, and from 0.817 to 0.893, respectively, while the execution time is significantly reduced, and the fastest running speed is increased by 25\(\times \). The results demonstrate that the coarsening and refinement strategy adopted by the MERIT framework produces high-quality embeddings, scaling up the graph embedding algorithms for both node classification and link prediction tasks.

Fig. 5
figure 5

On the Reddit dataset, the performance and execution time for node classification vary with the coarsening level in the MERIT framework. The report displays Micro-F1 results and execution time in hours, respectively, on the left and right sides. Notably, \(m=0\) denotes the use of the initial embedding

Full size image
Table 2 On the Flickr dataset, the paper presents statistics for the performance and execution time for link prediction under various graph embedding methods and coarsening levels of the MERIT framework
Full size table

Experimental comparison

The paper conducts a link prediction task to evaluate the performance of the MERIT framework on various datasets using the AUROC evaluation metric, with higher scores indicating better performance. Two preprocessed datasets are used for evaluation. The first dataset has 2700 nodes and 11,000 edges, while the second comprises over 40,000 nodes and 150,000 edges. The paper compares the performance of various recent works and presents their average results on the test set in Table 3.

  • HARP [39]: HARP is a hierarchical framework based on iterative learning methods like DeepWalk and Node2Vec. The framework implements two folding schemes, edge folding and

  • HSRL [24]: The paper proposes a framework that is composed of two components: hierarchical sampling and representation learning. Hierarchical sampling discovers the hierarchical topological information of the global network using a strategy that is aware of the community structure. Representation learning focuses on learning node embeddings with low dimensionality while preserving the hierarchical topological information of the network.

  • NECL [12]: The paper proposes a novel and efficient network embedding method which preserves the local structural features of the nodes. The framework is a modularized graph compression layout-based network representation learning method.

Table 3 This section provides statistics on the time performance and link prediction accuracy of various graph embedding methods, using the CORA and DBLP datasets. The statistics are presented in terms of the evaluated graph embedding methods
Full size table

Table 3 shows that MERIT outperforms other methods significantly, especially on large-scale datasets like DBLP. For the CORA dataset, the performance improvements achieved by MERIT(DW) on Deepwalk, HARP(DW), and NECL(DW) are 2%, 6%, and 0.6%, respectively. For HSRL(DW), although there is a reduction in performance of 1.4%, the operating speed improves by a factor of 10. Similarly, the performance improvements achieved by MERIT(NV) are 1.4%, 4.6%, and 0.8% for Node2Vec, HARP(NV), and NECL(NV), respectively. For HSRL(NV), there is a 1.3% reduction in performance, but the operating speed increases by a factor of 25. For large-scale graphs like DBLP, MERIT(DW) achieves performance improvements of 4.7%, 21%, and 2.1% for Deepwalk, HARP(DW), and NECL(DW), respectively. For HSRL(DW), despite a reduction in performance of 2%, the operating speed increases by a factor of 7. In the Node2Vec-based approach, the performance improvements achieved by MERIT for Node2Vec, HARP(NV), HSRL(NV), and NECL(NV) are 29%, 35%, 3.8%, and 9%, respectively, with the running time being greatly reduced.

MERIT not only improves the embedding quality but also greatly shortens the runtime, especially on the DBLP dataset, implying that MERIT is more suitable for large-scale graphs. Additionally, it is unclear how the logic of a method like HARP extends to other embedding methods (e.g., GraRep and NetMF), since such an approach requires modifying the embedding method to preset its initialized embedding values.

Memory consumption

This study investigates the impact of MERIT on memory consumption reduction, focusing on MERIT (NetMF) due to the high memory usage of NetMF, which involves a dense target matrix. Deepwalk and Node2vec are not discussed here, since their embedding learning methods generate training data on the fly with minimal memory consumption compared to storage space. Figure 6 depicts the memory consumption of MERIT(NetMF) on PPI, Flicker and DBLP as the coarsening level increases. The paper observed that MERIT significantly reduced memory consumption as the coarsening degree increased. The memory consumption for the first level of coarsening is reduced by 45%, and it continues to decrease with increasing coarsening level. This memory reduction is consistent with our expectation, as both rows and columns in the factored matrix reduce by almost half with one level of coarsening.

Fig. 6
figure 6

Figure 6 illustrates the memory overhead of MERIT (NetMF) at different coarsening levels on PPI, Flicker, and DBLP datasets. The horizontal axis shows the coarsening level (\(m = 0\) is the baseline embedding), and the vertical axis shows the memory consumption in GB

Full size image

Choice for Coarsening Level

The results of the experiments are presented in Figs. 3 and 4 for coarsening levels 1 to 2 on PPI, Fig. 5 for coarsening level 5 on Reddit, and Table 2 for coarsening level 6 on Flickr. In addition, the optimal coarsening levels for CORA and DBLP are shown in Table 3, which are 1 and 4, respectively. Based on the results, this study suggests that using only a limited range of coarsening levels (0 to 3) generally provides the best quality embeddings and efficient computation for graphs with a moderate number of nodes (i.e., < 10,000). However, for large-scale graphs (i.e., >10,000 nodes), higher coarsening levels (above 3) can produce high-quality embeddings with considerably faster computation time. Therefore, considering the appropriate coarsening level is crucial for generating the most refined embeddings while greatly reducing the computation time. Modifications made are listed in the table below.

Table 4 Node classification results on PPI dataset
Full size table
Table 5 Link prediction results on PPI dataset
Full size table

Multi-level Framework Comparison

In order to further demonstrate the advantages of the multi-level graph embedding refinement framework proposed in this paper on large-scale graphs, this compared three basic embedding methods (DeepWalk, Node2vec, and NetMF) and three other graph embedding frameworks (MILE, GraphZoom, and MERIT) in terms of their performance on node classification and link prediction tasks using preprocessed PPI dataset, as shown in Tables 4 and  5. These three methods (MILE, GraphZoom, and MERIT) all showed improvements in terms of accuracy and speed, but their performance levels varied as the coarsening degree increased. For example, as shown in Table 4, the use of coarsening levels can improve the performance of the three basic embedding methods. The micro-f1 score was significantly improved in the range of coarsening levels from \(\textit{m}\,=\,1\) to 2, while the speed was also significantly improved. It is worth noting that the proposed framework demonstrated the best node classification results at all coarsening levels and outperformed other models in terms of acceleration ratio by 22\(\times \). As for the link prediction results in Table 5, the proposed MERIT framework outperformed other models at coarsening level \({m}\,=\,2\), although it did not achieve the best results at \(m\,=\,1\) or \(m=3\). In addition, at coarsening level \(m=3\), the MERIT framework showed an acceleration ratio of up to 29\(\times \), indicating its ability to generate high-quality embeddings while performing basic tasks. Since performance results can be influenced by different datasets and affected by computer performance and memory, this paper does not compare different datasets in this regard.

In summary, the experiments demonstrate that the proposed multi-level graph embedding refinement framework preserved the black box characteristics of the original multi-level graph embedding framework while enhancing its coarsening and thinning methods to achieve a better balance between effectiveness and efficiency.

Fig. 7
figure 7

This study compared the classification accuracy of different kernel combinations of MERIT and MILE on the CORA, PPI, and DBLP datasets. DeepWalk (DW) was selected as the embedding kernel, and MERIT C and MERIT R respectively denote the proposed coarsening and refining kernels in MERIT, while MILE C and MILE R represent the coarsening and refining kernels in MILE. The blue curves represent the results of MERIT, and the yellow curves represent those of MILE

Full size image

Ablation analysis on MERIT kernels

To investigate the effectiveness of the proposed MERIT kernels, this study compared each MERIT kernel with the corresponding kernel from MILE while fixing other kernels. As shown in Fig. 7, when fixing the coarsening kernel and comparing the refining kernels of MERIT and MILE, the refining kernel of the proposed framework can improve the graph embedding results over that of MILE, especially when the coarsening level is high. This indicates that the improved graph convolutional network for refinement in this study can effectively alleviate over-smoothing and improve the embedding quality. Similarly, when comparing the coarsening kernels of MERIT and MILE while fixing the refining kernels, the coarsening kernel of MERIT can also improve the quality of graph embedding over that of MILE, indicating that the spectral distance-constrained graph coarsening algorithm in this study can indeed preserve the critical graph structure and provide a useful input to the underlying graph embedding method. When combining the MERIT coarsening and refining kernels, the algorithm outperforms any other kernel in MILE in terms of classification accuracy. This suggests that the MERIT coarsening and refining kernels play a useful and unique role in improving embedding performance and their combination can further enhance the embedding results.

Conclusion

This paper proposes a multi-level graph embedding refinement (MERIT) framework. The coarsening part of the framework is improved using a spectral distance approach that limits the difference between the original and coarsened graphs. Additionally, the proposed framework enhances the graph convolutional network model by incorporating initial values and identity mapping to solve the over-smoothing problem that arises during the embedding refinement process. The multi-level graph embedding refinement framework treats the graph embedding method as a black box, enabling the application of existing graph embedding methods to large-scale graphs, thereby shortening the embedding time and improving its efficiency. Future research will build on this work by exploring methods and frameworks for large-scale dynamic graph embedding and by adopting the graph embedding framework proposed in this paper for further research.