Introduction

In statistical quality control, acceptance sampling is one of the most important tools to control and enhance quality. This sampling is a testing procedure where samples of lots are compared with set standards. The nature of a lot can be raw material, components, or finished goods. Inspection of a lot can occur after production or before supplying to the producer. The customer’s inspection is made after receiving the product. Inspection by the producer is termed outgoing inspection, and that by the customer is known as incoming inspection [1]. There are two primary types of the acceptance sampling plan, variable acceptance and attribute acceptance. Variable acceptance plans are based on characteristics that can be measured, while attribute acceptance plans are based on binary decisions [1]. According to Montgomery [1], acceptance sampling plans can be classified into two groups: variables and attributes. Variables are evaluated on mathematical scales, attributes deal with qualitative characteristics and are stated as binary results. Acceptance sampling plans for attributes can be managed easily. Attribute acceptance sampling plans are easier to execute than variable acceptance plans, therefore, their application is common in the industry to examine lots. According to Montgomery [2], if the customer’s process identifies no faulty items, and no other valid reason for inspection exists, supplies can be accepted without inspection. If the customer observes a high percentage of failures and many defective items, then 100% inspection is proposed. Acceptance sampling is midway between these two cases and is applied when only samples of lots are examined. Acceptance sampling is beneficial in reducing the cost of inspections while ensuring that the product meets standard specifications. Acceptance sampling is a useful tool to test sensitive, expensive items or when the legal liabilities are potentially greater. In acceptance sampling, there are two undesirable possible outcomes: a good lot may be rejected or a bad lot may be accepted. The first situation, when a good lot is rejected, is termed manufacturer’s risk and denoted by α, while the second situation, when a bad lot is accepted, is called consumer’s risk and denoted by β [3]. Schilling [4] applied software including Excel, Minitab and Statgraphics to study acceptance sampling plans. Attribute sampling plans have different classes: single, double, multiple sequential and skip lot sampling plans. Single and double acceptance sampling plans are used mostly because they are more practical and easy.

In practice, single and double acceptance sampling plans are used due to their usefulness and ease. The single sampling plan is simple and easy to apply. The plan involves only one sample and is used to study attributes. This plan has two parameters: the number of units selected from a lot, denoted by n, and the number of defective items to be allowed, denoted by c. If more than c items are found to be faulty, the lot will be excluded. In case of rejection of the lot, corrective measures are taken, or the lot is sent back to the manufacturer. Usually, all items are in the lot are inspected, and faulty items are replaced with good items. If the number of defective items x is less than or equal to c, the lot will be accepted. Conventional acceptance sampling plans have been discussed by many scholars in detail [5]. In Reference [6], Liu developed new single sampling plans for three-class attributes. In the Reference [7], Liu proposed new techniques to develop attribute single acceptance sampling plans. Examples are given to illustrate newly developed approaches. In conventional sampling plans, the probability \(p\) of an item being faulty has an exact value. However, in practical decision making, the exact value of \(p\) is typically not known, due to vagueness arising from test procedures, individual decisions, or estimation. In this situation, fuzzy set theory is applied. This concept is used to express and study vagueness emerging from uncertain and individual opinions. In the Reference [8], Sadeghpour Gildeh proposed a single acceptance sampling plan that treats \(p\) as a fuzzy number, using it to develop a fuzzy characteristic (FOC) curve band. According to these researchers, the width of the band depends upon the uncertainty about \(p\), and for zero acceptance number, this band becomes convex. The degree of convexity is directly proportional to the sample size n. Single acceptance sampling plans with vague parameters that used fuzzy probability [9] suggested a plan based on the Poisson model in a fuzzy environment. When n is large and the probability of fraction items \(p\) is small and imprecise, a fuzzy Poisson distribution is employed. The resulting operating characteristic (OC) curve is presented with detailed examples, and the OC bands for fuzzy binomial distributions and fuzzy Poisson distributions are compared. Buckley [10] proposed a comparison of single sampling plans with and without inspection errors. This comparison shows that there is a lower operating characteristic band to a sampling plan without inspection errors for handling quality. The effects of improper classification of good items and of faulty items on the fuzzy probability of acceptance are discussed. According to them, improper classification of good items decreases the fuzzy probability of acceptance, and improper classification of faulty items increases the fuzzy probability of acceptance. In this work [21], Turanoğlu developed a sampling plan using the fuzzy probabilities. Further OC curve in the fuzzy environment are presented, and the concept is illustrated with examples. Acceptance sampling is a viable and inexpensive alternative to expensive complete scrutiny. This sampling provides an opportunity to measure the quality of a whole lot and to decide the lot’s acceptance or rejection. This approach saves material and time in inspection and enhances inspection quality and efficiency. Though acceptance sampling is a useful measure, it is difficult to determine its exact parameters. It is easier to define these parameters as verbal variables. In this article, they gave elastic definitions to sample size, acceptance number and probability of faulty items. They analyzed single and double acceptance sampling plans when the parameters N, n, p, c are vague, and all characteristics including operating characteristic (OC) curve, acceptance probability, average sample number (ASN), (AOQL), and average total inspection were studied with inexact parameters. These results show all options of ATI, ASN, and OC curves. In Jamkhaneh [12], the researchers suggested reliability measures for fuzzy conditions. The fuzzy Weibull distribution is employed to describe device lifetimes. Formulas for all reliability functions, including reliability function, hazard function, and their α-cuts, are proposed. They also suggested fuzzy functions of series systems and parallel systems. They presented fuzzy reliability curves with detailed examples. Afshari [13] recommended a fuzzy multiple deferred state sampling plan by attribute where the fraction \(p\) of malfunctioning items is imprecise. Both probability theory and fuzzy set theory are applied to study this plan. Venkatesh [14] suggested a sampling plan employing an exponential model in a fuzzy environment. The concept is illustrated with an example and the conclusion is made that a substantial change occurs in gastrin plasma level.

In Venkateh [15], the authors proposed applying the fuzzy Weibull distribution to acceptance sampling. The acceptance sampling plan is illustrated by example from medical field. Acceptance probability for crisp and fuzzy parameters is calculated. The fuzzy acceptance probability is found to be more flexible and to give more information. Acceptance probability against samples to predict sample size is presented graphically. In Venkateh [16], comparison of gamma distribution and generalized exponential distribution in the fuzzy environment is presented. The comparison showed that acceptance sampling plan results for the fuzzy gamma distribution is better than for the fuzzy generalized exponential distribution. Tong [17] proposed a fuzzy acceptance sampling plan for the situation where sampling parameters are presented as vague numbers for quality inspection of vague quality characteristics. This sampling plan is better than the conventional fuzzy acceptance sampling plan. The sampling plan consists of three situations with different sampling parameters. The fuzzy operating characteristic (FOC) curve with this newly proposed method has two bounds and is more flexible and informative. Elango [18] developed an acceptance sampling plan that used the fuzzy gamma distribution and found that it was better than a plan using the fuzzy generalized exponential distribution. Aryal [20] probability distributions were applied and investigated in reliability. A neutrosophic acceptance sampling plan was explored by Aslam Aslam [23]. Transmuted inverse Weibull distribution is applied in the acceptance sampling plan [22].

In this study, single acceptance sampling plan based on transmuted Weibull distribution is proposed. The fuzzy proportion of faulty items and fuzzy acceptance probability is used to construct the fuzzy OC curve. The results are described by numerical examples and an application of real data is considered for illustration.

Design of the proposed plan

The mathematical model of transmuted Weibull is given as

$$ \begin{aligned} f\left(t, \sigma , \lambda , \eta \right) & = {\frac{\eta }{\sigma }{\left(\frac{t}{\sigma }\right)}^{\eta -1}e}^{{\left(-\frac{t}{\sigma }\right)}^{\eta }}\left[1-\lambda +2\lambda {e}^{{\left(-\frac{t}{\sigma }\right)}^{\eta }}\right], \\ & 0< t<\infty , \lambda >0, \eta >0, \sigma >0, \end{aligned} $$
(1)

where \(\lambda\ and\ \eta \) are shape parameters and \(\sigma \) is the scale parameter, the average of the transmuted Weibull model is

$$\mu = \sigma\Gamma 1+\frac{1}{\eta } \left(1+\lambda +\lambda {2}^{\frac{-1}{\eta }}\right)$$
(2)

The cumulative distribution function of transmuted Weibull model is given by

$$F\left(x\right) = \left[1-{e}^{{\left(-\frac{x}{\sigma }\right)}^{\eta }}\right]\left[1+\lambda {e}^{{\left(-\frac{x}{\sigma }\right)}^{\eta }}\right]$$
(3)

Suppose that \({t}_{0}\) is the termination time and let \({t}_{0} = a{\mu }_{0};\) where \(a\) is termed the termination ratio. The cumulative distribution function introduced in Eq. (3) can be modified as

$${F}_{T}\left({t}_{0}, \lambda , \eta \right) = \left[1-{e}^{{\left(-\frac{a{\mu }_{0}}{\frac{\mu }{b}}\right)}^{\eta }}\right]\left[1+\lambda {e}^{{\left(-\frac{a{\mu }_{0}}{\frac{\mu }{b}}\right)}^{\eta }}\right]$$
(4)

By following Stephens [11], the lot acceptance probability is given by

$$L\left(p\right) = \left[\sum_{i = 0}^{n}\left(\begin{array}{c}n\\ i\end{array}\right){p}^{i}{\left(1-p\right)}^{n-i}\right].$$
(5)

By following Jamkhaneh and Gildeh [9], the probability of fraction of faulty items is given by

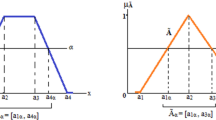
$$ \begin{aligned} \tilde{p }K & = \left(K, {b}_{2}+K, {b}_{3}+K, {b}_{4}+K\right);{p}_{K}\in \tilde{p }K\left[\alpha \right], \\& {q}_{K}\in \tilde{q }K\left[\alpha \right], {p}_{K}+\mathrm{qk} = 1, \end{aligned} $$
(6)

where \({b}_{i} = {a}_{i}-{a}_{2}\), i  = 2, 3, 4 and \(K = \left[\mathrm{0, 1}-{b}_{4}\right]\).

Based on the information, α-cut of \(\tilde{p }K\) is given as follows:

$$\tilde{p }K\left(\alpha \right) = \left(K+\left({b}_{2}+K-K\right)\alpha , {b}_{3}+K+\left({b}_{3}-{b}_{4}\right)\alpha \right).$$
(7)

Similarly, the value of α-cut of \(\tilde{p }K\) at \(\alpha \) = 0 is given by

$$\tilde{p }K\left(0\right) = \left(K, {b}_{4}+K\right), $$
(8)

where proportion (\(p\)) is the \({\mathrm{F}}_{\mathrm{T}}\left({\mathrm{t}}_{0}, {\alpha }, \uplambda \right)\) in Eq. (4).

Fuzzy acceptance sampling plan (ASP)

The proposed plan will be implemented using the following steps.

  1. Step 1.

    Select a random sample of size \(n\) from the lot ant note the number of defective items for time \({\mathrm{t}}_{0}\).

  2. Step 2.

    Fix α-cut and compute the probability of acceptance using the above-mentioned formulas are given in Eqs. (10) and (11).

  3. Step 3.

    A lot of the product will be rejected if the number of defective exceed from \(c\), otherwise, accept the lot of the product.

Lot acceptance probability using fuzzy approach

By following Turanoğlu et al. [21] Kaya and Kahraman (2012), the lot acceptance probability using the fuzzy-logic is given by

$${\tilde{p }}_{k} \alpha \left\{\left(\begin{array}{c}n\\ k\end{array}\right){p}^{k} {q}^{n-k}|p\in p \alpha , q\in q \alpha \right\}, 0 \le \alpha \le 1.$$
(9)

Note here that

$${\tilde{p }}_{k} \alpha = \left[{p}_{kl}, {p}_{kr}\right]$$
$${p}_{kl} \alpha = min\left\{\left(\begin{array}{c}n\\ k\end{array}\right){p}^{k} {q}^{n-k}|p\in p \alpha , q\in q \alpha \right\}$$
$${p}_{kr} \alpha = max\left\{\left(\begin{array}{c}n\\ k\end{array}\right){p}^{k} {q}^{n-k}|p\in p \alpha , q\in q \alpha \right\}$$
$${\tilde{p }}_{k} \alpha = \left[{p}_{kl}, {p}_{kr}\right]$$
$${p}_{kl} \alpha = min\left\{\left(\begin{array}{c}n\\ k\end{array}\right){p}^{k} {q}^{n-k}|p\in p \alpha , q\in q \alpha \right\}$$
$${p}_{kr} \alpha = max\left\{\left(\begin{array}{c}n\\ k\end{array}\right){p}^{k} {q}^{n-k}|p\in p \alpha , q\in q \alpha \right\}.$$

The lot acceptance probability when c  = o is derived as follows:

$${\tilde{p }}_{K}\left(0\right)\left[0\right] = {\left(1-{{\tilde{p }}_{K}}^{U}\left[\alpha \right]\right)}^{n}, {\left(1-{{\tilde{p }}_{K}}^{L}\left[\alpha \right]\right)}^{n}, $$
(10)

where

\({{\tilde{p }}_{K}}^{L} = \) \(K\) \({{\tilde{p }}_{K}}^{U} = \) \({b}_{4}+K\) and \(n\) is the sample size.

Similarly, the probability of acceptance at c  = 0, and α  = 0 is given by

$$ \begin{aligned} {\tilde{p }}_{K}\left(1\right)\left[0\right] & = {\left(1-{{\tilde{p }}_{K}}^{U}\left[\alpha \right]\right)}^{n}+n{\left(1-{{\tilde{p }}_{K}}^{U}\left[\alpha \right]\right)}^{n-1}, \\ & {\left(1-{{\tilde{p }}_{K}}^{L}\left[\alpha \right]\right)}^{n}+n{\left(1-{{\tilde{p }}_{K}}^{L}\left[\alpha \right]\right)}^{n-1}. \end{aligned} $$
(11)

Here, \({{\tilde{p }}_{K}}^{L}\left[\alpha \right], {{\tilde{p }}_{K}}^{U}\left[\alpha \right]\) is evaluated using the cumulative distribution function of the transmuted Weibull model. The cumulative distribution function of the transmuted Weibull model under fuzzy-logic is given by

$$\stackrel{\sim }{F\left(x\right)} = \left[1-{e}^{{\left(-ab/\mu /\mu \_0 \right)}^{\stackrel{\sim }{\eta }}}\right]\left[1+\stackrel{\sim }{\lambda }{e}^{{\left(-ab/\mu /\mu \_0 \right)}^{\stackrel{\sim }{\eta }}}\right], $$
(12)

where \(\stackrel{\sim }{\widehat{\eta }}\), \(\stackrel{\sim }{\widehat{\sigma }}\), and \(\stackrel{\sim }{\widehat{\lambda }}\) are considered as trapezoidal fuzzy numbers.

The benefit of the OC curve under fuzzy logic is that lot acceptance probability can be evaluated at different values of fraction of faulty items. The size of the band of fuzzy OC curve highlights the uncertainty in the process; the higher the size of the band is, higher the uncertainty and less the quality. Similarly, the lower size of the band indicates less uncertainty and high quality. The mean ratio in the function influences the width of the curve. The higher mean ratio results in a lower width, and lower value increases the size of the band of FOC. The general form of the imprecise proportion is indicated by \({\tilde{p }}_{K}\left[\mathrm{\alpha }\right]\), while acceptance probability as \({\tilde{P }}_{K}\left(c\right)\left[\mathrm{\alpha }\right]\). The fuzzy proportion and fuzzy acceptance probability at \(n\)  = 5, \(k\)  = 0.01, and \(c\)  = 0 will be (0.00, 0.001), and (0.94, 0.97) separately. The fuzzy proportion and acceptance probability are calculated as (0.02, 0.028), and the acceptance probability (0.96, 0.97), respectively, at \(K\)  = 0.01, and \(c\)  = 1.

Application of the proposed plan

In this section, the application of the proposed plan is given using the real data that are taken from the industry. The data of fatigue life data of Yarn with a 2.3% strain level are taken from Quesenberry and Kent [19]. Quesenberry and Kent [19] showed that the data follow transmuted Weibull distribution. The data consist of 100 values as shown in Table 1.

Table 1 The size of the Yarn is presented at a 2.3% strain level
Full size table

According to Aryal and Tsokos [20], estimates of parameters of transmuted Weibull distribution are \(\widehat{\eta }\) = 1.7187616, \(\widehat{\sigma }\) = 330.2877498, and \(\widehat{\lambda }\) = 0.7502233. Suppose these estimated parameters of transmuted Weibull distribution are approximate values (fuzzy) and we treat these estimates as trapezoidal fuzzy numbers to calculate the fraction of faulty items as a fuzzy number \(\tilde{P }\). Suppose imprecise estimates of parameters are \(\stackrel{\sim }{\widehat{\eta }}\)  = (0.718, 1.2181.718, 2.218), \(\stackrel{\sim }{\widehat{\sigma }}\) = (328.287, 329.288, 330.287, 331.28774), and \(\stackrel{\sim }{\widehat{\lambda }}\)(0.730, 0.740, 0.750, 0.760).

Let \(\mu /{\mu }_{0}\) = 1, 2, 3 at \(c\) = 0, \(n\) = 5, \(a\) = (0.05, 0.06, 0.07, 0.08). Proportion of defective items using these values will be \(\stackrel{\sim }{\mathrm{p}}\) = (0.1422055, 0.2251823, 0.3407913, 0.4662092) at \(\upmu /{\upmu }_{0}\) = 1; according to previous researches, the largest value will be selected as proportion. In this case, proportion will be (0.4662092), similarly at \(\upmu /\upmu \_0\) = 2, \(\stackrel{\sim }{\mathrm{p}}\)  = (0.07401295, 0.12024158, 0.18925649, 0.27179549), proportion value (0.27179549). For \(\upmu /{\upmu }_{0}\)  = 3, \(\stackrel{\sim }{\mathrm{p}}\)  = (0.05001334, 0.01819692, 0.13080042, 0.19116059), proportion will be 0.019116059 and \(K\)  = (0.01, 0.02, 0.03, 0.04, 0.05). Using all values, fuzzy OC curves were developed for comparison purpose at different values of parameters of OC curve, sample sizes \(n\)  = (5, 25, 50, 100), and acceptance numbers \(c\)  = (0, 1, 2).

Discussions

The size of the fuzzy OC curve is the function of the mean ratio. An increase or decrease in the mean ratio has an impact on the width of the band of the OC curve. Figure 1 displays fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 1, acceptance number \(c\)  = 0: (a) \(n\)  = 5, (b) \(n\)  = 25, (c) \(n\)  = 50, (d) \(n\)  = 75. Figure 2 shows fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 2, acceptance number \(c\)  = 0: (a) \(n\)  = 5, (b) \(n\)  = 25, (c) \(n\)  = 50, (d) \(n\)  = 75. The comparison between Figs. 1 and 2 indicates that an increase in the mean ratio reduces the uncertainty of the fuzzy OC curve. Similarly, Fig. 3 presents OC curve of transmuted Weibull distribution with mean ratio  = 3, acceptance number c  = 0 and sample sizes (a) \(n\)  = 5, (b) \(n\)  = 25, (c) \(n\)  = 50, (d) \(n\)  = 75. Furthermore, Figs. 4 and 5 indicate fuzzy OC curve of transmuted Weibull distribution with different mean ratios and acceptance number \(c\) = 1. Figure 6 indicates when c  = 0 and the mean ratio is 8, the fuzzy OC curve almost becomes crisp. Furthermore, Figs. 7, 8, and 9 highlight the impact of the mean ratio on the width of the fuzzy OC curve. Finally, in Figs. 10, 11, and 12, behavior of the fuzzy OC curve with different ratios is highlighted and concluded that an increase in mean ratio enhances the quality and reduces uncertainty. In Table 2, acceptance probability of transmuted Weibull distribution is at \(c\) = 0, \(\alpha \) = 0.While acceptance probability at \(c\) = 1, \(\alpha \) = 0 is shown in Table 3. Similarly, in Table 4, acceptance probability is presented at mean ratio 2. Likewise, in Table 5, acceptance probability is displayed at mean ratio 3.

Fig. 1
figure 1

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 1, acceptance number \(c\)  = 0: a \(n\)  = 5, b \(n\) = 25, c \(n\) = 50, d \(n\) = 75

Full size image
Fig. 2
figure 2

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 2, acceptance number \(c\)  = 0: a \(n\)  = 5, b \(n\)  = 25, c \(n\)  = 50, d \(n\)  = 75

Full size image
Fig. 3
figure 3

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 3, acceptance number \(c\)  = 0: a \(n\)  = 5, b \(n\)  = 25, c \(n\)  = 50, d \(n\)  = 75

Full size image
Fig. 4
figure 4

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 1, acceptance number \(c\)  = 1: a \(n\)  = 5, b \(n\)  = 25, c \(n\)  = 50, d \(n\)  = 75

Full size image
Fig. 5
figure 5

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 3, acceptance number \(c\) = 1: a \(n\) = 5, b \(n\) = 25, c \(n\) = 50, d \(n\) = 75

Full size image
Fig. 6
figure 6

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 8, acceptance number \(c\) = 1: a \(n\) = 5, b \(n\) = 25, c \(n\) = 50, d \(n\) = 75

Full size image
Fig. 7
figure 7

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 1, acceptance number \(c\) = 0 and \(n\) = 25

Full size image
Fig. 8
figure 8

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 2, acceptance number \(c\) = 0 and \(n\) = 25

Full size image
Fig. 9
figure 9

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 3, acceptance number \(c\) = 0 and \(n\) = 25

Full size image
Fig. 10
figure 10

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 1, acceptance number \(c\) = 0 and \(n\) = 50

Full size image
Fig. 11
figure 11

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 3, acceptance number \(c\) = 0 and \(n\) = 50

Full size image
Fig. 12
figure 12

Operating characteristic curve of fuzzy OC curve of transmuted Weibull distribution with mean ratio  = 2, acceptance number \(c\) = 0 and \(n\) = 50

Full size image
Table 2 The fuzzy acceptance probability of transmuted Weibull distribution at \(c\) = 0, \(\upmu /{\upmu }_{0}\) = 1 and \(\alpha \) = 0
Full size table
Table 3 Acceptance probability for transmuted Weibull distribution at \(c\) = 1 and \(\upmu /{\upmu }_{0}\) = 1
Full size table
Table 4 Acceptance probability for transmuted Weibull distribution at \(c\) = 1, \(\mu /{\mu }_{0}\) = 2
Full size table
Table 5 Acceptance probability for transmuted Weibull distribution at \(c\) = 1 and \(\mu /{\upmu }_{0}\) = 3
Full size table

Comparative study

Omari [22] proposed the sampling plan for transmuted Generalized Inverse Weibull distribution (TGIWD) when the parameters are crisp but in the proposed plan fuzzy parameters are used. When the data are fuzzy, the evaluation of the lot of product with fuzzy acceptance sampling is more appropriate than the conventional sampling plans. The operating characteristic values in AS plan based on TGIWD are precise numbers but in the suggested plan values are in the fuzzy form. The OC values of both plans are shown in Figs. 13 and 14, respectively. The results indicate that fuzzy OC curves are more flexible than conventional OC curves. In addition, the fuzzy OC curve explains intermediate OC values. The fraction of faulty items is denoted by (\(\tilde{p }\)) in fuzzy form. This value is calculated utilizing the distribution function of transmuted Weibull distribution (TWD) but in (TGIWD), this is an assumed and crisp value. Fuzzy transmuted Weibull distribution (FTWD) can be used to deal with fuzzy data. The sampling plan with \(n\) = 7, \(c\) = 2, \(t/{\mu }_{0} = 0.942, \upmu /{\upmu }_{0} = 4\) has OC value \(0.996473\) with a given probability \(0.90\) in the TGIWD, see Omari [22]. The fuzzy OC value of the proposed sampling plan with the same parameters for (FTWD) is (0.9178, 0.9988). It shows in our proposed plan OC values can be presented in a fuzzy form which is not possible in crisp (TGIWD). The band of fuzzy OC curve of the proposed plan indicates the degree of uncertainty which is not possible to show in the OC curve of (TGIWD) [23].

Fig. 13
figure 13

OC curve of transmuted Weibull distribution (TWD)

Full size image
Fig. 14
figure 14

OC curve of transmuted generalized inverse Weibull distribution (TGIWD)

Full size image

Conclusions

In this research, transmuted Weibull model is used to design a single acceptance sampling plan in fuzzy conditions. The fraction of faulty items is treated as a trapezoidal fuzzy number denoted by (\(\tilde{p }\)). This value is calculated utilizing the distribution function of transmuted Weibull distribution than assumed value. The fuzzy OC curve based on this \(\tilde{p }\) is used to assess the performance of acceptance sampling. Fuzzy operating characteristic (FOC) curves are designed for different combinations of sample sizes and parameters have been tabulated. It is determined from this study that one can use the suggested plan if there is vagueness in the product’s quality. The comparative study showed that the proposed plan is quite effective in uncertain environments. The proposed sampling plan can be extended to neutrosophic statistics distributions in future research.