The development trend of China’s aging population: a forecast perspective

Abstract

To accurately predict the aging population in China, a novel grey prediction model (CFODGMW(1,1, $\alpha$) model) is established in this study. The CFODGMW(1,1, $\alpha$) model has all the advantages of the weighted least square method, combined fractional-order accumulation generation operation and grey prediction model with time power term, which makes it have excellent prediction performance. Compared with the traditional grey prediction model based on the least square method and the first-order accumulation operation, the CFODGMW(1,1, $\alpha$) model has stronger adaptability. The proposed model and its competing models are used to analyze the aging population in five regions of China. The results show that the prediction performance of the CFODGMW(1,1, $\alpha$) model is better than other models. Based on this, the CFODGMW(1,1, $\alpha$) model is used to predict the aging population in China in the next 4 years, and some suggestions are given based on the development trend of the aging population.

Introduction

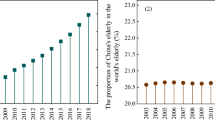
Population aging refers to the process in which the number of the elderly ($\ge$65 years old) keeps increasing and the proportion of the total population keeps rising. Recently, China’s population aging has become an arresting problem. Figure 1 shows the number and growth rate of China’s total population and aging population (the data used for mapping comes from China’s National Bureau of Statistics-NBS, https://data.stats.gov.cn/). It can be seen from Fig. 1 that the growth rate of China’s total population is far less than that of the aging population. In the face of the growing aging population, a series of problems such as pension, medical care and assistance follow. Therefore, accurate prediction of China’s aging population is helpful for the government to formulate corresponding policies.

Fig. 1

The number and growth rate of China’s aging population and total population from 2005 to 2019

Considering the exponential growth law of population and the applicable scope of the grey prediction model (GM model), this paper chooses the GM model to analyze and forecast the aging population in China. The GM model is a vital component of the grey system theory put forward by the famous Chinese scholar Deng [1]. Due to its excellent predictive performance, the GM model and its variants have been widely used in various areas of society [2,3,4,5,6,7]. The GM(1,1) model is the benchmark model of all grey variant models. The improvement work on it has never stopped. These improvement schemes mainly focus on the expansion of the model, accumulative order, initial value, background value and parameter estimation. Since the background value and initial value are irrelevant to the focus of this article, we will not cover the work of these two parts. The work of the other three parts is shown as follows:

• (1) Expansion of the model. To further expand the applicable scope of the GM model, Cui et al. put forward the NGM(1,1,k,c) model, which can simultaneously fit the time series with homogeneous exponential law and the time series with approximately non-homogeneous exponential series [8]. Qian et al. proposed the GM(1,1, ${t^\alpha }$) model with time power term and proved that GM(1,1) and NGM(1,1,k) model are special expressions of this model [9]; Inspired by Qian et al., Luo and Wei put forward another grey model with time term, namely, GMP(1,1,N) model [10]. Similar to GM(1,1, ${t^\alpha }$) model, GMP(1,1,N) model can also be transformed into other grey forecasting models by changing its parameters. Liu et al. analyzed the modeling process and mechanism of the GM(1,1,${t^\alpha }$) and GMP(1,1,N) model and found that these two models have certain defects. Based on this, Liu et al. proposed the OPGM(1,1,$\alpha$) model with all the advantages of the two models [11]. Although the GMP(1,1,N) and OPGM(1,1,$\alpha$) model have excellent predictive ability, their modeling mechanisms are too complex to be universal. Therefore, the GM(1,1,${t^\alpha }$) model with strong adaptability is the best choice for predictive analysis.

• (2) Accumulative order. The traditional GM model is built on the basis of the first-order cumulative generation operation (1-AGO), which aims to reduce the randomness of time series to achieve the purpose of accurate prediction. However, some scholars have found that the predictive accuracy of the GM model based on the 1-AGO is even lower than that of the GM model based on initial sequence modeling in some cases [12]. To solve this problem, Wu proposed the idea of the fractional-order accumulative generation operation (r-AGO) [13]. The idea of r-AGO is to establish a programming problem based on the model, and then use the intelligent optimization algorithms to solve the programming problem to obtain the accumulation order r that make the model have the minimum error. If the benefit brought by the accumulative operation is too small, the order of the r-AGO is 0, that is, the original time series is used for modeling. If the accumulative operation can greatly enhance the predictive accuracy of the predictive model, then the algorithms can find the best order to build the model. Since r-AGO can stably improve the performance of forecasting models, many grey system models based on r-AGO have been developed [14, 15]. In addition, inspired by Wu  [13], many other fractional-order accumulation operations have come into being. For instance, inspired by the conformable fractional derivative, Ma et al. proposed the conformable fractional grey prediction model [16]. Subsequently, Chen et al. put forward the grey forecasting model with the fractional-order Hausdorff accumulation operation and proved the superiority of the proposed model by cases [17]. Based on Wu’s research  [13], Liu et al. proposed the weighted r-AGO [18] and so on.

• (3) Parameter estimation. Similar to other regression prediction models, GM models usually utilize the least square method (LSM) to estimate the structural parameters of the models. Indeed, the LSM is a good method because it is easy to understand, but it is antiquated and limits the predictive performance of the models to some extent. To further optimize the GM models, some scholars proposed to use other parameter estimation methods to estimate the structural parameters of the models. These methods include partial least square (PLS) [19], nonlinear least square (NLS) [20, 21], and the weighted least square method (WLS) [22, 23]. Among these methods, the weighted least square method has the simplest mechanism and powerful performance.

With the above discussion, we know that the GM(1,1,${t^\alpha }$) is an ideal model, the r-AGO and the WLS are measures that can stably enhance the performance of the GM models. To accurately predict China’s aging population, this paper establishes an optimized GM(1,1,${t^\alpha }$) model based on the GM(1,1,${t^\alpha }$) model, r-AGO and WLS. Compared with previous studies, the contributions of this paper are as follows:

• (1) We use the midpoint formula to solve the problem that GM(1,1,${t^\alpha }$) model is difficult to be solved.

• (2) We propose a new combined fractional-order accumulation operator.

• (3) We use the weighted least square method with strong compatibility to estimate the parameters of the proposed model.

• (4) This paper uses the proposed model to predict China’s aging population in the next 4 years, and gives corresponding suggestions based on the prediction results.

The other parts of this article are arranged as follows: the next section gives the necessary knowledge including the definition of the GM(1,1, ${t^\alpha }$) model and combined r-AGO. The third section discusses the concepts, properties and solution methods of the proposed model. The fourth section proves the feasibility and effectiveness of the proposed model through five real cases. The fifth section describes the application of the proposed model in China’s aging population. The conclusion is given in the last section.

Prerequisite knowledge

Traditional GM(1,1,${t^\alpha }$) model and its optimized discrete form

Supposing there is a time sequence ${X^{\left( 0 \right) }} = \{ {x^{\left( 0 \right) }}\left( m \right) ,m = 1,2,3, \ldots ,n\},n \ge 4,$ then

$$\begin{aligned} {X^{\left( 1 \right) }} = \left\{ {x^{\left( 1 \right) }}\left( m \right) = \sum \limits _{j = 1}^m {{x^{\left( 0 \right) }}\left( j \right) } ,m = 1,2,3, \ldots ,n\right\} \end{aligned}$$

(1)

is called the first-order accumulative generation operation (1-AGO) sequence of ${X^{\left( 0 \right) }}$.

Based on the above conditions, the grey equation of the GM(1,1,${t^\alpha }$) model is expressed as

$$\begin{aligned} {[{x^{\left( 1 \right) }}\left( t \right) ]'_t} + a{x^{\left( 1 \right) }}\left( t \right) = b\cdot {t^\alpha } + c. \end{aligned}$$

(2)

Fig. 2

Schematic diagram of the difference quotient method

Usually, the predictive formula of GM models is the solution of the grey differential equation. Obviously there is no exact solution for Eq. (1). When Qian et al. put forward the model, they did not provide a solving method for the model, but only used $\alpha$ = 2 to establish the model for prediction, which greatly restricted the predictive ability of the GM(1,1,${t^\alpha }$) model. In the past, people usually used the forward difference formula [22] or the backward difference formula [24] to approximate the derivative to discretize the differential equation similar to Eq. (1). However, these two methods are not the best methods. According to the difference quotient method shown in Fig. 2, we can see that the accuracy of the midpoint formula is much higher than that of the forward difference formula and the backward difference formula. Next, we estimate the errors of the three difference quotient formulas. Performing Taylor expansion of $f(a + h)$ at point a to get

$$\begin{aligned} f(a + h) = f(a) + hf'(a) + \frac{{{h^2}}}{2}f''(\zeta ),\zeta \in [a,a + h].\qquad \end{aligned}$$

(3)

Substituting the above equation into the forward difference formula $f'(a) = \frac{{f(a + h) - f(a)}}{h} + \varepsilon$, we can get

$$\begin{aligned} f'(a)= & {} \frac{{f(a) + hf'(a) + \frac{{{h^2}}}{2}f''(\zeta ) - f(a)}}{h} + \varepsilon \nonumber \\= & {} f'(a) + \frac{h}{2}f''(\zeta ) + \varepsilon , \end{aligned}$$

(4)

that is

$$\begin{aligned} \varepsilon = - \frac{h}{2}f''(\zeta ). \end{aligned}$$

(5)

Therefore, the truncation error of the forward difference formula is O(h). Similarly, we can know that the truncation errors of the backward difference formula and the midpoint formula are O(h) and $O({h^2})$. Obviously, the midpoint formula has the least error. Therefore, we use the midpoint formula to discretize Eq. (2), and then we can get

$$\begin{aligned} {x^{\left( 1 \right) }}\left( {t + 1} \right) - {x^{\left( 1 \right) }}\left( {t - 1} \right) = - 2a{x^{\left( 1 \right) }}\left( t \right) + 2b{t^\alpha } + 2c. \end{aligned}$$

(6)

Let ${\mu _1} = - 2a,{\mu _2} = 2b,{\mu _3} = 2c$, and then Eq. (6) can be expressed by

$$\begin{aligned} {x^{\left( 1 \right) }}\left( {t + 1} \right) = {x^{\left( 1 \right) }}\left( {t - 1} \right) + {\mu _1}{x^{\left( 1 \right) }}\left( t \right) + {\mu _2}{t^\alpha } + {\mu _3}. \end{aligned}$$

(7)

Equation (7) is called the optimized discrete GM(1,1,${t^\alpha }$) model (ODGM(1,1,${t^\alpha }$) model). Similar to the regression prediction model, the parameters $\mu _1,\mu _2,\mu _3$ of the ODGM(1,1, ${t^\alpha }$) model are estimated by using the LSM, that is,

where

$$\begin{aligned} Y = \left( {\begin{array}{*{20}{c}} {{x^{\left( 1 \right) }}\left( 3 \right) - {x^{\left( 1 \right) }}\left( 1 \right) }\\ {{x^{\left( 1 \right) }}\left( 4 \right) - {x^{\left( 1 \right) }}\left( 2 \right) }\\ \vdots \\ {{x^{\left( 1 \right) }}\left( n \right) - {x^{\left( 1 \right) }}\left( {n - 2} \right) } \end{array}} \right) ,B = \left( {\begin{array}{*{20}{c}} {{x^{\left( 1 \right) }}\left( 2 \right) }&{}{{2^\alpha }}&{}1\\ {{x^{\left( 1 \right) }}\left( 3 \right) }&{}{{3^\alpha }}&{}1\\ \vdots &{} \vdots &{} \vdots \\ {{x^{\left( 1 \right) }}\left( {n - 1} \right) }&{}{{{(n - 1)}^\alpha }}&{}1 \end{array}} \right) . \end{aligned}$$

Once the estimated parameters

of the ODGM(1,1,${t^\alpha }$) are obtained by the least square method (LSM), the time response function the model can be expressed as

Since the ODGM(1,1, ${t^\alpha }$) model is built using the 1-AGO, it is necessary to carry out the 1-order inverse AGO (1-IAGO) on Eq. (9) to obtain the predicted values, that is,

According to the introduction of the ODGM(1,1,${t^\alpha }$) model, we can still find some deficiencies.

• (1) The ODGM(1,1,${t^\alpha }$) model is built based on the 1-AGO. Although a sequence with weakened randomness can be obtained by 1-AGO, this does not mean that the prediction performance of the model is improved.

• (2) Similar to the traditional regression model, the ODGM(1, 1,${t^\alpha }$) model uses the LSM to solve the structural parameters of the model. Indeed, the LSM is a good method, but it is too simple and limits the predictive performance of the model to some extent.

These two points provide ideas for the optimization scheme of this article. This article will discuss the optimization measures of the ODGM(1,1,${t^\alpha }$) model in detail in the next section.

The combined fractional-order accumulative generation operation

The advantage of fractional-order accumulation generation operation (r-AGO) is that it can choose the most suitable order to build the model through algorithms. Compared with the traditional 1-AGO, it is more adaptable. Obviously, the r-AGO can solve the first deficiency described in the previous section. At present, there are two popular r-AGOs, namely the r-AGO proposed by Wu [13] and the fractional-order Hausdorff accumulation generation operation ($\delta$-HAGO) proposed by Chen et al. [17]. To further enhance the predictive ability of the model, we combine these two measures and propose a new r-AGO, which is defined as follows.

Theorem 1

If ${X^{\left( 0 \right) }}$ is the original time series and

$$\begin{aligned} {H^{\left( 0 \right) }}= & {} \left\{ {h^{\left( 0 \right) }}\left( k \right) = \sum \limits _{p = 1}^k {x^{\left( 0 \right) }}\left( p \right) \right. \nonumber \\&\left. \cdot [{p^\delta } - {{(p - 1)}^\delta }] ,\delta \in {R^ + },k = 1,2,3, \cdots ,n\right\} \nonumber \\ \end{aligned}$$

(11)

is the fractional-order Hausdorff accumulation generation sequence of ${X^{\left( \mathrm{{0}} \right) }}$, then the combined fractional-order accumulation generation operator (CF-AGO) of ${X^{\left( \mathrm{{0}} \right) }}$ is

$$\begin{aligned} {h^{\left( r \right) }}\left( k \right)&= \sum \limits _{l = 1}^k {\frac{{\Gamma (r + k - l)}}{{\Gamma (k - l + 1)\Gamma (r)}}\cdot {h^{\left( 0 \right) }}(l)}\nonumber \\&= \sum \limits _{l = 1}^k \frac{{\Gamma (r + k - l)}}{{\Gamma (k - l + 1)\Gamma (r)}}\nonumber \\&\quad \cdot \sum \limits _{p = 1}^l {{x^{\left( 0 \right) }}\left( p \right) \cdot [{p^\delta } - {{(p - 1)}^\delta }]} . \end{aligned}$$

(12)

Proof

According to the method proposed by Chen et al. [17], the $\delta$-HAGO of ${X^{\left( \mathrm{{0}} \right) }}$ can be given as

$$\begin{aligned} {h^{\left( 0 \right) }}(k) = \sum \limits _{p = 1}^k {{x^{\left( 0 \right) }}\left( p \right) \cdot [{p^\delta } - {{(p - 1)}^\delta }]},k = 1,2,3, \ldots . \end{aligned}$$

(13)

When $r=1$, according to the 1-AGO, we can get

$$\begin{aligned} {h^{\left( 1 \right) }}\left( k \right)&= \sum \limits _{l = 1}^k {\frac{{(k - l + 1) \ldots (k - l + r - 1)}}{{(r - 1)!}}\cdot {h^{\left( 0 \right) }}\left( l \right) }\nonumber \\&= \sum \limits _{l = 1}^k {{h^{\left( 0 \right) }}\left( l \right) }. \end{aligned}$$

(14)

Similarly, when $r=2$, the 2-AGO of the $\delta$-HAGO of ${X^{\left( \mathrm{{0}} \right) }}$ is

$$\begin{aligned} {h^{\left( 2 \right) }}\left( k \right)&= \sum \limits _{l = 1}^k \frac{{(k - l + 1)}}{{(2 - 1)!}}\cdot {h^{\left( 0 \right) }}\left( l \right) \nonumber \\ \quad&= \sum \limits _{l = 1}^k {(k - l + 1)\cdot {h^{\left( 0 \right) }}\left( l \right) }. \end{aligned}$$

(15)

Supposing the n-AGO of the $\delta$-HAGO of ${X^{\left( \mathrm{{0}} \right) }}$ is

$$\begin{aligned} {h^{\left( n \right) }}\left( k \right) = \sum \limits _{l = 1}^k {\frac{{(k - l + 1) \ldots (k - l + n - 1)}}{{(n - 1)!}}\cdot {h^{\left( 0 \right) }}\left( l \right) }, \end{aligned}$$

(16)

then, when $r=n+1$, we have

$$\begin{aligned}&{h^{\left( {n + 1} \right) }}\left( k \right) =\sum \limits _{l = 1}^k \sum \limits _{j = 1}^l {\frac{{(l - j + 1) \ldots (l - j + n - 1)}}{{(n - 1)!}}}\nonumber \\&\qquad \cdot {h^{\left( 0 \right) }}\left( j \right) \nonumber \\&\quad =\sum \limits _{j = 1}^2 \Big [\frac{{(1 - j + 2) \ldots (2 - j + n - 1)(2 - j + n)}}{{n!}}\Big ]\nonumber \\&\qquad \cdot {h^{\left( 0 \right) }}\left( j \right) +\cdots + \sum \limits _{j = 1}^k {\frac{{(k - j + 1) \ldots (k - j + n - 1)}}{{(n - 1)!}}}\nonumber \\&\qquad \cdot {h^{\left( 0 \right) }}\left( j \right) \nonumber \\&\quad =\sum \limits _{j = 1}^3 \Big [\frac{{(3 - j + 1)\ldots (3 - j + n - 1)(n + 3 - j)}}{{n!}}\Big ]\nonumber \\&\qquad \cdot {h^{\left( 0 \right) }}\left( j \right) + \cdots + \sum \limits _{j = 1}^k {\frac{{(k - j + 1) \ldots (k - j + n - 1)}}{{(n - 1)!}}}\nonumber \\&\qquad \cdot {h^{\left( 0 \right) }}\left( j \right) =\cdots \nonumber \\&\quad = \sum \limits _{j = 1}^k {\frac{{(k - j + 1) \ldots (k - j + n)}}{{n!}}\cdot {h^{\left( 0 \right) }}\left( j \right) .} \end{aligned}$$

(17)

Therefore, the r-AGO of the $\delta$-HAGO of ${X^{\left( \mathrm{{0}} \right) }}$ is

$$\begin{aligned} {h^{\left( r \right) }}\left( k \right)= & {} \sum \limits _{l = 1}^k \frac{{(k - l + 1)\ldots (k - l + r - 1)}}{{(r-1)!}}\nonumber \\&\cdot {h^{\left( 0 \right) }}\left( l \right) ,r \in {N^ + }. \end{aligned}$$

(18)

According to the concept of Gamma function, Eq. (18) can be converted to

$$\begin{aligned} {h^{\left( r \right) }}\left( k \right)&= \sum \limits _{l = 1}^k {\frac{{\Gamma (r + k - l)}}{{\Gamma (k - l + 1)\Gamma (r)}}\cdot {h^{\left( 0 \right) }}(l)} \nonumber \\ \quad&= \sum \limits _{l = 1}^k \frac{{\Gamma (r + k - l)}}{{\Gamma (k - l + 1)\Gamma (r)}}\cdot \sum \limits _{p = 1}^l {x^{\left( 0 \right) }}\left( p \right) \nonumber \\&\quad \cdot [{p^\delta } - {{(p - 1)}^\delta }] . \end{aligned}$$

(19)

By the broad definition of the combinatorial number [25], it can be seen that when $r \in {R^ + }$, Eq. (19) is also true.

This completes the proof. $\square$

Theorem 2

If ${H^{\left( 0 \right) }}$ is the fractional-order Hausdorff accumulation generation sequence of ${X^{\left( \mathrm{{0}} \right) }}$, and

$$\begin{aligned} {H^{\left( { - r} \right) }}\mathrm{{ = }}\{ {h^{\left( { - r} \right) }}\left( 1 \right) ,{h^{\left( { - r} \right) }}\left( 2 \right) , \ldots ,{h^{\left( { - r} \right) }}\left( n \right) \} ,r \in {R^ + } \end{aligned}$$

(20)

is the fractional-order inverse accumulative generation sequence of ${H^{\left( \mathrm{{0}} \right) }}$, then the kth term in ${H^{\left( \mathrm{{-r}} \right) }}$ can be represented by

$$\begin{aligned} {h^{\left( { -r} \right) }}\left( k \right)= & {} \sum \limits _{l = 0}^{k - 1} {{( - 1)}^l}\cdot \frac{{\Gamma (r + 1)}}{{\Gamma (l + 1)\Gamma (r + 1 - l)}}\nonumber \\&\cdot {h^{\left( 0 \right) }}\left( {k - l} \right) ,k = 1,2,3, \ldots ,n. \end{aligned}$$

(21)

Proof

Case 1: When $r=1$, $k=1$, according to the 1-order inverse AGO, we can get

$$\begin{aligned} {h^{\left( { - 1} \right) }}\left( 1 \right) = \sum \limits _{l = 0}^{k-1} {{{( - 1)}^l}\cdot \frac{{r!}}{{l!(r-l)!}}\cdot {h^{\left( 0 \right) }}\left( k-l \right) = {h^{\left( 0 \right) }}\left( 1 \right) }. \end{aligned}$$

(22)

At the same time, when $k = 2,3,4, \ldots$,we can get

$$\begin{aligned} {h^{\left( { - 1} \right) }}(k)&= \sum \limits _{l = 0}^r {{{( - 1)}^l}\cdot \frac{{r!}}{{l!(r - l)!}}{h^{\left( 0 \right) }}(k - l)}\nonumber \\&= {h^{\left( 0 \right) }}(k) - {h^{\left( 0 \right) }}(k - 1). \end{aligned}$$

(23)

Case 2: When $r=2$,$k=1$, we obtain

$$\begin{aligned} {h^{\left( { - 2} \right) }}\left( 1 \right) = \sum \limits _{l = 0}^{k-1} {{{( - 1)}^l}\cdot \frac{{r!}}{{l!(r - l)!}}\cdot {h^{\left( 0 \right) }}\left( {k - l} \right) } = {h^{\left( 0 \right) }}\left( 1 \right) . \end{aligned}$$

(24)

When $k=2$, we know that

$$\begin{aligned} {h^{\left( { - 2} \right) }}(2)&= \sum \limits _{l = 0}^{k - 1} {{{( - 1)}^l}\cdot \frac{{r!}}{{l!(r - l)!}}\cdot {h^{\left( 0 \right) }}(k - l)}\nonumber \\&= {h^{\left( 0 \right) }}\left( 2 \right) - 2{h^{\left( 0 \right) }}\left( 1 \right) . \end{aligned}$$

(25)

When $k = 3,4, \ldots$, we can get

$$\begin{aligned}&{h^{\left( { - 2} \right) }}(k) = \sum \limits _{l = 0}^r {{{( - 1)}^l}\cdot \frac{{r!}}{{l!(r - l)!}}\cdot {h^{\left( 0 \right) }}(k - l)} \nonumber \\&\quad = {h^{\left( 0 \right) }}\left( k \right) - 2{h^{\left( 0 \right) }}\left( {k - 1} \right) + {h^{\left( 0 \right) }}\left( {k - 2} \right) . \end{aligned}$$

(26)

Case 3: Assuming that when $r=n$,

$$\begin{aligned} \begin{aligned} {h^{\left( { - n} \right) }}\left( k \right) = \left\{ \begin{array}{l} \sum \limits _{l = 0}^{k - 1} {{{( - 1)}^l}\cdot \frac{{\Gamma (n + 1)}}{{\Gamma (l + 1)\Gamma (n - l + 1)}}\cdot {h^{\left( 0 \right) }}\left( {k - l} \right) ,k = 1,2,3, \ldots ,n} \\ \sum \limits _{l = 0}^n {{{( - 1)}^l}\cdot \frac{{\Gamma (n + 1)}}{{\Gamma (l + 1)\Gamma (n - l + 1)}}\cdot {h^{\left( 0 \right) }}\left( {k - l} \right) ,k = n + 1,n + 2, \ldots } \end{array} \right. \end{aligned} \end{aligned}$$

(27)

holds, then when $r=n+1$, we can get

$$\begin{aligned}&{h^{\left( { - n - 1} \right) }}\left( k \right) = {h^{\left( { - n} \right) }}\left( k \right) - {h^{\left( { - n} \right) }}\left( {k - 1} \right) \nonumber \\&\quad = \sum \limits _{l = 0}^n {{{( - 1)}^l}\cdot \frac{{n!}}{{l!(n - l)!}}\cdot {h^{\left( 0 \right) }}\left( {k - l} \right) }\nonumber \\&\qquad - \sum \limits _{l = 0}^n {{{( - 1)}^l}\cdot \frac{{n!}}{{l!(n - l)!}}\cdot {h^{\left( 0 \right) }}\left( {k - 1 - l} \right) } \nonumber \\&\quad = {h^{\left( 0 \right) }}\left( k \right) - \Bigg [\frac{{n!}}{{1!(n - 1)!}} + \frac{{n!}}{{0!(n - 0)!}}\Bigg ]\nonumber \\&\qquad \cdot {h^{\left( 0 \right) }}\left( {k - 1} \right) + \Bigg [\frac{{n!}}{{2!(n - 2)!}}\nonumber \\&\qquad + \frac{{n!}}{{1!(n - 1)!}}\Bigg ]\cdot {h^{\left( 0 \right) }}\left( {k - 2} \right) \nonumber \\&\qquad - \left[ \frac{{n!}}{{3!(n - 3)!}} + \frac{{n!}}{{2!(n - 2)!}}\right] \cdot {h^{\left( 0 \right) }} \left( {k - 3} \right) + \cdots \nonumber \\&\qquad + {( - 1)^n}\Big [\frac{{n!}}{{n!(n - n)!}} + \frac{{n!}}{{(n - 1)!(n - n + 1)!}}\Big ]\nonumber \\&\qquad \cdot {h^{\left( 0 \right) }}\left( {k - n} \right) \nonumber \\&\qquad + {( - 1)^{n + 1}}\frac{{n!}}{{n!(n - n)!}}\cdot {h^{\left( 0 \right) }}\left( {k - 1 - n} \right) , \end{aligned}$$

(28)

and

$$\begin{aligned} \begin{aligned}&{h^{\left( { - n - 1} \right) }}(k) = {h^{\left( { - n} \right) }}(k) - {h^{\left( { - n} \right) }}(k - 1)\\&\quad = \sum \limits _{l = 0}^{k - 1} {{{( - 1)}^l}\cdot \frac{{n!}}{{l!(n - l)!}} \cdot {h^{\left( 0 \right) }}(k - l)} \\&\qquad - \sum \limits _{l = 0}^{k - 2} {{{( - 1)}^l} \cdot \frac{{n!}}{{l!(n - l)!}}\cdot {h^{\left( 0 \right) }}(k - 1 - l)} \\&\quad = {h^{\left( 0 \right) }}(k) - \left[ \frac{{n!}}{{1!(n - 1)!}} + \frac{{n!}}{{0!(n - 0)!}}\right] \cdot {h^{\left( 0 \right) }}(k - 1) \\&\qquad + \left[ \frac{{n!}}{{2!(n - 2)!}} + \frac{{n!}}{{1!(n - 1)!}}\right] \cdot {h^{\left( 0 \right) }}(k - 2)\\&\qquad + \cdots + {( - 1)^{k - 1}}\cdot \left[ \frac{{n!}}{{(k - 1)!(n - k + 1)!}}\right. \\&\qquad \qquad \qquad \left. + \frac{{n!}}{{(k - 2)!(n - k + 2)!}}\right] \cdot {h^{\left( 0 \right) }}\left( {1} \right) . \end{aligned}\nonumber \\ \end{aligned}$$

(29)

It is easy to see that the coefficient of the lth term ${h^{\left( 0 \right) }}\left( {k - l} \right)$ in the expansion of ${h^{\left( { - n - 1} \right) }}\left( k \right)$ is

$$\begin{aligned} \begin{array}{l} {( - 1)^l}\cdot \Big [\frac{{n!}}{{l!(n - l)!}} + \frac{{n!}}{{(l - 1)!(n - l + 1)!}}\Big ] = {( - 1)^l}\cdot \frac{{(n + 1)!}}{{l!(n - l + 1)!}}, \end{array} \end{aligned}$$

(30)

that is,

$$\begin{aligned} {h^{\left( { - n - 1} \right) }}(k) = \left\{ \begin{array}{l} \sum \limits _{l = 0}^{k - 1} {{{( - 1)}^l}\cdot \frac{{(n + 1)!}}{{l!(n - l + 1)!}}\cdot {h^{\left( 0 \right) }}(k - l)} \\ \sum \limits _{l = 0}^{n + 1} {{{( - 1)}^l}\cdot \frac{{(n + 1)!}}{{l!(n - l + 1)!}}\cdot {h^{\left( 0 \right) }}(k - l)} \end{array} \right. . \end{aligned}$$

(31)

In summary, we can get

$$\begin{aligned} {h^{\left( { - r} \right) }}\left( k \right) = \left\{ \begin{array}{l} \sum \limits _{l = 0}^{k - 1} {{{( - 1)}^l}\cdot \frac{{\Gamma (r + 1)}}{{\Gamma (l + 1)\Gamma (r - l + 1)}}\cdot {h^{\left( 0 \right) }}\left( {k - l} \right) ,k = 1,2,3, \cdots ,r} \\ \sum \limits _{l = 0}^r {{{( - 1)}^l}\cdot \frac{{\Gamma (r + 1)}}{{\Gamma (l + 1)\Gamma (r - l + 1)}}\cdot {h^{\left( 0 \right) }}\left( {k - l} \right) ,k = r + 1,r + 2, \ldots } \end{array} \right. ,r \in {N^ + }. \end{aligned}$$

(32)

Then, when $1 \le k \le r,$

$$\begin{aligned} {h^{\left( { - r} \right) }}(k) = \sum \limits _{l = 0}^{k - 1} {{{( - 1)}^l}\cdot \frac{{\Gamma (r + 1)}}{{\Gamma (l + 1)\Gamma (r - l + 1)}}\cdot {h^{\left( 0 \right) }}(k - l)}, \end{aligned}$$

(33)

when $r + 1 \le k \le n,l \le k-1,$ that is, $r + 1 \le l \le k - 1$,$\frac{{r!}}{{l!(r - l)!}} = 0$. (According to the nature of the Gamma function, when the function value is negative integer, it is infinite, and its reciprocal is 0).

Therefore, we have

$$\begin{aligned}&h^{\left( { - r} \right) }(k) = \sum \limits _{l = 0}^r {{{( - 1)}^l}\cdot \frac{{r!}}{{l!(r - l)!}}{h^{\left( 0 \right) }}(k - l)}\nonumber \\&\quad = \sum \limits _{l = 0}^r {{{( - 1)}^l}\cdot \frac{{r!}}{{l!(r - l)!}} \cdot {h^{\left( 0 \right) }}(k - l)} \nonumber \\&\qquad + \sum \limits _{l = r + 1}^{k - 1} {{{( - 1)}^l} \cdot \frac{{r!}}{{l!(r - l)!}}\cdot {h^{\left( 0 \right) }}(k - l)} \nonumber \ \\&\quad = \sum \limits _{l = 0}^{k - 1} {{{( - 1)}^l}\cdot \frac{{\Gamma (r + 1)}}{{\Gamma (l + 1)\Gamma (r + 1 - l)}}\cdot {h^{\left( 0 \right) }}(k - l)}. \end{aligned}$$

(34)

By generalizing Eq. (34), the kth term in ${H^{\left( \mathrm{{-r}} \right) }}$ is

$$\begin{aligned} {h^{\left( { -r} \right) }}\left( k \right)= & {} \sum \limits _{l = 0}^{k - 1} {{( - 1)}^l}\cdot \frac{{\Gamma (r + 1)}}{{\Gamma (l + 1)\Gamma (r + 1 - l)}}\nonumber \\&\cdot {h^{\left( 0 \right) }}\left( {k - l} \right) ,k = 1,2,3, \ldots ,n. \end{aligned}$$

(35)

By the broad definition of the combinatorial number [25], it can be seen that when $r \in {R^ + }$, Eq. (35) is also true, and it completes the proof. $\square$

Theorem 2 tells us that

$$\begin{aligned} {h^{\left( { 0} \right) }}\left( k \right)= & {} \sum \limits _{l = 0}^{k - 1} {{( - 1)}^l}\cdot \frac{{\Gamma (r + 1)}}{{\Gamma (l + 1)\Gamma (r + 1 - l)}}\nonumber \\&\cdot {h^{\left( r \right) }}\left( {k - l} \right) ,k = 1,2,3, \ldots ,n. \end{aligned}$$

(36)

In this paper, Eq. (12) is used to generate accumulative sequence, while Eq. (36) is used to restore output sequence.

The proposed model

Based on the knowledge in Section “Prerequisite knowledge”.  this section will give the definition of the CFODGMW(1,1,$\alpha$) model.

For a given original time series ${X^{\left( 0 \right) }}$, if it satisfies Theorems 1 and 2, then the following equation:

$$\begin{aligned} {h^{\left( r \right) }}\left( {k + 1} \right) = {h^{\left( r \right) }}\left( {k - 1} \right) + {\mu _1}\cdot {h^{\left( r \right) }}\left( k \right) + {\mu _2}\cdot {k^\alpha } + {\mu _3}\qquad \end{aligned}$$

(37)

is called the combined fractional ODGM(1,1,$\alpha$) based on weighted least square (WLS) (abbreviated as CFODGMW(1, 1,$\alpha$)), where ${\mu _1}$ is the development modulus, and ${\mu _2}\cdot {k^\alpha } + {\mu _3}$ is grey action.

Parameters’ estimation of the CFODGMW(1,1,$\alpha$) model

Let $k=2,3, \ldots ,n$ in Eq. (37), and we get the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} {h^{\left( r \right) }}\left( 3 \right) - {h^{\left( r \right) }}\left( 1 \right) = {\mu _1}\cdot {h^{\left( r \right) }}\left( 2 \right) + {\mu _2} \cdot {2^\alpha } + {\mu _3}\\ {h^{\left( r \right) }}\left( 4 \right) - {h^{\left( r \right) }}\left( 2 \right) = {\mu _1}\cdot {h^{\left( r \right) }}\left( 3 \right) + {\mu _2} \cdot {3^\alpha } + {\mu _3}\\ \vdots \\ {h^{\left( r \right) }}\left( n \right) - {h^{\left( r \right) }}\left( {n - 2} \right) = {\mu _1}\cdot {h^{\left( r \right) }}\left( {n - 1} \right) + {\mu _2} \cdot {(n - 1)^\alpha } + {\mu _3} \end{array} \right. \end{aligned}$$

(38)

and its matrix form is

$$\begin{aligned} \mathrm{X}\psi = \Upsilon , \end{aligned}$$

(39)

where

$$\begin{aligned}&\Upsilon = \left( {\begin{array}{*{20}{c}} {{h^{\left( r \right) }}\left( 3 \right) - {h^{\left( r \right) }}\left( 1 \right) }\\ {{h^{\left( r \right) }}\left( 4 \right) - {h^{\left( r \right) }}\left( 2 \right) }\\ \vdots \\ {{h^{\left( r \right) }}\left( n \right) - {h^{\left( r \right) }}\left( {n - 2} \right) } \end{array}} \right) ,\\&\mathrm{X} = \left( {\begin{array}{*{20}{c}} {{h^{\left( r \right) }}\left( 2 \right) }&{}{{2^\alpha }}&{}1\\ {{h^{\left( r \right) }}\left( 3 \right) }&{}{{3^\alpha }}&{}1\\ \vdots &{} \vdots &{} \vdots \\ {{h^{\left( r \right) }}\left( {n - 1} \right) }&{}{{{(n - 1)}^\alpha }}&{}1 \end{array}} \right) . \end{aligned}$$

According to linear algebra knowledge, there is no exact solution to Eq. (39). Let the residual vector is $\tau = {\left[ {\varepsilon (2), \cdots ,\varepsilon (n)} \right] ^T}$, and we have

$$\begin{aligned} \tau = \Upsilon - \mathrm{X}\psi . \end{aligned}$$

Then, the estimated value of the parameter set $\psi$ is

According to the extremum existence condition, it is easy to know that the WLS estimation of the structural parameters of the CFODGMW(1,1,$\alpha$) model is

where W is the weight matrix.

The forecasting formula of the CFODGMW(1,1,$\alpha$) model

According to Eq. (37), we can get

$$\begin{aligned}&h^{\left( r \right) }\left( {k + 1} \right) = {h^{\left( r \right) }}\left( {k - 1} \right) + {\mu _1}{h^{\left( r \right) }}\left( k \right) + {\mu _2}{k^\alpha } + {\mu _3}\nonumber \\&\quad = ({\mu _1}^2 + 1){h^{\left( r \right) }}\left( {k - 1} \right) + {\mu _1}{h^{\left( r \right) }}\left( {k - 2} \right) \nonumber \\&\qquad + {\mu _2}{k^\alpha } + {\mu _1}{\mu _2}{(k - 1)^\alpha } + ({\mu _1} + 1){\mu _3}\nonumber \\&\quad = ({\mu _1}^2 + 1){h^{\left( r \right) }}\left( {k - 3} \right) \nonumber \\&\qquad + [{\mu _1}({\mu _1}^2 + 1) + {\mu _1}]{h^{\left( r \right) }}\left( {k - 2} \right) \nonumber \\&\qquad + ({\mu _1}^2 + 1){\mu _2}{(k - 2)^\alpha }\nonumber \\&\qquad + {\mu _1}{\mu _2}{(k - 1)^\alpha } + {\mu _2}{k^\alpha } + [({\mu _1}^2 + 1) + ({\mu _1} + 1)]{\mu _3}\nonumber \\&\quad = \{ {\mu _1}[{\mu _1}({\mu _1}^2 + 1) + {\mu _1}] + ({\mu _1}^2 + 1)\} {h^{\left( r \right) }}\left( {k - 3} \right) \nonumber \\&\qquad + [{\mu _1}({\mu _1}^2 + 1) + {\mu _1}]{h^{\left( r \right) }}\left( {k - 4} \right) + {\mu _2}{k^\alpha }\nonumber \\&\qquad + {\mu _1}{\mu _2}{(k - 1)^\alpha } + ({\mu _1}^2 + 1){\mu _2}{(k - 2)^\alpha }\nonumber \\&\qquad + {\mu _2}[{\mu _1}({\mu _1}^2 + 1) \nonumber \\&\qquad + {\mu _1}]{(k - 3)^\alpha } + {\mu _3}[{\mu _1}({\mu _1}^2 + 1) + {\mu _1}]\nonumber \\&\quad = \{ {\mu _1}[{\mu _1}({\mu _1}^2 + 1) + {\mu _1}] + ({\mu _1}^2 + 1)\} {h^{\left( r \right) }}\left( {k - 5} \right) \nonumber \\&\qquad + \left\langle \begin{array}{c} {\mu _1}\{ {\mu _1}[{\mu _1}({\mu _1}^2 + 1) + {\mu _1}] + \\ ({\mu _1}^2 + 1)\} + [{\mu _1}({\mu _1}^2 + 1) + {\mu _1}] \end{array} \right\rangle {h^{\left( r \right) }}\left( {k - 4} \right) \nonumber \\&\qquad + {\mu _2}{k^\alpha } + {\mu _1}{\mu _2}{(k - 1)^\alpha } + ({\mu _1}^2 + 1){\mu _2}{(k - 2)^\alpha }\nonumber \\&\qquad + {\mu _2}[{\mu _1}({\mu _1}^2 + 1)\nonumber \\&\qquad + {\mu _1}]{(k - 3)^\alpha } + ({\mu _1}^2 + 1)\} {(k - 4)^\alpha }\nonumber \\&\qquad + {\mu _3}\bigg \langle \{ {\mu _1}[{\mu _1}({\mu _1}^2 + 1) + {\mu _1}] + ({\mu _1}^2 + 1)\} \nonumber \\&\qquad + [{\mu _1}({\mu _1}^2 + 1) + {\mu _1}] \bigg \rangle \nonumber \\&\quad = \cdots = {S_{k - 1}}{h^{\left( r \right) }}\left( 2 \right) + {S_{k - 2}}{h^{\left( r \right) }}\left( 1 \right) \nonumber \\&\qquad + {\mu _2}\left[ \sum \limits _{i = 1}^{k - 2} {{S_i}{{(k - i + 1)}^\alpha }} \right] + {Z_{k - 1}}{\mu _3}. \end{aligned}$$

(42)

where ${S_1} = {\mu _1},{S_2} = (1 + \mu _1^2),{S_n} = {\mu _1}{S_{n - 1}} + {S_{n - 2}},n \ge 3,{Z_1} = 1,{Z_i} = {S_{i - 1}} + {Z_{i - 1}}.$

Then, we substitute the

obtained by the WLS into Eq. (42), and the recursive formula of the model can be shown by

According to Theorem 2, we can get

Therefore, the prediction formula of CFODGMW(1,1,$\alpha$) is

Properties of the CFODGMW(1,1,$\alpha$) model

Convertibility

1.When the weight matrix W and structural parameters of the CFODGMW(1,1,$\alpha$) model takes different values, we have the following conclusions.

• (1) When $W = I$, the criterion for parameter estimation of the CFODGMW(1,1,$\alpha$) model is the least square criterion, that is,

  

• (2) When $W = diag\{ \frac{1}{{{{[{h^{\left( r \right) }}\left( 2 \right) ]}^2}}},\frac{1}{{{{[{h^{\left( r \right) }}\left( 3 \right) ]}^2}}}, \ldots ,\frac{1}{{{{[{h^{\left( r \right) }}\left( n \right) ]}^2}}}\}$, the criterion for parameter estimation of the CFODGMW(1, 1,$\alpha$) model is the minimum mean square relative error criterion, that is,

  

• (3) When $\delta = 1,r = 0,\alpha = 0,W = I$, the CFODGMW(1, 1,$\alpha$) model degenerates to the DGM(1,1) model  [24] based on midpoint difference.

• (4) When $\delta = 1,r = 0,\alpha = 1,W = I$, the CFODGMW(1, 1,$\alpha$) model degenerates to the NDGM(1,1,k) model  [26] based on midpoint difference.

Unbiasedness

Unbiasedness means that the forecasting model can completely fit a time series. Since the modeling mechanism of the CFODGMW(1,1,$\alpha$) model is too complex, it is very difficult to directly prove the unbiasedness of the model using the formula. Therefore, we use examples to prove that the model is unbiased.

Theorem 3

The CFODGMW(1,1,$\alpha$) model is unbiased for time series satisfying the homogeneous or non-homogeneous laws.

Proof

Case 1: When $\delta = 1,r = 0,\alpha = 0, W = I$, Eq. (37) (CFODGMW(1,1,$\alpha$)) is transformed into

$$\begin{aligned} {x^{\left( 1 \right) }}\left( {k + 1} \right) = {x^{\left( 1 \right) }}\left( {k - 1} \right) + {\mu _1}{x^{\left( 1 \right) }}\left( k \right) + {\mu _2}. \end{aligned}$$

(48)

Obviously, Eq. (48) is the expression of the DGM(1,1) model based on midpoint difference. When the time series satisfies the homogeneous law, that is,${X_{\mathrm{Fit}}} + {X_\mathrm{Pre}} = \{ 2 \cdot {3^k},k = 1,2,3,4,5\} + \{ 2 \cdot {3^k},k = 6,7\}$. The ${X_\mathrm{Fit}}$ is applied to establish the model, and ${X_\mathrm{Pre}}$ is applied to test the predictive ability of the model.

According to Eq. (41), we can get

Then, we bring

into Eq. (48), and then according to the 1-IAGO, we can obtain

Case 2: When $\delta = 1,r = 0,\alpha = 1,W = I$, Eq. (37) is turned into

$$\begin{aligned} {x^{\left( 1 \right) }}\left( {k + 1} \right) = {x^{\left( 1 \right) }}\left( {k - 1} \right) + {\mu _1} \cdot {x^{\left( 1 \right) }}\left( k \right) + {\mu _2} \cdot {k^\alpha } + {\mu _3}.\qquad \end{aligned}$$

(50)

Then, Eq. (50) is the expression of the NDGM(1,1,k) model. When the time series satisfies the non-homogeneous law, that is, ${X_\mathrm{Fit}} + {X_\mathrm{Pre}} = \{ 2 \cdot {3^k}+2,k = 1,2,3,4,5\} + \{ 2 \cdot {3^k}+2,k = 6,7\}$. The ${X_\mathrm{Fit}}$ is applied to establish the model, and ${X_\mathrm{Pre}}$ is applied to test the predictive ability of the model.

According to Eq. (41), we can get

Then, we bring

into Eq. (50), and then according to the 1-IAGO, we can obtain

Therefore, this complete the proof. $\square$

Note that since there are many time series that conform to the homogeneous exponential law or approximate non-homogeneous exponential law in real life, the CFODGMW(1,1,$\alpha$) model has a wide application background.

The solution method of the CFODGMW(1,1,$\alpha$) model

From the expression of the CFODGMW(1,1,$\alpha$) model, it can be seen that the CFODGMW(1,1,$\alpha$) model is built on the basis of the r,$\alpha$,$\delta$. Then, the most important task is to determine the r, $\alpha$, $\delta$ of the CFODGMW(1,1,$\alpha$) model. To solve the parameters r, $\alpha$, $\delta$, we consider establishing a programming model with error minimization as the objective function and the modeling process of the model as constraints. This programming model can be expressed by

Obviously, the traditional method is difficult to solve the above-mentioned planning problem. Here, we use the whale optimization algorithm (WOA) [27] to solve the above planning problem to obtain the parameters r, $\alpha$, $\delta$ that make the model have the smallest error. The calculation process of the CFODGMW(1,1,$\alpha$) model is shown in Fig. 3.

Fig. 3

Schematic diagram of the calculation process of the CFODGMW(1,1,$\alpha$) model

Validity

In this section, the aging population of five regions in China is taken as cases to verify the validity of the proposed model. The five data sets are from the statistical yearbook for each region, as shown in Table 1. The models used for comparison include exponential curve model (ECM), GM(1,1) model [1], polynomial regression model (PR) [28],FGM(1,1) model [29],OGM(1,1) model [30] and GMP(1,1,N) model with excellent predictive performance [10]. The aging population from 2010 to 2016 are applied to build models, and the last three data are applied to test the predictive ability of the models. The MAPEs of the seven predictive models are shown in Table 2. In addition, to facilitate readers to observe the gap between the models, we visualized the data in Table 2, as shown in Fig. 4.

It can be seen from Fig. 4 that in the fitting stage, the CFODGMW(1,1,$\alpha$) model has a winning rate of 60%, which is much higher than that of other models. Therefore, the fitting performance of CFODGMW(1,1,$\alpha$) model is better than that of its competitors. According to Fig. 4 (right) we can clearly see that the winning rate of the CFODGMW(1,1,$\alpha$) model is 100%, which means that the prediction performance of the CFODGMW(1,1,$\alpha$) model is the best among all models. Therefore, the validity of the CFODGMW(1,1,$\alpha$) model is confirmed.

Table 1 The number of aging populations in five regions of China from 2010 to 2019 (10,000)

Table 2 MAPEs of seven predictive models in five cases

Fig. 4

The rank of the seven predictive models in the five cases (the larger the value, the better the performance)

Application

Collection of raw data

The original data on China’s aging population from 2005 to 2019 are collected from the NBS, and it is shown in Table 3.

Table 3 China’s aging population (10,000) from 2005 to 2019

Table 4 The predicted results of the proposed model and its comparative models

Table 5 The errors of the proposed model and its comparative models (APE and MAPE)

Evaluation index of model performance

It is an important part of data analysis to evaluate the predictive performance of the model [31]. The MAPE and APE are applied to judge the predictive performance of the models. Their definitions are as follows

Numerical results

The parameters $r=0$, $\delta =1.00492011229591$ and $\alpha$= 3.49253638869618 of the CFODGMW(1,1,$\alpha$) model are obtained by using the whale optimizer. The table containing the calculation time of each part of the algorithm is placed in the Appendix. The predicted results and prediction errors of the CFODGMW(1,1,$\alpha$) model and its competing models are shown in Tables 4 and 5, respectively. Similarly, to facilitate review, we visualized the data in Tables 4 and 5, as shown in Fig. 5.

Fig. 5

The curves, APE (%) and MAPE (%) of the seven models in the case of China’s aging population

According to the MAPE shown in Fig. 5, we can see that the GMP(1,1,N) model and FGM(1,1) model have better fitting performance than the CFODGMW(1,1,$\alpha$) model during the training phase, which means that these two models are also tools with excellent fitting performance. Although the GMP(1,1,N) model and FGM(1,1) model have better fitting performance than CFODGMW(1,1,$\alpha$) model, we can see that there is little difference in their fitting performance. It is worth noting that the pink bar representing the CFODGMW(1,1,$\alpha$) model is the lowest in the test phase, meaning that its predictive performance is better than the other models. From the first figure shown in Fig. 5, we can see that the curve of CFODGMW(1,1,$\alpha$) model is very close to the curve of the real value, which indicates that the development trend of CFODGMW(1,1,$\alpha$) model conforms to the actual situation. The APE in Fig. 5 also implies that the performance of the CFODGMW(1,1,$\alpha$) model is better than other models. In summary, compared with other models, the CFODGMW(1,1,$\alpha$) model is more suitable for analyzing China’s aging population. Beside, the running time of WOA in this case is shown in Table 6.

Forecasts and suggestions

Since the CFODGMW(1,1,$\alpha$) model has won the competition with other models, this section will use it to forecast China’s aging population from 2020 to 2023 and give some corresponding policy recommendations according to the predicted results. Inspired by the idea of metabolism [32], based on the parameters r, $\delta$ and $\alpha$ of the CFODGMW(1,1,$\alpha$) model described in Section “Numerical results”, the original data from 2008 to 2019 are used to establish the CFODGMW(1,1,$\alpha$) model to predict China’s aging population from 2020 to 2023. The number of the aging population in the past 4 years is shown in Fig. 6.

Fig. 6

The growth rate and number of China’s aging population in the next 4 years

According to the data shown in Fig. 6, it can be seen that the aging population in China will further increase in the next few years, which is bound to have a huge impact on the development of Chinese society.

On the one hand, the sustained growth of the aging population and the declining birth rate indicates that China will completely become an “aging country”. The main reason for this phenomenon can be attributed to the fact that young people in China are under great pressure in life, and their salary cannot support them to raise a newborn. In addition, the early “family planning” in China also contributed to this phenomenon. Based on this, this article gives two related suggestions

• 1. To curb the surge in housing prices, the biggest living pressure of Chinese young people comes from the continuous increase in housing prices. Lower housing prices will inevitably lead to social unrest in China, but the Chinese government can control housing prices to stabilize, which can reduce the pressure on the younger generation.

• 2. Promoting the birth subsidy program. China should encourage young people to have children, and provide certain financial assistance to parents with multiple newborns.

On the other hand, with the increase in the aging population, their huge medical expenditure directly promotes the increase in the total dependency ratio of the society, thereby reducing the growth rate of GDP, which has a certain hindering effect on the economic development of Chinese society. Given this situation, the Chinese government should speed up the coverage of insurance business, expand the applicable scope of the insurance business, so that more aging population can enjoy the benefits of insurance business.

Conclusion

Considering the exponential growth law of population and the applicable scope of the grey forecasting model, this paper proposes an optimized discrete grey forecasting model based on the WLS and combined fractional-order accumulation operation. By analyzing the modeling mechanism of the proposed model, it is found that the CFODGMW(1,1,$\alpha$) model can be transformed into other types of GM models by changing its structural parameters, and it is unbiased for the time series satisfying homogeneous or non-homogeneous laws. These two aspects prove that CFODGMW(1,1,$\alpha$) model is a kind of prediction model with excellent predictive performance. Subsequently, the CFODGMW(1,1,$\alpha$) model and its comparative models are used to study China’s aging population. Numerical results show that the prediction performance of the CFODGMW(1,1,$\alpha$) model is better than other prediction models. At the end of the article, the CFODGMW(1,1,$\alpha$) model is used to forecast the aging population in China in the next 4 years, and some corresponding recommendations are given according to the forecast results.

In addition, although the CFODGMW(1,1,$\alpha$) model is a forecasting model with excellent predictive performance, it still has some defects. According to its modeling steps, we can see that the information of the first data in the time series is ignored when the CFODGMW(1,1,$\alpha$) model is built, and the information is hard-won and it is a shame to waste it. How to make full use of the first data to build a more reasonable CFODGMW(1,1,$\alpha$) model is still a problem.

Appendix

See Table 6.

Table 6 The running time of each part of the algorithm