Introduction

With the breakthroughs in both theory and applications of the evolutionary computing (EC), the evolutionary optimization algorithms have attracted a great deal of research interest, and a large amount of research results have been published in the literature [1, 31, 39, 41]. Generally, the EC algorithms can be roughly divided into the categories of genetic algorithms, genetic programming, evolution strategies, and evolution programming. Through simulating the interactions among the individuals in the fish schooling or bird flocking, the particle swarm optimization (PSO) algorithm has been presented in [16] with the purpose of exploring the searching space, which is made possible by automatically adjusting the current velocities and the current positions of the particles according to the competition and cooperation among the particles. Serving as a powerful evolutionary technique, the PSO algorithm is capable of discovering the globally optimal solution in an efficient yet effective way in the research areas of parameter optimization, neural network training, clustering analysis, combination optimization, pattern recognition, image processing and so forth [1, 5, 6, 8, 17, 20, 22, 30, 32, 36, 41, 46, 50].

Unfortunately, like other population-based EC approaches, the PSO algorithm still has the issue of easily getting trapped in the local optima when dealing with large-scale complex optimization problems. As such, it is of vital importance to develop advanced strategies/variants to improve the optimization capability of conventional PSO algorithm [44]. Up to now, many researchers have devoted tremendous efforts in improving the searching ability of the existing PSO algorithms and developing advanced PSO variants with aim to alleviate premature convergence, see, e.g., [28, 41, 42]. To be more specific, a PSO algorithm with saturation and time-delay has been developed in [42] to ensure the convergence and increase the possibility of escaping from local optimum. Recently, an N-state Markovian jumping PSO variant has been presented in [28] to adjust evolutionary state according to the N-state Markov chain [4, 7, 18, 21, 56, 57], showing better exploration ability than that of other algorithms. It is noted that the competitiveness of these advanced variants (in terms of both the convergence rate and the searching ability) have mostly been demonstrated via numerical simulations, and there is a lack of rigorous proof of the performance from the theoretical viewpoint. The objective of this paper is, therefore, to further improve the performance of the PSO algorithm from both aspects of theory and simulation.

Over the past few decades, much research effort has been made to the analysis of the convergence of the PSO algorithms, and a variety of efficient approaches have been presented in the literature [13, 19, 24, 29, 33, 39]. To be more specific, in [33], the first and most important empirical study has been reported by Eberhart and Shi regarding the PSO algorithm. The convergence analysis of the PSO algorithm has been studied in [24] from the theoretical aspect, and further insights have been provided in [13, 19, 29, 39]. Based on these existing results, we can draw the following conclusions on the performance of the PSO algorithm: 1) the exploration and exploitation ability of the PSO algorithm to control the population diversity are vitally important for its efficiency as an optimizer; and 2) as with the other population-based optimizers, higher population diversity is desirable in the early exploration stage, while lower population diversity is preferable in the later/terminal convergence stage. These conclusions, without any doubts, provide some insights into the mechanism of how the PSO algorithm behaves well. Nevertheless, there is still room to further improve the terminal convergence of the PSO algorithm. It is noticed that, in [49], the traditional particle swarm optimizer has been interpreted as a proportional-integral controller. Following this line, in this paper, we endeavor to develop the PSO algorithm based on the proportional-integral-derivative (PID) strategy and also analyze the terminal convergence of this PID-like PSO (PIDLPSO) algorithm.

As is well known, the proportional-integral-derivative (PID) control strategy has been widely applied in industry (e.g. aerospace and industrial robotics) owing to its advantages of simple structure, few tuning parameters, outstanding control performance and so on, see [2, 52] and the reference therein. Proportional control can be easily implemented where the output of the controller is proportional to the error signal of the input. By using proportional control alone, the controlled system would suffer from the steady-state error that cannot be eliminated. As such, the integral control is introduced to form the proportional-integral (PI) control strategy, which ensures that the output of the controlled system traces the input precisely. In addition, the derivative control strategy has the advantages of quick action and advanced adjustment, which is conducive to improving the performance of controlled object with large time-delays effectively, though it cannot easily remove the residual error. Therefore, the PID control strategy has become more and more popular in practice because it combines the merits of (1) timeliness and rapidity of the proportional control; (2) the residual elimination ability of the integral control; and (3) the advanced adjustment ability of the derivative control.

Inspired by the insight that the particle swarm optimizer could be approximately a PI controller [48], in this paper, the derivative control strategy is introduced into the PSO algorithm with aim to further enhance the optimization ability and improve the convergence rate. As compared with the traditional PSO algorithm, such a PID-like PSO (PIDLPSO) algorithm owns the following two advantages: (1) the overshoot problem during the stage of the terminal convergence of the particle dynamics can be adequately resolved through adjusting the change of deviation signal; and (2) more historical information can now be utilized that is beneficial for explore the problem space more thoroughly.

In connection with the discussions made so far, the main objective of this paper is to put forward a novel PIDLPSO algorithm with rigorous mathematical proof of the terminal convergence. The main contributions of this paper are summarized in threefold as follows.

  1. (1)

    A novel PIDLPSO algorithm is proposed to alleviate the overshoot problem and accelerate convergence during the later/terminal stage of the particle dynamics, where the velocity of the particle is updated according to the past momentum, the present positions (including the personal best position and the global best position), as well as the future trend of the positions.

  2. (2)

    For the proposed PIDLPSO algorithm, the convergence conditions and the final positions are obtained by means of the Routh stability criterion and the final value theorem of the Z-transformation.

  3. (3)

    The proposed PIDLPSO algorithm is comprehensively verified from the aspects of population diversity, searching ability and convergence rate. Also, it is demonstrated that the PIDLPSO algorithm has more competitive ability in achieving the global optimum than five other popular PSO algorithms.

The structure of this paper is outlined as follows. Section 2 formulates the problem to be studied for the PSO algorithm. Section 3 puts forward a novel PIDLPSO algorithm and analyze its convergence conditions. Experimental results are presented in Sect. 4 with detailed discussions, and Sect. 5 outlines the conclusions and future directions.

Notation. The Z-transform of a vector implies that every element of this vector has taken the Z-transform.

Problem formulation

In the typical PSO algorithm developed [16], the particles, referred to as the feasible candidates, are employed to explore and exploit in the D-dimensional searching space by continuously adjusting the velocity vector \(v_{i}(k)=(v_{i1}(k),v_{i2}(k),...,v_{iD}(k))\) and the position vector \(x_{i}(k)=(x_{i1}(k),x_{i2}(k),...x_{iD}(k))\), respectively. According to the competition and cooperation among the particles, the position of the i-th particle is justified towards two directions, where one direction is the personal best position \(p_\mathrm{best}\) represented by \(p_\mathrm{best}= (p_{1}, p_{2}, \ldots , p_{D})\), and the other one is the globally optimal position \(g_\mathrm{best}\) represented by \(g_\mathrm{best}= (g_{1}, g_{2}, \ldots , g_{D})\). Specifically, the velocity and the position of the i-th particle at the \((k+1)\)-th iteration are updated as follows:

$$\begin{aligned} \left\{ \begin{aligned} {v_{i}}(k+1)=\,&\omega v_{i}(k)+c_{1}r_{1}(p_\mathrm{best}-x_{i}(k))\\&+c_{2}r_{2}(g_\mathrm{best}-x_{i}(k)),\\ x_{i}(k+1)=\,&x_{i}(k)+v_{i}(k+1), \end{aligned} \right. \end{aligned}$$
(1)

where k is the number of recent iterations of the i-th particle in the D-dimensional problem space, \(\omega \) is the inertia weight, \(c_1\) and \(c_2\) called the cognitive and social parameters are the acceleration coefficients, and \(r_1\), \(r_2\) are constants selected on the interval [0, 1].

The main objective of this paper is to 1) put forward a novel PIDLPSO algorithm; 2) analyze its terminal convergence by means of the Routh stability criterion and the final value theorem of the Z-transformation; and 3) obtain the conditions for convergence and the position of the final particle of the proposed PIDLPSO algorithm.

The PIDLPSO algorithm and its terminal convergence analysis

Motivated by interactions among the individuals in the fish schooling or bird flocking, the PSO algorithm has been proposed in [16] with the purpose of exploring the searching space by updating a linear summation of the particle’s past momentum and current search direction. To the best of the authors’ knowledge, in the later/terminal stage of the evolution of the particle dynamics. Very little attention has been paid to the overshoot problem of the particle dynamics caused by the past momentum, and such an overshoot phenomenon could lead to oscillations which, in turn, slow down the convergence significantly especially for high-dimensional complex optimization problems [48].

According to the similarity between the PSO algorithm and the PI strategy [49], in this paper, we would like to propose a novel PIDLPSO algorithm, which is a yet another PSO variant, to better keep the tradeoff between the exploration and the exploitation with hope to alleviate the overshoot problem during the terminal stage of the convergence of the particle dynamics, where the PIDLPSO updates the velocity and position based on three factors, namely, the past momentum, the present positions (including the personal best position and the global best position), and the future trend of the position. Meanwhile, by combining the Routh stability criterion and the final value theorem of the Z-transformation, we shall obtain the convergence conditions of the PIDLPSO algorithm to be developed. The framework and convergence proof of the proposed PIDLPSO algorithm will be illustrated in details.

As discussed previously, the traditional PSO algorithm could be interpreted as a PI strategy and, in this context, a novel PSO variant is developed by introducing the following derivative term

$$\begin{aligned} \begin{aligned} \xi _i(k)=k_D(e_i(k)-e_i(k-1)), \end{aligned} \end{aligned}$$
(2)

where \(k_D\) is control coefficient and

$$e_i(k)=c_{1}r_{1}p_\mathrm{best}+c_{2}r_{2}g_\mathrm{best}-c_{1}r_{1}x_{i}(k)-c_{2}r_{2}x_{i}(k).$$

In the proposed PIDLPSO algorithm, the velocity and position of the i-th particle at the \((k + 1)\)-th iteration are updated as follows:

$$\begin{aligned} \left\{ \begin{aligned} {v_{i}}(k+1)=&\omega v_{i}(k)+c_{1}r_{1}(p_\mathrm{best}-x_{i}(k))\\&+c_{2}r_{2}(g_\mathrm{best}-x_{i}(k))+\xi _i(k),\\ x_{i}(k+1)=&x_{i}(k)+v_{i}(k+1), \end{aligned} \right. \end{aligned}$$
(3)

The following lemma will be used in obtaining our main results.

Lemma 1

[14] (1) The PSO system does not have an equilibrium point if \(p_\mathrm{best}\ne g_\mathrm{best}\). (2) If \(p_\mathrm{best}=g_\mathrm{best}=x\) is time invariant, then there is a unique equilibrium point at \(v_*=0\) and \(x_*=g_\mathrm{best}\).

Remark 1

Compared to the conventional PSO algorithm, a new term \(\xi _i(k)\) has been added to the particle dynamics whose coefficient, the derivative control gain \(k_D\), will be adequately designed to alleviate the overshoot problem by smoothening the terminal convergence of the particle dynamics. The convergence conditions and the position of the final particle are to be investigated in a mathematically rigorous way, and this constitutes the main contribution of this paper.

Theorem 1

The novel PIDLPSO algorithm is convergent if the following inequality holds

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\omega -1}{c_{1}r_{1}+c_{2}r_{2}}<k_D<\frac{\omega +1}{c_{1}r_{1}+c_{2}r_{2}}-\frac{1}{2},\\&0<c_{1}r_{1}+c_{2}r_{2}<4. \end{aligned}\right. \end{aligned}$$
(4)

Moreover, the final position of the i-th particle in the PIDLPSO algorithm is

$$\begin{aligned} {x_i(\infty )=g_\mathrm{best}.} \end{aligned}$$
(5)

Proof

Considering (2) and (3), we have immediately that

$$\begin{aligned} x_{i}(k+1)=x_{i}(k)+\omega v_{i}(k)+e_{i}(k)+\xi _i(k). \end{aligned}$$
(6)

Letting \(k=k+1\), it follows that

$$\begin{aligned} \begin{aligned} x_{i}(k+2)=&x_{i}(k+1)+\omega v_{i}(k+1)\\&+(k_D+1)e_{i}(k+1)-k_D e_{i}(k). \end{aligned} \end{aligned}$$
(7)

According to (2), we obtain

$$\begin{aligned} x_{i}(k+2)= & {} \frac{c_{1}r_{1}p_\mathrm{best}+c_{2}r_{2}g_\mathrm{best}-e_i(k+2)}{c_{1}r_{1}+c_{2}r_{2}}, \end{aligned}$$
(8)
$$\begin{aligned} x_{i}(k+1)= & {} \frac{c_{1}r_{1}p_\mathrm{best}+c_{2}r_{2}g_\mathrm{best}-e_i(k+1)}{c_{1}r_{1}+c_{2}r_{2}}, \end{aligned}$$
(9)
$$\begin{aligned} \omega v_{i}(k+1)= & {} \omega \frac{e_i(k)-e_i(k+1)}{c_{1}r_{1}+c_{2}r_{2}}. \end{aligned}$$
(10)

Substituting (8)–(10) into (7), one has

$$\begin{aligned} \begin{aligned}&e_{i}(k+2)+((k_D+1)(c_{1}r_{1}+c_{2}r_{2})-\omega -1)e_{i}(k+1)\\&\quad +(\omega -k_D(c_{1}r_{1}+c_{2}r_{2}))e_{i}(k)=0.\\ \end{aligned} \end{aligned}$$
(11)

Taking the Z-transform of (11), we obtain

$$\begin{aligned} \begin{aligned} e_{i}(z)=\frac{Az^{2}+Bz}{Cz^{2}+Dz+E} \end{aligned} \end{aligned}$$
(12)

where

$$\begin{aligned} A= & {} e_{i}(0), \\ B= & {} 2e_{i}(1)+((k_D+1)(c_{1}r_{1}+c_{2}r_{2})-\omega -1)e_{i}(0), \\ C= & {} 1, \\ D= & {} (k_D+1)(c_{1}r_{1}+c_{2}r_{2})-\omega -1, \\ E= & {} \omega -k_D(c_{1}r_{1}+c_{2}r_{2}). \end{aligned}$$

Taking the linear difference transformation

$$\begin{aligned} z=\frac{\mu +1}{\mu -1}, \end{aligned}$$

we arrive at

$$\begin{aligned} \begin{aligned} e_{i}(\mu )=\frac{A(\frac{\mu +1}{\mu -1})^{2}+B\frac{\mu +1}{\mu -1}}{C(\frac{\mu +1}{\mu -1})^{2}+D\frac{\mu +1}{\mu -1}+E} \end{aligned} \end{aligned}$$
(13)

The characteristic equation of (13) is calculated as follows:

$$\begin{aligned} \begin{aligned}&(c_{1}r_{1}+c_{2}r_{2})\mu ^{2}+(2-2\omega +2k_D(c_{1}r_{1}+c_{2}r_{2}))\mu \\&\quad +2+2\omega -(2k_D+1)(c_{1}r_{1}+c_{2}r_{2})=0. \end{aligned} \end{aligned}$$
(14)

By utilizing the Routh stability criterion, we obtain the system stability conditions as follows:

$$\begin{aligned} \left\{ \begin{aligned}&c_{1}r_{1}+c_{2}r_{2}>0,\\&2-2\omega +2k_D(c_{1}r_{1}+c_{2}r_{2})>0,\\&2+2\omega -(2k_D+1)(c_{1}r_{1}+c_{2}r_{2})>0,\\ \end{aligned}\right. \end{aligned}$$
(15)

and therefore

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\omega -1}{c_{1}r_{1}+c_{2}r_{2}}<k_D<\frac{\omega +1}{c_{1}r_{1}+c_{2}r_{2}}-\frac{1}{2},\\&0<c_{1}r_{1}+c_{2}r_{2}<4. \end{aligned}\right. \end{aligned}$$
(16)

By means of the final value theorem of the Z-transform, we obtain that

$$\begin{aligned} {e_{i}(\infty )={\lim _{z \rightarrow 1}}(z-1)e_{i}(z)=0.} \end{aligned}$$
(17)

Hence, the PIDLPSO algorithm will converge to

$$\begin{aligned} {x_i(\infty )=\frac{c_{1}r_{1}p_\mathrm{best}+c_{2}r_{2}g_\mathrm{best}}{c_{1}r_{1}+c_{2}r_{2}}}. \end{aligned}$$
(18)

Finally, it follows from \(p_\mathrm{best}=g_\mathrm{best}\) that

$$\begin{aligned} {x_i(\infty )=g_\mathrm{best}} \end{aligned}$$
(19)

which ends the proof. \(\square \)

Remark 2

So far, a novel PIDLPSO algorithm has been proposed in which a new derivative control term is introduced so as to govern the smoothening process of the terminal convergence during the final stage of the dynamics evolution of the particles, thereby alleviating the overshoot/oscillation problems. In this PIDLPSO algorithm, the new derivative control term is mainly to fine-tune the future trend of the positions and hence provides yet another design freedom (in addition to the past momentum and the present positions) for improving the transient behaviors of the terminal convergence of the particle dynamics.

Remark 3

Comparing to the numerous versions of the PSO variants, our proposed PIDLPSO exhibits the following distinctive features: 1) a derivative control term is introduced to alleviate the overshoot problem and accelerate convergence during the later/terminal stage of the particle dynamics; 2) the convergence conditions and the final positions are obtained by means of the Routh stability criterion and the final value theorem of the Z-transformation; and 3) the PIDLPSO algorithm is more competitive (in achieving the global optimum) than several other popular PSO algorithms as demonstrated in the next section.

Simulation Experiments

In this section, the superiority of proposed PIDLPSO algorithm is demonstrated by comparing with five widely employed PSO variants in terms of population diversity, convergence rate and searching ability.

In the experiments, the population size is set as \(m=20\) and the dimension of the searching space is \(D=20\). For the PIDLPSO algorithm, the inertia weight \(\omega =0.729\), the acceleration coefficients \(c_1=c_2=1.5\), \(r_1=r_2=0.5\). The performance of the PIDLPSO algorithm with different settings of the derivative control \(K_D\) is shown in Table 1. It can be seen that the PIDLPSO algorithm demonstrates competitive performance when \(k_D=0.155\).

Population Diversity

In this paper, the variance (population spatial distribution) and the entropy (particle activity) are employed to describe the population diversity. The variance of the population in the k-th iteration is defined as follows

$$\begin{aligned} S_i(k)=\frac{1}{m}\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{D}({x_{i}^{j}(k)-{\bar{x}^j(k)})}^{2}, \end{aligned}$$
(20)

where D denotes the dimension of the searching space, m is the number of the particles in the population, \(x_{i}^{j}(k)\) indicates the i-th particle in the j-th dimension, and \(\bar{x}^j(k)\) denotes the mean of the j-th dimension over all particles in the k-th iteration.

Figures 1 and 2 depict the variance of the population dynamics of the typical PSO algorithm and the proposed PIDLPSO algorithm when the iterations are set to 5000 and 20000, respectively. It is clearly seen from the figures that, with the number of iterations increasing, the population variance gradually decreases until it converges, which indicates that all the particles are dispersed to explore the whole space with the purpose of discovering globally optimal solution in the global exploration stage. Contrarily, during the local exploitation process, the others are inspired to move towards the globally optimal particle until convergence. Note that the population variance of the PIDLPSO is higher than that of the typical PSO algorithm, which illustrates the particle distribution of the PIDLPSO algorithm is more dispersed so as to search the whole space more thoroughly.

Fig. 1
figure 1

Variation curves of population variance, when the maximum number of iterations is 5000

Full size image
Fig. 2
figure 2

Variation curves of population variance, when the maximum number of iterations is 20000

Full size image

In the k-th iteration, the particles are divided into Q subsets denoted by {\(S_1(k),S_2(k),\ldots ,S_Q(k) \)}. For \(\forall p,q\in \{1, 2,\ldots , Q\}\), we have

$$\begin{aligned} S_p(k)\cap S_q(k)= \emptyset , \ \ \bigcup \limits _{q=1}^Q S_q(k)=A(k), \end{aligned}$$

where A(k) is the whole swarm set. The number of the particles in each subset is represented by

$$\{|S_1(k)|,|S_2(k)|,\ldots ,|S_Q(k)| \},$$

and then the population entropy is defined as follows

$$\begin{aligned} Ep=-\sum \limits _{j=1}^{Q}{p_{j}\lg ({p_{j}}}), \end{aligned}$$
(21)

where

$$\begin{aligned} p_{j}=\frac{|S_j(k)|}{m} \end{aligned}$$

with m denoting the number of individuals in the whole swarm.

The dynamic curves of the population entropy with the number of iterations are depicted for the PSO algorithm and the PIDLPSO algorithm in Fig. 3. We can see that the population entropy is higher during the early stage of the iterations, the particles are distributed into the whole space to explore the globally optimal solution, and the curves of population entropy contain a large number of particle exploration information. While the population entropy is lower in the last stage of the iterations, which illustrates that other particles are encouraged to move towards the globally optimal particle. Therefore, the population entropy of the final curve is lower and more stable, which indicates that the PIDLPSO algorithm is convergent.

Fig. 3
figure 3

Variation curves of population entropy

Full size image

Optimization Performance

In this subsection, the searching ability of the PIDLPSO algorithm is tested and verified through a large number of simulation and comparison experiments. Note that the details of all the test functions are given in Table 2, which includes the dimension, the threshold, and etc.

Table 1 Statistics results of the PIDLPSO algorithm under different \(K_D\) conditions
Full size table
Table 2 The test function configuration
Full size table
Table 3 Statistical results of six PSO algorithms
Full size table

In order to demonstrate the optimality of the PIDLPSO algorithm, in this paper, various improved PSO variants reported in recent literatures are employed for optimization capability evaluation via four widely-used test functions. In the consideration of evaluation factors, the comparisons are conducted from the following four aspects: (1) minimum; (2) mean; (3) standard deviation; and (4) success ratio.

Table 3 lists the statistical results for various PSO variants. It is seen from Table 3 that, compared with other PSO variants, the PIDLPSO algorithm has the smallest or near the smallest minimum, mean and standard deviation, which illustrates that the proposed PIDLPSO algorithm is more competitive in searching performance. In addition, it should be noted that the success ratio is another significant indicator to assess the convergence characteristics, which illustrates the capability of jumping out of the local optimum. It is demonstrated from Table 3 that the success ratio of our PIDLPSO algorithm is the biggest reaching 100% for four benchmark functions, which is further verified that the PIDLPSO algorithm is better than other algorithms, especially in getting rid of local optimum.

Convergence analysis

Convergence rate

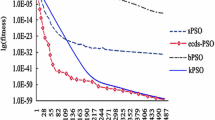
It is worth noting that the convergence rate is a crucial metric to assess the convergence of the PSO algorithms. The convergence rate of various PSO variants is illustrated in Figs. 4, 5, 6 and 7, where the abscissa and the ordinate respectively represents the iteration number and the mean fitness values of various PSO variants. It is clearly shown that the convergence rate of the proposed PIDLPSO algorithm is more competitive than that of other algorithms on the most test functions. In detail, it can be seen from Figs. 5, 6 and 7 that the convergence rate of the PIDLPSO algorithm is the fastest than that of other PSO variants. Although, in Fig. 4, the proposed PIDLPSO algorithm is not the best in convergence rate, its fitness values are small enough to satisfy the convergence performance. In general, the convergence rate of the PIDLPSO algorithm is more excellent than that of others.

Fig. 4
figure 4

PSO algorithms convergence characteristics of Sphere

Full size image
Fig. 5
figure 5

PSO algorithms convergence characteristics of Schwefel 2.22

Full size image
Fig. 6
figure 6

PSO algorithms convergence characteristics of Schwefel 1.2

Full size image
Fig. 7
figure 7

PSO algorithms convergence characteristics of Penalized 1

Full size image

Step response

In essence, the particle swarm optimizer could be approximately regarded as the PI strategy, similarly, the proposed PIDLPSO algorithm could be considered as a PID strategy in this paper. The step response curves of the two methods are shown in Fig. 8. It can be clearly seen that, compared with the typical PSO algorithm, the proposed PIDLPSO algorithm provides better control performance and reduce the overshoot problem. It owes the introduction of derivative control, which expands the search space of the particles and increases the probability of escaping from the local optimum.

Fig. 8
figure 8

The step response curve of the algorithms

Full size image

Theoretical simulation

According to Theorem 1, all the particles will eventually converge to

$$\begin{aligned} {x_{i}(\infty )=g_\mathrm{best}.} \end{aligned}$$
(22)

Figures 9 and 10 plot the tendencies of \(x_i(k)\) and \(g_\mathrm{best}\) when the maximum number of iterations is 4000 and 20000, respectively. It can be seen from the figures that, as the number of iterations increases, the two curves of \(x_i(k)\) and \(g_\mathrm{best}\) will coincide, that is, the particles will converge.

Fig. 9
figure 9

The convergence curve of the PIDLPSO algorithm, when the maximum number of iterations is 4000

Full size image
Fig. 10
figure 10

The convergence curve of the PIDLPSO algorithm, when the maximum number of iterations is 20000

Full size image

Conclusion

In this paper, motivated by the similarity in traditional PSO algorithm and PI control strategies, a novel PIDLPSO algorithm has been designed by introducing the derivative item with the purpose of alleviating the overshoot problem caused by past momentum. With this novel tactics, the PIDLPSO algorithm has not only maintained the accuracy of the solution but also enhanced the convergence rate. Furthermore, with the help of Routh stability criterion and final value theorem of the Z-transformation, the convergence conditions and the final positions have been gained for the PIDLPSO algorithm. The superiorities of proposed algorithm have been evaluated from the perspectives of population diversity, convergence rate and searching ability. Experimental results have exhibited the superiorities of designed PIDLPSO algorithm over other state-of-the-art PSO variants on four wide-ranging benchmark functions including both one-peak and multi-peak cases. In the future, we will research into some new directions which include, but are not limited to, the investigations on (1) how to analyze the convergence of the modified PSO algorithms with time-varying parameters [55] and (2) how to apply the PIDLPSO algorithm to other research fields such as deep learning [10, 15, 26, 38, 43, 54, 58], fault detection [3, 11, 12], signal processing [23, 25, 27, 34, 35, 37, 40, 45, 47, 51] and multi-objective optimization [9, 53].