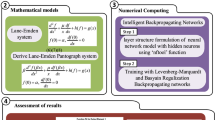
Abstract
The current study is related to present a novel neuro-swarming intelligent heuristic for nonlinear second-order Lane–Emden multi-pantograph delay differential (NSO-LE-MPDD) model by applying the approximation proficiency of artificial neural networks (ANNs) and local/global search capabilities of particle swarm optimization (PSO) together with efficient/quick interior-point (IP) approach, i.e., ANN-PSOIP scheme. In the designed ANN-PSOIP scheme, a merit function is proposed by using the mean square error sense along with continuous mapping of ANNs for the NSO-LE-MPDD model. The training of these nets is capable of using the integrated competence of PSO and IP scheme. The inspiration of the ANN-PSOIP approach instigates to present a reliable, steadfast, and consistent arrangement relates the ANNs strength for the soft computing optimization to handle with such inspiring classifications. Furthermore, the statistical soundings using the different operators certify the convergence, accurateness, and precision of the ANN-PSOIP scheme.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The delay differential model is one of the historical and prominent differential model discovered four centuries ago and has numerous applications in scientific areas like economical states, population dynamics, communication networks, transport, and engineering models [1,2,3,4]. Beretta et al.[5] used the delay-dependent factors to function the geometric consistency based on the delay differential model. To solve the delay differential systems, Frazier [6] used the wavelet Galerkin scheme along with the Taylor series, Rangkuti et al. [7] applied the coupled variation iteration scheme and Chapra [8] implemented the Runge–Kutta method. The current study is about the pantograph differential model that is a form of delay differential system and has a variety of applications in medicine, chemical kinetics, light absorption, ships controlling, biology, chemistry, engineering, physics, electrodynamics, quantum mechanics, infectious diseases, electronic models, physiological kinetics and control problems [9, 10]. Due to the paramount significance of these models, a variety of analytical/numerical schemes has been proposed. To mention a few of them are the Dirichlet series that is applied to get the analytical solutions of the multi-pantograph (MP) delay differential system [11]. For higher order MP nonlinear delay differential system, one-dimensional approach based on differential transforms has been proposed [12]. The Taylor polynomials technique and numerical differential transform scheme are implemented to the solutions of the MP delay differential system [13]. Some more potential recent studies of delay differential system arising in different fields solved with numerical or analytical schemes can be seen in [14,15,16,17].
The study of the historical Lane–Emden model that involves singularity at the origin is considered very important for the researchers due to the numerous applications in the cooling of the radiators, system of the gas cloud, cluster galaxies, and polytrophic star models. The Lane–Emden systems used to model the dusty fluids [18], physical forms of the science systems [19], density state of gasiform star [20], catalytic diffusion reactions [21], stellar configuration [22], the electromagnetic theory [23], mathematical physics [24], quantum/classical mechanics [25], oscillating magnetic areas [26], isotropic continuous media [27] and stellar structure systems [28]. It is always difficult to solve the Lane–Emden model due to a singular point, hard and grim nature. Some existing techniques that have been used to solve the singular problems shown in the ref [29,30,31]. The standard notation of the Lane–Emden system is shown as [32]:
where \(\Omega \ge 1\) is the value of shape factor and \(\chi = 0\) represents the singular point at the origin. The motive of the current work is to solve numerically nonlinear second-order Lane–Emden multi-pantograph delay differential (NSO-LE-MPDD) model along with a grander system understanding by applying the stochastic methods through the artificial neural networks (ANNs), optimized with both global and local search competences, particle swarm optimization (PSO) and interior-point (IP) approach, i.e., ANN-PSOIP algorithm. Some well-known submissions are HIV infection model [33], nonlinear Bratu’s systems [34], heat conduction dynamics based on singular nonlinear human head model [35], singular three-point model [36], Thomas–Fermi model [37], multi-singular nonlinear models [38], model of heartbeat dynamics [39], singular periodic model [40], prey-predator models [41] and nonlinear singular functional differential model [42, 43]. The generic form of the NSO-LE-MPDD model is shown as [44]:
where a is the constant and the pantographs appear twice in the first and second derivative terms of the Eq. (2). The system model represented in Eq. (2) is a type of functional differential equations with multi-pantograph delays, i.e., a kind of proportional delay that exists in more than one terms. This Lane–Emden pantograph model has not solved before using the stochastic ANN-PSOIP algorithm. Some main topographies of the proposed integrated computational heuristic of ANN-PSOIP method are concisely provided as:
-
A mathematical NSO-LE-MPDD system is numerically solved by applying the integrated heuristic of neuro-swarming computing intelligent ANN-PSOIP algorithm.
-
The matching/overlapping of the numerical results from the designed approach with the reference solutions of the NSO-LE-MPDD system established the worth/value of the ANN-PSOIP algorithm.
-
Certification of the performance is ratified via statistical explorations to find the solutions for multiple execution of the ANN-PSOIP algorithm in terms of Theil’s inequality coefficient (TIC), variance account for (VAF), semi-interquartile (SI) range and Nash Sutcliffe efficiency (NSE) performance operators.
-
Beside the precise/practical outcomes for the nonlinear Lane–Emden pantograph second-order delay differential system, easy understanding, extensive applicability, consistency, smooth operations and robustness are other significant advantages.
The remaining portions of this work are planned as: In the next section, the suggested framework is presented using the ANN-PSOIP algorithm. In the folowing section, the mathematical formulation of the performance measures is described. In the next section, the detailed discussions of the numerical results are provided. In the last section, the conclusions together with future research guidance are listed.
Design methodology
The proposed ANN-PSOIP algorithm for numerical results of the NSO-LE-MPDD model is categorized into two steps.
-
Introduced an objective function using the differential system and associated boundary/initial conditions.
-
The optimal combination of PSO and IP algorithm, i.e., PSOIP algorithm is provided in the form of preliminary material along with pseudocode.
ANN modeling
Mathematical models of the NSO-LE-MPDD system are accumulated with the strength of feed-forward ANNs, which designate the continuous mapping for an approximate solution \(\hat{U}(\chi )\) and its derivatives up to second order based on the log-sigmoid \(H(\chi ) = \left( {1 + \exp ( - \chi )} \right)^{ - 1}\) activation functions given respectively as follows:
where \({\varvec{b}} = [b_{1} ,b_{2} ,b_{3} ,...,b_{m} ],\,\,{\varvec{c}} = [c_{1} ,c_{2} ,c_{3} ,...,c_{m} ]\) and \({\varvec{a}} = [a_{1} ,a_{2} ,a_{3} ,...,a_{m} ]\) are the weight vectors. The log-sigmoid activation function is normally used exhaustively for the hidden layers due to established strength of stability, efficiency, and accuracy in the majority of the applications in diversified fields.
For solving the NSO-LE-MPDD system, an error-based merit function is written as:
where \(\xi_{{\text{Fit - 1}}}\) is the merit functions related to the differential model and \(\xi_{{\text{Fit - 2}}}\) represents the initial conditions, respectively, shown as:
where \(hN = 1,\,\,F_{m} = F(\chi_{m} ),\,\,\hat{U}_{m} = \hat{U}(\chi_{m} )\,\,{\text{and}}\,\,\,\chi_{m} = mh.\), while h be the step size.
Optimization procedure: PSO-IP algorithm
A kind of memetic computing paradigm through hybrid computational heuristics of global search efficacy of particle swarm optimization (PSO) aided with rapid local refinements with efficient interior-point (IP) algorithm, i.e., PSOIP, is ratified for the parameter optimization for NSO-LE-MPDD system due to their established strength of accuracy, convergence, and stability over the standalone techniques based on global and local search methodologies [45].
PSO is a global search optimization process in which the process of search space, a candidate single result relating the procedure of optimization is represented as a particle. For the PSO optimization, preliminary swarms spread into the larger. To modify PSO parameters, the scheme delivers optimal outcomes iteratively \({\varvec{P}}_{LB}^{\Phi - 1}\) and \({\varvec{P}}_{GB}^{\Phi - 1}\), that is the position and velocity of swarm, mathematically shown as:
where Xi and Vi are ith position and velocity of the particle, respectively, \(\Phi\) be the flight index or cycle of the algorithm, \(\Psi \in [0,1][0,1]\) is the inertia weight, \(\Phi_{1}\) and \(\Phi_{2}\) are cognitive and social acceleration constants, respectively, while r1 and r2 are the random positive real number between 0 and 1.
PSO is a global search optimization process represented in Eqs. (7–8) used as an operational alternate of the genetic algorithms [46] for NSO-LE-MPDD system. Kennedy and Eberhart suggested PSO, i.e., a famous global search easy implementation algorithm introduced at the last of the previous century and required short requirements of the memory [47]. Few recent applications of the PSO are fuel ignition model [48], balancing stochastic U-lines problems [49], nonlinear physical systems [50], feature classification [51] and operation scheduling of microgrids [52].
The PSO rapidly converges to hybrid with an appropriate local search approach by using the PSO values as a primary weight. Therefore, a rapid and operative local search approach based on interior-point (IP) algorithm is implemented to adjust the solutions attained by the designed optimization algorithm. Few recent submissions of the IP algorithm are active noise control systems [53], mixed complementarity monotone systems [54], simulation of aircraft parts riveting [55], nonlinear system identification [56] and economic load dispatch model [57].
The pseudo code for the combination of PSOIP algorithm trains the ANN along with the essential parameter settings of PSO and IP algorithm are given in Table 1. The scheme based on optimization becomes impulsive by a slight change to set the parameters, thus, it needs numerous experiences, repetitions, and information on necessary optimization imitations of suitable settings using the hybrid of PSO-IP algorithm.
Performance procedures
In the current study, the statistical forms of the Nash Sutcliffe efficiency (NSE), Theil’s inequality coefficient (TIC), semi-interquartile (SI) range, and variance account for (VAF) are presented to nonlinear Lane–Emden pantograph second-order delay differential system.
The mathematical formulations of TIC is presented as:
where \(U_{i}\) and \(\hat{U}_{i}\) be the reference and estimation solutions for the ith input of nonlinear Lane–Emden pantograph second-order delay differential system. The desire/optimal value of TIC is 0 for the perfect scenarios.
The mathematical formulations of VAF and error in VAF (EVAR) are presented as:
here ‘var’ stands for variance operator, and the desire/optimal values of VAF and EVAF are 100 and 0 for the perfect modelling scenarios.
Mathematical expression for SIR metric is given as follows:
The mathematical based definition of NSE and error in NSE (ENSE) are given respectively as follows
The desire/optimal values of NSE and ENSE are o and 1 for the perfect scenario, respectively.
Results and discussions
In this section, the details for solving three problems of the NSO-LE-MPDD system are provided.
Problem-I
Consider a NSO-LE-MPDD model based equation is written as:
The true result of the Eq. (13) is \(1 + \chi^{4}\) and the merit function is given as:
Problem-II
Consider a NSO-LE-MPDD model based equation involving trigonometric values in its forcing factor is given as:
The exact solution of the Eq. (15) is \(\cos (\chi )\) and the fitness function becomes as:
Problem-III
Consider a NSO-LE-MPDD model based equation is written as:
The exact form of the solution of the Eq. (17) is \(1 + \chi^{3}\) and the merit function is given as:
The optimization of the NSO-LE-MPDD model-based problems I–III is accomplished by the hybrid of PSOIP algorithm for 60 independent executions to get the ANN parameters for 10 neurons. The values of the ANN-PSOIP algorithm using the best values of the weight vector are plotted in Fig. 1 and the mathematical illustrations of the proposed numerical solutions are shown as:
Optimization is performed for solving the NSO-LE-MPDD model-based problems I-III using the ANN-PSOIP algorithm for 60 independent executions. In Fig. 1, a set of best weight vectors and comparison of the reference, mean and obtained results of the NSO-LE-MPDD model-based problems I-III using 10 neurons is presented. It is indicated that the reference, mean and proposed results overlapped over one another for all the examples of the NSO-LE-MPDD model. This overlapping of the outcomes designates the accomplishment and excellence of the ANN-PSOIP algorithm. Figure 2 represents the absolute error (AE) values and performance investigations of the ANN-PSOIP approach for the NSO-LE-MPDD model-based problems I–III. The Fig. 2a shows the AE plots for all the problems of the model. It is resulted that the AE values exist around 10−04 to 10−07, 10−04 to 10−05 and 10−05 to 10−07 for the problems I-III, respectively. The Fig. 2b represents the performance measures for all the problems in terms of the fitness, TIC, EVAF and ENSE. It is observed that the fitness values exist around 10−10 to 10−11 for Problem-I, while the fitness lie around 10−09 to 10−10 for Problems II and III. The values of the TIC gages for all the Problems lie 10−08 to 10−09 ranges. Furthermore, the EVAF and ENSE gages values for Problem I lie 10−07 to 10−08 range, while the EVAF and ENSE values for Problems II and III lie around 10−08–10−09.
The statistical soundings for the designed ANN-PSOIP algorithm through the Fitness, TIC, EVAF and ENSE values using the boxplots and histogram values for the NSO-LE-MPDD model-based problems I-III are presented in Figs. 3, 4, 5 and 6. It is indicated that maximum fitness, TIC, EVAF and ENSE values are found to be around 10−06 to 10−08, 10−04 to 10−08, 10−02 to 10−08 and 10−04–10−06, respectively. One may realize from these solutions that most of the independent executions got specific and reasonable accuracy for the statistical values of TIC, EVAF and ENSE.
To find the statistical measures, minimum (Min), median (Med), Mean, and SI operatives are performed for 60 independent runs using the ANN-PSOIP algorithm for solving the NSO-LE-MPDD model-based problems I–III. The statistic values using these gages are presented in Table 2 for solving all the problems. These numerical values are calculated adequate and adequate, which designates the precision and accuracy of the designed ANN-PSOIP scheme. Further analysis of performance is conducted by the implementation of the proposed integrated heuristic ANN-PSOIP for optimization problem based on multiple neurons in the hidden layers, i.e., 5, 10, and 15 neuron-based network models. It is shown that with the increase of the number of neurons the accuracy and stability of the ANN-PSOIP increase but at the cost of more computations. Therefore, there is always a trade-off between the complexity and accuracy, so increasing the neurons more than 10 in the networks, the complexity of the algorithm increases rather more rapidly while very little advantage or gain in the accuracy and convergence.
Conclusion
In this study, a novel submission of stochastic numerical computing solvers is proposed to solve the NSO-LE-MPDD model-based equations using 10 numbers of neurons optimized with the global/local search proficiencies of particle swarm optimization enhanced with the rapid refinement of decision variables by manipulating the local search strength via interior-point algorithm. An objective function is designed using the differential system/initial conditions and then optimization is performed by the hybrid of local/global competencies of particle swarm optimization and interior-point algorithm, respectively. The accuracy and exactness of the designed scheme are certified by finding identical solutions with the exact/reference results having 5–7 decimal places of precision for solving all the problems of the NSO-LE-MPDD model. Statistical interpretation through performance measures of TIC, ENSE and EVAF based on 60 trials/executions for obtaining the solution of NSO-LE-MPDD model-based equations in terms of semi-interquartile range, mean and median authenticate the robustness, accurateness and trustworthiness of the proposed scheme.
In the future, the proposed ANN-PSOIP algorithm can be used as an accurate/efficient stochastic numerical approach for singular higher order models [58,59,60], biological models [61, 62], prediction differential model [63], dynamical investigations of computational fluid models [64,65,66,67,68] and stiff nonlinear systems [69,70,71,72,73,74,75]. Moreover, the polynomial, radial, wavelet, support vector machine-based neural networks looks promising to be exploited in future for the improved performance [76].
References
Li W, Chen B, Meng C, Fang W, Xiao Y, Li X, Hu Z, Xu Y, Tong L, Wang H, Liu W (2014) Ultrafast all-optical graphene modulator. Nano Lett 14(2):955–959
Kuang Y (ed) (1993) Delay differential equations: with applications in population dynamics, vol 191. Academic Press, Cambridge
Niculescu SI (2001) Delay effects on stability: a robust control approach, vol 269. Springer Science & Business Media, Berlin
Li DS, Liu MZ (2000) Exact solution properties of a multi-pantograph delay differential equation. J Harbin Inst Technol 32(3):1–3
Beretta E, Kuang Y (2002) Geometric stability switch criteria in delay differential systems with delay dependent parameters. SIAM J Math Anal 33(5):1144–1165
Frazier MW (1999) Background: complex numbers and linear algebra. An introduction to wavelets through linear algebra, pp 7–100
Rangkuti YM, Noorani MSM (2012) The exact solution of delay differential equations using coupling variational iteration with Taylor series and small term. Bull Math 4(01):1–15
Chapra SC (2012) Applied numerical methods. McGraw-Hill, Columbus
Bogachev L, Derfel G, Molchanov S, Ochendon J (2008) On bounded solutions of the balanced generalized pantograph equation. In: Chow P-L, Yin G, Mordukhovich B (eds) Topics in stochastic analysis and nonparametric estimation, vol 145. The IMA volumes in mathematics and its applications. Springer, New York, pp 29–49
Soleymani KV, Sedighi HK (2011) On the numerical solution of generalized pantograph equation. World Appl Sci J 13(12):2531–2535
Liu MZ, Li D (2004) Properties of analytic solution and numerical solution of multi-pantograph equation. Appl Math Comput 155(3):853–871
Koroma MA, Zhan C, Kamara AF, Sesay AB (2013) Laplace decomposition approximation solution for a system of multi-pantograph equations. Int J Math Comput Sci Eng 7(7):39–44
Sezer M, Şahin N (2008) Approximate solution of multi-pantograph equation with variable coefficients. J Comput Appl Math 214(2):406–416
Zhu Q (2019) Stabilization of stochastic nonlinear delay systems with exogenous disturbances and the event-triggered feedback control. IEEE Trans Autom Control 64(9):3764–3771
Zhu Q (2018) Stability analysis of stochastic delay differential equations with Lévy noise. Syst Control Lett 118:62–68
Wang H, Zhu Q (2020) Global stabilization of a class of stochastic nonlinear time-delay systems with SISS inverse dynamics. IEEE Trans Autom Control 65(10):4448–4455
Zhu Q, Huang T (2020) Stability analysis for a class of stochastic delay nonlinear systems driven by G-Brownian motion. Syst Control Lett 140:104699
Flockerzi D, Sundmacher K (2011) On coupled Lane–Emden equations arising in dusty fluid models. In: Journal of physics: conference series, vol 268, no 1. IOP Publishing, p 012006
Mandelzweig VB, Tabakin F (2001) Quasi linearization approach to nonlinear problems in physics with application to nonlinear ODEs. Comput Phys Commun 141(2):268–281
Luo T, Xin Z, Zeng H (2016) Nonlinear asymptotic stability of the Lane–Emden solutions for the viscous gaseous star problem with degenerate density dependent viscosities. Commun Math Phys 347(3):657–702
Rach R, Duan JS, Wazwaz AM (2014) Solving coupled Lane–Emden boundary value problems in catalytic diffusion reactions by the Adomian decomposition method. J Math Chem 52(1):255–267
Abbas F, Kitanov P, Chimene S, Rehmani A (2020) Analytical approach to study the generalized Lane–Emden model arises in the study of stellar configuration. Appl Math 14(3):1–10
Khan JA, Raja MAZ, Rashidi MM, Syam MI, Wazwaz AM (2015) Nature-inspired computing approach for solving non-linear singular Emden–Fowler problem arising in electromagnetic theory. Connect Sci 27(4):377–396
Bhrawy AH, Alofi AS, Van Gorder RA (2014) An efficient collocation method for a class of boundary value problems arising in mathematical physics and geometry. In: Abstract and applied analysis, vol 2014. Hindawi Publishing Corporation
Ramos JI (2003) Linearization methods in classical and quantum mechanics. Comput Phys Commun 153(2):199–208
Dehghan M, Shakeri F (2008) Solution of an integro-differential equation arising in oscillating magnetic fields using He’s homotopy perturbation method. Prog Electromagn Res 78:361–376
Radulescu V, Repovs D (2012) Combined effects in nonlinear problems arising in the study of anisotropic continuous media. Nonlinear Anal Theory Methods Appl 75(3):1524–1530
Taghavi A, Pearce S (2013) A solution to the Lane–Emden equation in the theory of stellar structure utilizing the Tau method. Math Methods Appl Sci 36(10):1240–1247
Wazwaz AM (2001) A new algorithm for solving differential equations of Lane–Emden type. Appl Math Comput 118(2):287–310
Shawagfeh NT (1993) Non-perturbative approximate solution for Lane–Emden equation. J Math Phys 34(9):4364–4369
Liao S (2003) A new analytic algorithm of Lane–Emden type equations. Appl Math Comput 142(1):1–16
Sabir Z et al (2020) Novel design of Morlet wavelet neural network for solving second order Lane–Emden equation. Math Comput Simul 172:1-14
Umar M et al (2020) Stochastic numerical technique for solving HIV infection model of CD4+ T cells. Eur Phys J Plus 135(6):403
Hassan A et al (2019) Design of cascade artificial neural networks optimized with the memetic computing paradigm for solving the nonlinear Bratu system. Eur Phys J Plus 134(3):122
Raja MAZ et al (2018) A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head. Eur Phys J Plus 133(9):364
Sabir Z et al (2020) Design of stochastic numerical solver for the solution of singular three-point second-order boundary value problems. Neural Comput Appl 33(7):2427-2443
Sabir Z et al (2018) Neuro-heuristics for nonlinear singular Thomas-Fermi systems. Appl Soft Comput 65:152–169
Raja MAZ et al (2019) Numerical solution of doubly singular nonlinear systems using neural networks-based integrated intelligent computing. Neural Comput Appl 31(3):793–812
Umar M et al (2020) A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment. Eur Phys J Plus 135(7):1–23
Sabir Z, Raja MAZ, Guirao JL, Shoaib M (2020) A neuro-swarming intelligence-based computing for second order singular periodic non-linear boundary value problems. Front Phys 8:224
Umar M et al (2019) Intelligent computing for numerical treatment of nonlinear prey–predator models. Appl Soft Comput 80:506–524
Sabir Z et al (2020) Neuro-swarm intelligent computing to solve the second-order singular functional differential model. Eur Phys J Plus 135(6):474
Sabir Z et al (2019) Stochastic numerical approach for solving second order nonlinear singular functional differential equation. Appl Math Comput 363:124605
Adel W et al (2020) Solving a new design of nonlinear second-order Lane–Emden pantograph delay differential model via Bernoulli collocation method. Eur Phys J Plus 135(6):427
Shi Y, Eberhart RC (1999) Empirical study of particle swarm optimization. In: Proceedings of the 1999 congress on evolutionary computation-CEC99 (Cat. No. 99TH8406), vol 3. IEEE, pp 1945–1950
Shi Y (2001) Particle swarm optimization: developments, applications and resources. In: Proceedings of the 2001 congress on evolutionary computation (IEEE Cat. No. 01TH8546), vol 1. IEEE, pp 81–86
Engelbrecht AP (2007) Computational intelligence: an introduction. Wiley, New York
Raja MAZ (2014) Solution of the one-dimensional Bratu equation arising in the fuel ignition model using ANN optimised with PSO and SQP. Connect Sci 26(3):195–214
Aydoğan EK, Delice Y, Özcan U, Gencer C, Bali Ö (2019) Balancing stochastic U-lines using particle swarm optimization. J Intell Manuf 30(1):97–111
Raja MAZ, Zameer A, Kiani AK, Shehzad A, Khan MAR (2018) Nature-inspired computational intelligence integration with Nelder-Mead method to solve nonlinear benchmark models. Neural Comput Appl 29(4):1169–1193
Ibrahim RA, Ewees AA, Oliva D, Elaziz MA, Lu S (2019) Improved salp swarm algorithm based on particle swarm optimization for feature selection. J Ambient Intell Humaniz Comput 10(8):3155–3169
Takano H, Asano H, Gupta N (2020) Application example of particle swarm optimization on operation scheduling of microgrids. In: Frontier applications of nature inspired computation. Springer, Singapore, pp 215–239
Raja MAZ, Aslam MS, Chaudhary NI, Khan WU (2018) Bio-inspired heuristics hybrid with interior-point method for active noise control systems without identification of secondary path. Front Inf Technol Electron Eng 19(2):246–259
Sicre MR, Svaiter BF (2018) A $$\mathcal {O}$$(1/k3/2) hybrid proximal extragradient primal–dual interior point method for nonlinear monotone mixed complementarity problems. Comput Appl Math 37(2):1847–1876
Stefanova M, Yakunin S, Petukhova M, Lupuleac S, Kokkolaras M (2018) An interior-point method-based solver for simulation of aircraft parts riveting. Eng Optim 50(5):781–796
Umenberger J, Manchester IR (2018) Specialized interior-point algorithm for stable nonlinear system identification. IEEE Trans Autom Control 64(6):2442–2456
Raja MAZ, Ahmed U, Zameer A, Kiani AK, Chaudhary NI (2019) Bio-inspired heuristics hybrid with sequential quadratic programming and interior-point methods for reliable treatment of economic load dispatch problem. Neural Comput Appl 31(1):447–475
Hu W, Zhu Q, Karimi HR (2019) Some improved Razumikhin stability criteria for impulsive stochastic delay differential systems. IEEE Trans Autom Control 64(12):5207–5213
Sabir Z et al (2020) Integrated intelligent computing paradigm for nonlinear multi-singular third-order Emden-Fowler equation. Neural Comput Appl. https://doi.org/10.1007/s00521-020-05187-w
Sabir Z et al (2020) Heuristic computing technique for numerical solutions of nonlinear fourth order Emden-Fowler equation. Math Comput Simul 178:534–548
Shoaib M et al (2021) A stochastic numerical analysis based on hybrid NAR-RBFs networks nonlinear SITR model for novel COVID-19 dynamics. Comput Methods Programs Biomed 202:105973
Cheema TN et al (2020) Intelligent computing with Levenberg–Marquardt artificial neural networks for nonlinear system of COVID-19 epidemic model for future generation disease control. Eur Phys J Plus 135(11):1–35
Sabir Z et al (2020) Design of a novel second-order prediction differential model solved by using Adams and explicit Runge–Kutta numerical methods. Math Probl Eng 2020
Ahmad I et al (2019) Novel applications of intelligent computing paradigms for the analysis of nonlinear reactive transport model of the fluid in soft tissues and microvessels. Neural Comput Appl 31(12):9041–9059
Ilyas H et al (2021) Intelligent computing for the dynamics of fluidic system of electrically conducting Ag/Cu nanoparticles with mixed convection for hydrogen possessions. Int J Hydrogen Energy 46(7):4947–4980
Awan SE et al (2021) Numerical computing paradigm for investigation of micropolar nanofluid flow between parallel plates system with impact of electrical MHD and Hall current. Arab J Sci Eng 46(1):645–662
Ilyas H et al (2021) A novel design of Gaussian WaveNets for rotational hybrid nanofluidic flow over a stretching sheet involving thermal radiation. Int Commun Heat Mass Transf 123:105196
Sabir Z et al (2019) A computational analysis of two-phase casson nanofluid passing a stretching sheet using chemical reactions and gyrotactic microorganisms. Math Probl Eng 2019
Premkumar M, Sowmya R, Jangir P, Nisar KS, Aldhaifallah M (2021) A new metaheuristic optimization algorithms for brushless direct current wheel motor design problem. https://doi.org/10.32604/cmc.2021.015565
Jadoon I et al (2021) Design of evolutionary optimized finite difference based numerical computing for dust density model of nonlinear Van-der Pol Mathieu’s oscillatory systems. Math Comput Simul 181:444–470
Jumani TA, Mustafa MW, Hussain Z, Rasid MM, Saeed MS, Memon MM, Khan I, Nisar KS (2020) Jaya optimization algorithm for transient response and stability enhancement of a fractional-order PID based automatic voltage regulator system. Alex Eng J 59(4):2429–2440
Sabir Z et al (2020) Design of neuro-swarming-based heuristics to solve the third-order nonlinear multi-singular Emden-Fowler equation. Eur Phys J Plus 135(6):1–17
Palmer JM et al (2010) Novel mechanism of rapamycin in GVHD: increase in interstitial regulatory T cells. Bone Marrow Transplant 45(2):379–384
Muhammad U et al (2021) Computational intelligent paradigms to solve the nonlinear SIR system for spreading infection and treatment using Levenberg–Marquardt backpropagation. Symmetry 13(4):618. https://doi.org/10.3390/sym13040618
Sabir Z et al (2021) Integrated intelligence of neuro-evolution with sequential quadratic programming for second-order Lane–Emden pantograph models. Math Comput Simul 188:87–101
Mehmood A et al (2019) Nature-inspired heuristic paradigms for parameter estimation of control autoregressive moving average systems. Neural Comput Appl 31(10):5819–5842
Acknowledgements
Taif University Researchers Supporting Project Number (TURSP-2020/77), Taif University, Taif, Saudi Arabia.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sabir, Z., Raja, M.A.Z., Le, DN. et al. A neuro-swarming intelligent heuristic for second-order nonlinear Lane–Emden multi-pantograph delay differential system. Complex Intell. Syst. 8, 1987–2000 (2022). https://doi.org/10.1007/s40747-021-00389-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-021-00389-8