Introduction

Welding tasks exist in various industrial manufacturing processes. Especially in the shipbuilding process, welding workload accounts for 40\(\%\) of the total workload. Shipbuilding, known as a labor-intensive industry, requires a considerable number of skilled technicians to weld in enclosed and hazardous surroundings. Thanks to the development of industrial robotics, automated welding is gradually replacing manual welding by means of equipping welding manipulators on the shipbuilding production line [1, 2]. Nonetheless, path planning for a specific welding task such as spot welding or arc welding, which is often completed by skilled welding technicians with an offline programming teach pendant, is still challenging automated welding. When dealing with a complex welding task operated on different workpieces with various shapes, it is rather tedious teaching on-line or programming off-line due to the existent of multifarious pose switching of the welding torch which demands many path planning queries. In view of the demand for flexible and high-efficiency welding, a reliable, safe, and automated path planning technology serving for pose switching of the welding torch is urgently needed.

In the field of welding, the term path planning may be formulated as a constrained Traveling Salesman Problem (TSP) [3] while in this paper we study a new method to find an elegant collision-free path in configuration space of the welding manipulator which connects the initial configuration and the target configuration [4].

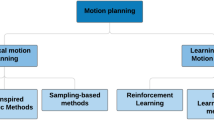
Most existing path planning methods for robots focus on their performance in one domain they pursue. The sampling-based method is one of the most popular path planning methods owing to its probabilistic completeness. The sampling-based planning algorithms mainly include the multi-query algorithm Probabilistic Roadmap Method(PRM) [5, 6] and the single-query method Rapidly exploring Random Trees (RRT) [7, 8]. The algorithms mentioned above can almost always find a feasible path (i.e., a sequence of valid states) when sampling in low-dimension state space like a 2-D or 3-D map for wheeled mobile robots [9, 10] and Unmanned Aerial Vehicle [11]. However, when searching for a feasible path in high-dimension state space like the configuration space of a six-DOF welding manipulator, the computational complexity of the sampling-based method shows an exponential growth trend due to the dimensional explosion of sampling space. To better apply the sampling-based algorithms to the high-dimension path planning(e.g. manipulator planning), many improved methods have been proposed. In [12], a new variation path planning method based on PRM and lazy-PRM for industrial manipulators was proposed to reduce the time spent on the roadmap construction. Cao et. al. adopted the idea of target gravity to accelerate the path search speed in [13] and in [14] an improved sampling-based method using learned critical sources and local sampling is developed to go through narrow passages more quickly. Despite the fact that those methods increase the planning efficiency and inherit the superiority of traditional RRT algorithm, the sampling-based planning method is actually a probabilistic search-based offline method with uncertainty and the planning time may tend to infinity in a complex environment especially a narrow passage.

One of the alternative methods for high-dimension manipulator path planning is based on Artificial Potential Field (APF) which is an online method proposed in [15]. Compared with the sampling-based search algorithm mentioned before, the APF algorithm plans the same path each time for the same task which is meaningful in industrial scenario [16] while both of the two algorithms’ performance suffers from finding a path in high-dimension state space. Furthermore, it should be noted that the APF algorithm, as a local planner, may converge to a local optimal solution and lacks completeness. In view of the aforementioned characteristics, scholars have proposed many improved APF algorithms for path planning in high-dimension state space such as [17, 18]. Another path planning method treats the path planning problem as a constrained optimal control problem and solves it by a nonlinear model predictive controller (MPC) [19], but this method is model dependent and requires computing power and memory resources. What is even more unacceptable is that it is a local planning algorithm as APF does.

With the development of machine learning and deep learning, the learning-based method becomes an elegant alternative method for robot path planning [20]. For example, the Motion Planning Networks(MPNet) based on deep learning [21] aims to train a model that is able to generate an end-to-end collision-free path in the obstacle space for the given start and goal configurations of a robot, yet the representation of the whole workspace with obstacles is needed and its completeness depends on the replanning method(e.g. RRT). Nevertheless, the existing learning-based planning methods often rely on traditional search algorithms (such as RRT) or optimal control algorithms, so that they inevitably inherit the disadvantages of basic algorithms. In addition, a large amount of sample data is needed, and sampling efficiency needs to be improved urgently. There is still a need to balance exploration and utilization to obtain better performance.

In recent years, owing to the amazing performance of various robot controllers or planners based on Deep Reinforcement Learning (Deep-RL) as described in [22,23,24,25,26], many researchers turn to Deep-RL which shows excellent prospects for solving path planning problems in high-dimensional continuous state and action spaces. At the same time, deep reinforcement learning itself has also received more attention from researchers [27,28,29]. Xue et al. [30] proposed an obstacle avoidance path planning method based on a Deep-RL algorithm applied in discretized actions, they introduced sub-goals to guide the mobile robot to the final goal. In [31] a continuous action space Deep-RL algorithm was used for navigation of a mobile robot in simulated environments and the authors believe that the continuous Deep-RL algorithm is an effective collision-free decision-maker for a mobile vehicle.

Compared with the mobile robots, a welding manipulator with high-dimension continuous action space seems to be not that easy to handle by Deep-RL algorithms directly due to the tremendous exploration space and the sampling inefficiency. The exploration–exploitation trade-off is at the heart of reinforcement learning which restricts the convergence of the algorithm thus the balance of exploration and exploitation must be considered when doing path planning using Deep-RL. In [32] a dynamic obstacle avoidance approach for robot manipulator base on a continuous Deep-RL algorithm [33] was proposed and a well-designed reward function was presented to avoid the sparse reward and increase useful exploitation. In Sangiovanni et al. [34], presented a hybrid control method that combines the Deep-RL policy and the PRM policy (i.e. a sampling-based method) to achieve collision-free path planning for anthropomorphic robot manipulators. Hua et al. [35] proposed a path planner for a redundant robot in a narrow duct based on the Deep Deterministic Policy Gradient (DDPG) algorithm [36], this method reduces the exploration space by decoupling the self-motion from the motion for obstacle avoidance; however, the manipulator must be redundant. It can be seen from the related work above that most scholars try to improve the convergence performance of reinforcement learning by adopting models which is inherent in the environment. This is indeed an area worth continuing to study. Aside from reinforcement learning itself, it is possible to mine information from the environment so that the agent could have a certain innate wisdom.

In this paper, we propose an informed learning-based path planner for a 6-DOF welding manipulator in the semi-closed and narrow environment which is common in real welding scenarios, see in Fig. 1. The model-free Deep-RL algorithm DDPG is adopted to train an agent that is able to navigate the welding manipulator in configuration space so that the welding torch can reach the target position in the workspace finally without any collision on the path. For the purpose of speeding up the convergence, we provide the agent the informed knowledge by introducing the inverse kinematics of the welding manipulator. To avoid the agent’s excessive exploitation due to the prior knowledge and encourage exploration for obstacle avoidance, we introduce a hybrid method of Deep-RL and inverse kinematics of robot manipulator which will be discussed later in detail. The main contributes of this paper are as follows:

  • A well-designed interactive environment with high fidelity in simulation scenario is developed. Our modeling method provides a new physical modeling solution based on CoppeliaSim as a substitute for gym or mujoco for Deep-RL algorithms.

  • We utilize the inverse kinematics based action as the prior knowledge to reduce the unnecessary exploration in the state-action space thus the learning speed is accelerated.

  • To avoid excessive exploitation caused by the presence of prior knowledge based on inverse kinematics, the effect of the inverse kinematics based action is adjusted dynamically by introducing the gain module.

  • We design a method for accelerating deep reinforcement learning training process by combining a inverse kinematics module, which provides researchers with a new idea that is different from improving the deep reinforcement learning algorithm itself.

Fig. 1
figure 1

The considered 6-DOF welding manipulator in the semi-closed and narrow environment simulated in a robot simulation platform CoppeliaSim

Full size image

The rest of this paper is structured as follows. The theoretical background is introduced in the next section followed by our modified method in the subsequent section. Then we demonstrate the relevant elegant performance of the proposed method with several experiment results. At last, we provides the conclusion.

Background

In this section, we give an overview of the background theories for the proposed Deep-RL-based collision-free path planner, including the kinematics modeling of a welding manipulator used in this research, the Sequential Decision-Making model, and the model-free Deep-RL algorithm: DDPG.

Kinematics modeling

The kinematics of a manipulator mainly studies the displacement relationship, velocity relationship, and acceleration relationship between different links or joints. In this research, we should model the kinematics of the used six-DOF welding manipulator as shown in Fig. 1. Denavit–Hartenberg (D–H) [37] representation has been widely used in kinematic modeling and analysis of series manipulator and has become the standard method for modeling kinematics. Therefore, the detailed standard D–H parameters are shown in Table 1. Using the D–H parameters, the Homogeneous Transformation Matrix (HTM) of the last link relative to the base link can be obtained as

(1)

where the \({\varvec{q}}=\left[ q_1,q_2,\ldots ,q_6\right] \in {\mathbb {R}}^6\) is the joint angle variable drawn from the Configuration Space (C-space), represents the HTM of ith link relative to the one of the previous links denoted as follows:

(2)

The last link is usually called an end flange, and an end-effector with a reference frame is fixed on it, e.g., a welding torch. In practice, the task is executed by the end-effector in Cartesian space, and the end-effector’s HTM refer to the base link can be computed by , for simplicity, both sides of the equation can be written as

$$\begin{aligned} {\varvec{x}}_e={\mathrm {fkine}}({\varvec{q}}), \end{aligned}$$
(3)

where \({\varvec{x}}_e=[{\varvec{p}}_e \ \varvec{\phi }_e]^T\in {\mathbb {R}}^6 \) is a pose, with \({\varvec{p}}_e\) being the three-dimensional position and \( \varvec{\phi }_e\) the orientation (e.g. Euler angles) in the Cartesian space.

Table 1 Standard D–H parameters of the used welding manipulator
Full size table

Most of the motion specified by the task is defined in Cartesian space, thus it is inevitable to map the end-effector’s Cartesian motion to the motion in joints in C-space. In robotics, given the end-effector’s Cartesian velocity \(\dot{{\varvec{x}}}_e\) relative to itself, the corresponding velocity of joints’ angles \(\dot{{\varvec{q}}}\) is as follows:

$$\begin{aligned} \dot{{\varvec{q}}} = J({\varvec{q}})^{\dagger }\dot{{\varvec{x}}}_e, \end{aligned}$$
(4)

where \(J({\varvec{q}})\) is a \(6\times {6}\) Jacobian matrix for a 6-DOF manipulator, and it can be a known matrix once the joint position \({\varvec{q}}\) is given [38]. It is worth noting that the pseudo-inverse of the matrix \(J({\varvec{q}})^{\dagger }\) is computed due to the existence of singularity.

The inverse kinematics (IK) problem of manipulator is to find a correct and proper joint configuration \({\varvec{q}}\) drawn from the C-space which satisfies the equation \({\varvec{x}}_e^* ={\mathrm {fkine}}({\varvec{q}})\), the term \({\varvec{x}}_e^*\) represents the target pose of end-effector.

figure a

In general, the traditional solutions to the inverse kinematics problem include closed-form solutions and numerical solutions. The closed-form solutions consist of algebraic and geometric methods, they solve the problem faster than numerical solutions yet they depend on the model of manipulator and lack generalization ability. On the other hand, the numerical solutions do not rely on the model of manipulator which mainly refer to iterative methods.

Among all of the iterative methods, the algorithm based on the Pseudo Inverse of the Jacobian matrix [39] and the one based on Damped Least-Squares(DLS) [40] are most popular, both of them can converge to an optimal or approximately optimal solution \({\varvec{q}}^*\) based on an initial guess \({\varvec{q}}_{\mathrm{init}}\). Unfortunately, sometimes these methods may not converge to a definite solution due to the presence of singularity or the initial guess is not proper enough. From the perspective of optimization theory, the Pseudo Inverse method is faster than the DLS method and can be implemented readily in practice.

In this research, the pseudo-inverse-based method (see in Algorithm 1) is considered to find a iteration direction in the C-space which minimizes the error between \({\varvec{x}}_e^*\) and current pose \({\varvec{x}}_e\). In Line 4, we use the difference of pose \(\varDelta {\varvec{x}}_e\) instead of the velocity \(\dot{{\varvec{x}}}_e\) in Eq. 4, and then \(\dot{{\varvec{q}}}_{\mathrm{inv}}\) is obtained in Line 5. The \(\varDelta {\varvec{x}}_e\) is computed as follows:

$$\begin{aligned} {\varvec{x}}_e\ominus {\varvec{x}}_e^*\doteq \left[ \begin{array}{l} {\varvec{p}}_e^*-{\varvec{p}}_e\\ \mathrm {vex}\left( {\varvec{R}}_e^*{\varvec{R}}_e^{T}-{\varvec{I}}_{3\times 3}\right) \\ \end{array}\right] , \end{aligned}$$
(5)

where the \({\varvec{R}}_e\in {\mathbb {R}}^{3\times 3}\) is the rotation matrix form of the orientation vector \(\varvec{\phi }_e\). The function \(\mathrm {vex}(\cdot )\) can be seen in [41] which aims to compute the increment of \({\varvec{R}}_e^*\) relative to \({\varvec{R}}_e\).

The Markov decision process

In a wide sense of the word, Reinforcement Learning (RL) solves the sequential decision problems by finding the decision sequence which maximizes the expected cumulative return. A Markov Decision Process (MDP) is a typical model of sequential decision problem which is described by a tuple \(({\mathcal {S}},{\mathcal {A}},\pi ,{\mathcal {P}},r,\gamma ,H)\). In this tuple, \({\mathcal {S}}\) is a complete set of all existing states, \({\mathcal {A}}\) is a set of all actions, both of them can be discrete or continuous. The policy \(\pi \) can be divided into a stochastic one \(a\sim \pi (\cdot |s)\) and a deterministic one \(a=\mu (s)\), where \(a\in {\mathcal {A}}\), \(s\in {\mathcal {S}}\). The state transition probability function \({\mathcal {P}}: {\mathcal {S}}\times {\mathcal {A}}\times {\mathcal {S}}\rightarrow [0,1]\) denotes the dynamics of the environment: the probability of reaching \(s_{t+1}\) after taking action \(a_t\) at the environment state \(s_t\). In some cases, the state transition function can be deterministic.

Fig. 2
figure 2

The interaction between the agent and the environment [42]

Full size image

The reward function \(r=R(s_t,a_t)\), which is a scalar obtained from the environment when taking action \(a_t\) at observing a state \(s_t\), implies the goal of a RL problem. Until now, we can use the MDP and \(\pi \) to generate sequence as follows:

$$\begin{aligned} s_0,a_0,r_0,s_1,a_1,r_1,s_2,\ldots ,s_{H-1},a_{H-1},r_{H-1},s_{H}, \end{aligned}$$

where \(H\in {\mathbb {N}}^+\) is a time or step horizon of an episode. It is also called a trajectory which is generated by the interaction between the agent and the environment, see in Fig. 2. The agent mainly plays the role of a policy \(\pi \) while the environment define the state transition model and output the reward signal.

The discounted return at time step t is defined as follows:

$$\begin{aligned} G_t\doteq \sum _{k=0}^{H-t-1}\gamma ^kR\left( s_{t+k},a_{t+k}\right) , 0 \le t < H, \end{aligned}$$
(6)

where the term \(\gamma \in [0,1]\) denotes the discount factor. To evaluate the performance of the policy \(\pi \), we can compute the expectation of the total reward in one episode:

$$\begin{aligned} J_\pi ={\varvec{E}}_\pi \left[ \sum _{t=0}^{H-1}\gamma ^tR\left( s_t,\pi (\cdot |s_t)\right) \right] , \end{aligned}$$
(7)

where the policy and the environment models are stochastic.

In general, the RL algorithms aim to find the optimal or asymptotically optimal policy \(\pi _\theta ^*(\cdot |s)\) with parameters \(\theta \). In recent years, scholars use deep neural networks (DNN) to represent the parameters of policy and therefore the iteration of policy is carried out by training the policy network weights. This method is called Deep Reinforcement Learning (Deep-RL) which interests more and more researchers all over the world from different domains [43] such as robotics.

Deep deterministic policy gradient

In this subsection, we focus on one of the state-of-the-art Deep-RL algorithm: deep deterministic policy gradient algorithm (DDPG) which was proposed in [36] and it is shown in Algorithm 2. This algorithm is suitable for training an agent or policy to control a robot such as a 6-DOF welding manipulator to accomplish a specify task with position or torque, because its policy can output an action that is high dimensional and continuous.

figure b

The motivation of DDPG is actually to allow Deep Q-learning Network [44] to expand to continuous action domain with a deterministic actor. Like the algorithm DQN, a pioneering work that combines reinforcement learning and the deep learning, DDPG trains an action-value function network \(Q^\pi (s,a)\) to approximate the Bellman function:

$$\begin{aligned} Q^\pi (s_t,a_t)={\mathbb {E}}_\pi \left[ G_t|s_t,a_t\right] , \end{aligned}$$
(8)

where the deterministic policy \(\pi \) is \(a = \mu (s)\) which maps the current state to a specific action. The action-value function network is trained by minimize the loss function:

$$\begin{aligned} L(\theta ^Q)={\mathbb {E}}\left[ \left( Q\left( s_t,a_t|\theta ^Q\right) -y_t\right) ^2\right] , \end{aligned}$$
(9)

where the label \(y_t\) is given by

$$\begin{aligned} y_t= R(s_t,a_t)+\gamma Q\left( s_{t+1},\mu \left( s_{t+1}\left| {\bar{\theta }}^\mu \right) \right| {\bar{\theta }}^Q\right) \end{aligned}$$
(10)

in which the action-value network \(Q\left( s,a|{\bar{\theta }}^Q\right) \) and the policy network \(\mu \left( s|{\bar{\theta }}^\mu \right) \) represents the target network, respectively. The purpose of introducing target network is to make the training process more stable.

On the other hand, the DDPG algorithm utilize the actor-critic framework-based DPG algorithm [45] to maintain the policy \(\mu (s)\), and in this framework, the action-value network is called critic network while the policy network is called actor network. The deterministic policy gradient is proved to be as follows:

$$\begin{aligned} \nabla _{\theta ^\mu }J={\mathbb {E}}\left[ \nabla _{a}Q\left( s,a|\theta ^Q\right) |_ {s=s_t,a=\mu (s_t)}\nabla _{\theta ^\mu }\mu \left( s|\theta ^\mu \right) |_{s=s_t}\right] \nonumber \\ \end{aligned}$$
(11)

which represents the performance of the actor network, we can update the actor network using this equation.

An experience replay buffer which is designed for off-policy updating denoted as \({\mathcal {R}}\) is used to store the transition tuple (\(s_t,a_t,r_t,s_{t+1}\)) see in Algorithm 2 Line 11. The predicted network \(\theta ^\mu \) and \(\theta ^Q\) are updated using Eqs. 11 and 9, respectively, with the sampled minibatch experience replay transitions. To train the target network more stably, a soft update technic as Algorithm 2 Line 16 shows is employed.

Due to the determinacy, the actor may coverage to a local optimum, and this is harmful to the agent to explore for higher reward in the environment. Thus, in Algorithm 2 Line 8, a stochastic process noise, Ornstein–Uhlenbeck, is added to the actor’s action to enhance exploration and protect the robot in the environment at the same time.

Methodology

In this section, we introduce in detail the hybrid collision-free path planning method of Deep-RL and inverse kinematics for the 6-DOF welding manipulator.

The interaction environment

To solve the path planning problem with the Deep-RL framework, we must convert the primal problem to a sequential decision problem, namely the Markov decision process (MDP). To this end, we need to define the interface between the agent and the environment in Fig. 2.

Fig. 3
figure 3

This is the schematic diagram of our method. In this diagram, apart from the DDPG learning framework, we add an Inverse kinematics module in series with a gain module. The Update1 represents the update of the network Q(s, a) and the Update2 represents the update of the network \(\mu (s)\)

Full size image

State space

In the real world, the state set may be extremely massive or even infinite, so enumerating all the states is unrealistic. In practice, we usually select some important characteristics as the state information. It should be noted that the state information of Deep-RL represents the environmental information perceived by the agent and implies the influence brought about by the actions of that agent. State information is the basis for the agent to make decisions and evaluate its long-term benefits, namely accumulative reward, and the quality of the state design directly determines the convergence, convergence speed, and final performance of the Deep-RL algorithm.

Task analysis is the soul of state design. In this research, the goal of the collision-free path planning task is to train an agent that drives the joints of the welding manipulator without any collision to minimize the distance between the end-effector of the welding manipulator and its target position. In the light of the given task, the state observed from the environment at time step t is designed as a stacked vector:

$$\begin{aligned} \varvec{s_t}=\left[ {\varvec{q}},{\varvec{p}}_e,d_{\mathrm{tar}}, \mathrm{collision} \right] \in {\mathcal {S}}, \end{aligned}$$
(12)

where \({\varvec{q}}\in {\mathbb {R}}^6\) is the joint position of the welding manipulator, and \({\varvec{p}}_e\in {\mathbb {R}}^3\) is the end-effector reference frame’s Cartesian position relative to the target frame. The scalar \(d_{\mathrm{tar}}\) denotes the Euclidean distance between the end-effector reference frame’s origin and the origin of the target frame. The last element collision is a Boolean that indicates whether the collision occurs between the links of the welding manipulator and obstacles in the environment, it can be obtained by the CoppeliaSim API function. It is obvious that the dimension of the state vector is

$$\begin{aligned} \mathbf {dim}(\varvec{s_t})=\mathbf {dim}({\varvec{q}}) +\mathbf {dim}({\varvec{p}}_e)+2, \end{aligned}$$
(13)

where \(\mathbf {dim}(\cdot )\) means the dimension of a vector.

Action space

When applying Deep-RL algorithm to an actual problem, perhaps the most intuitive part is the definition of the action space \({\mathcal {A}}\). In this research, the actor in the environment is a 6-DOF welding manipulator; thus, the control method of the agent for the manipulator can be velocity control mode intuitively as follows:

$$\begin{aligned} \varvec{a_t} = \dot{{\varvec{q}}}\in {\mathcal {A}}, \end{aligned}$$
(14)

where \(\dot{{\varvec{q}}}\in {\mathbb {R}}^6\) is the target angular velocity within the limitation of each rotation joint driven by a servo motor. The dimension of the action space is

$$\begin{aligned} \mathbf {dim}(\varvec{a_t})=6 \end{aligned}$$
(15)

Reward signal

Contrary to the definition of action space mentioned aforehand, the reward signal, which implies the goal of the specified problem, determines whether the agent can finally learn the desired skills, and directly affects the convergence speed and final performance of the algorithm as the state space does. After considering our problem, we define the reward signal consists three parts.

The first part is designed for the end-effector approaching a specific target position. We utilize a nonlinear piecewise function to compute this part of the reward:

$$\begin{aligned} r_1= {\left\{ \begin{array}{ll} -\frac{1}{2}d_{\mathrm{tar}}^2&{} d_{\mathrm{tar}}\le \delta \\ -\delta \left( \left| d_{\mathrm{tar}}\right| -\frac{1}{2}\delta \right) &{} d_{\mathrm{tar}}>\delta , \end{array}\right. } \end{aligned}$$
(16)

where \(d_{\mathrm{tar}}\) is the Euclidean distance between the end-effector and its target position, the parameter \(\delta \) is the turning point of the function. The popular explanation for \(r_1\) is the longer the distance \(d_{\mathrm{tar}}\), the smaller the reward.

The second part is designed for the purpose of avoiding collision, so in this part, we give a large penalty according to the current collision condition.

$$\begin{aligned} r_2= {\left\{ \begin{array}{ll} -C_\mathrm{o} &{} \text {if }\mathrm{collision} \\ 0 &{} \text {otherwise} \end{array}\right. } , \end{aligned}$$
(17)

where \(C_\mathrm{o}\in {\mathbb {R}}^+\) is a constant by which we can regulate the penalty. The collision state collision is a Boolean as mentioned in Eq. 12.

The third part is relative to the norm of the current action \(\dot{{\varvec{q}}}\) as shown in Eq. 18, that means we expect the agent to take smaller actions for safety.

$$\begin{aligned} r_3 = -\left\| \dot{{\varvec{q}}}\right\| ^2 . \end{aligned}$$
(18)

Finally, we can construct the total reward signal as follows:

$$\begin{aligned} r_t\left( \varvec{s_t},\varvec{a_t}\right) = \lambda _1r_1+\lambda _2r_2+\lambda _3r_3\in {\mathbb {R}}, \end{aligned}$$
(19)

where \(\lambda _i\in {\mathbb {R}}^+\) denotes the constant scaling factor which is designed to make the contribution of each reward component to the final reward at a close level, so that each target reward can be taken into account by the agent to the same extent.

The training process

Although the Deep-RL algorithm DDPG as shown in Algorithm 2 has achieved elegant results on many robotic operation tasks in Mujoco environment such as reacherObstacle in which the agent is required to move a 5-DOF manipulator to the target position without collision, the complexity of learning mapping relationship between state space \({\mathcal {S}}\) and action space \({\mathcal {A}}\) in the path planning problem is so high that it requires amazing training time steps and even millions of steps are commonplace.

To be honest, training a policy model for a path planning problem from scratch using the DDPG algorithm is irrational. Thus, in this paper, we aim to speed up the DDPG training process for the collision-free path planning problem via a hybrid method of DDPG and inverse kinematics of the welding manipulator as shown in Fig. 3.

The path planning problem for a welding manipulator actually contains two sub-problems, one is moving the end-effector to its target position while the other is avoiding collision during the moving process. If the collision avoidance is not in consideration, moving the end-effector to its target position can be solved by a sequential dynamic model shown in Eq. 20.

$$\begin{aligned} {\varvec{q}}_{t+1}={\varvec{q}}_t+\dot{{\varvec{q}}}_{\mathrm{inv}}\cdot \text {d}t, \end{aligned}$$
(20)

where \(\text {dt}\) is the sampling period, \(\dot{{\varvec{q}}}_{\mathrm{inv}}\) is obtained as Line 5, Algorithm 1 shows.

Due to the presence of obstacles, we need to correct the \(\dot{{\varvec{q}}}_{\mathrm{inv}}\) generated by the inverse kinematics module to avoid collision. To this end, we might as well use the action \(\varvec{a_t}\) selected by the policy network of DDPG to share the task of avoiding obstacles as Eq. 21 shows.

$$\begin{aligned} {\varvec{q}}_{t+1}={\varvec{q}}_t +(\dot{{\varvec{q}}}_{inv}+\varvec{a_t})\cdot \text {dt}. \end{aligned}$$
(21)

In this way, there is no need for the DDPG agent to learn from scratch since the inverse kinematics module will constraint the search space between the start and goal region as well as guide the welding manipulator move to the target position so that the agent’s responsibility is just to correct the output of inverse kinematics module for collision avoidance. In other words, the invalid exploration which discourage the welding torch moving to the target position is lessened, thus the search space is reduced significantly which is beneficial to speed up the training process of the agent.

figure c

However, we find that when training with dynamic model Eq. 21, the excessive exploitation of the inverse kinematics module leads the agent to overlook the objective of collision avoidance and the policy converge to local a optimum. We blame this failure on the changeless usage of \(\dot{{\varvec{q}}}_{\mathrm{inv}}\) generated by the inverse kinematics module. It is the fixed \(\dot{{\varvec{q}}}_{\mathrm{inv}}\) that restricts the exploration of the agent for collision avoidance. Thus we add a time-varying gain module to encourage exploration in the early time of one episode with a relatively large growth rate and increase the exploitation in the later time by applying a lower growth rate when the manipulator ought to be near the goal position. The gain module is an increasing nonlinear function \(\ln (x)\) of time step t as shown in Eq. 22.

$$\begin{aligned} {\mathcal {G}}(t)=\ln (t+1), \end{aligned}$$
(22)

where \(t=0,\ldots ,T-1\) and the hybrid dynamic model which balances the exploitation and exploration is as follows:

$$\begin{aligned} {\varvec{q}}_{t+1}={\varvec{q}}_t+ \left( {\mathcal {G}}(t)\cdot \dot{{\varvec{q}}}_{\mathrm{inv}}+\varvec{a_t}\right) \cdot \text {d}t. \end{aligned}$$
(23)

The integral training process of our collision-free path planning method is described in Algorithm 3.

Experiments and analysis

In this section, we evaluate the performance of our proposed hybrid method through several path planning experimental results in the simulation system. We also prove the progress of our method through comparative analysis.

Experimental system description

The simulation experiment system is roughly divided into three parts. The first part is the interaction environment which mainly includes a welding manipulator with obstacle around it as shown in Fig. 1 and we model them in a well-known open-source robot simulator CoppeliaSim with high fidelity. The simulator CoppeliaSim provides remote interface functions for collision detection between specific robot entity and obstacles, thus we can determine the Boolean collision in Eq. 17 which indicates whether any collision occurs when the welding manipulator is at a certain joint angle \({\varvec{q}}\) . In general, this part, as a server application, provides an interface for the exchange of state information and action input as shown in Fig. 2. When receiving the action information, namely the joints’ angular velocity \(\dot{{\varvec{q}}}\in {\mathbb {R}}^6\) predicted by the agent, the environment server application will update the current state \(\varvec{s_t}\) of the welding manipulator as described in Eq. 12 to its transition state \(\varvec{s_{t+1}}\), and the joints’ angle is updated with Eq. 23, where \( \text {d}t \) is set to 0.05 in second. To make the simulation closer to the real situation, we must constraint the action \(\varvec{a_t}\) or \(\dot{{\varvec{q}}}\) in a bounded range: \(\dot{{\varvec{q}}}_{\text {min}}\le \dot{{\varvec{q}}}\le \dot{{\varvec{q}}}_{\text {max}} \). In the meanwhile the joint angle \( {\varvec{q}} \) should meet the joint limit requirements which are very crucial to the safety of the welding manipulator, otherwise, the links of the welding manipulator may collide with each other.

After the update of the state, the acquisition of the instant reward signal instead of a sparse one is pivotal. The constant parameters which formulate the reward signal are instantiated as follows: the \(\delta \) in Eq. 16 is set to 0.05, the \(C_\mathrm{o}\) in Eq. 17 is set to 200, the \(\lambda _i\) in Eq. 19 set to \(\lambda _1=2000, \lambda _2=1, \lambda _3=1 \), respectively. It needs to be pointed out that these parameters are carefully picked up through a large number of experiments. Different parameters will directly affect the convergence of the algorithm.

Table 2 Choice of key parameters for the DDPG agent
Full size table

The second part is the DDPG agent represented by four fully connected deep neural networks constructed by a famous deep learning framework Pytorch and their respective update method for internal neural network weights. All of those networks are trained by an Adam optimizer using a certain number (Mini-batch size M) of transitions data sampled from the replay buffer \({\mathcal {R}}\) at each time step. All of the aforementioned four networks including two actor networks and two critic networks have two hidden layers respectively. The actor networks approximate the deterministic policy function \(\varvec{a_t}=\mu (\varvec{s_t})\); thus, the dimension of the input layer equals to the state dimension \( \mathbf {dim}(\varvec{s_t})\) while the output layer equals to \( \mathbf {dim}(\varvec{a_t})\). On the other hand, the critic networks approximate the action-value function \(Q(\varvec{s_t},\varvec{a_t})\) thus the dimension of the input layer equals to the sum of the action dimension \( \mathbf {dim}(\varvec{a_t})\) and the state dimension \(\mathbf {dim}(\varvec{s_t})\) while the dimension of the output layer equals to one because the action value is a real scalar. The choice of key parameters for the DDPG agent is shown in Table 2.

The third part is the inverse kinematics module. We perform the inverse kinematics calculation according to the current position of joints \({\varvec{q}}\) to obtain \(\dot{{\varvec{q}}}_{\mathrm{inv}}\) at each time step. This part will be executed in Matlab. More specifically, we set up a pure kinematic model of the welding manipulator synchronize with the one in simulator CoppeliaSim, and the instantaneous Jacobian matrix as shown in Eq. 4 is computed at each time step which is used to obtain \(\dot{{\varvec{q}}}_{\mathrm{inv}}\).

Fig. 4
figure 4

The relation chart of the simulation system

Full size image

These three parts communicate through remote Application Programming Interface (API) or engine as shown in Fig. 4. The whole training phase is implemented on a PC (CPU 3.6 GHz, RAM 16 GB).

Fig. 5
figure 5

The learning curves of the training process for three tasks which different gain module \({\mathcal {G}}(t)\). These curves represent the convergence of different training strategies

Full size image
Fig. 6
figure 6

The path planning solutions conducted by our method for three single-query tasks rendered in CoppeliaSim. For each solution, we select some pivotal way points to express the complete safe path

Full size image

Experimental results and analysis

In various algorithms of path planning, the proposed learning-based path planning algorithm can be classified as a global and single query path planning method. To validate the effectiveness of the proposed method, we test the learning-based planner with three different path planning tasks. Each task was specified with an initial position \({\varvec{q}}_s\in {\mathbb {R}}^6\) drawn from the configuration space and a target end-effector’s Cartesian position \({\varvec{p}}_e^*\in {\mathbb {R}}^3\) relative to the welding manipulator’s reference frame.

Fig. 7
figure 7

Distance between the current end-effector’s Cartesian position and the target Cartesian position

Full size image
Fig. 8
figure 8

Cartesian position of the end-effector of the welding manipulator along the path in the workspace of the welding manipulator

Full size image
Fig. 9
figure 9

Performance comparison of our algorithm and sampling-based algorithms by three histograms, where a illustrates the success rate while b and c illustrates average path length in C-space and Cartesian space, respectively

Full size image

Performance evaluation

We evaluate the performance of our method on the three single-query test tasks from different domains. First of all, it is known that the objective of the Deep-RL algorithm is to maximize the cumulative reward in one episode with finite time steps and, therefore, it is necessary to analyze the trend of the reward curve or the learning curve vs training episode number which reflects whether the target deterministic policy model has converged as well as the learning efficiency. We show the learning curves of the three test tasks, respectively, in Fig. 5. For each specified path planning task, we train the policy model using different gain module noted as \({\mathcal {G}}(t) \). When \({\mathcal {G}}(t)=0\), it means that the inverse kinematics module is removed and the agent should learn from scratch which is abandoned in our research. To exploit the inverse kinematics module during the training phase, we need a non-zero \({\mathcal {G}}(t)\); thus, we adopt \({\mathcal {G}}(t)=\ln (t+1)\) as shown in Eq. 22. To reveal the progress of the proposed time-varying gain module, we also adopt a fixed gain module \( {\mathcal {G}}(t)=2 \) as contradistinction. After comparison, we find that different selection of gain module \({\mathcal {G}}(t)\) leads to significantly different learning curve when dealing with the same task. Our method which adopts a time-varying gain module \({\mathcal {G}}(t)=\ln (t+1)\) achieved the best performance in terms of the convergence as the red curves in Fig. 5 show. The red curves in Fig. 5a–c finally converge without exception to a near-zero level from which we can infer that the learned agents have accomplished the specified tasks in the light of our reward design mechanism. On the other hand, when \({\mathcal {G}}(t)=0\) or \({\mathcal {G}}(t)=2\), the learning curves fail to converge like the red curves do in the same range of training episodes; therefore, it can be seen that our method has significantly improved convergence performance and convergence speed which is a credit to the introduction of the proposed inverse kinematics module and gain module.

Second, we need to confirm whether the final deterministic policy model mentioned above can be used to generate a collision-free path that is a solution to the respective specified task. The collision-free path in configuration space of the welding manipulator can be obtained indirectly by way of sampling a trajectory \({\varvec{s}}_0,{\varvec{a}}_0,{\varvec{s}}_1,\ldots ,{\varvec{a}}_T,{\varvec{s}}_T\) using the final policy model and then construct the solution \(\left\{ {\varvec{q}}_i\right\} \), \(i=0,1,\ldots ,T\) from \(\left\{ {\varvec{s}}_i\right\} \) where \({\varvec{s}}_0\) is equivalent to the state when the welding manipulator is at the configuration of \({\varvec{q}}_{s}\). Consistent with the previous assumption, the policy model trained by our method described in Algorithm 3 which employs both the gain module \({\mathcal {G}}(t)=\ln (t+1)\) and inverse kinematic module can generate a unique collision-free path in the configuration space which fulfills respective task requirements. We render the path intuitively and succinctly in the simulator CoppeliaSim as Fig. 6 shows.

In addition to collision avoidance, the path should ensure that the end-effector of the welding manipulator is at its target position \({\varvec{p}}_e^*\) finally. Although all of the three models trained by different \({\mathcal {G}}(t)\) can generate a collision-free path for respective task, only the model trained by \({\mathcal {G}}(t)=\ln (t+1)\) is able to move the end-effector to its target position. To intuitively reflect the performance of the models in the control of end-effector’s position, we plot the distance between the end-effector and its target Cartesian position vs the path steps as Fig. 7 shows. It is clear that all of the red curves that represent our method eventually drop to zero or near-zero while other curves fail to drop as the red ones do, the second half of these failed curves fluctuates around a number significantly greater than zero, which shows that those learned policy fails to convergence and is trapped in local optima. On the other hand, as shown in Fig. 8, obviously, only our proposed training method can move the end-effector to its target position. However, the policy learned by other training methods (e.g. \( {\mathcal {G}}(t)=2 \) or \( {\mathcal {G}}(t)=0 \)) controls the manipulator arm to gradually move toward the non-target direction and the movement step is gradually reduced, which can also indicate that these paths fall into the local optimum. The above description indicates that only the policy trained by our method can successfully complete all given tasks including collision avoidance and moving the end-effector to its target position.

Comparison with other methods

In this paper, we introduce an alternative collision-free path planning algorithm for industry manipulators. As we all know, for the path planning problem in high-dimensional sampling space, e.g. the configuration space of industry manipulators, the sampling-based method is one of the most efficient algorithms. To demonstrate the progress of our algorithm, the three experimental path planning tasks which have been used to test our algorithm are now used to query several staple sampling-based single-query path planning algorithm, i.e. RRT-Connect [46], RRT [7], RRTStar [47], and BiTRRT [48]. We utilize the open-source motion planning library “The Open Motion Planning Library”(OMPL) [49] to implement the above planning algorithm on the three test tasks.

We select three performance indicators to evaluate the performance of different algorithms from different dimensions. The first performance indicator is the success rate for a single-query path planning task in a specified number of times and the other two indicators aim to measure path length in configuration space and workspace, namely Cartesian space. Generally speaking, the success rate of path planning means the robustness of the algorithm while the length of the planned path represents the optimality of the path. In Fig. 9, we reveal our algorithm’s performance through comparison with other algorithms.

First, since the path generated by the converged model is deterministic and successful each time, the success rate of our path planner based on the policy model is 100\(\%\). However, in line with expectations, the success rate of sampling-based planning algorithms is relatively low, and the highest success rate is only just about 70\(\%\) which is got by the RRT-Connect algorithm. This is obviously not allowed in industrial scenarios, so our algorithm has unique advantages over those sampling-based planning algorithms. Second, as we all know, from the perspective of path length, only optimal RRT algorithms such as RRTStar [47] can find the optimal or asymptotical optimal path, but they may require a huge number of samples to achieve such optimality. our algorithm achieves the same performance as BiTRRT does which is better than any other algorithms, In other words, the path generated by a well-trained policy using our method can be comparable to an optimal sampling-based path planning algorithm.

Conclusion and future work

In this research, we propose a hybrid algorithm of DDPG and Inverse kinematics as an alternative global and single-query path planning algorithm for industry welding manipulator. Simulation results in high-fidelity virtual scenario show that our improvements to the original algorithm DDPG have greatly increased its convergence performance and convergence speed and the well-trained policy model is able to generate a collision-free path for a specified task. In industry robot systems like automatic welding robot systems that require extremely high stability and safety, our algorithm may be competitive comparing with other sampling-based algorithms because the sampling-based algorithm can not guarantee 100\(\%\) success rate of planning. Furthermore, our algorithm can also produce path planning results comparable to those of optimality or progressive optimality algorithms in terms of path length. In summary, our algorithm provides an alternative solution for teaching-free automatic path planning of actual welding robots or other industrial robots.

Despite the progress of the proposed algorithm, we still have lots of future work to do. We always remember that the model-free deep reinforcement learning algorithm such as DDPG in this paper is born with the characteristics of low sample efficiency. Although we promote the sample efficiency greatly in this research, we will still go on to develop a more elegant method to accelerate the convergence of the Deep-RL algorithm for path planning. On the other hand, we also wish our algorithm can be applied to real-world robots to complete sim-to-real tasks.