A memetic discrete differential evolution algorithm for the distributed permutation flow shop scheduling problem

Abstract

The distributed manufacturing has become a prevail production mode under the economic globalization. In this article, a memetic discrete differential evolution (MDDE) algorithm is proposed to address the distributed permutation flow shop scheduling problem (DPFSP) with the minimization of the makespan. An enhanced NEH (Nawaz–Enscore–Ham) method is presented to produce potential candidate solutions and Taillard’s acceleration method is adopted to ameliorate the operational efficiency of the MDDE. A new discrete mutation strategy is introduced to promote the search efficiency of the MDDE. Four neighborhood structures, which are based on job sequence and factory assignment adjustment mechanisms, are introduced to prevent the candidates from falling the local optimum during the search process. A neighborhood search mechanism is selected adaptively through a knowledge-based strategy which focuses on the adaptive evaluation for the neighborhood selection. The optimal combinations of parameters in the MDDE algorithm are testified by the design of experiment. The computational results and comparisons demonstrated the effectiveness of the MDDE algorithm for solving the DPFSP.

Introduction

In the context of globalization, intelligent manufacturing has become a common production mode. With the increasing cooperation between factories, distributed manufacturing systems have been widely applied [1, 2]. The distributed scheduling contributes to reduce the management risk and improve the efficiency of transportation [3, 4]. Among various types of scheduling problems, the flow shop scheduling problem has attracted widespread attention from researchers [5, 6]. The permutation flow shop scheduling problem (PFSP) is one of the classic combinatorial optimization problems, which has been proved as an NP-hard problem [7, 8]. Due to its importance in engineering applications and academic, certain methods have been proposed to solve the PFSP [9, 10].

Fig. 1

The production model in distributed environment

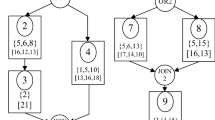
The distributed permutation flow shop scheduling problem (DPFSP) is a generalization of classical permutation flow shop scheduling problem, which is used to fill the gap between practical application and academic research [5, 11], as shown in Fig. 1. The DPFSP is expressed as $\mathrm{{DP}}/\mathrm{{prmu}}/C_{max}$ , where DP represents the distributed factory; prmu represents permutation features, and $C_{max}$ represents the target is to minimize the maximum completion time. In the DPFSP, there are F factories with the same m machines. In addition to the constraints of PFSP, DPFSP also stipulates that once a job is assigned to a factory, it is not allowed to be re-distributed. The processing times of the jobs do not differ between factories [12, 13]. This additional dimension minimizes the maximum global makespan of Ffactories to determine the jobs that should be assigned to each factory. Therefore, from the specific situation of $F=1$ in [14], DPFSP is a typical PFSP problem. For DPFSP, several integer linear programming models and two factory assignment methods based on dispatching rules were proposed by Naderi [11]. Recently, several meta-heuristics have been developed to solve the DPFSP, including Iterated Greedy Algorithm (IG) [15, 16], Estimation of Distributed Algorithm (EDA) [1], Discrete Artificial Bee Colony (ABC) and Iterated Local Search Algorithm (ILS) [13]. Differential Evolution Algorithms have rarely been studied to solve the DPFSP.

Differential evolution (DE) algorithm [17] is an intelligent optimization algorithm, including three critical components, mutation, crossover, and selection. In DE, three operations are repeated after population initialization until the termination condition is satisfied. The convergence result of DE is mainly determined by the mutation operation and the crossover operation [18, 19]. To improve the performance of DE, researchers have proposed a series of improvement measures from the aspects of mutation strategy, population size, parameter design and fusion of other algorithms.

In terms of mutation strategy, Zhang and Sanderson [20] proposed a new mutation strategy “$\mathrm{{DE}}$/current-to-pbest ” to update the scale factor in an adaptive way to enhance the optimization performance (JADE). The jSO [21] is a variant of iL-SHADE algorithm [22] and it is the winner algorithm in the CEC2017 benchmark. In the jSO, a mutation strategy named “$\mathrm{{DE}}$/current-to-pBest-w/1” is proposed. For the size of the population, Tanabe and Fukunaga proposed an adaptive algorithm (LSHADE) [23], which is based on linear population size reduction (LPSR). In LSHADE, the LPSR rule is applied to save expensive evaluations. For the parameters, Mohamed, Hadi, Fattouh and Jambi proposed LSHADE-SPACMA [24], which adopted a semi-parametric adaptive method based on randomization and self-adaptation. Furthermore, a hybridization framework is introduced between the modified versions of LSHADE-SPA and the Covariance Matrix Adaptation Evolution Strategy (CMA-ES). In recent years, DE has been fused with other algorithms to improve its performance. The search mechanism of DE is introduced into the Biogeography-Based Optimization algorithm (BBO) to improve the anti-rotation of the algorithm (TDBBO) [25]. The simulation results of TDBBO based on the CEC2017 benchmark test suit show that TDBBO has better accuracy and convergence speed than the most advanced BBO. In the Gravitational Search Algorithm (GSA), the crossover and mutation operations of DE are used to realize the diversity of population, which is named SGSADE [26].

DE and its variant algorithms have been widely used in production scheduling problems. The IDESAA algorithm which was integrated with the simulated annealing (SA) and DE was proposed by Xiuli and Xiajing [27] to solve the distributed flexible job-shop scheduling problem. A hybrid DE algorithm based on set model (eEDA) with distribution estimation algorithm is proposed by Zhou et al. [28] to solve the scheduling problem of reentrant hybrid flow shop. A discrete differential evolution (DDE) algorithm was designed by Zhang et al. [29] to solve the distributed blocking flow-shop scheduling. In the following research work, the author designed a CDE algorithm based on DDE to solve the distributed limited-buffer flow shop scheduling problem [30]. Wang et al. [31] proposed a novel hybrid discrete differential evolution (HDDE) algorithm for solving the blocking flow-shop scheduling problem. In HDDE, the permutations between jobs are discrete, thus the algorithm is directly operated in the discrete domain. Furthermore, a local search strategy based on the inserted neighborhood structure is introduced into the algorithm to enhance the ability of local search.

Inspired by the framework of MDDE, the MDDE is proposed to address the DPFSP. The search operator of the general heuristic is randomly searched during the prime search process, which leads to the phenomenon of undesirable search efficiency. In general, the effectiveness in the search process is promoted by the previously acquired prior knowledge. An effective method of decomposition and coordination is formed by cooperative optimization. First, a constructive method named DNEH+T is used to create initial population for the MDDE. Second, a discrete mutation strategy is proposed to generate new solutions. Finally, four neighborhood search mechanisms and local search strategies are embedded in the MDDE to further improve the quality of solutions. Meanwhile, an appropriate neighborhood search mechanism is adaptively selected by a knowledge-based optimization strategy and is applied to promote the global search capacity of the MDDE.

The effectiveness of the four integration strategies in the MDDE are demonstrated by the experimental results. The contributions in this study are summarized as follows.

• An improved NEH method is designed to generate potential candidate solution and the Taillard’s acceleration method is adopted to ameliorate the efficiency of the insertion process for jobs.

• A new discrete mutation strategy is proposed for MDDE algorithm to ameliorate the exploration ability. In the discrete mutation strategy, the best solution information is used to balance the diversity of population and the greediness of mutation.

• Four neighborhood structures based on job sequence and factory assignment adjustment mechanisms are designed to enhanced the search around the current best candidate solution. Furthermore, an appropriate neighborhood search mechanism is adaptively selected by a knowledge-based optimization strategy.

The structure of this study is as follows. The definition and details of DPFSP and the traditional DE are introduced in “Background”. The proposed MDDE algorithm are introduced in “MDDE for DPFSP with minimizing makespan”. The related experimental analysis and discussion are in “The experiments and comparisons”. The conclusion and future works are suggested in “Conclusions and future research”.

Background

The distributed permutation flow shop scheduling problem

According to the literature [32], the DPFSP is described as follows. A set of jobs J is processed in F factories, where $J={j_1,j_2,\ldots ,j_n}$ and $F={f_1,f_2,\ldots ,f_l}$ . Each factory includes an identical flow shop with M machines, $M={m_1,m_2,\ldots ,m_m}$. In each factory, the operation of jobs j on machine i is denoted as $O_{ij}$. One job is processed on the only one machine at a time and each job has to go through all the machines in the factory to which it is assigned. In addition, each operation is not interrupted once it started. The setting time of the machine and the transmission time between operations are not considered. The notations in this study are shown as follows.

i	Index for machines where $i=1,2,\ldots ,m$
$\omega$	The scaling factor
j	Index for jobs where $j=1,2,\ldots ,n$
F	The number of factories
f	Index for factories where $f=1,2,\ldots ,l$
Cr	Crossover rate
n	The number of jobs
NP	The population size
m	The number of machines
$P_{1}$	Neighborhood search random value
$P_{j,i}$	The processing time of operation $O_(j,i)$ on machine $M_i$
Avg	The average
$I_{i,k,f}$	The idle time
$W_{i,k,f}$	Indicates the completion time of the job in position k on machine i in factory f
$X_{j,k,f}$	Binary variable that takes values 1 if job j occupies position k in factory f , and 0 otherwise

In this study, the purpose is to minimize the maximum completion time (completion time) with the sequence of jobs in the assigned factory. DPFSP detailed mixed-integer programming model is shown in the literature of Naderi and Ruiz [11]. Therefore, the maximum completion time minimization is calculated as follows.

$$\begin{aligned}&\mathrm{{min}} C_{max} \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{k=1}^{n}\sum _{f=1}^{F}X_(j,k,f) =1, \forall _{j} \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{j=1}^{n}\sum _{f=1}^{F}X_(j,k,f) =1, \forall _{k} \end{aligned}$$

(3)

$$\begin{aligned}&I_{i,k,f}+\sum _{j=1}^{n}\cdot P_{j,i}+W_{i,k+1,f}-W_{i,k,f}\nonumber \\&\quad -\sum _{j=1}^{n}X_(j,k,f)\cdot P_{j,i+1}- I_{i+1,k,f}=0, \forall _{k<n,i<m,f} \end{aligned}$$

(4)

$$\begin{aligned} C_{f}= & {} \sum _{i=1}^{m-1}\sum _{j=1}^{n}X_(j,1,f)\cdot P_{j,i} +\sum _{k=1}^{n-1}I_(m,k,f)\nonumber \\&+\sum _{j=1}^{n}\sum _{k=1}^{n}X_(j,k,f)\cdot P_{j,m} ,\forall _{f} \end{aligned}$$

(5)

$$\begin{aligned}&C_{max} \ge C_{f}, \forall _{f} \end{aligned}$$

(6)

$$\begin{aligned}&I_{i,k,f} \ge 0, \forall _{i,k<n,f} \end{aligned}$$

(7)

$$\begin{aligned}&W_{i,k,f} \ge 0, \forall _{k,i<m,f} \end{aligned}$$

(8)

$$\begin{aligned}&X_{j,k,f} \in \{0,1\} ,\forall _{j,k,f} \end{aligned}$$

(9)

The constraint set (2) ensures that each job is assigned to only one location in a factory. All n positions that must occupy nF are indicated in the constraint set (3). The constraint set (4) is expressed as the idle time of the machine i after the job execution is completed at the position k of the factory f and before the job processing is started at the position $k+1$, where $k\le n$. The completion time of different factories is expressed in the constraint set (5), while the completion time of the entire problem is represented by the constraint set (6). Constraint sets (7)–(9) define the decision variables. The constraint sets (7) and (8) ensure that the completion time of each job and the machine idle time before the next job which is processed are non-negative.

Compared with traditional single factory scheduling problem, scheduling problem in distributed factory is more complex. n jobs need to be assigned to F suitable factories. The possible combination for assigning jobs to factory $f_{1}$ is $\left( {\begin{array}{c}n\\ f_{1}\end{array}}\right)$ and there are $f_{1}!$ sequences in each of the combinations. $f_{h}$ represents the number of jobs assigned to factory h.The result of n jobs assigned to F factories is $\left( {\begin{array}{c}n\\ f_{1}\end{array}}\right) f_{1}! \times \left( {\begin{array}{c}n-f_{2}\\ f_{2}\end{array}}\right) f_{2}! \times \cdots \times \left( {\begin{array}{c}n-\sum _{h=1}^{F-1}{f_{h}}\\ f_{F}\end{array}}\right) f_{F}!$ . The result of the problem is n!.

In addition, there are different ways to assign n jobs to F different factories. The number of these methods is $\left( {\begin{array}{c}n+F-1\\ F-1\end{array}}\right)$.

So, the complexity of the DPFSP is $\left( {\begin{array}{c}n+F-1\\ F-1\end{array}}\right) n!$.

Fig. 2

The example of DPFSP

• Factory 1: The maximum completion time $C_{max}$ of the job sequence 1, 2, 3 is 41.

• Factory 2: The maximum completion time $C_{max}$ of the job sequence 4, 5, 6 is 37. So, the maximum completion time in the example is 41.

When the number of jobs is 6 and the number of factories is 2, the DPFSP problem complexity is 5040.

$$\begin{aligned} f_{(1)}(6,2)= \left( \begin{array}{c} 6+2-1 \\ 2-1 \\ \end{array} \right) 6! = \left( \begin{array}{c} 7 \\ 1 \\ \end{array} \right) 6!=7*720=5040 \end{aligned}$$

Brief introduction to DE algorithm

Traditional DE algorithm is an intelligent metaheuristic method introduced by Storn and Price [17]. The convergence result of DE is mainly determined by the mutation operator and the crossover operator. Starting from the random initialization of individuals in the population, it creates new candidate solutions by mutation strategy and crossover operator, and then the selection operators are used to determine the next generation of target individuals. Furthermore, the control parameters of DE play an important role in balancing the convergence speed of the algorithm and diversity of population, such as population size NP, scaling factor $\omega$, crossover rate Cr. The basic DE algorithm process is procedure as follows.

• Step 1: Initialization phase. The algorithm randomly generates NP particles to form the initial population and set the parameters.

• Step 2: Mutation phase. Mutation vector $\mathbf {v} _{i,g}$ is created in DE using the “$\mathrm{{DE}}/rand/1$” mutation strategy. Two vectors are randomly selected in “$\mathrm{{DE}}/rand/1$”. The difference of the two vectors is multiplied by the scaling factor $\omega$ and added to a third randomly selected vector as follows.

  $$\begin{aligned} \mathbf {v}_{i,j} = \mathbf {x}_{r_{1},j}+\omega \cdot (\mathbf {v}_{r_{2},j}-\mathbf {v}_{r_{3},j} ), r_{1} \ne r_{2} \ne r_{3} \ne i \end{aligned}$$

  (10)

  where $r_{1}$, $r_{2}$, and $r_{3}$ are different from each other and randomly selected indexes of the [1, NP] .

• Step 3: Crossover phase. The mutation vector $\mathbf {v} _{i,g}^{g}$ generated by the mutation operation is used for crossover operation to generate a trial vector $\mathbf {u} _{i,g}^{g}$.

  $$\begin{aligned} \mathbf {u}_{i,j}^{g}=\left\{ \begin{array}{l} \mathbf {v}_{i,j}^{g}, \mathrm{{if}}(rand(0,1) \le Cr \ or \ j = j_{rand}) \\ \mathbf {x}_{i,j}^{g}, \qquad \mathrm{{otherwise}} \end{array} \right. \end{aligned}$$

  (11)

  where $i \in [ 1, NP]$ and $j \in [1,D]$, $Cr \in [0,1]$ is crossover rate, a random integer uniformly distributed in [1, D] is represented by $j_rand$, D is the dimension of the search space.

• Step 4: Selection phase. The options are as follows.

  $$\begin{aligned} \mathbf {x}_{i}^{g+1}=\left\{ \begin{array}{l} \mathbf {u}_{i}^{g}, \mathrm{{if}}(f(u_{i}^{g}) <f(x_{i}^{g}) ) \\ \mathbf {x}_{i}^{g}, \qquad \mathrm{{otherwise}} \end{array} \right. \end{aligned}$$

  (12)

• Step 5: If a stopping criterion is not satisfied, the result is output; otherwise it returns to step 2.

MDDE for DPFSP with minimizing makespan

The DE algorithm was originally designed to solve the continuous optimization problem, it is not used to directly generate discrete job sequences. Therefore, the MDDE algorithm for solving the problem of blocking flow shop scheduling is proposed by Wang et al. [27]. Inspired by the HDDE algorithm, the MDDE algorithm for solving the DPFSP with a makespan criterion is presented. The details of MDDE algorithm details include population initialization, mutation and crossover operator design, local search and variable neighborhood search, and elite retention strategies.

Initial population of DNEH+T

The principle of distributing two kinds of jobs to the factories is proposed by Naderi and Ruiz [11]. The first is to assign the job to the factory with the lowest current makespan, excluding the inserting job (denoted as NEH1). The second is the lowest current makespan (denoted NEH2) after the job is assigned to the factory. The “NEH” is the Nawaz–Enscore–Ham algorithm which is one of the most effective heuristic algorithms. An improved NEH (DNEH + Dipak) was proposed by Shao et al. [4] to solve the distributed no-wait flow shop scheduling problem (DNWFSP).

Fig. 3

The examples of Initial population

In this study, a modified version of DNEH + Dipak is applied to construct the initial population, which is named as DNEH + T. The detail of DNEH + T method is described as follows.

Supposing s is a sequence of k jobs to be assigned, assigning the k jobs to two factories, the steps are as follows.

• Step 1: According to the principle of the shortest processing time (SPT Rule), the total processing time of each job is arranged in ascending order, obtaining a new sequence $s^{'}$ of jobs to be assigned.

• Step 2: Insert the first two jobs of $s^{'}$ into the two factories, respectively.

• Step 3: Insert the third job of $s^{'}$ into all possible locations in the two factories, respectively. Find the best factory location for the job.

• Step 4: Repeat the Step 3 until all jobs of $s^{'}$ have been allocated.

In addition, the insertion process of jobs using Taillard’s acceleration method [33] greatly increase the speed of operation. The pseudo-code of initial population is shown in Algorithm 1. The detailed application rules of DNEH + T are shown in Fig. 3.

The job permutation-based mutation operator

Mutation operator is one of the significant operators of DE algorithms. A good mutation operator can prevent the algorithm from falling into the local optimal solution, and makes the algorithm perform well in solving speed and precision. Inspired by the LSAHDE [21] algorithm, the mutation strategy $current-to-pbest/1$ is used in the MDDE algorithm.

$$\begin{aligned} \mathbf {v}_{i,g} = \mathbf {x}_{i,g}\oplus \omega \otimes (\mathbf {v}_{pb,g}-\mathbf {x}_{i,g} )\oplus \omega \otimes (\mathbf {x}_{r1,g}-\mathbf {x}_{r2,g} )\nonumber \\ \end{aligned}$$

(13)

where $x_{pb,g}$ is the best individual at the current generation g. $x_{r_{1},g}$ and $x_{r_{2},g}$ are two different individuals at the current population. $x_{i,g}$ is the individual involved in mutation. $v_{i,g}$ is the offspring individual of $x_{i,g}$ by the mutation operation. The definitions of ‘−’, ‘$\otimes$’ and ‘$\oplus$’ in Eq. (13) are separately described as follows.

$$\begin{aligned} \triangle _{1}= & {} \omega \otimes (\mathbf {x}_{r1,g}-\mathbf {x}_{r2,g} )\nonumber \\\Leftrightarrow & {} \sigma _{j}= \left\{ \begin{array}{l@{\quad }l} \mathbf {x}_{r1,g}-\mathbf {x}_{r2,g}, &{} \mathrm{{if}} \ rand(0,1) <\omega \\ 0, &{} \mathrm{{otherwise}}. \end{array} \right. \end{aligned}$$

(14)

$$\begin{aligned} \triangle _{2}= & {} \omega \otimes (\mathbf {x}_{pb,g}-\mathbf {x}_{i,g} )\nonumber \\\Leftrightarrow & {} \pi _{j}= \left\{ \begin{array}{l@{\quad }l} \mathbf {x}_{pb,g}-\mathbf {x}_{i,g}, &{} \mathrm{{if}} \ rand(0,1) <\omega \\ 0, &{} \mathrm{{otherwise}}. \end{array} \right. \end{aligned}$$

(15)

where $\triangle _{1}$ and $\triangle _{2}$ are temporary vector.

$$\begin{aligned} \mathbf {v}_{i,g}=\mathbf {x}_{i,g}\oplus \triangle _{1}\oplus \triangle _{2} =\mathrm{{mod}}((\mathbf {x}_{i,g}+\triangle _{1}+\triangle _{2}+n),n)\nonumber \\ \end{aligned}$$

(16)

where ‘mod’ represents the mathematical operation of Mod. n is the dimension of the individual. The detailed pseudo-code of mutation operator is shown in Algorithm 2.

From Algorithm 2, $v_{i,g}$ does not represent a complete sequence, as individual jobs are repeated multiple times or lost. Mutant individuals are used to enhance the perturbation to the target individuals to increase the exploitation and exploration ability of the algorithm. Therefore, the legitimate target individuals are obtained through the following crossover operators.

Crossover operator

The mutant individual $V_{i,g}$ and the target individual $x_{i,g-1}$ are combined to generate a trial individual $u_{i,g}$ by crossover operator. The purpose of crossover operation is to transform the unreasonable sequence of jobs produced by mutation operation into reasonable sequence of jobs. The details are as follows.

Fig. 4

The examples of crossover operators

Assuming that $v_{i}$ is a sequence of repeated jobs produced by the mutation operation, and $x_{i}$ is a sequence containing non-repeated jobs. The length of $v_{i}$ and $x_{i}$ is n.

• Step 1: From $j=1$ to n, if $rand() \>Cr$ or the job is not the first time appear in $v_{i}$, the job is deleted from $v_{i}$. Assigning $v_{i}$ that completes the step to $V_{i}$, that is, $V_{i} = v_{i}$.

• Step 2: Remove jobs contained in $V_{i}$ from $x_{i}$ and assigning the $x_{i}$ that completes the step to $U_{i}$, that is, $U_i=x_i$.

• Step 3: Each job is fetched from $V_i$ and re-inserted to any possible location in $U_i$, until the best location for the job is found.

The detailed process is shown in Fig. 4. Assuming that $u_i= (5,0,2,3,5,4)$ is the mutation sequence.

Switching mechanism based on neighborhood structures

The main ideas of neighborhood search are divided into the following aspects. First, a local minimum in a neighborhood structure is not necessarily applied to another neighborhood structure. Second, the global optimal value is the local optimal value involving all possible neighborhood structures. Finally, for various problems, the local optimal values of multiple neighborhoods are relatively close to each other [4]. In the design of the neighborhood, supposing that if the schedule in the factory of the largest makespan (represented as the critical factory $f_\mathrm{{c}}$) is not changed, the solution makespan is not reduced. In MDDE, four neighborhood structures are introduced in this paper, improving the exploitation and exploration ability of the algorithm. These neighborhood structures are divided into two categories. One is assignment based on factory, including Critical-swap-multi $(N_1)$ and Critical-insert-multi $(N_2)$. The other is adjustment based on job order, including Critical-swap-single $(N_3)$ and Critical-insert-single $(N_4)$. An example of the four neighborhood structures is shown in Fig. 5. The detailed descriptions of the four neighborhood structures are as follows.

Fig. 5

Neighborhood structures of MDDE

• $N_1$: A job J is randomly selected from the $f_\mathrm{{c}}$ factory. Randomly select a job $J_f$ from other factories, and then exchange the positions of J and $J_f$ respectively. Then, $F-1$ new solutions are generated, and the current optimal solution is selected as the next neighborhood for local search.

• $N_2$: A job J is randomly selected from the factory $f_\mathrm{{c}}$, and insert it into a randomly selected position in other factories.

• $N_3$: Randomly select l jobs from the factory $f_\mathrm{{c}}$. A job J is randomly selected from l jobs and exchanged with other $l-1$ jobs in the factory.

Neighborhood structure based local search

The local search takes a significant effect in the MDDE algorithm. Four local search methods are used to improve the solution as shown in Fig. 6. $\mathrm{{LS}}\_\mathrm{{insert}}\_\mathrm{{critical}}\_\mathrm{{factory1}}$ and $\mathrm{{LS}}\_\mathrm{{insert}}\_\mathrm{{critical}}\_\mathrm{{factory2}}$ indicate that a job is taken from the critical factory $f_\mathrm{{c}}$ and inserted into all other factories or critical factory. The location of the best makespan is chosen for that factory. Each job in the critical factory is exchanged with each job of another factory as shown in $\mathrm{{LS}}\_\mathrm{{swap}}$. $\mathrm{{LS}}\_\mathrm{{insert}}$ means that a pair of job taken from critical factory and non-critical factory and then they are inserted into other factories respectively to find the best completion time. The local search is terminated when the maximum makespan is no longer improved.

Fig. 6

Local search methods of MDDE

The MDDE algorithm

The general diagram of MDDE algorithm is shown in Fig. 7. The detailed pseudo-code of MDDE is summarized in Algorithm 3.

Fig. 7

Generic diagram of MDDE

In the initialization stage, the $DNEH+T$ method is introduced to generate potential candidate solution. The improved mutation strategies are used to assist in the exploration and exploitation of the algorithms. A switching mechanism is designed to determine whether to enter variable neighborhood search after the crossover operation of MDDE to reduce the complexity of the algorithm. A switch probability $P_{1}$ is given and a random number between 0 and 1 is generated after each mutation operation of the population. If the random number is less than probability $P_{1}$, the individual enters variable neighborhood search and local search. The selection of neighborhood is also one of the important factors to improve the search ability of the algorithm. Finally, the target individuals in the population are selected for the next generation by greedy selection.

In this paper, the knowledge used to guide search is divided into two kinds: knowledge of problem and knowledge of algorithm optimization.

For the distributed permutation flow-shop scheduling problem, optimal sequence of jobs needs to be found to minimize the maximum completion time. In the process of algorithm search, it is easy to find multiple local optimal solutions. In order to further optimize the current solution, it is necessary to set the neighborhood structure of the solution. A local optimum is optimal in a certain neighborhood, but it may not be optimal after changing the neighborhood. At this point, the solution has room for improvement. Therefore, the design of reasonable neighborhood structure based on problem knowledge can guide the evolution of individuals.

The local search of variable neighborhood is the key operation in this algorithm. In this section, four neighborhood structures are designed and a knowledge-based neighborhood selection strategy is proposed. The feedback results of local search in the neighborhood during the evolution of the algorithm are extracted to decide whether to switch neighborhoods or not. When there are still potential candidate solutions in the neighborhood, the local search is continued in the neighborhood. The algorithm switches to the next neighborhood to continue searching, when potential candidate solution is not found in this neighborhood. The historical information in the evolution process of the algorithm is extracted as a kind of guiding knowledge to switch neighborhood search, which helps to further enhance the exploitation ability of MDDE.

The experiments and comparisons

In this section, the optimal combinations of parameters in the MDDE algorithm are testified by the DOE. Afterwards, MDDE is compared with the other four state-of-the-art algorithms. The computational simulation used the benchmark proposed by Naderi and Ruiz [11], which is extension of the Taillard [34] benchmark. The small instance problem of DPFSP has been well solved by various algorithms, so the algorithm in this study is used to solve the large instance of DPFSP. The number of factories is set to $F={2,3,\ldots ,7 }$. More details are found at http://soa.iti.es.

Design of the experiments

The same experimental conditions are used in the experiment, including the same stopping criteria and the same programming language. All algorithms are programmed with MATLAB (2016b). The experiments run on a PC with 3.4 GHz Intel (R) Core i7-6700 CPU, 16GB RAM and 64-bit OS to ensure the fairness of the algorithm. The average relative percentage deviation (ARPD) index is used to measure the results and is calculated as follows.

$$\begin{aligned} \mathrm{{ARPD}}=\frac{1}{R}\cdot \sum _{i=1}^{R}\frac{C_{i}-C_\mathrm{{opt}}}{C_\mathrm{{opt}}}\cdot 100 \end{aligned}$$

(17)

where $C_i$ represents the solution generated by the specific algorithm in the ith experiment of the given instance. R is expressed as the number of runs. $C_\mathrm{{opt}}$ is represented as the optimal value of the results of all algorithms. ARPD represents the minimum found by all the algorithms in this paper.

Table 1 ANOVA results for parameter of MDDE

In this study, the termination time of all comparison algorithms is set to $T_\mathrm{{max}} = n \times m \times f \times C$ millisecond (ms), and the time-level $C=5,15,30$. All comparison algorithms are run independently 10 times on the benchmark function.

Fig. 8

Main effects plot of parameters

Parameters analysis

The parameter calibration experiments contribute to improve the efficiency and performance of the algorithm because the control parameters have an important influence in DE [35]. In this section, the DOE method is used to determine a suitable set of parameters for MDDE [32]. MDDE has four critical parameters: Cr (crossover rate), $\omega$ (scaling factor), $P_1$, NP (population size). The selected parameters are as follows: $Cr\in {0.3,0.5,0.6}$, $\omega \in {0.5,0.6,0.7}$, $P_1\in {0.2,0.4,0.5}$, $NP \in {20,40,50}$. The configurations of all possible combinations of the four parameters are $3\times 3\times 3\times 3=81$. Since the calibration algorithm using the same example result in over fitted results [36], 52 instances of randomly generated with various numbers of jobs, machines, and factories. Each parameter combination is executed 5 times. Following the literature [37], the experimental results are analyzed by the multivariate analysis of variance (ANOVA). In the DOE experiment, the parameters have a distinctiveness effect on the algorithm, when the confidence level of the P value is less than 0.05. The results of ANOVA are reported in Table 1.

Table 2 Calculation results of ARPD value with $C=5$

Table 3 Calculation results of ARPD value with $C=15$

Table 4 Calculation results of ARPD value with $C=30$

After running all parameter configurations, the results show that the parameters $P_1$ and NP have no significantly effect on MDDE. According to the results from Table 1, the P values of parameters Cr and $\omega$ are less than the confidence level ($\alpha = 0.05$), indicating that these parameters have a greater impact on MDDE than other parameters. Meanwhile, the parameters Cr corresponds to the greatest F-ratio. It suggests that the parameters Cr have the greatest effect on the average performance of MDDE among all factors of consideration. From Fig. 8, the parameters are selected as follows: $Cr=0.5$, $\omega =0.5$, $P_1=0.4$, and $NP=50$.

Analysis and discussion

In this study, the proposed MDDE algorithm is compared with the four optimal competitive algorithms for FSFP. The details of four comparison algorithms are described as follows.

• In the HDDE algorithm [31], discrete mutation and crossover operators, and local search are used to solve the problem of blocking flow shop scheduling.

• An efficient hybrid DDE algorithm is used to solve distributed blocking flow shop scheduling problem, including a unique elitist retain strategy and a biased selection operator [29].

• The CDE algorithm is used to solve the distributed finite buffer flow shop scheduling problem, using two constructive heuristics to create excellent initialization [30].

• A two-stage Iterated greedy algorithm [5] is used to solve the distributed permutation flow shop scheduling problem, which includes construction improvement, destruction procedures, and a local search.

The MDDE algorithm is used to test on 720 large-scale instances. The ARPD values grouped by the number of factories F are listed in Table 2, 3 and 4, where the best results are shown in boldface. From Table 2, 3 and 4, the performance of MDDE is better than other variants on the most instances. The reason is that MDDE algorithm uses a knowledge-based ensemble strategy, which improves the search accuracy of the algorithm. The mean and 95% Fisher’s least-significant difference (LSD) interval for MDDE is presented in Fig. 9, 10 and 11. Therefore, the proposed MDDE algorithm is slightly better than the other four comparison algorithms.

Statistical tests show that MDDE algorithm has significant improvement compared with the comparison algorithms. In this study, Wilcoxon’s sign rank test [38] is selected for nonparametric statistical tests. From Table 5, $R^+$ represents that the sum of ranks for the functions of MDDE is better than the comparison algorithm in the row, and $R^-$ represents that the sum of ranks the functions of the comparison algorithm is superior to the MDDE.

It is worth noting that in pair-wise comparison, MDDE is the first algorithm in the row. The statistical results are listed in Table 5, MDDE is significantly better than the other four comparison algorithms in the case of $C=15$.

In 120 instances, the ARPD of MDDE is smaller than that of the HDDE, DDE, CDE and IG, which means that MDDE has obtained a better solution. The classical trend graphs of MDDE and the comparison algorithms are shown in Figs. 12, 13, 14, 15, 16 and 17. In these figures, the horizontal axis represents the index of the instances in the test suit, and the vertical axis represents the test results obtained by MDDE and the four comparison algorithms on all the instances. In this paper, the algorithm is tested on 120 instances when $F=2$, $F=3$, $F=4$, $F=5$, $F=6$, $F=7$ respectively. There are 120 points on the horizontal axis, and each point corresponds to the ARPD value of the five algorithms. Since the 120 instances are not related to each other, the ARPD value on each instance of the algorithm has no correlation.

Bonferroni–Dunn test and Friedman’s test are addressed to further illustrate the significant differences between MDDE and the four comparison algorithms, as shown in Figs. 18, 19, 20 and 22. The ARPD values between different plants are compared in Figs. 18, 19, 20 and 22, and the maximum runtime is set to $T_\mathrm{{max}} = n \times m \times f \times 15$ ms. To assess the significance level of MDDE and other comparison algorithms, the Bonferroni–Dunn test is used to calculate the critical differences between the algorithms to compare their differences with $\alpha = 0.05$ and $\alpha = 0.1$. Although there is no significant difference between MDDE and the comparison algorithms in individual cases, the rank of MDDE is the smallest among all the test cases. From Figs. 18, 19, 20, 21 and 22, the proposed MDDE algorithm ranks first in all dimensions.

The effectiveness of discrete mutation strategy, the neighborhood structures and local search method are validated by the above experimental analysis. Furthermore, compared with the state-of-the-art algorithms from the literatures, the proposed MDDE algorithm for solving the DPFSP is effective. The main reasons are summarized as follows.

First, the DE algorithm is an efficient intelligent optimization algorithm, which has been applied in various fields. Although DE is sensitive to parameters including the crossover rate and mutation factor, it generally provides excellent results on various complex problems. In addition, an excellent initial solution assists the algorithm in increasing the diversity of the population to discover the potential candidate solution. A poor initial population unnecessarily increases the number of searches or causes the algorithm to converge at local optima. In MDDE, the constructive DNEH + T method is used to initialize the population to increase the population diversity, and the Taillard’s method is used to speed up the operational efficiency of the algorithm.

Third, the neighborhood search is one of the important factors which affect the performance of the algorithm. In MDDE, an appropriate neighborhood search mechanism is adaptively selected by a knowledge-based optimization strategy, which enhances the global search ability of the proposed algorithm. The experiments show that each local search method plays a different role in the overall performance of the algorithm. Since various local search methods are explored in different solution spaces, the mixing local search helps to avoid local optimum. At the same time, the results prove that this integration strategy is better than a single local search strategy.

It is noteworthy that the ensemble strategy focuses on improving the global search capability in the stage of exploration, including the discrete mutation strategy, neighborhood search and local search. Individuals in the population become similar when the MDDE algorithm falls into the local optimal solution. Mutation strategies and crossover operations will not produce new individuals and will lead to population stagnation. For example, when MDDE algorithm falls into local optimum, even if new mutation strategy is applied in MDDE, none of the mutation strategies can help MDDE escape from the local optimal. However, the neighborhood search mechanism helps the algorithm to search the direction that is introduced to another neighborhood.

Fig. 9

The variance plot of the algorithms at $C=5$

Fig. 10

The variance plot of the algorithms at $C=15$

Fig. 11

The variance plot of the algorithms at $C=30$

Table 5 Rankings obtained through the Wilcoxon signed-rank test

Fig. 12

ARPD of F=2

Fig. 13

ARPD of F=3

Fig. 14

ARPD of F=4

Fig. 15

ARPD of F=5

Fig. 16

ARPD of F=6

Fig. 17

ARPD of F=7

At the same time, the local search mechanism is complementary to the neighborhood search mechanism, which increases the small-range search capability of the algorithm. In addition, the current suitable neighborhood search mechanism is adaptively selected by the knowledge-based optimization strategy, which enables the algorithm to implement a closed-loop control system. Significant differences between the MDDE algorithm and the comparison algorithms are shown in Table 5. Results with significant differences are marked ‘yes’ and highlighted in bold. The experiment results show that MDDE outperforms other comparison algorithms. According to Table 5, MDDE proves to be significantly different from the majority of comparison algorithms by using Wilcoxon’s test. The convergence accuracy and stability of MDDE are superior to other comparison algorithms, as shown in Figs. 9, 10 and 11. From Figs. 18, 19, 20, 21, 22 and 23, MDDE is superior to other comparison algorithms because it ranks higher than all comparison algorithms.

Fig. 18

Rankings for F=2

Fig. 19

Rankings for F=3

Fig. 20

Rankings for F=4

Fig. 21

Rankings for F=5

Fig. 22

Rankings for F=6

Fig. 23

Rankings for F=7

Performance analysis of each component of MDDE

In this section, the contributions of each strategy and mechanism to the MDDE algorithm are analyzed experimentally. The MDDE mainly consists of DNEH initialization method, discrete mutation strategy and adaptive neighborhood search strategy. Three sets of experiments are conducted to verify the contribution of these strategies. In the first experiment (N-DNEH), the improved NEH initialization method is removed. In the second experiment (N-Mutation), the discrete mutation and crossover strategy is removed. The adaptive neighborhood search strategy is removed in the third experiment (N-LocalSearch). The three algorithms are run on each instance 10 times and the terminal time is $30*m*n$. Table 6 is obtained according to the calculation method of ARPD. In each instance, the smallest value corresponds to the best result. The value with the best result is highlighted in bold.

Table 6 The computational results of all variants of MDDE

It can be seen from the Table 6 that the results of MDDE are better than MDDE(N-DNEH), so it can be concluded that the improved NEH initialization method contributes to the quality of the initial solution of the algorithm. The results of MDDE are also superior to the MDDE(N-Mutation) because the discrete variation strategies guarantee the feasibility of solutions. The results of the MDDE(N-LocalSearch) are poor, because the local search method effectively improves the exploitation of the algorithm and helps the algorithm to find the global optimal solution quickly.

Fig. 24

The 95% confidence interval plot

The 95% confidence interval plot is shown in Fig. 24. As can be seen from the figure, the MDDE performs better than the other variables in all cases, indicating that each component has a significant impact on the proposed algorithm.

Flow shop scheduling problem has n! possible sequences. It’s expensive to list all the possible sequences. In the flow-shop scheduling problem, all the jobs must pass through all the machines in the same order, and the jobs with higher total machining time have higher priority than those with lower total machining time. The NEH method is a classical initialization method. The method can generate a very good sequence of jobs and solve the large-scale flow-shop scheduling problem well in both static and dynamic scheduling. The DNEH+T method is an improved version of NEH method, which is used to initialize the population. It can generate a good sequence of jobs and effectively solve the permutation flow shop scheduling problem.

DE algorithm has an efficient global optimization capability. The mutation strategy is an operation in the DE algorithm. The current individual and the differential vector are used to form the mutation strategy, in which the scaling factor is used to control the influence of the differential vector. This method can avoid falling into local optimum in the process of solving and improve the speed and accuracy.

In the process of iteration, multiple local optimal solutions are generated. The goal is to find a global optimal solution. Since a local optimal solution may not be optimal in all neighborhoods, the neighborhood needs to be changed to obtain the global optimal solution. In general, variable neighborhood search is a local search method, which can further optimize the current optimal solution.

In the process of solving, DNEH+T is used to generate a good initial solution, which is conducive to the further search of the algorithm. The mutation strategy in DE avoids the local optimum and increases the global searching ability of the algorithm. The variable neighborhood search strategy further optimizes the current optimal solution and enhances the local search ability of the algorithm. The combination of the three works balances the exploration and exploitation capabilities of the algorithm.

Conclusions and future research

In this paper, a memetic discrete differential evolutionary algorithm is proposed to solve the DPFSP problem. In the proposed MDDE, the neighborhood structure based on knowledge exchange mechanism strengthens the exploration and exploitation ability of MDDE. MDDE algorithm adopts knowledge-based integration strategy, which improves the search precision of the algorithm. MDDE algorithm is used to test 720 large instances. The results show that in most instances, MDDE performs better than other variants of DE. Wilcoxon’s sign rank test and Friedman test are used to analyze the data. The results show that in the case of $C=15$, MDDE is superior to the other four comparison algorithms in terms of solution diversity and convergence accuracy.

The future research is to develop the multi-target MDDE and design a certain self-learning method to improve the search ability of MDDE. The MDDE algorithm is used to solve other distributed scheduling problems, such as the distributed dynamic scheduling problems. Furthermore, adopting MDDE to real-world optimization is also the main direction of future research.