Generalized complex q-rung orthopair fuzzy Einstein averaging aggregation operators and their application in multi-attribute decision making

Abstract

The recently proposed q-rung orthopair fuzzy set, which is characterized by a membership degree and a non-membership degree, is effective for handling uncertainty and vagueness. This paper proposes the concept of complex q-rung orthopair fuzzy sets (Cq-ROFS) and their operational laws. A multi-attribute decision making (MADM) method with complex q-rung orthopair fuzzy information is investigated. To aggregate complex q-rung orthopair fuzzy numbers, we extend the Einstein operations to Cq-ROFSs and propose a family of complex q-rung orthopair fuzzy Einstein averaging operators, such as the complex q-rung orthopair fuzzy Einstein weighted averaging operator, the complex q-rung orthopair fuzzy Einstein ordered weighted averaging operator, the generalized complex q-rung orthopair fuzzy Einstein weighted averaging operator, and the generalized complex q-rung orthopair fuzzy Einstein ordered weighted averaging operator. Desirable properties and special cases of the introduced operators are discussed. Further, we develop a novel MADM approach based on the proposed operators in a complex q-rung orthopair fuzzy context. Numerical examples are provided to demonstrate the effectiveness and superiority of the proposed method through a detailed comparison with existing methods.

Introduction

The intuitionistic fuzzy set (IFS), which was pioneered by Atanassove [1], is a generalization of the fuzzy set (FS) [2]. The IFS is an important tool for coping with unreliable and difficult information. The prominent characteristic of the IFS is that it assigns each element a membership grade and a non-membership grade, whose sum is ≤ 1. Therefore, the IFS has received increasing research attention since it was proposed [3, 4]. However, in many cases, the IFS cannot work effectively, for example, when a decision maker provides information for which the aforementioned sum is > 1. For example, if he/she assigns 0.52 as the membership grade and 0.63 as the non-membership grade, we note that 0.52 + 0.63 ${ \nleqq }1$. To deal with such problems, Yager [5] pioneered the notion of the Pythagorean FS (PFS) as a useful tool to describe uncertain and unreliable information effectively, where the sum of the square of membership grade and the square of the non-membership grade is limited to [0,1]. Sometimes, the PFS cannot work effectively. For example, when a decision maker assigns 0.9 as the membership grade and 0.7 as the non-membership grade, $0.9^{2} + 0.7^{2} = 0.81 + 0.47 = 1.28 > 1$; thus, the PFS is not applicable. Yager [6] developed the q-rung orthopair FS (q-ROFS) for handling such situations, where the sum of the q-power of the membership grade and the q-power of the non-membership grade is constrained to [0,1]. For this example, we have $0.9^{4} + 0.7^{4} = 0.66 + 0.24 = 0.9$. Clearly, the q-ROFS is more general than the IFS and PFS (see Fig. 1). Because of its advantages, the q-ROFS is a fundamental tool for processing troublesome fuzzy data, and it is used in the fields of aggregation operators, similarity measures (SMs), hybrid aggregation operators, etc. Various studies have been performed on q-ROFSs, as described below.

• 1. Operator-based approaches: According to the aggregation operators, many scholars have successfully developed operators for the q-ROFS environment. For instance, Liu and Wang [7] developed aggregation operators using q-ROFSs. Garg and Chen [8] investigated neutrality aggregation operators for q-ROFSs. Using the new score function, Peng et al. [9] presented exponential and aggregation operators based on q-ROFSs. Xing et al. [10] established point-weighted aggregation operators based on q-ROFSs.

• 2. Measures-based approaches: The SM is useful for accurately examining the degree of similarity between any two objects. Many scholars have applied SMs in different environments. For example, Wang et al. [11] used a cosine function to evaluate the SMs for q-ROFSs. Du [12] established Makowski-type distance measures based on generalized q-ROFSs. Peng and Liu [13] examined information measures for q-ROFSs.

• 3. Hybrid operator-based approaches: For investigating the relationships between objects, the hybrid aggregation operators play an essential role in the realistic decision environment. Scholars have investigated various hybrid aggregation operators based on the q-ROFS, for example, Archimedean Bonferroni mean operators [14], Maclaurin symmetric mean operators [15], Muirhead mean operators [16], power Maclaurin symmetric mean operators [17], Heronian mean operators [18], partitioned Bonferroni mean operators [19], partitioned Maclaurin symmetric mean operators [20], and others [21,22,23,24,25,26,27,28,29,30,31,32,33].

Fig. 1

Geometric comparison of the q-ROFS, PFS, and IFS

Figure 1 presents the geometric representations of the IFSs, PFSs, and q-ROFSs. As shown, the q-ROFSs provide the largest amount of space for expressing the fuzzy information. Ramot et al. [34] introduced the complex FS (CFS), which extended the range of the membership grades from real numbers to complex numbers with unit discs. The CFS is an extension of the FS for coping with uncertainty and unreliability. Additionally, Ramot et al. [35] reintroduced the notion of complex fuzzy logic. However, the CFS is completely different from the complex fuzzy number proposed by Buckley [36]. Furthermore, Alkouri and Salleh [37] developed the complex IFS (CIFS), which extended the range of the membership and non-membership grades from real numbers to complex numbers with a unit disc. In contrast to the IFS, which can process only one-dimensional information, the CIFS can cope with two-dimensional information; hence, information loss can be avoided. Kumar and Bajaj [38] developed complex intuitionistic fuzzy soft sets with distance measures and entropies. Garg and Rani [39, 40] proposed correlation coefficients and aggregation operators based on the CIFS. Rani and Garg [41, 42] introduced distance measures and power aggregation operators based on the CIFS.

Recently, Ullah et al. [43] proposed the complex PFS (CPFS), which is useful for efficiently describing uncertain and unreliable information. A characteristic of CPFS is that the sum of the square of the real part (and imaginary part) of complex membership grade and the square of the real part (and imaginary part) of complex non-membership grade is limited to [0,1]. Sometimes, the CPFS cannot work effectively; for example, when a decision maker provides $0.9{\text{e}}^{{i2\pi \left( {0.8} \right)}}$ for the complex membership grade and $0.7{\text{e}}^{{i2\pi \left( {0.7} \right)}}$ for the complex non-membership grade, $0.9^{2} + 0.7^{2} = 0.81 + 0.47 = 1.28 > 1$ and $0.8^{2} + 0.6^{2} = 0.64 + 0.49 = 1.13 > 1$, making the CPFS inapplicable. To solve such problems, we developed a complex q-rung orthopair FS (Cq-ROFS) characterized by complex membership and non-membership grades, i.e., $0.9^{4} + 0.7^{4} = 0.66 + 0.24 = 0.9$ and $0.8^{4} + 0.7^{4} = 0.41 + 0.24 = 0.65$. In the Cq-ROFS, the sum of the q-power of the real part (and imaginary part) of the complex membership grade and the q-power of the real part (and imaginary part) of the complex non-membership grade is constrained to [0,1]. The Cq-ROFS is more general than the CIFS and CPFS.

Real-life situations involve numerous complex circumstances, and data measures are useful for handling uncertain data. Various data measures, e.g., similitude, separation, and entropy, are used in the decision-making process, for example, in design acknowledgment, clinical determination, and bunching investigation. Some existing MADM methodologies for fuzzy information are based on the PFS and q-ROFS, because they have shortcomings. In the proposed Cq-ROFS, the sum of the q-power of the real part (and imaginary part) of the complex membership grade and the q-power of the real part (and imaginary part) of the complex non-membership grade is constrained to [0,1]. It is more general and can express a wider information scope. Next, the q-ROFS is turned into a fundamental tool to process troublesome fuzzy data. Now, we provide an example. Assume that XYZ Corp. chooses to set up biometric‐based participation gadgets (BBPGs) in all its workplaces throughout the nation. For this, the organization invites a specialist to provide the data with respect to the (i) shows of BBPGs and (ii) creation dates of BBPGs. The organization must select the optimal model of BBPGs with its creation date at the same time. Here, the issue includes two-dimensional information: the BBPG model and the creation date of the BBPGs. Obviously, they cannot be expressed precisely by the q-ROFS, because the q-ROFS cannot handle multiple types of one-dimensional information simultaneously. The sufficiency terms in the Cq-ROFS can be utilized to determine an organization’s choice with regard to the model of the BBPGs, and the stage terms can be utilized to express the organization’s judgment regarding the creation date of the BBPGs.

Keeping the advantages of the Cq-ROFS, the objectives of this study were as follows:

• 1. To propose the notion of Cq-ROFS and its operational laws, which was the basis of this study

• 2. To aggregate complex q-rung orthopair fuzzy numbers (Cq-ROFNs), we extend the Einstein operations (EOs) to Cq-ROFSs and propose a family of complex q-rung orthopair fuzzy Einstein averaging operators, such as the complex q-rung orthopair fuzzy Einstein weighted averaging (Cq-ROFEWA) operator, the complex q-rung orthopair fuzzy Einstein ordered weighted averaging (Cq-ROFEOWA) operator, the generalized complex q-rung orthopair fuzzy Einstein weighted averaging (GCq-ROFEWA) operator, and the generalized complex q-rung orthopair fuzzy Einstein ordered weighted averaging (GCq-ROFEOWA) operator. Desirable properties and special cases of the introduced operators are discussed.

• 3. To develop a novel MADM approach in the complex q-rung orthopair fuzzy context based on the proposed operators

• 4. To demonstrate the effectiveness and superiority of the proposed method by comparing numerical results with the results of existing methods

The remainder of this paper is organized as follows. In the next section, we briefly review existing concepts such as PYFSs, CPYFSs, q-ROFSs, and their operational laws. In the following section, the concept of the Cq-ROFS and its operational laws are investigated. In the next section, we extend the EOs to Cq-ROFSs and propose a family of complex q-rung orthopair fuzzy Einstein averaging operators, such as the Cq-ROFEWA, Cq-ROFEOWA, GCq-ROFEWA, and GCq-ROFEOWA operators. Desirable properties and special cases of the introduced operators are discussed. In the following section, we develop a novel approach for MADM in the complex q-rung orthopair fuzzy context based on the proposed operators. Finally, a detailed comparison is performed between existing methods and the proposed approach. The conclusions are presented in the last section.

Preliminaries

In this section, we briefly review existing concepts such as PYFSs, CPYFSs, q-ROFSs, and their operational laws. In this study, the finite universal set is denoted as $X$.

Definition 1

[15] A PYFS ${\mathbb{E}}$ on a finite universal set $X$ is given by:

$$ {\mathbb{E}} = \left\{ {\left( {{\mathcal{T}}_{{\mathbb{E}}}^{{\prime}} \left( X \right),{\mathcal{N}}_{{\mathbb{E}}}^{{\prime}} \left( X \right)} \right):X \in X} \right\}, $$

(1)

where ${\mathcal{T}}_{{\mathbb{E}}}^{{\prime}}$ and ${\mathcal{N}}_{{\mathbb{E}}}^{{\prime}}$ represent the membership and non-membership grades, respectively, under the following condition: $0 \le {\mathcal{T}}_{{\mathbb{E}}}^{\prime 2} + {\mathcal{N}}_{{\mathbb{E}}}^{\prime 2} \le 1$. The hesitancy degree is defined as ${\mathcal{H}}_{{\mathbb{E}}} = \left( {1 - {\mathcal{T}}_{{\mathbb{E}}}^{\prime 2} - {\mathcal{N}}_{{\mathbb{E}}}^{\prime 2} } \right)^{\frac{1}{2}}$. The Pythagorean fuzzy number (PYFN) is given as ${\mathbb{E}} = \left( {{\mathcal{T}}_{{\mathbb{E}}}^{{\prime}} ,{\mathcal{N}}_{{\mathbb{E}}}^{{\prime}} } \right)$.

Definition 2

[43] A CPYFS ${\mathbb{E}}$ on a finite universal set $X$ is given as follows:

$$ {\mathbb{E}} = \left\{ {\left( {{\mathcal{T}}_{{\mathbb{E}}}^{{\prime}} \left( X \right),{\mathcal{N}}_{{\mathbb{E}}}^{{\prime}} \left( X \right)} \right):X \in X} \right\} \to , $$

(2)

where ${\mathcal{T}}_{{\mathbb{E}}}^{{\prime}} = {\mathcal{T}}_{{\mathbb{E}}} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{{\mathbb{E}}} }} }}$ and ${\mathcal{N}}_{{\mathbb{E}}}^{{\prime}} = {\mathcal{N}}_{{\mathbb{E}}} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{{\mathbb{E}}} }} }}$ represent the complex-valued membership grade and complex-valued non-membership grade, respectively, under the following conditions: $0 \le {\mathcal{T}}_{{\mathbb{E}}}^{2} + {\mathcal{N}}_{{\mathbb{E}}}^{2} \le 1$ and $0 \le {\mathcal{W}}_{{{\mathcal{T}}_{{\mathbb{E}}} }}^{2} + {\mathcal{W}}_{{{\mathcal{N}}_{{\mathbb{E}}} }}^{2} \le 1$. Further, the complex-valued hesitancy degree is defined as ${\mathcal{H}}_{{\mathbb{E}}} = \left( {1 - {\mathcal{T}}_{{\mathbb{E}}}^{2} - {\mathcal{N}}_{{\mathbb{E}}}^{2} } \right)^{\frac{1}{2}} {\text{e}}^{{i2\pi \left( {1 - {\mathcal{W}}_{{{\mathcal{T}}_{{\mathbb{E}}} }}^{2} - {\mathcal{W}}_{{{\mathcal{N}}_{{\mathbb{E}}} }}^{2} } \right)^{\frac{1}{2}} }}$. The complex PYFN is given as ${\mathbb{E}} = \left( {{\mathcal{T}}_{{\mathbb{E}}} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{{\mathbb{E}}} }} }} ,{\mathcal{N}}_{{\mathbb{E}}} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{{\mathbb{E}}} }} }} } \right)$.

Definition 3

[24] A q-ROFS ${\mathbb{E}}$ on a finite universal set $X$ is given as:

$$ {\mathbb{E}} = \left\{ {\left( {{\mathcal{T}}_{{\mathbb{E}}}^{{\prime}} \left( X \right),{\mathcal{N}}_{{\mathbb{E}}}^{{\prime}} \left( X \right)} \right):X \in X} \right\} \to , $$

(3)

where ${\mathcal{T}}_{{\mathbb{E}}}^{{\prime}}$ and ${\mathcal{N}}_{{\mathbb{E}}}^{{\prime}}$ represent the membership and non-membership grades, respectively, under the following condition: $0 \le {\mathcal{T}}_{{\mathbb{E}}}^{\prime q} + {\mathcal{N}}_{{\mathbb{E}}}^{\prime q} \le 1$. The hesitancy degree is given as ${\mathcal{H}}_{{\mathbb{E}}} = \left( {1 - {\mathcal{T}}_{{\mathbb{E}}}^{\prime q} - {\mathcal{N}}_{{\mathbb{E}}}^{\prime q} } \right)^{\frac{1}{q}}$. The q-rung orthopair fuzzy number (q-ROFN) is given as ${\mathbb{E}} = \left( {{\mathcal{T}}_{{\mathbb{E}}}^{{\prime}} ,{\mathcal{N}}_{{\mathbb{E}}}^{{\prime}} } \right)$.

Definition 4

[24] For any two q-ROFNs ${\mathbb{E}}_{1} = \left( {{\mathcal{T}}_{1}^{{\prime}} ,{\mathcal{N}}_{1}^{{\prime}} } \right)$ and ${\mathbb{E}}_{2} = \left( {{\mathcal{T}}_{2}^{{\prime}} ,{\mathcal{N}}_{2}^{{\prime}} } \right)$ with any $\delta > 0$,

• 1. ${\mathbb{E}}_{1} \oplus {\mathbb{E}}_{2} = \left( {\left( {\frac{{{\mathcal{T}}_{1}^{\prime q} + {\mathcal{T}}_{2}^{\prime q} }}{{1 + {\mathcal{T}}_{1}^{\prime q} {\mathcal{T}}_{2}^{\prime q} }}} \right)^{\frac{1}{q}} ,\left( {\frac{{{\mathcal{N}}_{1}^{{\prime}} {\mathcal{N}}_{2}^{{\prime}} }}{{\left( {1 + \left( {1 - {\mathcal{N}}_{1}^{\prime q} } \right)\left( {1 - {\mathcal{N}}_{2}^{\prime q} } \right)} \right)^{\frac{1}{q}} }}} \right)} \right);$

• 2. ${\mathbb{E}}_{1} \otimes {\mathbb{E}}_{2} = \left( {\left( {\frac{{{\mathcal{T}}_{1}^{{\prime}} {\mathcal{T}}_{2}^{{\prime}} }}{{\left( {1 + \left( {1 - {\mathcal{T}}_{1}^{\prime q} } \right)\left( {1 - {\mathcal{T}}_{2}^{\prime q} } \right)} \right)^{\frac{1}{q}} }}} \right),\left( {\frac{{{\mathcal{N}}_{1}^{\prime q} + {\mathcal{N}}_{2}^{\prime q} }}{{1 + {\mathcal{N}}_{1}^{\prime q} {\mathcal{N}}_{2}^{\prime q} }}} \right)^{\frac{1}{q}} } \right);$

• 3. $\delta {\mathbb{E}}_{1} = \left( {\left( {\frac{{\left( {1 + {\mathcal{T}}_{1}^{{'q}} } \right)^{\delta } - \left( {1 - {\mathcal{T}}_{1}^{{'q}} } \right)^{\delta } }}{{\left( {1 + {\mathcal{T}}_{1}^{{'q}} } \right)^{\delta } + \left( {1 - {\mathcal{T}}_{1}^{{'q}} } \right)^{\delta } }}} \right)^{{\frac{1}{q}}} ,\left( {\frac{{\left( 2 \right)^{{\frac{1}{q}}} {\mathcal{N}}_{1}^{{'\delta }} }}{{\left( {\left( {2 - {\mathcal{N}}_{1}^{{'q}} } \right)^{\delta } + \left( {{\mathcal{N}}_{1}^{{'q}} } \right)^{\delta } } \right)^{{\frac{1}{q}}} }}} \right)} \right);{\text{ and}}$

• 4. ${\mathbb{E}}_{1}^{\delta } = \left( {\left( {\frac{{\left( 2 \right)^{{\frac{1}{q}}} {\mathcal{T}}_{1}^{{'\delta }} }}{{\left( {\left( {2 - {\mathcal{T}}_{1}^{\prime q} } \right)^{\delta } + \left( {{\mathcal{T}}_{1}^{\prime q} } \right)^{\delta } } \right)^{{\frac{1}{q}}} }}} \right),\left( {\frac{{\left( {1 + {\mathcal{N}}_{1}^{\prime q} } \right)^{\delta } - \left( {1 - {\mathcal{N}}_{1}^{\prime q} } \right)^{\delta } }}{{\left( {1 + {\mathcal{N}}_{1}^{\prime q} } \right)^{\delta } + \left( {1 - {\mathcal{N}}_{1}^{\prime q} } \right)^{\delta } }}} \right)^{{\frac{1}{q}}} } \right).$

Definition 5

[24] For any q-ROFN ${\mathbb{E}}_{1} = \left( {{\mathcal{T}}_{1}^{{\prime}} ,{\mathcal{N}}_{1}^{{\prime}} } \right)$, the score function and accuracy function are defined as follows:

$$ {\mathcal{S}}\left( {{\mathbb{E}}_{1} } \right) = {\mathcal{T}}_{1}^{\prime q} - {\mathcal{N}}_{1}^{\prime q} , $$

(4)

$$ {\mathbb{H}}\left( {{\mathbb{E}}_{1} } \right) = {\mathcal{T}}_{1}^{\prime q} + {\mathcal{N}}_{1}^{\prime q} , $$

(5)

where ${\mathcal{S}}\left( {{\mathbb{E}}_{1} } \right) \in \left[ { - 1,1} \right]$ and ${\mathbb{H}}\left( {{\mathbb{E}}_{1} } \right) \in \left[ {0,1} \right]$.

Cq-ROFSs and their operational laws

In this section, we propose the Cq-ROFSs and their operational laws.

Definition 6

A Cq-ROFS ${\mathbb{E}}$ on a finite universal set $X$ is given as:

$$ {\mathbb{E}} = \left\{ {\left( {{\mathcal{T}}_{{\mathbb{E}}}^{{\prime}} \left( X \right),{\mathcal{N}}_{{\mathbb{E}}}^{{\prime}} \left( X \right)} \right):X \in X} \right\}, $$

(6)

where ${\mathcal{T}}_{{\mathbb{E}}}^{{\prime}} = {\mathcal{T}}_{{\mathbb{E}}} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{{\mathbb{E}}} }} }}$ and ${\mathcal{N}}_{{\mathbb{E}}}^{{\prime}} = {\mathcal{N}}_{{\mathbb{E}}} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{{\mathbb{E}}} }} }}$ represent the degrees of the complex-valued membership and complex-valued non-membership, respectively, under the following conditions:$0 \le {\mathcal{T}}_{{\mathbb{E}}}^{q} + {\mathcal{N}}_{{\mathbb{E}}}^{q} \le 1, 0 \le {\mathcal{W}}_{{{\mathcal{T}}_{{\mathbb{E}}} }}^{q} + {\mathcal{W}}_{{{\mathcal{N}}_{{\mathbb{E}}} }}^{q} \le 1,$ and $q \ge 1$. The complex-valued hesitancy degree is given as ${\mathcal{H}}_{{\mathbb{E}}} = \left( {1 - {\mathcal{T}}_{{\mathbb{E}}}^{q} - {\mathcal{N}}_{{\mathbb{E}}}^{q} } \right)^{\frac{1}{q}} {\text{e}}^{{i2\pi \left( {1 - {\mathcal{W}}_{{{\mathcal{T}}_{{\mathbb{E}}} }}^{q} - {\mathcal{W}}_{{{\mathcal{N}}_{{\mathbb{E}}} }}^{q} } \right)^{\frac{1}{q}} }}$. The Cq-ROFN is given as ${\mathbb{E}} = \left( {{\mathcal{T}}_{{\mathbb{E}}} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{{\mathbb{E}}} }} }} ,{\mathcal{N}}_{{\mathbb{E}}} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{{\mathbb{E}}} }} }} } \right)$.

Definition 7

For any two Cq-ROFNs ${\mathbb{E}}_{1} = \left( {{\mathcal{T}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{1} }} }} ,{\mathcal{N}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{1} }} }} } \right)$ and ${\mathbb{E}}_{2} = \left( {{\mathcal{T}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{2} }} }} ,{\mathcal{N}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{2} }} }} } \right)$

• 1.
  $$ {\mathbb{E}}_{1}^{c} = \left( {{\mathcal{N}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{1} }} }} ,{\mathcal{T}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{1} }} }} } \right); $$
• 2.
  $$ \begin{aligned} {\mathbb{E}}_{1} \vee {\mathbb{E}}_{2} & = \Big( \max \left( {{\mathcal{T}}_{1} ,{\mathcal{T}}_{2} } \right){\text{e}}^{{i2\pi \max \left( {{\mathcal{W}}_{{{\mathcal{T}}_{1} }} ,{\mathcal{W}}_{{{\mathcal{T}}_{2} }} } \right)}} ,\\ &\quad \min \left( {{\mathcal{N}}_{1} ,{\mathcal{N}}_{2} } \right){\text{e}}^{{i2\pi \min \left( {{\mathcal{W}}_{{{\mathcal{N}}_{1} }} ,{\mathcal{W}}_{{{\mathcal{N}}_{2} }} } \right)}} \Big);{\text{ and}} \end{aligned} $$
• 3.
  $$ \begin{aligned} {\mathbb{E}}_{1} \wedge {\mathbb{E}}_{2} & = \Big( \min \left( {{\mathcal{T}}_{1} ,{\mathcal{T}}_{2} } \right){\text{e}}^{{i2\pi \min \left( {{\mathcal{W}}_{{{\mathcal{T}}_{1} }} ,{\mathcal{W}}_{{{\mathcal{T}}_{2} }} } \right)}} ,\\ &\quad \max \left( {{\mathcal{N}}_{1} ,{\mathcal{N}}_{2} } \right){\text{e}}^{{i2\pi \max \left( {{\mathcal{W}}_{{{\mathcal{N}}_{1} }} ,{\mathcal{W}}_{{{\mathcal{N}}_{2} }} } \right)}} \Big). \end{aligned} $$

Next, we investigate Einstein’s operational laws for Cq-ROFNs, which are defined as follows.

Definition 8

For any two Cq-ROFNs ${\mathbb{E}}_{1} = \left( {{\mathcal{T}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{1} }} }} ,{\mathcal{N}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{1} }} }} } \right)$ and ${\mathbb{E}}_{2} = \left( {{\mathcal{T}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{2} }} }} ,{\mathcal{N}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{2} }} }} } \right)$ with any $\delta > 0,$

$$1. \quad{\mathbb{E}}_{1} \oplus {\mathbb{E}}_{2} = \left( {\left( {\frac{{{\mathcal{T}}_{1}^{q} + {\mathcal{T}}_{2}^{q} }}{{1 + {\mathcal{T}}_{1}^{q} {\mathcal{T}}_{2}^{q} }}} \right)^{\frac{1}{q}} {\text{e}}^{{i2\pi \left( {\frac{{{\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} + {\mathcal{W}}_{{{\mathcal{T}}_{2} }}^{q} }}{{1 + {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} {\mathcal{W}}_{{{\mathcal{T}}_{2} }}^{q} }}} \right)^{\frac{1}{q}} }} ,\left( {\frac{{{\mathcal{N}}_{1} {\mathcal{N}}_{2} }}{{\left( {1 + \left( {1 - {\mathcal{N}}_{1}^{q} } \right)\left( {1 - {\mathcal{N}}_{2}^{q} } \right)} \right)^{\frac{1}{q}} }}} \right){\text{e}}^{{i2\pi \left( {\frac{{{\mathcal{W}}_{{{\mathcal{N}}_{1} }} {\mathcal{W}}_{{{\mathcal{N}}_{2} }} }}{{\left( {1 + \left( {1 - {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right)\left( {1 - {\mathcal{W}}_{{{\mathcal{N}}_{2} }}^{q} } \right)} \right)^{\frac{1}{q}} }}} \right)}} } \right);$$

$$2. \quad{\mathbb{E}}_{1} \otimes {\mathbb{E}}_{2} = \left( {\left( {\frac{{{\mathcal{T}}_{1} {\mathcal{T}}_{2} }}{{\left( {1 + \left( {1 - {\mathcal{T}}_{1}^{q} } \right)\left( {1 - {\mathcal{T}}_{2}^{q} } \right)} \right)^{\frac{1}{q}} }}} \right){\text{e}}^{{i2\pi \left( {\frac{{{\mathcal{W}}_{{{\mathcal{T}}_{1} }} {\mathcal{W}}_{{{\mathcal{T}}_{2} }} }}{{\left( {1 + \left( {1 - {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} } \right)\left( {1 - {\mathcal{W}}_{{{\mathcal{T}}_{2} }}^{q} } \right)} \right)^{\frac{1}{q}} }}} \right)}} ,\left( {\frac{{{\mathcal{N}}_{1}^{q} + {\mathcal{N}}_{2}^{q} }}{{1 + {\mathcal{N}}_{1}^{q} {\mathcal{N}}_{2}^{q} }}} \right)^{\frac{1}{q}} {\text{e}}^{{i2\pi \left( {\frac{{{\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} + {\mathcal{W}}_{{{\mathcal{N}}_{2} }}^{q} }}{{1 + {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} {\mathcal{W}}_{{{\mathcal{N}}_{2} }}^{q} }}} \right)^{\frac{1}{q}} }} } \right);$$

$$3.\quad \delta {\mathbb{E}}_{1} = \left( {\left( {\frac{{\left( {1 + {\mathcal{T}}_{1}^{q} } \right)^{\delta } - \left( {1 - {\mathcal{T}}_{1}^{q} } \right)^{\delta } }}{{\left( {1 + {\mathcal{T}}_{1}^{q} } \right)^{\delta } + \left( {1 - {\mathcal{T}}_{1}^{q} } \right)^{\delta } }}} \right)^{\frac{1}{q}} {\text{e}}^{{i2\pi \left( {\frac{{\left( {1 + {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} } \right)^{\delta } - \left( {1 - {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} } \right)^{\delta } }}{{\left( {1 + {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} } \right)^{\delta } + \left( {1 - {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} } \right)^{\delta } }}} \right)^{\frac{1}{q}} }} ,\left( {\frac{{\left( 2 \right)^{\frac{1}{q}} {\mathcal{N}}_{1}^{\delta } }}{{\left( {\left( {2 - {\mathcal{N}}_{1}^{q} } \right)^{\delta } + \left( {{\mathcal{N}}_{1}^{q} } \right)^{\delta } } \right)^{\frac{1}{q}} }}} \right){\text{e}}^{{i2\pi \left( {\frac{{\left( 2 \right)^{\frac{1}{q}} {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{\delta } }}{{\left( {\left( {2 - {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right)^{\delta } + \left( {{\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right)^{\delta } } \right)^{\frac{1}{q}} }}} \right)}} } \right);{\text{ and}}$$

$$4. \quad{\mathbb{E}}_{1}^{\delta } = \left( {\left( {\frac{{\left( 2 \right)^{\frac{1}{q}} {\mathcal{T}}_{1}^{\delta } }}{{\left( {\left( {2 - {\mathcal{T}}_{1}^{q} } \right)^{\delta } + \left( {{\mathcal{T}}_{1}^{q} } \right)^{\delta } } \right)^{\frac{1}{q}} }}} \right){\text{e}}^{{i2\pi \left( {\frac{{\left( 2 \right)^{\frac{1}{q}} {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{\delta } }}{{\left( {\left( {2 - {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} } \right)^{\delta } + \left( {{\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} } \right)^{\delta } } \right)^{\frac{1}{q}} }}} \right)}} ,\left( {\frac{{\left( {1 + {\mathcal{N}}_{1}^{q} } \right)^{\delta } - \left( {1 - {\mathcal{N}}_{1}^{q} } \right)^{\delta } }}{{\left( {1 + {\mathcal{N}}_{1}^{q} } \right)^{\delta } + \left( {1 - {\mathcal{N}}_{1}^{q} } \right)^{\delta } }}} \right)^{\frac{1}{q}} {\text{e}}^{{i2\pi \left( {\frac{{\left( {1 + {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right)^{\delta } - \left( {1 - {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right)^{\delta } }}{{\left( {1 + {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right)^{\delta } + \left( {1 - {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right)^{\delta } }}} \right)^{\frac{1}{q}} }} } \right).$$

Definition 9

For any q-ROFN ${\mathbb{E}}_{1} = \left( {{\mathcal{T}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{1} }} }} ,{\mathcal{N}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{1} }} }} } \right),$ the score function and accuracy function are defined as follows:

$$ {\mathcal{S}}\left( {{\mathbb{E}}_{1} } \right) = \frac{1}{2}\left( {{\mathcal{T}}_{1}^{q} + {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} - {\mathcal{N}}_{1}^{q} - {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right), $$

(7)

$$ {\mathbb{H}}\left( {{\mathbb{E}}_{1} } \right) = \frac{1}{2}\left( {{\mathcal{T}}_{1}^{q} + {\mathcal{W}}_{{{\mathcal{T}}_{1} }}^{q} + {\mathcal{N}}_{1}^{q} + {\mathcal{W}}_{{{\mathcal{N}}_{1} }}^{q} } \right), $$

(8)

where ${\mathcal{S}}\left( {{\mathbb{E}}_{1} } \right) \in \left[ { - 1,1} \right]$ and ${\mathbb{H}}\left( {{\mathbb{E}}_{1} } \right) \in \left[ {0,1} \right].$

Theorem 1

For any two Cq-ROFNs ${\mathbb{E}}_{1} = \left( {{\mathcal{T}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{1} }} }} ,{\mathcal{N}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{1} }} }} } \right)$ and ${\mathbb{E}}_{2} = \left( {{\mathcal{T}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{2} }} }} ,{\mathcal{N}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{2} }} }} } \right)$ with any $\delta ,\delta_{1} ,\delta_{2} > 0,$

• 1. ${\mathbb{E}}_{1} \oplus {\mathbb{E}}_{2} = {\mathbb{E}}_{2} \oplus {\mathbb{E}}_{1} ;$

• 2. ${\mathbb{E}}_{1} \otimes {\mathbb{E}}_{2} = {\mathbb{E}}_{2} \otimes {\mathbb{E}}_{1} ;$

• 3. $\delta \left( {{\mathbb{E}}_{1} \oplus {\mathbb{E}}_{2} } \right) = \delta {\mathbb{E}}_{1} \oplus \delta {\mathbb{E}}_{2} ;$

• 4. $\left( {{\mathbb{E}}_{1} \otimes {\mathbb{E}}_{2} } \right)^{\delta } = {\mathbb{E}}_{1}^{\delta } \otimes {\mathbb{E}}_{2}^{\delta } ;$

• 5. $\delta_{1} {\mathbb{E}}_{1} \oplus \delta_{2} {\mathbb{E}}_{1} = \left( {\delta_{1} + \delta_{2} } \right){\mathbb{E}}_{1} ;{\text{ and}}$

• 6. ${\mathbb{E}}_{1}^{{\delta_{1} }} \otimes {\mathbb{E}}_{1}^{{\delta_{2} }} = {\mathbb{E}}_{1}^{{\delta_{1} + \delta_{2} }} .$

The proof of Theorem 1 is presented in the "Appendix".

Theorem 2

For any two Cq-ROFNs ${\mathbb{E}}_{1} = \left( {{\mathcal{T}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{1} }} }} ,{\mathcal{N}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{1} }} }} } \right)$ and ${\mathbb{E}}_{2} = \left( {{\mathcal{T}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{2} }} }} ,{\mathcal{N}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{2} }} }} } \right),$

• 1. ${\mathbb{E}}_{1}^{c} \vee {\mathbb{E}}_{2}^{c} = \left( {{\mathbb{E}}_{1} \wedge {\mathbb{E}}_{2} } \right)^{c} ;$

• 2. ${\mathbb{E}}_{2}^{c} \wedge {\mathbb{E}}_{1}^{c} = \left( {{\mathbb{E}}_{1} \vee {\mathbb{E}}_{2} } \right)^{c} ;$

• 3. ${\mathbb{E}}_{1}^{c} \oplus {\mathbb{E}}_{2}^{c} = \left( {{\mathbb{E}}_{1} \otimes {\mathbb{E}}_{2} } \right)^{c} ;$

• 4. ${\mathbb{E}}_{1}^{c} \otimes {\mathbb{E}}_{2}^{c} = \left( {{\mathbb{E}}_{1} \oplus {\mathbb{E}}_{2} } \right)^{c} ;$

• 5. $\left( {{\mathbb{E}}_{1} \vee {\mathbb{E}}_{2} } \right) \oplus \left( {{\mathbb{E}}_{1} \wedge {\mathbb{E}}_{2} } \right) = {\mathbb{E}}_{1} \oplus {\mathbb{E}}_{2} ;{\text{ and}}$

• 6. $\left( {{\mathbb{E}}_{1} \vee {\mathbb{E}}_{2} } \right) \otimes \left( {{\mathbb{E}}_{1} \wedge {\mathbb{E}}_{2} } \right) = {\mathbb{E}}_{1} \otimes {\mathbb{E}}_{2} .$

Proof

Similar to the case of Theorem 1, the proofs are omitted.

Theorem 3

For any three Cq-ROFNs ${\mathbb{E}}_{1} = \left( {{\mathcal{T}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{1} }} }} ,{\mathcal{N}}_{1} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{1} }} }} } \right)$, ${\mathbb{E}}_{2} = \left( {{\mathcal{T}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{2} }} }} ,{\mathcal{N}}_{2} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{2} }} }} } \right)$, and ${\mathbb{E}}_{3} = \left( {{\mathcal{T}}_{3} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{3} }} }} ,{\mathcal{N}}_{3} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{3} }} }} } \right),$

• 1. $\left( {{\mathbb{E}}_{1} \vee {\mathbb{E}}_{2} } \right) \wedge {\mathbb{E}}_{3} = \left( {{\mathbb{E}}_{1} \wedge {\mathbb{E}}_{3} } \right) \vee \left( {{\mathbb{E}}_{2} \wedge {\mathbb{E}}_{3} } \right);$

• 2. $\left( {{\mathbb{E}}_{1} \wedge {\mathbb{E}}_{2} } \right) \vee {\mathbb{E}}_{3} = \left( {{\mathbb{E}}_{1} \vee {\mathbb{E}}_{3} } \right) \wedge \left( {{\mathbb{E}}_{2} \vee {\mathbb{E}}_{3} } \right);$

• 3. $\left( {{\mathbb{E}}_{1} \vee {\mathbb{E}}_{2} } \right) \oplus {\mathbb{E}}_{3} = \left( {{\mathbb{E}}_{1} \oplus {\mathbb{E}}_{3} } \right) \vee \left( {{\mathbb{E}}_{2} \oplus {\mathbb{E}}_{3} } \right);$

• 4. $\left( {{\mathbb{E}}_{1} \wedge {\mathbb{E}}_{2} } \right) \oplus {\mathbb{E}}_{3} = \left( {{\mathbb{E}}_{1} \oplus {\mathbb{E}}_{3} } \right) \wedge \left( {{\mathbb{E}}_{2} \oplus {\mathbb{E}}_{3} } \right);$

• 5. $\left( {{\mathbb{E}}_{1} \vee {\mathbb{E}}_{2} } \right) \otimes {\mathbb{E}}_{3} = \left( {{\mathbb{E}}_{1} \otimes {\mathbb{E}}_{3} } \right) \vee \left( {{\mathbb{E}}_{2} \otimes {\mathbb{E}}_{3} } \right);{\text{ and}}$

• 6. $\left( {{\mathbb{E}}_{1} \wedge {\mathbb{E}}_{2} } \right) \otimes {\mathbb{E}}_{3} = \left( {{\mathbb{E}}_{1} \otimes {\mathbb{E}}_{3} } \right) \wedge \left( {{\mathbb{E}}_{2} \otimes {\mathbb{E}}_{3} } \right).$

Proof

Similar to the case of Theorem 1, the proofs are omitted.

Complex q-rung orthopair fuzzy Einstein arithmetic aggregation operators

In this section, we propose complex q-rung orthopair fuzzy Einstein aggregation operators.

Complex q-rung orthopair fuzzy Einstein weighted averaging operator

The complex q-rung orthopair fuzzy Einstein weighted averaging operator is investigated, and its properties are discussed.

Definition 10

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right),i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the Cq-ROFEWA operator is given as ${\text{Cq-ROFEWA}}:{{\aleph }}^{n}\to {\aleph }$, and defined by:

$$ \begin{aligned} & {\text{Cq-ROFEWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\\ &\quad ={\omega }_{1}{\mathbb{E}}_{1}\oplus {\omega }_{2}{\mathbb{E}}_{2}\oplus , \cdots , \oplus {\omega }_{n}{\mathbb{E}}_{n}={\oplus }_{i=1}^{n}{\omega }_{i}{\mathbb{E}}_{i} \end{aligned} $$

(9)

Here, the symbol $\aleph$ represents the family of Cq-ROFNs, and the weight vector is defined as $\sum_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\in [\text{0,1}]$.

Remark 1

By substituting ${\omega }_{i}=\frac{1}{n}$ for all instances of $i$, the Cq-ROFEWA operator is reduced to the complex q-rung orthopair fuzzy averaging (Cq-ROFA) operator, as follows:

$$ \begin{aligned} {\text{Cq-ROFA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right) & =\frac{1}{n}\left({\mathbb{E}}_{1}\oplus {\mathbb{E}}_{2}\oplus , \cdots , \oplus {\mathbb{E}}_{n}\right)\\ & =\frac{1}{n}{\oplus }_{i=1}^{n}{\mathbb{E}}_{i }. \end{aligned} $$

(10)

According to Einstein’s operational laws, we obtain the following result.

Theorem 4

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right),i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the aggregating value from Definition 10 is a Cq-ROFN, and:

$${\text{Cq-ROFEWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)=\left(\begin{array}{c}{\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{n}{\mathcal{N}}_{i}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{n}{\left(2-{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left({\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{n}{\mathcal{W}}_{{\mathcal{N}}_{i}}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{n}{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left({\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right)}\end{array}\right). $$

(11)

The proof of Theorem 4 is presented in the Appendix.

Theorem 5

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right)\in {\text{Cq-ROFN}},i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the relationship between the Cq-ROFEWA and Cq-ROFWA operators is expressed as follows:

$$ \begin{aligned} & {\text{Cq-ROFEWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\\ &\quad \le {\text{Cq-ROFWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right), \end{aligned} $$

where the weight vector is defined by $\sum_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\in [\text{0,1}].$

The proof of Theorem 5 is presented in the Appendix.

The Cq-ROFEWA operator has the following properties.

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right)\in {\text{Cq-ROFN}},i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs and the weight vector is defined by $\sum_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\in [\text{0,1}]$. Then, we have the following:

• 1. Idea: When ${\mathbb{E}}_{i}={\mathbb{E}}_{0}=\left({\mathcal{T}}_{0}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{0}}},{\mathcal{N}}_{0}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{0}}}\right),\forall i$, ${\text{Cq-ROFEWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)={\mathbb{E}}_{0}$.

• 2. Boundedness: Let ${\mathbb{E}}_{i}^-=\left(\text{min}\left({\mathcal{T}}_{i}\right){\text{e}}^{i2\pi \text{min}\left({\mathcal{W}}_{{\mathcal{T}}_{i}}\right)},\text{max}\left({\mathcal{N}}_{i}\right){\text{e}}^{i2\pi \text{max}\left({\mathcal{W}}_{{\mathcal{N}}_{i}}\right)}\right),{\mathbb{E}}_{i}^{+}=\left(\text{max}\left({\mathcal{T}}_{i}\right){\text{e}}^{i2\pi \text{max}\left({\mathcal{W}}_{{\mathcal{T}}_{i}}\right)},\text{min}\left({\mathcal{N}}_{i}\right){\text{e}}^{i2\pi \text{min}\left({\mathcal{W}}_{{\mathcal{N}}_{i}}\right)}\right)$; then, ${\mathbb{E}}_{i}^-\le {\text{Cq-ROFEWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\le {\mathbb{E}}_{i}^{+}$.

• 3. Monotonicity: If ${\mathbb{E}}_{i}\le {\mathbb{E}}_{i}^{{^{\prime}}{^{\prime}}},\forall i$, ${\text{Cq-ROFEWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\le {\text{Cq-ROFEWA}}\left({\mathbb{E}}_{1}^{{^{\prime}}{^{\prime}}},{\mathbb{E}}_{2}^{{^{\prime}}{^{\prime}}},\ldots,{\mathbb{E}}_{n}^{{^{\prime}}{^{\prime}}}\right)$.

Proofs of these properties are presented in the Appendix.

Complex q-rung orthopair fuzzy Einstein ordered weighted averaging operator

Definition 11

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right),i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the Cq-ROFEOWA operator is given by ${\text{Cq-ROFEOWA}}:{{\aleph }}^{n}\to {\aleph }$

$$ \begin{aligned} & {\text{Cq-ROFEOWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)={\omega }_{1}{\mathbb{E}}_{O\left(1\right)} \\ &\quad \oplus {\omega }_{2}{\mathbb{E}}_{O\left(2\right)}\oplus , \cdots , \oplus {\omega }_{n}{\mathbb{E}}_{O\left(n\right)}={\oplus }_{i=1}^{n}{\omega }_{i}{\mathbb{E}}_{O\left(i\right)} \end{aligned} $$

(12)

where the symbol $\aleph$ represents the family of Cq-ROFNs, and the weight vector is defined by $\sum_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\in [\text{0,1}]$. $\left(O\left(1\right),O\left(2\right),\ldots,O\left(n\right)\right)$ is a permutation of $\left(i=\text{1,2},\ldots,n\right)$ such that ${\mathbb{E}}_{O\left(i\right)}\le {\mathbb{E}}_{O\left(i-1\right)}.$

Remark 2

By substituting ${\omega }_{i}=\frac{1}{n}$ for all instances of $i$, the Cq-ROFEOWA operator is reduced to the complex q-rung orthopair fuzzy ordered averaging (Cq-ROFOA) operator, as follows:

$$ \begin{aligned} & {\text{Cq-ROFA}}\left( {{\mathbb{E}}_{1} ,{\mathbb{E}}_{2} , \ldots ,{\mathbb{E}}_{n} } \right) \\ &\quad = \frac{1}{n}\left( {{\mathbb{E}}_{{O\left( 1 \right)}} \oplus {\mathbb{E}}_{{O\left( 2 \right)}} \oplus , \cdots , \oplus {\mathbb{E}}_{{O\left( n \right)}} } \right) \\ &\quad = \frac{1}{n} \oplus _{{i = 1}}^{n} {\mathbb{E}}_{{O\left( i \right)}} . \end{aligned} $$

(13)

According to Einstein’s operational laws, we examine the following results.

Theorem 6

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right),i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the aggregating value from Definition 11 is a Cq-ROFN, and

$$\text{Cq-ROFEOWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)=\left(\begin{array}{c}{\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{n}{\mathcal{N}}_{O\left(i\right)}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{n}{\left(2-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left({\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{n}{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{n}{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left({\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

(14)

where the weight vector is defined by $\sum_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\in [\text{0,1}]$. $\left(O\left(1\right),O\left(2\right),\ldots,O\left(n\right)\right)$ is a permutation of $\left(i=\text{1,2},\ldots,n\right)$ such that ${\mathbb{E}}_{O\left(i\right)}\le {\mathbb{E}}_{O\left(i-1\right)}$. When we consider ${\mathcal{N}}_{O\left(i\right)}^{q}=1-{\mathcal{T}}_{O\left(i\right)}^{q}$, Eq. (14) is converted into the following equation:

$${\text{Cq-ROFEOWA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)=\left(\begin{array}{c}{\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}},\\ {\left(1-\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(1-\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}}\end{array}\right).$$

Proof

Similar to the case of Theorem 4, the proof is omitted.

Next, we discuss the properties of this operator.

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right)\in {\text{Cq-ROFN}},i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs and the weight vector is defined by $\sum_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\in [\text{0,1}]$. Then, we have:

• 1. Idea: When ${\mathbb{E}}_{i}={\mathbb{E}}_{0}=\left({\mathcal{T}}_{0}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{0}}},{\mathcal{N}}_{0}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{0}}}\right),\forall i$, $\text{Cq-ROFEOWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)={\mathbb{E}}_{0}$.

• 2. Boundedness: Let ${\mathbb{E}}_{i}^-=\left(\text{min}\left({\mathcal{T}}_{i}\right){\text{e}}^{i2\pi \text{min}\left({\mathcal{W}}_{{\mathcal{T}}_{i}}\right)},\text{max}\left({\mathcal{N}}_{i}\right){\text{e}}^{i2\pi \text{max}\left({\mathcal{W}}_{{\mathcal{N}}_{i}}\right)}\right),{\mathbb{E}}_{i}^{+}=\left(\text{max}\left({\mathcal{T}}_{i}\right){\text{e}}^{i2\pi \text{max}\left({\mathcal{W}}_{{\mathcal{T}}_{i}}\right)},\text{min}\left({\mathcal{N}}_{i}\right){\text{e}}^{i2\pi \text{min}\left({\mathcal{W}}_{{\mathcal{N}}_{i}}\right)}\right)$; then, ${\mathbb{E}}_{i}^-\le \text{Cq-ROFEOWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\le {\mathbb{E}}_{i}^{+}$.

• 3. Monotonicity: If ${\mathbb{E}}_{i}\le {\mathbb{E}}_{i}^{{^{\prime}}{^{\prime}}},\forall i$, $\text{Cq-ROFEOWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\le \text{Cq-ROFEOWA}\left({\mathbb{E}}_{1}^{{^{\prime}}{^{\prime}}},{\mathbb{E}}_{2}^{{^{\prime}}{^{\prime}}},\ldots,{\mathbb{E}}_{n}^{{^{\prime}}{^{\prime}}}\right)$.

Generalized complex q-rung orthopair fuzzy Einstein weighted averaging operator

Definition 12

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right),i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the GCq-ROFEWA operator is given by ${\text{GCq-ROFEWA}}:{{\aleph }}^{n}\to {\aleph }$

$$ \begin{aligned} & \text{GCq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\\ &\quad ={\left({\omega }_{1}{\mathbb{E}}_{1}^{\delta }\oplus {\omega }_{2}{\mathbb{E}}_{2}^{\delta }\oplus , \cdots , \oplus {\omega }_{n}{\mathbb{E}}_{n}^{\delta }\right)}^{\frac{1}{\delta }}={\left({\oplus }_{i=1}^{n}{\omega }_{i}{\mathbb{E}}_{i}^{\delta }\right)}^{\frac{1}{\delta }}\to \end{aligned} $$

(15)

where the symbol $\aleph$ represents the family of Cq-ROFNs, and the weight vector is defined by $\sum_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\in [\text{0,1}]$, $\delta >0$.

Remark 3

By substituting ${\omega }_{i}=\frac{1}{n}$ for all instances of $i$, the GCq-ROFEWA operator is reduced to the generalized complex q-rung orthopair fuzzy averaging (GCq-ROFA) operator, as follows:

$$ \begin{aligned} & {\text{GCq-ROFA}}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right) \\ &\quad ={\left(\frac{1}{n}\left({\mathbb{E}}_{1}^{\delta }\oplus {\mathbb{E}}_{2}^{\delta }\oplus , \cdots , \oplus {\mathbb{E}}_{n}^{\delta }\right)\right)}^{\frac{1}{\delta }}={\left(\frac{1}{n}{\oplus }_{i=1}^{n}{\mathbb{E}}_{i}^{\delta }\right)}^{\frac{1}{\delta }} \end{aligned} $$

(16)

When $\delta =1$, the GCq-ROFEWA operator is reduced to the Cq-ROFEWA operator.

Using Einstein’s operational laws, the following result is obtained.

Theorem 7

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right),i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the aggregating value from Definition 12 is a Cq-ROFN, and:

$$\begin{aligned}&\text{GCq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\hfill\\ &\quad =\left(\begin{array}{c}\frac{{\left(2\right)}^\frac{1}{q}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{i}^{q}\right)}^{\delta }+3{\left({\mathcal{T}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{i}^{q}\right)}^{\delta }-{\left({\mathcal{T}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{2\delta }}}{{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{i}^{q}\right)}^{\delta }+3{\left({\mathcal{T}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{i}^{q}\right)}^{\delta }-{\left({\mathcal{T}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}+\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{i}^{q}\right)}^{\delta }+3{\left({\mathcal{T}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{i}^{q}\right)}^{\delta }-{\left({\mathcal{T}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}^\frac{1}{q}}{\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }+3{\left({\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }-{\left({\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{2\delta }}}{{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }+3{\left({\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }-{\left({\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}+\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }+3{\left({\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }-{\left({\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}^\frac{1}{q}}\right)},\\ {\left(\frac{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{i}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{N}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{i}^{q}\right)}^{\delta }-{\left(1-{\mathcal{N}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}-\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{i}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{N}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{i}^{q}\right)}^{\delta }-{\left(1-{\mathcal{N}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{i}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{N}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{i}^{q}\right)}^{\delta }-{\left(1-{\mathcal{N}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}+\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{i}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{N}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{i}^{q}\right)}^{\delta }-{\left(1-{\mathcal{N}}_{i}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}-\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}+\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}\right)}^\frac{1}{q}}\end{array}\right).\end{aligned}$$

(17)

Proof

Similar to the case of Theorem 4, the proof is omitted.

Generalized complex q-rung orthopair fuzzy Einstein ordered weighted averaging operator

Definition 13

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right),i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the GCq-ROFEOWA operator is given by $\text{GCq-ROFEOWA}:{{\aleph }}^{n}\to {\aleph }$

$$ \begin{aligned} & \text{GCq-ROFEOWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\\ &\quad ={\left({\omega }_{1}{\mathbb{E}}_{O\left(1\right)}^{\delta }\oplus {\omega }_{2}{\mathbb{E}}_{O\left(2\right)}^{\delta }\oplus , \cdots , \oplus {\omega }_{n}{\mathbb{E}}_{O\left(n\right)}^{\delta }\right)}^{\frac{1}{\delta }}\\ &\quad ={\left({\oplus }_{i=1}^{n}{\omega }_{i}{\mathbb{E}}_{O\left(i\right)}^{\delta }\right)}^{\frac{1}{\delta }}\to \end{aligned} $$

(18)

where the symbol $\aleph$ represents the family of Cq-ROFNs, and the weight vector is defined by $\sum_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\in [\text{0,1}]$, $\delta >0$.

Remark 4

By substituting ${\omega }_{i}=\frac{1}{n}$ for all instances of $i$, the GCq-ROFEOWA operator is reduced to the generalized complex q-rung orthopair fuzzy ordered averaging (GCq-ROFOA) operator, as follows:

$$ \begin{aligned} & \text{GCq-ROFOA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right) \\ &\quad ={\left(\frac{1}{n}\left({\mathbb{E}}_{O\left(1\right)}^{\delta }\oplus {\mathbb{E}}_{O\left(2\right)}^{\delta }\oplus , \cdots , \oplus {\mathbb{E}}_{O\left(n\right)}^{\delta }\right)\right)}^{\frac{1}{\delta }} \\ &\quad ={\left(\frac{1}{n}{\oplus }_{i=1}^{n}{\mathbb{E}}_{O\left(i\right)}^{\delta }\right)}^{\frac{1}{\delta }} \end{aligned} $$

(19)

When $\delta =1$, the GCq-ROFEOWA operator is reduced to the Cq-ROFEOWA operator.

According to Einstssein’s operational laws, we obtain the following result.

Theorem 8

Suppose that ${\mathbb{E}}_{i}=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right),i=\text{1,2},\ldots,n$ comprise the family of Cq-ROFNs; then, the aggregating value from Definition 13 is a Cq-ROFN, and

$$\begin{aligned} & \text{GCq-ROFEOWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\\ &\quad =\left(\begin{array}{c}\frac{{\left(2\right)}^\frac{1}{q}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }+3{\left({\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }-{\left({\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{2\delta }}}{{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }+3{\left({\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }-{\left({\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}+\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }+3{\left({\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }-{\left({\mathcal{T}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}^\frac{1}{q}}{\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }+3{\left({\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }-{\left({\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{2\delta }}}{{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }+3{\left({\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }-{\left({\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}+\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }+3{\left({\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(2-{\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }-{\left({\mathcal{W}}_{{\mathcal{T}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}^\frac{1}{q}}\right)},\\ {\left(\frac{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }-{\left(1-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}-\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }-{\left(1-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }-{\left(1-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}+\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }-{\left(1-{\mathcal{N}}_{O\left(i\right)}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}-\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}{\left(\begin{array}{c}{\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}+\\ 3{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}+\\ {\left(\begin{array}{c}{\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }+3{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}-\\ {\prod }_{i=1}^{n}{\left\{{\left(1+{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{N}}_{O\left(i\right)}}^{q}\right)}^{\delta }\right\}}^{{\omega }_{i}}\end{array}\right)}^{\frac{1}{\delta }}\end{array}\right)}\right)}^\frac{1}{q}}\end{array}\right). \end{aligned}$$

(20)

Proof

Similar to the case of Theorem 4, the proof is omitted.

In Eq. (20), $\delta$ plays a key role in the aggregation of the Cq-ROFNs. The parameter $\delta$ takes a special number; then, the GCq-ROFEWA operator can be reduced. For example, when $\delta = 1$, Eq. (20) is converted into Eq. (14).

MAGDM approach based on proposed operators

Description of decision-making problem

Suppose an MAGDM problem in which $A = \left\{ {x_{1} ,x_{2} , \ldots ,x_{m} } \right\}$ represents the family of alternatives, and $G = \left\{ {G_{1} ,G_{2} , \ldots ,G_{n} } \right\}$ represents the family of finite attributes with weight vector $\omega = \left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} } \right)$. The decision matrix $A = \left( {{\mathbb{E}}_{ij} } \right)_{m \times n}$ is given by decision makers through evaluation of the attribute ${G}_{j}$ under the alternative${x}_{i}$, which is represented by the Cq-ROFN. The complex q-rung orthopair fuzzy decision matrix is presented in Table 1.

Table 1 Complex q-rung orthopair fuzzy decision matrix

We use the proposed operators to solve this decision-making problem, and the steps are as follows.

Step 1: Normalize the decision matrix with respect to.

$$ {r}_{ij} =\left({\mathcal{T}}_{ij}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{ij}}},{\mathcal{N}}_{ij}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{ij}}}\right)=\left\{\begin{array}{cc}{\mathbb{E}}_{ij}^{c}& j \quad \text{is benefit types}\\ {\mathbb{E}}_{ij}& j \quad \text{is cost types}\end{array}\right.$$

(21)

Step 2: Use Eq. (20) to aggregate the normalized decision matrix.

$${r}_{i}=GCq-ROFO{{W}}A\left({r}_{i1},{r}_{i2},\ldots,{r}_{in}\right),i=\text{1,2},3,\ldots,m$$

Step 3: Use Eq. (7) to examine the score values of the aggregated values obtained in step 2.

Step 4: Rank all the alternatives according to the score values from step 3, and select the best one.

Step 5: End.

Illustrative numerical example

An example was taken from the area of the investment, where the investor wishes to invest money in a standard company. After a careful analysis, five possible alternatives represented by $A=\left\{{x}_{1},{x}_{2},\ldots,{x}_{m}\right\}$ were considered, as shown in Table 2.

Table 2 Symbols of the alternatives

Furthermore, these alternatives were evaluated using four attributes represented by $G=\left\{{G}_{1},{G}_{2},\ldots,{G}_{n}\right\}$, which are presented in Table 3.

Table 3 Representations of the attributes

The weight vector for the given attributes was given as $\omega =\left\{\text{0.25,0.15,0.4,0.2}\right\}$; then, the complex q-rung orthopair fuzzy decision matrix was obtained, as shown in Table 4.

Table 4 Complex q-rung orthopair fuzzy decision matrix

The steps of the decision-making process were as follows:

Step 1: Normalize the decision matrix and obtain the results shown in Table 5.

Table 5 Normalized complex q-rung orthopair fuzzy decision matrix

Step 2: Obtain the aggregation results using Eq. (20), which are presented in Table 6.

Table 6 Aggregation values of the Cq-ROFNs

Step 3: Obtain the scores of the aggregated values using Eq. (7), which are presented in Table 7.

Table 7 Score values of the Cq-ROFNs

Step 4: Rank all the alternatives and select the best one.

$${\mathbb{E}}_{5}\le {\mathbb{E}}_{4}\le {\mathbb{E}}_{1}\le {\mathbb{E}}_{3}\le {\mathbb{E}}_{2}$$

Hence, the best alternative is ${\mathbb{E}}_{2}$, which represents the furniture company.

Step 5: End.

Effect of parameter ${{\delta}}$

In this subsection, we examine the effect of the parameter δ on the ranking results. We obtained the ranking results for different values of the parameter δ, as shown in Table 8 ($q$ was 1).

Table 8 Effect of the parameter $\updelta$, for $\text{q}=1$

As shown in Table 8, the parameter $\delta$ affected the ranking results. However, the best alternative did not change.

Effect of parameter ${{q}}$

In this subsection, we examine the effect of the parameter $q$ on the ranking results. We obtained the ranking results for different values of $q$, as shown in Table 9 ($\delta$ was 1).

Table 9 Effect of the parameter $\text{q}$ for $\updelta =1$

As indicated by Table 9, the parameter $q$ affected the ranking results. However, the best alternative did not change.

Advantages and comparative analysis

The proposed method was compared with existing approaches to highlight its advantages.

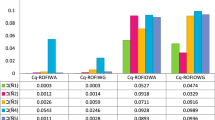
We compared Garg and Rani’s method [40] based on the power aggregation operators for the CIFS and Garg and Rani’s method [42] based on the aggregation operators for the CIFS with the proposed method for the CPFS and Cq-ROFS. The results are presented in Table 10 and Fig. 2.

Table 10 Comparison of the proposed method with existing approaches

Fig. 2

Graphical representation of Table 10

Figure 2 contains five alternatives represented by ${\mathbb{E}}_{i}\left(i=\text{1,2},\text{3,4},5\right)$. To identify the best alternative among them, we adopt four types of operators, whose representations are presented in Table 10. Two of the operators existed previously, and the other two are newly proposed herein.

As indicated by Table 10 and Fig. 2, we obtained the same ranking results for the four methods. This validates the proposed method.

Furthermore, the geometric interpretations of the range of Cq-ROFSs and the existing methods are shown in Fig. 3, which represents the unit disc in a complex plane.

Fig. 3

Range for Cq-ROFS and the existing approaches

The advantages of the proposed method are explained below.

First numerical example for comparison

An example is taken from the area of the investment, where the investor wishes to invest money in a stranded company. After a careful analysis, we consider the five possible alternatives represented by $A=\left\{{x}_{1},{x}_{2},\ldots,{x}_{5}\right\}$, as shown in Table 2. The alternatives are evaluated using four attributes represented by $G=\left\{{G}_{1},{G}_{2},\ldots,{G}_{4}\right\}$, as shown in Table 3. The weight vector for the given attributes is given as $\omega =\left\{\text{0.25,0.15,0.4,0.2}\right\}$, and the normalized complex q-rung orthopair fuzzy decision matrix is presented in Table 11.

Table 11 Normalized complex q-rung orthopair fuzzy decision matrix

Using Eqs. (20) and (7) for $\delta =20$, then the score values of the alternatives are obtained, as shown in Table 12 and Fig. 4.

Table 12 Score values of the proposed methods

Fig. 4

Graphical representation of Table 12

Then, all the alternatives are ranked as follows, and the best one is selected.

$${\mathbb{E}}_{5}\le {\mathbb{E}}_{4}\le {\mathbb{E}}_{3}\le {\mathbb{E}}_{2}\le {\mathbb{E}}_{1}$$

Hence, the best alternative is ${\mathbb{E}}_{1}$, which represents the furniture company.

The proposed method is compared with existing approaches in Table 13 and Fig. 5.

Table 13 Comparison of the proposed method with existing approaches

Fig. 5

Graphical representation of Table 13

Figure 5 shows five alternatives represented by ${\mathbb{E}}_{i}\left(i=\text{1,2},\text{3,4},5\right)$. Because the two existing methods based on the CIFS [40] and [42] could not solve this problem, they are not included in Fig. 5. In this example, we select the complex Pythagorean fuzzy information form.

Therefore, this example demonstrates the advantages of the proposed method.

Second numerical example for comparison

An example is taken from the area of the investment, where the investor wishes to invest money in a stranded company. After a careful analysis, we consider the five possible alternatives represented by $A=\left\{{x}_{1},{x}_{2},\ldots,{x}_{5}\right\}$, as shown in Table 2, which are evaluated using four attributes represented by $G=\left\{{G}_{1},{G}_{2},\ldots,{G}_{4}\right\}$, as shown in Table 3. The weight vector for the given attributes is given as $\omega =\left\{\text{0.25,0.15,0.4,0.2}\right\}$, and the normalized complex q-rung orthopair fuzzy decision matrix is presented in Table 14.

Table 14 Normalized complex q-rung orthopair fuzzy decision matrix

Using Eqs. (20) and (7) for $\delta =20$, the score values of the alternatives are obtained, as shown in Table 15 and Fig. 6.

Table 15 Score values of the proposed method

Fig. 6

The graphical representation of the Table 15

Then, all the alternatives are ranked as follows, and the best one is selected.

$${\mathbb{E}}_{1}\le {\mathbb{E}}_{3}\le {\mathbb{E}}_{4}\le {\mathbb{E}}_{2}\le {\mathbb{E}}_{5}$$

Hence, the best alternative is ${\mathbb{E}}_{5}$, which represents the furniture company.

The proposed method is compared with existing approaches in Table 16 and Fig. 7.

Table 16 Comparison of the proposed method with existing approaches

Fig. 7

Graphical representation of Table 16

Figure 7 shows five alternatives represented by ${\mathbb{E}}_{i}\left(i=\text{1,2},\text{3,4},5\right)$, as the methods based on the CIFS and CPFS cannot solve this problem. In Fig. 7, only the proposed method is shown, indicating that the proposed method is more general than the other methods.

Defense budget

Next, we discuss the defense budget of Pakistan. Information regarding the defense budget, national saving scheme, deposit and reserves, and development expenditure and revenue account for this country is presented below. According to this information, we discuss the strength and capability of armies or which one is powerful militaries.

• 1. The total defense budget of the Pakistan army removes the lion’s share:

  • Pakistan army budget: 0.476%;

  • Pakistan air force budget: 0.21%;

  • Pakistan navy budget: 0.11%;

  • Pakistan’s inter-service budget: 0.20%.

• 2. The total national saving scheme budget of Pakistan removes the lion’s share:

  • Pakistan investment deposit account budget: 0.8%;

  • Pakistan’s other accounts budget: 0.5%;

  • Pakistan total receipts budget: 0.17%;

  • Pakistan net receipts budget: 0.13%.

• 3. The total deposit and reserves budget of Pakistan removes the lion’s share:

  • Pakistan zakat collection account budget: 0.25%;

  • Pakistan civil and criminal deposit amount budget: 0.16%;

  • Pakistan’s personal deposit budget: 0.11%;

  • Pakistan’s post office welfare found budget: 0.1%.

• 4. The total development expenditure and revenue account budget of Pakistan take away the lion’s share:

  • Pakistan health budget: 0.27%;

  • Pakistan culture and religion budget: 0.15%;

  • Pakistan’s social protection budget: 0.17%;

  • Pakistan’s education budget: 0.18%.

Using Eq. (11), we obtain the following values: the imaginary part and the non-membership values are considered as zero, with weight vectors (0.2,0.2,0.2,0.3). Then, we have the following:

• Defense budget of Pakistan: 0.249.

• National saving scheme of Pakistan: 0.4

• Deposit and reserves of Pakistan: 0.155.

• Development expenditure and revenue account for Pakistan: 0.1925.

The ranking values of the foregoing results clearly indicate that the best alternative is the national saving scheme of Pakistan, with a score of 0.4. Similarly, we can analyze the budgets of any country.

The key advantages of the proposed approach are as follows:

• 1. The complex q-rung orthopair fuzzy Einstein aggregation operators generalize the existing Einstein aggregation operators.

• 2. The complex q-rung orthopair fuzzy Einstein aggregation operators take into account the refusal grade compared with complex intuitionistic and complex Pythagorean fuzzy Einstein aggregation operators.

• 3. The proposed method based on the proposed operators is more general than some existing methods, as the parameters $\delta \text{and} q$ can be changed.

The Cq-ROFS contains two complex-valued functions called the complex-valued membership and complex-valued non-membership grades. Because Cq-ROFN ${\mathbb{E}}=\left({\mathcal{T}}_{\mathbb{E}}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{\mathbb{E}}}},{\mathcal{N}}_{\mathbb{E}}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{\mathbb{E}}}}\right)$ satisfies the conditions $0\le {\mathcal{T}}_{\mathbb{E}}^{q}+{\mathcal{N}}_{\mathbb{E}}^{q}\le 1, 0\le {\mathcal{W}}_{{\mathcal{T}}_{\mathbb{E}}}^{q}+{\mathcal{W}}_{{\mathcal{N}}_{\mathbb{E}}}^{q}\le 1, \text{and} q\ge 1$, the CIFSs and CPFSs are clearly special cases of the proposed Cq-ROFS. By setting $q=1$, the proposed Cq-ROFS is converted into a CIFS, and by setting $q=2$, the proposed Cq-ROFS is converted into a CPFS. Moreover, the foregoing discussions indicate that the proposed method is more general and accurate than some existing approaches. The proposed method is useful for designing intelligent systems in real applications, such as image recognition.

Conclusion

This paper proposes the Cq-ROFS and its operational laws. An MADM method based on complex q-rung orthopair fuzzy information was investigated. To aggregate the Cq-ROFNs, we extended the EOs to Cq-ROFSs and proposed a family of complex q-rung orthopair fuzzy Einstein averaging operators, such as the Cq-ROFEWA operator, the Cq-ROFEOWA operator, the GCq-ROFEWA operator, and the GCq-ROFEOWA operator. Desirable properties and special cases of the introduced operators were discussed. Additionally, we developed a novel approach for MADM in the complex q-rung orthopair fuzzy context based on the proposed operators. Numerical examples were presented to demonstrate the effectiveness and superiority of the proposed method via comparison with existing methods. The main contributions of this study are as follows:

• 1. The concept of the Cq-ROFS was proposed in the form of polar coordinates belonging to a unit disc in a complex plane.

• 2. Complex q-rung orthopair fuzzy Einstein averaging operators were introduced, such as the Cq-ROFEWA operator, Cq-ROFEOWA operator, GCq-ROFEWA operator, and GCq-ROFEOWA operator. Desirable properties and special cases of the introduced operators were discussed.

• 3. An MADM method based on the proposed operators was developed, which is more general than some existing methods, as the parameters $\delta\text{ and}$ $q$ can be changed.

In the future, we will extend the present work to consider (1) aggregation operators for different FSs, e.g., the linguistic neutrosophic set [44], probabilistic linguistic information [45], linguistic D number [46], interval type-2 FS [47], T-spherical FS [48, 49], and others [50], and (2) MADM methods [51,52,53,54,55,56,57,58,59], which will be more flexible for future directs.

Appendix

Proof 1

We know that $0\le {\mathcal{T}}_{\mathbb{E}}^{q}+{\mathcal{N}}_{\mathbb{E}}^{q}\le 1, 0\le {\mathcal{W}}_{{\mathcal{T}}_{\mathbb{E}}}^{q}+{\mathcal{W}}_{{\mathcal{N}}_{\mathbb{E}}}^{q}\le 1$, then $0\le {\mathcal{T}}_{\mathbb{E}}^{q}\le 1-{\mathcal{N}}_{\mathbb{E}}^{q}, 0\le {\mathcal{W}}_{{\mathcal{T}}_{\mathbb{E}}}^{q}\le 1-{\mathcal{W}}_{{\mathcal{N}}_{\mathbb{E}}}^{q}$ and $0\le {\mathcal{N}}_{\mathbb{E}}^{q}\le 1-{\mathcal{T}}_{\mathbb{E}}^{q}, 0\le {\mathcal{W}}_{{\mathcal{N}}_{\mathbb{E}}}^{q}\le 1-{\mathcal{W}}_{{\mathcal{T}}_{\mathbb{E}}}^{q}$ implies that $0\le {\left({\mathcal{N}}_{\mathbb{E}}^{q}\right)}^{\delta }\le {\left(1-{\mathcal{T}}_{\mathbb{E}}^{q}\right)}^{\delta }, 0\le {\left({\mathcal{W}}_{{\mathcal{N}}_{\mathbb{E}}}^{q}\right)}^{\delta }\le {\left(1-{\mathcal{W}}_{{\mathcal{T}}_{\mathbb{E}}}^{q}\right)}^{\delta }$ implies that

$$ \begin{aligned} & {\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}} \\ & \quad \le {\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }-{\left({\mathcal{N}}_{\mathbb{E}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left({\mathcal{N}}_{\mathbb{E}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }-{\left({\mathcal{W}}_{{\mathcal{N}}_{\mathbb{E}}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }+{\left({\mathcal{W}}_{{\mathcal{N}}_{\mathbb{E}}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}} \end{aligned} $$

and

$$ \begin{aligned} & \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{\delta }}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{\delta }+{\left({\mathcal{N}}_{1}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{\delta }}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)}\\ &\quad \le \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{\delta }}{{\left({\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left({\mathcal{N}}_{1}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{\delta }}{{\left({\left(1+{\mathcal{W}}_{{\mathcal{T}}_{\mathbb{E}}}^{q}\right)}^{\delta }+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)} \end{aligned} $$

Thus,

$$ \begin{aligned} & {\left({\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}\right)}^{q} \\ &\quad +{\left(\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{\delta }}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{\delta }+{\left({\mathcal{N}}_{1}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)\right)}^{q}\le 1 \end{aligned} $$

$$\begin{aligned} & {\left({\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta } +{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}\right)}^{q}\\ &\quad +{\left(\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{\delta }}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)\right)}^{q}\le 1 \end{aligned} $$

Moreover,

$$ \begin{aligned} & {\left({\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}\right)}^{q}\\ &\quad +{\left(\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{\delta }}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{\delta }+{\left({\mathcal{N}}_{1}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)\right)}^{q}=0 \end{aligned} $$

$$ \begin{aligned} & {\left({\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}\right)}^{q}\\ &\quad +{\left(\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{\delta }}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)\right)}^{q}=0 \end{aligned} $$

If and only if ${\mathcal{T}}_{1}={\mathcal{N}}_{1}={\mathcal{W}}_{{\mathcal{T}}_{1}}={\mathcal{W}}_{{\mathcal{N}}_{1}}=0$.

$$ \begin{aligned} & {\left({\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}\right)}^{q}\\ &\quad +{\left(\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{\delta }}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{\delta }+{\left({\mathcal{N}}_{1}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)\right)}^{q}=1 \end{aligned} $$

$$ \begin{aligned} & {\left({\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}\right)}^{q}\\ &\quad +{\left(\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{\delta }}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)\right)}^{q}=1 \end{aligned} $$

If and only if ${\mathcal{T}}_{1}^{q}+{\mathcal{N}}_{1}^{q}=1,{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}+{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}=1$. Thus, $\delta {\mathbb{E}}_{1}={\mathbb{E}}_{4}$ is also Cq-ROFNs.

Proof 2

We examine the following parts (1,3,5), and the others is similar with them.

• 1. Let us consider the part (1), we have

$$\begin{aligned} {\mathbb{E}}_{1}\oplus {\mathbb{E}}_{2}&=\left({\left(\frac{{\mathcal{T}}_{1}^{q}+{\mathcal{T}}_{2}^{q}}{1+{\mathcal{T}}_{1}^{q}{\mathcal{T}}_{2}^{q}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}}{1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}}\right)}^\frac{1}{q}},\left(\frac{{\mathcal{N}}_{1}{\mathcal{N}}_{2}}{{\left(1+\left(1-{\mathcal{N}}_{1}^{q}\right)\left(1-{\mathcal{N}}_{2}^{q}\right)\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\mathcal{W}}_{{\mathcal{N}}_{1}}{\mathcal{W}}_{{\mathcal{N}}_{2}}}{{\left(1+\left(1-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)\left(1-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)\right)}^\frac{1}{q}}\right)}\right)\hfill \\ &=\left({\left(\frac{{\mathcal{T}}_{2}^{q}+{\mathcal{T}}_{1}^{q}}{1+{\mathcal{T}}_{2}^{q}{\mathcal{T}}_{1}^{q}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}}{1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}}\right)}^\frac{1}{q}},\left(\frac{{\mathcal{N}}_{2}{\mathcal{N}}_{1}}{{\left(1+\left(1-{\mathcal{N}}_{2}^{q}\right)\left(1-{\mathcal{N}}_{1}^{q}\right)\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\mathcal{W}}_{{\mathcal{N}}_{2}}{\mathcal{W}}_{{\mathcal{N}}_{1}}}{{\left(1+\left(1-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)\left(1-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)\right)}^\frac{1}{q}}\right)}\right)\hfill \\& ={\mathbb{E}}_{2}\oplus {\mathbb{E}}_{1}\end{aligned}$$

• 1. The proof of part (2) is straightforward.

• 2. Let us consider the part (3), we have

$${\mathbb{E}}_{1}\oplus {\mathbb{E}}_{2}=\left({\left(\frac{{\mathcal{T}}_{1}^{q}+{\mathcal{T}}_{2}^{q}}{1+{\mathcal{T}}_{1}^{q}{\mathcal{T}}_{2}^{q}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}}{1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}}\right)}^\frac{1}{q}},\left(\frac{{\mathcal{N}}_{1}{\mathcal{N}}_{2}}{{\left(1+\left(1-{\mathcal{N}}_{1}^{q}\right)\left(1-{\mathcal{N}}_{2}^{q}\right)\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\mathcal{W}}_{{\mathcal{N}}_{1}}{\mathcal{W}}_{{\mathcal{N}}_{2}}}{{\left(1+\left(1-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)\left(1-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)\right)}^\frac{1}{q}}\right)}\right)$$

Is equivalent to

$${\mathbb{E}}_{1}\oplus {\mathbb{E}}_{2}=\left(\begin{array}{c}{\left(\frac{\left(1+{\mathcal{T}}_{1}^{q}\right)\left(1+{\mathcal{T}}_{1}^{q}\right)-\left(1-{\mathcal{T}}_{2}^{q}\right)\left(1-{\mathcal{T}}_{2}^{q}\right)}{\left(1+{\mathcal{T}}_{1}^{q}\right)\left(1+{\mathcal{T}}_{1}^{q}\right)+\left(1-{\mathcal{T}}_{2}^{q}\right)\left(1-{\mathcal{T}}_{2}^{q}\right)}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)-\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)+\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}{\mathcal{N}}_{2}}{{\left(\left(2-{\mathcal{N}}_{1}^{q}\right)\left(2-{\mathcal{N}}_{2}^{q}\right)+{\mathcal{N}}_{1}^{q}{\mathcal{N}}_{2}^{q}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}{\mathcal{W}}_{{\mathcal{N}}_{2}}}{{\left(\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)+{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

We will consider for real part $a=\left(1+{\mathcal{T}}_{1}^{q}\right)\left(1+{\mathcal{T}}_{1}^{q}\right),b=\left(1-{\mathcal{T}}_{2}^{q}\right)\left(1-{\mathcal{T}}_{2}^{q}\right),c={\mathcal{N}}_{1}^{q}{\mathcal{N}}_{2}^{q},d=\left(2-{\mathcal{N}}_{1}^{q}\right)\left(2-{\mathcal{N}}_{2}^{q}\right)$ and similarly for imaginary part ${a}^{{\prime}}=\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right),{b}^{{\prime}}=\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right),{c}^{{\prime}}={\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q},{d}^{{\prime}}=\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)$, then

$${\mathbb{E}}_{1}\oplus {\mathbb{E}}_{2}=\left({\left(\frac{a-b}{a+b}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}^{{^{\prime}}}-{b}^{{^{\prime}}}}{{a}^{{^{\prime}}}+{b}^{{^{\prime}}}}\right)}^\frac{1}{q}},\frac{{\left(2c\right)}^\frac{1}{q}}{{\left(d+c\right)}^\frac{1}{q}}{\text{e}}^{i2\pi \frac{{\left(2{c}^{{^{\prime}}}\right)}^\frac{1}{q}}{{\left({d}^{{^{\prime}}}+{c}^{{^{\prime}}}\right)}^\frac{1}{q}}}\right)$$

By Einstein operational laws, we get

$$\begin{aligned} \delta \left({\mathbb{E}}_{1}\oplus {\mathbb{E}}_{2}\right)&=\delta \left({\left(\frac{a-b}{a+b}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}^{{\prime}}-{b}^{{\prime}}}{{a}^{{\prime}}+{b}^{{\prime}}}\right)}^\frac{1}{q}},\frac{{\left(2c\right)}^\frac{1}{q}}{{\left(d+c\right)}^\frac{1}{q}}{\text{e}}^{i2\pi \frac{{\left(2{c}^{{\prime}}\right)}^\frac{1}{q}}{{\left({d}^{{\prime}}+{c}^{{\prime}}\right)}^\frac{1}{q}}}\right)\hfill\\ &=\left(\begin{array}{c}{\left(\frac{{\left(1+\frac{a-b}{a+b}\right)}^{\delta }-{\left(1-\frac{a-b}{a+b}\right)}^{\delta }}{{\left(1+\frac{a-b}{a+b}\right)}^{\delta }+{\left(1-\frac{a-b}{a+b}\right)}^{\delta }}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+\frac{{a}^{{\prime}}-{b}^{{\prime}}}{{a}^{{\prime}}+{b}^{{\prime}}}\right)}^{\delta }-{\left(1-\frac{{a}^{{\prime}}-{b}^{{\prime}}}{{a}^{{\prime}}+{b}^{{\prime}}}\right)}^{\delta }}{{\left(1+\frac{{a}^{{\prime}}-{b}^{{\prime}}}{{a}^{{\prime}}+{b}^{{\prime}}}\right)}^{\delta }+{\left(1-\frac{{a}^{{\prime}}-{b}^{{\prime}}}{{a}^{{\prime}}+{b}^{{\prime}}}\right)}^{\delta }}\right)}^\frac{1}{q}},\\ \frac{{\left(2\right)}^\frac{1}{q}{\left(\frac{{\left(2c\right)}^\frac{1}{q}}{{\left(d+c\right)}^\frac{1}{q}}\right)}^{\delta }}{{\left({\left(2-\frac{2c}{d+c}\right)}^{\delta }+{\left(\frac{2c}{d+c}\right)}^{\delta }\right)}^\frac{1}{q}}{\text{e}}^{i2\pi \frac{{\left(2\right)}^\frac{1}{q}{\left(\frac{{\left(2{c}^{{\prime}}\right)}^\frac{1}{q}}{{\left({d}^{{\prime}}+{c}^{{\prime}}\right)}^\frac{1}{q}}\right)}^{\delta }}{{\left({\left(2-\frac{2{c}^{{\prime}}}{{d}^{{\prime}}+{c}^{{\prime}}}\right)}^{\delta }+{\left(\frac{2{c}^{{\prime}}}{{d}^{{\prime}}+{c}^{{\prime}}}\right)}^{\delta }\right)}^\frac{1}{q}}}\end{array}\right)\hfill\\ &=\left(\begin{array}{c}{\left(\frac{{a}^{\delta }-{b}^{\delta }}{{a}^{\delta }+{b}^{\delta }}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{{a}^{{\prime}}}^{\delta }-{{b}^{{\prime}}}^{\delta }}{{{a}^{{\prime}}}^{\delta }+{{b}^{{\prime}}}^{\delta }}\right)}^\frac{1}{q}},\\ \frac{{\left({2c}^{\delta }\right)}^\frac{1}{q}}{{\left({d}^{\delta }+{c}^{\delta }\right)}^\frac{1}{q}}{\text{e}}^{i2\pi \frac{{\left({{2c}^{{\prime}}}^{\delta }\right)}^\frac{1}{q}}{{\left({{d}^{{\prime}}}^{\delta }+{{c}^{{\prime}}}^{\delta }\right)}^\frac{1}{q}}}\end{array}\right)\hfill\\ & =\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta } {\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }-{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta } {\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{\delta }{\mathcal{N}}_{2}^{\delta }}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{\delta }{\left(2-{\mathcal{N}}_{2}^{q}\right)}^{\delta }+{{\mathcal{N}}_{1}^{q}}^{\delta }{{\mathcal{N}}_{2}^{q}}^{\delta }\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{\delta }{\mathcal{W}}_{{\mathcal{N}}_{2}}^{\delta }}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{\delta }+{{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}}^{\delta }{{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}}^{\delta }\right)}^\frac{1}{q}}\right)}\end{array}\right)\end{aligned} $$

In other hand, we examine that

$$\begin{aligned}\delta {\mathbb{E}}_{1}&=\left({\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}},\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{\delta }}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{\delta }+{\left({\mathcal{N}}_{1}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{\delta }}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)}\right)\hfill \\&=\left({\left(\frac{{a}_{1}-{b}_{1}}{{a}_{1}+{b}_{1}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{1}^{{\prime}}-{b}_{1}^{{\prime}}}{{a}_{1}^{{\prime}}+{b}_{1}^{{\prime}}}\right)}^\frac{1}{q}},\left(\frac{{\left(2{c}_{1}\right)}^\frac{1}{q}}{{\left({d}_{1}+{c}_{1}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2{c}_{1}^{{\prime}}\right)}^\frac{1}{q}}{{\left({d}_{1}^{{\prime}}+{c}_{1}^{{\prime}}\right)}^\frac{1}{q}}\right)}\right)\end{aligned}$$

and

$$\begin{aligned} \delta {\mathbb{E}}_{2}&=\left({\left(\frac{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{\delta }-{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{\delta }+{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}},\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{2}^{\delta }}{{\left({\left(2-{\mathcal{N}}_{2}^{q}\right)}^{\delta }+{\left({\mathcal{N}}_{2}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{2}}^{\delta }}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{\delta }+{\left({\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{\delta }\right)}^\frac{1}{q}}\right)}\right)\hfill \\&=\left({\left(\frac{{a}_{2}-{b}_{2}}{{a}_{2}+{b}_{2}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{2}^{{\prime}}-{b}_{2}^{{\prime}}}{{a}_{2}^{{\prime}}+{b}_{2}^{{\prime}}}\right)}^\frac{1}{q}},\left(\frac{{\left(2{c}_{2}\right)}^\frac{1}{q}}{{\left({d}_{2}+{c}_{2}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2{c}_{2}^{{\prime}}\right)}^\frac{1}{q}}{{\left({d}_{2}^{{\prime}}+{c}_{2}^{{\prime}}\right)}^\frac{1}{q}}\right)}\right)\end{aligned}$$

where ${a}_{1}={\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta },{b}_{1}={\left(1-{\mathcal{T}}_{1}^{q}\right)}^{\delta },{c}_{1}={\left({\mathcal{N}}_{1}^{q}\right)}^{\delta },{d}_{1}={\left(2-{\mathcal{N}}_{1}^{q}\right)}^{\delta },{a}_{2}={\left(1+{\mathcal{T}}_{2}^{q}\right)}^{\delta },{b}_{2}={\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta },{c}_{2}={\left({\mathcal{N}}_{2}^{q}\right)}^{\delta },{d}_{2}={\left(2-{\mathcal{N}}_{2}^{q}\right)}^{\delta },{a}_{1}^{{\prime}}={\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta },{b}_{1}^{{\prime}}={\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta },{c}_{1}^{{\prime}}={\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta },{d}_{1}^{{\prime}}={\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta },{a}_{2}^{{\prime}}={\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta },{b}_{2}^{{\prime}}={\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta },{c}_{2}^{{\prime}}={\left({\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{\delta },{d}_{2}^{{\prime}}={\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{\delta }.$

$$ \delta {\mathbb{E}}_{1}\oplus \delta {\mathbb{E}}_{2}=\left(\begin{array}{c}{\left(\frac{{a}_{1}-{b}_{1}}{{a}_{1}+{b}_{1}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{1}^{^{\prime}}-{b}_{1}^{^{\prime}}}{{a}_{1}^{^{\prime}}+{b}_{1}^{^{\prime}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2{c}_{1}\right)}^\frac{1}{q}}{{\left({d}_{1}+{c}_{1}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2{c}_{1}^{^{\prime}}\right)}^\frac{1}{q}}{{\left({d}_{1}^{^{\prime}}+{c}_{1}^{^{\prime}}\right)}^\frac{1}{q}}\right)}\end{array}\right)\oplus \left(\begin{array}{c}{\left(\frac{{a}_{2}-{b}_{2}}{{a}_{2}+{b}_{2}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{2}^{^{\prime}}-{b}_{2}^{^{\prime}}}{{a}_{2}^{^{\prime}}+{b}_{2}^{^{\prime}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2{c}_{2}\right)}^\frac{1}{q}}{{\left({d}_{2}+{c}_{2}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2{c}_{2}^{^{\prime}}\right)}^\frac{1}{q}}{{\left({d}_{2}^{^{\prime}}+{c}_{2}^{^{\prime}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$$\begin{aligned} &\quad\quad\quad\quad=\left(\begin{array}{c}{\left(\frac{\frac{{a}_{1}-{b}_{1}}{{a}_{1}+{b}_{1}}+\frac{{a}_{2}-{b}_{2}}{{a}_{2}+{b}_{2}}}{1+\left(\frac{{a}_{1}-{b}_{1}}{{a}_{1}+{b}_{1}}\right)\left(\frac{{a}_{2}-{b}_{2}}{{a}_{2}+{b}_{2}}\right)}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{\frac{{a}_{1}^{^{\prime}}-{b}_{1}^{^{\prime}}}{{a}_{1}^{^{\prime}}+{b}_{1}^{^{\prime}}}+\frac{{a}_{2}^{^{\prime}}-{b}_{2}^{^{\prime}}}{{a}_{2}^{^{\prime}}+{b}_{2}^{^{\prime}}}}{1+\left(\frac{{a}_{1}^{^{\prime}}-{b}_{1}^{^{\prime}}}{{a}_{1}^{^{\prime}}+{b}_{1}^{^{\prime}}}\right)\left(\frac{{a}_{2}^{^{\prime}}-{b}_{2}^{^{\prime}}}{{a}_{2}^{^{\prime}}+{b}_{2}^{^{\prime}}}\right)}\right)}^\frac{1}{q}},\\ \left(\frac{{2\left(\frac{{c}_{1}{c}_{2}}{\left({d}_{1}+{c}_{1}\right)\left({d}_{2}+{c}_{2}\right)}\right)}^\frac{1}{q}}{{\left(1+\left(1-\frac{2{c}_{1}}{{d}_{1}+{c}_{1}}\right)\left(1-\frac{2{c}_{2}}{{d}_{2}+{c}_{2}}\right)\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{2\left(\frac{{c}_{1}^{^{\prime}}{c}_{2}^{^{\prime}}}{\left({d}_{1}^{^{\prime}}+{c}_{1}^{^{\prime}}\right)\left({d}_{2}^{^{\prime}}+{c}_{2}^{^{\prime}}\right)}\right)}^\frac{1}{q}}{{\left(1+\left(1-\frac{2{c}_{1}^{^{\prime}}}{{d}_{1}^{^{\prime}}+{c}_{1}^{^{\prime}}}\right)\left(1-\frac{2{c}_{2}^{^{\prime}}}{{d}_{2}^{^{\prime}}+{c}_{2}^{^{\prime}}}\right)\right)}^\frac{1}{q}}\right)}\end{array}\right)\\ &\quad\quad\quad\quad =\left(\begin{array}{c}{\left(\frac{{a}_{1}{a}_{2}-{b}_{1}{b}_{2}}{{a}_{1}{a}_{2}+{b}_{1}{b}_{2}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{1}^{^{\prime}}{a}_{2}^{^{\prime}}-{b}_{1}^{^{\prime}}{b}_{2}^{^{\prime}}}{{a}_{1}^{^{\prime}}{a}_{2}^{^{\prime}}+{b}_{1}^{^{\prime}}{b}_{2}^{^{\prime}}}\right)}^\frac{1}{q}},\\ {\left(\frac{2{c}_{1}{c}_{2}}{\left({d}_{1}{d}_{2}+{c}_{1}{c}_{2}\right)}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{2{c}_{1}^{^{\prime}}{c}_{2}^{^{\prime}}}{\left({d}_{1}^{^{\prime}}{d}_{2}^{^{\prime}}+{c}_{1}^{^{\prime}}{c}_{2}^{^{\prime}}\right)}\right)}^\frac{1}{q}}\end{array}\right) \end{aligned}$$

$$\quad\quad\quad\quad =\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta } {\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }-{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta } {\left(1+{\mathcal{T}}_{1}^{q}\right)}^{\delta }+{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{\delta }+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{\delta }}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{\delta }{\mathcal{N}}_{2}^{\delta }}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{\delta }{\left(2-{\mathcal{N}}_{2}^{q}\right)}^{\delta }+{{\mathcal{N}}_{1}^{q}}^{\delta }{{\mathcal{N}}_{2}^{q}}^{\delta }\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{\delta }{\mathcal{W}}_{{\mathcal{N}}_{2}}^{\delta }}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{\delta }{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{\delta }+{{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}}^{\delta }{{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}}^{\delta }\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

Hence $\delta \left({\mathbb{E}}_{1}\oplus {\mathbb{E}}_{2}\right)=\delta {\mathbb{E}}_{1}\oplus \delta {\mathbb{E}}_{2}$.

• 3. The proof of part (4) is straightforward.

• 4. Let us consider the part (5), we have

$${\delta }_{1}{\mathbb{E}}_{1}=\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}}-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}}}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}}+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{{\delta }_{1}}}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\delta }_{1}}+{\left({\mathcal{N}}_{1}^{q}\right)}^{{\delta }_{1}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{{\delta }_{1}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\delta }_{1}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\delta }_{1}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$$\quad\quad =\left(\begin{array}{c}{\left(\frac{{a}_{1}-{b}_{1}}{{a}_{1}+{b}_{1}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{1}^{{\prime}}-{b}_{1}^{{\prime}}}{{a}_{1}^{{\prime}}+{b}_{1}^{{\prime}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2{c}_{1}\right)}^\frac{1}{q}}{{\left({d}_{1}+{c}_{1}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2{c}_{1}^{{\prime}}\right)}^\frac{1}{q}}{{\left({d}_{1}^{{\prime}}+{c}_{1}^{{\prime}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$${\delta }_{2}{\mathbb{E}}_{1}=\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{2}}-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{2}}}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{2}}+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{2}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{2}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{2}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{2}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{2}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{{\delta }_{2}}}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\delta }_{2}}+{\left({\mathcal{N}}_{1}^{q}\right)}^{{\delta }_{2}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{{\delta }_{2}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\delta }_{2}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\delta }_{2}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$$\quad\quad=\left(\begin{array}{c}{\left(\frac{{a}_{2}-{b}_{2}}{{a}_{2}+{b}_{2}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{2}^{{\prime}}-{b}_{2}^{{\prime}}}{{a}_{2}^{{\prime}}+{b}_{2}^{{\prime}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2{c}_{2}\right)}^\frac{1}{q}}{{\left({d}_{2}+{c}_{2}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2{c}_{2}^{{\prime}}\right)}^\frac{1}{q}}{{\left({d}_{2}^{{\prime}}+{c}_{2}^{{\prime}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

where ${a}_{1}={\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}},{b}_{1}={\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}},{c}_{1}={\left({\mathcal{N}}_{1}^{q}\right)}^{{\delta }_{1}},{d}_{1}={\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\delta }_{1}},{a}_{2}={\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\delta }_{2}},{b}_{2}={\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\delta }_{2}},{c}_{2}={\left({\mathcal{N}}_{2}^{q}\right)}^{{\delta }_{2}},{d}_{2}={\left(2-{\mathcal{N}}_{2}^{q}\right)}^{{\delta }_{2}},{a}_{1}^{{\prime}}={\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}},{b}_{1}^{{\prime}}={\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}},{c}_{1}^{{\prime}}={\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\delta }_{1}},{d}_{1}^{{\prime}}={\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\delta }_{1}},{a}_{2}^{{\prime}}={\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\delta }_{2}},{b}_{2}^{{\prime}}={\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\delta }_{2}},{c}_{2}^{{\prime}}={\left({\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\delta }_{2}},{d}_{2}^{{\prime}}={\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\delta }_{2}}$. Then

$$ \begin{aligned} {\delta }_{1}{\mathbb{E}}_{1}\oplus {\delta }_{2}{\mathbb{E}}_{1} & =\left(\begin{array}{c}{\left(\frac{{a}_{1}-{b}_{1}}{{a}_{1}+{b}_{1}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{1}^{{\prime}}-{b}_{1}^{{\prime}}}{{a}_{1}^{{\prime}}+{b}_{1}^{{\prime}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2{c}_{1}\right)}^\frac{1}{q}}{{\left({d}_{1}+{c}_{1}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2{c}_{1}^{{\prime}}\right)}^\frac{1}{q}}{{\left({d}_{1}^{{\prime}}+{c}_{1}^{{\prime}}\right)}^\frac{1}{q}}\right)}\end{array}\right)\\ &\quad \oplus \left(\begin{array}{c}{\left(\frac{{a}_{2}-{b}_{2}}{{a}_{2}+{b}_{2}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{2}^{{\prime}}-{b}_{2}^{{\prime}}}{{a}_{2}^{{\prime}}+{b}_{2}^{{\prime}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2{c}_{2}\right)}^\frac{1}{q}}{{\left({d}_{2}+{c}_{2}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2{c}_{2}^{{\prime}}\right)}^\frac{1}{q}}{{\left({d}_{2}^{{\prime}}+{c}_{2}^{{\prime}}\right)}^\frac{1}{q}}\right)}\end{array}\right) \end{aligned}$$

$$\quad =\left(\begin{array}{c}{\left(\frac{\frac{{a}_{1}-{b}_{1}}{{a}_{1}+{b}_{1}}+{\frac{{a}_{2}-{b}_{2}}{{a}_{2}+{b}_{2}}}}{1+\left(\frac{{a}_{1}-{b}_{1}}{{a}_{1}+{b}_{1}}\right)\left(\frac{{a}_{2}-{b}_{2}}{{a}_{2}+{b}_{2}}\right)}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{\frac{{a}_{1}^{{\prime}}-{b}_{1}^{{\prime}}}{{a}_{1}^{{\prime}}+{b}_{1}^{{\prime}}}+\frac{{a}_{2}^{{\prime}}-{b}_{2}^{{\prime}}}{{a}_{2}^{{\prime}}+{b}_{2}^{{\prime}}}}{1+\left(\frac{{a}_{1}^{{\prime}}-{b}_{1}^{{\prime}}}{{a}_{1}^{{\prime}}+{b}_{1}^{{\prime}}}\right)\left(\frac{{a}_{2}^{{\prime}}-{b}_{2}^{{\prime}}}{{a}_{2}^{{\prime}}+{b}_{2}^{{\prime}}}\right)}\right)}^\frac{1}{q}},\\ \left(\frac{{2\left(\frac{{c}_{1}{c}_{2}}{\left({d}_{1}+{c}_{1}\right)\left({d}_{2}+{c}_{2}\right)}\right)}^\frac{1}{q}}{{\left(1+\left(1-\frac{2{c}_{1}}{{d}_{1}+{c}_{1}}\right)\left(1-\frac{2{c}_{2}}{{d}_{2}+{c}_{2}}\right)\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{2\left(\frac{{c}_{1}^{{\prime}}{c}_{2}^{{\prime}}}{\left({d}_{1}^{{\prime}}+{c}_{1}^{{\prime}}\right)\left({d}_{2}^{{\prime}}+{c}_{2}^{{\prime}}\right)}\right)}^\frac{1}{q}}{{\left(1+\left(1-\frac{2{c}_{1}^{{\prime}}}{{d}_{1}^{{\prime}}+{c}_{1}^{{\prime}}}\right)\left(1-\frac{2{c}_{2}^{{\prime}}}{{d}_{2}^{{\prime}}+{c}_{2}^{{\prime}}}\right)\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$$=\left(\begin{array}{c}{\left(\frac{{a}_{1}{a}_{2}-{b}_{1}{b}_{2}}{{a}_{1}{a}_{2}+{b}_{1}{b}_{2}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{a}_{1}^{{\prime}}{a}_{2}^{{\prime}}-{b}_{1}^{{\prime}}{b}_{2}^{{\prime}}}{{a}_{1}^{{\prime}}{a}_{2}^{{\prime}}+{b}_{1}^{{\prime}}{b}_{2}^{{\prime}}}\right)}^\frac{1}{q}},\\ {\left(\frac{2{c}_{1}{c}_{2}}{\left({d}_{1}{d}_{2}+{c}_{1}{c}_{2}\right)}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{2{c}_{1}^{{\prime}}{c}_{2}^{{\prime}}}{\left({d}_{1}^{{\prime}}{d}_{2}^{{\prime}}+{c}_{1}^{{\prime}}{c}_{2}^{{\prime}}\right)}\right)}^\frac{1}{q}}\end{array}\right)$$

$$ \begin{aligned} & =\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}} -{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{{\delta }_{1}+{\delta }_{2}}}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}+{{\mathcal{N}}_{1}^{q}}^{{\delta }_{1}+{\delta }_{2}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{{\delta }_{1}+{\delta }_{2}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\delta }_{1}+{\delta }_{2}}+{{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}}^{{\delta }_{1}+{\delta }_{2}}\right)}^\frac{1}{q}}\right)}\end{array}\right)\\ &\quad =\left({\delta }_{1}+{\delta }_{2}\right){\mathbb{E}}_{1}. \end{aligned}$$

Hence ${\delta }_{1}{\mathbb{E}}_{1}\oplus {\delta }_{2}{\mathbb{E}}_{1}=\left({\delta }_{1}+{\delta }_{2}\right){\mathbb{E}}_{1}$.

• 5. The proof of part (6) is straightforward.

Proof 4

Using the process of mathematical induction to prove the Eq. (11), if $n=2$, then.

$$\text{Cq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)={\omega }_{1}{\mathbb{E}}_{1}\oplus {\omega }_{2}{\mathbb{E}}_{2}$$

By Theorem 1, the result of ${\omega }_{1}{\mathbb{E}}_{1}\oplus {\omega }_{2}{\mathbb{E}}_{2}$ is also Cq-ROFN, Using the Definition (8), we get

$${\omega }_{1}{\mathbb{E}}_{1}=\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{{\omega }_{1}}}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}+{\left({\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{{\omega }_{1}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$${\omega }_{2}{\mathbb{E}}_{2}=\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{2}^{{\omega }_{2}}}{{\left({\left(2-{\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{2}}^{{\omega }_{2}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

then

$$\text{Cq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)={\omega }_{1}{\mathbb{E}}_{1}\oplus {\omega }_{2}{\mathbb{E}}_{2}$$

$$ \begin{aligned} & =\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{{\omega }_{1}}}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}+{\left({\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{{\omega }_{1}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}\right)}^\frac{1}{q}}\right)}\end{array}\right) \\ &\quad \oplus \left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{2}^{{\omega }_{2}}}{{\left({\left(2-{\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{2}}^{{\omega }_{2}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right)}\end{array}\right) \end{aligned} $$

$$=\left(\begin{array}{c}{\left(\frac{\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}}+\frac{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}}{1+\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}}\right)\left(\frac{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}\right)}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}}+\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}}{1+\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}}\right)\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}\right)}\right)}^\frac{1}{q}},\\ \left(\frac{\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{{\omega }_{1}}}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}+{\left({\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}\right)}^\frac{1}{q}}\right)\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{2}^{{\omega }_{2}}}{{\left({\left(2-{\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right)}{{\left(1+\left(1-\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{1}^{{\omega }_{1}}}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}+{\left({\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}\right)}^\frac{1}{q}}\right)\left(1-\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{2}^{{\omega }_{2}}}{{\left({\left(2-{\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right)\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{{\omega }_{1}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}\right)}^\frac{1}{q}}\right)\left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{2}}^{{\omega }_{2}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right)}{{\left(1+\left(1-\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{1}}^{{\omega }_{1}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}\right)}^\frac{1}{q}}\right)\left(1-\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{2}}^{{\omega }_{2}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right)\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$$=\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}{\left(1+{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{T}}_{1}^{q}\right)}^{{\omega }_{1}}{\left(1-{\mathcal{T}}_{2}^{q}\right)}^{{\omega }_{2}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{1}}^{q}\right)}^{{\omega }_{1}}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{2}}^{q}\right)}^{{\omega }_{2}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}\left({\mathcal{N}}_{1}^{{\omega }_{1}}{\mathcal{N}}_{2}^{{\omega }_{2}}\right)}{{\left({\left(2-{\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}{\left(2-{\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{N}}_{1}^{q}\right)}^{{\omega }_{1}}{\left({\mathcal{N}}_{2}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{{\omega }_{1}}{\mathcal{W}}_{{\mathcal{N}}_{2}}^{{\omega }_{2}}\right)}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{1}}^{q}\right)}^{{\omega }_{1}}{\left({\mathcal{W}}_{{\mathcal{N}}_{2}}^{q}\right)}^{{\omega }_{2}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

For $n=2$, the result is kept. We suppose that it is true for $n=k$, then the Eq. (11), we have

$$\text{Cq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{k}\right)=\left(\begin{array}{c}{\left(\frac{{\prod }_{i=1}^{k}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\prod }_{i=1}^{k}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{k}{\mathcal{N}}_{i}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{k}{\left(2-{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k}{\left({\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{k}{\mathcal{W}}_{{\mathcal{N}}_{i}}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{k}{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k}{\left({\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

We will prove for $n=k+1$, such that

$$\begin{aligned} Cq-ROFEWA\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{k+1}\right) & =\left(\begin{array}{c}{\left(\frac{{\prod }_{i=1}^{k}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\prod }_{i=1}^{k}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{k}{\mathcal{N}}_{i}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{k}{\left(2-{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k}{\left({\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{k}{\mathcal{W}}_{{\mathcal{N}}_{i}}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{k}{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k}{\left({\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right)}\end{array}\right)\\ &\quad \oplus \left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{k+1}^{q}\right)}^{{\omega }_{k+1}}-{\left(1-{\mathcal{T}}_{k+1}^{q}\right)}^{{\omega }_{k+1}}}{{\left(1+{\mathcal{T}}_{k+1}^{q}\right)}^{{\omega }_{k+1}}+{\left(1-{\mathcal{T}}_{k+1}^{q}\right)}^{{\omega }_{k+1}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{k+1}}^{q}\right)}^{{\omega }_{k+1}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{k+1}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{k+1}}^{q}\right)}^{{\omega }_{k+1}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{k+1}}^{q}\right)}^{{\omega }_{k+1}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{k+1}^{{\omega }_{k+1}}}{{\left({\left(2-{\mathcal{N}}_{k+1}^{q}\right)}^{{\omega }_{k+1}}+{\left({\mathcal{N}}_{k+1}^{q}\right)}^{{\omega }_{k+1}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{k+1}}^{{\omega }_{k+1}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{k+1}}^{q}\right)}^{{\omega }_{k+1}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{k+1}}^{q}\right)}^{{\omega }_{k+1}}\right)}^\frac{1}{q}}\right)}\end{array}\right) \end{aligned} $$

$$=\left(\begin{array}{c}{\left(\frac{{\prod }_{i=1}^{k+1}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k+1}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k+1}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k+1}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\prod }_{i=1}^{k+1}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k+1}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k+1}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k+1}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{k+1}{\mathcal{N}}_{i}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{k+1}{\left(2-{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k+1}{\left({\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{k+1}{\mathcal{W}}_{{\mathcal{N}}_{i}}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{k+1}{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{k+1}{\left({\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

For $n=k+1$, the result is also kept. Hence the Eq. (11), is kept for all $n$.

Proof 5

Let $\text{Cq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)=\left({\mathcal{T}}_{i}^{q}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}},{\mathcal{N}}_{i}^{q}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}}\right)={\mathbb{E}}_{i}^{q}$ and $\text{Cq-ROFWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)=\left({\mathcal{T}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{i}}},{\mathcal{N}}_{i}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{i}}}\right)={\mathbb{E}}_{i}$. Firstly, we check for real part of complex-valued membership grades, such that

$$ \begin{aligned} & {\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}} \\ &\quad \le \sum_{i=1}^{n}{\omega }_{i}\left(1+{\mathcal{T}}_{i}^{q}\right)+\sum_{i=1}^{n}{\omega }_{i}\left(1-{\mathcal{T}}_{i}^{q}\right)=2 \end{aligned} $$

then,

$$ \begin{aligned} & {\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}\\ &\quad \le {\left(1-{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{i}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}\iff {\mathcal{T}}_{i}^{p}={\mathcal{T}}_{i}\iff {\mathcal{T}}_{1}\\ &\quad ={\mathcal{T}}_{2}=\ldots={\mathcal{T}}_{n}. \end{aligned} $$

At the same time, it is also kept for imaginary part of complex-valued membership grade. Next, we check for real part for non-membership grade, we get

$$\begin{aligned} & \frac{2{\left({\prod }_{i=1}^{n}{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(2-{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}+{\left({\prod }_{i=1}^{n}{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}}\\ &\quad \ge \frac{2{\prod }_{i=1}^{n}{\left({\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}}{\sum_{i=1}^{n}{\omega }_{i}\left(2-{\mathcal{N}}_{i}^{q}\right)+\sum_{i=1}^{n}{\omega }_{i}{\mathcal{N}}_{i}^{q}}\ge {\prod }_{i=1}^{n}{\left({\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}} \end{aligned}$$

$$\Rightarrow {\left(\frac{2{\left({\prod }_{i=1}^{n}{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(2-{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}+{\left({\prod }_{i=1}^{n}{\mathcal{N}}_{i}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}\ge {\prod }_{i=1}^{n}{\left({\mathcal{N}}_{i}\right)}^{{\omega }_{i}}$$

$$\Rightarrow {\mathcal{N}}_{i}^{p}\ge {\mathcal{N}}_{i}\iff {\mathcal{N}}_{1}={\mathcal{N}}_{2}=\ldots={\mathcal{N}}_{n}$$

At the same time, it is also kept for imaginary part of complex-valued non-membership grade. Then the score value of the above, such that

$$\begin{aligned} \mathcal{S}\left({\mathbb{E}}_{i}^{p}\right)&=\frac{1}{2}\left({{\mathcal{T}}_{i}^{p}}^{q}+{{\mathcal{W}}_{{\mathcal{T}}_{i}}^{p}}^{q}-{{{\mathcal{N}}_{i}}^{p}}^{q}-{{\mathcal{W}}_{{\mathcal{N}}_{i}}^{p}}^{q}\right)\\ & \le \frac{1}{2}\left({\mathcal{T}}_{i}^{q}+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}-{{\mathcal{N}}_{i}}^{q}-{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)=\mathcal{S}\left({\mathbb{E}}_{i}\right) \end{aligned} $$

When $\mathcal{S}\left({\mathbb{E}}_{i}^{p}\right)<\mathcal{S}\left({\mathbb{E}}_{i}\right)$, then by definition of score function, we have

$$ \text{Cq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right) <\text{Cq-ROFWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right) $$

When $\mathcal{S}\left({\mathbb{E}}_{i}^{p}\right)=\mathcal{S}\left({\mathbb{E}}_{i}\right)$, then by definition of accuracy function, we have

$$ \begin{aligned} {\mathbb{H}}\left({\mathbb{E}}_{i}^{p}\right) & =\frac{1}{2}\left({{\mathcal{T}}_{1}^{p}}^{q}+{{\mathcal{W}}_{{\mathcal{T}}_{1}}^{p}}^{q}-{{{\mathcal{N}}_{1}}^{p}}^{q}-{{\mathcal{W}}_{{\mathcal{N}}_{1}}^{p}}^{q}\right)\\ & =\frac{1}{2}\left({\mathcal{T}}_{i}^{q}+{\mathcal{W}}_{{\mathcal{T}}_{i}}^{q}+{{\mathcal{N}}_{i}}^{q}+{\mathcal{W}}_{{\mathcal{N}}_{i}}^{q}\right)={\mathbb{H}}\left({\mathbb{E}}_{i}\right) \end{aligned} $$

$$\text{Cq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)=\text{Cq-ROFWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)$$

therefore

$$\text{Cq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)\le \text{Cq-ROFWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)$$

Proof (Property 1: Idempotency)

• 1. We know that ${\mathbb{E}}_{0}=\left({\mathcal{T}}_{0}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{T}}_{0}}},{\mathcal{N}}_{0}{\text{e}}^{i2\pi {\mathcal{W}}_{{\mathcal{N}}_{0}}}\right)\in \text{Cq-ROFN},i=\text{1,2},\ldots,n$, then

$$\text{Cq-ROFEWA}\left({\mathbb{E}}_{1},{\mathbb{E}}_{2},\ldots,{\mathbb{E}}_{n}\right)=\left(\begin{array}{c}{\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{0}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{0}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{T}}_{0}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{T}}_{0}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{0}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{0}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{0}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{0}}^{q}\right)}^{{\omega }_{i}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{n}{\mathcal{N}}_{0}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{n}{\left(2-{\mathcal{N}}_{0}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left({\mathcal{N}}_{0}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\prod }_{i=1}^{n}{\mathcal{W}}_{{\mathcal{N}}_{0}}^{{\omega }_{i}}}{{\left({\prod }_{i=1}^{n}{\left(2-{\mathcal{W}}_{{\mathcal{N}}_{0}}^{q}\right)}^{{\omega }_{i}}+{\prod }_{i=1}^{n}{\left({\mathcal{W}}_{{\mathcal{N}}_{0}}^{q}\right)}^{{\omega }_{i}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$$=\left(\begin{array}{c}{\left(\frac{{\left(1+{\mathcal{T}}_{0}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}-{\left(1-{\mathcal{T}}_{0}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}}{{\left(1+{\mathcal{T}}_{0}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}+{\left(1-{\mathcal{T}}_{0}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}}\right)}^\frac{1}{q}{\text{e}}^{i2\pi {\left(\frac{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{0}}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}-{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{0}}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}}{{\left(1+{\mathcal{W}}_{{\mathcal{T}}_{0}}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}+{\left(1-{\mathcal{W}}_{{\mathcal{T}}_{0}}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}}\right)}^\frac{1}{q}},\\ \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{N}}_{0}^{\sum_{i=1}^{n}{\omega }_{i}}}{{\left({\left(2-{\mathcal{N}}_{0}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}+{\left({\mathcal{N}}_{0}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}\right)}^\frac{1}{q}}\right){\text{e}}^{i2\pi \left(\frac{{\left(2\right)}^\frac{1}{q}{\mathcal{W}}_{{\mathcal{N}}_{0}}^{\sum_{i=1}^{n}{\omega }_{i}}}{{\left({\left(2-{\mathcal{W}}_{{\mathcal{N}}_{0}}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}+{\left({\mathcal{W}}_{{\mathcal{N}}_{0}}^{q}\right)}^{\sum_{i=1}^{n}{\omega }_{i}}\right)}^\frac{1}{q}}\right)}\end{array}\right)$$

$$ = \left( {{\mathcal{T}}_{0} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{T}}_{0} }} }} ,{\mathcal{N}}_{0} {\text{e}}^{{i2\pi {\mathcal{W}}_{{{\mathcal{N}}_{0} }} }} } \right) = {\mathbb{E}}_{0} $$

• 2. Proof (Property 2: Boundedness)

We know that $f\left( x \right) = \frac{1 - x}{{1 + x}},x \in \left[ {0,1} \right]$, then $f^{\prime}\left( x \right) = \frac{ - 2}{{\left( {1 + x} \right)^{2} }} < 0$, thus $f\left( x \right)$ is decreasing function. We check for real part of membership grade, such that ${\mathcal{T}}_{i.min}^{q} \le {\mathcal{T}}_{i}^{q} \le {\mathcal{T}}_{i.max}^{q} \forall i = 1,2, \ldots ,n$, then $f\left( {{\mathcal{T}}_{i.min}^{q} } \right) \le f\left( {{\mathcal{T}}_{i}^{q} } \right) \le f\left( {{\mathcal{T}}_{i.max}^{q} } \right),\forall i$ implies that $\frac{{1 - {\mathcal{T}}_{i.max}^{q} }}{{1 + {\mathcal{T}}_{i.max}^{q} }} \le \frac{{1 - {\mathcal{T}}_{i}^{q} }}{{1 + {\mathcal{T}}_{i}^{q} }} \le \frac{{1 - {\mathcal{T}}_{i.min}^{q} }}{{1 + {\mathcal{T}}_{i.min}^{q} }},\forall i$ and the weight vector is discussed above, we have

$$ \begin{aligned} &\left( {\frac{{1 - {\mathcal{T}}_{i.\max }^{q} }}{{1 + {\mathcal{T}}_{i.\max }^{q} }}} \right)^{{\omega_{i} }} \le \left( {\frac{{1 - {\mathcal{T}}_{i}^{q} }}{{1 + {\mathcal{T}}_{i}^{q} }}} \right)^{{\omega_{i} }} \le \left( {\frac{{1 - {\mathcal{T}}_{i.\min }^{q} }}{{1 + {\mathcal{T}}_{i.\min }^{q} }}} \right)^{{\omega_{i} }} \hfill \\ &\quad \Rightarrow \mathop \prod \limits_{i = 1}^{n} \left( {\frac{{1 - {\mathcal{T}}_{i.\max }^{q} }}{{1 + {\mathcal{T}}_{i.\max }^{q} }}} \right)^{{\omega_{i} }} \le \mathop \prod \limits_{i = 1}^{n} \left( {\frac{{1 - {\mathcal{T}}_{i}^{q} }}{{1 + {\mathcal{T}}_{i}^{q} }}} \right)^{{\omega_{i} }} \le \mathop \prod \limits_{i = 1}^{n} \left( {\frac{{1 - {\mathcal{T}}_{i.\min }^{q} }}{{1 + {\mathcal{T}}_{i.\min }^{q} }}} \right)^{{\omega_{i} }} \hfill \\ &\quad \Leftrightarrow \left( {\frac{{1 - {\mathcal{T}}_{i.\max }^{q} }}{{1 + {\mathcal{T}}_{i.\max }^{q} }}} \right)^{{\mathop \sum \limits_{i = 1}^{n} \omega_{i} }} \le \mathop \prod \limits_{i = 1}^{n} \left( {\frac{{1 - {\mathcal{T}}_{i}^{q} }}{{1 + {\mathcal{T}}_{i}^{q} }}} \right)^{{\omega_{i} }} \le \left( {\frac{{1 - {\mathcal{T}}_{i.\min }^{q} }}{{1 + {\mathcal{T}}_{i.\min }^{q} }}} \right)^{{\mathop \sum \limits_{i = 1}^{n} \omega_{i} }} \hfill \\ &\quad\Leftrightarrow \left( {\frac{2}{{1 + {\mathcal{T}}_{i.\max }^{q} }}} \right) \le 1 + \mathop \prod \limits_{i = 1}^{n} \left( {\frac{{1 - {\mathcal{T}}_{i}^{q} }}{{1 + {\mathcal{T}}_{i}^{q} }}} \right)^{{\omega_{i} }} \le \left( {\frac{2}{{1 + {\mathcal{T}}_{i.\min }^{q} }}} \right) \hfill \\ &\quad\Leftrightarrow \left( {\frac{{1 + {\mathcal{T}}_{i.\min }^{q} }}{2}} \right) \le \frac{1}{{1 + \mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{1 - {\mathcal{T}}_{i}^{q} }}{{1 + {\mathcal{T}}_{i}^{q} }}} \right)^{{\omega_{i} }} }} \le \left( {\frac{{1 + {\mathcal{T}}_{i.\max }^{q} }}{2}} \right) \hfill \\ &\quad\Leftrightarrow \left( {1 + {\mathcal{T}}_{i.\min }^{q} } \right) \le \frac{2}{{1 + \mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{1 - {\mathcal{T}}_{i}^{q} }}{{1 + {\mathcal{T}}_{i}^{q} }}} \right)^{{\omega_{i} }} }} \le \left( {1 + {\mathcal{T}}_{i.\max }^{q} } \right) \hfill \\ &\quad \Leftrightarrow \left( {{\mathcal{T}}_{i.\min }^{q} } \right) \le \frac{2}{{1 + \mathop \prod \nolimits_{i = 1}^{n} \left( {\frac{{1 - {\mathcal{T}}_{i}^{q} }}{{1 + {\mathcal{T}}_{i}^{q} }}} \right)^{{\omega_{i} }} }} - 1 \le \left( {{\mathcal{T}}_{i.\max }^{q} } \right) \hfill \\ &\quad \Leftrightarrow \left( {{\mathcal{T}}_{i.\min }^{q} } \right) \le \frac{{\mathop \prod \nolimits_{i = 1}^{n} \left( {1 + {\mathcal{T}}_{i}^{q} } \right)^{{\omega_{i} }} - \mathop \prod \nolimits_{i = 1}^{n} \left( {1 - {\mathcal{T}}_{i}^{q} } \right)^{{\omega_{i} }} }}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {1 + {\mathcal{T}}_{i}^{q} } \right)^{{\omega_{i} }} + \mathop \prod \nolimits_{i = 1}^{n} \left( {1 - {\mathcal{T}}_{i}^{q} } \right)^{{\omega_{i} }} }} \le \left( {{\mathcal{T}}_{i.\max }^{q} } \right) \hfill \\ &\quad \Leftrightarrow {\mathcal{T}}_{i.\min } \le \left( {\frac{{\mathop \prod \nolimits_{i = 1}^{n} \left( {1 + {\mathcal{T}}_{i}^{q} } \right)^{{\omega_{i} }} - \mathop \prod \nolimits_{i = 1}^{n} \left( {1 - {\mathcal{T}}_{i}^{q} } \right)^{{\omega_{i} }} }}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {1 + {\mathcal{T}}_{i}^{q} } \right)^{{\omega_{i} }} + \mathop \prod \nolimits_{i = 1}^{n} \left( {1 - {\mathcal{T}}_{i}^{q} } \right)^{{\omega_{i} }} }}} \right)^{\frac{1}{q}} \le {\mathcal{T}}_{i.\max } \hfill \\ \end{aligned} $$

It is also kept for the imaginary part of membership grade, such that

$$ {\mathcal{W}}_{{{\mathcal{T}}_{i.\min} }} \le \left( {\frac{{\mathop \prod \nolimits_{i = 1}^{n} \left( {1 + {\mathcal{W}}_{{{\mathcal{T}}_{i} }}^{q} } \right)^{{\omega_{i} }} - \mathop \prod \nolimits_{i = 1}^{n} \left( {1 - {\mathcal{W}}_{{{\mathcal{T}}_{i} }}^{q} } \right)^{{\omega_{i} }} }}{{\mathop \prod \nolimits_{i = 1}^{n} \left( {1 + {\mathcal{W}}_{{{\mathcal{T}}_{i} }}^{q} } \right)^{{\omega_{i} }} + \mathop \prod \nolimits_{i = 1}^{n} \left( {1 - {\mathcal{W}}_{{{\mathcal{T}}_{i} }}^{q} } \right)^{{\omega_{i} }} }}} \right)^{\frac{1}{q}} \le {\mathcal{W}}_{{{\mathcal{T}}_{i.\max} }} $$

Similarly, when we consider $g\left( y \right) = \frac{2 - y}{y},y \in \left[ {0,1} \right]$, then $g^{\prime}\left( y \right) = \frac{ - 2}{{y^{2} }} < 0$, then the function is decreasing, so the followings are kept.

$$ {\mathcal{N}}_{i.\min} \le \frac{{\left( 2 \right)^{\frac{1}{q}} \mathop \prod \nolimits_{i = 1}^{n} {\mathcal{N}}_{i}^{{\omega_{i} }} }}{{\left( {\mathop \prod \nolimits_{i = 1}^{n} \left( {2 - {\mathcal{N}}_{i}^{q} } \right)^{{\omega_{i} }} + \mathop \prod \nolimits_{i = 1}^{n} \left( {{\mathcal{N}}_{i}^{q} } \right)^{{\omega_{i} }} } \right)^{\frac{1}{q}} }} \le {\mathcal{N}}_{i.\max} $$

It is also kept for the imaginary part of non-membership grade, such that

$$ {\mathcal{W}}_{{{\mathcal{N}}_{i.\min} }} \le \frac{{\left( 2 \right)^{\frac{1}{q}} \mathop \prod \nolimits_{i = 1}^{n} {\mathcal{W}}_{{{\mathcal{N}}_{i} }}^{{\omega_{i} }} }}{{\left( {\mathop \prod \nolimits_{i = 1}^{n} \left( {2 - {\mathcal{W}}_{{{\mathcal{N}}_{i} }}^{q} } \right)^{{\omega_{i} }} + \mathop \prod \nolimits_{i = 1}^{n} \left( {{\mathcal{W}}_{{{\mathcal{N}}_{i} }}^{q} } \right)^{{\omega_{i} }} } \right)^{\frac{1}{q}} }} \le {\mathcal{W}}_{{{\mathcal{N}}_{i.\max} }} $$

From the above discussion, we get

$$ {\mathcal{T}}_{i.\min} \le {\mathcal{T}}_{i} \le {\mathcal{T}}_{i.\max} $$

$$ {\mathcal{W}}_{{{\mathcal{T}}_{i.\min} }} \le {\mathcal{W}}_{{{\mathcal{T}}_{i} }} \le {\mathcal{W}}_{{{\mathcal{T}}_{i.\max} }} $$

$$ {\mathcal{N}}_{i.\min} \le {\mathcal{N}}_{i} \le {\mathcal{N}}_{i.\max} $$

$$ {\mathcal{W}}_{{{\mathcal{N}}_{i.\min} }} \le {\mathcal{W}}_{{{\mathcal{N}}_{i} }} \le {\mathcal{W}}_{{{\mathcal{N}}_{i.\max} }} $$

So, ${\mathcal{S}}\left( {{\mathbb{E}}_{i} } \right) = \frac{1}{2}\left( {{\mathcal{T}}_{i}^{q} + {\mathcal{W}}_{{{\mathcal{T}}_{i} }}^{q} - {\mathcal{N}}_{i}^{q} - {\mathcal{W}}_{{{\mathcal{N}}_{i} }}^{q} } \right) \le \frac{1}{2}\left( {{\mathcal{T}}_{i.max}^{q} + {\mathcal{W}}_{{{\mathcal{T}}_{i.max} }}^{q} - {\mathcal{N}}_{i.min}^{q} - {\mathcal{W}}_{{{\mathcal{N}}_{i.min} }}^{q} } \right) = {\mathcal{S}}\left( {{\mathbb{E}}_{i}^{ + } } \right)$ and ${\mathcal{S}}\left( {{\mathbb{E}}_{i} } \right) = \frac{1}{2}\left( {{\mathcal{T}}_{i}^{q} + {\mathcal{W}}_{{{\mathcal{T}}_{i} }}^{q} - {\mathcal{N}}_{i}^{q} - {\mathcal{W}}_{{{\mathcal{N}}_{i} }}^{q} } \right) \ge \frac{1}{2}\left( {{\mathcal{T}}_{i.min}^{q} + {\mathcal{W}}_{{{\mathcal{T}}_{i.min} }}^{q} - {\mathcal{N}}_{i.max}^{q} - {\mathcal{W}}_{{{\mathcal{N}}_{i.max} }}^{q} } \right) = {\mathcal{S}}\left( {{\mathbb{E}}_{i}^{ - } } \right)$, then we get

$$ {\mathbb{E}}_{i}^{ - } \le \text{Cq-ROFEWA}\left( {{\mathbb{E}}_{1} ,{\mathbb{E}}_{2} , \ldots ,{\mathbb{E}}_{n} } \right) \le {\mathbb{E}}_{i}^{ + }. $$

• 3. The proof of property 3 is similar to property 2.