Skip to main content
SpringerLink
Log in

Exponentiated Generalized Kumaraswamy Distribution with Applications

  • Published:
Annals of Data Science Aims and scope Submit manuscript

Abstract

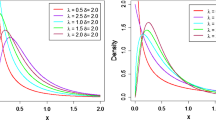
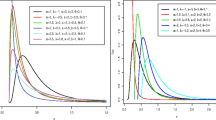
In this article, we introduced and studied exponentiated generalized Kumaraswamy distribution. We derived mathematical properties including quantile function, moment generating function, ordinary moments, probability weighted moments, incomplete moments, and Rényi entropy. The expressions of order statistics are also derived. Here we discuss the parameter estimation by using the method of maximum likelihood. We showed resilience of the introduced distribution over existing some well-known distributions by using real dataset applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Arya G, Elbata I (2015) On the exponentiated generalized modified Weibull distribution. Commun Stat Appl Methods 22:333–348

    Google Scholar 

  2. Alzaatreh A, Lee C, Famoye F (2013) A new method for generating families of continuous distributions. Metron 71(1):63–79

    Article  Google Scholar 

  3. Azzalini A (1985) A class of distributions which includes the normal ones. Scand J Stat 12(2):171–178

    Google Scholar 

  4. Cordeiro GM, De Andrade TAN, Bourguignon M, da- Silva FSG (2017) The exponentiated generalized standardized half-logistic distribution. Int J Stat Probab 6(3):24–42

    Article  Google Scholar 

  5. Cordeiro GM, de Castro M (2011) A new family of generalized distribution. J Stat Comput Simul 81(7):883–898

    Article  Google Scholar 

  6. Cordeiro GM, Gomes AE, da-Silva CQ (2014) Another extended Burr III model: some properties and applications. J Stat Comput Simul 84(12):2524–2544

    Article  Google Scholar 

  7. Cordeiro GM, Ortega EMM, da Cunha DCC (2013) The exponentiated generalized class of distributions. J Data Sci 11(1):1–27

    Google Scholar 

  8. De Andrade TAN, Bourguignon M, Cordeiro GM (2016) The exponentiated generalized extended exponential distribution. J Data Sci 14(3):393–414

    Google Scholar 

  9. Dumonceaux R, Antle CE (1973) Discriminating between the log-normal and Weibull Distribution. Technometrics 15(4):923–926

    Article  Google Scholar 

  10. Elbatal I, Muhammed HZ (2014) Exponentiated generalized inverse Weibull distribution. Appl Math Sci 8:3997–4012

    Google Scholar 

  11. Elgarhy M, Hassan AS, Rashed M (2016) Garhy-generated family of distributions with application. Math Theory Model 6:1–15

    Google Scholar 

  12. Eugene N, Lee C, Famoye F (2002) Beta-normal distribution and its applications. Commun Stat Theory Methods 31(4):497–512

    Article  Google Scholar 

  13. Gupta RC, Gupta PL, Gupta RD (1998) Modeling failure time data by Lehman alternatives. Commun Stat Theory Methods 27(4):887–904

    Article  Google Scholar 

  14. Hassan AS, Elgarhy M (2016) Kumaraswamy Weibull-generated family of distributions with applications. Adv Appl Stat 48:205–239

    Google Scholar 

  15. Hassan AS, Elgarhy M (2016) A new family of exponentiated Weibull-generated distributions. Int J Math Appl 4:135–148

    Google Scholar 

  16. Hassan AS, Hemeda SE (2016) The additive Weibull-g family of probability distributions. Int J Math Appl 4:151–164

    Google Scholar 

  17. Haq MA, Butt NS, Usman RM, Fattah AA (2016) Transmuted power function distribution. Gazi Univ J Sci 29(1):177–185

    Google Scholar 

  18. Kumaraswamy P (1980) Generalized probability density function for double-bounded random-processes. J Hydrol 46(1–2):79–88

    Article  Google Scholar 

  19. Lemonte AJ (2014) A new exponential-type distribution with constant, decreasing, increasing, upside-down bathtub and bathtub-shaped failure rate function. Comput Stat Data Anal 62:149–170

    Article  Google Scholar 

  20. Mansoor M, Tahir MH, Alzaatreh A, Ghazali SSA (2016) An extended Fréchet distribution: properties and applications. J Data Sci 14:167–188

    Google Scholar 

  21. Marshall AN, Olkin I (1997) A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families. Biometrika 84(3):641–652

    Article  Google Scholar 

  22. Oguntunde PE, Adejumo AO, Balogun OS (2014) Statistical properties of the exponentiated generalized inverted exponential distribution. Appl Math 4:47–55

    Google Scholar 

  23. Rényi A (1961) On measures of entropy and information. In: Proceedings of the fourth Berkeley symposium on mathematical statistics and probability, vol 1, pp 547–561

  24. Ristic MM, Balakrishnan N (2011) The gamma-exponentiated exponential distribution. J Stat Comput Simul 82(8):1191–1206

    Article  Google Scholar 

  25. Shakeel M, ul Haq MA, Hussain I, Abdulhamid AM, Faisal M (2016) Comparison of Two New Robust Parameter Estimation Methods for the Power Function Distribution. PloS ONE 11(8):e0160692

    Article  Google Scholar 

  26. Shakeel M, Rehmat N, ul Haq MA (2017) Comparison of the robust parameters estimation methods for the two-parameters Lomax distribution. Cogent Math 4(1):1279397

    Article  Google Scholar 

  27. Sharma D, Chakrabarty TK (2016) On size biased Kumaraswamy distribution. arXiv:1609.09278

  28. Shuaib KM, Robert K, Lena HI (2016) Transmuted Kumaraswamy distribution. Stat Transit New Ser 17(2):183–210

    Article  Google Scholar 

  29. Shaw WT, Buckley IR (2009) The alchemy of probability distributions: beyond Gram–Charlier expansions, and a skew-kurtotic-normal distribution from a rank transmutation map. arXiv:0901.0434

  30. Silva AO, da Silva LCM, Cordeiro GM (2015) The extended Dagum distribution: properties and application. J Data Sci 13:53–72

    Google Scholar 

  31. Zografos K, Balakrishnan N (2009) On families of beta- and generalized gamma-generated distributions and associated inference. Stat Methodol 6(4):344–362

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Vice Presidency for Graduate Studies and Scientific Research, Jeddah University, Jeddah, Saudi Arabia

    M. Elgarhy

  2. Institute of Statistical Studies and Research (ISSR), Cairo University, Giza, Egypt

    M. Elgarhy

  3. College of Statistical and Actuarial Sciences, University of the Punjab, Lahore, Pakistan

    Muhammad Ahsan ul Haq

  4. Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan

    Qurat ul Ain

Authors
  1. M. Elgarhy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Muhammad Ahsan ul Haq
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qurat ul Ain
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Muhammad Ahsan ul Haq.

Appendix

Appendix

The elements of the observed Fisher information matrix \(I^{-1}(\Theta )\) are given by

$$\begin{aligned} U_{aa}= & {} -\,\frac{n}{a^{2}}+-\left( {b\alpha -1} \right) \sum _{i=1}^n {\left\{ {\frac{x_i ^{a}\left( {\ln x_i } \right) ^{2}}{\left[ {1-x_i ^{a}} \right] }+\left[ {\frac{x_i ^{a}\left( {\ln x_i } \right) }{\left[ {1-x_i ^{a}} \right] }} \right] ^{2}} \right\} } \\&\quad +\,b\alpha \left( {\beta -1} \right) \sum _{i=1}^n {\left\{ {\frac{-\left( {b\alpha -1} \right) \left( {\ln x_i } \right) ^{2}\left[ {1-x_i ^{a}} \right] ^{b\alpha -2}x_i ^{a}}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \right. } \\&\quad \left. +\,\frac{\left( {\ln x_i } \right) ^{2}\left[ {1-x_i ^{a}} \right] ^{b\alpha -1}x_i ^{a}}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] } {-\,b\alpha \left[ {\frac{\ln x_i \left[ {1-x_i ^{a}} \right] ^{b\alpha -1}x_i ^{a}}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \right] ^{2}} \right\} \end{aligned}$$
$$\begin{aligned} U_{ab}= & {} -\,\alpha \sum _{i=1}^n {\frac{x_i ^{a}\left( {\ln x_i } \right) }{1-x_i ^{a}}} +\alpha \left( {\beta -1} \right) \sum _{i=1}^n {\frac{\left[ {1-x_i ^{a}} \right] ^{b\alpha -1}x_i ^{a}\ln x_i }{1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }}} \\&+\,b\alpha ^{2}\left( {\beta -1} \right) \sum _{i=1}^n {\left\{ {\frac{\left[ {1-x_i ^{a}} \right] ^{b\alpha -1}\ln \left( {1-x_i ^{a}} \right) x_i ^{a}\ln x_i }{1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }}} \right. } \\&\left. {+\,\frac{\left[ {1-x_i ^{a}} \right] ^{2b\alpha -1}\ln \left( {1-x_i ^{a}} \right) x_i ^{a}\ln x_i }{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] ^{2}}} \right\} \\ U_{a\alpha }= & {} -b\sum _{i=1}^n {\frac{x_i ^{a}\left( {\ln x_i } \right) }{1-x_i ^{a}}} +b\left( {\beta -1} \right) \sum _{i=1}^n {\frac{\left[ {1-x_i ^{a}} \right] ^{b\alpha -1}x_i ^{a}\ln x_i }{1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }}} \\&+\,b^{2}\alpha \left( {\beta -1} \right) \sum _{i=1}^n {\left\{ {\frac{\left[ {1-x_i ^{a}} \right] ^{b\alpha -1}\ln \left( {1-x_i ^{a}} \right) x_i ^{a}\ln x_i }{1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }}} \right. }\\&\left. {+\,\frac{\left[ {1-x_i ^{a}} \right] ^{2b\alpha -1}\ln \left( {1-x_i ^{a}} \right) x_i ^{a}\ln x_i }{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] ^{2}}} \right\} \\ U_{a\beta }= & {} b\alpha \sum _{i=1}^n {\frac{\left( {\ln x_i } \right) \left[ {1-x_i ^{a}} \right] ^{b\alpha -1}x_i ^{a}}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }}\\ \end{aligned}$$
$$\begin{aligned} U_{bb}= & {} -\,\frac{n}{b^{2}}-\alpha ^{2}\left( {\beta -1} \right) \sum _{i=1}^n \left\{ \frac{\left( {\ln \left( {1-x_i ^{a}} \right) } \right) ^{2}\left[ {1-x_i ^{a}} \right] ^{b\alpha }}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }\right. \\&\left. +\left[ {\frac{\ln \left( {1-x_i ^{a}} \right) \left[ {1-x_i ^{a}} \right] ^{b\alpha }}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \right] ^{2} \right\} \\ U_{b\alpha }= & {} \sum _{i=1}^n {\ln \left( {1-x_i ^{a}} \right) } -\left( {\beta -1} \right) \sum _{i=1}^n {\left\{ {\frac{\ln \left( {1-x_i ^{a}} \right) \left[ {1-x_i ^{a}} \right] ^{b\alpha }}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \right\} } \\&-\alpha b\left( {\beta -1} \right) \sum _{i=1}^n {\left\{ {\frac{\left( {\ln \left( {1-x_i ^{a}} \right) } \right) ^{2}\left[ {1-x_i ^{a}} \right] ^{b\alpha }}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \right. } \left. {+\left[ {\frac{\ln \left( {1-x_i ^{a}} \right) \left[ {1-x_i ^{a}} \right] ^{b\alpha }}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \right] ^{2}} \right\} \\ U_{b\beta }= & {} -\alpha \sum _{i=1}^n {\frac{\left[ {1-x_i ^{a}} \right] ^{b\alpha }\ln \left( {1-x_i ^{a}} \right) }{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }}\\ \end{aligned}$$
$$\begin{aligned} U_{\alpha \alpha }= & {} -\,\frac{n}{\alpha ^{2}}-b^{2}\left( {\beta -1} \right) \sum _{i=1}^n {\left\{ {\frac{\left( {\ln \left( {1-x_i ^{a}} \right) } \right) ^{2}\left[ {1-x_i ^{a}} \right] ^{b\alpha }}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \right. } \\&\quad \left. {+\,\left[ {\frac{\ln \left( {1-x_i ^{a}} \right) \left[ {1-x_i ^{a}} \right] ^{b\alpha }}{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \right] ^{2}} \right\} \\ U_{\alpha \beta }= & {} -b\sum _{i=1}^n {\frac{\left[ {1-x_i ^{a}} \right] ^{b\alpha }\ln \left( {1-x_i ^{a}} \right) }{\left[ {1-\left[ {1-x_i ^{a}} \right] ^{b\alpha }} \right] }} \\ U_{\beta \beta }= & {} \frac{-n}{\beta ^{2}} \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Elgarhy, M., Haq, M.A.u. & ul Ain, Q. Exponentiated Generalized Kumaraswamy Distribution with Applications. Ann. Data. Sci. 5, 273–292 (2018). https://doi.org/10.1007/s40745-017-0128-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40745-017-0128-x

Keywords

Search

Navigation