Introduction

The structure of forest landscapes, including the composition and the configuration of the landscape, impacts the provision of multiple ecosystem services (ES) and must thus be addressed by forest management planning. It plays a critical role in maintaining ecological integrity, which encompasses a wide range of ecological functions and processes, ultimately leading to the provision of several ecosystem services [1,2,3,4]. The functions include for example facilitating habitat connectivity, regulating carbon sequestration, supporting water provision and enhancing erosion control activities. Moreover, various biological, chemical, and physical processes that occur within ecosystems, influence the flow of energy, matter, and nutrients (i.e., nitrogen fixation, succession, disturbances and resilience) and thus the provision of ecosystem services [4, 5]. Nevertheless, the escalating global demand for food, fuel, and fiber has resulted in intensified fiber production and more homogenous forest landscape mosaics that impact the vulnerability to pests and diseases [6] and to wildfires [7,8,9] as well as the biodiversity conservation [10,11,12]. This trend impacts the ecological integrity of forest landscaped and poses detrimental effects to the sustainability of global forest resources management. In response to this challenge, forest management planning endeavors to reconcile the growing demand for forest products while simultaneously striving to create target landscape structures that can effectively sustain ecological integrity and thus fulfill green certification standards, account for aesthetic considerations, comply with nature or biodiversity conservation and tackle problems arising from landscape fragmentation [7, 13••, 14,15,16].

Forest management model development should encompass the recognition of spatial configurations of landscape patches and management interventions, in addition to incorporating traditional temporal and compositional characteristics. Hence, there is a critical need to integrate nonlinear relationships between decision variables, such as among schedules of stand-level management options, while controlling the spatial arrangement of patches to achieve multiple forest management objectives [1, 17, 18•]. This concept, termed spatial forest planning, entails the systematic integration of spatial information and landscape features into forest management planning, leveraging both spatial information technologies and analytical solution techniques to formulate optimal forest management plans [13••, 18•]. Unlike conventional forest planning, spatial forest planning emphasizes the spatial organization of forest management activities by considering spatial features such as the size, shape, and juxtaposition of forest patches (e.g., land use patterns, habitat connectivity, adjacency, green-up delay) distributed across the landscape. Modelling techniques such as linear programming and integer programming (i.e., exact methods) have often been used to indicate which forest stand to treat in each period to meet management objectives subject to certain political, silvicultural, environmental and other planning constraints. In fact, they are valuable tools for optimizing forest management planning processes, considering spatial and temporal dynamics, and balancing multiple objectives and constraints to achieve sustainable forest management outcomes. In that process, concerns with the spatial distribution of management options have also long been included explicitly in decision models to address the provision of ecosystem services that depend on the landscape structure. The literature reports that both exact mathematical methods (i.e., mixed integer programming) and heuristic techniques (i.e., simulated annealing) have been used increasingly in spatial forest planning efforts to produce optimal or near-optimal solutions, with relatively shorter computational times. In fact, characterizing and controlling the spatio-temporal structure of forest landscape with those methods encapsulated in a decision support system (DSS) has been a promising as well as challenging research endeavor in forest management planning [13••, 18•, 19,20,21,22]. Coordinating management planning across multiple forest ownerships in larger areas with modeling efforts addressing spatial details and neighborhoods has also become part of spatial planning [23]. Spatial requirements on the distribution of management options over the landscape are often expressed in the form of minimum and maximum harvesting area limits, adjacency (i.e., green up delay) restrictions, connectivity and proximity, and core area. The spatial forest model is unique in the sense that spatial conditions become a target objective just like any typical product flow objective.

Some literature reviews have examined spatial considerations in forest management planning. De Pellegrin Llorente [13••] explored factors such as wildlife habitat, invasive species, and harvesting costs, recommending tradeoff analyses and parallel processing for better understanding of forest dynamics. Belavenutti [24] focused on industrial forest plantations, highlighting hierarchical planning approaches for biodiversity conservation and nature protection. Yoshimoto [25•] emphasized research gaps in incorporating forest carbon sequestration into optimization frameworks. Baskent et al. [26, 27•] reviewed multiple-use forest management planning and ecosystem service assessments, while Franca et al. [4] focused on economic benefits in forest certification. Blanco and Lo [21] examined forest modeling, emphasizing integrated approaches driven by climate change impacts. Most recent review papers have focused on a specific topic such as optimization and multi-criteria forest management [25•, 26, 28], landscape management [13••], economics of forest planning [4, 29], current state of forest modelling [21] and techniques and approaches used in industrial plantations [24]. However, they do not focus specifically on the exploration of the techniques and methods used for the concept of spatial forest planning.

Earlier reviews by Baskent and Keles [18•] and Shan et al. [22] highlighted adjacency and green-up relationships in forest management planning, discussing limitations of MIP and heuristic parameter selection. However, the conceptual framework defined in these reviews has become outdated, motivating a reassessment to incorporate new approaches supporting spatial planning for multiple ecosystem services. This paper aims to provide a comprehensive review and analysis of spatial forest planning initiatives since 2005 (as there was a similar review by that time), focusing on the use of analytical solution techniques such as optimization methods and heuristics in designing forest mosaics and understanding the implications of spatial arrangements on the provision of ecosystem services. It explores any developments in spatial forest modeling in terms of modelling architecture, modeling techniques, solution approaches, spatial database and multiple ecosystem services, contributing to both advancing knowledge in spatial forest planning and ultimately promoting the conservation and sustainable use of forest ecosystems. For that purpose, this paper provides an overview of the contextual background regarding spatial forest management planning problems, challenges, trends, innovations, and scientific progress witnessed in the last two decades. The objective of this scientific paper is to provide a comprehensive literature review that examines the prevalent approaches and methodologies used as analytical solution techniques in spatial forest planning. This includes an in-depth analysis of exact techniques, meta-heuristics, artificial intelligence, game theory, and other spatially explicit methods employed to address spatial problems in forest management planning. Additionally, the review aims to identify and discuss emerging trends, current challenges, and future opportunities in the field, offering insights into potential advancements and applications of these methodologies in spatial forest planning.

Review Method

We planned the work to address the connections among the concept, approaches, and techniques used in spatial forest planning based on scientific knowledge. The literature review was set to cover the scientific publications from 2005 to 2023. Nevertheless, it was considered some of the earlier references and reviews were relevant to lay out the ground to the introduction and the discussion of spatial planning. The literature was retrieved from Journal Citation Reports (JCR) journals. Firstly, we used the term “spatial forest planning” to retrieve all papers published in the period 2005–2023 in the ISI Web of Knowledge. Secondly, additional keywords were used in further queries in order to ensure the retrieval of other papers addressing issues relevant to spatial forest planning from the same database (e.g., “spatially explicit harvest scheduling”, “Spatial pattern”, “Landscape structure”, “adjacency”, “green up delay”, “opening size”, “habitat connectivity”, “core areas”, "edge effects” combined with the terms “forest management planning” or “harvest scheduling”.

The literature review was meticulously structured, categorizing decision-making methods into their main classes and providing detailed insights into the specific types of decision methods employed by the researchers across various studies. Additionally, the review systematically categorized ecosystem services, shedding light on the diverse dimensions explored by the researchers. A temporal perspective was also incorporated by classifying the literature based on publication years. Each publication was scrutinized to discern the predominant decision-making methods, specific decision-making techniques, and the spectrum of ecosystem services addressed in the respective research endeavors (Annex 1). To enhance clarity, comprehensive tables and graphs were crafted, offering a visual representation that facilitated a nuanced understanding of the literature review.

The full set of papers retrieved was examined to exclude duplicate records as well as to select the references that were relevant to the objectives of this review. Afterwards each article underwent a comprehensive scientific analysis that delved into various aspects of spatial forest planning. The in-depth analysis covered a wide range of aspects, including the conceptual approaches utilized, the spatial elements incorporated, the specific DSS and methods employed, the ecosystem services integrated, spatial planning concepts addressed, the risks and uncertainties dealt with, and the pertinent policies and regulations considered. These results were then synthesized to determine the contributions made by these studies to the broader understanding of the contribution of spatial planning to the efficiency and the effectiveness of forest ecosystem management planning. The analysis also aimed at identifying the strengths and weaknesses of these contributions to the implementation of spatial forest planning in practical real-world applications. Furthermore, potential challenges that may arise in future work were identified and discussed.

Approaches/Methods and Decision-Making Techniques Used in Spatial Forest Planning

The design of the landscape mosaic often involves the use of exact or heuristic solution techniques [30, 31, 32•, 33, 34, 35••]. However, integrating spatial features can substantially increase the computational complexity of the problem, almost rendering it intractable [18•, 22, 36]. Therefore, it may become necessary to scale down and simplify the problem to attain a manageable solution within a hierarchical process. Eyvindson et al. [3] demonstrated this approach by integrating the upper hierarchical level with a subset of lower hierarchical level issues, forming a comprehensive optimization problem solved with a variation of the goal programming technique with an iterative methodology. The landscape-level management plans generated through this iterative process exhibited significant improvements in strategic solutions, approaching the global optimum. This suggests that when a problem becomes exceptionally challenging and difficult to solve, a hierarchical approach has the potential to facilitate the incorporation of spatial factors into practical applications and enable the utilization of exact solution techniques at the landscape level.

Various approaches have been developed and extensively documented in the literature to span both individual classes of methods and the integration of exact methods with heuristic strategies [37,38,39,40,41]. The literature review indicates that the number of papers utilizing exact methods were predominantly used (44 papers, 39%) by the researchers followed by the number of researches using heuristics methods (34 papers, 30%) (Fig. 1a). The exact methods typically involve algorithms or techniques that guarantee optimal solutions within certain computational constraints. Heuristic methods, however, are approximate algorithms that aim to find relatively good or near optimal solutions quickly. Only 10% of the literature (11 papers) combined both exact and heuristic methods in their decision-making approaches. This meaningful amount of research suggests a hybrid approach, possibly leveraging the strengths of both types of methods. A reasonable proportion of the literature (25 paper, 22%) falls into the category of "Other," which may include conceptual papers, review articles, or studies that apply other decision-making methods such as Multi-Criteria Decision Analysis (MCDA) and Artificial Intelligence (AI).

Fig. 1
figure 1

The classification of the number of publications according to the class (a) and types of methods (b) used. “Exact/heuristic” classification refers to the papers that either combine exact and heuristic methods or uses both methods

Full size image

Regarding the detailed classification of decision-making methods into "types of decision-methods”, researchers predominantly favor MIP representing 19% of decision-making methods in spatial forest management, followed by simulated annealing (SA) heuristics at 11% (Fig. 1b). Other notable methods include integer programming (10%), linear programming (9%), and tabu search (4%). Less common methods such as genetic algorithm, threshold accepting, ant colony, cellular automata, and great deluge heuristics were also utilized, reflecting a diverse range of approaches. Some researchers explored alternative solutions with less common exact methods like goal and dynamic programming. Despite their complexity, these methods were tested for novel perspectives in spatial forest management. The distribution of publications shows an increasing trend from 2015 onward, indicating a growing interest in the subject during this period (Fig. 2).

Fig. 2
figure 2

The evolution of the publications over time

Full size image

Exact Optimization Techniques

Exact optimization refers to an algorithm that guarantees finding the best possible solution to a given problem within a specified set of constraints and conditions. These techniques are characterized by their ability to systematically explore all possible solutions to identify the one that optimally satisfies the problem's objective function. However, they may be computationally intensive and time-consuming, especially for complex problems with a large search space. They include linear programming, integer programming, dynamic programming and mixed-integer linear programming. They have been extensively used in forest planning, particularly in solving the harvest scheduling problem [31, 35••, 42••, 43, 44]. Over the last three decades, however, the exact methods have been also tailored to solve spatial forest planning problem that include spatial variables describing key elements of habitat reserve such as core area and connectivity, as well as adjacency and opening size constraints. A thorough exploration of the specific applications, limitations, and implementations of exact techniques has been cautiously undertaken in Section “Spatial forest planning with ecosystem services: Case studies and applications “to avoid redundancy within the review. The section offers a comprehensive and in-depth exploration, providing detailed insights into the practical uses of exact techniques in spatial forest planning.

While the optimal solutions are achieved with the exact techniques as their major strengths, such approaches have still some drawbacks:

  • It is often cumbersome to formulate and find a feasible solution for real forest management planning problems involving many ecosystem services and management objectives, requiring spatial consideration and stochastic approach [18•, 22, 45, 46]

  • Reconfiguring forests to reduce the problem size due to computation difficulties can result in a loss of spatial detail and resolution.

  • In most of the exact techniques, forest re-stratification is performed a priori which limits the ability of solution techniques to explore alternative spatial configurations for improved solutions.

  • Most of the approaches involve a significant pre-processing compilation to enumerate sets, still requiring more computational time and memory usage.

  • Due to the linearity of the relationships among the decision variables, model building is complicated by the need to address issues involving non-linear relationships between the decision choices, such as those related to spatial patterns, wildlife habitat, and fire behavior integration. [47, 48].

Contemporary forest management planning is a multifaceted endeavor, encompassing a multitude of ecosystem services, diverse objectives, and involving multiple ownerships and stakeholders. It necessitates the projection of the future forest with multiple intervention entries, such as multiple harvests, spanning multiple rotation periods to ensure the long-term sustainability of ecosystem services [27•, 35••, 49]. As forest management planning paradigm expand in scope and complexity, relying solely on exact methods for formulation becomes increasingly challenging and unwieldy. This challenge arises from the growing size and complexity of the spatial data and variables involved, necessitating more flexible and scalable approaches to modeling and decision-making, such as heuristics. Thus, various types of methods can well be developed and used to solve spatial forest planning problem.

Meta-heuristic/Combinatorial optimization techniques

In the pursuit of search techniques that offer enhanced convenience and simplicity within the domain of spatial forest modeling, significant developments have been taken through the evolution of metaheuristic approaches. Meta-heuristic or combinatorial optimization techniques are powerful methods used to find high-quality solutions to complex problems where the search space is combinatorial in nature, meaning that the solution is a combination of discrete elements or decisions. They are general problem-solving strategies that guide the search for solutions in large, complex solution spaces. Metaheuristics are characterized by their flexibility, simplicity, and ability to provide near-optimal solutions within a reasonable amount of time. They often draw inspiration from natural phenomena or human problem-solving processes and typically involve iterative improvement processes that gradually refine candidate solutions. These techniques are widely applied in various fields including forestry due to difficulties in formulating and solving NP-hard problems such as spatial forest planning. A variety of heuristic techniques have been employed to address spatial forest problems, such as simulated annealing (SA) [17, 50], tabu search (TS) [51], genetic algorithms (GA) [52, 53], threshold accepting (TA) [19] and various other hybrid algorithms [30, 54•].

However, the effectiveness of meta-heuristics varies based on the complexity of the planning problem, encompassing the diverse range of management objectives, ecosystem services, and the design of the model with the rational configuration of its parameters [30, 55]. In fact, these techniques are closely aligned with optimization methods but emphasize a problem-specific approach rather than a purely algorithmic one [56]. In another review conducted by Kangas et al. [33], metaheuristics are described as tailored to the specific problem at hand, focusing on escaping local optima. Furthermore, Pellerin et al. [54•] highlight the advancement towards heuristics and hybrid metaheuristics in addressing resource-constrained project scheduling problems. In fact, hybrid metaheuristics combine various metaheuristic algorithms, as well as other optimization techniques, to create more powerful and effective problem-solving approaches. For example, a hybrid metaheuristic may combine genetic algorithms with simulated annealing or tabu search to improve exploration and exploitation capabilities.

In metaheuristics, effectively exploring the solution space is vital for finding optimal solutions. In spatial forest planning, the quality of solutions heavily relies on the search technique used between consecutive iterations. Developing and employing an efficient neighborhood search technique is crucial for improving heuristic results. Bettinger and Zhu [57] introduced a novel approach that incorporates unused decision options into a solution, addressing any resulting problems by selecting better alternatives for affected spatial units. Although the study highlighted the significance of this approach, its superiority over traditional methods was not precisely quantified. Examples of metaheuristics include genetic algorithms, simulated annealing, tabu search, particle swarm optimization, and ant colony optimization.

The simulated annealing (SA) technique, inspired by metallurgical annealing, explores the solution space by gradually accepting worse solutions with decreasing probability, escaping local optima to converge near-optimal solutions. SA is a stochastic neighborhood search method that examines forest management plans, proposing changes to single characteristics like harvest time or activity. It is highly parameterized and combines intensification and diversification to improve solution quality. Bettinger and Zhu [57] propose evaluating solution quality by comparing results with exact techniques for relaxed problems or estimating a global optimum from heuristic solutions. Cyr et al. [58] used both SA and MIP techniques sequentially to determine the effects of wildfire and wildlife habitat (Caribou population) on harvest level, that were implemented on an area varying from 50 to 1000 km2 with adjacency constraints. Unit restricted model (URM) was used to control the shape (low perimeter/area ratio) or harvesting units. They found that the combination of heuristics and exact models was beneficial in achieving a spatially constrained harvest schedule that accounted for wildlife requirements and maximized annual allowable cut. Similarly, Chen et al. [2012] developed a spatial forest planning model that integrated timber revenue and habitat quality for a forest landscape in northeast China with SA based on the area restricted model (ARM) of adjacency constraints. The study explored three different management strategies: first, maximizing forest net present value (NPV) without spatial limitations; second, optimizing the management of various levels of suitable habitats while considering constraints related to green-up periods and opening sizes over a span of two periods. The results demonstrated that allowing for habitat generation led to a reduction in total NPV ranging from 40.7% to 74.4%. The impact of adjacency constraints on NPV and habitat quality was determined to be moderate. Furthermore, imposing restrictions on the amount of suitable habitat had a significant negative effect on overall timber benefits in spatial planning problems.

Tabu search has commonly been used in solving spatial forest management problems over a number of decades. Different from SA, the heuristic maintains a short-term memory of recently visited solutions and avoids revisiting them. This helps escape local optima and allows exploration of different regions of the solution space. As well, tabu search utilizes various types of solution change methods to intensify and diversity the solution to arrive a global optimum. In a typical adjacency and opening size based spatial forest planning, Bettinger et al. [59] explored three types of decision choices or moves, that included a change to the harvest timing of a single management unit (1-opt moveFootnote 1), the swapping of two management unit's harvest timing (2-opt moves), and the swapping of three management unit's harvest timing (3-opt moves). They tested four reversion rates (0, 3, 6 and 9 reversion intervals) in three types of s-metaheuristics; threshold accepting, tabu search and the raindrop methods [60] in combination with three types of moves.

Reversion, which involves resuming a search from a previously found local optimum, seeks to enhance the search of the best solution by focusing on established high-quality local optima and uncover potentially improved solutions within the same neighborhood. Bettinger et al. [59] used a 1841-hectare hypothetical forest that was divided into 87 management units and solved it with MIP based on URM with pairwise adjacency constraints (one period green-up) to find out the global optimum. They concluded that (a) reversion does improve the quality of the solutions generated, and (b) the rate of reversion is an important factor that can affect solution quality.

Dong et al. [61••] evaluated the performances of various variants of neighborhood, hybrid and reversion search techniques compared to the traditional 1-opt moves. They indicated that the performances of all the enhanced search techniques of SA generated systematically better results than a conventional search strategy, at the expense of additional computational time. However, the reversion search technique employing the exchange version of 2-opt moves was found to be the most suitable strategy to solve the problem with at least a 1% increase in the objective function. In a similar yet larger problem, however, changing simultaneously the treatment schedule in more than one stand does not improve much the performance of SA [62]. Later, the same authors such as Dong et al. [63•, 64, 65, 66•] as well as Qin et al., [5] used various combination of neighborhood search techniques such as 1-opt moves and 2-opt moves in SA heuristic to solve three typical spatial problems involving non-spatial model, ARM and URM models with different parameters. Their objective was to investigate various management activities for both timber production and carbon stocks by adhering to maximum harvest opening size and even-flow timber constraints with various neighborhood search techniques. The study emphasized the sensitivity of optimal solutions in forest management planning to various factors such as neighborhood search techniques, problem complexity, and parameter rationality. It advocated for the generation of multiple independent solutions before applying heuristics, underscoring its importance. For instance, the effectiveness of a neighborhood search strategy (a combination of 1-opt and the swapping version of 2-opt move) improved significantly (10%) from smaller to larger scenarios, based on objective function comparisons. The study recommended utilizing both polynomial and exponential functions for parameter estimation in the Simulated Annealing framework. Regarding carbon management, a non-linear pattern was observed in balancing carbon management with conventional timber harvest due to challenges in maintaining consistent harvests, initial age class structures, and arranging harvesting activities [5, 65].

Similar to tabu search approach, "raindrop" has been developed and used for addressing spatial forest problems [60]. This method incrementally enhances solutions through a series of iterative changes that can be chosen either randomly or in a deterministically. During these iterations, a harvest unit period is selected at random, without consideration for potential constraint violations. If any adjacency constraints are violated during this process, they are promptly rectified in a spreading wave-like fashion. The next best alternative for the affected management unit is then incorporated into the solution. Any other management units subsequently impacted by this change are added to the list of affected units. This iterative process continues until all constraint violations have been resolved. Zhu and Bettinger [60] tested the method in the context of spatial forest planning to maximize NPV subject to wood flow and area adjacency constraints. They compared its performance to that of similar heuristics. Their results indicate that the effectiveness of these heuristics depends on the initial condition of the forest, particularly its age class distribution. Notably, the modified raindrop method exhibited superior performance when applied to forests with young age class distributions. While one advantage of this method lies in its reliance on only two parameters (the total number of iterations and the number of iterations before reverting to the best solution), a drawback is the increasing amount of time needed to solve the same problem. Hence, it is suggested that the raindrop method is best suited for smaller problems characterized by relatively young age class structures.

Inspired by the principles of natural selection and evaluation mechanisms, genetic algorithms (GA) stand out as powerful stochastic optimization algorithms employing probabilistic operators [52]. Their distinguishing feature lies in their operation with a population of solution vectors, setting them apart from many other heuristics. These algorithms operate by maintaining a population of potential solutions and applying selection, crossover, and mutation operators to iteratively evolve towards improved solutions. Genetic algorithms have found applications in diverse fields, including spatial forest planning, as demonstrated by the work of Lu and Eriksson [52]. An intriguing example of genetic algorithms in action can be found in the study conducted by Fotakis et al. [53]. The study utilized genetic algorithms to optimize timber harvest while minimizing sedimentation in water runoff to safeguard water quality and prevent soil erosion. The genetic algorithm strategically placed old forest stands near streams, reducing sedimentation levels significantly. This approach generated a Pareto front of non-dominating solutions, demonstrating the trade-offs between timber harvest and soil conservation. By offering a spectrum of solutions that reconcile these goals, the genetic algorithm provided crucial insights for spatial forest planning.

Other Metaheuristics

In addition to well-known metaheuristics like SA, TS and GA, other heuristics are occasionally applied in spatial forest modeling. For instance, Wei and Hoganson [67] and later Henderson and Hoganson [68] developed a learning-based dynamic programming solution heuristic to address spatial forest management problems efficiently. Their approach decomposes the problem into smaller sub-problems, using windowing techniques to avoid dimensionality issues and accelerate solution search times. Parameters such as size, direction, and overlap define each sub-problem, aiming to comply with core area constraints over time and create large contiguous patches of adjacent stands as habitat. They incorporate a learning-based strategy to improve future problem setups based on past solutions, aiming for superior outcomes within shorter timeframes while minimizing suboptimal results. Their analysis revealed solution outcomes ranging from nearly 1% to 32% of the global optimum, considering spatial constraints.

Neto et al. [69] introduced a Monte Carlo tree search method to address spatial harvest scheduling, aiming to minimize forest fragmentation while maximizing NPV and connectivity index. Their multi-objective approach found efficient solutions with a slight NPV decrease (5%) but significant connectivity index increases (up to 200%). Heinonen [70] similarly used graph theory and minimum spanning tree (MST) to optimize NPV and habitat connectivity in a forest landscape, improving connectivity of broadleaf-rich patches with moderate NPV loss. Garcia-Gonzalo et al. [45] introduced a technique to incorporate climate change uncertainty into harvest planning to optimize NPV across various scenarios and spatial restrictions for a 1000-stand forest. They utilized the Progressive Hedging (PH) algorithm, similar to Simulated Annealing, breaking down the problem into autonomous sub-problems for simpler solving [71]. Non-anticipativity constraints (i.e., time consistency) were relaxed using a quadratic penalty term in the objective function, acting as soft constraints. This approach aimed to minimize infeasibilities across different sets of variables and climate scenarios. Adjacency constraints were included through the "minimum infeasible cluster formulation" with the ARM model. The PH-based stochastic programming method outperformed deterministic models, achieving improved and feasible objective functions with an average time savings of 90% and maximum average gaps of 4%.

Some researchers are trying to deal with risk and uncertainty which are rarely regarded as part of spatial forest planning that would be disrupted by fire, pests, or even on-the-ground conditions. Murray et al. [72] investigated spatial uncertainty in 351 management units, with an average size of 12 ha subject to adjacency restrictions to mitigate sedimentation limits, stress on flora and fauna, and degradation of the environment. They used some forms of URM type of approach with MIP to simultaneously address dispersion, disruption, and uncertainty and minimize total uncertainty associated with potential adjacency violations in forest planning. They found that incorporating risks and uncertainty would reduce benefits from 17 to 65%.

Similar to SA and TS, cellular automata (CA) are discrete dynamic systems used infrequently in spatial forest planning. CA involves a grid of stands that change over discrete time intervals following specific rules based on their present condition and neighboring stands. Zeng et al. [73] utilized CA to minimize wind damage risk in forest planning, considering stand composition and spatial configuration. They developed a model to minimize wind damage by arranging clear-cuts next to opening gaps, reducing vulnerable stand edges. Although CA yielded lower harvest levels, it effectively minimized wind damage. Similarly, Mathey et al. [74] developed a computationally efficient CA algorithm to maximize cumulative harvest volume and clustered late-seral forests, demonstrating a trade-off between objectives. Their results highlighted sensitivity to local and strategic constraints, comparable to SA search. Pascual et al. [75] examined the impact of harvesting costs on distribution using the dynamic treatment units (DTUs) approach to optimize NPV and enhance treatment clustering using CA heuristic. They observed that maximizing NPV favored final harvesting over thinning, positioning harvest blocks near forest roads, and creating more compact DTUs compared to plans focused solely on timber production. Compact harvest blocks were achieved by minimizing the proportion of cut-uncut boundaries, while an aggregated landscape was achieved by maximizing cut-cut boundaries between treatment units. Furthermore, CA outperformed SA with an increasing number of spatial units.

Ant colony optimization (ACO), inspired by the foraging behavior of ants, uses artificial ants to build solutions and reinforce paths based on pheromone levels, eventually converging to optimal or near-optimal solutions. Infrequently applied in forest planning, the ACO algorithm was put to the test in optimizing the harvesting patterns within a forest landscape. The primary objectives were to minimize the risk of wind damage and ensure a sustainable and consistent flow of periodic harvests, as demonstrated in the study by Zeng et al. [76]. In comparison to SA and TS, ACO exhibited logical performance, consistently maintaining a relatively even distribution of periodic timber harvesting while minimizing the risk of wind damage. However, similar to other heuristic algorithms, the sensitivity of ACO to parameters governing pheromone updates and schedule selection was notable.

Nonetheless, the prevailing consensus indicates that SA has demonstrated comparable performance to TA, Great Deluge (GD), Ga and TS with 1-opt and 2-opt moves. As stated by a number of researchers heuristic methods may well be combined with exact techniques to generate a new method where the exact techniques can be used for solving the non-spatial dimension, and the heuristic methods are used for solving the spatial dimension of the problems. Most of the researchers indicated that heuristics used in solving aspatial forest management problem are sensitive to the search reversion rates, decision choices (n-opt moves), parameters used and the problem characteristics.

While less commonly utilized in spatial forest modeling, other operational research techniques such as neural networks, artificial intelligence, and game theory show promise in addressing spatially oriented forest management problems. For instance, Yemshanov et al. [11] developed a novel modeling approach integrating habitat connectivity and timber production in forest management planning using a Stackelberg game-theoretic approach for woodland caribou in Ontario, Canada. They formulated a game between policy makers and companies, treating it as a bi-level optimization problem with seven different combinations of objectives. The spatial aspect involved ensuring connectivity of protected habitat patches and accessibility of unprotected patches for harvesting, requiring control over the connectivity of subnetworks. They highlighted the potential of bi-level game-theoretic approaches in spatial forest planning, noting a trade-off between protection and harvesting levels.

Spatial Forest Planning with Ecosystem Services: Case Studies and Applications

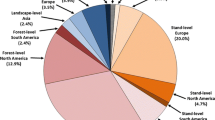
Ecosystem services, the benefits provided by ecosystems, are integrated into spatial forest planning in various combinations. Wood and non-wood forest products (NWFP) are the most prominent services, comprising 40.44% of references, indicating a focus on resource utilization and sustainable management. Biodiversity conservation follows at 33.33%, emphasizing attention to spatial structure and forest fragmentation. Climate regulation, particularly carbon storage and sequestration, is addressed in 7.11% of references, reflecting recognition of forests' role in mitigating climate change. Regulatory services, such as managing wildfire and wind damage, are discussed in 7.54% of references, highlighting concerns for forests' protective functions. Multiple ecosystem services are considered in 9.13% of references, acknowledging their interconnectedness and the need for holistic management. Water provision, erosion prevention, and cultural services each constitute smaller percentages, reflecting specific but less emphasized aspects. Overall, the diverse range of ecosystem services addressed in the literature underscores the multifaceted considerations in spatial forest management planning.

Spatial Constraints (Biodiversity Conservation)

Biodiversity conservation has been handled with a number of proxy indicators such as opening size, adjacency, core area and connectivity, mainly representing various aspects of spatial forest structure [76, 78]. In fact, quantifying, measuring and modeling landscape pattern or structure has long been the primary focus of spatial forest planning. Many researchers have focused on restoring habitat connectivity, reducing habitat fragmentation, and preserving suitable old growth habitats to establish spatial forest integrity [10, 17, 34, 44, 79, 80]. Both the exact models and heuristics have been used to generate solutions to control landscape fragmentation and establish spatial integrity in a landscape through designing harvest scheduling activities.

A green-up or adjacency constraint regulates the time interval between harvesting neighboring forest units and limits the extent of clear-cutting or unharvested stands. While "adjacency" refers to the spatial relationship between forest patches, green-up indicates the temporal differences between the contiguous forest units. While there is a slight or subtle differences between adjacency and green-up concepts, both are often used interchangeably. In general, however, "adjacency" refers to the time difference between harvested units in spatial proximity, aiming to maintain a contiguous forest landscape and prevent negative ecological impacts from edges or boundaries. Different types of adjacency concepts include immediate adjacency, point-touch adjacency, and distance adjacency, each defining various aspects of spatial configurations between stands. By combining distance adjacency with green-up delay constraints, forest connectivity over time can be ensured, creating corridors of width d meters connecting unharvested stands [81]. Goycoolea et al. [42••] distinguished between dynamic and static green-up constraints, where dynamic constraints enforce adjacency at the stand level within the unit restriction model, while static constraints operate at the cluster level, requiring adjacent stands within a clear-cut area to be harvested simultaneously. These constraints mimic model behavior and contribute to the planning process.

An alternative definition of adjacency considers both spatial and non-spatial attributes. Forest units are deemed adjacent if they are within a specified proximity, regardless of physical touch. Additionally, stands with thematic attributes within proximity can form wildlife habitat clusters, like old forests or native forests. Minimum area requirements for such clusters are often imposed in harvest scheduling with adjacency constraints [82]. Unlike the URM, Ríos-Mercado et al. [83] introduced the green unit restriction model (GURM), where nearby native or old forest stands are selected as wildlife reserves or protection areas to remain standing throughout the planning horizon. The GURM adjacency constraint aims to establish a maximum distance between native forest stands.

In integrating spatial features into harvest scheduling models, algorithms defining adjacency constraints are crucial. Various methods have been developed to minimize the number of adjacency constraints within spatial planning models like URM and ARM. Spatial relationships among stands are stored using adjacency lists and adjacency matrices, each influencing the effectiveness of spatial harvest scheduling. Kašpar et al. [84] introduced four types of adjacency matrices, including pairwise constraints from an adjacency list, and constraints derived from analytical algorithms like triangular adjacency matrices, row adjacency matrices, and row triangular adjacency matrices. Comparing the time efficiency of solving URM-based harvest scheduling models using these matrices, their study found that the choice of adjacency constraints significantly impacts problem-solving time. Pairwise adjacency constraints from a regular adjacency list may suffice for addressing URM-based harvest schedules.

Opening size in spatial forest planning refers to the extent of forest units scheduled for treatment, whether contiguous or adjacent, within the same time period. Modeling techniques for opening size vary, with one approach being the URM, where harvesting areas are predetermined based on a specific number of adjacent stands and treated as fixed in size. Another approach is the ARM, where spatial units are dynamically combined into overlapping harvesting blocks composed of all adjacent stands within a maximum opening size limit. The ARM model allows harvesting two adjacent units if the total harvested area does not exceed the desired maximum opening size. However, this approach overlooks the maximum width limitation, a legal requirement in many countries. Murray [85•] introduced both the URM and ARM models. Additionally, the extended area restriction model (EARM) has been proposed, where adjacency is defined as strong (full adjacency) or weak (half adjacency or point-touch adjacency) based on the number of shared points between units. While the URM is relatively straightforward to solve, the ARM presents challenges in formulation and solution. However, researchers have developed new approaches to enhance solution efficiency. For instance, Goycoolea et al. [43] contributed to solutions for both ARM and EARM. In ARM-based models, defining feasible clusters, or cliques, for harvesting is essential [86]. A clique comprises units (stands, cells) that are mutually adjacent, termed immediate adjacency. The largest subset of mutually adjacent units is known as a "maximal clique," and the approach is termed maximal clique-cluster (MCC) formulation. Adjacency constraints are fulfilled by selectively harvesting a single viable cluster from the set of feasible clusters intersecting each maximal clique. Goycoolea et al. [43] emphasized the significance of clique definition and utilization, as model performance depends on clique characteristics, with certain sets of cliques outperforming others.

Adjacency and opening size constraints are readily handled in heuristic modeling techniques like simulated annealing, tabu search, genetic algorithms, and cellular automata in a more flexible manner. However, exact modeling methods such as integer programming and mixed-integer programming face great challenges due to the NP-hard complexity of the spatial forest management problem, making it difficult to solve in a reasonable time. Goycoolea et al. [43] and Goycoolea et al. [42••] attempted to address this challenge by formulating adjacency and opening size constraints in exact modeling approaches using LP-relaxation through a clique representation of a projected problem with integer variables. They developed MIP based harvest scheduling models subject to maximum area constraints based on the EARM approach by projecting strong valid inequalities from the node packing problem to the cluster packing problem. They also re-defined clusters to be adjacent when within a certain proximity, termed distance adjacency. Testing their approach on both hypothetical and real case study areas, they demonstrated that their tight formulation allowed for the "branch and bound" method to solve medium-sized EARM instances relatively quickly, achieving solutions within a 1% margin of the optimal solution. In their study, Goycoolea et al. [42••] investigated three MIP formulations based on the ARM concept, applying a static green-up delay concept. The first formulation, termed the Path Formulation, involves identifying all possible paths or potential infeasible configurations of a harvesting cluster and establishing constraints to prevent each of these infeasibilities. Specifically, this formulation ensures that the maximum number of stands in a cluster harvested in the same period is equal to the total number of stands minus one at most. Adjacency constraints are imposed for each path, and simultaneous harvesting of all stands composing each path (minimally infeasible cluster) is prohibited to ensure a feasible solution. This formulation enforces adjacency restrictions on every path, disallowing the concurrent harvesting of all stands within each pathway, forming the minimal infeasible cluster, to obtain a feasible solution.

The second formulation, called Cluster Packing Formulation, focused on defining variables for all feasible harvesting clusters and imposing constraints to ensure that no selected pair of clusters overlapped or shared adjacent stands [31]. The third formulation, known as the Bucket Formulation, entailed predefining buckets and assigning stands to each bucket in a manner that represented a harvested cluster [87]. They applied three formulations in four case forests using dynamic green-up delay concept, ensuring all stands were harvested once over the planning horizon without multiple harvests. The Clique-Cluster Packing formulation outperformed Path and Bucket formulations, achieving optimality ranging from 1% to 7.16%, influenced by forest size and formulation tightness. Green-up constraints posed challenges, with varying effects based on the number of green-up periods constraint. Introduction of volume, ending age, and green-up constraints led to encountering some infeasible solutions, highlighting formulation sensitivity. Martins et al. [88] introduced the connected-bucket model, extending the bucket model with additional constraints on bucket connectivity and stand adjacency, using Dantzig-Wolfe decomposition and finding superior results with the branch-and-price approach in most cases.

Augustynczik et al. [89] compared two methods for clustering forest harvesting activities in a planning model: Minimum Spanning Tree (MST) as integer linear programming and SA as a heuristic technique. MST used graphical representation with stands as vertices and connections as edges, while SA considered connectivity with an immediate adjacency concept. MST, though more time-consuming, offered a precise solution, while SA, with quadratic penalty functions, provided a quicker alternative. Testing on a 2365.8-hectare forest with 236 stands, MST reduced NPV by 3.9% to 7.3%, while SA reduced it by 7.6% to 15.4%. Previous SA formulations by Bachmatiuk et al. [62] narrowed this gap to 1.9% to 8.7%, suggesting a promising alternative for better connectivity, especially in larger forest planning problems.

Yoshimoto and Konoshima [35••] proposed a 0–1 integer programming method for formulating the scheduling problem of allowing multiple harvests over time by using common matrix algebra. They used the concept of Model I formulation to avoid concurrent harvest among adjacent units by different treatments. Green-up constraints is handled by adding a constraint through modification of the activity adjacency element based on two kinds of adjacency matrices; one is an ordinary spatial adjacency matrix for the forest unit location, and the other is a newly introduced activity adjacency matrix to identify concurrent harvesting activities in a set of possible treatments for one forest unit.

Gharbi et al. [16] introduced the Full Adjacent Unit (FAU) model, a MIP approach combining ARM and URM without prior enumeration. FAU utilizes a "full adjacent units" constraint per stand to prevent simultaneous harvesting of adjacent stands, ensuring linearity between constraints and stand count, reducing problem complexity. Tested on real forests, FAU demonstrated insensitivity to forest size and structure while generating superior results compared to counterparts in terms of model size and solution quality [16].

Yoshimoto and Asente [79] developed an exact model of focal point aggregation to address connectivity among aggregated units in clusters, enhancing connectivity between isolated wildlife patches. Focal point aggregation involves aggregating a specific unit (focal point) with its adjacent units, meeting spatial requirements. They utilized the Maximum Flow constrained Model I (MF-Model I) approach by Yoshimoto and Asente [79], incorporating area restrictions via linkage constraints between temporal and spatial features of harvest scheduling. MF-Model I identifies complete connectivity among aggregated units in clusters under maximum opening size restrictions, solving spatial issues like focal-point aggregation while considering no-harvest prescriptions. The number of focal points, periods, and minimum habitat size significantly affect optimization and computational burden. Incorporating maximum flow constraints and spatial constraints addresses spatial challenges, but optimal solutions for larger problems within defined CPU time frames remain challenging due to exponential growth of constraints and integer variables. Despite theoretical feasibility, practical limitations persist for larger forest management problems.

Yoshimoto and Asante [90] addressed inter-temporal unit aggregation issues in forest management using modified dynamic MF-Model I and MF-Model II approaches without prior enumeration to generate possible clusters (Model IV by [91, 92••]). Their method allows spatial units (stands) to merge into different clusters (candidate harvest blocks) over the planning horizon, termed "inter-temporal aggregation". This dynamic problem is complex to solve exactly, but their proposed approaches incorporate a spatial connection module with maximum flow constraints and sequential triangle connection to optimize solutions. They introduced an additional module to manage cluster shapes, preventing long elongated clusters. While clusters cannot be harvested simultaneously (representing a one-period green-up delay), their formulation doesn't account for delays exceeding one period between clusters. St. John and Tóth [90] suggested that their Model IV is compatible with various formulations and computationally viable for spatially explicit harvest scheduling.

Fustel et al. [93] introduced a spatial forest model using MIP to minimize wind exposure during storms by reducing the susceptibility of edges between adjacent stands. They established thresholds for allowable differences between neighboring stands and found that it was feasible to reduce vulnerable edge length while experiencing moderate reductions in NPV, leading to clustering of dominant stand heights among neighboring stands. In a recent study, Ríos-Mercado et al. [83] formulated a forest harvesting problem with adjacency and environmental constraints based on the extended URM model (GURM) using IP. They tested the effects of parameters such as distance between harvested units, timber volume, green-up period, and minimum forest reserve. They found that maximum area inversely affected the URM and GURM models, with larger regions resulting in reduced profit and time.

Climate Regulation, Carbon Stock and Sequestration

The review also touches upon the incorporation of climate change in spatial forest planning, emphasizing the need to balance wood production with carbon storage and sequestration. Incorporating climate change concerns into spatial forest planning is essential as management interventions and spatial constrains (e.g., adjacency and opening size) and resultant spatial patterns directly influence growing stock or biomass levels and, consequently, carbon storage. Despite the significance of this issue, only around 7% of the literature reviewed specifically addressed climate regulation in spatial planning. Dong et al. [14, 65] and Qin et al. [5] utilized neighborhood search techniques within the Simulated Annealing heuristic framework to explore management activities maximizing timber production and carbon stocks while adhering to constraints like maximum harvest opening size and even-flow timber requirements. Their findings suggested significant potential for carbon stock increases over the next 30 years, with average carbon density rising by the end of the planning horizon across different initial age class structures. Garcia-Gonzalo et al. [45] pioneered integrating climate change uncertainty into spatial harvest planning using PH and ARM methods to optimize NPV under 32 climate change scenarios and spatial adjacency restrictions. The review highlights the effectiveness of incorporating climate change uncertainty into spatial forest management planning, with the PH-based stochastic programming methodology demonstrating superiority over deterministic models. Marto et al. [94], Marques et al. [39], and Marques et al. [40, 41] integrated carbon sequestration, wood production, and biodiversity conservation into spatial forest planning using various decision support approaches such as MIP, GP and MCDA. They presented trade-offs among ecosystem services in a Pareto Frontier, showing that maximizing average carbon stock and biodiversity often comes with a lower net present value. Qin et al. [5] examined the effects of carbon prices on trade-offs between forest carbon and timber management objectives, demonstrating through Simulated Annealing metaheuristic that higher carbon prices led to an increase in non-harvested units and a decline in harvested units with alternative prescriptions while maintaining a consistent total percentage of harvested units due to even flow constraints. They basically demonstrated the effects of carbon-prices on the optimal spatial and temporal assignments of alternative management prescriptions by considering adjacency constraints of assigned management prescriptions.

Others (Water Provision, Erosion Control and Recreation)

The integration of various ecosystem services in spatial forest planning is essential for ensuring sustainable forest management. Forest planners are adopting holistic strategies to balance timber harvesting with preserving soil integrity, enhancing water resources, and providing recreational services. This approach addresses economic goals while fostering resilience and well-being in forest ecosystems. However, the review found that studies incorporating water provision, erosion prevention, and cultural services in spatial forest planning are limited, comprising less than 4% of the literature (Fig. 3). Fotakis et al. [53] introduced an innovative method that integrated soil preservation into timber production using genetic algorithms. They strategically located old forest stands along the stream network to mitigate sedimentation while optimizing timber harvest, demonstrating trade-offs between timber harvest and soil conservation. In contrast, Rodrigues et al. [95] integrated timber production and soil erosion but did not address spatial characteristics for soil erosion prevention or timber yield optimization. None of the studies developed a decision support system to control the spatial arrangement of forest stands for water provision. Nevertheless, recent studies by Lundholm et al. [20], Knoke et al. [96], and Botequim et al. [80] have emphasized the importance of recreation, water provision, and quality in traditional forest management planning. While these studies provide valuable insights into forest multi-functionality, they overlook detailed spatial management strategies, highlighting a gap in current research methodologies. There is a pressing need for comprehensive spatial forest planning models that go beyond generic trade-offs and incorporate nuanced spatial control measures. These measures are crucial for achieving a delicate balance among soil preservation, water provision, recreation, and timber production, ultimately ensuring the long-term health and resilience of forest ecosystems.

Fig. 3
figure 3

The distribution of the number of publications according to the ecosystem services

Full size image

Regulating Services (Forest Fire and Wind)

In forest fire management, fuel treatments and fires can interact with each other across both time and space. However, the planning of fuel treatment activities poses complicated decision-making problems with spatial and temporal dimensions [8, 47, 48]. Forest management planning approaches need to treat potential fire loss estimates as indigenous parameters [7]. They developed a methodology based on fire occurrence, suppression, and spatial spread models, a fire protection value model that identifies crucial stands, the harvesting of which can have a significant influence on the spread of fires across the landscape, and a spatially explicit timber harvest scheduling model. Based on the method, they demonstrated that integrated fire—forest management planning could result in an 8.1% increase in NPV when compared with traditional planning [7].

Troncoso et al. [97] developed spatially explicit URM based harvest scheduling models aimed at maximizing harvesting volume while considering adjacency constraints on flammable landscapes to reduce fire risks. They utilized a fire threat index constructed by analyzing spatial relationships between stands to identify stands at higher risk of fire or those capable of reducing potential volume losses from fire damage. Integrating this index into their analysis resulted in notable benefits: a more than 1% increase in total harvested volume, a 19% growth in standing volume, and an 18% decrease in the total area affected by fire. The study highlighted the sensitivity of results to landscape structure, with a diverse distribution of ignition probabilities across heterogeneous landscapes leading to a more significant increase in final volume compared to cases with more evenly distributed ignition probabilities in homogeneous forest areas.

Altamimi et al. [98] introduced an innovative artificial intelligence modeling approach called Deep Reinforcement Learning (DRL) for dynamic decision-making problems. Based on traditional reinforcement learning which is a type of machine learning paradigm where an agent learns to make decisions by interacting with an environment, DRL utilizes neural networks to learn through direct interaction with the environment, updating Q-functions with on-policy and off-policy approaches to address the curse of dimensionality [98]. They developed a DRL-based forest model to prevent and mitigate wildfire risks by determining efficient management policies considering factors such as timber volume, flammability, and wind direction. Results showed that the DRL policy closely resembled the exact optimum Markov decision process solution and outperformed GA solutions as benchmarks for large-scale model policies. DRL is praised for its ability to estimate near-optimal policies even for complex problems with a high number of possible decisions.

In their recent work, Ferreira et al. [9] focused on spatial optimization in forest management by integrating a wildfire resistance index into MIP formulations. Their approach addressed the flammability of individual stands and landscape features impacting fire spread between neighboring stands, utilizing clear-cut openings based on ARM with a path formulation to represent full adjacency. However, they encountered challenges in reaching optimal solutions, prompting them to explore alternative methods such as using minimal unfeasible clusters and barrier clusters. Belavenutti et al. [99] developed a spatial optimization algorithm using a multi-criteria distance function and breadth-first search to prioritize forest and fuel management treatments in a linear fuel break network in a Western US national forest. They analyzed 13 implementation scenarios considering wildfire hazard, treatment costs, and harvest revenues. Their findings showed that prioritizing wildfire encounter rate and optimizing large fuel break networks led to reduced net revenue and harvested timber, highlighting the trade-offs inherent in wildfire management strategies.

Challenges and Future Directions

Spatial forest harvest scheduling is a complex management task influenced by various factors including diverse forest owner interests, competing objectives, and the consideration of multiple ecosystem services. The process requires extensive spatial data and incorporates new spatial requirements such as habitat connections and riparian buffers. Managing spatial information introduces uncertainty, especially regarding spatial distribution, location, and boundaries of harvest units and habitat patches. Wei and Murray [46] highlighted the sensitivity of URM to spatial data uncertainty, indicating challenges in spatial forest planning. Persistent challenges in spatial forest planning include addressing evolving complexities and developing effective spatial harvest scheduling models. Future research should focus on innovative solutions to enhance the effectiveness of spatial forest models, addressing challenges, and identifying research priorities in forest management planning.

  • Challenges related to spatial data and its sources: Database development is crucial for spatial forest modeling but is often neglected in planning efforts, resulting in deficiencies. Research advocates for integrating high-resolution spatial data from remote sensing and LiDAR into harvest scheduling models to improve spatial accuracy. Modern technologies like remote sensing and operational research offer novel spatial planning techniques. Integration of spatial optimization models with tree-level data enables tree selection based on economic and spatial criteria, while representing trees as polygons facilitates spatial optimization by minimizing perimeter boundaries and adhering to adjacency constraints [100].

  • Spatial scale and complexity: Navigating spatial considerations involves managing hierarchical planning frameworks and multi-level decision-making structures. Addressing spatial scaling and cross-boundary concerns requires seamless coordination across diverse regions and jurisdictions. Coping with spatial heterogeneity and evolving landscapes poses challenges, necessitating agile planning approaches for effective adaptation.

  • New solution techniques: Emerging technological advancements, such as cloud computing, AI, DRL, and game theory, are being combined with spatial DSS to address forest modeling and planning challenges. The Internet of Things (IoT) presents opportunities to integrate spatial information into automated systems, especially in forest modeling applications. Cloud computing expands access to advanced DSS for previously underserved user groups. Object-oriented design facilitates the creation of flexible and adaptable DSS. Future challenges involve hybridizing various metaheuristics and exact algorithms, augmented by artificial intelligence [98] and strategies like self-adaptation and iterative scheduling techniques, to optimize decision-making in forest planning [54•, 56, 101].

  • International conventions and guidelines: International initiatives like forest certification programs and the European Green Deal establish spatial constraints to promote responsible forest stewardship. Guidelines emphasize strategically distributing forest patches and corridors to preserve ecological diversity, while regulating openings near biological reserves to safeguard conservation areas [102,103,104].

  • Integration of multiple objectives with multiple ecosystem services: Future research should focus on integrating a broader range of ecosystem services as management objectives in spatial harvest scheduling models. This includes biodiversity conservation, carbon sequestration, wildfire prevention, water quality, and aesthetic-recreation, all considered simultaneously. Developing multi-objective optimization frameworks and associated spatial planning models will aid in understanding the trade-offs and synergies among these conflicting goals [40].

  • Climate change adaptation: Incorporating climate change impacts into spatial harvest scheduling models is essential. More research should aim to develop climate-resilient spatial planning strategies and assess how changing climate conditions affect forest growth, disturbance regimes, spatial forest pattern and the ecosystem services.

  • Dynamic models: Moving beyond static models, future research should emphasize dynamic spatial harvest scheduling models. These models should account for changing forest conditions over time, including forest growth, disturbance events (e.g., wildfires, insect outbreaks), and land-use changes.

  • Uncertainty Analysis: Effective methods for quantifying and addressing uncertainty in spatial harvest scheduling models are needed. This includes incorporating stochastic modeling techniques and conducting sensitivity analyses to assess the robustness of scheduling decisions to various sources of uncertainty. While some initiatives account for wildfire into spatial modeling [7, 8, 97], the spatial forest models should fully incorporate the catastrophic and spatially-contagious effects of natural disturbances such as wildfire, storm and insect out-break as they are spatially progressing stochastic events. One alternative strategy would involve the development of fire-smart landscape pattern, which entail the optimal layout of fuel breaks and the integration of fire-resisted forest stands spatially arranged with other forested areas to enhance overall fire resilience and mitigation in fire-prone forest ecosystems.

  • Spatial optimization algorithms: The pursuit of progress in optimization algorithms, encompassing diverse search techniques and meticulous parameter determination effort, especially within the realm of metaheuristics such as genetic algorithms, simulated annealing, and tabu search, should be actively undertaken. This exploration effort should be directed towards enhancing the efficiency and precision of addressing the formidable challenges posed by large-scale spatial harvest scheduling problems, bringing us closer to attaining solutions that approach the global optimum.

  • Operational constraints: Consideration of operational constraints, such as road networks, fire breaks, equipment limitations, and budgetary constraints, is crucial. Models should account for these practical yet spatial factors to ensure the feasibility of on-the-ground scheduling solutions to spatial planning.

  • Policy alignment: Management policies and thus guidelines should ensure the clear definition and incorporation of spatial requirements embedded in the sustainability standards (i.e., green certification) in harvest scheduling models.

  • Multi-stakeholder engagement: There is a need for the integration of methods to address landscape functions and processes across various land-use sectors (forestry, agriculture, terrestrial water, and urban areas) in order to engage stakeholders in spatial landscape planning with a wider spatial characteristics considered. Developing sound governance models and tools that facilitate collaborative decision-making among diverse stakeholders, including forest owners, communities, and conservation organizations, is essential in effective spatial forest modeling process. Ensuring that the interests and concerns of all parties including the indigenous and local knowledge systems are incorporated into harvest scheduling decisions that is crucial for sustainable forest management.

  • Capacity building: Invest in training and capacity-building programs to equip forest managers and researchers with the skills and knowledge needed to apply advanced spatial harvest scheduling models effectively.

  • Real-time DSS: Developing real-time DSS that can adapt spatial harvest scheduling plans based on emerging information and changing conditions. Real-time spatial forest model would be possible with the improved data sharing and interoperability, real-time monitoring and adaptive spatial planning approach which involves the dynamic and flexible management of forest landscape in response to changing environmental conditions, societal needs, and stakeholder preferences.

Discussion and Conclusion

The paper presents a thorough review of any scientific papers dealing particular with spatial aspects in forest management planning, focusing on spatial forest modeling and analytical solution techniques. It examines various spatial features such as harvest block size, adjacency requirements, core areas, habitat connectivity, and fire spread. Analytical solution methods, including exact and heuristic approaches, are discussed, alongside case studies assessing their performance. Recent advancements in spatial forest modeling, particularly in exact solution techniques, are highlighted, but the importance of heuristic techniques for real-world problems is also emphasized. The paper highlights the ongoing advocacy for heuristic techniques in addressing large-scale, real-world problems in spatial forest planning, especially concerning multiple ecosystem services and constraints. It highlights further the potential of artificial intelligence to overcome computational constraints to the use of both exact and heuristic techniques. It emphasizes the integration of regulating, supporting, and cultural services in objective functions, beyond provisioning services. The paper identifies emerging requirements and unresolved challenges in spatial forest planning, concluding with critical future developments such as hybrid modeling techniques, quantifying landscape fragmentation, and comprehensive characterization of various forest ecosystem services. Additionally, it underscores the growing enthusiasm in the field to implement innovative approaches for enhancing sustainability and effectiveness in spatial forest modeling initiatives.

The philosophy of ecosystem management planning underscores the importance of understanding ecosystem services, forest patch/stand characteristics, and decision-making techniques for sustainable forest ecosystem management. This approach relies on real-time spatial data and integrates landscape indicators/metrics into the planning framework. Spatial planning is crucial within this framework, aiming to regulate the spatial arrangement of the forest landscape to sustain desired ecosystem services while meeting stakeholder requirements. Establishing structural management objectives, defining spatial interventions, and quantifying spatial requirements are essential for selecting appropriate solution techniques, understanding forest dynamics, and controlling spatial patterns using performance indicators.

Understanding spatial dynamics is crucial for informed decision-making in forest management, enabling the formulation of effective solutions applicable on the ground. Leveraging spatial modeling tools helps understand the causal basis of management interventions and their consequences on forest structure and goals. A holistic systems approach is essential, synthesizing inductive and deductive reasoning to establish a scientific framework and explore spatial relationships among management objectives, including ecosystem services. The challenge lies in determining optimal spatial arrangements across landscapes to maximize multiple objectives while ensuring resilience to natural disturbances. Future research aims to uncover ecologically stable forest configurations that meet diverse management objectives sustainably, balancing public demands with ecosystem conservation.

As for the modeling techniques, both exact and heuristic solution techniques have been successfully used in spatial forest planning. The performance and the successful use of various analytical solution techniques highly depend on the robust architectural design and formulation of the spatial features/characteristic in exact solution techniques and in the case of heuristics is quite sensitive to the types of decision choices or moves, system functions and parameters used within the model. Utilizing heuristic search is commonly recommended in situations where the abundance of decision variables can lead to spatial problems of substantial magnitude within the feasible region [74]. Heuristic search techniques are both fast and efficient in generating solutions, even when dealing with numerous small-scale forest units [105]. These techniques are quite flexible that facilitate alternative formulations of the planning problems and interpretation of the results. Nonetheless, the proximity of the near-optimal solutions to the global optimum and the requirements for parameterization consistently introduce uncertainty when assessing the quality of heuristic-generated solutions as compared to exact modeling techniques [106]. In the meantime, they do not guarantee to optimize management objectives due mainly to their inability to explore all the possible options in a given simulation time and to make inter-temporal trade-offs among the alternatives. There are, however, certain areas to improve the performance of metaheuristics in spatial forest planning as hinted by Bettinger and Boston, [107••] and Baskent et al. [26]. These include hybridization with exact models, process improvements, reversion strategies, destruction and reconstruction strategies, intelligent or dynamic parameterization approaches, intelligent termination or transitioning approaches, and seeding strategies.

Great improvements have been observed since 2005 in formulating various modifications of URM and ARM based harvest scheduling problems with the exact approaches to represent and solve spatial planning problems with a relatively reasonable size of forests in a reasonable computation time [35••, 42••, 43, 79]. In fact, exact approaches are unique, systematic and mathematically rigorous in formulating spatial forest management problems as they seek and find the optimal solution. They are excellent models for small-sized forest management problems with fewer constraints and decision variables, such as ecosystem services and requirements. However, as problem size and the number of ecosystem services and spatial constraints increase, solving larger forest management problems becomes challenging and computationally burdensome. Real-large forest problems involving various spatial requirements like habitat connectivity, core area, harvest block size, and adjacency constraints may be impossible to solve within a reasonable computational time. Therefore, it is crucial to recognize that hybridization or integration of heuristics and the exact approach offers significant benefits to researchers involved in both heuristic and exact modeling domains [56, 79, 108]. The use of hybrid techniques is still rare yet gaining importance particularly in the context of collective decision-making, focusing on the robustness and simplicity [54•, 109]. A solution achieved through heuristics holds the potential to be scrutinized through the prism of the exact method, harnessing optimal metrics such as a gap. Likewise, the exact methodology can capitalize on an integer-feasible solution originating from heuristics, employing it as an initial starting point. This strategic move expedites the pursuit of a conclusive solution, all the while achieving computational efficiency. The general solution in developing solution techniques would seem to proceed on three alternative paths; the development and use of increasingly more sophisticated meta-heuristic solution techniques, approaches and development of alternative mathematical formulations by exact optimization methods and/or inventing totally new solution techniques such artificial intelligence (e.g., as deep reinforcement learning [11, 98].

In conclusion, this review paper provides a comprehensive review regarding the state of the art in spatial forest planning and outlines some future directions to improve its effectiveness in the sustainable management and conservation of ecosystem services. The synthesis of knowledge presented here aims to contribute to the advancement of spatial forest planning strategies and their integration into sustainable management of forest ecosystems.