1 Introduction

High seas are dangerous for ship traffic and offshore engineering activities. Since recent times, radar observation methods are being developed to detect phase-resolved waves at the coast and near harbours and for coastal and ocean engineering activities to reduce the downtime of activities that can only take place during low wave conditions, such as helicopter landing, windmill placements and side-by-side loading operations.

The first attempt in analysing radar images was mainly to retrieve the statistical properties of the waves, such as the peak period \(T_\mathrm{p}\), the directional normalized spectrum and surface currents, using the so-called 3DFFT method (Young et al. 1985; Ziemer and Rosenthal 1987). Although the 3DFFT method is quite successful to determine such characteristic parameters of the sea, efforts to obtain phase-resolved information about the surrounding wave field were not successful (Naaijen and Blondel 2012). An inversion technique using a modulation transfer function (MTF) was used in Borge et al. (2004) to estimate the sea surface elevation. The derivation of the MTF required external information, for instance obtained from in situ measurement. A processing system, called Remocean, also used MTF to estimate the sea surface elevation in coastal areas; see (Ludeno et al. 2014, 2015; Punzo et al. 2016). An empirical method without using any external calibration was introduced in Dankert and Rosenthal (2004). The method required the radar images to be free of shadowing effects which can only be achieved when the radar is mounted very high relative to the significant wave height. Another approach based on variational data assimilation was proposed in Aragh and Nwogu (2008) and Aragh et al. (2008) to find the optimal wave profiles that minimize the difference between images and a wave model prediction; this led to an approximation of the multi-directional spectrum over part of the frequency band.

The aim of this Part 2 is to show that even for high seas that were numerically simulated in Part 1 (Van Groesen et al. 2017), radar observations can be used to observe and predict extreme waves ahead in time to support safer sea traffic, dynamic positioning and ocean engineering activities.

Methods based on the dynamic averaging and evolution scenario (DAES) developed earlier in Wijaya et al. (2015) will be shown to be applicable also for such extreme seas, now using nonlinear simulations instead of linear theory to observe and evolve reconstructed sea states. Physical restrictions caused by the restricted area observed by the radar determine the maximal prediction horizon. For the standard X-band radar settings taken here, the scanning area is restricted to 2000 m around the ship. With a radar height of 30 m above sea level, this leads to a prediction horizon with an accuracy above 80% of approximately 120 s, which is reasonably close to the physical largest prediction horizon of 150 s.

The simulated nonlinear waves of Draupner seas in Part 1 will be used for the radar investigations in a smaller semicircle of radius 2 km. By first designing synthetic radar images by adding the effects of shadowing, these images are then used to reconstruct the sea using DAES. It will be shown that the reconstructed seas are reasonably accurate, with correlation above 80% compared to the original undisturbed seas. Taking a sea reconstruction at one instant as the initial sea state, a prediction can be made for future sea states until the time that waves from the outer domain have reached the position of the radar, which defines the prediction time.

In Sect. 2, we briefly describe the main properties of Draupner seas studied in Part 1, as much as needed for the successive radar application. In the next section, we present the details of the nonlinear version of the dynamic averaging and evolution scenario, DAES. In Sect. 4, we present the results for reconstructing and predicting a specific high wave occurrence, namely, the three successive freak crests described in Part 1. Conclusions and discussion are in the last section.

2 Draupner seas and simulations

Draupner seas have been introduced in Part 1 as seas that have the same characteristic sea parameters as the sea during which the iconic Draupner wave was recorded from the Draupner platform in the North Sea (Haver 2004); see Part 1 for further details and references. This subsection describes briefly the Draupner sea parameters that will be used to synthesize radar images.

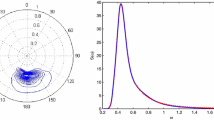
Figure 1 shows the 2D Draupner spectrum obtained from the data of the European Centre for Medium-Range Weather Forecasts, Reading, UK, (Cavaleri et al. 2016), but rotated over an angle of 13\(^\circ \) in the western direction to have the maximum energy flux directed towards the south. Of special interest is the very wide spreading, with two low-frequency lobes 60\(^\circ \) separated.

Fig. 1
figure 1

The 2D spectrum rotated over an angle of 13\(^\circ \) to the west to have the main energy propagation to the south

Full size image

The spectrum is scaled such that the significant wave height is 12 m and has 120\(^\circ \) spreading. The peak period is 14.45 s and the water depth is 70 m. In Part 1 is described in much detail how the seas have been simulated. Using the spectrum properties and \(H_\mathrm{s}\) mentioned above, explicit expressions for a random linear analytic sea were obtained. Over a rectangular numerical area of more than 60 km\(^2\), at distinct update times, new linear sea states are used as influx data outside a large semicircle; a nonlinear wave model then calculates the evolution into the semicircle until the next update, and so on.

The use of a nonlinear wave model is needed because in steep nonlinear seas, extreme waves will undergo nonlinear changes that may dramatically change the local properties (Gibson and Swan 2007, Adcock et al. 2015). Moreover, in Part 1, Table 2, substantial differences in crest height, position and time of the freak event are listed for the event that will be studied as example in this part.

The wave model used is the HAWASSI-AB code with third-order nonlinearity of Kurnia and Van Groesen (2014, 2015, 2017). A total of 40 seas were simulated and investigated, in total more than 8000 waves through each point of the domain.

For the illustration of the radar application, we choose the sea identified as 17m13, one of the seas described in detail in Part 1. This sea contains the wave with the highest crest of 21.73 m that was found in the ensemble. This high crest is preceded by two other very high crests above 18 m, so three successive freak crests. For the purpose of the radar application, a coordinate shifting is applied so that the maximum amplitude happens just in front of the origin of the coordinate system where the radar is located, with the main wave direction from north to south for decreasing values of y. The sea at the time when the highest crest occurs is shown in Fig. 2.

Fig. 2
figure 2

At the top, a snapshot of nonlinear Draupner waves in a semicircle of 2 km at the time when the maximum elevation of 21.73 m occurs. The location of the freak wave is at \(x=0,y=85\). Below that the same sea for \(x>0\), with the left part replaced by the elevation on a cross section at \(x=0\)

Full size image

3 From synthetic radar images to reconstructed high seas

To prevent confusion, from now on the nonlinearly simulated seas will be called the ‘true’ seas, to distinguish from ‘shadowed’ seas, and later from ‘reconstructed’ and ‘predicted’ seas. The shadowing effect in radar images, discussed below, provide partial and severely distorted information about the true sea. The reconstructed sea will result when we improve the shadowed sea to resemble the true sea better. In this section, the methods presented in Wijaya et al. (2015) are extended to become applicable to high, nonlinear Draupner-like seas.

For typical marine incoherent radars operated at the X-band frequency (9.5 GHz) with wavelength around 2–4 cm, the small ripples induced by the wind on the sea surface cause a radar return. These return signals received at the radar will produce a radar backscatter plot for every rotation of the radar, with rotation time denoted by \(\Delta t\), which is typically between 1 and 2 s. This radar backscatter has no direct relation with the (significant) wave height of the surrounding waves. The longer waves are visible in radar images due to modulations of the radar cross section. Of the various modulations in the radar mechanism, we will only consider the shadowing effect in this paper; this is the effect that for low grazing angles waves further away will be partly or completely blocked by waves closer to the radar. Therefore, radar images of a sea state give only a very poor representation of the sea. In Wijaya and Van Groesen (2016), it was shown that the amount of shadowing with increasing distance from the radar can be used to characterize the significant wave height directly from the images without any empirical constants or further external information, but here we will use the a priori information about the significant wave height.

3.1 Synthetic radar images

The shadowed seas will now be constructed first, which will produce synthetic radar images by adding the shadowing effect.

Shadowing is greatly determined by the dimensionless number which is the ratio between the radar height \(H_\mathrm{r}\) and the significant wave height \(H_\mathrm{s}\); the smaller this ratio, the more shadowing and the more distorted the images will be. For the radar height, we take as example \(H_\mathrm{r} = 30\) m above the still water level, which is a reasonable value for large ships such as oil and gas tankers. This then leads to a rather small ratio of \(H_\mathrm{r}/H_\mathrm{s}=2.5\) for Draupner seas.

Fig. 3
figure 3

In the upper plot, a shadowed image on a semicircle; zero values in the observation area \(500<r<2000\) represent the shadowed area. In the lower plot, part of the same density image for \(x>0\), with the left part replaced by the cross section along \(x=0\) showing the elevation of the shadowed image along that line

Full size image

To obtain synthetic images for a radar located at \(x =0,y=0\), snapshots \(\eta (\mathbf x ,m\Delta t)\) from the given nonlinear sea are taken at discrete time differences \(\Delta t=3\) s which is approximately a quarter peak wave period. The images are restricted to the radar observation domain, which is a ring-shaped area between 500 and 2000 m in the northern semicircle; the small semicircle with \(r < 500\) is the blind area of the radar where the radar backscatter is too high to be useful due to specular scatter from the sea surface (Skolnik 1969). Then the effect of shadowing is applied to obtain distorted images \(R_\mathrm{m}(x)\) that will serve as synthetic radar images outside the blind zone. The area where the waves are not visible by the radar due to shadowing will be given the value 0. Figure 3 illustrates the severe effects of shadowing. Yet, for this high sea the visibility (percentage of the time the wave is visible at a point) does not differ much from the visibility of relatively low seas as in Wijaya et al. (2015).

3.2 Nonlinear DAES

Having designed the shadowed sea and obtained the synthetic radar images, the aim is now to reconstruct as much as possible the true sea, for which the method in Wijaya et al. (2015) will be adapted to become applicable for nonlinear seas. This method is the so-called DAES, the dynamic averaging and evolution scenario. The dynamic evolution is only completely described and determined when both the elevation and the surface potential are known. For that reason, we will use in the following the word ‘sea state’ to express succinctly the combination of these two quantities. The procedure consists of data assimilation in an ongoing evolution of the sea state; the assimilation is performed with updates that are obtained by dynamic averaging of successive shadowed sea states to enhance the quality of the updates. The evolution also advances waves from the ring-shaped radar-observation area into the blind area surrounding the radar. The reconstruction using linear evolution has shown to work well for low, possibly multi-modal, seas; the correlation for the elevation between the reconstructed and the true sea was above 90% in Wijaya et al. (2015). Moreover, using one reconstructed sea state as initial value, a prediction of the expected sea states in future time can be obtained by evolution of the initial value, without using any updates. It was shown in that same paper that until the maximal physical prediction horizon, linear uni- and multi-modal low sea states could be predicted in the radar area with correlations above 90%.

The linear simulations in DAES use standard Fourier methods to advance the waves with the exact dispersion relation extremely fast. For the high Draupner seas, we will follow the same method, but now using the third-order nonlinear AB-code to evolve the updated sea states and to calculate a prediction. A preliminary result for reconstructing nonlinear long-crested seas has been discussed in Wijaya (2016). Some details of the procedure are now described.

To improve the quality of the shadowed sea state, two operations are performed (Wijaya et al. 2015). To obtain an update for the dynamics, say at \(t=0\), the procedure uses three successive shadowed sea states, to be denoted by \(R_{-2},R_{-1},R_0\), at times \(t=-2\Delta t,-\Delta t\) and \(t=0\). The shadowed sea states \(R_{-2},R_{-1}\) are evolved linearly over two and one time step, respectively, to the same time \(t=0\) as the shadowed sea state \(R_0\), and then at that time the average is taken to get the dynamically averaged sea state:

$$\begin{aligned} AR_0=\frac{1}{3}(R_0+\mathcal{E}(R_{-1})+\mathcal{E}^2(R_{-2})). \end{aligned}$$

Here, \(\mathcal E\) denotes the linear evolution over one time step. This averaged sea state contains the information about the shadowed sea state over the radar-observation domain \(500<r<2000\), and is taken as initial value \(U_0=AR_0\) for the start of the nonlinear evolution until the next update at time \(3\Delta t\). During this time interval, the waves will start to advance into the blind zone \(r<500\) m. For the next update, a spatially smooth superposition will be taken of a new dynamically updated averaged sea state \(AR_3\) and the evolved sea state, as follows:

$$\begin{aligned} U_{1}(\mathbf {x})=\left( \frac{1}{2}AR_3+\frac{1}{2}\mathcal{E}^3_\mathrm{nl}(U_{0})\right) (1-\chi _\mathrm{rad}) +\mathcal{E}^3_\mathrm{nl}(U_{0})\chi _\mathrm{rad}. \end{aligned}$$

Here, \(\mathcal{E}_\mathrm{nl}^3\) denotes the nonlinear evolution operator over three time steps, \(3\Delta t\). The function \(\chi _\mathrm{rad}\) is a smooth characteristic function of the blind area: equal to 1 in the blind area and monotonically decreasing to 0 in the outer area over a distance of one-third wave length. The update \(U_{1}\) is then obtained in the blind zone as the nonlinear evolution of the previous update over \(3\Delta t\), and in the outer area as the average of the update in the outer region \(AR_3\) and the nonlinear evolution of the previous update \(\mathcal{E}^3_\mathrm{nl}(U_{0})\). Continuing in this way, this evolution scenario transports the waves further into the blind area and also improves the quality in the outside region, leading to the reconstructed sea states at time steps \(\Delta t\).

3.3 Quality of reconstruction

From a practical point of view, of most interest is the quality of the reconstructed sea elevation at the radar position and in a circular area around the radar that occupies the ship. The quality will depend on various factors: the amount of shadowing determined by the ratio \(H_\mathrm{r}/H_\mathrm{s}\), the area of the radar observation and the quality of the evolution operator. The use of synthetic data makes it possible to quantify the reconstruction by comparing the reconstructed sea with the true sea. As an example, the elevation of the reconstructed sea and the true sea along the cross section in the main propagation direction of the waves at \(x=0\) m is shown in Fig. 4 for the time that the highest wave is close to the radar.

Fig. 4
figure 4

The reconstructed wave profile at \(x=0\) in the north–south direction y (red dashed line) and the actual wave elevation (blue solid line). The extreme crest of 21.73 m is estimated by the reconstructed waves to have a height of 17.9 m (color figure online)

Full size image

This plot indicates that the DAES method can reconstruct the waves quite well, especially near the radar location; further away from the radar the resemblance is somewhat less because shadowing is more severe there and fewer updates have been assimilated. The time signal of the reconstructed elevation at the radar location is shown in the upper plot of Fig. 5 and compared with the elevation of the true sea. At the initial stages of the process, the reconstructed waves are poor because the entrance into the blind zone of waves from outside is not yet complete near the radar. After a certain initiation time, the phase and amplitude of the reconstructed elevation signal are in good agreement with the signal of the true sea. To measure the quality quantitatively, the correlation of the elevation of the reconstructed and the true sea in a radius of 200 m around the radar is shown in the lower plot of Fig. 5; the averaged correlation turns out to be 92%.

Fig. 5
figure 5

The upper plot shows the time signal of the elevation of the reconstructed waves (red dashed) and that of the true sea elevation (blue solid) at the radar location. The lower plot gives the correlation of the reconstructed and the true elevation in the area around the radar of radius 200 m (color figure online)

Full size image

4 Prediction of high waves

4.1 Prediction horizon

To be able to detect the sea near the radar ahead in time, the reconstructed sea state at a specific time is used as the initial condition for a successive nonlinear evolution without updates, leading to the predicted sea. Provided the simulation is faster than real time, this can give warnings for high waves in advance. How far ahead in time the sea near the radar can be calculated depends fundamentally on the size of the observation area and the speed of the most energy-carrying waves. Roughly speaking, it is the time in which such most energy-carrying waves will evolve from the outer observation ring to the radar position. For the seas under investigation, this leads to a value somewhere between \(2000/V_\mathrm{g}\approx 150\) s and \(2000/C_\mathrm{p}\approx 90\) s, where \(V_\mathrm{g}\) and \(C_\mathrm{p}\) are, respectively, the group and phase velocity at peak frequency.

Fig. 6
figure 6

Averaged correlation of the elevation in a circular area of 200 m around the radar between predictions starting with an initial sea state of the true sea compared to the elevation of the true sea (blue solid), and the correlation between predictions starting from a reconstructed sea state compared to the true sea states (red dashed) (color figure online)

Full size image
Fig. 7
figure 7

With \(t=0\) s, the time when the freak wave happens, subplot a shows the reconstructed sea at time 60 s before the freak wave event takes place; this sea state is taken as initial sea for the prediction. b The predicted sea at the time of the freak wave event in a smaller domain \(-1000<x<1000\) and \(-500<y<1500\). c The cross section at \(x=0\) and \(t=0\) of the predicted (red dashed) and the true elevation (blue solid). d The time signal of the predicted (red dashed) and the true elevation (blue solid) at the position of the freak wave (color figure online)

Full size image

The quality of prediction will be measured as the correlation between the elevation of the predicted sea and the true sea in a circular radar area of 200 m. Averaged over 40 different initial sea states, with 48 s time difference between successive initial states, two different comparisons are considered to measure correlations of elevation as function of time, as shown in Fig. 6. The elevation correlation is taken over the circular area of 200 m around the radar.

First, to check the numerical procedure and calculate the maximal prediction horizon, the solid blue curve is the correlation between an elevation prediction starting from a true sea state and the elevation of the true sea. The correlation is nearly maximal (value 1) when it can be expected, i.e. until the most energy-carrying waves in the prediction evolution have passed the radar area. After that, the correlation shows a sharp decrease near \(t=135\) s, when most energy-carrying waves have passed the radar position; this indicates that 135 s is the physically maximal prediction horizon, which could only be achieved if there would be no reconstruction errors from shadowing.

But in practice, such reconstruction errors will be present. This is seen by the red dotted line in the same picture. That line results when the prediction starts from a reconstructed sea state and thus contains errors; the correlation of the elevation of the initial reconstructed sea (at time \(t=0\)) with the true sea is 93.8%. Advancing in time, the elevation prediction remains above 85 % until 100 s and decays gradually till a value of 80% at 120 s, faster compared to the result of the true sea.

4.2 Prediction of freak waves

This section discusses the possibility of detecting the highest of the three successive freak crests using information from the reconstructed seas. To investigate the possibility and the quality of prediction, we calculated predictions with initial conditions from the reconstructed sea at three different times: \(t= -60, -45\) and \(-30\) s before the freak event.

Figure 7 shows the results for the prediction starting at \(t=-60\) s. Subplot (a) shows the reconstructed sea that is taken as initial state, and subplot (b) the predicted sea at \(t=0\), the time of the true freak crest. Subplot (c) is the cross section along the \(y-\)axis at \(x=0\): the blue line denotes the true wave elevation and the red dashed line the predicted elevation. Note that at \(t=0\) s a prediction of the maximum crest height of 17.5 m is obtained, compared to the true value 21.73 m. Subplot (d) shows elevation signals at the position of the freak crest, the true (blue) and the predicted (red dashed) elevation. Although the prediction of the crest height is not very accurate, an expected freak wave with a crest height of 1.45 times the significant wave height is predicted.

A better prediction result is achieved by starting the prediction closer to the time of the freak event. This is shown in two successive plots with similar information as in the previous plot, now starting the prediction at time \(t=-45\) s in Fig. 8 and starting the prediction at \(t=-30\) in Fig. 9. The maximum crest height is then slightly better predicted, as 18.44 and 18.82 m, respectively, just as the prediction of the location of the freak crest.

Fig. 8
figure 8

The same as in Fig. 7, but now for starting the prediction 45 s before the freak event

Full size image
Fig. 9
figure 9

The same as in Fig. 7, but now for starting the prediction 30 s before the freak event

Full size image

5 Discussion

To put the results obtained here in perspective, a comparison will be made with similar results in Wijaya et al. (2015) of linear bi-modal low seas with \(H_\mathrm{s}\approx 3 \) m and \(H_\mathrm{r}/H_\mathrm{s}=5\) and wide spreading caused by the presence of a low-amplitude swell with \(T_\mathrm{p}=16\) s under an angle of 135\(^{\circ }\) with a wind wave system with \(T_\mathrm{p}=9\) s.

Compared to these seas, the reconstruction of the shadowed Draupner sea has approximately the same quality; the high correlation with the real sea and the reconstructions in Fig. 5 shows that also for the high nonlinear Draupner seas a good reconstruction can be made. This good reconstruction of the sea states results in a reasonably good prediction of the waves ahead of time. With the maximal prediction horizon around 120 s, the prediction obtained for the reconstructed sea is still above 85% until 110 s, which is slightly longer than the time for the waves to travel with the phase speed from the outer ring and less than the time to transport the energy to the radar from the outer regions.

In the time interval in which the highest of three successive freak crests approach the radar, the reconstruction and prediction identifies the wave quite well, although the crest height is slightly lower, some 17.9 m for the reconstruction and 18.82 m for the prediction instead of 21.73 m. From the quality of reconstruction and prediction, we can conclude that this freak event can be predicted around 60 s in advance of its appearance, which seems the largest possible time interval.