Micrositing variability and mean flow scaling for marine turbulence in Ramsey Sound

Abstract

We present turbulence results from two acoustic Doppler current profiler measurement campaigns carried out in Ramsey Sound at two locations within 50 m of one another. The first measurements were taken in 2009 and the second in 2011; both include a complete spring–neap cycle. In this paper we characterise turbulence through turbulent kinetic energy (TKE) density and integral lengthscales and their relationships with one another and with mean flow parameters. We briefly describe the methods used to calculate these parameters. We find that a flood–ebb asymmetry is present in the data from both measurement campaigns, but although the flood tides are similar at both locations, the ebb tides are much more energetic in the 2011 data than the 2009 data. We suggest that this may be due to differences in seabed features between the two measurement locations. Dimensional analysis is employed to investigate how TKE scales with mean flow velocity; we find that the expected quadratic scaling is not well supported by the data at either measurement location. As a consequence, flows that have more energetic turbulence may instead appear to be less turbulent if judged by turbulence intensity. We investigate the correlation between lengthscales and TKE density and find that it is highly site-specific: it should not be assumed that for a given measurement location highly energetic turbulence is associated with larger flow structures or vice versa.

1 Introduction

Tidal stream turbines (TSTs) represent a renewable energy source that is gradually becoming more important. In addition to a dedicated test site in Orkney with eight berths for full-scale pilot devices (Norris and Droniou 2007), there are already individual devices supplying power to the grid (MacEnri et al. 2011) and the first commercial array is due to be installed in 2017. For conventional designs, the principle of operation is very similar to the familiar horizontal-axis wind turbines, although there are unique technological and environmental challenges (Fraenkel 2002; Batten et al. 2008; Willis et al. 2010).

One of these environmental challenges is turbulence in the tidal currents, which will induce fluctuating loads on the device. Such fluctuations will not only shorten the fatigue life of mechanical components but also entail strong transient peak loads. Understanding the nature of turbulence at deployment sites is thus not only of intrinsic scientific interest, but is also significant for device developers. Although much work has been carried out on the investigation of marine turbulence at particular sites (Osalusi et al. 2009; Thomson et al. 2012), no general model yet exists, necessitating investigation on a site-by-site basis. In the work presented here, we look at two sets of results from a single site at slightly different measurement locations (‘micrositing’) in order both to assess the turbulence at this site and to examine how much relatively small changes in position can influence the turbulence conditions experienced by a TST. Other micrositing studies are reported in the literature: Gooch et al. (2009) interpolated from acoustic Doppler current profiler (ADCP) transects to predict flow characteristics over roughly a square kilometre off the coast off Marrowstone Island in Puget Sound, and Palodichuk et al. (2013) used a series of observations from a station-keeping vessel-mounted survey to observe variation in hydrokinetic resource in the Admiralty Inlet (also in Puget Sound). Both these studies, however, examined micrositing insofar as it affected mean flow characteristics, rather than the turbulence characteristics we are primarily interested in here. Ultimately, we hope that this work can inform developers not just in respect of their initial device design but also in their ongoing modelling efforts (Masters et al. 2011; Chapman et al. 2013).

The site we examine here is Ramsey Sound, a narrow channel between Ramsey Island and the Pembrokeshire coast. The most important mean flow characteristics of this site, obtained from boat transects, have been previously reported in Fairley et al. (2013) and Evans et al. (2015). The bathymetry of the site is complex, with the centre of the channel running as deep as 70 m in places, a stack that pierces the surface at low water (Horse Rock) and a large ridge (the Bitches) extending from Ramsey Island into the middle of the channel (see Fig. 1). The seabed throughout the channel is swept bedrock. A map of the northern part of the channel is shown in Fig. 1, with the measurement locations indicated; Fig. 2 depicts the bathymetry in the immediate vicinity of the measurement locations. Evans et al. (2015) presents the bathymetry of Ramsey Sound in more detail.

Fig. 1

Map of the northern end of Ramsey Sound taken from Admiralty Chart, with measurement locations marked by circles (2009 in yellow, 2011 in red) (colour figure online)

Fig. 2

Detailed view of seabed bathymetry at the measurement locations, looking from south to north; Trwyn Ogof Hen is the land feature visible at top left (cf. Fig. 1). ADCP locations marked with circles (2009 in yellow, 2011 in red). Image credit: Paul Evans (colour figure online)

Both sets of measurements we present in the current study were taken with bed-mounted RDI WorkHorse Sentinel ADCPs, operated with a ping frequency of 600 kHz, a sample frequency of 2 Hz and a bin depth of 1 m. These devices are the most appropriate tools currently available for taking measurements of marine turbulence throughout the water column over a period of time, and measurements of these kinds are the most important for TST applications. ADCPs work by emitting pulses of sound and measuring the Doppler shift in the echoes. Typically an ADCP will have four transceivers (although configurations with three or five are also possible), each of which emits a ping along a fixed direction called a ‘beam’. Each beam can take velocity measurements at multiple distances from the device, throughout the entire water column—note, however, that it is only possible to measure the component of velocity along the direction of the beam. It is this remote sensing capability that makes ADCPs so useful in measuring marine turbulence. Other devices such as acoustic Doppler velocimeters (ADVs) can sample at higher frequencies, allowing the use of additional spectral analyses that are not viable with ADCP data, but cannot measure remotely. Historically this has meant that ADVs cannot be used to obtain data from mid-column; however, recent work (Thomson et al. 2013; Kilcher et al. 2014) has demonstrated a system that corrects for the motions of an ADV on a mooring line with synchronous measurements from an inertial sensor. Nonetheless, the methods for turbulence analysis with ADCP data are well established, and the capacity for simultaneous measurements throughout most of the water column means that ADCPs remain one of the most useful tools for assessing marine turbulence.

The first data set was recorded between 11/09/09 and 29/09/09 (“campaign A”); the second between 20/10/11 and 7/11/11 (“campaign B”). Thus, both data sets incorporate at least one complete spring–neap cycle. The second device was deployed 46.8 m away from the first, east–south–east of the original deployment location. At the first site, the water depth varied from 32.1 to 37.7 m, while the second site was slightly shallower, with the water depth in the range 31.1–37.0 m. The mean flow characteristics for both campaigns are depicted in Fig. 3, which shows the mean current velocities from the bin nearest 20 m above the seabed, in Fig. 4, which shows mean velocity profiles, and in Table 1, which details the most important tidal harmonics.

Fig. 3

Mean flow velocities taken from the bin closest to 20 m above the seabed for (top) campaign A and (bottom) campaign B. Black line shows north–south component, with positive values northward; red line shows east–west component, with positive values eastward (colour figure online)

Fig. 4

Comparison of mean longitudinal velocity profiles from ebbs (left) and floods (right). Campaign A results are in black, campaign B results in red. Pale lines show profiles of individual phases, while bold lines show overall ebb or flood profiles for a given campaign (colour figure online)

Table 1 Table of tidal harmonic components for the measurement campaigns, calculated from flow velocity record shown in Fig. 3

From the point of view of TST operation, the most important characteristics of turbulence are its strength and the size of the eddies present. The most direct metric of the strength of turbulence is the turbulent kinetic energy (TKE). TKE is typically measured as a quantity $\frac{1}{2}q^{2}$, called the TKE density. This represents the amount of energy contained in turbulent fluctuations per kilogramme of fluid. Measuring eddy size is somewhat more difficult; normally we use a lengthscale, which is simply a parameter with the dimensions of length that is related to the typical size of an eddy in the flow. A measure of eddy size is useful in that it allows us to assess the scale on which turbulent effects are likely to take place, e.g., will a single large eddy affect the whole rotor disc simultaneously, or will separate eddies impinge on separate blades. In addition to turbulence magnitude and lengthscales, we also investigate the friction velocity, which although not of direct interest in TST applications is important in characterising the transfer of momentum in a turbulent boundary layer.

2 Method

We begin by dividing our data into floods, ebbs and slacks. As we are interested in the extremes of turbulent loading, we disregard the slack data in the present study, and for each flood and ebb phase examine only an hour of data centred around the time of maximum mean flow. Flow direction is constrained by the channel to run almost perfectly north–south, with floods from the south and ebbs from the north (see Fig. 3). The mean flow velocity is greater on floods than on ebbs, by 4.2 % in campaign A and 34.4 % in campaign B (cf. Evans et al. 2015).

Our calculations are based on a conventional right-handed Cartesian axis system, with the x-dimension aligned with the mean flow (or longitudinal) direction and the z-direction positive upwards. We use u, v and w to denote the velocities in the x, y and z directions, respectively. The only velocities we have direct access to are the along-beam components measured by each beam. The record associated with the ith beam is denoted $b_{i}$, with positive values indicating flow towards the ADCP. As a simple quality control, we discard all data from any bin in which fewer than 90 % of samples return a valid reading.

The calculation of TKE density and Reynolds stresses, detailed in Sects. 2.1 and 2.3 below, makes use of the variance method, which is well attested in the literature (Lu and Lueck 1999b; Stacey et al. 1999). This method relies on making two important assumptions about the properties of the turbulence in the region of flow seen by the ADCP. First, we must assume that the statistics of the flow (that is, properties such as the mean velocity and the velocity variances) are uniform across the volume of fluid occupied by the beam spread. Second, we must assume that these statistics are temporally stationary over our averaging period, i.e., the mean quantities do not significantly change during the time we are calculating their average values.

To check the validity of the homogeneity assumption, Lu and Lueck (1999a) suggest tests based on the error velocity, e. e is defined as the difference between two independent estimates of vertical velocity from the ADCP beam data; these two independent estimates can be made because the data from four beams overdetermine the vertical velocity. If horizontal homogeneity is a valid assumption, the expectation of e is zero. We tested this by comparing the mean value of e to its standard deviation and found that the mean exceeded the standard deviation in fewer than 0.1 % of samples. This is a far stronger confirmation of homogeneity than that reported in Lu and Lueck (1999a); it is likely that this improvement is due to the exclusion of slack data in the current study.

2.1 Calculation of TKE density and turbulence intensity

As mentioned above, TKE density is a measure of the energy contained in turbulent velocity fluctuations. It can be expressed as

$$\begin{aligned} \tfrac{1}{2}q^{2} = \frac{1}{2} (\langle u ^{\prime 2} \rangle + \langle v ^{\prime 2} \rangle + \langle w ^{\prime 2} \rangle ), \end{aligned}$$

(1)

where the prime indicates a fluctuating component of velocity, i.e., that part of the velocity due to turbulence, and angle brackets are used to denote a time-averaged quantity; we employ a 10 min rolling mean.

We begin by taking the time-averaged variance of the beam velocities (which we denote $\langle b_{i}^{\prime 2} \rangle$ for the ith beam), which gives us a set of four linear expressions involving the five turbulent velocity variances and covariances $\langle u^{\prime 2} \rangle$, $\langle v^{\prime 2} \rangle$, $\langle w^{\prime 2} \rangle$, $\langle u^{\prime } w^{\prime } \rangle$ and $\langle v^{\prime } w^{\prime } \rangle$. Our assumption of spatial homogeneity in flow statistics allows us to eliminate the covariance terms.

One final assumption needs to be made still, regarding the proportion of $\tfrac{1}{2}q^{2}$ attributable to the vertical fluctuations. We express this assumption as $\tfrac{1}{2}w^{\prime 2} = \xi \cdot \tfrac{1}{2} q^{2}$; following the work of Nezu and Nakagawa (1993), we take $\xi = 0.1684$. With this final assumption, we can calculate TKE density as

$$\begin{aligned} \tfrac{1}{2}q ^{2} = \frac{\sum _{i} \langle b _{i} ^{\prime 2} \rangle }{4 \sin ^{2} \theta (1 - \xi (1 - 2\cot ^{2} \theta ))}, \end{aligned}$$

(2)

where $\theta$ is the beam angle, i.e., the angle at which the beams are inclined to the vertical. Although TKE density is the most direct measure of the energy of turbulent fluctuation in a marine current, it is common practice in industry to report turbulence intensity (TI) instead. This is the ratio of the magnitude of turbulent fluctuations to the magnitude of the mean flow and is usually expressed as a percentage. In the current work, we report TI as $q {/} \langle | \mathbf {u} | \rangle$, although a common alternative is to use the variance of the magnitude of the horizontal velocity (i.e., $\text {Var}(|(u,v,0)|)$) in place of q. This elides the contributions of vertical fluctuations and purely directional changes in the horizontal and is thus a greatest lower bound on the value we report.

2.2 Calculation of turbulent lengthscales

Lengthscales are a measure of the size of eddies present in a turbulent flow. Although they have units of length, they do not precisely correspond to the size of a particular structure; instead, it is better to interpret them as showing when structures become larger or smaller. It should of course be borne in mind that a single lengthscale is of necessity a simplification, as real turbulent flows contain a range of eddy sizes, from the largest energy-bearing structures to the smallest scales at which turbulent energy is dissipated.

Lengthscales can be computed in a number of different ways; Stacey et al. (1999) suggest that a simple quadratic expression may provide a reasonable first approximation, while Dillon (1982) suggests a mixing lengthscale based on the ratio of the Reynolds stress to the square of the mean shear. In this paper we use the integral lengthscale, which describes the most coherent lengthscale. As such it is not a measure of the most energetic scale, but instead the scale over which the fluctuating velocity is best correlated with itself. It is calculated by integrating the time-lagged autocorrelation coefficient, $R_{ii}(t,\tau )$ of the along-beam velocity. This coefficient is defined as

$$\begin{aligned} R_{ii}(t,\tau ) = \frac{\langle b _{i} ^{\prime } (t) b _{i} ^{\prime } (t + \tau ) \rangle }{\langle b _{i} ^{\prime 2} (t)\rangle }. \end{aligned}$$

(3)

$R_{ii}(t,\tau )$ is definitionally 1 for zero lag, and in general decreases with increasing lag. If we denote the first time for which decorrelation occurs by $\tau _{0}$, then we can define the integral lengthscale as

$$\begin{aligned} l_{i} (t) = \langle u \rangle \cdot \int _{\tau = 0} ^{\tau _{0}} R_{ii}(t, \tau ) \mathrm{d} \tau . \end{aligned}$$

(4)

We multiply the integral by the mean longitudinal velocity, $\langle u \rangle$, to convert from units of time to units of length.

Note that this calculation of $l_{i}$ takes data from only a single beam, and, therefore, we can obtain four independent estimates of the integral lengthscale. Furthermore, as we are using data from only a single beam, the assumptions of homogeneity and stationarity that are required in the calculation of TKE density are not necessary here.

2.3 Calculation of friction velocity

In this study, we use two independent ways of estimating friction velocity $u_{\tau }$: line fitting to the mean Reynolds stress profile, and log-law fitting to the mean velocity profile. For the Reynolds stress profile, we consider only the longitudinal–vertical component $\langle - u ^{\prime } w ^{\prime } \rangle$, which can be calculated in a similar manner to TKE density (Stacey et al. 1999). In a turbulent channel of depth H, we can expect total stress (i.e., Reynolds stress plus viscous stress) to vary according to the relationship $\langle - u^{\prime } w^{\prime } \rangle + \nu \frac{\partial \langle u \rangle }{\partial z}= u_{\tau }^{2} (1 - \frac{z}{H})$ (Stacey et al. 1999). In a turbulent flow outside the viscous sublayer, the viscous stress $\nu \frac{\partial \langle u \rangle }{\partial z}$ is negligible in comparison to the Reynolds stress throughout the water depth, and thus we expect a linear profile of $\langle - u ^{\prime } w ^{\prime } \rangle$ whose slope is related to $u_{\tau }$:

$$\begin{aligned} \langle - u^{\prime } w ^{\prime } \rangle = u _{\tau } ^{2} \left( 1 - \frac{z}{H}\right) \end{aligned}$$

(5)

Note that this profile shape dictates that Reynolds stress decrease to zero at the surface; a two-parameter linear least squares fit cannot guarantee that this is preserved. However, we have found that the difference in estimates of $u_{\tau }$ between allowing free variation of both line-fitting parameters and constraining the profile to zero at the surface is very small, on the order of 3 %. In our results we present only unconstrained estimates.

The mean velocity profile can also be used to estimate $u _{\tau }$, using the law of the wall. This law states that in a turbulent boundary layer, between the small viscous sublayer very near the wall and the main flow, the mean velocity profile will vary logarithmically:

$$\begin{aligned} \langle u \rangle = \frac{u _{\tau }}{\kappa } \ln \frac{z}{z _{\delta }}, \end{aligned}$$

(6)

$z _{\delta }$ the roughness lengthscale. A two-parameter linear least squares fit of the mean velocity to the log-law yields an estimate of both $u_{\tau }$ and $z_{\delta }$. The central difficulty with using this method is that we do not know a priori where the logarithmic layer ends; in fact, although strictly speaking the log-layer should occupy only part of the column, empirically-observed velocity profiles are frequently well-approximated logarithmically. We overcome this by carrying out a sequence of logarithmic fits. The first fit is to a small set of only the first eight near-bed points; we then fit with the first nine points and so on until we have carried out a fit for the complete water column. Note that this assumes the log-layer occupies at least the portion of the water column corresponding to the first eight bins. We assess the goodness of fit by measuring the mean relative error; our estimate for $u _{\tau }$ is taken from an average across all fits that have a mean error of less than 5 %.

3 Results

3.1 TKE density

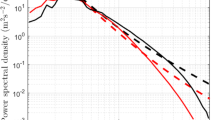
In Fig. 5, we show the TKE density profiles for both measurement campaigns, split into floods and ebbs. We can see that there are two important asymmetries: first between ebb and flood, which is present in both measurement campaigns, and second between campaign A and campaign B, which is more noticeable on the ebb than the flood.

Fig. 5

Comparison of mean TKE profiles from ebbs (left) and floods (right). Campaign A results are in black, campaign B results in red. Pale lines show profiles of individual phases, while bold lines show overall ebb or flood profiles for a given campaign (colour figure online)

In both campaigns, the flood phases are more energetic than the ebbs. However, while the flood phases are very similar in magnitude between the campaigns, with their mean value differing by less than 5 %, this is not the case in the ebbs. Here, the mean TKE density from campaign B is 140 % greater than seen in campaign A, and the profile shape is significantly different. This is far greater than the increase in mean flow magnitude, which is only 9.4 % in the principal semidiurnal constituent. While the mean profile from campaign A shows a slight decline from its maximum at the bed as we go up the water column, the campaign B profile has its maximum at the water surface, with another local maximum 5 m above the bed and a minimum at 23 m above the bed.

Campaign A’s mean flood profile is almost perfectly parabolic in the bottom 30 m (a least-squares quadratic fit gives $R^{2} = 0.9924$), whereas campaign B’s is only slightly better-fitted by a quadratic fit ($R^{2} = 0.9026$) than a linear fit ($R^{2} = 0.8712$). It is not clear why this is the case, given that there is a fundamental asymmetry in the water column between the no-slip seabed and free-slip water surface. For symmetrical channels, with two no-slip walls, we expect the TKE profile to have a peak near each channel boundary (Jarrin 2008), but no such feature is evident in the near-bed region of the profiles found in this study. Note, however, that near the wall, energy-bearing structures reduce in size but the vertical resolution of the ADCP remains the same. This means it is possible that such a peak exists in the flow, but is not picked up in our measurements due to being under-resolved.

The turbulence characteristics must be determined by the parameters of the problem: in this case, the geometry of the sound and the mean flow characteristics. It, therefore, follows by a simple dimensional argument that we should expect TKE density (which has units of m$^{2}$ s$^{-2}$) to vary as the square of some appropriate velocity scale, the most obvious choice being the mean velocity. However, when we plot whole-phase mean velocity against TKE density, as seen in the top panels of Figs. 6 and 7, the measured data seems to indicate that the relationship is simply linear. In Table 2, we tabulate measures of correlatedness and goodness of fit for the datasets depicted in these figures. It is important to note that when fitting to $\langle | \mathbf {u} | \rangle ^{2}$ and $u _{\tau } ^{2}$, we are carrying out a linear fit to the squared velocities, rather than a quadratic fit to the velocities themselves. This distinction is important because a quadratic fit, having an extra degree of freedom over a linear fit, will always be better in an $R^{2}$ sense when fitting to the same data set: the comparison would, therefore, not reveal anything meaningful.

Fig. 6

Data from campaign A, showing mean velocity against TKE density (top), mean velocity against TI (middle) and friction velocity (estimated from log-law fit) against TKE (bottom). Left-hand column shows ebb data and right-hand column shows flood data

Fig. 7

Data from campaign B, using the same format as Fig. 6

As we can see from the values of $R^{2}$ in this table, a linear relationship between $\langle | \mathbf {u} | \rangle$ and $\tfrac{1}{2}q^{2}$ is better supported by the data than a quadratic one in all cases except for campaign B ebbs. The differences are very small, however: for instance, on campaign A floods, the linear relationship has an $R^{2}$ of 0.9369, while the quadratic relationship has one of 0.9258. This margin is insufficient to firmly conclude that a linear fit is better than a quadratic one. If we suppose the flow in Ramsey Sound to be dominated by turbulence generated near the bed, a reasonable alternative to mean velocity scaling is to take $u_{\tau }$ as the pertinent velocity scale rather than $\langle | \mathbf {u} | \rangle$. This is not borne out by the data, however, as we see in the bottom panels of Figs. 6 and 7 and in Table 2, which show that the correlation between $u _{\tau }$ and $\tfrac{1}{2}q^{2}$ is poorer than that between $\langle | \mathbf {u} | \rangle$ $\tfrac{1}{2}q^{2}$.

Table 2 Parameters relating to the data plotted in Figs. 6 and 7

Recall that turbulence intensity is defined by the ratio $q {/} \langle | \mathbf {u} | \rangle$, expressed as a percentage: in other words, it is the ratio of the magnitudes of the turbulent fluctuation velocity and the mean velocity. If the expected quadratic scaling of the TKE with mean velocity had obtained, TI would collapse on to a single value for a given location and tidal phase, e.g., all campaign A ebbs would have the same TI value (albeit with some scatter), all campaign B floods would have the same TI value, etc. In other words, TI would be selected only by the channel geography and bathymetry upstream of the measurement location. However, the results we have actually observed demonstrate that TI does not collapse as we might anticipate. Instead, we see a negative correlation between TI and mean velocity. In other words, as the mean flow gets faster, the turbulence intensity decreases; this is despite the fact that faster flows are also correlated with more energetic turbulence. Thus we have a situation where more energetic turbulence frequently appears less intense when measured in terms of TI, the prevailing metric for the strength of turbulence in the industrial sector.

3.2 Lengthscales

The mean lengthscale results are depicted in Fig. 8. We see that larger eddies are present on the floods than on the ebbs (by 120 %, on average) and that larger structures were observed during campaign A in comparison to campaign B (by 37 %). The flood–ebb asymmetry is qualitatively similar to what we see with the TKE density, which leads us to suspect that there may be a straightforward link between how energetic the turbulence on a particular tide is and the size of the corresponding eddies.

Fig. 8

Mean integral lengthscales across all floods and ebbs from both campaigns. Panels on left show mean ebb lengthscales and panels on right show mean flood lengthscales. Top panels show data from campaign A and bottom panels data from campaign B. Profile colours indicate beam used to calculate integral lengthscales: blue beam 1; green beam 2; red beam 3; cyan beam 4. Uncertainty in results is indicated by dashed lines, which show the range of values one standard deviation above and below the mean. The standard deviations are calculated from the set of phase-mean lengthscales (colour figure online)

We explore this possible link in Fig. 9. By averaging across the entire water column and hour-long sampling period for each phase, we obtain a single characteristic mean TKE density and (with an additional averaging across all beams) a single characteristic mean lengthscale. These were plotted against one another, and we carried out a linear least squares fitting to see how well one can predict large turbulent structures given an energetic mean flow (or vice versa).

Fig. 9

Mean lengthscale against mean TKE density for data from a campaign A and b campaign B. Black triangles show flood data, red circles show ebb data. Each data point corresponds to a complete flood or ebb phase. Lines of best fit (by linear least squares) are shown, corresponding in colour to the data points they are fitted to. Solid lines minimise error in lengthscale fit, dashed lines minimise error in TKE density fit (colour figure online)

As seen in the second panel of Fig. 9, this relationship is well borne-out in the data from campaign B (see Table 3 for further details): the two parameters are well-correlated, and a linear fit shows a reasonable $R^{2}$ value (0.795 for a fit to all phases). Campaign A, however, did not clearly demonstrate such a relationship in either the flood or ebb; on the flood, TKE and lengthscale are correlated very weakly, and on the ebb they are in fact anticorrelated. It is clear from a simple inspection of the data that there is no obvious linear relationship, and this is borne out by the $R^{2}$ values in Table 3. Fitting all data together does apparently show a relationship, but the fit is mediocre ($R^{2} = 0.5819$), and it is clear by examining the top panel of Fig. 9 that this relationship only appears because the line thus obtained approximately passes through the centroids of the clearly separated flood and ebb populations.

Table 3 Parameters of the relationship between TKE density and lengthscale

One possible explanation for the lack of obvious relationship emerging from the campaign A data is simply a scarcity of data points. In order to investigate whether this could shed light on any underlying relationship, we divided each tide into 10 min subsets and repeated the fitting procedure. For campaign B, the effect was negligible; for campaign A, there was some improvement, but not to such an extent as to satisfactorily demonstrate our hypothesised relationship between lengthscale and $\tfrac{1}{2}q^{2}$.

3.3 Friction velocities

As we mention in Sect. 2.3, our two estimates of friction velocity are independent of one another; it is, therefore, interesting to see how well they correspond. We present the overall mean values in Table 4, but this does not show the whole story. Obviously there is variation from phase to phase: the question is, does $u _{\tau }$ estimated from the Reynolds stress profile track $u _{\tau }$ estimated from a log law fit?

Table 4 Estimates of friction velocity ($u _{\tau }$) in cm $\cdot$ s $^{-1}$

We find, in fact, that in most cases the two estimates track each other rather well (see Table 4), particularly on campaign B. Here, measuring the correlatedness of the two $u_{\tau }$ estimates with the Pearson coefficient R, we find that across all floods, the two estimates are correlated with $R = 0.9339$, while across all ebbs they are correlated with $R = 0.8109$. Note that for the ebb, one outlying Reynolds stress estimate of $u_{\tau }$ was replaced with an estimate based on constraining the fitted profile to zero at the surface (see Sect. 2.3). On campaign A, the correlation is somewhat less strong on the flood phases ($R = 0.7028$) and significantly weaker on the ebb phases ($R = 0.1809$). Despite this weak correlation, the mean values of the two estimates vary by only 26 %.

4 Discussion and conclusions

The data presented in this paper are drawn from a single location and the measurements at the two sites were not taken simultaneously; we must, therefore, be cautious about extrapolating our results too far. Nonetheless, we can draw some conclusions regarding the effect of relatively small changes in location on marine turbulence. The large flood–ebb asymmetry in Ramsey Sound turbulence is already attested (Togneri and Masters 2012), and these results show that this asymmetry persists elsewhere in the channel; what is novel in the data presented here, though, is that the ebb TKE density can vary by 140 % at locations separated by less than 50 m. It is unlikely that the difference in ebb TKE density between the two campaigns is explained by the changes in mean flow alone: although campaign B did see greater mean flow velocities, this increase (9.4 % in the amplitude of the principal tidal constituent, see Table 1) was much smaller than the increase in TKE density. Furthermore, while the flood–ebb asymmetry increases in mean flow terms from campaign A to campaign B, the opposite is the case when we examine the turbulence. It is reasonable to presume, then, that the differences in turbulence characteristics are not simply due to variation in the mean flow over the time elapsed between the two campaigns, and, therefore, that similar differences in mean turbulent properties at points with similar separations may be found elsewhere in Ramsey Sound and other deployment locations. We would, therefore, strongly advise that turbine developers make sure that any assessment of site turbulence is carried out using measurements from the actual proposed turbine location, rather than using a nearby site as a proxy. More ideal still would be to carry out simultaneous turbulence measurements from several ADCPs spread across the planned deployment area, although the cost of this may be prohibitive.

It is possible that the differences seen between the two measurement campaigns are due to the seabed features at the two locations (see Fig. 2). Campaign A’s measurement location is south of a trench with a smooth floor, while that of campaign B is south of a rougher outcropping. A separated flow off this feature might go some way to explaining why we tend to see a maximum in TKE density roughly 5 m off the seabed in campaign B ebbs. A study of the mean flow in Ramsey Sound (Evans et al. 2015) did not show variation in the gross flow characteristics on comparable spatial scales except in the wake of large surface-piercing features, however; so if the bathymetry is the cause then we must consider that certain features strongly influence the turbulence characteristics without a similarly strong effect on the mean flow.

The scaling of phase-mean TKE density does not behave exactly as we might expect. As we discuss in Sect. 3.1, the data do not clearly support the expected quadratic relationship with velocity scales, whether mean velocity or friction velocity. Furthermore, in light of the great increase in ebb TKE density greatly from campaign A to campaign B, far in excess of the change in mean velocity (and not accompanied by a similar increase in flood TKE density), one would expect that if mean flow velocity was the dominant velocity scale governing TKE density there would be a significant change in the relationship between them, but this is not evident in the parameters we have investigated.

This suggests that there is some other factor outwith those investigated here, varying between the two measurement campaigns that has an influence on the turbulent environment of the channel. Perhaps more importantly, this means that the use of TI in industry to characterise the strength of turbulence at TST deployment locations may be somewhat misleading. The fact that TKE density does not climb as fast as the square of the mean velocity means that TI falls as mean velocity increases, since TI is essentially the ratio of the square root of TKE density to mean velocity. This means, then, that tidal phases with high mean current speeds will appear to have weaker turbulence when measured by the metric of TI, even although the turbulence in these phases is in fact more energetic.

Integral lengthscales, as depicted in Fig. 8, are estimated using data from only a single beam, and thus we have four independent estimates. In our calculation of the TKE density using the variance method, as discussed in Sect. 2.1, we have assumed statistical homogeneity over the beam spread, and if this holds we should expect the independent estimates of integral lengthscale to be similar to one another. Although the mean lengthscales do differ between beams, most pronouncedly in campaign B floods where the estimates from beam 2 and 3 differ by up to 68 %, in most cases there is significant variance in the lengthscale estimates and the results from each beam overlap to within one standard deviation. The exceptions to this observation are near the seabed in campaign B: in the bottom 4 m on ebbs and the bottom 11 m on floods, some beams do not agree within this margin of error. This indicates that the assumption of homogeneity is less satisfactory in these parts of the flow. It is surprising that homogeneity is, by this measure, less well-supported in the near-bed region than the near-surface region, as in the near-bed region the beams are measuring from points that are closer together and thus the homogeneity assumption is less stringent here.

Using $R^{2}$ values of linear fits, we have shown that for the campaign B data, there is a fairly good correlation between larger turbulent structures and more energetic turbulence ($R^{2} = 0.797$ over all tides). However, this correlation is not as well borne out in data from campaign A. Fitting over all campaign A tides does seem to show a reasonable fit, but looking at the actual data as plotted in Fig. 6 indicates that this is simply an artefact of the best fit line passing roughly through the centroids of the very clearly separated flood and ebb populations This separation is not present in campaign B; although the floods do tend to be more energetic and have larger lengthscales than the ebbs, both flood and ebb data lie along a similar trendline and there is a great deal of overlap. What we observe in the campaign A data, on the other hand, suggests that there is a weak correlation between TKE density and turbulent lengthscales on the flood, but on the ebb there is a relatively narrow range of TKE densities and a much wider scatter in lengthscale, with little correlation between them. We conclude, then, that any relationship between lengthscale and TKE density is site-specific and should not be presumed to hold a priori.

It is pleasing to see that our two independent estimates of friction velocity track each other very well in most cases. This agreement not only increases our confidence in the measure of $u_{\tau }$ itself, but also suggests that it is reasonable to treat the Sound as a channel fully occupied by a turbulent boundary layer, as we have done throughout our analyis. Although data on the bed friction is not of immediate utility for calculating loads and performance of TSTs, it is useful in larger basin-scale models for predicting power extraction on an array or multi-array scale (Neill et al. 2009; Robins et al. 2014).