1 Introduction

Continuous soil and streambed erosion modeling attempts to describe the natural processes occurring in the landscape and in the streambeds, accordingly, of a basin over large periods of time (e.g., weekly, monthly, annual), due to rainfall events which take place in the under study period of time, as well as to quantify the sediment yield that reaches the outlet of the basin, through its watercourses. It is important to understand the major processes affecting sediment delivery to surficial water bodies in order to tailor effective mitigation and outreach activities (Ricker et al. 2008). The purpose of this paper is to present continuous simulation efforts of soil and streambed erosion processes in the basin of Kosynthos River (district of Xanthi, Thrace, northeastern Greece), as well as to compare the computed sediment load values with field measurements at the basin outlet.

In recent decades, three categories of models (empirical, conceptual and physically-based) have been developed in order to quantify the processes of detachment, transport, and deposition of eroded soil (Renschler and Harbor 2002).

Empirical models are simple, but they do not describe in detail the mechanisms of the physical processes (Hrissanthou 2005). They are created for certain conditions and limitations, as a result of field measurements and observations. The main drawback of these models is their lack of effectiveness in an environment that differs from the one they were primarily created for. Some common empirical models, amongst others, are the Musgrave Equation (Musgrave 1947), the Dendy-Boltan Method (Dendy and Boltan 1976), the Sediment Delivery Ratio Method (Renfro 1975), the Sediment Rating Curve (Campbell and Bauder 1940) and the Pacific Southwest Interagency Committee (PSIAC) Method (Pacific Southwest Interagency Committee 1968). However, the most widely used empirical model is the Universal Soil Loss Equation (USLE; Wischmeier and Smith 1978). A modification of USLE is the MUSLE (Modified Universal Soil Loss Equation; Williams 1975), while a revision of USLE is the RUSLE (Revised Universal Soil Loss Equation; Renard et al. 1996).

Conceptual models are a mixture of empirical and physically-based models, and their use is therefore more applicable to answer general questions (Beck 1987). Some examples of conceptual models are the: Sediment Concentration Graph (Johnson 1943), Renard-Laursen Model (Renard and Laursen 1975), Unit Sediment Graph (Rendon-Herrero 1978), Sediment Routing Model (Williams and Hann 1978), Discrete Dynamic Model (Sharma and Dickinson 1979) and Agricultural Catchment Research Unit (ACRU; Schulze 1995).

In physically-based models, fundamental physical equations, concerning streamflow and sediment transport in a basin, are solved (Merritt et al. 2003). They describe the natural procedure by combining all the individual physical components into a composite model. The physical basis of these models can, in principle, contribute to overcoming many of the shortcomings of the empirical models (Marino and Simonovic 2001). Some of the most well known physically-based models are Erosion Kinematic Wave Model (Hjelmfelt et al. 1975), Quasi-Steady State (Foster et al. 1977), Areal Non-Point Source Watershed Environment Response Simulation (ANSWERS; Beasley et al. 1980), Chemical Runoff and Erosion from Agricultural Management Systems (CREAMS; Knisel 1980), Water Erosion Prediction Project (WEPP; Laflen et al. 1991) and European Soil Erosion Model (EUROSEM; Morgan et al. 1998).

In this study, the variation with time of the following physical processes is quantified: runoff resulting from rainfall, soil erosion due to rainfall and runoff, inflow of soil erosion products into streams, and sediment transport in streams. The quantification of the variation with time of the above physical processes leads to the derivation of sediment graphs at the basin outlet.

The continuous version of the deterministic distributed hydrologic model HEC-HMS (USACE 2010) is used to simulate the flow in the sub-basins. The result is the derivation of continuous runoff hydrographs which, along with the rainfall amount, are used as the decisive input data to the soil erosion model. The outcome of the soil erosion model is the final available quantity of soil, which reaches the streams. Subsequently, the essential for continuous modeling parameter of baseflow is taken into account, in order to calculate the total flow that runs on the streambed, which, in combination with the transport capacity of the stream, determines whether there is a deposition or detachment of soil particles on the streambed and what is the final quantity of sediment, that reaches the outlet of the basin. A brief theoretical model description is given below.

2 Model Description

2.1 Rainfall-Runoff Submodel

The Soil Conservation Service-Curve Number (SCS-CN) method (SCS 1993) is widely used in hydrology; it is one of the simplest and most efficient methods for computing the amount of runoff along with the hydrologic losses of a rainfall event, in a specific area. The hydrologic losses estimated by the above method are mainly due to rainfall water infiltration. The hydrologic losses due to evapotranspiration may not be a necessary parameter for event-based calculations. Contrarily, it is a crucial one in continuous hydrologic modeling, because it accounts for the largest part of the rainfall losses over a long period of time. Among the methods used in estimating reference evapotranspiration is the universally acceptable FAO-56 Penman-Monteith method, due to its better performance in many regions of the world when compared with other models (Allen et al. 1998). This method has been extensively tested and is found as one of the most common and effective methods for estimating reference evapotranspiration in a variety of climates.

The transformation of rainfall excess into runoff hydrograph is achieved on the basis of the theory of unit hydrograph. In concrete terms, the dimensionless synthetic unit hydrograph created by the Soil Conservation Service is used, which is a result of a long-term analysis of a large number of hydrographs in various basins. In the dimensionless synthetic unit hydrograph of SCS (1993), discharges and time steps are expressed as a fraction of the peak discharge and as a fraction of the rise time of the unit hydrograph, respectively. The peak discharge is calculated as a function of the rise time, which again is calculated as a function of the time of concentration.

The applied composite rainfall-runoff submodel includes an exponential recession model to represent the time variation of baseflow (Barnes 1939).

The routing of the runoff (direct runoff + baseflow) hydrograph from the outlet of a sub-basin to the outlet of the whole basin is enabled by means of Muskingum-Cunge model, which is based on the well known hydrologic routing Muskingum model. In contrast to the hydrologic Muskingum model, the Muskingum-Cunge model is considered as hybrid one, namely it constitutes a combination of hydrologic and hydraulic approach. A detailed description of the rainfall-runoff submodel can be found in Kaffas and Hrissanthou (2014).

2.2 Soil Erosion Submodel

Sediment is detached from soil surface both by the raindrop impact and shearing force of flowing water (Jain and Das 2009). Thus, soil erosion is mainly due to rainfall and runoff. For the estimate of soil erosion due to rainfall in a sub-basin, the following basic equations of Poesen (1985) are used:

$$ {q}_{rs}=C(KE){r}_s^{-1} \cos a $$
(1)
$$ {q}_r={q}_{rs}\left[0.301 \sin a+0.19{D}_{50}^{-0.22}\left(1-{e}^{2.42 \sin a}\right)\right] $$
(2)

where: q rs is the mass of detached particles per unit area [kg/m2]; C is the soil cover factor; KE is the rainfall kinetic energy [J/m2]; r s is the soil resistance to drop detachment [J/kg]; a is the slope gradient [°]; q r is the downslope splash transport per unit width [kg/m]; and D 50 is the median particle diameter [m].

The soil cover factor C is not included in the original relationship of Poesen for splash detachment, because this relationship is valid for bare soils. In order to take into account the decrease of splash detachment because of the vegetation, the dimensionless vegetation factor C of the USLE is considered as appropriate to express the vegetation influence (Hrissanthou 2002).

The rainfall kinetic energy, KE [J/m2], and the resistance of the soil material, r s [J/kg], are given by the following equations (Poesen 1985):

$$ KE=\beta N $$
(3)
$$ \begin{array}{cc}\hfill {r}_s=1836.5+175.7 \ln {D}_{50},\hfill & \hfill \mathrm{f}\mathrm{o}\mathrm{r}\kern0.5em 0.0001m<{D}_{50}<0.0007m\hfill \end{array} $$
(4)

where: β is a factor proportional to the square of the mean fall velocity of the raindrops [J/(m2 mm)]; and N is the rainfall amount [mm].

In the model of Poesen, in contrast to the empirical USLE, the physical sub-processes of the rainfall erosion are quantified, e.g., splash detachment, upslope and downslope splash transport. However, the correlation of the influencing parameters of the rainfall erosion is enabled in an empirical way (Hrissanthou 2002).

Soil erosion due to runoff is estimated through the sediment transport by runoff as follows (Nielsen et al. 1986):

$$ {q}_f={r}_e{q}_t $$
(5)

where: q f is the sediment transport per unit width by runoff [m3/(s m)]; r e is the entrainment ratio (r e  = 1 for noncohesive soils, r e  < 1 for cohesive soils); and q t is the sediment transport capacity per unit width by runoff [m3/(s m)].

The sediment transport capacity by runoff, q t , is computed by the modified formula of Engelund and Hansen (1967):

$$ {q}_t=0.04\frac{{\left(2g/f\right)}^{1/6}}{{\left({\rho}_s/\rho -1\right)}^2{g}^{1/2}{D}_{50}}{q}^{5/3}{s}^{5/3} $$
(6)

where: g is the gravitational acceleration [m/s2]; f is the friction factor; ρ s is the sediment density [kg/m3]; ρ is the water density [kg/m3]; q is the runoff rate per unit width [m3/(s m)]; and s is the energy slope.

The friction factor, f, is given by Engelund and Hansen (1967):

$$ f=2g{h}_os/{u}^2 $$
(7)

where: h o is the flow depth [m]; and u is the mean flow velocity [m/s].

The sediment supply to the main stream of a sub-basin is estimated by means of a comparison between the available sediment, q r  + q f , in the sub-basin area and the sediment transport capacity by runoff, q t . If the available sediment exceeds the sediment transport capacity by runoff, deposition occurs, and the sediment transported to the main stream of the sub-basin equals the sediment transport capacity. If the available sediment in a sub-basin is less than the sediment transport capacity by runoff and if the erosive forces of the flow exceed the resistance of the soil to detachment by flow, detachment occurs; in this case, it is assumed that sediment transported to the main stream of the sub-basin equals the available sediment.

2.3 Stream Sediment Transport Submodel

The sediment yield at the outlet of the main stream of a sub-basin is estimated by means of a comparison between the available sediment in the stream and the sediment transport capacity by streamflow. If the available sediment in the main stream exceeds the sediment transport capacity by streamflow, deposition occurs, and the sediment yield is equal to sediment transport capacity; if the available sediment is less than the streamflow sediment transport capacity, bed detachment may occur; in this case, it is assumed that the sediment yield is equal to the available sediment.

Sediment transport capacity by streamflow is estimated from the sediment concentration in the stream, which is computed by the relationships of Yang and Stall (1976):

$$ \begin{array}{l} \log {c}_t=5.435-0.286 \log \frac{w{D}_{50}}{\nu }-0.457 \log \frac{u_{\ast }}{w}\\ {}+\left(1.799-0.409 \log \frac{w{D}_{50}}{\nu }-0.314 \log \frac{u_{\ast }}{w}\right) \log \left(\frac{us}{w}-\frac{u_{cr}s}{w}\right)\end{array} $$
(8)
$$ \begin{array}{cc}\kern1em \frac{u_{cr}}{w}=\frac{2.5}{ \log \left({u}_{\ast }{D}_{50}/\nu -0.06\right)}+0.66,\kern1em & \kern1em 1.2<\frac{u_{\ast }{D}_{50}}{\nu }<70\kern1em \end{array} $$
(9)
$$ \begin{array}{cc}\kern1em \frac{u_{cr}}{w}=2.05,\kern1em & \kern1em if\kern0.5em \frac{u_{\ast }{D}_{50}}{\nu}\ge 70\kern1em \end{array} $$
(10)

where: c t is the total sediment concentration by weight [ppm]; w is the terminal fall velocity of sediment particles [m/s]; D 50 is the median particle diameter [m]; v is the kinematic viscosity of the water [m2/s]; s is the energy slope; u is the mean flow velocity [m/s]; u cr is the critical mean flow velocity [m/s]; and u * is the shear velocity [m/s].

Equation (8) was determined from the concept of unit stream power (rate of potential energy expenditure per unit weight of water, symbolized with the product us) and dimensional analysis. A critical situation is considered in this equation for the beginning of sediment particle motion, as in most sediment transport equations.

3 Application to Kosynthos River Basin

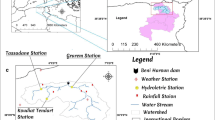
The submodels described above were combined to form a mathematical model. This composite mathematical model is applied to Kosynthos River basin (district of Xanthi, Thrace, northeastern Greece) in order to simulate continuous sediment graphs of the years 2005–2009. Kosynthos River basin is a rather large basin, with an area of about 237 km2, consisting of forest (74 %), bush (4.5 %), urban area (1.5 %) and an area with no significant vegetation (20 %) (Fig. 1). The dominant rocks are granite-diorite, marble, gneiss-granite and migmatite. The structure of the rocks (low percentage of deep percolation), as well of the soil (semi-permeable) favour a relatively high runoff. The highest altitude of the basin is about 1700 m. The length of the main stream of the basin is about 35 km.

Fig. 1
figure 1

Soil cover map of Kosynthos River basin

Full size image

The rainfall-runoff submodel (HEC-HMS 3.5) was ran continuously for the period 2005–2009, and more specifically from 1st January 2005 until 21st January 2009. In this way, a continuous hydrograph of the latter period was obtained and thus, a thorough perspective of the variation of the direct and total flow. In addition, it is easier for the component of evapotranspiration to be incorporated into the model, since evapotranspiration is usually calculated on a monthly or annual basis. The monthly values of evapotranspiration, for the study area, as they were calculated by the FAO-56 Penman-Monteith method, vary between 20 and 125 mm. The continuous nature of the hydrograph enables the development of a continuous sediment graph. The whole basin was divided into ten natural sub-basins, so that more detailed calculations can be performed (Fig. 2).

Fig. 2
figure 2

Map of the main streams of the ten sub-basins

Full size image

The estimation of the model parameters was achieved by means of rainfall data (time step 10 min) from the meteorological station of Oraio, as well as by means of topographical, geological, main stream and soil cover maps. The meteorological station of Oraio is located in the centre of gravity of the basin (Fig. 2), at an elevation of 800 m. However, it has to be noted that the rainfall data of only one meteorological station is not representative for the whole basin, especially for the sub-basins located near the outlet of the whole basin.

Moreover, the Laboratory of Hydrology and Hydraulic Structures, Civil Engineering Department, Democritus University of Thrace, carried out ten field measurements of bed load and suspended load near the outlet of Kosynthos River basin (Fig. 2); these included: four in November-December 2005, two in April 2006 and four in May 2007 (Table 1). Along with the ten complete measurements (bed load and suspended load), there are 18 additional measurements, in which either only the bed load or only the suspended load or neither is available (Table 2). In concrete terms, the date of the measurements, the rainfall depth, the rainfall intensity, the stream discharge, the suspended load transport rate and the bed load transport rate are given in Table 2.

Table 1 Measured values of stream discharge, suspended load transport rate and bed load transport rate near the outlet of Kosynthos River basin
Full size table
Table 2 Rainfall data and measured values of stream discharge, suspended load transport rate and bed load transport rate near the outlet of Kosynthos River basin
Full size table

Metallinos and Hrissanthou (2010) established nonlinear regression relationships between sediment transport on the one hand and stream discharge, rainfall depth and rainfall intensity on the other hand for Kosynthos River basin. While bed load transport depends mainly on the hydraulic characteristics of the streams, e.g., stream discharge, suspended load transport depends on both hydraulic and rainfall characteristics, e.g., rainfall depth, rainfall intensity. This fact can be justified as follows: when soil erosion products, due to rainfall and runoff, reach the streams, they are transported in the streams as suspended material, because they are very fine. Contrarily, bed load consists mainly of coarse material and originates from stream bed erosion (Metallinos and Hrissanthou 2010). Thus, the bed load transport rate q b [kg/(m s)] was determined as an exponential function of the stream discharge Q (m3/s) by means of Eq. (11) and the suspended load transport rate Q s [g/s] as a hyperbolic function of the daily rainfall depth N [mm] by means of Eq. (12):

$$ {q}_b=0.002{e}^{0.284Q} $$
(11)
$$ {Q}_s=251{N}^{0.915} $$
(12)

In this way, 18 additional measurements of sediment values (bed load + suspended load) became available (28 in total), which allows a more thorough evaluation of the under study mathematical model.

The cross section of Kosynthos River, where the measurements were performed (Fig. 2), was divided into sub-sections. The stream discharge of the whole cross section is the sum of the stream discharges of the sub-sections. The stream discharge in each sub-section results as the product of the mean velocity and the cross-sectional area of the sub-section. The mean velocity was measured separately in each sub-section by means of an impeller flow meter (Metallinos and Hrissanthou 2010). Measurements of suspended load transport and bed load transport were carried out at the same time as the stream discharge measurements.

As far as suspended load is concerned, the measurements were carried out by taking a sample of water from the centre of the cross section and by infiltrating it through a filter paper. When infiltration has been completed, the filter paper is put into a laboratory oven. By dividing the dry mass of the suspended sediment by the water volume of the sample, the concentration of the suspended sediment is determined. The suspended load transport rate results by multiplying the suspended sediment concentration by the stream discharge of the whole cross section (Angelis et al. 2012).

For the measurement of the bed load transport, a net trap was put on the bed, in the middle of the whole cross section. The trapped bed load was put into a laboratory oven, in order to dry out residual humidity. The bed load transport rate is determined by dividing the dry mass of the trapped sediment by the measurement duration and the width of the sediment trap (Metallinos and Hrissanthou 2010).

3.1 Determination of the Rainfall-Runoff Submodel Parameters

The sensitivity of the hydrologic model to the parameter CN (curve number) of the SCS rainfall excess model dictates a detailed determination of the CN. The curve number was estimated for each sub-basin by processing the soil cover map and by using the available soil permeability data for the basin.

Another crucial parameter of the SCS model for the transformation of rainfall excess to runoff hydrograph is the concentration time, which was computed by the Turazza-Giandotti formula (Giandotti 1934).

The determined parameters of the Muskingum-Cunge routing model are: (a) the main stream length of each sub-basin (main stream map); (b) the average slope of the main stream of each sub-basin (contour map); (c) the geometric characteristics of the cross sections (estimated); (d) the Manning coefficient depending on the roughness of the streambed (estimated).

A “manual” calibration was carried out for the parameters that cannot be determined by means of tables and/or maps. Thus, two parameters of the baseflow model were determined manually (Kaffas and Hrissanthou 2014).

In Table 3, the area, the curve number and the concentration time, resulting from the Giandotti formula, are given for each sub-basin. In Table 4, the length, the bed slope, the bottom width, the shape of the cross section and the Manning coefficient are given for each routing reach.

Table 3 Area, curve number and concentration time values for each sub-basin
Full size table
Table 4 Length, bed slope, bottom width, cross section shape and Manning coefficient
Full size table

3.2 Determination of the Soil Erosion Submodel Parameters

Apart from the parameters of the rainfall-runoff submodel, some additional parameters needed to be determined for the application of the model of Poesen (1985).

The soil slope gradient can be found, as the reach bed slope, using the contour map, while the median particle diameter of the soil surface was estimated in the size order of suspended particles. The factor β (Eq. 5) was taken as equal to 12.5 J/(m mm2) (Poesen 1985).

Wischmeier and Smith (1978) give detailed tables with soil cover factor C values for different types of soil cover and land use. On the basis of these tables, the following values of soil cover factor were taken: 0.004 for forest area, 0.03 for areas covered by bushes, 0.001 for urban areas and 0.2 for areas with no significant vegetation. The final soil cover factor value, for each sub-basin, was calculated by the following type:

$$ C={F}_{forest}\cdot {C}_{forest}+{F}_{bush}\cdot {C}_{bush}+{F}_{urban}\cdot {C}_{urban}+{F}_{noveg}\cdot {C}_{noveg} $$
(13)

where: F forest is the percentage of sub-basin area covered by forest; F bush is the percentage of sub-basin area covered by bush; F urban is the percentage of sub-basin covered by urban area; and F no veg is the percentage of sub-basin area covered by no significant vegetation.

The entrainment ratio, r e (Eq. 5), was determined by testing different values of r e and comparing the sediment yield values of the mathematical model with the field measurements at the basin outlet. After trial computations, r e was taken as equal to 0.7. However, the above manner of r e determination has as a consequence that this parameter loses its physical meaning in relation to soil cohesion and becomes rather an arithmetic calibration factor (Hrissanthou 2002). Table 5 displays the soil slope gradient and the soil cover factor values, for each sub-basin.

Table 5 Soil slope gradient and soil cover factor values for each sub-basin
Full size table

3.3 Determination of the Stream Sediment Transport Submodel Parameters

The additional input data for the stream sediment transport submodel, with reference to the foregoing submodels, concern the main stream of each sub-basin. The median diameter of the transported bed load was estimated on the basis of the granulometric composition of bed load samples. The median diameter of stream suspended particles was taken as equal to that of the soil surface, because the soil erosion products are transported in the streams in suspension.

4 Quantitative Results

In Fig. 3, the computed sediment graph (bed load + suspended load) at the basin outlet is illustrated for the period November 2005 - January 2009. In Fig. 4, the measured sediment discharge values are depicted in the sediment graph of Fig. 3. However, in Fig. 4, the linear scale of the sediment discharge axis is augmented in relation to the scale of the same axis in Fig. 3, so that the comparison between measured and computed values can be visualized. The black-colored arithmetic values in Fig. 4 refer to the measured sediment discharge, while the orange-colored ones refer to the values determined by means of the regression relationships (Metallinos and Hrissanthou 2010).

Fig. 3
figure 3

Sediment graph of November 2005 - January 2009

Full size image
Fig. 4
figure 4

Sediment graph of November 2005–January 2009 with measured sediment discharge values

Full size image

In Table 6, the measured sediment values along with the computed ones are given for each date. In the “measured sediment discharge” column of Table 6, the arithmetic values without asterisk refer to the measured sediment discharge values, while the arithmetic values provided with an asterisk refer to the values determined by means of the regression relationships (Metallinos and Hrissanthou 2010).

Table 6 Measured and computed sediment discharges
Full size table

Table 6 contains 28 ratios of measured to computed sediment discharge values. In ten of them, the measured sediment discharge resulted by means of field measurements, while in the remaining 18 ratios, the measured sediment discharge resulted by means of regression analysis. The mean value of the 28 ratios given in Table 6, amounts to 2.20, the mean value of the ten ratios is 4.59, while the mean value of the 18 ratios is 0.86.

Efficiency criteria are commonly used by hydrologists to provide an objective assessment of the closeness of the simulated behaviour to the observed measurements (Krause et al. 2005). For the comparison between computed and measured sediment discharge values, the following criteria were used: root mean square error (RMSE), relative error, efficiency E, linear correlation coefficient r, and determination coefficient r 2.

RMSE [kg/s] is defined mathematically as follows:

$$ RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum_{i=1}^n\Big({O}_i-{P}_i}\Big){}^2} $$
(14)

where: O i is the observed daily sediment discharge value for the day i [kg/s]; P i is the predicted daily sediment discharge value for the day i [kg/s]; and n is the number of pairs of observed and predicted sediment discharge values.

The perfect value for RMSE is 0. The smaller the RMSE is, the better the correlation between the observed and the predicted values is.

The relative error [%] is expressed as:

$$ relativeerror=\frac{O_i-{P}_i}{O_i}\times 100 $$
(15)

The efficiency E proposed by Nash and Sutcliffe (1970) is expressed by the following equation:

$$ E=1-\frac{{\displaystyle \sum_{i=1}^n{\left({O}_i-{P}_i\right)}^2}}{{\displaystyle \sum_{i=1}^n{\left({O}_i-\overline{O}\right)}^2}} $$
(16)

where: Ō is the observed overall mean daily sediment discharge [kg/s]. The range of E lies between 1 (perfect fit) and − ∞.

The degree of linear dependence between computed and measured sediment discharge values is expressed by the linear correlation coefficient r:

$$ r=\frac{{\displaystyle \sum_{i=1}^n\Big({O}_i}-\overline{O}\Big)\left({P}_i-\overline{P}\right)}{\sqrt{{\displaystyle \sum_{i=1}^n{\left({O}_i-\overline{O}\right)}^2}}\sqrt{{\displaystyle \sum_{i=1}^n{\left({P}_i-\overline{P}\right)}^2}}} $$
(17)

where: \( \overline{P} \) is the predicted overall mean daily sediment discharge [kg/s].

The value of r is such that − 1 ≤ r ≤ + 1. The + and - signs are used for positive and negative linear correlations, respectively. A perfect correlation of ± 1 occurs when all the data points lie exactly on a straight line.

The determination coefficient r 2 is defined as the squared value of the linear correlation coefficient, in the case of linear regression between computed and measured sediment discharge values. It gives the percentage of the total variation in computed sediment discharge that can be explained by the linear relationship between computed and measured sediment discharge. The range of r 2 lies between 0 and 1. A value of zero means no correlation at all, whereas a value of 1 means that the dispersion of the prediction is equal to that of the observation (Krause et al. 2005).

The value of RMSE for the present data amounts to 0.79 kg/s. The relative error varies between the values −93.87 and 185.78 %, and has an average value of 16.17 %. The efficiency E was found to be 0.52. The correlation coefficient amounts to 0.88, while the determination coefficient r 2 equals 0.77 (Fig. 5). In Fig. 5, apart from the basic regression line, two other lines are shown: the line of perfect agreement between computed and measured sediment discharge values, as well as the corresponding regression line that passes through the intersection point of the two coordinate axes. The slope of the last line (1.19) is greater than 1.0, which means that the mathematical model used in this study overpredicts sediment yield at the basin outlet.

Fig. 5
figure 5

Linear regression line between computed and measured sediment discharge values

Full size image

From Table 6, it is evident that the estimate of the sediment discharge, by means of nonlinear regression analysis, implies a better agreement between computed and measured sediment discharge. From the arithmetic values of the statistical efficiency criteria, it is concluded that the deviation between computed and measured sediment discharge values is not considerable. Additionally, the degree of linear dependence between computed and measured sediment discharge values is very high.

The comparison between computed and measured stream discharge values at the outlet of Kosynthos River basin, for the time periods given above, provided slightly better results, concerning the closeness of the predicted to the observed arithmetic results (Kaffas and Hrissanthou 2014), than the comparison between computed and measured sediment discharge values, which was anticipated because of the complicate nature of the soil erosion and sediment transport processes.

5 Discussion

The present study constitutes an extension of the study described in Kaffas and Hrissanthou (2014). In the previous study, continuous hydrographs for relatively long time periods were computed for the outlet of Kosynthos River basin, by means of the same hydrologic model described shortly in the present study. This hydrologic model is combined with a soil erosion model and a stream sediment transport model, in the present study, in order to generate continuous sediment graphs at the outlet of Kosynthos River basin. The three models are connected with each other through the fact that the output of the hydrologic model is the input to the soil erosion model, while the output of the soil erosion model is the input to the stream sediment transport model. It could be stated that the connection of the models through the input-output data ensures the almost parallel running of the models, which approximates the natural reality.

The Yang formula (Yang and Stall 1976) used in this study is valid for sand beds, while the beds of the main streams of the basin considered consist of gravel and sand. Nevertheless, it is believed that the transported bed load belongs mostly to the sand category, whereas gravel transport takes place, usually, under flood conditions (Hrissanthou et al. 2010).

In previous publications of the second author, different versions of the present model were used (Hrissanthou 2002, 2005). The main differences between the previous model versions and the present model version are summarized below: (a) The time variation of stream discharge and sediment discharge, on a hourly time basis, at the basin outlet is computed in the present model version. In other words, hydrographs and sediment graphs, on a hourly time basis, are computed at the basin outlet, in the present model version. Nevertheless, in the previous model versions, total monthly values of water volume and sediment yield at the basin outlet were computed. (b) A different rainfall-runoff submodel was used in the previous versions, that is based on a water balance condition in the root zone of the soil. In the present model version, the well known SCS method is used for the production of hydrographs. (c) A second soil erosion submodel (Schmidt 1992) was used alternatively in a previous version, which provided annual sediment yield values of the same size order as the soil erosion submodel of Poesen (1985). However, in the present model version, the sediment discharge values on a hourly time basis, according to both soil erosion submodels, display a significant disagreement. (d) In the present study, sediment discharge measurements at the basin outlet are available, so that a comparison between computed and measured values of sediment discharge can be made. In the previous studies, sediment yield values at the basin outlet were not available. (e) The previous model versions were applied to Nestos River basin, downstream of Platanovrysi Dam, with an area of 838 km2 (Hrissanthou 2002) and to Kompsatos River basin with an area of 567 km2 (Hrissanthou 2005). Both basins are neighbouring to Kosynthos River basin, with an area of 237 km2, considered in the present study.

6 Conclusions

The full benefit of an erosion prediction model is gained through the use of a continuous simulation model. By continuous simulation it is meant that the model follows the time variation of the physical processes related to erosion, which are affected by management decisions and climatic environment (Lal 1994).

The combination of a hydrologic model with a soil erosion model and a stream sediment transport model enables the transition of the hydrograph, due to a rainfall event, at a basin outlet to the corresponding sediment graph. In other words, the variation with time of the sediment discharge at the basin outlet is computed on the basis of the variation with time of the stream discharge due to the rainfall event (Hrissanthou and Theodorakopoulos 2005).

Consequently, through the continuous hydromorphologic modeling for a relatively long time period in a relatively large basin, a more realistic representation of the runoff, soil erosion and sediment transport processes can be achieved.

Finally, it is believed that the deviations between computed and measured sediment discharge values for single rainfall events can be mitigated by means of the continuous hydromorphologic modeling, because of the integrating effect obtained through use of a long simulation period.