A combined SPH-DEM approach for extremely deformed granular packings: validation and compression tests

Abstract

We present a novel smoothed particle hydrodynamics-discrete element method (SPH-DEM) approach for the simulation of deformable granular media. First, we show how the method converges to the analytical solution in a simple contact mechanics problem, namely the Hertz contact law for elastic spherical grains. Second, we analyze the evolution of a 2D packing of disks under uniaxial compression, displaying the evolution of key metrics of the packing such as the coordination number and the vertical stress. We show that the code produces data in quantitative agreement with what is known from literature. Finally, we demonstrate that our SPH-DEM coupling can be used to study packings of deformable grains from the onset of jamming to extremely compacted states, reaching packing fractions of $\phi \simeq 0.995$.

1 Introduction

Smoothed particle hydrodynamics (SPH) was introduced in 1977 in the field of astrophysics [16, 29], and since then, the maturity of the method, the fields where it is used, and the range of applications have significantly increased. Among the numerous applications the method has been used for, the following can be mentioned: water wave impact on coastal structures [1], flow around ships [31], sloshing of liquids in carrier tanks [44], flooding [46], tsunami generation [52], flow in porous media [21, 38], fluid–solid elastic interaction [24, 53], or bird strikes on aircraft components [17].

To extend the fields of application of SPH, many studies have coupled it with other methods, addressing in this way multiphysics problems [12]. Discrete element method (DEM) is not an exception in this context, and in the literature, SPH-DEM couplings were presented. These algorithms were used to study fluid–solid interaction [5, 22] or impact of two solid objects — recently giving high importance to the contact models used for solid–solid interaction [48, 49]— in a regime of high deformations.

Being able to simulate highly deformed solids is of paramount importance in many fields. An extremely wide and interdisciplinary example is the study of granular matter. The way the deformability of the constituents of a granular packing can drastically change the macroscopic properties of the system has been observed in several contexts. An important example is the discharge of particles from a silo, where the flow field and clogging statistics are dramatically different for hard and soft grains [2, 50]. Also, in many fileds, softness is a fundamental quality of particles: In biology, it is known that forces associated with cell–cell interactions, (and the resulting force chains) can impact the transmission of information in cells [40]. Deformable grains are of main interest in the food industry as well, where the change of the properties can have direct consequences on the quality of the product [47]. As a final example, from a more fundamental point of view, recent experiments on photoelastic disks have shown that asperities play a central role in the transition from a variable to a persistent force chain regime in granular packings [26]. This raises question on the role of irregularities in jamming transitions.

In the last years, a number of mesh-free numerical approaches have been proposed to explore phenomena in deformable granular packings [4, 33,34,35]. These approaches are fruitful alternatives to more established mesh-based methods [20, 39]. Despite its wide range of applications, and to the best of our knowledge, the SPH paradigm has never been systematically applied to quantitatively study a granular packing composed of deformable grains.

SPH has been utilized to simulate granular matter at both macroscopic and grain scales. At the macroscopic scale, it has been used to study granular flows as a continuum [32], disregarding grain deformation. At the grain scale, with DEM coupling, it has been applied to investigate problems involving solid–fluid [24] and solid–solid impacts at the single particle level [49]. However, a comprehensive study involving a set of particles is missing. Sharing the mathematical framework of previous SPH-DEM implementations and their interest toward highly deformable particles, our work aims to investigate the effect of mutual grain deformation on the global properties of the system, at the mesoscale level.

In our present contribution, we present an SPH-DEM coupling aiming at taking the best from both methods: the ability to simulate large deformations from SPH, and the specialized contact models for granular systems developed by the DEM community (e.g., cohesive forces). Specifically, our goal is twofold: first overcoming one of the main limitations of DEM models, undeformable particles, and second, extending the use of SPH to particle resolved simulations in the field of granular materials.

Here, we demonstrate how our coupling of SPH-DEM provides a viable tool to address the study of packings of deformable grains. This numerical approach enables the extraction of detailed information about the number of contacts, overlaps, grain shape, and contact forces in mesoscale systems. Moreover, the data produced can be used to calibrate existing DEM models that participated in taking into consideration particle deformation [15], thus allowing to transfer our results on an industrially relevant scale. Furthermore, the great flexibility in the possible geometries allows to study the effects of the shape on different levels, from aspect ratio, to asymmetric particles, to the presence of irregularities on the surface of interest.

2 Methods

2.1 SPH-DEM

We use an in-house version of the software LIGGGHTS [25], where we coupled an SPH package [25] to work with the variety of contact models available in LIGGGHTS. The SPH implementation we are using was originally designed for the simulation of continuum mechanics problems, with the aim of replicating large deformation events [14, 28]. It uses a total Lagrangian formalism, with a viscous force for stabilization, and a correction force for the suppression of zero energy modes, further details can be found in [14]. The DEM code was specifically developed for granular materials, and it offers several contact models that can account from repulsion, to friction, to cohesion. The coupling is therefore a bridge between continuum mechanics and granular matter, with the goal of studying the packings of deformable grains.

The SPH and DEM interplay is illustrated in Fig. 1. The DEM force models are used to calculate the contact interaction between the boundaries of different grains. The SPH interaction is used to compute the internal stress of a grain, starting from the mutual displacement of its discretization points. For example, when a grain is stretched, the distances between the discretization points increase along the direction of stretching. The SPH interaction calculates the internal tensile stress, which results in a force that pulls the points back to their equilibrium positions, restoring the grain to its original shape. Similarly, when two grains are pressed against each other, the discretization points inside each grain are pushed closer along the direction of contact. This change triggers the SPH model to compute the stress inside the grain and the corresponding reaction force, which aims to restore the grain to its original shape.

Fig. 1

SPH-DEM pair interaction. (a) A snapshot from the simulations showing grains in contact. The discretization points are represented by black dots and the colored areas show the shape of each grain. (b) A close-up of the contact at the center, where the dashed lines represent the DEM contact radius of two points. The DEM interaction occurs only between points belonging to different grains. The overlap between the contact radii, in magenta, is used to calculate DEM repulsive forces. The resulting displacement modifies the mutual distances between points belonging to the same grain. The internal stress of the material is computed using the SPH interaction

2.1.1 SPH interaction

The SPH code in our simulations is used for the computation of the physics at the single grain scale, specifically, how the material reacts to deformations. This involves the calculation of the strain tensor in each grain and, using a given material model — in this work restricted to linear elasticity — the computation of the corresponding stress tensor. The stress tensor then defines the force applied on each discretization point, which is used for time integration. Technical specifications of the SPH code are reported in Appendix A.1.

It is worth noting that the SPH interaction is only computing the internal stress tensor of each grain, so the pair interactions are computed only between discretization points belonging to the same grain. The contact interaction between two grains, which causes their deformation, is computed by the DEM part of the code.

2.1.2 DEM interaction

The interaction between grains is handled by the DEM code, which is activated when the discretization points on the boundaries of two grains come into contact: Each of these points has an associated contact radius $r_c$. In case two points come closer than the sum of the contact radii, the DEM model calculates the corresponding force between them.

We point out that since the aim of DEM interactions is to simulate contact interaction between grains, the pair interactions are computed only between discretization points belonging to different grains. As a consequence, points within the same grain can be closer than $r_c$, without this causing any internal stress because of repulsive forces.

In the following, we only use repulsive forces, namely the Hertz contact law, excluding cohesive and frictional models, that we leave for future research. It is worth noting that, although the DEM model has no tangential force, the discretized grains are not completely frictionless. The discretization process indeed is inherently unable to produce perfectly smooth surfaces, and the resulting discretized surfaces will show some "bumps", as can be seen in Fig. 1. This geometry induces frictional effects, which magnitude depends on the specific contact configuration. In Appendix B, we elaborate this point, giving a method to estimate the friction coefficient of the discretized grains.

We stress that the precise functional form of the contact law is not critical as far as the interpenetration of grains boundaries is small enough. While we keep this interpenetration as low as possible, we underline that in this scheme it is a necessary ingredient for the interaction to happen. In order to avoid the effects of an unphysical large volumetric interpenetration of the grains, the stiffness of the contact model — that we express here in terms of the associated Young’s modulus — $Y_c$ needs to be higher than the stiffness defined in the material properties of the grain. To be more precise, we consider two discretization points with identical properties $r_c$, $Y_c$, and Poisson’s ratio $\nu _c$, in contact. If they interact via a normal force of the type $F_{ij} = k \sqrt{\frac{r_c}{2}}\delta _{ij}^\frac{3}{2}$, where $k = \frac{4Y_c}{3(1-\nu _c^2)}$, we found that the simulations produce the desired behavior, is to say small grain interpenetration, already for $Y_c = 5 E$, where E is the Young’s modulus of the material of the grain. More details on the DEM interaction are described in Appendix A.2.

3 3D uniaxial compression

3.1 Simulation setup

We consider here a well-known system to benchmark the simulation results against an analytical solution. Therefore, the problem we tackle is the contact force between linear elastic, frictionless spheres, which can be analytically solved for small overlaps [27]. The relation between the overlap $\delta$ and the contact force F, for two spheres of radius $R_1$ and $R_2$, is:

$$\begin{aligned} F = \frac{1}{D}\sqrt{\frac{R_1R_2}{R_1+R_2}}\delta ^\frac{3}{2} \text {.} \end{aligned}$$

Given that r is the distance center to center of the two spheres, the overlap is $\delta = R_1 + R_2 - r$. The quantity $D = \frac{3}{4} \bigl ( \frac{1-\nu _1^2}{E_1} + \frac{1-\nu _2^2}{E_2}\bigr )$, where $\nu _1$, $\nu _2$ are the Poisson’s ratios and $E_1$, $E_2$ the Young’s moduli of the two bodies. In our simulations, we always used identical particles, so the above expression of the force becomes $F = \frac{\sqrt{2R}}{3 (1- \nu ^2)} E\delta ^{\frac{3}{2}}$. Using the undeformed radius of the particle R as unit of length, the non-dimensional force becomes $F^* = \frac{\sqrt{2}}{3(1-\nu ^2)} \delta ^{*\frac{3}{2}}$. We will present our analysis in terms of this force, hence the only relevant parameter is the Poisson’s ratio, that we chose to be $\nu = 0.4$, in the range of common values for hydrogel particles ($0.3-0.5$) [7, 8].

Fig. 2

Discretization scheme. (a) To simulate a disk, discretization points are placed following concentric rings. The blue area is representing the disk to be discretized. The contact radius, here not represented, of the most external points touches exactly the border of the original disk (b) A sphere is composed of a sequence of disks, of different radii, along the direction perpendicular to the ring plane. For major visual clarity, the represented radii of the discretization points are smaller than their contact radius $r_c$

To produce the data to compare with the Hertz law, the implemented numerical setup consists of three aligned purely elastic spheres, discretized as in Fig. 2. The two external spheres are slowly pushed against the one in the middle, and then the center to center distance and the contact force are measured.

Fig. 3

Sketch of the rigid cap, with a thickness of $3.5 r_c$. As the discretization becomes finer, $r_c$ decreases. This parameter is determined by the discretization pace, meaning that the fraction of particles included in the cap also decreases. For the coarser simulation with $N_{sphere} = 107$, the fraction of particles included in the cap is $N_{caps}/N_{tot} \simeq 0.3$, while for the case with $N_{sphere} = 3731$, is reduced to $N_{caps}/N_{tot} \simeq 0.04$

To push the spheres we define, on the external side of the two lateral spheres, a spherical cap, sketched in Fig. 3. The spherical caps will move as a rigid body, at constant velocity, pushing the two spheres against the central one. The movement is parallel to the line connecting the centers of the three spheres so that no shear components are introduced. The magnitude of the compression velocity is orders of magnitude slower than the speed of sound in the material, and the compression can be considered quasi-static. Since the simulation can be considered in equilibrium at every moment, the force applied to the cap is equal to the contact force between the particles. For this reason, we measure the force acting on the solid caps. At the center of each sphere, there is an SPH particle which is considered the center of the deformed sphere. These particles are used to compute the distance center to center and the overlap between the grains.

3.2 Convergence

The arrangement of discretization points can have effects on the computation of physical observables such as stress and strain [9, 11]. Some of these problems are caused by an uneven arrangement of the discretization points, some others by the intrinsic instability of the lattice used to place these points. We decided to use an arrangement that can accurately reproduce the shape of a sphere. All the external points are placed on the surface of a sphere of radius $R-r_c$, this reduces the shape irregularities that will be observed if, instead, we were choosing a lattice arrangement. In the last case, the points would be placed on the surface of a sphere only when the lattice sites coincide with it, an eventuality that can be met only for a small number of lattice points, and along a few directions. The internal volume of the sphere is discretized by a superposition of concentric spherical shells. More details on discretization can be found in Appendix C.

We performed simulations for different levels of discretization to study the convergence of the simulation to the solution. In Fig.  4 we report the results obtained for the force-overlap relation using $N_{sphere} = 107,\, 195,\, 3731$ discretization points per sphere. The number of points is determined by our code after we choose the discretization length, that in this case are $a = 0.25, 0.20, 0.08$ mm, respectively. The qualitative behavior is always captured, also for the coarser discretization, although eventually showing a significant quantitative disagreement with the data obtained from finer simulations. Starting from $N_{sphere} = 195$ the solution is satisfactory for high levels of compression. For $\delta /R > 0.15$, the measured relative force difference with respect to the full resolution simulation is ${\Delta F/F} < 0.1$ at most. For small overlaps, the differences are larger, this can be expected since: i) the details of the surface discretization play a dominant role at the onset of the contact; ii) the SPH approximation is less accurate on the surface where discretization points have fewer neighbors. For the simulation with $N_{sphere} = 3731$, we see that the data is in good agreement with the analytical solution until $\delta /R \simeq 0.1$, which is satisfactory since we do not expect the Hertz law to hold for large overlaps.

Fitting a function of the form $F = A' \delta ^{\gamma '}$ to the simulation data, where $A'$ and $\gamma '$ are fitting parameters, we want to verify that the Hertz contact law is recovered with increasing accuracy by simulations with finer discretization. The fit is done excluding the values of $\delta > 0.15$, and the results are plotted in Fig. 5. We report the results for one additional simulation with $N_{sphere} = 1028$, previously not shown for the sake of visual clarity. For each discretization, we estimated the exponent and its uncertainty by considering three independent datasets produced by varying the stiffness of the particles. For every dataset, the fit was iterated ten times on random subsets, obtaining a distribution for the parameter $\gamma$. The value of $\gamma$ and the error bar were calculated as the mean and the standard deviation of this distribution. We observe that the relative deviation from the analytical solution decreases with an increasing number of discretization points. For the finer discretization, the error in the evaluation of the exponent in the contact force law is $\Delta \gamma /\gamma _{Hertz} \simeq 0.09$ reaching a good agreement also according to this metric.

Fig. 4

Force against overlap, data from different discretizations. $N_{sphere}$ is the number of discretization points per sphere in the simulation. The dashed lines represent the fits $F = A'\delta ^{\gamma '}$ on the different datasets

Fig. 5

Fitted exponent on data from simulations with different resolution and stiffness. $N_{sphere}$ is the number of discretization points per sphere. The error bars indicate plus/minus one standard deviation

4 2D compression

4.1 Simulation setup

Fig. 6

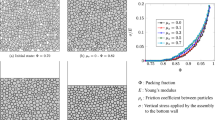
Snapshots of the system configuration at the beginning and toward the end of the 2D compression. The particles are represented with a slightly reduced radius to distinguish their boundaries. In (a), we present a configuration with packing fraction $\phi \simeq 0.81$. In (b), a compressed state with packing fraction $\phi \simeq 0.99$

The system studied in this section is composed by $N_{mol} = 300$ 2D disks, enclosed by walls. The grains radii were randomly extracted in the interval $[1,2] \text { mm}$, following a uniform distribution. Two snapshots taken from the simulation are shown in Fig. 6. The simulations were run for nearly incompressible grains, choosing this time the Poisson’s ratio to be $\nu = 0.45$, another commonly observed value for hydrogel particles [7, 8]. The packing is adiabatically compressed, at constant velocity, by a moving piston. The evolution of quantities such as the coordination number, overlaps, and stress is studied.

To generate the initial configuration, we first start from a purely DEM simulation performed in LAMMPS [45]. Inspired by the procedure described by Herrmann [18] to produce a granular packing, a mixture of grains is poured from a height between ${150}~{\hbox {mm}}$ and ${200}~{\hbox {mm}}$ into a box of length ${62.7}~{\hbox {mm}}$. The energy is dissipated via inelastic collisions, and the grains settle under the effect of the gravitational acceleration $g_0$. Once the configuration is relaxed, we drastically reduce gravity to $g_1 = 0.005 g_0$, keeping the stiffness of the particles fixed, to reach a state where the overlaps are as small as possible.

Since the considered interaction potential is linear elastic, we expect the overlap to linearly decrease with the gravitational acceleration. We can estimate the overlap considering the balance between the elastic force and the force caused by the pressure of the packing. Considering the equivalent hydrostatic pressure at the bottom of the packing $P_H = \rho g_0 h$, hence a typical value of the respective force $F_H \simeq \pi R^2 P_H$, and equating with the elastic normal force $F_{el} = k_n \delta$ the expected relative overlap is $\delta /R \simeq \pi R \rho g h/k_n$. Following this approximation, we can estimate the overlap to change from $\delta /R \simeq 10^{-4}$ with the initial gravitational acceleration to $\delta /R \simeq 10^{-6}$ when the gravity is reduced. The packing we are obtaining has then minimal overlaps between the different grains, and this is important because in the next step we restart the simulation from the configuration thus obtained, considering undeformed particles.

Every DEM particle is replaced by a disk, discretized by SPH particles, which center and radius are identical to the starting DEM particle. The discretization is done following the strategy mentioned in Appendix C.1, the average density of discretization points is ${25.7}~{\hbox {mm}^{-2}}$, corresponding to a discretization length $a ={0.2}~{\hbox {mm}}$. This implies that the number of discretization points per grain varies, from a minimum of $N_{disc}^{(min)} = 81$ to a maximum of $N_{disc}^{(max)} = 321$, using a total of $N_{at}^{(tot)} = 52172$ discretization points for the grains. In this simulation, also the walls are discretized using point particles, with pace $a_{wall} = {0.1}~{\hbox {mm}}$, reaching a total of $N^{tot} = 54288$ points.

When replacing a DEM particle with our discretized disk, we reduce the symmetry of the system. Unlike the DEM particle, which is rotationally invariant, the periodicity of the external boundary of our disks depends on the level of discretization. Nonetheless, we want to emphasize that initializing all the particles in the same orientation does not induce any angular order in the contact orientation. The initial packing lacks any angular order, so setting all the particles in the same orientation is equivalent to randomly initializing their rotations. Randomly rotating the disks would produce different, but statistically equivalent evolutions of the system. In principle, for the particles in contact with the walls we introduce an angular order. However, the disks are not discretized following a lattice, which could induce an order, and we do not observe any significant interlocking effects arising from the discretization.

Fig. 7

Graphical representation of the simulation protocol. The packing fraction is varied by moving the top wall of the system. Every relaxation step (plateau) has the same duration as the previous compression (or decompression). The dashed line denotes the start of the compression when the data are sampled

The initial packing is contained in a box of length $62.7 \text { mm}$ and height larger than the maximum height of the particles. To obtain a more compact configuration before sampling, we apply some cycles of compression, reaching the maximum packing fraction $\phi _{max} \simeq 0.995$. The simulation protocol is graphically represented in Fig. 7. Considering the speed of sound in the medium to be $c_s$, the following protocol is followed:

• (i) the system is compressed at a velocity of $v = 5 \times 10^{-3}c_s$ until it reaches a compact configuration with a packing fraction of approximately $\phi = 0.80$;

• (ii) the piston is then held fixed, and the system is allowed to relax. During this relaxation, energy is dissipated through collisions. The packing fraction, although high, has not yet reached a value where the contact network prevents any movement of the particles;

• (iii) the system is compressed again, this time at a velocity of $v = 10^{-3}c_s$, until it reaches a maximum packing fraction of $\phi _{max}$. The piston is held fixed at this position to allow the system to relax. In this state, particles are no longer free to move and are highly deformed;

• (iv) the system is decompressed until it reaches again the state at $\phi \simeq 0.81$;

• (v) repetition of the compression with $v = 10^{-3}c_s$ to $\phi _{max}$ and again relaxation, keeping the strain constant;

• (vi) again decompression to reach $\phi \simeq 0.81$ but now with a lower velocity $v = 2.5 \times 10^{-4}c_s$, followed by another relaxation step;

• (vii) finally, the system is compressed again, this time the piston is moved with velocity $v = 1 \times 10^{-4}c_s$ until reaching $\phi _{max}$. Note that data sampling was performed only in the final (seventh) phase of our simulation protocol.

4.2 Results

During the compaction, we studied the evolution of the coordination number and the stress. To compute the coordination number Z, we exclude all the disks in contact with the wall, which naturally have a lower number of contacts. Above jamming, we expect to observe an increase of the contact number of the type $Z-Z_0 \propto (\phi - \phi _0)^\frac{1}{2}$, where $Z_0$ is the coordination number at jamming. The scaling law of the excess contact number has not only been derived on theoretical grounds [13, 51] but has also been consistently observed, numerically and in experiments across a variety of systems [10, 30, 36, 37]. As a phenomenon, it is a solid and universal signature characterizing a granular system close to jamming.

Fig. 8

Evolution of coordination number during the compression. The dashed line is a fit where the scaling $(\phi -\phi _0)^\frac{1}{2}$ is imposed. Via fit we obtain $Z_0 = 3.3$, $\phi _0 = 0.84$, and $b_1 = 5.3$. The dotted line is the result from a fit where the exponent is a fit parameter while we fixed $\phi _0 = 0.84$ and $Z_0 = 3.3$. We obtain $\gamma = 0.501$, and $b_2 = 5.4$

In Fig.  8, we show the evolution of the excess contact number. Since $Z_0$ varies for several reasons, such as friction [43] and preparation of the packing [23], we do not have a priori knowledge of what is the exact value of $Z_0$ for our system. We expect it to be $3< Z_0 < 4$, since for two-dimensional disks the coordination number varies smoothly between these two values depending on the friction coefficient [42]. We estimate $Z_0$ and its corresponding packing fraction $\phi _0$ from fitting on the data $Z-Z_0' = b'(\phi - \phi _0')^\frac{1}{2}$, where $b'$, $Z_0'$ and $\phi _0'$ are fit parameters. We obtain $Z_0 = 3.3$, $\phi _0 = 0.84$, in line with values expected from theory. Furthermore we obtain $b = 5.3$, in close agreement with what was observed in literature for a similar system (i.e., $b = 5.1$) [6]. Keeping $Z_0$, $\phi _0$ to the values found above, we then perform a second fit $Z - 3.3 = b'(\phi - 0.84)^{\gamma '}$, with $\gamma '$ and $b'$ being fit parameters. We find $\gamma = 0.501$ and $b = 5.4$, in perfect agreement with previous observations.

In Fig. 9, we show the measured vertical stress against the packing fraction for two systems. The initial spatial configuration is the same, but in one case the particles are two times stiffer. $\sigma _{y,0}^*$, a small but finite value, is the measured vertical stress for the configuration at $\phi _0$. As it is expected, the data collapse on the same curve. At the grain scale, the systems are following different evolutions. It is possible to observe a non-monotonic behavior in each dataset. These are caused by local rearrangements of the particles, shear band formation, which release internal stress from the grains. We notice also a small systematic difference comparing the two datasets, this is caused by the uncertainty in the determination of $\phi _0$, and hence $\sigma _{y,0}^*$.

Fig. 9

Evolution of the vertical stress $\sigma _{y}^* =\sigma _{y}/E$ with the packing fraction during compression. The results of simulations with different Young’s moduli are plotted. The data collapse on the same curve. The small systematic difference is caused by the uncertainty in the determination of $\phi _0$ and $\sigma _{y,0}^*$

Fig. 10

Detail from the initial part of the compression, $\sigma _{y}^* = \sigma _{y}/E$. For very small strains, we observe a linear response of the system, as expected if the particles were interacting via harmonic springs. We obtained the dashed line from a linear fit on the log-log scale

Finally in Fig. 10 we focus on the very beginning of the compression, stopping at strains $(\phi /\phi _0 -1) < 0.02$. Considering a system of soft grains, interacting through repulsive normal forces of the type $f \propto \delta ^{\alpha }$, we know that the pressure, above a critical packing fraction $\phi _c$, scales with a power law $\sigma \propto (\phi - \phi _c)^\alpha$ [36], where $\phi _c$ indicates the onset of jamming. For small strains, the grains composing the system behave as linear springs. In Fig. 10, we show that the measured vertical stress linearly scales with the distance from $\phi _0$, the best estimation we have for $\phi _c$. From a linear fit $y = \alpha ' x + c'$ on the data in the figure, we find that the slope of the line is $\alpha = 1.07$, meaning that the code is correctly reproducing an affine response of the packing to deformations.

4.3 Computational Time

The DEM and SPH codes were originally developed in LAMMPS. As with most packages, the computational time scales as ${\mathcal {O}}(N/P)$ [45], where N is the total number of particles and P is the processor count. Varying some parameters can radically change the computational time with one of the most important being the SPH kernel length, h. This parameter is crucial for determining the number of neighbors each particle is interacting with, which scales as $(h/a)^D$, where a and h are the discretization pace and the kernel length, respectively, and D is the dimension of the system. This was confirmed by direct inspection of the CPU time in a 2D simulation, varying only h. We found that the CPU time scales approximately as $(h/a)^{1.9}$, indicating that the DEM part of the code has a minor impact on the total computational time.

5 Conclusions

As a first result, we presented, in a 3D simulation, how the code can, given the geometry, the material model, and the contact model, reproduce an analytically known solution for a contact mechanics problem. The Hertzian law, relating the force to the overlap of two linear elastic, frictionless spheres, was recovered with increasing precision enhancing the level of discretization.

We also tackled a more complex system, in a 2D setup, studying the behavior of 300 disks under compression, and comparing the results to what is known from the literature. The code successfully reproduced the complex phenomenology of a granular packing beyond jamming. We observed, as expected, a linear scaling of the pressure for small strains [36]. Furthermore, the evolution of the coordination number correctly reproduced the typical $Z - Z_0 = b(\phi -\phi _0)^\frac{1}{2}$ behavior [30, 37]. Using this law, we were able to approximately evaluate the coordination number and the packing fraction at the onset of jamming, obtaining results fully compatible with the literature [3, 10, 30, 36].

The SPH-DEM approach here used shows itself to be a promising tool for the study of compressed granular materials. Among the many problems we imagine it could be used for, there is the understanding of how macroscopic properties of granular materials are influenced by the underlying deformability of their grains. As an example, deeply jammed systems, where the change in shape of the particles might have a huge effect, have been mainly studied using undeformable particles [41, 54], or considering small deformations [19]. Our method shows potential as a valuable tool for studying the extremes packing fractions observed in these systems. We are indeed able to produce in detail information on the evolution of the number of contacts and their orientation, the stress distribution in the packing, and the shape of the grains. Most important, this is even possible at extreme deformations that were computationally inaccessible (or only with extreme computational effort), or shadowed by the inability of classical DEM to predict contact forces at extremely large grain deformation.

Furthermore, although in this work we presented only grains of regular shape, the method can be used for arbitrary complex geometries, for example to study the role of anisotropies in packings of deformable particles. However, it is important to note that the optimal arrangement of discretization points is not always straightforward, and more research needs to be done in that direction. Another challenging aspect of the method is the evaluation of the friction coefficient between grains. The computation is not trivial as it depends on the specific contact configuration and can vary smoothly between zero and a finite value. In Appendix B, we provide an analytical estimation of the maximum friction coefficient for our discretization technique.

Finally, our method also offers a significant advantage in its easy extension to situations involving cohesion, due to the implementation into the LIGGGHTS framework that allows us to access a variety of cohesion models. We believe that foams, emulsions, hydrogel packings, and cells, to mention a few, are good candidates as object of study with this method. The applications could range from the engineering of batteries in the automotive industry to the optimization of silo flow, or the food and pharma industry.

Appendices

A code technical specifications

1.1 A.1 SPH technical specifications

Table 1 Details of the SPH implementation

To define the behavior of a given material, is to say how the stress tensor is computed from the strain tensor, two models need to be specified: the material strength model, that computes the off diagonal elements of the stress tensor; and an equation of state (EOS) that computes its diagonal elements. This two are chosen to be linear elastic and the stress strain relation is

$$\begin{aligned} \varvec{\sigma }_{ij} = K \text {Tr}(\varvec{\epsilon })\delta _{ij} + 2 G \biggl ( \varvec{\epsilon }_{ij} - \frac{1}{3} \text {Tr}(\varvec{\epsilon }) \delta _{ij} \biggr ) \end{aligned}$$

Where $\varvec{\sigma }$ is the stress tensor, $\varvec{\epsilon }$ the strain tensor, K and G are the bulk and shear moduli of the material.

To fully determine the behavior of the SPH interaction, some additional parameters need to be specified: $q_1$, that defines the strength of a linear viscous force between SPH discretization points; $q_2$, a quadratic viscous term that we always set to zero; $k_{hg}$ that defines the strength of an hourglass correction force. Finally, the shape of the kernel function and its associated smoothing length, h, are crucial factors in the simulation. The former determines the weight of the pair interaction, while the latter defines the length within which particles interact. All the technical parameters specific to this implementation of SPH, together with the kernel type and its length h, are specified in the Table 1. The physical parameters defining the elastic properties of the material are reported in Table 2. While the Young’s modulus is an important parameter in our simulations, its absolute value is not significant, as scaling all Young’s moduli by the same factor produces the same dynamics. For completeness, we provide a list of the Young’s moduli and Poisson’s ratio used in this work, along with the speed of sound in the medium, defined as the longitudinal wave speed. The speed of sound is calculated using well known results from the theory of elasticity, giving $c_s = \sqrt{(K+\frac{4}{3}G)/\rho }$ in 3D and $c_s = \sqrt{E/\rho (1-\nu ^2)}$ in 2D [27].

Further details on the SPH code can be found in [14, 28] while the source code is available in LAMMPS [45] and LIGGGHTS [25].

Table 2 Elastic properties of grains

1.2 A.2 DEM technical specifications

The parameters of the DEM contact model are reported in Table 3. In all the simulations, the contact interaction is only normal, and hence there is no frictional interaction directly acting through the DEM model. It is worth noting that in spite of this, when two grains are in contact, some friction is introduced as a consequence of the discretization itself.

Table 3 Details of the DEM implementation

B Friction coefficient

As a result of the discretization, it is impossible to obtain perfectly smooth surfaces, although irregularities can be reduced by increasing the contact radius $r_c$, or the number of the points on the grain surface.

Fig. 11

Two different contact scenarios, corresponding to two different frictional behaviors. In (a), the contact force consist solely of the normal component, corresponding to the frictionless case. In (b), the boundary of the particles in touch "interlock", illustrating the maximum friction condition.

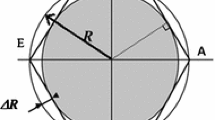
To estimate the friction coefficient, we start considering undeformed particles at the onset of the contact. We compute the friction coefficient as the ratio of the tangential over the normal components of the contact force between two points, $\mu _f = f_T/f_N$. This quantity is independent of the specific repulsive DEM contact model we choose and is defined by the geometrical parameters of the grain discretization. However, it does depend on the reciprocal orientation of the grains in contact, as sketched in Fig. 11. Keeping in mind that the friction coefficient depends on orientation, smoothly varying between zero and a maximal value when the interlocking between the asperities is more effective, we compute the maximum coefficient of friction.

The computation of the friction coefficient is a simple geometrical problem. Given a as the distance between two discretizaton points on the boundary of the same grain, and $r_c$ as the DEM contact radius of the discretization points in touch, then $\mu _f = \frac{1}{\sqrt{(4r_c/a)^2-1}}$. In our case, $r_c = a$ so we obtain $\mu _f = 1/\sqrt{15} \simeq 0.26$.

When particles are compressed, the arrangement of the discretization points changes, and consequently, the geometrical parameters involved in the computation of the friction coefficient. To estimate it, we start from the same scenario as before, but now considering a typical overlap between discretization points in a highly compressed configuration ($\phi \simeq 0.995$), where the distance between two contact points can be $r \simeq 1.6 r_c$, instead of $r \simeq 2 r_c$. In this case we obtain $\mu _f = \frac{1}{\sqrt{(2r/a)^2-1}}$, which gives approximately $\mu _f \simeq 1/\sqrt{9.9-1} \simeq 0.33$.

As explained in Appendix C.1,the distance between two neighboring discretization points is slightly different from the discretization length a. Nonetheless, this difference is small, and for the purpose of estimating the friction coefficient, we neglected it.

C Discretization algorithm

1.1 C.1 Discretization of a disk

We start by describing the discretization of a circumference, the extension to a circle is straightforward. The algorithm and the idea of the discretization are simple. In this study, we are interested in reproducing as accurately as possible the shape of the particles. For this reason, we choose an algorithm that respects as much as possible the geometry of the system we want to discretize. It is important to keep in mind that the external discretization points are interacting through a DEM potential, meaning that the points have an associated contact radius $r_c$. Hence, if we want to discretize a circumference of radius $R'$, we place the discretization points at distance $R = R'-r_c$. In the following, to keep the notation lighter, we will use R as the relevant radius. After the radius of the circumference R and the discretization pace a are defined, the code will determine the regular polygon, inscribed in the circumference of radius $R-r_c$, which side length $a'$ approaches a from above. The discretization points are then placed on the vertices of the polygon, hence at distance exactly R from the center of the ring. Obtaining as a discretization for a circumference the regular polygon inscribed in it.

A circle is then discretized as a series of concentric regular polygons. The vertices are placed at distance R from the center for the first one, $R-a$ for the second, $R-2a$ for the next one, and so on until the center of the circle is reached, where a particle is placed.

Eventually, the symmetry group $D_n$ of the polygon can be enforced, as it is the case in the presented simulations. For the compression of the disks, the symmetry of the rings is imposed to be $D_{8n}$ so that the points in the external circumference vary between 32 and 64, following multiples of eight, according to the size of the disk. In Fig. 2 is shown the case of a disk, discretized with symmetry $D_8$, where the approximation of the external circumference is made with a 64-sided polygon.

1.2 C.2 Discretization of a sphere

We describe first the discretization of a spherical shell, the algorithm for the sphere naturally follows from it. After the radius of the shell R and a discretization pace a are defined, the code places a series of circumferences, of different radius, parallel to each other, on the surface of the shell. Each couple of consecutive circumferences has distance which approaches a from below, and each circumference is discretized as described above. In this way we obtain a set of points, at fixed distance from the center, which distance with the nearest neighbor is always less than a.

To discretize a sphere of radius R, a series of shells are used. The first one of radius R, the second one $R-a$, the third one $R-2a$ and so on until the center of the sphere is reached.