1 Introduction

Natural disasters, such as rockfall events, pose a serious threat to people, especially in mountainous areas. Several works, such as [1,2,3,4], already describe how to simulate these events and discuss the appropriate modelling of protection structures. While [5, 6] use the coupling of the DEM and the FEM to analyse the interaction of rocks and the ground surface, [7] discusses different design strategies for flexible rockfall barriers.

Recently, the work of [8, 9] explained how to realize a multi-physics analysis of rock impact in an open-source code. The code that is used within this work is KRATOS [10,11,12,13]. Since this is an open-source code, it allows for further development by independent research groups and is publicly accessible. The development and use of open-source codes allows the reliable assessment of life threatening natural events for everyone and is of upmost importance for the safety of the society.

To model the impact scenario two different numerical methods are combined in a coupled simulation. The finite element method (FEM) is used to analyse the structural response to the impact, while the discrete element method (DEM) models and simulates the impacting objects. While the DEM represents a particle method [14,15,16], the FEM is concerned with the analysis of continuous, deformable bodies.

In contrast to continuum-based particle methods such as the material point method (MPM) [17, 18] or the particle finite element method (PFEM) [19, 20], the DEM describes single discrete particles, instead of a continuum, which is composed of particles. In the case of debris flows and avalanches, a continuum-based particle method such as MPM or PFEM would prove to be more useful. In the case of the simulation of rockfalls, the modelling of the impacting objects as discrete objects seems to make the most sense.

The DEM models the dynamics of spherical particles taking into account external forces such as gravity and contact with other particles or objects [14,15,16]. It can be used for many different particle shapes such as rectangles, cones, spheres and more; however, in this publication only spherical particles are considered. To describe more complex shapes, a set of spheres is connected within clusters. A cluster consists of several particles, which are used for contact detection and force evaluation. The mass and centre of gravity are described within the cluster shape and independent of the masses of the particles (for more information see [14, 15]).

Current state-of-the-art publications, such as [1, 3], use the FEM to model the geometry of the test objects. By using geometric objects such as surfaces and lines, the use of FEM in this case leads to complex and costly contact algorithms [16]. The use of spherical particles greatly simplifies contact detection and thus appears to be the more appropriate modelling method. Additionally, the general restriction of simple FEM geometries is alleviated since particle clusters can represent arbitrarily shaped objects.

The objective of this work is to show the applicability of the aforementioned coupling method and discuss the appropriate modelling of impacting objects. In contrast to standard finite element discretization of the impacting objects as provided in previous works, e.g. [1,2,3,4], the DEM in KRATOS uses clusters of single spheres to represent any desired, arbitrary shape. This allows a simple contact search but also raises the question how these clusters have to be defined to achieve adequate results. Since this work focuses on the appropriate modelling of the impacting objects, the application of the coupling algorithm and not on the exact analysis of detailed structural components, the results of a test resulting in an elastic structural response are used. Although large rockfall events often result in much higher impact energies, often generating plastic and possibly destructive structural responses, this behaviour is not considered for demonstrative simplicity.

From a formal point of view, the structure of the paper is as follows:

  • Section 2 briefly describes the underlying coupling theory and the respective components in this multi-physics simulation (see [8, 9] for detailed information).

  • Section 3 describes the experiment which will be used for validation and calibration.

  • Section 4 discusses the modelling of the numerical simulation used to replicate the experiment. Both the modelling of the structure itself and the modelling of the impacting object are discussed.

  • Section 5 presents the numerical results and explains each of the results in detail.

  • Section 6 finalizes this work with a conclusion and an outlook for future research.

2 DEM–FEM coupling

The general coupling of the two participating methods (DEM, FEM) was discussed in detail in recent publications such as [5,6,7, 15, 21]. In particular, [5,6,7] describe the possibility to apply the aforementioned coupling to analyse rockfall events modelling the interaction of the rock with the ground. Recently [8, 9] used the FEM to calculate the highly nonlinear structural response of protection nets to the extreme load cases of rockfall events (simulated by the DEM), allowing for a deeper understanding of the interaction of impacting objects with flexible tension structures.

Nevertheless, for the sake of completeness, a short introduction is given in the proceeding subsections expressing tensors with bold letters and scalar values with regular letters. A list of appropriate, more detailed publications on the respective topics is attached to the specific subsections.

2.1 DEM

As a particle method, the DEM is used to model single discrete particles. The movement of discrete particles can be effectively simulated, making DEM an advantageous method for modelling impacting objects. It offers the advantage that rigid objects of any shape can also be modelled as particle clusters, which greatly reduces the computational effort. This feature is used in this work to model the impacting objects.

Various contact laws may be formulated which can be applied to the case at hand. The contact of particles to arbitrary geometric objects such as points, lines and surfaces is always modelled in the present implementation as the contact of the geometric objects to a sphere. This sphere has a radius \(R_i\) and a geometrical centre \(\mathbf {C}_i\).

For the present work three variants are of particular interest (described in [21]), where \(d_e\) is used to express the smallest distance to the line element in contact. The geometric contact conditions are stated in Table 1.

Table 1 Geometric contact conditions
Full size table
Fig. 1
figure 1

Contact spherical particle—line [8, 21]

Full size image

The corresponding contact forces are calculated with the contact law [21], which is suitable for the respective application, and thus, the equation of motion is integrated based on Newton’s second law. In this study a Hertz–Mindlin spring-dashpot contact model (abbreviated as HM+D in [15]) is used. A sketch of the rheological contact model is shown in Fig. 2. The respective normal, tangent spring stiffness \(k_n\), \(k_t\) as well as the normal, and tangent damping coefficients \(c_n\), \(c_t\) are used to calculate the contact forces [9, 15, 21,22,23]. To restrict the maximum tangential force to the Coulomb’s friction limit the coefficient of friction \(\mu \) is applied.

Fig. 2
figure 2

DEM–DEM and DEM–FEM rheological models, adapted from [15]. a DEM–DEM. b DEM–FEM

Full size image

A detailed description of the contact algorithms, force evaluations, time integration, and other DEM-related topics would lie beyond the scope of this work. For a more detailed introduction to DEM see [14,15,16, 21,22,23,24].

2.2 FEM

The FEM is used in the context of this work to discretize the protective structure. As described in [25], the virtual work is set up with the involvement of the d’Alembert forces and the external virtual work \(\delta W_{\mathrm{ext}}\),

$$\begin{aligned} \begin{aligned} \delta W&= \int _{\varOmega _{0}} \varvec{\sigma }_{PK2}\cdot \delta \varvec{\varepsilon }_{\mathrm{GL}}~d\varOmega _{0} \\&\quad +\int _{\varOmega _{0}} \rho \dot{\mathbf {u}}\cdot \delta \mathbf {u}~d\varOmega _{0} - \delta W_{\mathrm{ext}} = 0. \end{aligned} \end{aligned}$$
(1)

As depicted in Eq. 1 the second Piola–Kirchhoff stress \(\varvec{\sigma }_{PK2}\), the work equivalent Green–Lagrange strain \(\varvec{\varepsilon }_{\mathrm{GL}}\), the density \(\rho \) as well as the degrees of freedom \(\mathbf {u}\) (here the displacements) and their second time derivative \(\ddot{\mathbf {u}} = \frac{\partial ^2\mathbf {u}}{\partial t^2}\) are integrated over the reference domain \(\varOmega _{0}\).

By evaluating Eq. 1 the following equilibrium equation results,

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {u}} + \mathbf {C}\dot{\mathbf {u}} + \mathbf {K}\mathbf {u} = \mathbf {f}_{\mathrm{ext}}, \end{aligned}$$
(2)

with the mass matrix \(\mathbf {M}\), the damping matrix \(\mathbf {C}\), the stiffness matrix \(\mathbf {K}\), and the external forces (the DEM contact forces in this context) \(\mathbf {f}_{\mathrm{ext}}\). Because of the very short time interval investigated in the field of rockfall simulation [4], explicit time integration is suitable for solving this system of equations, since small time steps are required to resolve the impact process with sufficient accuracy. This method does not require the complex solution of sometimes very large systems of equations. A diagonal mass matrix is used (point mass assumption) and Eq. 2 is solved with the help of Newton’s second law,

$$\begin{aligned} \ddot{\mathbf {u}} = \mathbf {M}^{-1}\left( \mathbf {f}_{\mathrm{ext}}-\mathbf {f}_{\mathrm{int}} - \mathbf {C}\dot{\mathbf {u}}\right) , \end{aligned}$$
(3)

using the internal forces \(\mathbf {f}_{\mathrm{int}}\) and the discrete nodal velocities \(\dot{\mathbf {u}}\).

2.3 Coupling procedure

The coupling procedure is described in detail in [8, 9]. The basic idea is the exchange of data between two stand-alone analyses. Figure 3 describes this idea. The respective steps can be summarized in the following enumeration (numbers relate to Fig. 4).

  1. 1.

    Solve DEM part, resulting in contact forces.

  2. 2.

    Transfer the forces with the help of a mapper [26] to the FEM part.

  3. 3.

    Solve FEM part, resulting in displacements, velocities and accelerations.

  4. 4.

    Transfer displacements, velocities and accelerations back to the DEM part.

  5. 5.

    If necessary: Calculate interface residuals [9, 27, 28].

  6. 6.

    If necessary: Repeat steps 1–5 until the interface residual reaches a given tolerance [9, 27, 28].

  7. 7.

    Advance in time.

Fig. 3
figure 3

Coupling interface DEM–FEM [8, 9]

Full size image

As known from other coupled multi-physics problems, such as fluid–structure interaction (FSI) [28], the direct explicit transfer of the interface data (forces, velocities, displacements) can lead to divergence problems in the staggered simulation. This problem is caused by large contact forces due to differences in velocities, acceleration, and highly different masses on both sides. In contrast to the weak coupling approach (direct exchange of data and subsequent proceeding in time [9]), the strong coupling approach, which is presented in [9] and depicted in Fig. 4, adds an additional iteration loop in each time step, which solves for the equilibrium between both numerical physics. This requires a Gauss–Seidel loop between DEM and FEM, which might need to be solved multiple times within one time step.

Fig. 4
figure 4

Strong coupling communication diagram [9]

Full size image

A more profound discussion of the aforementioned coupling scheme can be found in [8, 9].

3 Experiment

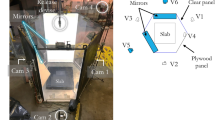
The experiment set-up is described below and depicted in Fig. 5. In the course of this work, only the required comparative data will be published, while the remaining data are not publicly accessible as property of Geobrugg. A standardized (SAEFL) concrete block was used, with a total weight of 180 kg (the concrete block weighs in itself 175 kg, the attached wire rope strap weighs 5 kg bringing the total weight of the block to 180 kg) and an edge length of 0.41 m impacts a \(3.9\times 3.9\,\hbox {m}^2\) DELTAX® G80/2 [29] (see Fig. 6) net which is spanned into a CTI frame with rigid boundaries (see [2] for a detailed description). The rigid boundaries are in this case 5/8” shackles connecting the mesh to the steel frame.

The block is dropped from a height of 2.0 m which results in an impact velocity of \(v=\sqrt{2.0\cdot 9.81\cdot 2.0}=6.261484\frac{\mathrm{m}}{\mathrm{s}}\). The same test is repeated twice, whereas (due to different pre-stresses) the initial sag, as a result of the dead load, varies from 0.05 to 0.10 m (labelled with exp_1, respectively, exp_2 hereafter). The tests are laid out to produce a rebound of the block without failure of any mesh wire.

Three main parameters are obtained from these tests by the means of a high-speed camera and an internal acceleration measuring device. The high-speed camera records at a resolution of \(1280\times 1024\) and a frame rate of 500 fps. The acceleration sensor is composed of a built-in triaxial accelerometer with a range up to 500 g and a sampling rate of 20,000 Hz and is incorporated in the test block. Deflection, i.e. the vertical displacement or sag of the mesh after impact, is measured directly through the analysis of the videos obtained from the high-speed camera. The block’s velocity is calculated by following the block’s trajectory over time in the high-speed video, based on the principle dx/dt. The velocity before impact is compared between the computed one, as explained above, and the result from the video analysis, to ensure the plausibility of the video analysis. The analysis of the accelerations obtained by the accelerometer yields the force evolution over time.

Fig. 5
figure 5

Photograph from the testing site in Walenstadt, Switzerland, showing the CTI frame

Full size image
Fig. 6
figure 6

Technical drawing of the DELTAX® G80/2 [29]

Full size image

The repeatability of the tests is deemed to be given. Five tests were carried out in total. The test block and the drop height are the same for all tests, i.e. the input parameters are kept constant. Three parameters are varying slightly, but all considered to be in a negligible range. The dimensions of the net panel itself is varying by +/\({-}\) 5%. The tensioning force when installing the net panel in the test frame is not directly measurable, this leads to a variation of the sag of +/\({-}\) 5 cm. Finally, the tensile strength of the material is varying between \(1700\,\hbox {N/mm}^2\) and \(2030\,\hbox {N/mm}^2\), with a mean value of \(1860\,\hbox {N/mm}^2\). This could be of importance when analysing the breaking load, although this variation is also deemed to be negligible in the practical application, since the lowest value is always considered. The tensile strength is of minor importance for this work as no damage in the mesh is observed.

4 Numerical modelling

4.1 Structural modeling

Due to the set-up of the experiment and the fine mesh of the used protection netting (see Fig. 6) a simplification of the net to a closed, homogeneous surface suggests itself. This assumption simplifies the structural modelling and allows the use of two-dimensional finite elements. Publications such as [1, 3] suggest a shell element to be used. While the advantages are clarified in the publication cited, this would mean an overhead for the underlying experiment. Due to its simplified set-up a membrane element [25] is used in this work. Carrying only in-plane stresses and omitting rotational nodal degrees of freedom an initially plane geometry possesses zero stiffness. As a remedy a minor pre-stress is applied to the structural model (see Table 2) to provide a non-singular stiffness matrix at the beginning of the simulation.

Table 2 Numerical properties for the structure
Full size table

The Young’s Modulus is tuned to the given value in Table 2 in order to achieve an initial sag due to dead load of \(\approx 0.05\,\hbox {m}\) (see Fig. 7), as described in the experimental set-up.

Fig. 7
figure 7

Initial static analysis to obtain equilibrium position for dead load (plot scaled by factor \(\times \) 10)

Full size image
Fig. 8
figure 8

Cluster refinement (1,8,56,296,1280,5408,22,232)

Full size image

With respect to the technical data sheets available on [29] the thickness of the membrane element is set to \(0.008\,\hbox {m}\), whereas the density of the membrane is derived from the provided weight of \(0.65 \frac{\mathrm{kg}}{\hbox {m}^2}\) DELTAX® mesh standard roll:

$$\begin{aligned} \rho = 0.65~\frac{\mathrm{kg}}{\mathrm{m}^2} / 0.008~\hbox {m} = 81.25~\frac{\hbox {kg}}{\hbox {m}^3}. \end{aligned}$$
(4)

As described in the experimental set-up in Sect. 3 the two tests that are investigated in this work show a rebound of the impacting sphere and no damage. Due to the observed structural response a simple elastic material model [25] and a Poisson’s ratio of \(\nu =0\) is applied in this work. In the course of this work it is shown that structural models with the right simplifications allow a correct assessment of the global behaviour. If a detailed analysis of the deformation behaviour and failure behaviour of individual structural elements is to be carried out, more attention must be paid to structural modelling. Publications such as [3, 30] a contain a very detailed description of the modelling and the state of the art.

4.2 Impacting object

In contrast to preceding works, such as [1, 2], this work proposes to model arbitrary objects with the help of discrete spherical element clusters. The advantage over standard finite element discretized objects is the simplified contact detection between arbitrary boundary objects and single spheres contained in the cluster [21].

As depicted in Fig. 8, the standardized experiment object is modelled with seven levels of refinement. Ranging from a representation as a single sphere to a detailed geometrical description with up to 22,232 spheres. Special algorithms are needed to create such refined cluster files. This work uses the sphere-tree algorithm described in [31, 32] as it is available in an online toolkit [33].

The density of the respective cluster is fitted to obtain a total cluster mass of 180 kg (see Sect. 3). Important DEM parameters, such as the coefficient of restitution \(\varepsilon \) [22] and the Young’s Modulus of the particle \(E_{\mathrm{p}}\), are varied with respect to Table 3 with their influence studied. The range in which \(E_{\mathrm{p}}\) is selected is based on experience gained from previous simulations.

Table 3 Cluster versions (visualized in Fig. 8)
Full size table

5 Validation

The experiment described in Sect. 3 produced results which are used to validate the proposed coupling algorithm [8, 9] and to investigate the influence of discrete element cluster refinement, time step, coefficient of restitution \(\varepsilon \), and the Young’s Modulus \(E_{\mathrm{p}}\) on the final solution of displacement, velocity, reaction forces \(F_{\mathrm{R}}\) and contact forces \(F_{\mathrm{C}}\). Furthermore, it is shown that simplified structural modelling allows an appropriate evaluation of the global structural behaviour.

Each of the aforementioned clusters, described in Table 3, is used in the numerical impact simulations. If not mentioned otherwise, a time step value of \(d_t = 10^{-5}\,\hbox {s}\) is used. The results with the label “small dt” follow from a simulation with \(d_t = 10^{-6}\,\hbox {s}\).

Although the simulated system set-up is more similar to exp_1, the experimental results for exp_2 are added to the result plots as it represents an experiment with the same impact velocity and the same of mass of the impacting object. The difference in the initial sag is a results of the test set-up and can hardly be controlled; thus, it allows error zones to be added in the result plots to show the variability of the experimental results.

Fig. 9
figure 9

Displacement of impacting objects

Full size image

5.1 Displacement

The simulated displacement values of the impacting object are compared to the experiment results. Figure 9 shows that the simulation results lie between the two experiment results.

It is noticeable that the refinement of the cluster shows a large influence as soon as the number of spheres is larger than one (\(c_1\)). To explain this behaviour the simulation is visualized at the time of maximum displacement in Figs. 11, 12, 13, 14, 15, 16 and 17 (see Fig. 10 for comparison to the experiment). Due to the fact, that the contact forces in DEM are calculated with the help of spring-dashpot models [15, 22, 23] the single sphere with one large radius experiences an indentation which is larger than it is for the clusters with more (smaller spheres). This has additional effects too, which become clear in Figs. 18 and 19. The single particle has a larger indention (Fig. 11) and thus decelerates slower (Fig. 18). This finally leads to lower contact/reaction forces and a longer duration of load application, as visualized in Fig. 19. The same behaviour is observed when decreasing the time step (see Fig. 9, label “c1 small dt”) and thus can be concluded to be a problem of the very rough representation of the original geometry as a single sphere.

Regarding the remaining refinement levels, a good agreement with the exp_1 is shown, as the initial sag of the numerical model due to dead load matches with the initial sag of the first experiment set-up exp_1 of 0.05 [m], while the displacements of all simulation results are within the error zone.

5.2 Velocity

Similar to the observations in Sect. 5.1 all cluster refinement levels again show good agreement with the experiment results in Fig. 18. The exception is again the single sphere which decelerates more slowly due to its larger indention (Fig. 11).

Fig. 10
figure 10

Maximal deflection, experiment

Full size image
Fig. 11
figure 11

Maximal deflection, cluster 1

Full size image
Fig. 12
figure 12

Maximal deflection, cluster 2

Full size image
Fig. 13
figure 13

Maximal deflection, cluster 3

Full size image

5.3 Forces

Lastly, the forces obtained from the numerical simulation are compared to the experiment results. Figure 19 shows the reaction forces in the structure as a sum over all boundary nodes. A good agreement for all cluster refinements >c_1 can be observed for both the force value as well as the contact time. Similar to the observations in the previous sections the roughest object representation performs poorly. The maximum force is below the experimentally obtained value and the time in which the object is in contact with the structure is too large. c_1, as the roughest object representation, is a single sphere, poorly representing the correct object shape. With regard to the forces, it can also be said that a more precise modelling of the exact object geometry plays a major role, even if the impact, as in this case, takes place without rotations.

Fig. 14
figure 14

Maximal deflection, cluster 4

Full size image
Fig. 15
figure 15

Maximal deflection, cluster 5

Full size image
Fig. 16
figure 16

Maximal deflection, cluster 6

Full size image
Fig. 17
figure 17

Maximal deflection, cluster 7

Full size image
Fig. 18
figure 18

Velocity of impacting objects

Full size image
Fig. 19
figure 19

Reaction forces \(F_{\mathrm{R}}\left( t\right) \)

Full size image
Fig. 20
figure 20

Reaction forces \(F_{\mathrm{R}}\left( t\right) \) and contact forces \(F_{\mathrm{C}}\left( t\right) \) for c1

Full size image

One more interesting behaviour that can be observed in the simulations is the difference between reaction forces \(F_{\mathrm{R}}\) (structural response, FEM) and contact forces \(F_{\mathrm{C}}\) (cluster interaction with boundary, DEM). Figure 20 illustrates the difference for a varying time step size, which is shown in Table 4. For simplicity, cluster c1 is used. The theoretical difference should be described by only the dead load of the protection net. Nevertheless strongly oscillating contact forces are observed for rather larger time steps, while the reaction forces remained smooth.

As visualized in Fig. 20, the contact forces \(F_{\mathrm{C}}\) for the largest time step (s1) strongly oscillate, while the respective reaction forces \(F_{\mathrm{R}}\) develop smoothly and exactly in the middle of the oscillations. This behaviour can also be observed for the next smaller time step (s2) as soon as the maximum force is reached. For the smallest time step (s3) the described behaviour is almost negligible.

Considerably large contact forces in combination with large time steps that are too big to resolve the contact interaction can lead

Table 4 Different time steps used for the simulation shown in Fig. 20
Full size table
Fig. 21
figure 21

Comparison of relative computational time

Full size image

to particles losing contact in one time step only to regain contact again in the next. As a result of this fretting, oscillating contact forces \(F_{\mathrm{C}}\) are generated. Since the contact points are located locally in the centre of the structure and are at some distance from the edge nodes at which the reaction forces are calculated, the influence of the initial oscillations on the reaction forces is negligible if the time steps are sufficiently small. With regard to the results in Fig. 20, it is clear that the correct time step is chosen because the results of the reaction forces for s2 and s3 match. The strong oscillations of the contact forces have only local influences due to the choice of a small time step but make a comparison to experimentally obtained results difficult. For this reason the reaction forces \(F_{\mathrm{R}}\) are chosen for comparison.

5.4 Results

With respect to the relative computational time for each simulation, as shown in Fig. 21, the effect of additional particles is negligible under \(\approx 10^3\) spheres. Additionally, considering the results in Sect. 5, the cluster version c5 is recommended for usage. It represents the best compromise between accuracy and computing effort, while also properly representing the geometry (see Fig. 8). It is also expected that the fine representation of the impacting object influences the simulation results favourably if the rotation of the object plays a crucial role (see also [8], where a simplified Attenuator is simulated by using an arbitrary shaped rock object).

The computational time for the simulation of the cluster c5 is discussed as an example. A total time of \(1108 s \approx 18.5\,\hbox {min}\) with an increased time step of \(d_t = 2\cdot 10^{-5}\,\hbox {s}\) for a total simulation time of \(0.3\,\hbox {s}\) is required. With respect to Fig. 9, the cluster leaves the reference axis of origin at \(\approx 0.25\,\hbox {s}\); thus, the simulation time could be further reduced by \(\approx 17\%\). The CPU system settings for this simulation are an Intel(R) Xeon(R) CPU E5-2623 v4 @ 2.60 GHz.

6 Conclusion

This contribution demonstrates that using the DEM for modelling an impacting object as well as simulating the interaction with the FEM structure is expedient. It allows modelling of any desired shape without requiring complex contact models between surfaces, lines and vertices. The strategy of using clusters of single spheres simplifies these contact models to a simple sphere contact detection. As shown in this work, this feature can be used to simulate standardized test objects, as illustrated in Fig. 8, as well as arbitrary shapes (see Fig. 22).

In cases of real rockfall scenarios it can be beneficial to simulate different, varying rock shapes to also capture the influence of sharp edges, and progressive fragmentation which result in a reduction of kinetic energy [6]. Additionally smaller sizes of impacting objects can cause a bullet effect [4]. The use of discrete element clusters in combination with cohesive forces, as described by [15], allows the cluster to break, reaching limit stresses, and ultimately allows modelling of cluster fragmentation.

Additionally a detailed discussion of the comparison between simulation results and test results highlights that a coarse description of the impacting object renders poor results (Figs. 9, 18, 19), while a reasonable representation of the impacting object geometry can be achieved without significantly increasing computational time (Fig. 21). The simplification of the structure to a closed surface (see Sect. 4.1) and the appropriate modelling of the impacting object (see Sect. 4.2) are confirmed to strike a good compromise between computational time and the approximation of the physically correct structural response (see Figs. 9, 18, 19). The relatively simplified modelling of the structure was shown to predict reasonably accurate global deformation behaviour and reaction forces. In combination with the high-performance modelling of the impacting objects as spherical clusters, this approach has advantages over current publications that use very complex structural models and thus require a lot of computing time. The contact forces and reaction forces of the structure were also compared. It was shown that relatively large time steps can lead to oscillating contact forces, which can be counteracted with smaller time steps restricting its influence on local parts of the structure. Although the contact forces can oscillate strongly, the reaction forces are relatively smooth. In addition to the elastic tests considered in this paper, experiments that lead to plastic deformations or even damage to the mesh were carried out too. It is expected that the application of plasticity constitution laws and damage models in the FEM part will also allow the reproduction of the results of the other experiments.

Fig. 22
figure 22

Arbitrary rock shape modelled with discrete element cluster

Full size image

The accurate assessment of life threatening natural events (such as rock slides, mud flow, and strong wind events) is of great value to society, with the open-source KRATOS [10, 12, 13] multi-physics software offering advanced analysis capabilities free of charge for all. The code is publicly accessible via a GitHub repository [34] with an installation guideline provided. KRATOS is designed in C++ and includes a Python interface to facilitate the advanced development and simulation. With easy access and a community where participation is highly appreciated, there is a great potential to further advance these simulation technologies. Such open-source projects are of upmost importance for the society, especially in times of extreme weather and environmental events.