A mathematical model for thermal expansion coefficient of periodic particulate composites

Abstract

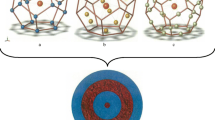
In this work, the authors introduce an octahedral body centered model transformed into a nine-layer spherical model, to simulate the periodic microstructure of particulate composites. This model takes into account the vicinity of internal and neighboring particles in the form of their deterministic configurations inside the matrix, along with the concept of interphase on the thermomechanical properties of the overall material. The latter is assumed to be homogeneous and isotropic. Next, by the use of this model, in association with classical elasticity approach, a closed form expression to calculate the thermal expansion coefficient of this category of composites is derived The theoretical predictions were compared with experimental results as well as with theoretical values yielded by formulae derived from other workers and they were found to be in good agreement.

Appendix

Let us remark some reliable theoretical formulas referring to thermal expansion coefficient of particulate composites.

• 1. Blackburn equation

  $$\begin{aligned} \gamma _C =\gamma _f +\frac{\frac{3}{2}\left( {1-\nu _f } \right) U_m \left( {\gamma _m -\gamma _f } \right) }{\frac{1}{2}\left( {1+\nu _f } \right) +U_m \left( {1-2\nu _f } \right) +\left( {1-2\nu _m } \right) \frac{E_f }{E_m }U_f } \end{aligned}$$

  (A1)

  where $\gamma$ is the cubic thermal expansion coefficient with $\gamma$ = 3$^{\alpha }$

• 2. Turner equation

  $$\begin{aligned} \gamma _C =\frac{U_m \cdot \gamma _m \cdot k_m +U_f \cdot \gamma _f \cdot k_f }{U_m \cdot k_m +U_f \cdot k_f } \end{aligned}$$

  (A2)

  where k denotes the bulk modulus

• 3. Kerner equation

  $$\begin{aligned} \gamma _C =\gamma _f U_f +\gamma _m U_m +\gamma _f U_m \left( {\gamma _m -\gamma _f } \right) q \end{aligned}$$

  (A3)

  where $q=\frac{\frac{1}{k_m }-\frac{1}{k_f }}{\frac{U_f }{k_f }+\frac{U_m }{k_m }+\frac{3}{4G_m }}$ The term containing the parameter q denotes the deviation of the values obtained from this expression when compared with the inverse mixing law.

• 4. Wang and Kwei equation

  $$\begin{aligned} \gamma _m =\gamma _m -U_f \cdot q\cdot \left( {\gamma _m -\gamma _f } \right) \end{aligned}$$

  (A4)

  where $q=\frac{\left( {\frac{3E_f }{E_m }} \right) U_f }{\frac{E_f }{E_m }\left[ {2U_f \left( {1-2\nu _m } \right) +1+\nu _m } \right] +2U_m \left( {1-2\nu _f } \right) }$

• 5. Tummala–Friedberg equation

  $$\begin{aligned} \gamma _m =\gamma _m -U_f \cdot q\cdot \left( {\gamma _m -\gamma _f } \right) \nonumber \\ q=\frac{\frac{1+\nu _m }{2E_m }}{\frac{1+\nu _m }{2E_m }+\frac{1-2\nu _f }{E_f }} \end{aligned}$$

  (A5)

• 6. Fahmi–Ragai equation

  $$\begin{aligned}&\alpha _C \nonumber \\&\quad =\alpha _m -\frac{3U_f \left( {\alpha _m -\alpha _f } \right) \left( {1-\nu _m } \right) }{2\left( {1-2\nu _f } \right) \left( {1-U_f } \right) \frac{E_m }{E_f }+2U_f \left( {1-2\nu _m } \right) +\left( {1+\nu _m } \right) }\nonumber \\ \end{aligned}$$

  (A6)