1 Introduction

Electric vehicles (EVs) have significantly lower mileage cost, reduced air pollution, less petroleum dependence, and better performance over conventional internal combustion engine (ICE) based vehicles [1]. Energy storage system (ESS) is the key factor in EV performance and reliability [2] as well as the main limiting factor during their commercialization process [3]. Due to the heavy, costly and bulky nature of a conventional ESS, EV characteristics, such as mileage is limited [4]. Although, the benefit of using EVs over ICE vehicles is clear in terms of fuel economy and pollution. However, the short service life of ESS and its replacement costs are the limiting factor for commercialization of EVs [5]. With the ongoing development of batteries in terms of increasing the capacity while reducing costs, EVs are becoming popular [6]. As a result, more and more efforts are devoted to improve ESS performance [7, 8].

The conventional ESS (battery or ultracapacitor(UC)) has either high energy or high power specifications [9]. Typically, the designer should oversize either the battery or UC, in order to meet both the energy and power demands of the EV, which is not practical due to the increase of cost, size and weight of the system [10]. Therefore, high energy/power characteristics of the battery/UC are combined to form a new ESS and provide the demand energy/power of the vehicle [11]. This provides an ESS with low cost and high performance while reducing the weight and improving the battery lifetime [12]. Recently, the idea of coupling battery and UC as a hybrid energy storage system (HESS) is proposed in order to moderate current stresses and peaks of the battery. This enables the designer to employ a smaller battery at lower cost while improving its lifetime [10, 13].

The HESS performance is strongly affected by its power distribution system (PDS) [14, 15]. Various HESS power distribution strategies are developed in recent years [16], and this field is getting more and more attention. Besides, there are limited reports on frequency-based control strategies. A dynamic programming strategy is developed in [17] for power distribution between battery and UC. This strategy develops an optimum controller for a specific driving cycle and is useful for off-line applications. Simple controllers such as battery-based [18] and UC-based [19] power management strategies for HESS are proposed, which are based on the battery and UC threshold levels (maximum and minimum power capacities). These controllers are online and show good performance.

A model predictive controller for power management of a plug-in hybrid EV with a hybrid ESS is designed in [20]. A cascade and adaptive control strategy is proposed for load compensating of a battery/UC HESS [21]. Adaptive HESS controller is proposed in [22, 23]. Other power management strategies are reported in the literature, such as fuzzy [24], optimal [25], mode decomposition [26], model predictive [27], dynamic programming [28], and neural network [29] strategies. Recently, the authors present a method based on the state of available power (SoP) and predict the power limitations for a given time frame in the future [30]. It is shown that the battery lifetime is improved by 2.6 times.

The basic idea of a frequency-based power management strategy is to moderate the battery current. The UC is assigned to provide the high frequency portion of the demand power, while the battery supports the remaining part. Wavelet filter is a powerful yet simple energy management method employed for different applications. The use of wavelet in energy management system for fuel cell vehicle [31], wind power [32], photovoltaic (PV) system [33], and wind-PV hybrid power [34] are reported. A frequency-based power management strategy is proposed for the HESS using Fourier method for a periodic pulsed current load [35].

This paper presents a new HESS power management (frequency-based) system to control the battery current using wavelet filter. A three-level Haar wavelet filter is employed. As a case study, powertrain modeling of an electric motorcycle is introduced in the Section 2. Section 3 discusses the HESS design procedure. A lifetime model for the Lithium iron phosphate (LiFePO4) battery, UC model, and HESS costs are discussed. Section 4 introduces the HESS power management. At first, a conventional UC-based power management is introduced, followed by SoP power management system. The wavelet-based power management system is discussed afterwards. Section 5 discusses the principles and tuning of power management optimization. Results and conclusion are presented in Sections 6 and 7.

2 Electric motorcycle modeling

An electric motorcycle (AVITA) has been designed and manufactured at Sharif University of Technology, Tehran, Iran. The high voltage bus of AVITA is provided by the batteries. Recently, the conventional Ni-MH batteries employed in EVs are replaced by Lithium-based batteries [36]. Particularly, the LiFePO4 battery is suggested to be a suitable option to be employed in EVs due to the good chemical and thermal behavior as well as its low cost [37]. A capacity depletion behavior and lifetime modeling of this battery are proposed in [17]. The battery cell of the electric motorcycle is “high capacity LFP26650P power cell”. The main characteristics of the electric motorcycle and the main specifications of its powertrain are listed in Tables 1 and 2, respectively.

Table 1 Main characteristics of electric motorcycle
Full size table
Table 2 Main specifications of the electric motorcycle powertrain
Full size table

Figure 1 shows a schematic power flow model of the driver, electric motorcycle powertrain model, vehicle dynamics, and the storage section. The core of the powertrain model is similar to that presented in [38]. This modeling platform has been used for hybrid electric [39], hybrid flywheel [40] and hybrid hydraulic [41] powertrain simulation and design. The results show that the developed powertrain passes the criteria, some of which are listed in Table 3.

Fig. 1
figure 1

Schematic power flow model of the electric motorcycle with ESS and HESS

Full size image
Table 3 Design criteria of electric motorcycle powertrain
Full size table

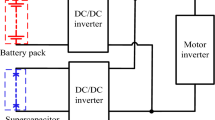
Figure 1a shows the electric motorcycle equipped with ESS, where the demand and actual ESS power are provided by the ESS, e.g. the battery. On the other hand, Fig. 1b shows the electric motorcycle equipped with HESS. The power demand is split between the battery and UC. A portion of the demand power (μ) is provided by the UC, while the rest of the demand power (1 − μ) is provided by the battery, where 0 < μ < 1. In the next section, different HESS architecture and power management systems are introduced and discussed.

3 HESS design

3.1 Battery lifetime model

The modeling and calculation of the state of charge (SoC) for the battery and UC are important while evaluating the HESS [42]. The generalized LiFePO4 battery life model is reported in [43], and is given by (1).

$$Q_{loss} = B\exp \left({\frac{{ {31700 + 370.3 \times C_{rate} } }}{{ {RT} }}}\right) \left( {A_{h} } \right)^{0.55}$$
(1)

where Qloss is the percentage of capacity loss; B is the pre-exponential factor depending on the Crate, which is the ratio of battery current to the battery capacity; R is the gas constant; T is the absolute temperature; Ah is the Ah-throughput expressed as Ah equals to cycle number multiplied by DoD multiplied by full cell capacity. This equation is proposed in [44]. The values of B at different Crate are listed in Table 4 [43].

Table 4 Values of B at different Crates
Full size table

The life capacity Ah which is a function of the current for the LiFePO4 battery cell with 2.6 Ah in each battery current is obtained using (1). And it is listed in Table 5 [17]. The life capacity is defined as the amount of charge that the battery can provide at a specific current before its capacity loss reaches 20% [17].

Table 5 Life capacity at different battery current
Full size table

For analyzing the vehicle performance, “driving cycles” are employed, where the vehicle speed is reported for a specific period of time to demonstrate a certain driving pattern. Generally, standard driving cycles are employed to estimate fuel consumption, vehicle emission and traffic assessment. It is shown that the performance of ESS or HESS depends on the aggressiveness of the driving cycle [45]. Therefore, in order to design and size the HESS, a specific driving cycle is considered to achieve the optimized battery size and associated costs.

The driving cycle capacity loss is given by [17]:

$$Q_{loss,DC} = \sum\limits_{k = 0}^{{t_{DC} }} {\frac{{I_{k} \frac{{{\text{d}}t}}{3600}}}{{L_{C} \left( {I_{k} } \right)}}}$$
(2)

where Ik is the battery current at the kth time step, and k is in the range of (0, driving cycle duration or tDC); dt is the time step of the calculation; LC is the life capacity and is a function of Ik determined by Table 5. Equation (3) calculates the 10-year capacity loss Qloss,10y [17]. It is a merit of how much loss is introduced to the battery. The obtained value from (3) is rounded up to the next integer, which shows the number of battery replacements, assuming the obtained value is greater than 1. Assuming consistent daily travel itineraries, the driving cycle capacity loss is divided by the driving cycle duration, multiplied by 3600 (to convert seconds to an hour), multiplied by 8 (to convert hours to a working day), multiplied by 250 (to convert working days to a working year) and then multiplied by 10, to estimate the 10-year capacity loss.

$$Q_{loss,10y} = Q_{loss,DC} /t_{DC} \times 3600 \times 8 \times 250 \times 10$$
(3)

Battery lifetime is expressed by (4). The factor of “0.2” is used, since the battery needs to be replaced once it reaches the 20% of its capacity.

$$T_{{life,bat}} = 0.2\frac{{C_{bat} }}{{Q_{loss,DC} }}\frac{{t_{DC} }}{3600 \times 8 \times 250}$$
(4)

where Cbat is the battery capacity in Ah.

3.2 UC model

Table 6 lists the UC module characteristics. Compared with the LiFePO4 battery, power specification of the UC (14.4 kW/kg) is much larger than that of the battery (1.53 kW/kg), and the energy specification of the UC (4.00 Wh/kg) is much smaller than that of the battery (134.55 Wh/kg).

Table 6 UC module characteristics
Full size table

3.3 HESS cost

The ESS cost is a major obstacle which should be overcome to make the EVs to be viable. Studies discuss the market trends and roadmaps for ESSs which show ongoing characteristics improvement and reduced costs. On the other hand, the reported studies and the number of patents on ESSs are growing fast in recent years.

The costs associated with LiFePO4 batteries, UCs and DC/DC converters are reported in literature. The configuration of the proposed HESS is “active topology” [7] with one DC/DC converter.

The cost of HESS for a 10-year period is calculated as:

$$C_{HESS,10y} = C_{ceil} {Q_{loss,10y} } \times 2.5 \times 500 + 12 \times 50 + 0.027 \times 15000$$
(5)

The following assumptions are made: a 2.5 kWh battery is used with the associated cost of 500 $/kWh. A 12 kW DC/DC converter is employed with the associated cost of 50 $/kW. A 0.027 kWh UC at the cost of 15000 $/kWh is used.

4 HESS power management

The HESS power management strategy strongly affects its performance [46]. In this paper, a wavelet-based power management based on the frequency of the demand current is developed to moderate the battery current fluctuations. The design targets are the battery lifetime and vehicle fuel consumption.

4.1 UC-based power management

Each HESS needs a power distribution control strategy (PDCS). The UC-based strategy is a conventional, yet simple PDCS which is in [18, 19]. A UC-based PDCS is proposed in [17]. At the beginning, the UC power is set to the demand power (PUC= Pdem). However, the UC power is limited by two bounds: the minimum and maximum levels of UC power, PUC,min and PUC,max, respectively. If there is any demand power left, which the UC could not provide, it would be supplied by the battery (Pbat= Pdem− PUC). Similarly, the battery power is limited by two bounds: the minimum and maximum levels of battery power, Pbat,min and Pbat,max, respectively.

4.2 SoP management

Another approach for power distribution management of HESS is based on the SoP, which is predicted power limits for a pre-defined time frame in the future. In other words, the energy storage power limitations are predicted for a certain period of time, in order to prevent it from violating maximum/minimum voltage and state of charge (SoC) constraints. Although the idea is not new [47], it is getting more attention recently [30, 48, 49]. Besides a few studies, this concept is rarely used along with the UC [30]. SoP-based PDS is in [30].

The maximum discharge power and minimum charge power based on the SoP is given by (6) and (7), respectively.

$$P_{UC,\hbox{max} }^{dis,SoP} = I_{UC,\hbox{max} }^{dis,tot} \left\{ {V_{OC,UC} (SoC_{UC} - I_{UC,\hbox{max} }^{dis,tot} \frac{\Delta t}{{C_{UC} }}) - R_{in,UC} I_{UC,\hbox{max} }^{dis,tot} } \right\}$$
(6)
$$P_{UC,\hbox{min} }^{chg,SoP} = I_{UC,\hbox{min} }^{chg,tot} \left\{ {V_{OC,UC} (SoC_{UC} - I_{UC,\hbox{min} }^{chg,tot} \frac{\Delta t}{{C_{UC} }}) - R_{in,UC} I_{UC,\hbox{min} }^{chg,tot} } \right\}$$
(7)

where \({\Delta t}\) is the specific time frame; SoCUC and VOC,UC are the SoC and open circuit voltage of UC during each time frame, respectively; CUC and Rin,UC are the capacitance and internal resistance of the UC, respectively; and \({I}\,^{dis,tot}_{UC, \text{max}}\) and \({\Delta t}\)\({I}\,^{chg,tot}_{UC, \text{min}}\) are the maximum UC current limits for the discharge and charge modes, respectively.

Detailed work of Section 4 can be found in [30].

4.3 Wavelet-based power management

The wavelet-based power management system is developed based on the frequency of the demand current to reduce the fluctuations of the battery current. A proper frequency filter is required for power management of the HESS. In this paper, the wavelet filter is used to distribute power between the battery and UC. The ESS demand power is analyzed by the wavelet filter and is divided into the high and low frequency parts. The UC provides the high frequency part, even if the demand power is lower than the maximum continuous power of the battery. The remaining part (low frequency one) is delivered by the battery.

Equation (8) presents the Morlet-Grossmann definition of the continuous wavelet transform (CWT) for a one-dimensional signal.

$$W\left( {\lambda ,u} \right) = \int\limits_{R} {x\left( t \right)\frac{1}{\sqrt \lambda }\psi } \left( {\frac{t - u}{\lambda }} \right){\text{d}}t\;\;\;\;\;\lambda > 0,u \in R$$
(8)

where t is the time; u is the location; W is the wavelet coefficient; x is the initial signal; λ is the size factor; and ψ is the mother function.

The reverse transform of continuous wavelet for reconstruction of the original signal x(t) is given by:

$$x\left( t \right) = \frac{1}{{K_{\psi } }}\mathop \int \limits_{{R^{ + } }} \mathop \int \limits_{R} W\left( {\lambda ,u} \right)\frac{1}{\sqrt \lambda }\psi \frac{t - u}{\lambda }\frac{{{\text{d}}\lambda {\text{d}}u}}{{\lambda^{2} }}$$
(9)

where Kψ is a constant value.

One of the most well-known mother wavelets is Haar wavelet, which has the shortest filter length in time domain compared with other wavelet basis. Haar is the simplest wavelet, which is equal to its inverse [50]. Therefore, the Haar wavelet function is the fastest for calculations and makes the decomposition calculations much simpler compared with the other basis due to the realization of wavelet transform strategy in a real-time situation [51]. In this paper, the Haar wavelet filter presented by (10) is employed for the decomposition of the demand power to distribute it between the battery and UC.

$$\psi (t) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {t \in [0,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})} \hfill \\ { - 1} \hfill & {t \in [{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2},1)} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(10)

Unlike CWT, the discrete wavelet transform (DWT) is employed to decompose a discrete signal into different resolution levels. The DWT and its inverse representations are given by (11) and (12), respectively.

$$\begin{aligned} W\left( {\lambda ,u} \right) = \int\limits_{R} {x\left( t \right)\frac{1}{\sqrt \lambda }\psi \frac{t - u}{\lambda }} {\text{d}}t \\ \lambda = 2^{j} ,u = k2^{j} ,j,k \in Z \end{aligned}$$
(11)
$$x(t) = \sum\limits_{j \in Z} {\sum\limits_{k \in Z} {W\left( {j,k} \right)\psi_{j,k} (t)} } \,$$
(12)

By using the Haar-wavelet-based N-channel filter bank [52], the input signal x(t) is decomposed by a low-pass filter H0(z) and high-pass filters Hk(z), k = 1,2,…,N − 1, into subband channels with the signal at that particular subband channel. The reconstruction filters Gk(z), k = 1,2,…,N − 1 are used for signal reconstruction [51].

The optimal level of wavelet decomposition should be chosen properly in order to meet the calculation simplicity and frequency requirements for a real-time system. For each wavelet decomposition level, the results are calculated and compared with the other cases to choose the best number of levels. Consider N = 2, then the decomposition and reconstruction filters become [H1(z), H0(z)]T and [G1(z), G0(z)]T, respectively.

The three-level Haar wavelet decomposition and reconstruction is employed. The down-sampling and up-sampling methods are used in the decomposition and reconstruction processes, respectively. The data size decreases by half in down-sampling operations while it doubles in the up-sampling operations [51].

Using the multilevel Haar wavelet filter, the electric power demand of the vehicle is decomposed to the smooth slow-variation power signal x0(n) and the transients (x1(n) + x2(n) +…+ xN(n)) power signal. The obtained power signals are distributed between battery and UC using the wavelet-based power management system.

5 Principles and tuning of power management optimization

Figure 2 shows the proposed power management system which is based on an initial decision on how to employ the wavelet controller. The demand power is received by the power management system. If the demand power is greater than a certain power level (activation power of the wavelet controller, pp), the wavelet controller is engaged and determines the battery and UC power shares accordingly.

Fig. 2
figure 2

The proposed power management system

Full size image

However, if the demand power is less than the activation power, a simple UC-based controller is engaged and the battery and UC powers are determined. The determined values are then checked with the battery/UC limits to make sure they do not exceed the power limits.

In order to determine the optimal level of wavelet decomposition as well as the optimal activation power, an optimization procedure is established as follows. Integer genetic algorithm is employed [53]. The target is defined as the battery capacity loss during one driving cycle (Qloss,DC), which needs to be minimized. Design variables are the level of wavelet decomposition ni and the activation power pp. The optimization parameters are listed in Table 7.

Table 7 Power management optimization problem
Full size table

Figure 3 shows the contour plot of the optimization objective function with respect to the pp and ni, respectively. It is found that the battery capacity loss is in the range of 1.46×10−5 Ah to 1.9×10−5 Ah.

Fig. 3
figure 3

Contour plot of Qloss,DC for the proposed power management system

Full size image

By analyzing the optimization results, the best capacity loss is found to be 1.46×10−5 Ah which is achieved when the conditions is:\(n_{i} = 29 , { }p_{p} = 1800{\text{ W}}\).

6 Results

After finding the optimal conditions for the wavelet controller, they are employed within the wavelet controller throughout this section. Figure 4 shows three plots for the UC power share during the FTP driving cycle. The top graph shows the power share for the whole FTP driving cycle. In order to clarify the results, the bottom-left graph shows an example of the UC discharging mode, while the bottom-right graph shows a charging instance as an example. The solid green line is for the UC-based PDS (PUC,U), the solid red line is for the SoP-based PDS (PUC,P) and the solid blue line is for the proposed wavelet PDS (PUC,W). As shown in Fig. 4, there is a large peak for the UC-based strategy at around 195 s. This is not desirable, since the UC drains quickly and would be idle for the moments after the peak. On the other hand, the proposed wavelet PDS has a higher UC power share for most of the time, compared with the other two methods.

Fig. 4
figure 4

UC power share for the whole, an interval during discharging mode, and charging mode of FTP driving cycle, for PUC,U, PUC,P, PUC,W strategies

Full size image

Another advantage of the proposed wavelet PDS is in the regenerative mode. As shown in Fig. 4, during the regenerative braking, the UC performs more efficiently under the wavelet PDS strategy, by providing larger UC power share to efficiently capture the recovery energy. Overall, it is noticed that the UC performance is the best for the wavelet PDS, followed by the SoP-based PDS and UC-based PDS.

An important parameter for the ESS is the SoC, which is a measure of the available energy. Figure 5 plots the UC SoC for the whole and interval duration of the FTP driving cycle. As discussed, the most effective UC power share belongs to the wavelet PDS, therefore, it is expected that the UC SoC remains higher for this strategy, compared with the other two strategies.

Fig. 5
figure 5

UC SoC for the whole and interval duration of FTP driving cycle, for UC-based (SoCUC,U), SoP-based (SoCUC,P) and wavelet based (SoCUC,W) strategies

Full size image

These results are in agreement with the ones reported by Fig. 4. This is due to the improved discharging/charging of the UC for the wavelet PDS, compared with the other two methods.

Figure 6 plots the battery power consumption for the whole and interval duration of the FTP driving cycle. As mentioned, the wavelet PDS engages the UC more efficiently during the discharging /charging modes, which enables the battery to have the lowest power consumption. This is evident from observing the battery power consumption shown in Fig. 6 and around 192 s, which shows that the battery power consumption is the lowest for the wavelet PDS, followed by the SoP PDS, and is the highest for the UC-based method. It is noticed that there are several battery power peaks associated with the UC-based PDS which is not desirable in terms of the battery lifetime. Overall, the wavelet and SoP PDSs show comparable results. As discussed, the wavelet PDS moderates the battery power consumption by effectively engaging the UC. This leads to lower battery SoC variations, compared with the other PDS strategies. Figure 7a shows the battery SoC for the duration of ten FTP driving cycles. When operating under the UC-based PDS strategy, the battery reaches the lower limit of 20% firstly, compared with the other two strategies.

Fig. 6
figure 6

Battery power consumption for the whole and interval duration of FTP cycle, for UC-based (PBat,U), SoP-based (PBat,P) and wavelet based (PBat,W) strategies

Full size image
Fig. 7
figure 7

Battery SoC and UC SoC

Full size image

The wavelet and SOP PDSs show comparable results. Therefore, these PDSs enable the motorcycle to drive for a longer range, compared with the UC-based method. This is possible due to the better management of the UC SoC, as shown in Fig. 5.

After showing the superior performance of the proposed wavelet PDS, compared with the UC-based and SoP-based PDSs, Fig. 7b compares the performance of the proposed HESS with an ESS. The battery/UC SoC of the proposed wavelet PDS and the battery SoC of an ESS are shown for the FTP driving cycle. As can be seen, the battery SoC for the wavelet remains above the one for the ESS. This is due to the UC contribution during the discharging/charging modes. The higher level of battery SoC provides higher mileage of the electric motorcycle equipped with the wavelet PDS, compared with the one equipped with an ESS.

Figure 8 shows the battery current fed to/from the battery during the whole and interval duration of the FTP driving cycle.

Fig. 8
figure 8

Battery current for the whole and interval duration of the FTP cycle, for ESS (IBat,B), UC-based (IBat,U), SoP-based (IBat,P) and wavelet based (IBat,W) strategies

Full size image

Note that the overall current fed to/drawn from the battery is the highest for the ESS (IBat,B), and is the least for the proposed wavelet HESS (IBat,W).

Performance comparison for different ESSs is summarized in Table 8. As can be seen, the battery lifetime for the ESS is 4.95 years, and is 10.66 years for the HESS equipped with SoP controller. On the other hand, the battery lifetime for the proposed HESS equipped with wavelet controller is 10.93 years, which shows an improvement of 120% and 3%, compared with the other two strategies, respectively.

Table 8 Comparison of different energy storage performance
Full size table

On the other hand, the number of battery replacement for a 10-year period of time is zero for the HESS equipped with the wavelet controller, while the ESS needs to be replaced two times. In terms of associated costs, the initial cost of the proposed HESS equipped with wavelet controller is about 1000 $ more than that of the ESS, while the total cost of the proposed HESS is about 1500 $ lower than that of the ESS. Finally, the energy recovery for the ESS is 102.5 Wh, while it is 126.3 Wh for the proposed HESS equipped with wavelet controller, which shows an improvement of 23%. This value is slightly higher than the one obtained for the SoP-based controller. Overall, the results demonstrate the effectiveness of the proposed HESS equipped with wavelet controller compared with the ESS, and the HESS equipped with UC-based and SoP-based controllers. This makes it suitable to replace the ESS and the latter methods.

7 Conclusion

A new frequency-based control strategy is proposed for power distribution management of an HESS. The proposed controller is designed based on the wavelet filter. If a certain input power level reaches (1800 W), the wavelet controller is engaged and the battery is assigned to provide the low frequency portion of the demand power, while the UC provides the high frequency portion. The frequency filter is a multi-level Haar wavelet filter with 29-level decomposition and reconstruction. An integer genetic algorithm optimization technique is employed to find the optimal level of wavelet decomposition as well as the optimal activation power.

As a case study, the powertrain of an electric motorcycle is modeled and examined for evaluating the ESS. The motorcycle is studied during the FTP driving cycle. The LiFePO4 battery type is considered and its life loss model based on the battery current is studied. To show the effectiveness of the proposed wavelet-based power management strategy, two other strategies are presented and studied: a UC-based strategy and a SoP-based strategy. The results show that the UC peak fluctuations of battery power are moderated by adding the UC. Moreover, the proposed HESS equipped with wavelet provides lower peaks of power fed to/drawn from the battery, compared with the other two HESSs. This is suitable in terms of improving the battery lifetime. Therefore, the battery life loss and number of battery replacement of the HESS equipped with the wavelet controller are the best. Specifically, there is an improvement of 120% and 3% for the battery lifetime, compared with ESS and SoP-based method. The energy recovery for the proposed algorithm is improved by 23%, compared with ESS and is slightly higher than the one for SoP-based controller. The initial cost of HESS is about 1000 $ higher than that of the ESS, while the 10-year overall cost of HESS with wavelet strategy is about 1500 $ lower than the ESS case.

Future work could be done by employing sophisticated control strategies for power distribution between battery and UC to improve the battery life cycle. In addition, the effect of battery temperature can be modeled to improve the life cycle estimation.