1 Introduction

Wind energy generation has attracted great interest due to its freely available, clean and renewable resource. The adoption of doubly-fed induction generators (DFIGs) for wind turbines has allowed the power rating of wind turbines to increase in AC grid [1]. The traditional DFIG converter system has many merits, such as small power capacity, low energy losses and cost, flexible power control [2,3,4]. However, it cannot easily satisfy the requirements of high-voltage direct-current (HVDC) transmission systems based on voltage-source conversion (VSC). Extra rectifiers are applied to connect the stator and traditional DIFG converter system with a DC bus, so that the cost increases due to this redundant structure [5].

Therefore, a DC-based converter system has been proposed to interface a DFIG with a DC grid. A diode-based converter interfaces the stator with the DC grid to simplify its structure and reduce its cost. A power control scheme for a DFIG is proposed with a diode-based rectifier connected to the DC Bus [6]. The stator frequency is regulated by an inner control method [7]. Torque ripple is reduced by resonant current controllers [8]. Operation and design issues are analyzed for a DFIG with a diode-based rectifier [9]. Self-sensing methods for regulating stator current and stator frequency are proposed for DFIG [10, 11]. But harmonics caused by diode-based rectifiers may reach from 5.97% to 11.66% and an active power filter should be applied to eliminate these [12, 13]. The IGBT-based DFIG converter system adopted in this paper, which consists of a rotor side converter (RSC) and a stator side converter (SSC), regulates DFIG more flexibly, with reduced harmonics [14, 15].

A DC-based converter system make it possible to regulate flux and current in the DFIG to minimize system loss and adapt it to various applications, because the SSC connects the stator to the DC grid and the stator is not confined to the AC grid. A SSC regulates its frequency and voltage to make the DFIG operate at low wind speed with fixed slip [14]. However system dissipation cannot be ignored, particularly at low and moderate torques.

Optimization strategies for DFIGs in AC and DC grids have been investigated as follows. Optimization of a DFIG in the AC grid only deals with the sharing of exciting current, while additional reactive power devices are needed to compensate reactive power [16]. The field weakening method is used to extend the rotor speed range of induction, and suitable flux and current trajectories are found to reduce system losses [17, 18]. The field weakening method is applied to a DFIG with a diode-based converter to improve its efficiency in a DC grid [19]. However, its efficiency only increases by 12% while the stator frequency increases by 200% at low torque and rotor speed. The higher stator frequency leads to more design difficulty and increases the cost of the diode-based converter. Optimization strategies for a DFIG with an IGBT-based converter system connecting to a DC grid are hardly mentioned in the literature, especially at the low speed and torque.

Field-oriented control techniques consisting of inner and outer loops are usually used to control DFIG power due to their simplicity [20, 21]. But it is difficult to choose suitable control parameters to ensure system stability under different conditions. Alternative control strategies have been proposed to overcome these drawbacks [22, 23]. Model predictive control (MPC) is an attractive solution for current, power, torque and flux control due to its easy design, fast dynamic response, high accuracy and small steady-state error under different conditions [24]. Compared with a PI controller, a MPC controller obtains faster responses and has less overshoot [25, 26]. MPC has been applied to DFIGs not only in the AC grid, but also in the DC grid [27,28,29,30]. However, MPC for a DFIG with two IGBT-based converters, to improve the dynamic and steady-state performance of the DFIG in the DC grid, is also hardly mentioned in the literature.

Considering the problems mentioned above, this study focuses on the optimization strategy to improve the efficiency of a DFIG with IGBT-based converters connected to a DC grid, which is the main contribution of this paper. Unlike previous optimization strategies for DFIGs, an optimization method for rotor flux and stator current is proposed to minimize system losses. The optimal values are analytically obtained and validated on a detailed model.

Furthermore, a coordinated MPC scheme for the RSC and the SSC is presented to overcome the drawbacks of the field-oriented control technique and improve the steady-state and dynamic performance of the DFIG. A stator current and rotor flux predictive method is used in the MPC controllers. Finally, experimental and simulation studies are carried out to validate the effectiveness.

2 System description

2.1 DC-based converter system

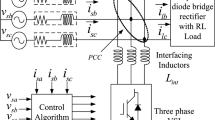
The DC-based converter system adopted in this paper is shown in Fig. 1.

Fig. 1
figure 1

DFIG with its DC-based converter system in DC grid

Full size image

The stator and rotor of DFIG are connected to the DC bus by the SSC and RSC. The stator voltage is not enslaved to the AC grid any more, and the SSC can regulate the stator voltage and frequency flexibly to control the stator current and compensate the stator reactive power. In addition, the RSC can regulate the rotor voltage flexibly to control the rotor flux.

2.2 Wind turbine model description

In this paper, the models of the gearbox and the wind turbine are merged into one part. And its maximum power point (MPP) curve assumed in this paper is approximatively given by [31]

$$\left\{ \begin{aligned} T_{opt} = 0.0667V_{w}^{2} \hfill \\ n_{ropt} = 111.8V_{w} \hfill \\ \end{aligned} \right.$$
(1)

where T opt (N·m), n ropt (krpm), and V w (m/s) are the optimum mechanical torque, optimum rotor speed, and wind speed respectively.

Wind turbine performance curves are shown in Fig. 2, as the rotor speed (n r ) ranges from 0.6 to 1.7 krpm. The solid line is for the curve of optimum mechanical torque. The other lines are the curves of mechanical torque (T m ) at the wind speeds of 9 and 15 m/s respectively.

Fig. 2
figure 2

Variation of wind turbine performance with rotor speed

Full size image

2.3 DFIG model description

The dynamic DFIG model in the dq synchronous frame can be expressed as [20, 21]

$$\left\{ \begin{aligned} u_{sd} = \frac{{{\text{d}}\psi_{sd} }}{{\text{d}}t} - \omega_{1} \psi_{sq} + R_{s} i_{sd} \hfill \\ u_{sq} = \frac{{{\text{d}}\psi_{sq} }}{{\text{d}}t} + \omega_{1} \psi_{sd} + R_{s} i_{sq} \hfill \\ u_{rd} = \frac{{{\text{d}}\psi_{rd} }}{{\text{d}}t} - \omega_{s} \psi_{rq} + R_{r} i_{rd} \hfill \\ u_{rq} = \frac{{{\text{d}}\psi_{rq} }}{{\text{d}}t} + \omega_{s} \psi_{rd} + R_{r} i_{rq} \hfill \\ \end{aligned} \right.$$
(2)
$$\left\{ \begin{aligned} \psi_{sd} = L_{s} i_{sd} + L_{m} i_{rd} \hfill \\ \psi_{sq} = L_{s} i_{sq} + L_{m} i_{rq} \hfill \\ \psi_{rd} = L_{r} i_{rd} + L_{m} i_{sd} \hfill \\ \psi_{rq} = L_{r} i_{rq} + L_{m} i_{sq} \hfill \\ \end{aligned} \right.$$
(3)
$$\left\{ \begin{aligned} T_{{\it m}} - T_{e} = J\frac{{{\text{d}}\omega_{m} }}{{\text{d}}t} = \frac{2\pi J}{60}\frac{{{\text{d}}{\it n}_{r} }}{{\text{d}}t} \hfill \\ T_{e} = 1.5n_{p} \frac{{L_{m} }}{{L_{r} }}(\psi_{rd} i_{sq} - \psi_{rq} i_{sd} ) \hfill \\ \end{aligned} \right.$$
(4)

where u sd , u sq , i sd , i sq , ψ sd , and ψ sq are the dq components of stator voltage, current and flux respectively; u rd , u rq , i rd , i rq , ψ rd , and ψ rq are the dq components of rotor voltage, current and flux respectively; ω 1, ω s , and ω m are synchronous, slip, and mechanical angular frequency respectively; L s , L r , and L m are the stator, rotor and mutual inductance respectively; R r and R s are the rotor and stator resistance respectively; T e is electromagnetic torque; J is generator rotational inertia; and n p is the number of pairs of poles.

3 Control strategy description

3.1 MPP control strategy

Rotor speed n r , here approximated by (1), is usually regarded as the tracked target to make the DFIG operate at its MPP. The MPP controller is given by (5), and its output is T e subject to a range limitation from T min to T max :

$$T_{e} = T_{opt} - k_{p} \left( {n_{ropt} - n_{r} } \right)$$
(5)

The dynamic responses of n r and T e increase in proportion to the rotor speed error with coefficient (k p ). The risk of mechanical faults increases with the variation speed of mechanical stress. Here k p is chosen as 0.0628.

3.2 Optimized control targets for DFIG

The rotor flux and the stator current are the control targets, which are optimized in this paper. Within the limitation of rated stator voltage, the proposed optimization method minimizes system losses. The maximum rotor flux is determined by rated stator voltage, because stator overvoltage causes danger and increases the design difficulty of the SSC.

From (3), when a rotor-oriented flux frame is adopted with its vector direction aligned with the q-axis, the rotor flux (ψ r ) and its dq components are given by

$$\left\{ \begin{array}{l} \psi_{rd} = 0 \hfill \\ \psi_{rq} = \psi_{r} \hfill \\ \end{array} \right.$$
(6)

The rotor currents are accordingly derived from (3):

$$\left\{ \begin{aligned} &i_{rd} = - \frac{{L_{m} i_{sd} }}{{L_{r} }} \hfill \\ &i_{rq} = \frac{{\psi_{r} - L_{m} i_{sq} }}{{L_{r} }} \hfill \\ \end{aligned} \right.$$
(7)

Substituting (7) into (3), the stator fluxes are obtained:

$$\left\{ \begin{aligned} &\psi_{sd} = \left( {L_{s} - \frac{{L_{m}^{2} }}{{L_{r} }}} \right)i_{sd} \hfill \\& \psi_{sq} = \frac{{L_{m} }}{{L_{r} }}\psi_{r} + \left( {L_{s} - \frac{{L_{m}^{2} }}{{L_{r} }}} \right)i_{sq} \hfill \\ \end{aligned} \right.$$
(8)

Substituting (6) into (4), the stator active current is given by

$$i_{sd} = \frac{{T_{e} L_{r} }}{{ - 1.5n_{p} L_{m} \psi_{r} }}$$
(9)

Ignoring both electromagnetic transient processes and the voltage drop due to the stator resistance, the stator voltage (u s ) and its dq components are obtained from (2):

$$\left\{ \begin{aligned} &u_{sd} = - \omega_{1} \psi_{sq} \hfill \\ &u_{sq} = \omega_{1} \psi_{sd} \hfill \\ \end{aligned} \right.$$
(10)
$$u_{s} = \sqrt {u_{sd}^{2} + u_{sq}^{2} } = \omega_{1} \sqrt {\psi_{sq}^{2} + \psi_{sd}^{2} }$$
(11)

It is well known that the rotor and stator resistances are approximately identical, and the rotor leakage reactance (L lr ) is far less than the mutual inductance (L m ) [32], namely,

$$\left\{ \begin{aligned} R_{s} \approx R_{r} \hfill \\ L_{r} \approx L_{m} \hfill \\ \end{aligned} \right.$$
(12)

From (8), (11), and (12), the rotor flux is approximately expressed as

$$\psi_{r} \approx \frac{{u_{s} }}{{\omega_{1} }} \le \psi_{r}^{*} \approx \frac{{V_{s} }}{{\omega_{1} }}$$
(13)

where V s and ψ * r are the rated stator voltage and rotor flux respectively.

With iron losses neglected, the total Joule losses (P l ) are given by

$$P_{l} = i_{r}^{2} R_{r} + i_{s}^{2} R_{s} = \frac{{\left( {i_{rd}^{2} + i_{rq}^{2} } \right)R_{r} + \left( {i_{sd}^{2} + i_{sq}^{2} } \right)R_{s} }}{2}$$
(14)

where i r and i s are the effective values of the rotor and stator current.

Substituting (7) and (9) into (14), if the DFIG operates at its MPP, the system losses are expressed as

$$P_{l} = 0.5\left( {R_{s} + R_{r} \frac{{L_{m}^{2} }}{{L_{r}^{2} }}} \right)\left( {\frac{{T_{opt} L_{r} }}{{ - 1.5n_{p} L_{m} \psi_{r} }}} \right)^{2} {\kern 1pt} + 0.5\left[ {i_{sq}^{2} \left( {R_{s} + R_{r} \frac{{L_{m}^{2} }}{{L_{r}^{2} }}} \right) - 2\frac{{\psi_{r} L_{m} R_{r} }}{{L_{r}^{2} }}i_{sq} + \frac{{R_{r} \psi_{r}^{2} }}{{L_{r}^{2} }}} \right]$$
(15)

From (12) and (15), it follows that

$$P_{l} = R_{s} \left[ {\left( {\frac{{T_{opt} }}{{1.5n_{p} \psi_{r} }} - \frac{{\psi_{r} }}{{2L_{r} }}} \right)^{2} + \left( {i_{sq} - \frac{{\psi_{r} }}{{2L_{r} }}} \right)^{2} + \frac{{T_{opt} }}{{1.5n_{p} L_{r} }}} \right]$$
(16)

We define a variable flux (ψ t ) that varies with T opt according to

$$\psi_{t} = \sqrt {\frac{{2L_{r} T_{opt} }}{{1.5n_{p} }}} {\kern 1pt}$$
(17)

The system losses (P fc ) resulting from the rotor flux and stator current optimization method are given by

$$P_{fc} = \left\{ \begin{aligned} &\frac{{R_{s} T_{opt} }}{{1.5n_{p} L_{r} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi_{t} {\kern 1pt} {\kern 1pt} \le {\kern 1pt} {\kern 1pt} \psi_{r}^{ *} \hfill \\ &R_{s} \left( {\frac{{T_{opt} }}{{1.5n_{p} \psi_{r}^{ *} }} - \frac{{\psi_{r}^{ *} }}{{2L_{r} }}} \right)^{2} { + }\frac{{R_{s} T_{opt} }}{{1.5n_{p} L_{r} }}{\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi_{r}^{ *} < \psi_{t} \hfill \\ \end{aligned} \right.$$
(18)

with

$$\psi_{r} = \left\{ \begin{aligned} \psi_{t} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi_{t} \le {\kern 1pt} {\kern 1pt} \psi_{r}^{ *} \hfill \\ \psi_{t}^{*} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi_{t} > {\kern 1pt} {\kern 1pt} \psi_{r}^{ *} \hfill \\ \end{aligned} \right.$$
(19)
$$i_{sq} = \left\{ \begin{aligned} \frac{{\psi_{t} }}{{2L_{r} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi_{t} \le {\kern 1pt} {\kern 1pt} \psi_{r}^{ *} \hfill \\ \frac{{\psi_{r}^{*} }}{{2L_{r} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi_{t} > {\kern 1pt} {\kern 1pt} \psi_{r}^{ *} \hfill \\ \end{aligned} \right.$$
(20)
$$i_{sd} = \left\{ \begin{aligned} &- \sqrt {\frac{{T_{opt} }}{{3n_{p} L_{r} }}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi_{t} {\kern 1pt} {\kern 1pt} \le {\kern 1pt} {\kern 1pt} \psi_{r}^{ *} \hfill \\ &- \frac{{T_{opt} }}{{1.5n_{p} \psi_{r}^{ *} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi_{r}^{ *} < \psi_{t} \hfill \\ \end{aligned} \right.$$
(21)

If DFIG operates in a non-optimization mode, the rotor flux and stator reactive current are equal to the rated value and zero respectively. In this case, the system losses (P u ) are given by

$$P_{u} = R_{s} \left( {\frac{{T_{opt} }}{{1.5n_{p} \psi_{r}^{*} }} - \frac{{\psi_{r}^{*} }}{{2L_{r} }}} \right)^{2} + R_{s} \left( {\frac{{\psi_{r}^{*} }}{{2L_{r} }}} \right)^{2} + \frac{{R_{s} T_{opt} }}{{1.5n_{p} L_{r} }}$$
(22)

If only the stator reactive current is optimized, system losses (P c ) are given by

$$P_{c} = R_{s} \left( {\frac{{T_{opt} }}{{1.5n_{p} \psi_{r}^{*} }} - \frac{{\psi_{r}^{*} }}{{2L_{r} }}} \right)^{2} + \frac{{R_{s} T_{opt} }}{{1.5n_{p} L_{r} }}$$
(23)

The output power of the wind turbine and the gearbox is equal to T opt ω opt when the DFIG operates at its MPP. In order to clearly illustrate the difference in system losses and efficiency between optimized and non-optimized operation, the decreased system losses ratio (Δη fc and Δη c ) and increased system efficiency (Δξ fc and Δξ c ) are defined by

$$\left\{\begin{aligned} \Delta \eta_{fc} = \frac{{P_{u} - P_{fc} }}{{P_{u} }} \hfill \\ \Delta \eta_{c} = \frac{{P_{u} - P_{c} }}{{P_{u} }} \hfill \\ \Delta \xi_{fc} = \frac{{P_{u} - P_{fc} }}{{T_{opt} \omega_{opt} }} \hfill \\ \Delta \xi_{c} = \frac{{P_{u} - P_{c} }}{{T_{opt} \omega_{opt} }} \hfill \\ \end{aligned} \right.$$
(24)

The parameters of wind power generation system are listed in Table 1. Based on (18)–(24), the curves of rotor flux, stator current, system losses, decreased system losses, and increased system efficiency are shown in Figs. 3 and 4. As the synchronous speed (n syn ) is 1500 rpm, Δη fc and Δη c increase from 25% to 82%, and from 25% to 50% when the rotor speed ranges from 1.2 n syn to 0.4 n syn , and Δξ fc and Δξ c increase from 1% to 19%, and from 1% to 12%. In [19], the improvement in efficiency varies from 0% to 12% when rotor speed n r decreases from 1.2n syn to 0.4n syn at low torque and rotor speed level.

Table 1 Parameters for the DFIG generation system
Full size table
Fig. 3
figure 3

Variations of losses, flux and current with rotor speed

Full size image
Fig. 4
figure 4

Decreased system losses and increased system efficiency

Full size image

Therefore, the proposed optimization method achieves better performance especially at low and moderate rotor speeds. Systems losses are reduced and system efficiency is improved.

The feasibility of operating a DFIG at low wind speed is validated with fixed slip in [14]. Hence, we focus on the coordinated MPC scheme using rotor flux and stator current predictive method to track the optimized control targets and improve the performance of the DFIG within the normal rotor speed range from 1.05 to 1.68 krpm in the following simulation and experiment.

3.3 Predictive model of DFIG

From (2) and (3), the state equation of DFIG can be derived in the form

$$\frac{{\text{d}}{\varvec{x}}}{{\text{d}}t} = {\varvec{Ax}} + {\varvec{Bu}}$$
(25)

where

$${\varvec{x}} = \left[ {\psi_{rd} \;\psi_{rq} \;i_{sd} \;{\kern 1pt} i_{sq}} \right]^{\text{T}} ,\quad {\varvec{u}} = \left[ {u_{rd} \;u_{rq} \;u_{sd} \;u_{sq}}\right]^{\text{T}} ,$$
$$\varvec{A} = \left[ {\begin{array}{*{20}c} {\frac{{- {R_{r}} }}{{ {L_{r} }}}} & {{\omega_{s}} } & {{ \beta R_{r} } }& {0} \\ {{\omega_{s}} } & {\frac{{ - {R_{r}} }}{{{L_{r}} }}} & {0} & {{ \beta R_{r} } } \\ {\frac{{{\beta R_{r}} }}{{{\alpha L_{r} }}}} & {\frac{{{\beta \omega_{r} }}}{{\alpha} }} & {\frac{{ { R_{s} }+ {\beta^{2} R_{r}} }}{{\alpha} }} & {{\omega_{1}} } \\ {\frac{{ - {\beta \omega_{r} }}}{{\alpha} }} & {\frac{{{\beta R_{r}} }}{{{\alpha L_{r} }}}} & {{\omega_{1}} } & {\frac{{ -{ R_{s} }+ {\beta^{2} R_{r}} }}{{\alpha} }} \\ \end{array} } \right],$$
$${{\varvec{B}}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ { - {\beta \mathord{\left/ {\vphantom {\beta \alpha }} \right. \kern-0pt} \alpha }} & 0 & 1 & 0 \\ 0 & { - {\beta \mathord{\left/ {\vphantom {\beta \alpha }} \right. \kern-0pt} \alpha }} & 0 & 0 \\ \end{array} } \right],\quad \left\{ \begin{aligned} &\alpha = \frac{{L_{r} L_{s} - L_{m}^{2} }}{{L_{r} }} \hfill \\ &\beta = \frac{{L_{m} }}{{L_{r} }} \hfill \\ \end{aligned} \right.$$

Stator current and rotor flux are the system state variables, and stator and rotor voltages are the system inputs for the RSC and the SSC respectively. The coefficient matrix A varies with rotor angular frequency. Rotor voltage is regulated by the RSC to confine rotor flux to its rated value with a coupled term including the stator current. Stator voltage is regulated by SSC to confine stator current to its reference with a coupled term including the rotor flux. The stator current and the rotor flux are therefore coupled strongly together. Separate controllers for the RSC and the SSC would generate system errors. Meanwhile it is difficult to decouple and ensure system stability over its full operational range using simple PI controllers. Therefore, coordinated MPC controllers for the RSC and the SSC are proposed to make the DFIG operate at its MPP and to improve its steady-state and transient performance, using a rotor flux and stator current predictive method without decoupling. The rotor flux is estimated from rotor and stator currents according to (3) [32]. Stator, rotor, and mutual inductances (L s , L r , L m ), are evaluated off-line.

The forward-difference Euler formula is adopted as the numerical approximation to predict the derivative for the next sample time:

$$\frac{{\text{d}}{\varvec{x}}}{{\text{d}}t} = \frac{\Delta {\varvec{x}}\left( k \right)}{\Delta t} \approx \frac{{{\varvec{x}}\left( {k + 1} \right) - {\varvec{x}}\left( k \right)}}{T}$$
(26)

where x is a state variable; T is the sampling period and k is the time stamp. The discrete predictive model for the DFIG is therefore given by

$${\varvec{x}}\left( {k + 1} \right) = \left( {{\varvec{A}}\left( k \right)T + {\varvec{I}}} \right){\varvec{x}}\left( k \right) + {\varvec{B}}T{\varvec{u}}\left( k \right)$$
(27)

3.4 Delay compensation

Current sampling and rotor flux calculation cannot occur simultaneously, and the sampled currents differ from the actual values at the time of calculation. These errors can be significant if the delay time is substantial. It is necessary to predict the stator current and the rotor flux for the sample time, to match the derivative prediction. They are estimated for sample time k by the previous values and expressed as

$${\varvec{x}}\left( k \right) = \left( {{\varvec{A}}\left( {k - 1} \right)T + {\varvec{I}}} \right){\varvec{x}}\left( {k - 1} \right) + {\varvec{B}}T{\varvec{u}}\left( {k - 1} \right)$$
(28)

3.5 Cost function

A cost function is the evaluation criterion to determine the optimum switching state for the next sample time and output the optimum vector with the least error. The stator current and rotor flux predictive method is used to keep the rotor flux stable and to track the stator current reference. Rotor flux and stator current targets are easily achieved by penalizing switching states that produce predictions distant from reference value. Thus the cost functions for the SSC and the RSC are defined as

$$\left\{ \begin{array}{l} g_{_{SSC}} = k_{1} \left| {i_{sd}^{*} - i_{sd}^{p} } \right| + k_{2} \left| {i_{sq}^{*} - i_{sq}^{p} } \right| \hfill \\ g_{_{RSC}} = k_{3} \left| {\psi_{rd}^{*} - \psi_{rd}^{p} } \right| + k_{4} \left| {\psi_{rq}^{*} - \psi_{rq}^{p} } \right| \hfill \\ \end{array} \right.$$
(29)

where k 1, k 2, k 3, and k 4 are the weight coefficients that influence relative performance against each of the control targets. In this paper, k 1, k 2, k 3, and k 4 are chosen as 1. Target values are denoted by the superscript “∗”, and the predicted values from (27) are denoted by the superscript “p”. The rotor flux reference values are obtained from (6) as

$$\left\{ \begin{aligned} &\psi_{rd}^{ *} = 0 \hfill \\ &\psi_{rq}^{ *} = \psi_{r} \hfill \\ \end{aligned} \right.$$
(30)

The stator current reference values are given from (4)–(6) and (20) as

$$\left\{ \begin{aligned} &i_{sd}^{ *} = \frac{{T_{opt} - k_{p} \left( {n_{opt} - n_{r} } \right)}}{{1.5n_{p} \beta \psi_{r} }} \hfill \\ &i_{sq}^{ *} = \frac{{\psi_{r} }}{{2L_{r} }} \hfill \\ \end{aligned} \right.$$
(31)

3.6 Coordinated and optimized control scheme

From the above analysis, the whole control scheme is shown in Fig. 5. The MPP model estimates the optimal speed and torque (n ropt , T opt ) using (1) according to the wind speed (V w ). The rotor flux and stator current reference values (ψ * rd , ψ * rq , i * sd , i * sq ) come from (30) and (31) with the inputs of T opt , n ropt , and n r . The rotor speed, and stator and rotor currents (n r , i sabc , i rabc ) are measured and transformed into their dq components (i sd , i sq , i rd , i rq ) in the synchronous frame. The rotor and stator currents (i sd (k), i sq (k), i rd (k), i rq (k)) for sample time k come from the delay compensation model illustrated by (28). The rotor fluxes (ψ rd (k), ψ rq (k)) for sample time k are estimated from the rotor and stator currents using (3). The predictive DFIG model in (27) is used to output the predicted rotor fluxes and stator currents (ψ rd (k + 1), ψ rd (k + 1), i sd (k + 1), i sq (k + 1)) for sample time k + 1. Cost functions given by (29) determine the optimum switching state during the next sampling period, which allows the optimum voltage vectors (s rabc , s sabc ) of the RSC and the SSC to be calculated using the inputs of predicted rotor fluxes and stator currents.

Fig. 5
figure 5

Control scheme for the RSC and the SSC

Full size image

4 Simulations

The DFIG system parameters in the following simulation and experiment are listed in Table 1.

Changes in rotor speed are modeled in a simulation platform to verify the feasibility of the proposed control scheme. During the first stage, n ropt is set to 1680 rpm which is assumed to be the rated rotor speed of the DFIG. Then at 0.3 s the rotor starts declining quickly during the transient stage, reaching 1050 rpm at 0.45 s, where it remains in the low-speed stage for the rest of the simulation. Simulation results are shown in Figs. 6, 7 and 8.

Fig. 6
figure 6

Rotor speed, flux, current, and torque variations during the transient stage of the simulation

Full size image
Fig. 7
figure 7

Rotor flux and stator current during the rated-speed stage of the simulation

Full size image
Fig. 8
figure 8

Rotor flux and stator current during the low-speed stage with a rotor speed of 1050 rpm

Full size image

4.1 Steady-state performance analysis

The rotor flux and stator current are stable and track their reference values closely before 0.3 s when DFIG operates at its rated rotor speed. n r is confined to its reference value, indicating that the DFIG operates at its MPP. The rotor flux amplitude remains stable at 1.03 Wb with a frequency of 6 Hz. The stator current (I s ) is a sine wave with amplitude of 6.3 A and frequency of 50 Hz. The stator reactive current is 3.77 A and, together with rotor reactive current, ensures the rotor flux stable. The filtered stator voltage amplitude is confined to 311 V. A phase difference exists between the stator current and the voltage.

At the rotor speed of 1050 rpm, the stator current amplitude is 3.87 A with its active and reactive current confined to their reference values of −2.79 and 2.68 A after 0.5 s, which accords with (31) and Fig. 3. The RSC confines the rotor flux to 0.732 Wb, which varies with T opt and accords with (19) and Fig. 3. The stator voltage amplitude declines to 227 V due to decreased rotor flux.

Thus, the MPC controllers make the DFIG operate steadily and track the optimized targets effectively.

4.2 Transient performance analysis

The transient performance is analyzed when rotor speed declines rapidly from 0.3 s in Fig. 6. Owing to the generator inertia and control delay, n r reaches its reference value at 0.45 s. With the stator active current reference increasing and rotor flux reference decreasing from 0.3 to 0.38 s, T e maintains its maximum value of 15 N·m to make n r fall quickly, and then reduces to its reference value, which accords with the expected behaviour of the MPP controller (5). The rotor flux and stator current closely follow their references values.

Thus, the transient performance of the DFIG is excellent when wind speed falls sharply, and all control targets are met smoothly and quickly.

5 Experiments

5.1 Test bench overview

A laboratory-scale experimental test bench was designed to verify the proposed control scheme. It consists of a DFIG, RSC, SSC, induction motor (IM), IM driver, and battery storage. Its schematic diagram and photograph are shown in Fig. 9 and Fig. A1 (as shown in the Appendix A) respectively. The IM is used to emulate a wind turbine, and its speed is controlled by the IM driver. Battery storage is connected with the stator and rotor, by the RSC and SSC respectively, to keep the DC bus voltage stable. Two du/dt filter inductors are added to the rotor and stator sides to protect the DFIG from sharp voltage changes. An incremental encoder and a torque sensor are used to measure the rotor position, speed, and torque. The proposed control scheme is implemented in a DSP28335 processing board with a switching frequency of 10 kHz. The stator voltage amplitude is obtained by the signal processing circuit to observe its variation directly.

Fig. 9
figure 9

Schematic diagram of the test bench

Full size image

5.2 Experimental results in normal speed range

A quasi-constant rotor speed ramping up from 1050 to 1680 rpm over 3 s was achieved using the induction motor. Rotor flux and stator current reference curves are presented in Fig. 3. An experimental comparison is made between the two control schemes with optimized and non-optimized targets, shown in Figs. 10–11.

Fig. 10
figure 10

Experiment results for the optimization control scheme

Full size image

In both figures n r increases from 1050 to 1680 rpm and follows its reference curve closely. T m ranges from 5.9 to 15 N·m and has the same trend as n r . This is consistent with the DFIG operating at its MPP in the two cases. The peak amplitude of the induced stator voltage, allowing for the effect of the low-pass filter, ramps from 227 to 311 V, which conforms to (12).

The stator current follows its reference value closely at rotor speeds of 1680 and 1050 rpm in Figs. 10 and 11. The peak stator current amplitude varies from 3.87 to 6.3 A in Fig. 10, and from 2.02 to 5.05 A in Fig. 11. The rotor peak current amplitude varies from 3.83 to 6.4 A and from 7.8 to 9 A respectively in the two cases. The optimized stator current supports the rotor flux using more reactive current than the non-optimized one. The optimized rotor current supports less reactive current than the non-optimized one. The rotor excitation frequency varies from 15 to 6 Hz in both cases.

The stator voltage in Fig. 10 has a different phase to the stator current which compensates reactive current according to (20). The stator voltage and current have the same phase in Fig. 11, and stator reactive current is zero. At the rated rotor speed, the losses of the DFIG between two cases are basically equal. Therefore, the losses of the DFIG are analyzed at the rotor speed of 1050 rpm (n r = 0.7 n syn ). The measured input power at low rotor speed is 648 W, and the output powers for the optimized and non-optimized cases are 628 and 610 W respectively. So we could get the increased system efficiency about 2.7% by (24), which accords with the result in Fig. 4b.

In addition, compared with the current and torque curves in [6], the curves in Fig. 10 have less harmonic contents and fewer steady-state errors, and are more smooth.

Thus, it could be concluded that the control scheme with optimized control targets can make DFIG operate steadily at its MPP over the whole operational speed range, and improve the system efficiency.

5.3 Experiment results during abrupt rotor speed variation

To validate the transient performance of the DFIG during an abrupt rotor speed variation, the rotor speed was changed sharply from 1680 to 1050 rpm in less than 0.1 s. The results are shown in Fig. 12.

Fig. 11
figure 11

Experiment results for non-optimization control scheme

Full size image
Fig. 12
figure 12

Experiment results in abrupt speed case

Full size image

n r reaches its reference value smoothly after 0.1 s, and T m varies from 15 to 5.9 N·m quickly with a small overshoot. The stator current tracks its reference value smoothly and quickly without overcurrent. The rotor current changes very quickly. The experiment results therefore accord with the simulated behavour shown in Fig. 6. Compared with the current and torque curves in [6], the curves in Figs. 11–12 have less overshoot and quicker dynamic response.

Thus, the coordinated MPC controllers improve the transient performance of DFIG when the rotor speed drops down sharply.

6 Conclusion

Based on the results and analysis, the following conclusions may be drawn:

  1. 1)

    The optimized control targets are analytically obtained and validated on the detailed model of system losses. And its parameters come from a practical DFIG system.

  2. 2)

    The optimized control targets effectively increase the system efficiency from 1% to 19% when rotor speed decreases from 1.2 n syn to 0.4 n syn , and minimize the system losses of a DFIG. The lower of the rotor speed is, the higher the increased system efficiency is.

  3. 3)

    The coordinated MPC controllers effectively track the optimized control targets to make DFIG operate at its MPP model, and improve the system efficiency about 2.7% at the rotor speed of 0.7 n syn in the experiment.

  4. 4)

    The coordinated MPC controllers make all control targets track their references within 0.15 s and without impulse when rotor speed drops down sharply in experiment. The transient performance of DFIG is improved.

In further study, this experiment will be extended to verify the effectiveness of the proposed control scheme over the full rotor speed range.