1 Introduction

Due to the high investment costs to connect to the grid, diesel fuel is still the only source for power generating in many islands and remote areas. Compared with the diesel-only system, stand-alone microgrids [1], incorporating various distributed energy resources and battery energy storage system (BESS), are able to weaken the dependence on fossil fuels, reduce the pollutant emissions, and economically meet the customer demands. Thus, it is essential to reasonably configure the stand-alone microgrids.

Significant work has been done on the planning of stand-alone microgrids. In planning studies, modeling the renewable energy resources (RESs) and the load needs to be considered firstly. A straightforward approach is to use historical meteorological data and the load in a typical year for planning purpose [2], [3]. The Markov models for the load and RESs are established to determine the optimal sizes for a stand-alone power system together with genetic algorithm in [4]. In addition, a Monte Carlo simulation technique is developed in [5] to create sequential time-series to model RESs and load behaviors. In [6], representative data of daily load and wind power profiles are used to consider the problem of sizing energy storage system. With this method, daily patterns of wind speed and the load can be taken into account as well as their correlation and randomness. However, the method fails to capture the wind patterns that obviously differ from the load.

Considerable work has been done on reliability evaluation, which also plays an essential role in power generation planning. A reliability index is usually treated as either an objective [3] or a constraint [2], [4], [7], which can be evaluated using analytical methods [7]–[8], or Monte Carlo simulation [9], [10]. To consider the impacts of the volatility of power outputs of the distributed generators on the system reliability, multistate models are developed in [11], [12]–[13]. Each state, generated by splitting the probability distributions of RESs, stands for a special power level with corresponding occurrence probability. However, these studies have paid little attention to modeling of the BESS used to balance power for RESs. A probabilistic model for BESS is introduced in [7], [8], considering multiple states of state of charge (SOC) and probability associated with each state.

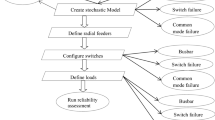
This paper considers the problems of planning of stand-alone microgrids, which consists of wind turbine generators (WTGs), diesel generators (DGs) and BESS, to supply energy to the load, as shown in Fig. 1. To capture the daily patterns and the correlation of the load and wind speed [14], clustering techniques [15] are utilized to cluster both of them simultaneously to generate scenarios for the planning studies. Then, an approximate analytical model for reliability evaluation of BESS is demonstrated, cooperating with multistate models for DGs [16] and WTGs [12], to assess the reliability performances of various system configurations. The proposed model for BESS takes into account the forced outage rates (FORs) of equipment, which is different from the one developed in [7], [8].

Fig. 1
figure 1

Schematic diagram of a stand-alone microgrid

Full size image

The remainder of this paper is organized as follows: Section 2 provides the methods to generate the operational scenarios. Section 3 presents the reliability modeling of WTGs, DGs and ESS. In Section 4, an optimal planning model is given. An application of the proposed method is demonstrated in Section 5. In Section 6, conclusions are drawn from the results. Finally, the derivations of partial equations are described in the Appendix.

2 Scenario generation

The methodology developed to capture the daily patterns [14], [17] of wind speed and load is based on the clustering techniques. With the method, some representational scenarios can be obtained along with their occurrence probabilities.

2.1 Clustering techniques

The aim of clustering is to group the data objects into multiple clusters in terms of similarity. The objects within a cluster are similar, whereas the objects of different clusters are dissimilar. The clustering technique applied in this paper is the k-mediods algorithm [15], which is a classical partitioning algorithm. The number of the clusters can be estimated by some techniques [18] or by rule of thumb. The latter is adopted to determine the number, and the clustering analysis is conducted with the help of R software [19].

2.2 Scenario generation for wind speed and load

The data objects to be clustered are selected from historical hourly wind and load resources in typical years. Each object represents a combination of average hourly values of the wind speed and the load on the same day, which is shown as

$$ Object_{i} = \left({w_{i1} ,w_{i2},\cdots,w_{i24},l_{i1},l_{i2},\cdots,l_{i24} } \right)^{\text{T}} \in {{\bf{R}}}^{48} $$
(1)

where Object i is the data object i; w and l are the wind speed and the load on day i of the chosen year, respectively. Considering one year of historical data, 365 objects are obtained. Owing to the fact that the units of the wind and the load are different, there is a need to perform a linear transformation on the original data using min–max normalization [20]. Then, these objects can be clustered by the aforementioned algorithm. Once the clustering analysis finishes, potential scenarios faced by the microgrid are obtained. The occurrence probability of each cluster, representing a scenario, can be further evaluated by

$$ \pi_{k} = {{{\text{Card}}\left( {C_{k} } \right)} \mathord{\left/ {\vphantom {{{\text{Card}}\left( {C_{k} } \right)} {365}}} \right. \kern-0pt} {365}} $$
(2)

where π k is the occurrence probability of cluster k; Card(C k ) is the number of objects contained in cluster k.

The wind profiles grouped in the same scenarios, as well as the load profiles, have similar daily patterns. In this paper, the fluctuating characteristics of these profiles are described by the probability distribution functions of the wind and the load at each hourly interval over the 24 h horizon. Figure 2 gives an example of the clustered wind profiles to illustrate the idea.

Fig. 2
figure 2

Fluctuating characteristics of the wind profiles in a special scenario

Full size image

The approaches to model the wind speed distributions at hour t in a scenario are presented in the following steps:

Step 1: Determine the theoretical distributions based on the estimated mean values and the variances of wind speed at hour t. Here, normal distribution is assumed [12].

Step 2: Split the probability density functions of the wind equally at hour t, according to the required accuracy. This paper considers a variation range of ± 3σ with a probability of 99.7 %. Let N W denote the number of discrete states. Then the discrete division of the probability can be calculated as Δ = 6/N W .

Step 3: Estimate the values and the probabilities of the discrete wind speed frames at hour t as:

$$ w_{k,t,n} = { \hbox{max} }\left\{ {\sigma_{k,t}^{2} {{\int_{{\left( {n - 1} \right)\Delta - 3}}^{n\Delta - 3} {yf\left( y \right)dy} } \mathord{\left/ {\vphantom {{\int_{{\left( {n - 1} \right)\Delta - 3}}^{n\Delta - 3} {yf\left( y \right)dy} } {\int_{{\left( {n - 1} \right)\Delta - 3}}^{n\Delta - 3} {f\left( y \right){\text{d}}y} }}} \right. \kern-0pt} {\int_{{\left( {n - 1} \right)\Delta - 3}}^{n\Delta - 3} {f\left( y \right){\text{d}}y} }}} + \overline{w}_{k,t} ,\; 0 \right\},\;\;n = 1,2, \cdots , \,\,N_{W} $$
(3)
$$ Pr_{w,k,t,n} = \int_{{\left( {n - 1} \right)\Delta - 3}}^{n\Delta - 3} {f\left( y \right){\text{d}}y} ,\;\;n = 2, \cdots ,N_{W} - 1 $$
(4)
$$ Pr_{w,k,t,n} = \int_{ - \infty }^{\Delta - 3} {f\left( y \right){\text{d}}y} ,\;\;\;n = 1,N_{W} $$
(5)

where w is the discrete wind speed; the subscripts k, t and n are the scenario index, the time index and the discrete state index, respectively; \( \overline{w} \) is the average value of the wind speed at hour t; σ is the standard variation of the wind speed at hour t; y is the standard normal distribution; Pr is the occurrence probability of the corresponding discrete state. Steps 1,2 and 3 are repeated for all the time intervals in each clustering scenario.

The load has similar modeling procedures as the wind speed; the details are not reported for the sake of brevity. Here, let Lk,t,i denote discrete value i of the load at hour t in scenario k, whose occurrence probability is represented as PrLoad{Lk,t,i}. The number of discrete states of the load is denoted as N L .

3 Reliability evaluation

Generally, the reliability evaluation of stand-alone microgrids is inclined to the generating capacity adequacy evaluation [9], which is different from the evaluation of the conventional generation system, due to the applications of RESs and BESS. The reliability of a stand-alone microgrid is influenced not only by the forced outage rates (FORs) of distributed generators, but also by the fluctuation of RESs. To consider these features in the clustering scenarios, an overall multistate modeling approach is described.

3.1 Wind energy system modeling

We use the available capacity probability tables (ACPTs) [21] to represent the characteristics of power outputs of a wind energy system (WES). Each ACPT is built in terms of the wind distribution at the considered time interval, which is different from the method used in [12]. The ACPTs vary with the time intervals due to the diverse wind distributions in the scenarios. The ACPT of the WES at each interval is developed as follows:

  1. 1)

    By means of a mathematical relationship between wind speed and power output [22], calculate the power outputs of one WTG under N W potential values of the wind speed at the considered time interval. The wind distribution and the availability of single WTG are combined to create the ACPT of the current time interval along with the calculated power outputs. We assume that availability of one WTG is modeled by the two-state Markov model [12].

  2. 2)

    Consider the WES consisting of NWTG identical WTGs. Determine the value and the probability of each power output level based on the performance of single WTG and the availability of the WTGs described by the binomial distribution [11]. Then an ACPT of WES is obtained [12].

Note that the number of capacity levels increases significantly with the addition of the WTGs involved in the microgrid, which will also increase computational burden. Therefore, the apportioning method [23] is used to reduce the ACPT, by which each level is apportioned among the assigned discrete states. In this paper, the maximum power output of all the WTGs facing the maximum wind speed at the current interval is regarded as the upper bound of the considered range. The probabilities of the assigned states are calculated with the method in [23], [16].

3.2 Diesel generating system modeling

For a diesel generating system including NDG identical DGs, a procedure similar to the WES’s is used to create its ACPT. Different from the ACPTs of the WES, the ACPT of the diesel generating system holds same for all the time intervals, which is only affected by the rated capacity of single DG and the availability of multiple DGs described by the binomial distribution [11] as well.

3.3 Battery energy storage system modeling

From the view of availability of the equipment, the BESS is characterized by two complementary states in this work: available and unavailable. Considering that its available state may correspond to diverse values of the state of charge (SOC), the available state is further subdivided equally into several states in term of the setting range of the SOC. Let SOCmax and SOCmin denote the maximum and minimum bounds of the SOC range, respectively. The interval ΔS is determined by (6), where NSOC represents the number of states including the divided states and the unavailable state.

$$ \Delta S = {{\left( {{\text{SOC}}_{ \hbox{max} } - {\text{SOC}}_{ \hbox{min} } } \right)} \mathord{\left/ {\vphantom {{\left( {{\text{SOC}}_{ \hbox{max} } - {\text{SOC}}_{ \hbox{min} } } \right)} {\left( {N_{\text{SOC}} - 1} \right)}}} \right. \kern-0pt} {\left( {N_{\text{SOC}} - 1} \right)}} $$
(6)

Consequently, a multistate model of the BESS is built, as shown in Fig. 3. Here, the first state at hour t in scenario k, denoted as sk,t,1, represents the unavailable state, and all the other states are the available states.

Fig. 3
figure 3

Multistate model of the BESS

Full size image

Due to the correlations of the SOC in time, the occurrence probabilities of the BESS states at hour t are determined by the probabilities of its states at hour t − 1, together with the corresponding states of the diesel generating system, the WES and the load during the time interval of t. We consider the BESS as a whole with a forced outage rate of FORBESS. In addition, assume that the state sk,0,1 has a probability of FORBESS, and all the other states occur equally with a probability of (1 – FORBESS)/(NSOC – 1) at hour 0 in scenario k.

Based on the above assumptions, the probability distribution of the states at hour t in scenario k can be calculated as (7) and (8). The expression of the conditional probability related to (8) and the derivation of (8) are illustrated in the Appendix.

$$ Pr_{\text{BESS}} \left\{ {s_{k,t,1} } \right\} = {\text{FOR}}_{\text{BESS}} $$
(7)
$$ \begin{aligned} Pr_{\text{BESS}} \left\{ {s_{k,t,f} } \right\} & = \sum\limits_{e = 2}^{{N_{\text{SOC}} }} {\sum\limits_{l = 1}^{{N_{L} }} {\sum\limits_{d = 0}^{{N_{\text{DG}} }} {\sum\limits_{g = 1}^{{N_{\text{WES}} }} {\left\{ {Pr_{\text{BESS}} \left\{ {s_{k,t - 1,e} } \right\}} \right.} } } } \\ & \, \cdot Pr_{\text{BESS}} \left\{ {s_{k,t,f} \left| {s_{k,t - 1,e} ,L_{k,t,l} ,P_{{{\text{DG,}}k ,t,d}} ,P_{{{\text{WES}},k,t,g}} } \right.} \right\} \\ & \, \cdot Pr_{\text{Load}} \left\{ {L_{k,t,l} } \right\} \cdot Pr_{\text{DG}} \left\{ {P_{{{\text{DG,}}k,t,d}} } \right\}\left. { \cdot Pr_{\text{WES}} \left\{ {P_{{{\text{WES}},k,t,g}} } \right\}} \right\}, \\ & \;\;f = 2,3, \cdots ,N_{\text{SOC}} \\ \end{aligned} $$
(8)

where l, d and g are the state indices of the load, the diesel generating system and the WES, respectively; f and e are the state indices of the BESS at different time intervals; PDG,k,t,d and PWES,k,t,g are the available capacities of the diesel generating system in state d and the WES in state g given by their own ACPTs; Pr is the occurrence probability of the considered state, distinguished by the subscripts of BESS, DG, and WES; NWES is the number of states of the WES.

3.4 System modeling

After modeling the load, the WES, the diesel generating system and the BESS are established, the overall states that the system are confronted with at hour t in scenario k can be obtained. Let SYS, L, D, G, and F denote the sets of states of the system, the load, the diesel generating system, the WES and the BESS, respectively. Then, l ∈ L = {1, 2, …, NL}; d ∈ D = {0, 1, 2, …, NDG}; g ∈ G = {1, 2, …, NWES}; f ∈ F = {1, 2, …, NSOC}. Let sys represent a certain state of the system. Moreover, the set SYS is determined by the Cartesian product of L, D, G, and F, i.e. SYS = L × D × G × F = {sys = (l, d, g, f) | l ∈ L, d ∈ D, g ∈ G, and f ∈ F}. In this way, the probability of the state sys at hour t in scenario k, denoted as PrSYS, k , t {sys}, can be calculated as:

$$ Pr_{{{\text{SYS,}}k ,t}} \left\{ {sys} \right\} = Pr_{\text{Load}} \left\{ {L_{k,t,l} } \right\}\cdot Pr_{\text{DG}} \left\{ {P_{{{\text{DG,}}k,t,d}} } \right\}\,\cdot Pr_{\text{WES}} \left\{ {P_{{{\text{WES}},k,t,g}} } \right\}\cdot Pr_{\text{BESS}} \left\{ {s_{k,t,f} } \right\} $$
(9)

Given the probabilities of overall states of the system, system reliability indices, such as loss of load expectation (LOLE) and loss of energy expectation (LOEE), can be calculated as follows:

  1. 1)

    The index LOLE is expressed as

$$ {\text{LOLE}} = 365 \cdot \sum\limits_{k = 1}^{{N_{C} }} {\sum\limits_{t = 1}^{{N_{T} }} {\sum\limits_{{sys \in \varvec{SYS}}} {\left\{ {\pi_{k} \cdot Pr_{{{\text{SYS,}}k ,t}} \left\{ {sys} \right\} \cdot I_{k,t,sys} } \right\}} } } $$
(10)

where N C is the number of the clusters; N T is the number of time intervals in a scenario, i.e. N T  = 24; Ik,t,sys is an indicator function given by (11).

$$ I_{k,t,sys} = \left\{ \begin{gathered} 1, \, L_{k,t,l} > MPS_{k,t,d,g,f} \hfill \\ 0, \, L_{k,t,l} \le MPS_{k,t,d,g,f} \hfill \\ \end{gathered} \right. $$
(11)

where MPSk,t,d,g,f is the maximum power output in state sys in the considered time interval, given by the sum of the available capacity of the diesel generating system in state d, the available capacity of the WES in state g, and the maximum discharge power of the BESS in state f.

  1. 2)

    The index of LOEE is determined by

$$ {\text{LOEE}} = 365 \cdot \sum\limits_{k = 1}^{{N_{C} }} {\sum\limits_{t = 1}^{{N_{T} }} {\sum\limits_{{sys \in \varvec{SYS}}} {\left\{ {\pi_{k} \cdot Pr_{{{\text{SYS,}}k ,t}} \left\{ {sys} \right\} \cdot M_{k,t} \left( {sys} \right)} \right\}} } } $$
(12)

If Lk,t,l is larger than MPSk,t,d,g,f in state sys, Mk,t(sys), denoting the loss of energy, is the absolute value of the difference between them; otherwise, Mk,t(sys) is zero.

4 Optimization formulation

Based on the obtained operational scenarios and the proposed reliability models, this section explains the optimization methods for the planning of stand-alone microgrids.

4.1 Problem formulation

For the microgrid shown in Fig. 1, we consider minimizing the present value of the costs occurring within the project lifetime, with the assumption that the load and the wind remain the same among the different years. The parallel number of the BESS (its series number is determined by the voltages of the BESS converter and the single battery), the numbers of the DGs and the WTGs, are selected as the decision variables, denoted as NBAT, NDG, and NWTG, respectively. Consequently, the problem can be formulated as

$$ \mathop { \hbox{min} }\limits_{{X \in \text{D}}} \, C_{\text{tot}} \left( X \right): = CI\left( X \right) + \sum\limits_{j = 1}^{T} {{{R_{j} \left( X \right)} \mathord{\left/ {\vphantom {{R_{j} \left( X \right)} {\left( {1 + r} \right)^{j} }}} \right. \kern-0pt} {\left( {1 + r} \right)^{j} }}} + {{SV\left( X \right)} \mathord{\left/ {\vphantom {{SV\left( X \right)} {\left( {1 + r} \right)^{T} }}} \right. \kern-0pt} {\left( {1 + r} \right)^{T} }} + {{\left( {M\left( X \right)\; + F\left( X \right)} \right)} \mathord{\left/ {\vphantom {{\left( {M\left( X \right)\; + F\left( X \right)} \right)} {\text{CRF}}}} \right. \kern-0pt} {\text{CRF}}} $$
(13)

where X is the decision vector; \( \text{D} \) is the range of the decision variables; Ctot is the sum of the present values of all the costs of the considered configuration; CI is the sum of the initial investment costs of all the equipment; R is the annual replacement costs of the equipment, due to the lifetime limits. In this paper, the battery lifetime is estimated by the Ah throughput aging model [2], [24]; T is the project lifetime; r is the discount rate; SV is the salvage costs of the equipment at the end of the project; M is the sum of the annual maintenance costs of the equipment, estimated as a proportion of their own initial investment costs; CRF is the capital recovery factor [2]. The more detailed calculations can be referred to [2], [3], [24]; and F is the annual fuel cost, given by

$$ F\left( X \right) = 365 \cdot \sum\limits_{k = 1}^{{N_{C} }} {\sum\limits_{t = 1}^{{N_{T} }} {\sum\limits_{{sys \in \varvec{SYS}}} {\left\{ {\pi_{k} \cdot Pr_{{{\text{SYS}},k,t}} \left\{ {sys} \right\} \cdot F_{k,t,sys} \cdot C_{fuel} } \right\}} } } $$
(14)

where Fk,t,sys is the fuel consumption of the DGs in state sys, determined by the relationship between power output and fuel consumption [2]; and C fuel is the fuel cost per liter.

To solve the problem in (13), the following constraints at each time interval in all the scenarios need to be considered:

  1. 1)

    Power balance: In each state sys ∈ SYS, the sum of the power output of diesel generating system, the power output of WES, and the discharge power of BESS plus the unmet load power should always be equal to the sum of the supplied load power and the charge power of BESS plus the dump load power. These quantities vary with the time, determined by the control strategies adopted in the system operation.

  2. 2)

    Operational constraints: In each state sys ∈ SYS, the operational constraints include power output limits of the DGs [6], maximum discharge and charge power limits of the BESS. Equation (15) to Eq. (18) describe the expressions of the constraints of the BESS. The energy transition of the BESS is expressed as (19) and (20).

$$ P_{{{\text{BESS}},{\text{dis}},k,t,sys}} \le MP_{{{\text{BESS}},{\text{dis}},k,t,sys}} $$
(15)
$$ P_{{{\text{BESS}},{\text{ch}},k,t,sys}} \le MP_{{{\text{BESS}},{\text{ch}},k,t,sys}} $$
(16)
$$ MP_{{{\text{BESS}},{\text{dis}},k,t,sys}} = { \hbox{min} }\,\left\{ {U_{\text{BESS}} I_{ \hbox{max} } ,U_{\text{BESS}} \frac{{C_{\text{BESS}} \left( {{\text{SOC}}_{k,t - 1,sys} - {\text{SOC}}_{ \hbox{min} } } \right)\eta_{\text{dis}} }}{\Delta t}} \right\} $$
(17)
$$ MP_{{{\text{BESS}},{\text{ch}},k,t,sys}} = { \hbox{min} }\left\{ {U_{\text{BESS}} I_{ \hbox{max} } ,\,U_{\text{BESS}} \frac{{C_{\text{BESS}} \left( {{\text{SOC}}_{ \hbox{max} } - {\text{SOC}}_{k,t - 1,sys} } \right)}}{{\eta_{\text{ch}} \Delta t}}} \right\} $$
(18)
$$ \begin{aligned} & {\text{if}}\;{\text{charge: }} \\ & {\text{SOC}}_{k,t,sys}^{{\prime }} = {\text{SOC}}_{k,t - 1,sys} + \frac{{P_{{{\text{BESS,ch,}}k,t,sys}} \Delta t\eta_{\text{ch}} }}{{U_{\text{BESS}} C_{\text{BESS}} }} ,\\ \end{aligned} $$
(19)
$$ \begin{aligned} & {\text{if}}\;{\text{discharge: }} \\ & {\text{SOC}}_{k,t,sys}^{{\prime }} = {\text{SOC}}_{k,t - 1,sys} - \frac{{P_{{{\text{BESS,dis,}}k,t,sys}} \Delta t}}{{U_{\text{BESS}} \eta_{\text{dis}} C_{\text{BESS}} }}. \\ \end{aligned} $$
(20)

where PBESS,dis,k,t,sys and PBESS,ch,k,t,sys are the discharge power and the charge power in state sys, respectively; MPBESS,dis,k,t,sys is the maximum discharge power; MPBESS,ch,k,t,sys is the maximum charge power; UBESS is the terminal voltage of BESS; Imax is the maximum permitted charge and discharge currents of the BESS; Δt is the time interval and set as 1 h; CBESS, ηch and ηdis are the rated capacity, the charge efficiency and the discharge efficiency of the BESS, respectively. In (17)–(20), SOCk,t−1,sys is the mean value of the SOC state f of the BESS, calculated as SOCk,t−1,sys = SOCmin + (f − 1.5)ΔS. The state of charge after transition, denoted as SOC′k,t,sys, is used to estimate the probability of BESS states in (23).

  1. 3)

    Reliability constraints:

    $$ \;{\text{LOLE}} \le {\text{LOLE}}_{\text{set}} $$
    (21)
    $$ \;{\text{LOEE}} \le {\text{LOEE}}_{\text{set}} $$
    (22)

    where LOLEset and LOEEset are the set values of reliability indices.

4.2 Solving method

Genetic algorithm [25] is applied to solve the optimization problem (13), which is no longer illustrated here for simplicity.

5 Case studies

A stand-alone microgrid (see in Fig. 1) is analyzed to explore the performance of the proposed method, which is located in the north area of Quebec of Canada. The hourly load and wind profiles of a typical year are shown in Fig. 4. The parameters associated with the method are: N C  = 12; N T  = 24; NSOC = 10; N L  = 3; N W  = 11; NWES = 8. The project lifetime and the discount rate are selected as 20 years and 3 %, respectively. The values of LOLEset and LOEEset are set as 8.76 h/yr and 11 550 kWh/yr, respectively. Some parameters related to the equipment are listed in Table 1. Additionally, the minimum load rate, the fuel curve intercept coefficient and the fuel curve slope of the DGs are 0.4, 0.077 27 L/h/kW, and 0.222 7 L/h/kW, respectively. The single WTG has a rated speed of 11 m/s, together with a cut-in speed of 3 m/s and a cut-out speed of 25 m/s. The lithium battery is considered, each with a voltage of 3.2 V, a charge/discharge efficiency of 0.95, and a lifetime throughput [2] of 1 152 kWh. The typical allowable range of SOC is from 0.1 to 0.9. The series number of the batteries is 240. And the battery life given in Table 1 refers to its float life [2].

Fig. 4
figure 4

Historical hourly data of the load and the wind during a typical year

Full size image
Table 1 Parameters related to the equipment (single unit)
Full size table
Table 2 Optimal results of the diverse configurations
Full size table

5.1 Scenario analysis

The k-mediods algorithm is applied to the given historical hourly data of the load and the wind, as shown in Fig. 4, and then the data are grouped into the expected clusters, some of which are reported in Fig. 5. Obviously, there are significant differences among the wind profiles in the obtained clusters, whereas the load profiles are similar and grouped tightly together.

Fig. 5
figure 5

Results of some clusters

Full size image

Therefore, compared with the load, it needs more states to model the wind speed distributions in each cluster. Moreover, the number of clusters also influences the performance of the clustering scenarios. The larger the number of clusters is, the easier it is to capture the daily patterns of the data, but the fewer objects there are in each cluster, and vice versa. Note that a large number of clusters may weaken the representativeness of scenarios. In this paper, the number of clusters is finally selected as 12 in terms of the local conditions of the studied microgrid.

5.2 Control strategy

In the stand-alone microgrid, the DGs serve as the main power sources, each with a power output greater than or equal to the minimum power level if they are working. Under this circumstance, at least one DG needs to be scheduled on all the time. When the wind is insufficient, the BESS is preferred to supply the load, and then increasing the power outputs of the operating DGs is considered as well as starting a new DG. If all these measures fail to meet the overall demands, a part of the load will be cut to ensure the power balance, referred to the unmet load. When the wind is abundant, some DGs are considered to be shut down, and the BESS may be charged by the excess wind power. The dump load may be activated in terms of the excess renewable energy as well.

5.3 Optimization results

5.3.1 Optimal configuration

Based on the clustering scenarios and the given control strategy, the optimal configuration of the study case is listed in Table 2. The table gives the optimal results of the wind-diesel system and the diesel-only system as well. Obviously, the configurations integrated with WES considerably reduce the system total cost compared with the diesel-only system. Introducing the BESS provides little help to the reductions in the system total cost; however, the BESS contributes to increase the penetration of wind power, reducing the need for large capacity diesel generating system, and consequently lowering the emission from the DGs, without violating the reliability constraints. Therefore, the wind-diesel-BESS system will gain more attentions in the future.

5.3.2 Sensitivity analysis of parameters

The number of states of the load, the BESS and the WES, affect the optimal configurations, for instance, Fig. 6 displays the impact of state number of the BESS on the system economics and the BESS capacity. From the figure, we can see that when the state number of the BESS increases more than 8, the variations in the system total cost and the BESS capacity becomes small, which indicates that this number can be treated as a threshold. As mentioned earlier, the lithium battery is applied in the case, which has a wide allowable range of SOC. Thus, more states are needed to model the BESS. Note that, the more states, the more accurate results, but the greater the computational burden. Thus, a tradeoff should be made between the modeling accuracy and the time. In the optimization process, diverse configurations consider the same wind distributions among all the scenarios. The number of wind states does not relate directly to the calculation of (8), thus its modeling accuracy has little effect on the overall calculation speed. Therefore, a large number of wind states at each time interval are suggested to present the daily patterns of the wind.

Fig. 6
figure 6

System total cost and parallel number of BESS versus state number of BESS. Note The values of system economics are the ratios of the corresponding system cost to the cost given in Table 2. We dealt with the remaining figures in the same way

Full size image

5.3.3 Sensitivity analysis of FORs

In order to illustrate the effects of the forced outage rates on the optimal configurations, FORs of the equipment in the diesel-wind-BESS system were varied from 0 to 0.10. Figure 7 shows the impacts of FORs on the capacities of diesel generating system, WES and BESS in the optimal configurations. Obviously, the number of DGs configured in the optimal results is mainly affected by its own FOR (as shown in Fig. 7a). In Fig. 7b, FORs of the equipment have no impact on the number of WTGs. As can be seen from Fig. 7c, when the FOR of single DG is not more than 0.02 in this case, a few DGs along with a large capacity BESS are capable of satisfying the system reliability indices, with better economic advantages as well. On the contrary, as the FOR of DG increases, the system with one or two DGs added, and with significantly decreased BESS capacity, can be more economical. Furthermore, the FOR of DG has much less influence on the capacities of WES and BESS.

Fig. 7
figure 7

Impacts of FORs of equipment on the capacities of equipment configured in the optimal configurations

Full size image

Figure 8 shows the system total cost as functions of the FORs of the equipment. The FOR of BESS barely affects the economics of the optimal configurations at different outage levels. The system total cost of the optimal configurations linearly increases as the FOR of single WTG increases. The reason is that, as the FOR of WTG increases, the reductions in total available energy from the WES result in that an added power output of the DGs is required to supply the load in certain time. Similarly, there is a significant increase in the system total cost at the DG FOR of 0.07 where the number of DGs increases, owing to that its own FORs play a decisive role in determining the optimal configurations. This change also occurs from the FORs of 0 to 0.02.

Fig. 8
figure 8

Impacts of FORs of the equipment on economics of optimal configurations

Full size image

Figure 9 and Fig. 10 demonstrate the comparisons of LOLE and LOEE of the diverse optimal configurations for different FORs of the equipment. Obviously, the DG FORs have significant effects on the system reliability performances. In addition, LOLE reaches nearly to the value of LOLEset at both the FORs of 0.01 and 0.06. When the DG FORs increase greater than these critical values, a new DG should be considered to satisfy the system reliability requirements. Note that two DGs, with a FOR of zero, are capable of supplying the overall demand. On the contrary, the reliability values of the optimal configurations fluctuate in a narrow range as the WTG FORs vary, due to the influence of the volatility of the wind power.

Fig. 9
figure 9

Impacts of FORs of the equipment on LOLE of optimal configurations

Full size image
Fig. 10
figure 10

Impacts of FORs of the equipment on LOEE of optimal configurations

Full size image

The results indicate that impacts of the WTG FORs on the system reliability can be neglected in the planning phase. The BESS has similar features on account of the task of storing wind power assigned by the control strategy.

6 Conclusion

In this paper, a novel method for the planning of stand-alone microgrids is introduced. For the obtained clustering scenarios, an overall multistate reliability model is established to investigate the impacts of FORs of the equipment on the optimal configurations. Moreover, an optimal planning model, with the objective of minimizing the system present cost, is illustrated. The proposed method is applied to a representative stand-alone microgrid. The sensitivity analysis of the parameters of the method indicates that the parameters chosen are suitable for solving the problem.

Likewise, sensitivity analysis of the FORs of the equipment has been conducted. The results show that the DGs, being the main power sources, play a vital role in the planning of a stand-alone microgrid. As the DG FORs increase, the installed capacity of the diesel generating system increases, unlike WES and BESS. However, the FORs of WES and BESS have little impact on the optimal configurations, due to their non-significant impacts on system reliability performance. In planning studies, to calculate the system reliability indices, it’s acceptable to assume that the WTGs have zero FORs, as well as the BESS acting as the role of storing the renewable energy.

Considering the load growth and the fluctuation of diesel cost not included in present work, planning of the stand-alone microgrids calls for further research effort.

7 Appendix

7.1 Expression of conditional probability related to (8)

This subsection presents the detailed expression of the conditional probability related to (8) in (23).

$$ \begin{aligned} & Pr_{\text{BESS}} \left\{ {s_{k,t,f} \left| {s_{k,t - 1,e} } \right.,L_{k,t,l} ,P_{{{\text{DG,}}k ,t,d}} ,P_{{{\text{WES}},k,t,g}} } \right\} \\ & \, = \left\{ \begin{gathered} 1,\;\;{\text{SOC}}_{k,t,sys}^{{\prime }} \in \left[ {{\text{SOC}}_{ \hbox{min} } + \left( {f - 2} \right) \cdot \Delta S,\;{\text{SOC}}_{ \hbox{min} } + \left( {f - 1} \right) \cdot \Delta S} \right) \hfill \\ 0,\;{\text{SOC}}_{k,t,sys}^{{\prime }} \notin \left[ {{\text{SOC}}_{ \hbox{min} } + \left( {f - 2} \right) \cdot \Delta S,\;{\text{SOC}}_{ \hbox{min} } + \left( {f - 1} \right) \cdot \Delta S} \right) \hfill \\ \end{gathered} \right. \\ \end{aligned} $$
(23)

Under the conditions that the system operates one hour with the given control strategy at hour t in scenario k, together with the BESS in state e, the load in state l, the WES in state g, and the diesel generating system in state d,if the state of charge SOC′k,t,sys calculated as (19) and (20) belongs to the interval in (23), the value of the conditional probability is 1, otherwise, the value is 0.

7.2 Derivation of (8)

Assume the BESS with a two-state Markov model [16] as well; its failure rate and repair rate are denoted as λ and μ, respectively. Note that its available state corresponds to various levels of the SOC. Besides the assumptions presented in Section 3.3, two additional assumptions are considered: if the BESS has a transition between its states: the transition from available state to unavailable state occurs at the end of time interval; the transition from unavailable state to available state occurs at the end of time interval as well, and the BESS after the transition inherits the SOC before failure.

If the FOR of BESS is zero, the equipment will always work. Then, the probabilities of the states shown in Fig. 3 can be calculated as (8). On the contrary, there needs to be a modification in (8) if the FOR of BESS is nonzero. Due to the assumption that the initial distribution of the probabilities of the states at hour 0 is stationary, the probabilities of the states subject to the stationary distribution at other time intervals as well [26]. In other words, the probability of the unavailable state is always FORBESS, and the cumulative probability of all the discrete states in which the BESS can work is 1 – FORBESS.

At the end of time t – 1, the BESS has a transition from state e to f if it is completely reliable. However, if the BESS has a nonzero FOR, the probability of the event of the transition from state e to state f should be modified as (1 – λΔt) · PrBESS{sk,t,f} on the premise of aformentioned assumptions.

Likewise, at the beginning of time t – 1, the BESS has a transition from state f to the unavailable state with a probability of λΔt · PrBESS{sk,t–1,f}. Then, at the end of time t – 1, the BESS will have a transition from the unavailable state to state f with a probability of FORBESS · μΔt · PrBESS{sk,t–1,f}/(1 – FORBESS). Note that

$$ \begin{aligned} & {\text{FOR}}_{\text{BESS}} \cdot \mu \Delta t \cdot {{Pr_{\text{BESS}} \left\{ {s_{k,t - 1,f} } \right\}} \mathord{\left/ {\vphantom {{Pr_{\text{BESS}} \left\{ {s_{k,t - 1,f} } \right\}} {\left( {1 - {\text{FOR}}_{\text{BESS}} } \right)}}} \right. \kern-0pt} {\left( {1 - {\text{FOR}}_{\text{BESS}} } \right)}} \\ & \, = \frac{\lambda }{\lambda + \mu } \cdot \mu \Delta t \cdot {{Pr_{\text{BESS}} \left\{ {s_{k,t - 1,f} } \right\}} \mathord{\left/ {\vphantom {{Pr_{\text{BESS}} \left\{ {s_{k,t - 1,f} } \right\}} {\left( {1 - \frac{\lambda }{\lambda + \mu }} \right)}}} \right. \kern-0pt} {\left( {1 - \frac{\lambda }{\lambda + \mu }} \right)}} \\ & \, = \lambda \Delta t \cdot Pr_{\text{BESS}} \left\{ {s_{k,t - 1,f} } \right\} \\ \end{aligned} $$
(24)

Therefore, the expression (1 – λΔt) · PrBESS{sk,t,f} has only to be further modified by λΔt · Pr{sk,t–1,f} at the end of time t – 1. Consequently, the modification is expressed as

$$ \overline{Pr }_{\text{BESS}} \left\{ {s_{k,t,f} } \right\} = \lambda \Delta t \cdot Pr_{\text{BESS}} \left\{ {s_{k,t - 1,f} } \right\} + \left( {1 - \lambda \Delta t} \right) \cdot Pr_{\text{BESS}} \left\{ {s_{k,t,f} } \right\},\;\;f = 2,3, \cdots ,N_{\text{SOC}} $$
(25)

where \( \overline{Pr }_{\text{BESS}} \left\{ {s_{k,t,f} } \right\} \) is the probability of state f considering the possible state transitions of the BESS.

In general, the FOR of the BESS is small, especially the converters [27], [28], and then the expression λΔt ≪ 1 is valid, where Δt = 1. Therefore, (25) can be simplified as (8), decoupling the unavailable state and the discrete SOC states.