Does driving-day-based tradable credit scheme outperform license plate rationing? Examination considering transaction cost

Abstract

This article models a novel driving-day-based tradable credit scheme (DD-TCS) to alleviate urban traffic congestion. In this model, car-using allowances (in terms of the number of days in a month, termed as “credit”) are freely and uniformly allocated to all travellers, who are also allowed to trade them in a market according to his/her travel needs (e.g. driving more or fewer days than the free endowment). As opposed to most studies on TCS, this paper explicitly considers the transaction cost (e.g. information cost of finding potential traders) in the trading market. To assess the feasibility of DD-TCS, we compare it against the license plate rationing (LPR) scheme, which has been practically implemented in many cities such as Beijing and Chengdu in China. Taking the performance of LPR as a benchmark, we quantify the threshold values of the transaction cost in DD-TCS when the two schemes yield equivalent performance (in terms of the total generalized cost). In numerical studies, we also compare the DD-TCS and LPR with the no-action case and the congestion pricing case (representing the theoretical optimum). Results show that both DD-TCS and LPR outperform the no-action case under certain conditions. With small transaction cost, DD-TCS may achieve a lower system cost that can be very close to the ideal optimum. In addition, parameter analysis shows that DD-TCS performs better than LPR in a wide range of transaction cost, where the threshold values appear to account for a considerable portion of the auto travel time. This implies that DD-TCS will be more appealing than LPR in practice because a transaction cost lower than the extremely large threshold values can be easily achieved for the trading market, e.g. via a mobile platform and modern communication techniques.

1 Introduction

License plate rationing (LPR) is a possible solution to reduce urban traffic congestion. It restricts private vehicles from entering a specified area on certain days based on the last digit of a license plate. As LPR can offer a quick congestion relief to local roadway network, it has become popular in many Chinese cities that suffer from dense and chaotic traffic, as well as in other cities around the world [1]. The implementation of LPR in China can be dated to the period of 2008 Beijing Olympic Games. The government adopted a highly restrictive LPR scheme known as odd–even rationing, in which private cars were only allowed to be driven on roads every other weekday. LPR then has been adopted since 2011. Later, many other Chinese cities, including Chengdu, Tianjin, and Hangzhou, have adopted similar LPR schemes to manage travel demand. However, empirical and theoretical studies have proved the following facts:

• 1. LPR is not a first-best policy. In fact, there is no guarantee that LPR can even be a second-best policy. It may never improve the system performance regardless of network configuration [2, 3, 5].

• 2. When it does improve the system performance, LPR makes it impossible to optimize the system cost by using other complementary policies [4, 5].

• 3. When the induced demand is considered, LPR always leads to welfare losses [6].

• 4. An over-restrictive LPR, e.g. the even–odd rationing, could make congestion worse when imposed on a rich population that can afford additional cars to bypass the policy [7].

Although it may not be an ideal tool of managing traffic congestion in the long run, it could be useful to deal with temporary traffic problems under certain conditions (as in the case of Beijing Olympic Games). To correct the shortcomings of a pure LPR policy, some new joint policies were developed, such as coupling the LPR with auto ownership control and turning the driving permits into tradable credits [1]. Tradable credit schemes (TCSs), as a new measure of traffic demand management, have attracted more and more attentions over the past few years [8]. In general, under a TCS, travellers who want to use the roadway resources will have to pay credits, rather than to pay tolls or tax in congestion pricing (CP). Initial credits may be free and distributed to the travellers by the government. Then, if roadway users need additional mobility credits, they may buy from a free trade market, or if they have extra credits, they may also sell them and gain monetary rewards. This will encourage travellers to cut down travel needs during rush hours and ease traffic congestion.

Insightful findings from existing studies demonstrate that TCS could be not only as efficient as the CP in managing travel demand, but also possess advantages in terms of revenue neutrality and social equity. For instance, Yang and Wang [9] proposed a TCS in which credits are universal for usage in a network and proved that a unique flow pattern of user equilibrium exists within homogeneous travellers. This work was expanded by Wang et al. [10]. They explored a case with heterogeneous travellers who have different values of time (VOTs). Another follow-up research is Nie’s [7] that compared an auction market and a negotiated market for the TCS. Wu et al. [11] further considered the effect of travellers’ income on their travel choices under TCS policy in a multimodal network. Gao et al. [12] studied a combinatorial problem of the optimal TCS design and bus system investment. Other forms of TCS models include a parking model [13], a bottleneck model [14], a park-and-ride model [15], and most recently a link-based cyclic TCS model [16].

Nonetheless, one big pitfall in TCS is the “transaction cost”, which is the cost incurred by traders in carrying out a transaction itself. As Coase [17] indicated that transaction cost is influenced by the costs of estimating the need and the amount of goods to be traded, acquiring trade information (e.g. finding potential traders), price negotiations, drawing up a contract and inspecting trade under contract terms, and so on. Fan and Jiang [8] and Nie [7] indicated that the transaction cost of TCS is associated with how the credits are delineated (e.g. trip-based and link-based or universal) and collected on roads, and it could be so considerable to prevent a trading market from working. Furthermore, the practicality of these TCS also relies on advanced roadside credit collection systems that impose credit charging on every links of the entire network.

To deal with the difficulty in designing a complex TCS with uncertain practicability, we build a simplified driving-day-based TCS model (DD-TCS) that can be readily implemented and need no more facilities than the current LPR system. Under the DD-TCS, the government freely allocate car-using allowances (in terms of the number of days in a month, termed as “credits”) to all travellers who are allowed to trade them in a market according to their travel needs. Basically, both the proposed DD-TCS and LPR manage travel demand via “driving days”, but the former allows trading and the latter uses regulation. DD-TCS is expected to receive more public acceptance than LPR in cities. For instance, low-income travellers may benefit from selling additional credits, while high-income travellers may enjoy better mobility by buying additional credits.

To conduct an apple-to-apple comparison between DD-TCS and LPR, we explicitly consider the impacts of transaction cost. Instead of directly measuring the transaction cost of DD-TCS that is very difficult, we seek to find the threshold value of the transaction cost that ensures the performance of DD-TCS no worse than that of the LPR as the benchmark scenario. Sensitivity analyses are also conducted to reveal the impacts of different wealth distributions in population. The comparison results may shed lights on the practicability and superiority of the DD-TCS over the regulatory LPR. More importantly, the findings in this paper would be used to promote the replacement of the LPR with DD-TCS, which might become the first type of TCS implemented in real world.

The rest of the paper is organized as follows. In Sect. 2, the LPR and DD-TCS models are introduced. Then, in Sect. 3, we develop the analytic solutions and discuss the results of numerical cases in Sect. 4; the sensitivity analysis of transaction cost and user heterogeneity is also presented in this section. The main findings are summarized in Sect. 5.

2 Models

2.1 Modelling framework

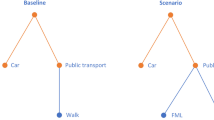
According to Nie’s work [1, 5], we consider a single origin–destination (O–D) corridor connecting the city centre and its suburb with two available travel modes: the auto via the highway and the public transit, as shown in Fig. 1. It is assumed that the total demand d is inelastic during the morning peak hours, which represents the demand of captive commuters. The commuters are considered to be heterogeneous in terms of their socio-economical characteristics. Let F(β) describe the distribution of travellers’ VOT denoted by β, and F(β) is a cumulative density function, defined as a continuous and strictly decreasing function of β. F(β_L) indicates the total number of travellers whose VOT $\beta \ge \beta_{\text{L}}$, where β_L is the minimum VOT. Let β_U be the maximum VOT among all commuters ($\beta_{\text{U}} > \beta_{\text{L}} > 0$); we have $F\left( {\beta_{\text{U}} } \right) = 0$. Conversely, for any given $q^{ *}$, the inverse function $F^{ - 1} \left( {q^{ *} } \right)$ identifies a unique $\beta^{ *}$, implying that there are $q^{ *}$ commuters with VOTs no less than $\beta^{ *}$. Particularly, $F^{ - 1} \left( d \right) = \beta_{\text{L}}$ and $F^{ - 1} \left( 0 \right) = \beta_{\text{U}}$.

Fig. 1

A commuting corridor with two travel modes

In the corridor, commuters’ travel disutility is composed of two types of costs, i.e. time and monetary cost components. Let $\tau \left( q \right)$ be the auto travel time on the highway, which is expressed as a strictly increasing and convex function of the highway flow q. The demand of the transit mode is thus (d − q), whose travel time γ is assumed to be a fixed value, being a sum of all time components including walking time to access/egress bus stops, waiting time at stops, and in-vehicle time (generally invariable to variations in transit demand) in the transit trip. Let c_A and c_T be the monetary costs per trip associated with travelling in auto and transit modes, respectively. c_A can be calibrated according to auto users’ average fuel consumption, parking fee at city centre, and any other out-of-pocket cost (e.g. congestion fee if any). c_T accounts for transit fare. Additionally, auto travellers incur costs for owing a private car, such as purchase cost and insurance cost, which is amortized over the study period with a unit cost and denoted by φ in this paper. Without loss of generality, it is hypothesized that the auto mode provides commuters a shorter travel time under the free-flow condition, but a higher monetary cost; that is, $\tau \left( 0 \right) < \gamma$ and c_A > c_T.

Therefore, the travel disutility of an individual commuter using the two travel modes (u_A for auto and u_T for transit) can be expressed as follows:

$$u_{\text{A}} = \beta \tau \left( q \right) + c_{\text{A}} + \varphi ,$$

(1)

$$u_{\text{T}} = \beta \gamma + c_{\text{T}} .$$

(2)

In the following sections, we will first model commuters’ travel choices under the LPR policy and then DD-TCS.

2.2 LPR models

Under the policy of LPR, the local authority regulates the usage of private cars with the expectation to alleviate the roadway traffic congestion. It limits the usage of private cars on valid days during a policy period (e.g. a week and a month) according to license plate numbers. For instance, the odd-and-even policy in Beijing (China) and the last digit policy in Chengdu (China) are the two most common forms of LPR policies in practice. In general, by rationing the valid days (denoted by $\lambda \in \left[ {0,1} \right]$, assumed to be continuous), the LPR policy manages to allow a proper portion of auto owners to utilize the roadway with less congestion. Thus, various values of λ represent how the LPR policy is implemented: λ = 1 indicates no rationing, λ = 0 means the strictest rationing, and for the two cases in Chengdu and Beijing, λ = 0.8 and 0.5, respectively.

Given the LPR ratio λ, the travel disutility of auto mode (Eq. 1) can be rewritten as

$$u_{\text{A}} = \lambda \left( {\beta \tau \left( {\lambda q_{\text{a}} } \right) + c_{\text{A}} } \right) + \left( {1 - \lambda } \right)\left( {\beta \gamma + c_{\text{T}} } \right) + \varphi ,$$

(3)

where q_a is the demand of auto owners and λq_a gives the average highway flow per day by assuming that the auto trips of auto owners are uniformly distributed during a policy period; $\lambda \left( {\beta \tau \left( {\lambda q_{\text{a}} } \right) + c_{\text{A}} } \right)$ yields the average travel cost per day by auto on the valid days, and $\left( {1 - \lambda } \right)\left( {\beta \gamma + c_{\text{T}} } \right)$ produces the average travel cost per day by transit when the private cars are ineligible.

2.2.1 User equilibrium condition under LPR

In a long term, the user equilibrium (UE) will be reached on the bimodal corridor when a traveller cannot minimize travel disutility by unilaterally changing the mode choice. Thus, we have $u_{\text{A}} \left( {\beta_{\text{e}} } \right) = u_{\text{T}} \left( {\beta_{\text{e}} } \right)$ for the individual (often referred as the indifferent traveller at UE) with VOT of β_e. For commuters with β > β_e, they have $u_{\text{A}} \left( \beta \right) < u_{\text{T}} \left( \beta \right)$, and vice versa. Let q_e be the demand of auto owners under UE, it can be obtained by first replacing β with $F^{ - 1} \left( {q_{\text{e}} } \right)$ in Eqs. (1) and (3) and then solving the following equation:

$$\lambda \left( {F^{ - 1} \left( {q_{\text{e}} } \right)\tau \left( {\lambda q_{\text{e}} } \right) + c_{\text{A}} } \right) + \left( {1 - \lambda } \right)\left( {F^{ - 1} \left( {q_{\text{e}} } \right)\gamma + c_{\text{T}} } \right) + \varphi - F^{ - 1} \left( {q_{\text{e}} } \right)\gamma - c_{\text{T}} = 0.$$

(4)

The performance of the LPR policy can be measured by the total system cost per day, which is the sum of all commuters’ travel cost under UE:

$$\begin{aligned} G_{\text{LPR}} & = \lambda \left( {\tau \left( {\lambda q_{\text{e}} } \right)\mathop \int \limits_{0}^{{q_{\text{e}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{A}} q_{\text{e}} } \right) + \left( {1 - \lambda } \right)\left( {\gamma \mathop \int \limits_{0}^{{q_{\text{e}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} q_{\text{e}} } \right) + \varphi q_{\text{e}} \\ & \quad + \gamma \mathop \int \limits_{{q_{\text{e}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} \left( {d - q_{\text{e}} } \right), \\ \end{aligned}$$

(5)

where $\int_{0}^{{q_{\text{e}} }} {F^{ - 1} } \left( w \right){\text{d}}w$ yields the cumulative VOTs of all commuters who have $\beta \ge \beta_{\text{e}}$ and own auto vehicles (travel by auto on valid days and by transit on other days); and $\int_{{q_{\text{e}} }}^{d} {F^{ - 1} } \left( w \right){\text{d}}w$ produces the cumulative VOTs of the others who have β < β_e and travel in the transit mode.

2.3 DD-TCS models

Unlike the above LPR model, the DD-TCS treats the designated valid days as “driving-day credits” and allows free trading of credits among credit holders (e.g. auto drivers or all-mode travellers). Generally, the credit market can be initialized by allocating/endowing credits free of charge to all travellers. Upon the usage of private cars, travellers are “charged” by the authority via ticketing their credits. The DD-TCS is thus revenue neutral and all traders are expected to benefit from trading the driving-day credits under perfect market assumption. As pointed out by Nie [18], however, the credit trading inevitably incurs transaction cost on the traders, such as information cost (e.g. finding other traders, and trading with other traders), bargaining cost, and inconvenience. To explicitly consider the impacts of transaction cost, the following models are established.

Let $x \in \left[ {0,1 - \lambda } \right],y \in \left[ {0,\lambda } \right]$ be the amount (also quantified as the ratio of valid days out of the policy period and assumed to be continuous variables) of credits bought and sold per trader during the policy period (e.g. 1 month). Equation (4) is thus rewritten as Eqs. (6–8) under three scenarios:

(1) Transit users sell and drivers buy, i.e. T–D scenario:

$$\begin{aligned} & \left( {\lambda + x} \right)(F^{ - 1} \left( {q_{\text{a}} } \right)\tau \left( {q_{\text{a}} \left( {\lambda + x} \right)) + c_{\text{A}} } \right) + \left( {1 - \lambda - x} \right)\left( {F^{ - 1} \left( {q_{\text{a}} } \right)\gamma + c_{\text{T}} } \right) + \varphi + xP_{\text{C}} \\ & \quad + xT_{\text{C}} F^{ - 1} \left( {q_{\text{a}} } \right) = F^{ - 1} \left( {q_{\text{a}} } \right)\gamma + c_{\text{T}} - yP_{\text{C}} + yT_{\text{C}} F^{ - 1} \left( {q_{\text{a}} } \right), \\ \end{aligned}$$

(6a)

$$y\left( {d - q_{\text{a}} } \right) = xq_{\text{a}} ,$$

(6b)

where the left-hand side (LHS) of Eq. (6a) represents the travel cost of auto owners (also the credit buyers), and the right-hand side (RHS) is that of transit users (i.e. credit sellers); Eq. (6b) shows the buying–selling conservation; P_C is the market price per credit; and T_C is the transaction cost in unit of time, e.g. minute per credit.

(2) Transit users and partial drivers sell and other drivers buy, i.e. T&D–D scenario:

$$\begin{aligned} & \left( {\lambda + x} \right)\left( {F^{ - 1} \left( {q_{\text{b}} } \right)\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right) + c_{\text{A}} } \right) + \left( {1 - \lambda - x} \right)\left( {F^{ - 1} \left( {q_{\text{b}} } \right)\gamma + c_{\text{T}} } \right) + \varphi \\ & \quad + xP_{\text{C}} + xT_{\text{C}} F^{ - 1} \left( {q_{\text{b}} } \right) = \left( {\lambda - y} \right)\left( {F^{ - 1} \left( {q_{\text{b}} } \right)\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right) + C_{\text{A}} } \right) \\ & \quad + \left( {1 - \lambda + y} \right)\left( {F^{ - 1} \left( {q_{\text{b}} } \right)\gamma + c_{\text{T}} } \right) + \varphi - yP_{\text{C}} + yT_{\text{C}} F^{ - 1} \left( {q_{\text{b}} } \right), \\ \end{aligned}$$

(7a)

$$\begin{aligned} & \left( {\lambda - y} \right)(F^{ - 1} \left( {q_{\text{a}} } \right)\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)) + c_{\text{A}} } \right) + \left( {1 - \lambda + y} \right)\left( {F^{ - 1} \left( {q_{\text{a}} } \right)\gamma + c_{\text{T}} } \right) + \varphi \\ & \quad - yP_{\text{C}} + yT_{\text{C}} F^{ - 1} \left( {q_{\text{a}} } \right) = F^{ - 1} \left( {q_{\text{a}} } \right)\gamma + c_{\text{T}} - yP_{\text{C}} + yT_{\text{C}} F^{ - 1} \left( {q_{\text{a}} } \right), \\ \end{aligned}$$

(7b)

$$y\left( {d - q_{\text{b}} } \right) = xq_{\text{b}},$$

(7c)

where q_b is the number of auto owners who buy credits; $\left( {q_{\text{a}} - q_{\text{b}} } \right)$ yields the number of auto owners who sell credits. The LHS and RHS of Eq. (7a) are the travel cost of auto owners who are buyers and sellers, respectively. The LHS and RHS of Eq. (7b) are the travel cost of credit sellers who are car owners and transit users, respectively.

(3) Considering the scenario that only auto drivers are endowed free credits, then trading can only occur among drivers, i.e. D–D scenario:

$$\begin{aligned} & \left( {\lambda + x} \right)\left( {F^{ - 1} \left( {q_{\text{b}} } \right)\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right) + c_{\text{A}} } \right) + \left( {1 - \lambda - x} \right)\left( {F^{ - 1} \left( {q_{\text{b}} } \right)\gamma + c_{\text{T}} } \right) + \varphi \\ & \quad + xP_{\text{C}} + xT_{\text{C}} F^{ - 1} \left( {q_{\text{b}} } \right) = \left( {\lambda - y} \right)\left( {F^{ - 1} \left( {q_{\text{b}} } \right)\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right) + C_{\text{A}} } \right) \\ & \quad + \left( {1 - \lambda + y} \right)\left( {F^{ - 1} \left( {q_{\text{b}} } \right)\gamma + c_{\text{T}} } \right) + \varphi - yP_{\text{C}} + yT_{\text{C}} F^{ - 1} \left( {q_{\text{b}} } \right), \\ \end{aligned}$$

(8a)

$$\begin{aligned} & \left( {\lambda - y} \right)(F^{ - 1} \left( {q_{\text{a}} } \right)\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)) + c_{\text{A}} } \right) + \left( {1 - \lambda + y} \right)\left( {F^{ - 1} \left( {q_{\text{a}} } \right)\gamma + c_{\text{T}} } \right) \\ & \quad + \varphi - yP_{\text{C}} + yT_{\text{C}} F^{ - 1} \left( {q_{\text{a}} } \right) = F^{ - 1} \left( {q_{\text{a}} } \right)\gamma + c_{\text{T}} , \\ \end{aligned}$$

(8b)

$$y\left( {q_{\text{a}} - q_{\text{b}} } \right) = xq_{\text{b}} ,$$

(8c)

where (8a) is the same as (7a) and the RHS of Eq. (8b) indicates the travel cost of transit users who have no credits to sell. From Eq. (8a, 8b), we can obtain that q_a is determined by

$$F^{ - 1} \left( {q_{\text{a}} } \right)\left( {\gamma - \tau \left( {\lambda q_{\text{a}} } \right)} \right) = \left( {c_{\text{A}} - c_{\text{T}} } \right) + \frac{\varphi }{\lambda }.$$

(8d)

The total system cost for DD-TCS under the above three scenarios is then expressed as follows:

T–D scenario:

$$\begin{aligned} G_{\text{TCS}} & = \left( {\lambda + x} \right)\left( {\tau \left( {q_{\text{a}} \left( {\lambda + x} \right) } \right)\mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{A}} q_{\text{a}} } \right) + \left( {1 - \lambda - x} \right)\left( {\gamma \mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} q_{\text{a}} } \right) \\ & \quad + \varphi q_{\text{a}} + \gamma \mathop \int \limits_{{q_{\text{a}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} \left( {d - q_{\text{a}} } \right) \\ & \quad + T_{\text{C}} \left( {x\mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + y\mathop \int \limits_{{q_{\text{a}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w} \right), \\ \end{aligned}$$

(9)

T&D–D scenario:

$$\begin{aligned} G_{\text{TCS}} & = \left( {\lambda + x} \right)\left( {\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right)\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{A}} q_{\text{b}} } \right) \\ & \quad + \left( {1 - \lambda - x} \right)\left( {\gamma \mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} q_{\text{b}} } \right) + \left( {\lambda - y} \right) \\ & \quad \quad \left( {\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right)\mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{A}} (q_{\text{a}} - q_{\text{b}} )} \right) \\ & \quad + \left( {1 - \lambda + y} \right)\left( {\gamma \mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} (q_{\text{a}} - q_{\text{b}} )} \right) + \varphi q_{\text{a}} + \gamma \mathop \int \limits_{{q_{\text{a}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} \left( {d - q_{\text{a}} } \right) \\ & \quad + T_{\text{C}} \left( {x\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + y\mathop \int \limits_{{q_{\text{b}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w} \right), \\ \end{aligned}$$

(10)

D–D scenario:

$$\begin{aligned} G_{\text{TCS}} & = \left( {\lambda + x} \right)\left( {\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right)\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{A}} q_{\text{b}} } \right) \\ & \quad + \left( {1 - \lambda - x} \right)\left( {\gamma \mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} q_{\text{b}} } \right) + \left( {\lambda - y} \right) \\ & \quad \quad \left( {\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right)\mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{A}} (q_{\text{a}} - q_{\text{b}} )} \right) \\ & \quad + \left( {1 - \lambda + y} \right)\left( {\gamma \mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} (q_{\text{a}} - q_{\text{b}} )} \right) + \varphi q_{\text{a}} + \gamma \mathop \int \limits_{{q_{\text{a}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} \left( {d - q_{\text{a}} } \right) \\ & \quad + T_{\text{C}} \left( {x\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + y\mathop \int \limits_{{q_{\text{b}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w} \right). \\ \end{aligned}$$

(11)

3 Analysis of system optimum of DD-TCS

Given a certain value of T_C, the system optimal (SO) condition of DD-TCS can be reached by minimizing G_TCS (Eqs. 9–11) with the corresponding constraints (Eqs. 6–8). Taking the T–D scenario for example, the following first-order conditions of G_TCS should hold with respect to the control variable, λ, and two state variables, i.e. the auto demand q_a and the credit trading quantity x under SO condition:

$$\frac{{\partial G_{\text{TCS}} }}{{\partial \lambda^{*} }} = 0,\quad \frac{{\partial G_{\text{TCS}} }}{{\partial q_{\text{a}}^{*} }} = 0,\quad \frac{{\partial G_{\text{TCS}} }}{{\partial x^{*} }} = 0.$$

(12)

Thus, we have three equations about three variables:

$$\begin{aligned} \frac{{\partial G_{\text{TCS}} }}{{\partial \lambda^{*} }} & = \left( {\tau \left( {q_{\text{a}}^{*} \left( {\lambda^{*} + x^{*} } \right)} \right)\mathop \int \limits_{0}^{{q_{\text{a}}^{*} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{A}} q_{\text{a}}^{*} } \right) + \left( {\lambda^{*} + x^{*} } \right)q_{\text{a}}^{*} \tau^{\prime } \left( {q_{\text{a}}^{*} \left( {\lambda^{*} + x^{*} } \right)} \right)\mathop \int \limits_{0}^{{q_{\text{a}}^{*} }} F^{ - 1} \left( w \right){\text{d}}w \\ & \quad - \left( {\gamma \mathop \int \limits_{0}^{{q_{\text{a}}^{*} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{T}} q_{\text{a}}^{*} } \right) = 0, \\ \end{aligned}$$

(13)

$$\begin{aligned} \frac{{\partial G_{\text{TCS}} }}{{\partial q_{a}^{*} }} & = \left( {\lambda + x^{*} } \right)\left( {\tau \left( {q_{\text{a}}^{*} \left( {\lambda^{*} + x^{*} } \right)} \right)F^{ - 1} \left( {q_{\text{a}}^{*} } \right) + \left( {\lambda^{*} + x^{*} } \right)\tau^{\prime } \left( {q_{\text{a}}^{*} \left( {\lambda^{*} + x^{*} } \right)} \right)\mathop \int \limits_{0}^{{q_{\text{a}}^{ *} }} F^{ - 1} \left( w \right){\text{d}}w + c_{\text{A}} } \right) +\\ & \quad \left( {1 - \lambda^{*} - x^{*} } \right)\left( {F^{ - 1} \left( {q_{\text{a}}^{*} } \right)\gamma + c_{\text{T}} } \right) + \\ & \quad \varphi - F^{ - 1} \left( {q_{\text{a}}^{*} } \right)\gamma - c_{\text{T}} + x^{*} T_{\text{C}} F^{ - 1} \left( {q_{\text{a}}^{*} } \right) - \\ & \quad T_{\text{C}} \frac{{x^{*} q_{\text{a}}^{*} }}{{d - q_{\text{a}}^{*} }}F^{ - 1} \left( {q_{\text{a}}^{*} } \right) + \frac{{x^{*} T_{\text{C}} d}}{{\left( {d - q_{\text{a}}^{*} } \right)^{2} }}\mathop \int \limits_{{q_{\text{a}}^{ *} }}^{d} F^{ - 1} \left( w \right){\text{d}}w = 0, \\ \end{aligned}$$

(14)

$$\begin{aligned} \frac{{\partial G_{\text{TCS}} }}{{\partial x^{*} }} & = q_{\text{a}}^{*} \left( {\lambda^{*} + x^{*} } \right)\tau^{\prime } \left( {q_{\text{a}}^{*} \left( {\lambda^{*} + x^{*} } \right)} \right)\mathop \int \limits_{0}^{{q_{\text{a}}^{ *} }} F^{ - 1} \left( w \right){\text{d}}w \, + \\ & \tau \left( {q_{\text{a}}^{*} \left( {\lambda^{*} + x^{*} } \right)} \right)\mathop \int \limits_{0}^{{q_{\text{a}}^{*} }} F^{ - 1} \left( w \right){\text{d}}w + (c_{\text{A}} - c_{\text{T}} )q_{\text{a}}^{*} - \\ & \gamma \mathop \int \limits_{0}^{{q_{\text{a}}^{*} }} F^{ - 1} \left( w \right){\text{d}}w + T_{\text{C}} \mathop \int \limits_{0}^{{q_{\text{a}}^{*} }} F^{ - 1} \left( w \right){\text{d}}w \, + \\ & \frac{{T_{\text{C}} q_{\text{a}}^{*} }}{{\left( {d - q_{\text{a}}^{*} } \right)}}\mathop \int \limits_{{q_{\text{a}}^{*} }}^{d} F^{ - 1} \left( w \right){\text{d}}w = 0. \\ \end{aligned}$$

(15)

Solving the above two equations can give us the optimal $\lambda^{*} ,q_{\text{a}}^{*} ,\,{\text{and}}\,x^{*}$ in the SO condition. The uniqueness of the optimal solution can be proved by convex analysis on the minimization of Eq. (9). In doing so, we take the second-order partial derivatives of Eq. (9) as follows:

$$\begin{aligned} \frac{{\partial G_{\text{TCS}} }}{{\partial \lambda^{2} }} & = q_{\text{a}} \tau^{\prime } \left( {q_{\text{a}} \left( {\lambda + x} \right)} \right)\mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + q_{\text{a}} \tau \left( {q_{\text{a}} \left( {\lambda + x} \right) } \right)\mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w \\ & \quad + \left( {\lambda + x} \right)q_{\text{a}}^{2} \tau^{\prime \prime } \left( {q_{\text{a}} \left( {\lambda + x} \right) } \right)\mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w\text{}, \\ \end{aligned}$$

(16)

$$\begin{aligned} \frac{{\partial^{2} G_{\text{TCS}} }}{{\partial q_{\text{a}}^{2} }} & = \left( {\lambda + x} \right)F^{{ - 1^{\prime } }} \left( {q_{\text{a}} } \right)\left( {\tau \left( {q_{\text{a}} \left( {\lambda + x} \right)} \right) - \gamma } \right) +\\ & \quad 2\left( {\lambda + x} \right)^{2} \tau^{\prime } \left( {q_{\text{a}} \left( {\lambda + x} \right)} \right)F^{ - 1} \left( {q_{\text{a}} } \right) + \\ & \quad \left( {\lambda + x} \right)^{3} \tau^{\prime \prime } \left( {q_{\text{a}} \left( {\lambda + x} \right)} \right)\mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w \, + \\ & \quad xT_{\text{C}} F^{{ - 1^{\prime } }} \left( {q_{\text{a}} } \right) - T_{\text{C}} \frac{x}{{\left( {d - q_{\text{a}} } \right)^{2} }}F^{ - 1} \left( {q_{\text{a}} } \right) - \\ & \quad T_{\text{C}} \frac{{xq_{\text{a}} }}{{d - q_{\text{a}} }}F^{{ - 1^{\prime } }} \left( {q_{\text{a}} } \right) + \frac{{2xT_{\text{C}} d}}{{\left( {d - q_{\text{a}} } \right)^{3} }}\mathop \int \limits_{{q_{\text{a}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w \, - \\ & \quad T_{\text{C}} \frac{{{\text{d}}x}}{{\left( {d - q_{\text{a}} } \right)^{3} }}F^{ - 1} \left( {q_{\text{a}} } \right)\text{}, \\ \end{aligned}$$

(17)

$$\frac{{\partial^{2} G_{\text{TCS}} }}{{\partial x^{2} }} = \left( {\lambda + x} \right)q_{\text{a}}^{2} \tau^{\prime \prime } \left( {q_{\text{a}} \left( {\lambda + x} \right) } \right)\mathop \int \limits_{0}^{{q_{\text{e}} }} F^{ - 1} \left( w \right){\text{d}}w + 2q_{\text{a}} \tau^{\prime } \left( {q_{\text{a}} \left( {\lambda + x} \right)} \right)\mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w.$$

(18)

From the definitions of $F\left( \cdot \right)$ and $\tau \left( \cdot \right)$, we know $F^{{ - 1^{\prime } }} \left( {q_{\text{a}} } \right) < 0$ and $\tau^{\prime } \left( \cdot \right) > 0,\tau^{\prime \prime } \left( \cdot \right) \ge 0$. Additionally, it is implicitly implied that the auto trip time should be less than that of transit trip, i.e. $\tau \left( {q_{\text{a}} \left( {\lambda + x} \right)} \right) \le \gamma$; otherwise, no one would buy credits to take auto trips. Thus, we can deduce that Eq. (17) is positive when T_C = 0, and there exists a range of T_C > 0 which makes (17) remain positive. As for the second derivative of λ and x, it is easy to see that Eqs. (16, 18) are always positive. Therefore, it suffices to conclude that the minimization of Eq. (9) is a convex problem, and the optimal solution is unique for a range of $T_{\text{c}} \ge 0$, of which the specific value range depends on the particular forms and values of $F\left( \cdot \right),\tau \left( \cdot \right),d,\lambda$, etc. For instance, in the following numerical study, we verified that when T_C = 24 min, $\frac{{\partial^{2} G_{\text{TCS}} }}{{\partial q_{\text{a}}^{2} }} = 0.0154 \approx 0$, and the second derivative of q_a increases with T_C decreasing. Thus, for $T_{\text{C}} \in \left[ {0,24} \right]$ min, the optimal solution of the DD-TCS is unique and it is the global optimum.

Given the optimal $q_{\text{a}}^{*}$ and $x^{*}$, the market price of credits, $P_{\text{c}}^{*}$, can be obtained by substituting the above results into Eq. (6a).

$$\begin{aligned} P_{\text{c}}^{*} & = \frac{{\left( {2q_{\text{a}}^{*} - d} \right)}}{d}T_{\text{C}} F^{ - 1} \left( {q_{\text{a}}^{*} } \right) + \frac{{\left( {\lambda + x^{*} } \right)\left( {d - q_{\text{a}}^{*} } \right)}}{{x^{*} d}}\left( {F^{ - 1} \left( {q_{\text{a}}^{*} } \right) \times \left( {\gamma - \tau \left( {q_{\text{a}}^{*} \left( {\lambda + x^{*} } \right)} \right)} \right) + c_{\text{T}} - c_{\text{A}} } \right) \\ & \quad - \frac{{\left( {d - q_{\text{a}}^{*} } \right)}}{{x^{*} d}}\varphi . \\ \end{aligned}$$

(19)

For other two T&D–D and D–D scenarios, the detailed SO conditions and convex analysis of the minimization problem are presented in “Appendices 1 and 2”, respectively. It is worth noting that the analysis in “Appendix 2” shows that the D–D scenario is very sensitive to the value of T_C. For a large T_C, the DD-TCS may directly degrade to the LPR, and no credit trading will occur; otherwise, the credit buyers under D–D scenario tend to buy credits as more as possible and always choose driving during the entire policy period.

4 Numerical case studies

In addition to the above-stated LPR and DD-TCS scenarios, this section includes two more cases for comparison: the no-action case and the ideal congestion pricing (CP) case. Parametric analysis will be conducted to reveal the impact of T_C values on the system performance of DD-TCS.

Following the works by Nie [1, 5], the VOT distribution among population is expressed by a first-order rational function, as follows:

$$F\left( \beta \right) = \frac{{d\left( {\beta_{\text{U}} - \beta } \right)}}{{\rho \beta + \beta_{\text{U}} }} \to F^{ - 1} \left( q \right) = \frac{{\beta_{\text{U}} \left( {d - q} \right)}}{\rho q + d},$$

(20)

where parameter $\rho > - 1$ indicates the wealth of the population: lower values represent wealthier population with higher VOTs, and vice versa. In particular, ρ = 0 describes a population with a uniformly distributed VOTs.

The relationship between the auto travel time and traffic flow is described using the following Bureau of Public Road (BPR) function:

$$\tau \left( q \right) = \tau_{0} \left( {1 + 0.15\frac{q}{C}} \right)^{4} ,$$

(21)

where τ₀ is the free-flow travel time and C denotes the highway capacity.

Table 1 summarizes the default values of all model parameters [7].

Table 1 Descriptions of model parameters [7]

4.1 Scenarios without transaction cost

This section examines the ideal situation when the transaction cost is negligibly small and can be assumed to be zero under DD-TCS. Table 2 summarizes the system performances of four scenarios: the no-action case, the LPR with λ = 0.5 and 0.8, respectively (representing two LPR cases that have been implemented in practice), and the DD-TCS.

Table 2 System performance metrics under scenarios without transaction cost

It is observed from Table 2 that compared with the no-action scenario, the system cost of LPR (λ = 0.8) and DD-TCS is reduced, while that of LPR (λ = 0.5) is increased by 3.25%. As for demand share, the transit users of LPR (λ = 0.5) and DD-TCS are increased and that of DD-TCS model is more than others, while the share of transit mode in LPR (λ = 0.8) is reduced. It is implied that regulating the use of auto is not always a good strategy to encourage more users to take transit mode, when the travel cost of the shifted demand is worse off than that of driving cars.

4.2 LPR versus DD-TCS with transaction cost

In reality, transaction cost may be greater than zero. This section examines when G_TCS is indifferent to LPR and finds the threshold value of T_C by sensitivity analyses. We consider three scenarios of DD-TCS, i.e. (1) T–D scenario, (2) T&D–D scenario, and (3) D–D scenario (see their descriptions and models in Sect. 2.3). A variety of numerical cases shows that the T&D–D always reduces to the T–D (i.e. $q_{\text{b}} = q_{\text{a}}$, trading only occurs between transit users and car owners), and the D–D always degrades to the LPR (see the analytic analysis in “Appendix 2”). Therefore, below we only report the results of T–D scenario and compare the results with three other policies (i.e. the no-action case, LPR with $\lambda = \left[ {0.5,0.8} \right]$, and the ideal CP).

Figure 2a, b shows the sensitivity analysis results of average system cost when transaction cost is changed from 0 to 120 min. Note that the average system cost of other three situations keeps unchanged. From Fig. 2a, b, we can see that the curves of the average system cost under DD-TCS have similar trend for different λ values. With the increase in T_C, the system cost per person of DD-TCS increases. Different λ values do affect the threshold value of T_C. It is seen from Fig. 3a (λ = 0.5), when 0 < T_C < 12 min, DD-TCS performs better than no-action case; when 12 min < T_C < 24 min, DD-TCS performs better than LPR but worse than no-action case; when T_C > 24 min, the performance of DD-TCS is the worst. When λ = 0.8, the threshold values of T_C are increased obviously relative to the case with λ = 0.5.

Fig. 2

Performances of DD-TCS with various T_C. q is the highway flow, i.e. $q = q_{\text{a}} \left( {\lambda + x} \right)$, which is converted into percentage by $\frac{q}{d} \times 100\%$; q_tr indicates the demand of transit users, i.e. $q_{\text{tr}} = d - q_{\text{a}}$, converted into percentage by $\frac{{q_{\text{tr}} }}{d} \times 100\%$

Fig. 3

Credit purchase changing with various T_C. Note that zone A means that car users who buy credits buy the most credits, that is, $x = 1 - \lambda$; zone B means this car users will buy the credits but they will not choose to drive every day in a month, that is, $x < 1 - \lambda$; zone C means this car uses rarely buy credits

Figure 2c–d shows the sensitivity analysis results of demand share when transaction cost is changed from 0 to 120 min. We can see that the curve of car users changes consistently with the curve of transit users and oppositely to the curve of car owners. Figure 2c (λ = 0.5) shows that when T_C is small (zone A), the q_a curve, i.e. the number of car owners, first coincides with the q curve, i.e. the highway flow, implying $\lambda + x = 1$ as verified in Fig. 3a. As T_C increases to zone B, q_a increases as well; however, the highway flow decreases due to $\lambda + x < 1$ (see Fig. 3a). When T_C reaches zone C, the number of auto owners and the highway flow gradually go down, and the demand of transit users increases. Similar findings are also observed in Fig. 2d for the scenario with λ = 0.8.

Figure 3a, b shows the sensitivity analysis results of transaction amount when transaction cost is changed from 0 to 120 min. We can see that the curves under DD-TCS with different λ have similar change, and different λ values only affect the initial value of x and the threshold value of T_C; with an increase in T_C, the transaction amount x remains unchanged at first, then decreases gradually, and finally keeps unchanged. In fact, we divide the three zones A, B and C according to the change in x. When x passes the turning point, the demand share begins to change oppositely.

4.3 Impacts of λ in LPR policy

Above analysis is specific to LPR with given λ = 0.8 and λ = 0.5. In order to find the optimal T_C threshold value, we need to find the optimal λ under the LPR policy. In the situation of LPR, we take the derivative of the total cost per person with respect to λ, find an optimal λ, and set it as a benchmark: $\mathop {\text{argmin}}\nolimits_{{\lambda \in \left[ {0,1} \right]}} G_{\text{LPR}}$ = 0.7897. Figure 4 shows the changes in G_LPR with λ.

Fig. 4

G_LPR changing with λ

In order to obtain the optimal threshold value of the transaction price T_C, in calculation, we use the $\lambda^{*}$ of LPR and perform the sensitivity analysis of T_C again. The variation of system cost per person G_TCS for T–D scenario is shown in Fig. 5. As Fig. 5 shows, when the transaction price T_C is equal to 72 min, the system cost per person of DD-TCS is the same as that of LPR, which is 29.6551 as shown in Fig. 4.

Fig. 5

G_TCS changing with different T_C for T–D scenario (λ = 0.7897)

In Table 3, we divide T_C by the auto travel time τ and transit travel time γ, and convert it into ratios. In reality, some technologies (e.g. mobile App) can facilitate credit trading; real T_C values can be much less than that listed in Table 3. In other words, DD-TCS is much superior to LPR.

Table 3 Transaction cost thresholds

4.4 Sensitivity analysis of population distribution

In order to set the right T_C threshold value for a specific population, we shall examine the impacts of population VOT distribution. According to Nie [1], VOT distributions depend on the parameter ρ. As Fig. 6 shows, the closer ρ is getting to − 1, the richer people are; the closer ρ is to 4, the poorer people are. Different ρ values represent people in different wealth classes, which affect how they behaviour in the system and thus the threshold value of T_C. Therefore, it is necessary to carry out sensitivity analysis of ρ.

Fig. 6

VOT distribution used in the numerical studies [1]

According to the previous work, there is an optimal $\lambda^{*}$ = 0.7897. Under the condition that the system cost per person of DD-TCS is equal to that of LPR, we calculate the values of T_C when ρ changes from − 0.5 to 4, and the results are shown in Fig. 7. We also calculate the demand share: the number of car owners q_a, highway flow q, and travellers who take transits $q_{\text{tr}} = d - q_{\text{a}}$ (all converted into percentage by dividing d). Figure 8 displays the results.

Fig. 7

T_C for different ρ (λ = 0.7897)

Fig. 8

T_C for different ρ (λ = 0.7897)

It is observed in Fig. 7 that with an increase in ρ, threshold value of T_C decreases gradually. Figure 8 indicates that with an increase in ρ, the number of car users (q) decreases gradually as well as the number of car owners (q_a), while the number of people who take transits is increased. It makes sense that the poorer population is less likely to own a car and drive on the road and is more likely to take transit.

From Fig. 7, we conclude that the poorer the population, the lower the transaction cost. In order to present an intuitive explanation to this conclusion, we define a proportion, that is, $\psi = \frac{{\mathop \int \nolimits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w*\frac{{\gamma - \tau \left( {q_{\text{a}} \left( {\lambda + x} \right)} \right)}}{\gamma }}}{{q_{\text{a}} }}$, which means auto users’ average travel time saving against transit users’. This variable reflects the auto owners’ willingness of transactions. Taking this proportional value as the target, sensitivity analysis was carried out with respect to ρ (see Fig. 9).

Fig. 9

Auto users’ travel time saving against transit users’ (in monetary units per person)

It is observed, with an increase in ρ, that the demand for buying credits, transaction amount, transaction cost, and traffic flow on the road all decrease, while the bus flow is increased. It makes sense that the poorer population are less likely to trade and drive on the road. This is in agreement with the results in Figs. 7 and 8.

5 Conclusions

In this study, we have established a DD-TCS model with particular consideration of transaction costs. Theoretical analyses are conducted for applying this model to a single origin–destination corridor under the SO situation. In numerical studies, we compared the performances of DD-TCS with the no-action case, LPR policy, and the ideal congestion pricing scenarios. Sensitivity analysis is conducted with respect to T_C, in which threshold values of T_C are obtained when the proposed DD-TCS and the benchmark-policy LPR yield equivalent performance (in terms of the total generalized cost). Results show that both DD-TCS and LPR may outperform the no-action case under certain conditions; DD-TCS may perform better than LPR in a wide range margin of transaction cost $T_{\text{C}} \ge 0$. The users’ heterogeneity with continuously distributed values of time is analysed with insightful findings: wealthier population may tolerate higher transaction cost and is willing to conduct credit trading under DD-TCS; furthermore, they tend to own and drive autos to commute, as they value their time more worthy. Therefore, it is believed that the DD-TCS has promising prospects in solving traffic congestion problem.

Appendices

Appendix 1: System optimal conditions for T&D–D scenario

1.1 First-order condition for T&D–D scenario

$$\begin{aligned} & \frac{{\partial G_{\text{TCS}} }}{\partial \lambda } = \left( {\lambda + x} \right)q_{\text{a}} \tau^{\prime } \left( {q_{\text{b}} \left( {\lambda + x} \right)} \right. + \\ & \left. {\left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)} \right)\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w \, +\\ & \left( {\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)} \right) - \gamma } \right) \\ & \mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + \left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)q_{\text{a}} \tau^{\prime } \left( {q_{\text{b}} \left( {\lambda + x} \right)} \, + \right. \\ & \left. { \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)} \right) \int_{{(q_{\text{b}} )}}^{{(q_{\text{a}} )}} {F^{( - 1)} } (w){\text{d}}w + q_{\text{a}} (c_{\text{A}} - c_{\text{T}} ) = 0, \\ \end{aligned}$$

(22)

$$\begin{aligned} \frac{{\partial G_{\text{TCS}} }}{{\partial q_{\text{a}} }} & = \left( {2\lambda + x - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)\tau^{\prime } \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)} \right)\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w \, + \\ & \quad \left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)F^{ - 1} \left( {q_{\text{a}} } \right)\left( {\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)} \right) - \gamma + c_{\text{A}} - c_{\text{T}} } \right) + \\ & \quad \varphi = 0, \\ \end{aligned}$$

(23)

$$\begin{aligned} \frac{{\partial G_{\text{TCS}} }}{\partial x} & = \left( {\lambda + x} \right)\frac{{q_{\text{b}} \left( {d - q_{\text{a}} } \right)}}{{d - q_{\text{b}} }}\tau^{\prime } \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)} \right)\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w \, + \\ & \quad \left( {\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)} \right) - \gamma } \right)\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w \, + \\ & \quad \left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)\frac{{q_{\text{b}} \left( {d - q_{\text{a}} } \right)}}{{d - q_{\text{b}} }}\tau^{\prime } \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - \frac{{xq_{\text{b}} }}{{d - q_{\text{b}} }}} \right)} \right) \mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w \, - \\ & \quad \frac{{q_{\text{b}} }}{{d - q_{\text{b}} }}\left( {\tau \left( {q_{\text{b}} \left( {\lambda + x} \right) + \left( {q_{\text{a}} - q_{\text{b}} } \right)\left( {\lambda - y} \right)} \right) - \gamma } \right)\mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w \, +\\ & \quad \frac{{q_{\text{b}} \left( {d - q_{\text{a}} } \right)}}{{d - q_{\text{b}} }}\left( {c_{\text{A}} - c_{\text{T}} } \right) + T_{\text{C}} \left( {\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + \frac{{q_{\text{b}} }}{{d - q_{\text{b}} }}\mathop \int \limits_{{q_{\text{b}} }}^{d} F^{ - 1} \left( w \right){\text{d}}w} \right) = 0. \\ \end{aligned}$$

(24)

Solving above equations leads to $\lambda^{*} ,q_{\text{a}}^{*} ,x^{*}$, and substituting $q_{\text{a}}^{*}$ into (7b), we have $q_{\text{b}}^{*}$. Substituting them into (7a) yields:

$$\begin{aligned} P_{\text{C}}^{*} & = \frac{{2q_{\text{b}}^{*} - d}}{d}T_{\text{C}} F^{ - 1} \left( {q_{\text{b}}^{*} } \right) + F^{ - 1} \left( {q_{\text{b}}^{*} } \right)\left( {\gamma - \tau \left( {q_{\text{b}}^{*} \left( {\lambda^{*} + x^{*} } \right) + \left( {q_{\text{a}}^{*} - q_{\text{b}}^{*} } \right)\left( {q_{\text{b}}^{*} - \frac{{x^{*} q_{\text{b}}^{*} }}{{d - q_{\text{b}}^{*} }}} \right)} \right)} \right) +\\ & \quad \left( {c_{\text{T}} - c_{\text{A}} } \right) . \\ \end{aligned}$$

(25)

1.2 Convexity analysis

Similar to the analysis process of T&D scenario, we take the second-order derivatives of G_TCS with respect to $\lambda ,q_{\text{a}} ,x$ (the detailed process are omitted due to complexity) and find that they are either always positive (for λ, x) or conditionally positive depending on T_C (for q_a). Thus, the minimization problem for T&D scenario is also convex for $0 \le T_{\text{C}} <$ certain positive value (which can be numerically found), and the above optimal solution ($\lambda^{*} ,q_{\text{a}}^{*} ,q_{\text{b}}^{*} ,x^{*} ,P_{\text{C}}^{*}$) is unique and global optimum.

Appendix 2: System optimal conditions for D–D scenario

2.1 The first-order condition

$$\begin{aligned} \frac{{\partial G_{\text{TCS}} }}{\partial \lambda } & = \left( {\lambda + x} \right)q_{\text{a}} \tau^{\prime } \left( {\lambda q_{\text{a}} } \right)\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + \left( {\tau \left( {\lambda q_{\text{a}} } \right) - \gamma } \right)\mathop \int \limits_{0}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w \, +\\ & \quad \left( {\lambda - \frac{{xq_{\text{b}} }}{{q_{\text{a}} - q_{\text{b}} }}} \right)q_{\text{a}} \tau^{\prime } \left( {\lambda q_{\text{a}} } \right)\mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + q_{\text{a}} \left( {c_{\text{A}} - c_{\text{T}} } \right) = 0, \\ \end{aligned}$$

(26)

$$\begin{aligned} &\frac{{\partial G_{\text{TCS}} }}{{\partial q_{\text{b}} }} = \left( {x + \frac{{xq_{\text{b}} }}{{q_{\text{a}} - q_{\text{b}} }}} \right)(F^{ - 1} \left( {q_{\text{b}} } \right)\left( {\tau \left( {\lambda q_{\text{a}} } \right) - \gamma } \right) + \\ & \quad\frac{{xq_{\text{a}} \left( {\tau \left( {\lambda q_{\text{a}} } \right) - \gamma } \right)}}{{(q_{\text{a}} - q_{\text{b}} )^{2} }}\mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w \, + \\ & \quad T_{\text{C}} \left( {(x - \frac{{xq_{\text{b}} }}{{q_{\text{a}} - q_{\text{b}} }})F^{ - 1} \left( {q_{\text{b}} } \right) - \frac{{xq_{\text{a}} }}{{(q_{\text{a}} - q_{\text{b}} )^{2} }}\mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w} \right) = 0, \\ \end{aligned}$$

(27)

$$\begin{aligned} \frac{{\partial G_{\text{TCS}} }}{\partial x} & = \left( {\tau \left( {\lambda q_{\text{a}} } \right) - \gamma } \right)\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w - \\ & \quad\frac{{q_{\text{b}} \left( {\tau \left( {\lambda q_{\text{a}} } \right) - \gamma } \right)}}{{q_{\text{a}} - q_{\text{b}} }}\mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w + \\ & \quad T_{\text{C}} \left( {\mathop \int \limits_{0}^{{q_{\text{b}} }} F^{ - 1} \left( w \right){\text{d}}w + \frac{{q_{\text{b}} }}{{q_{\text{a}} - q_{\text{b}} }}\mathop \int \limits_{{q_{\text{b}} }}^{{q_{\text{a}} }} F^{ - 1} \left( w \right){\text{d}}w} \right) \\ & \quad = 0. \\ \end{aligned}$$

(28)

Solving above equations leads to $\lambda^{*} ,q_{\text{b}}^{*} ,x^{*}$. Then, together with $q_{\text{a}}^{*}$ substituting them into (8b) yields

$$\begin{aligned} P_{\text{C}}^{*} & = \frac{{\lambda^{*} \left( {q_{\text{a}}^{*} - q_{\text{b}}^{*} } \right) - x^{*} q_{\text{b}}^{*} }}{{x^{*} q_{\text{b}}^{*} }}\left( {F^{ - 1} \left( {q_{\text{a}}^{*} } \right)\left( {\tau \left( {\lambda^{*} q_{\text{a}}^{*} } \right) - \gamma } \right) + c_{\text{A}} - c_{\text{T}} } \right) +\\ & \quad\frac{{\left( {q_{\text{a}}^{*} - q_{\text{b}}^{*} } \right)}}{{x^{*} q_{\text{b}}^{*} }} \varphi + T_{\text{C}} F^{ - 1} \left( {q_{\text{a}}^{*} } \right).\\ \end{aligned}$$

(29)

2.2 Convexity analysis

We find that the second-order derivative of λ is always larger than 0 and that of q_b is conditionally positive, depending on T_C. Moreover, the second-order derivative of x is 0. To verify, see Eq. (28) that is irrelevant to x. It is implied that G_TCS is a linear increasing function of x, if T_C makes $\frac{{\partial G_{\text{TCS}} }}{\partial x} > 0$, the optimal $x^{*} = 0$ so as to minimize G_TCS; in this case, the DD-TCS degrades to the LPR because no trading of credits happens. Otherwise, if T_C makes $\frac{{\partial G_{\text{TCS}} }}{\partial x} < 0$, the optimal $x^{*} = 1 - \lambda$.