1 Introduction

Slip/slide phenomenon usually causes insufficient braking and traction performance as well as early damaging of rails and wheels and is one of the critical issues that must be solved in order to supply more reliable and acceptable way of transportation. The required traction and braking efforts are performed by adhesion forces among wheels and rail. Adhesion is a highly complex event which depends on many factors, including surface properties, material types, temperature, velocity, etc. However, experimental results show that for each specific combination of these factors, there exists an optimum slip ratio which maximizes the adhesion force between wheel and rail as a function of each velocity value.

The main objective of the re-adhesion control strategy is to maintain the slip velocity at the optimal value. It is compulsory to derive or estimate the optimum slip ratio for specific vehicle velocity and environmental conditions. The slip ratio can be defined as a relative velocity proportion in the contact area. Hence, the evaluation performance of the slip ratio is directly coupled with the integrity of the vehicle speed information. Many methods have been suggested to estimate the railway vehicle velocity by using magnetic sensors such as Hall effect gear tooth active speed sensor, which are very accurate in velocity measurement. However, these methods are very expensive and sensitive to wheel–rail contact conditions (rain, sand, snow, dew, etc.). The other way of acquiring velocity information is to utilize global positioning system (GPS) signals. There are many well-known techniques in the literature that combine GPS information with other sensors such as the wheel speed sensor, accelerometer and inertial measurement unit (IMU) [1,2,3,4]. This kind of information can be also obtained by integrating indirect methods and different estimation approaches. One of these methods is detecting the excitations resulted from track irregularities with acceleration and angular rate measurements at different wheelsets, and another is through measurement of the time shift between the dynamic responses of two wheelsets with respect to the same track irregularity [5]. In addition, robust velocity estimation involving establishment of a dynamic friction model has also been investigated [6]. However, the slip/slide control systems based on vehicle velocity estimation do not meet the safety concerns of industrial applications. These systems demand an additional estimation process to track the optimal slip ratio.

Among the alternative methods, there exists an indirect detection and estimation process of the slip/slide conditions by measuring the voltage, current and speed of the alternative current (AC) traction motor through an extended Kalman filter (EKF) [7]. Another method is to control the slip/slide states by evaluating the wheel speed information of different axles together. If one of the axles in slip/slide state turns faster or slower than the others, the slipping or sliding axle can be detected and controlled unless all of the axles slip or slide at the same time. A trailer axle solves this kind of problem as well [8]. When a wheelset is accelerated higher than the pre-defined threshold, the reference torque of this wheelset will be decreased distinctly till the adhesion situation is recovered to the micro-slip region. This axle is assumed as a reference axle, and the adhesion forces on the other axles are expected to be maximized considering its wheel speed information.

A new method used to detect the slip velocity is based on the multi-rate EKF state identification which combines the multi-rate and EKF method to estimate the traction motor load torque. This method provides a faster detection of slip and improves the reliability and traction performance [9]. A re-adhesion control system based on the disturbance observer for examining the first resonant frequency of the bogie system to utilize adhesion more efficiently was also proposed in [10, 11]. However, these methods are not reliable enough for industrial real-time applications because the time derivative of the adhesion force cannot be estimated correctly when the adhesion force changes quickly in case of sudden slip [12]. Estimation accuracy of adhesion force among the wheel and rail is quite beneficial for the solution of slip/slide problem. The aim of the controller is to maximize the adhesion coefficient while sustaining the overall stability of the railway vehicle. The slip velocity is adjusted by keeping it in the stable region adjacent to the peak point of the adhesion coefficient. To achieve the sub-optimal slip velocity, which corresponds to the approximity of the maximum value of the adhesion coefficient, is also suitable for the controller performance. The relationship between the tractive force and the wheel slip is a nonlinear function of the wheel–rail contact condition. For this reason, an estimator that estimates the wheel–rail adhesion condition and a traction controller which adjusts the wheel slip velocity to the optimal value should be added to the control scheme. Several control methods have been proposed based on sliding mode controller, fuzzy logic, adaptive schemes in the literature [13–15].

In this paper, electric multiple units consisting of self-propelled carriages were used due to the superiority from the viewpoint of tractive effort. The railway vehicle is driven by 120 kW induction motors with a 750 V dc bus voltage which are controlled using the field-oriented control (FOC) method with an indirect vector control scheme. A robust adaptive re-adhesion control scheme to regulate the control torque of the traction motor was designed for not only suppressing the excessive wheel slip, which make the system unstable, but also optimizing the wheel slip to operate at the optimal adhesion point even if some system parameter uncertainties or disturbances exist. The adhesion coefficient and slip velocity were predicted through the second-order sliding mode observer. Optimal slip velocities at different wheel–rail contact conditions were found with a higher precision via the guidance of the optimal slip velocity seeking algorithm. By creating a Lyapunov candidate function, it was proved that the ultimate boundedness of the proposed strategy with time-varying disturbance and finite-time convergence of the proposed method were satisfied. The traction capability was also maintained after recovering adhesion. A steep grade railway was chosen in the simulations to test the performance of the controller in low adhesion conditions. On steep grades, the friction between wheel and rail is not able to transfer sufficient adhesion to overcome gravity.

The organization of the paper is as follows. Section 2 introduces the dynamic model of the longitudinal traction system that is used in the control system scheme. The proposed robust adaptive re-adhesion control strategy is described in Sect. 3. Section 4 gives the details of the optimal slip velocity estimator based on the second-order sliding mode observer, and Sect. 5 presents the simulation results of the robust adaptive approach. Finally, conclusions are provided in the last section.

2 Traction system dynamics model

The slip mechanism should be modeled to construct a slip control strategy. Therefore, a traction system dynamics model with the traction motor reference torque as input and the forward speed of the railway vehicle as output is built, which concentrates on two fundamental parts, i.e., the mechanical transmission and the outer condition. The input and output of the mechanical transmission part are the traction motor torque and angular velocities of wheels, respectively. The outer condition part produces the actual railway vehicle forward speed, which depends on the angular velocities of the wheels, actual adhesion level and various losses due to air resistance, rolling resistance, curve resistance, gradient resistance, etc. [16]. The mechanical transmission consists of a traction motor, a gearbox and two wheels which are coupled with each other through a wheelset axle and a brake system. The mechanical transmission model is demonstrated in Fig. 1.

Fig. 1
figure 1

Mechanical transmission model composed of traction motor, gearbox, wheelset axle, wheels and brake system

Full size image

The output torque of the traction motor (Tm,k) is derived as

$$J_{{{\text{m}},k}} \frac{{{\text{d}}\omega_{{{\text{m}},k}} }}{{{\text{d}}t}} = T_{{{\text{m}},k}} - T_{{{\text{t}},k}} ,$$
(1)

where Jm,k is the moment of inertia of the traction motor, ωm,k is the motor angular velocity, Tm,k is the traction motor input torque, Tt,k is the transmission output torque, the subscript k = {1, 2, …, l} is the serial number of the wheelset to which the traction motor are mounted, and l is the total number of traction shafts in the train.

The following inequality is always valid for all railway vehicle types:

$$l \le nm,$$
(2)

where n is the total number of wheelsets in each bogie and m is the number of the bogies. Usually, l = nm − 2. In our model, each bogie has two wheelset (n = 2), and the train is assumed to have three bogies (m = 3). The leading and trailing bogies are equipped with traction motors, while the wheelsets in the middle bogie have no traction motor. Thus, there exist four traction motors in total, which are equivalent to four traction shafts. The output torque of the traction motor is transmitted to the gearbox by a shaft, as stated in Eq. (3). The torque is then transmitted to the left and the right wheels via the wheelset axle. The distances from the gearbox to the left and right wheels are different; therefore, the spring constants and damping coefficients of the shaft on two sides are also different. Here, considering that the part of wheelset axle from the gearbox to right wheel is very short when compared with that to the left wheel, we neglect the spring constant and damping coefficient of the shaft on the motor side and the loss due to viscous friction that emerges in the gearbox. The gearbox scales the input torque and speed through a gear ratio (n k ).

$$\frac{{J_{{{\text{g}},k}} }}{{n_{k} }}\frac{{{\text{d}}\omega_{{{\text{m}},k}} }}{{{\text{d}}t}} = T_{{{\text{t}},k}} n_{k} - T_{{{\text{w}},k}}^{\text{R}} - T_{{{\text{w}},k}}^{\text{L}} ,$$
(3)

where the superscripts R and L refer to the right and left wheels, respectively; Jg,k is the moment of inertia of the gearbox; \(T_{{{\text{w}},k}}^{\text{R}} \;{\text{and}}\;T_{{{\text{w}},k}}^{\text{L}}\) are the traction torque of the right and left wheels, respectively; and t is time.

The drive shaft torque transmitted to the left wheel is given by

$$T_{{{\text{w}},k}}^{\text{L}} = K_{k} \left( {\frac{{\theta_{{{\text{m}},k}} }}{{n_{k} }} - \theta_{{{\text{w}},k}}^{\text{L}} } \right) + B_{k} \left( {\frac{{\omega_{{{\text{m}},k}} }}{{n_{k} }} - \omega_{{{\text{w}},k}}^{\text{L}} } \right),$$
(4)

where \(K_{k}\) is the spring constant; B k is the damping coefficient of the wheelset axle; \(\theta_{{{\text{w}},k}}^{\text{L}}\) and \(\omega_{{{\text{w}},k}}^{\text{L}}\) are the angular displacement and angular velocity of the wheelset axle to the left wheel, respectively. The wheels transmit the traction torque to the rail, and the amount of torque transmitted depends on the adhesion level between the wheel and rail, as represented in Eqs. (5) and (6).

$$J_{{{\text{w}},k}}^{\text{L}} \frac{{{\text{d}}\omega_{{{\text{w}},k}}^{\text{L}} }}{{{\text{d}}t}} = T_{{{\text{w}},k}}^{\text{L}} - T_{{{\text{a}},k}}^{\text{L}} ,$$
(5)
$$J_{{{\text{w}},k}}^{\text{R}} \frac{{{\text{d}}\omega_{{{\text{w}},k}}^{\text{R}} }}{{{\text{d}}t}} = T_{{{\text{w}},k}}^{\text{R}} - T_{{{\text{a}},k}}^{\text{R}} - J_{{{\text{br}},k}} \frac{{{\text{d}}\omega_{{{\text{w}},k}}^{\text{R}} }}{{{\text{d}}t}} - J_{{{\text{x}},k}} \frac{{{\text{d}}\omega_{{{\text{w}},k}}^{\text{R}} }}{{{\text{d}}t}},$$
(6)

where \(J_{{{\text{w}},k}}^{\text{R}}\) and \(J_{{{\text{w,}}k}}^{\text{L}}\) are the moment of inertia of the right and left wheels, respectively; \(\omega_{{{\text{w}},k}}^{\text{R}}\) is the angular velocity of the right wheel; Jx,k and \(J_{{{\text{br}},k}}\) are the moment of inertia of the wheelset axle and brake system, respectively; \(T_{{{\text{a}},k}}^{\text{R}}\) and \(T_{{{\text{a}},k}}^{\text{L}}\) are the adhesion torque of the right and left wheels, respectively:

$$T_{{{\text{a}},k}}^{\text{L}} = F_{{{\text{a}},k}}^{\text{L}} \cdot r_{{{\text{w}},k}}^{\text{L}} ,$$
(7)
$$T_{{{\text{a}},k}}^{\text{R}} = F_{{{\text{a}},k}}^{\text{R}} \cdot r_{{{\text{w}},k}}^{\text{R}} ,$$
(8)

where \(F_{{{\text{a}},k}}^{\text{R}}\) and \(F_{{{\text{a}},k}}^{\text{L}}\) are the adhesion forces of the right and left wheels, respectively; \(r_{{{\text{w}},k}}^{\text{R}}\) and \(r_{{{\text{w}},k}}^{\text{L}}\) are the effective radii of the right and left wheels, respectively.

To determine the adhesion force, the dynamic property of outer conditions must be taken into consideration as well. The maximum value of the adhesion mainly depends on the adhesion coefficient and the adhesion weight of the railway vehicle, which vary with time and vehicle’s position on the track. The adhesion coefficient is a function of the slip velocity, conditions of the wheel–rail contact, railway vehicle velocity and temperature in the contact area [17]. The forces and velocities that act on a single wheel are depicted in Fig. 2.

Fig. 2
figure 2

Forces and velocities that act on a single wheel [10]

Full size image

While the motor torque and the adhesion torque are adopted as input in this traction system model, the railway vehicle velocity and angular speed of the wheel are taken as output. The slip ratio, which is defined as the ratio of the relative velocity between wheel and rail in the contact area to the forward speed of the railway vehicle, is calculated for each driven wheel–rail interface as follows [18]:

$$\lambda_{k}^{{{\text{R}},{\text{L}}}} = \frac{{\nu_{{{\text{s}},k}}^{{{\text{R}},{\text{L}}}} }}{V},$$
(9)

where V is the forward speed of the railway vehicle; ν R,Ls,k is the slip velocity in the longitudinal direction defined as in Eq. (10):

$$\nu_{{{\text{s}},k}}^{{{\text{R}},{\text{L}}}} = V_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} - V,$$
(10)

where \(V_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}}\) is the peripheral velocity of the right or left wheel through the contact patch. Note that the superscript “R, L” of some variables throughout this paper means that the quantity is for the right or left wheel, and the related equation holds not only for the right wheel but also for the left wheel.

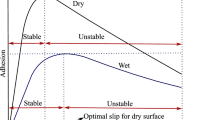
Slip generation is a highly nonlinear process, which varies continuously over time and can be modeled as the adhesion coefficient–slip characteristic curve depicted in Fig. 3. This function can be separated into three phases. In the first phase, the adhesion coefficient increases linearly with the slip velocity; in the second part, however, the adhesion coefficient presents a nonlinear relationship with the slip velocity. In both of the two phases, the function characteristic between adhesion coefficient and slip velocity is basically stable, and hence, the range of adhesion coefficient or slip velocity covering the two phases is regarded as a stable region [17]. At the endpoint of the second phase, the adhesion coefficient reaches its maximum value (\(\mu_{{{\text{a}},{ \hbox{max} }}}\)), which corresponds to the optimal slip velocity (\(\nu_{\text{s}}^{*}\)). In other words, the adhesion saturates at the point \(\left( {\nu_{\text{s}}^{*} , \mu_{{{\text{a}},{ \hbox{max} }}} } \right)\). If the traction torque remains steady when the current adhesion force strongly decreases, the characteristic function switches into the third phase, which is called as a slip region or an unstable region [19]. The main objective of the re-adhesion or slip control is to drive the slip velocity to the stable region of the characteristic function and to maintain the optimal slip velocity, which comes across to the maximum adhesion coefficient for best tractive effort.

Fig. 3
figure 3

Adhesion coefficient–slip velocity characteristic function [17]

Full size image

In Fig. 4, adhesion slip characteristics of the wheel–rail contact surface in different conditions such as “dry,” “wet,” “low” and “very low” [20] are shown, which are used for evaluation and simulation process of this paper.

Fig. 4
figure 4

Adhesion–slip characteristics in different wheel–rail contact conditions

Full size image

The tractive effort of the railway vehicle is evaluated as a sum of partial tangential forces of all driven shafts whose wheels are subjected to different adhesion coefficients and adhesion weights. To compute the slip velocity, it is necessary to know the angular velocity of the wheel \(( {\omega_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} })\) and the railway vehicle longitudinal velocity (V). The angular velocity \((\omega_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} )\) is obtained directly from the mechanical transmission model.

In this model, the vehicle velocity is actually evaluated from the adhesion coefficient \(( {\mu_{{{\text{a}},k}}^{{{\text{R}},{\text{L}}}} })\) and fed back into the system. Given the adhesion coefficient \((\mu_{{{\text{a}},k}}^{{{\text{R}},{\text{L}}}} )\) of a specific wheel, the adhesion forces \((F_{{{\text{a}},k}}^{{{\text{R}},{\text{L}}}} )\) can be evaluated for both wheels individually as in Eqs. (11) and (12):

$$F_{{{\text{a}},k}}^{\text{L}} = m_{{{\text{a}},k}}^{\text{L}} g\mu_{{{\text{a}},k}}^{\text{L}} ,$$
(11)
$$F_{{{\text{a}},k}}^{\text{R}} = m_{{{\text{a}},k}}^{\text{R}} g \mu_{{{\text{a}},k}}^{\text{R}} ,$$
(12)

where \(F_{{{\text{a}},k}}^{\text{L}}\) and \(F_{{{\text{a}},k}}^{\text{R}}\) are the adhesion forces of the left and right wheels, respectively; g is the gravitational acceleration; \(\mu_{{{\text{a}},k}}^{\text{L}}\) and \(\mu_{{{\text{a}},k}}^{\text{R}}\) are adhesion coefficients of the left and right wheels, respectively; \(m_{{{\text{a}},k}}^{\text{L}}\) and \(m_{{{\text{a}},k}}^{\text{R}}\) are the adhesion mass of the left and right wheels, respectively; and

$$m_{{{\text{a}},k}}^{\text{L}} = m_{{{\text{a}},k}}^{\text{R}} = \frac{1}{2nm}m_{\text{stc}} ,$$
$$m_{\text{stc}} = m_{\text{vb}} + \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} \left( {2m_{{{\text{w}},ij}} + m_{{{\text{x}},ij}} + m_{{{\text{br}},ij}} } \right) + \mathop \sum \limits_{i = 1}^{m} m_{{{\text{b}},i}} + \mathop \sum \limits_{k = 1}^{l} \left( {m_{{{\text{m}},k}} + m_{{{\text{g}},k}} } \right),$$

where \(m_{\text{stc}}\) is the total static mass of the railway vehicle, \(m_{\text{vb}}\) is the railway vehicle body mass, \(m_{{{\text{b}},i}}\) is the mass of the bogie, \(m_{{{\text{m}},k}}\) is the mass of the motor, \(m_{{{\text{g}},k}}\) is the mass of the gearbox, \(m_{{{\text{x}},ij}}\) is the wheelset axle mass, \(m_{{{\text{br}},ij}}\) is the mass of the brake system, \(m_{{{\text{w}},ij}}\) is the wheel mass, the subscript j = {1, 2, …, n}refers to the wheelset axle number in one bogie, and the subscript i = {1, 2, …, m} refers to the bogie number.

The adhesion torque for each traction wheelset is described as

$$T_{{{\text{a}},k}} = r_{{{\text{w}},k}}^{\text{L}} F_{{{\text{a}},k}}^{\text{L}} + r_{{{\text{w}},k}}^{\text{R}} F_{{{\text{a}},k}}^{\text{R}} .$$
(13)

The adhesion torque is fed back into the mechanical transmission as described in Eqs. (7) and (8). There is also another way to calculate the adhesion torque by approaching from the traction motor side, as represented in Eqs. (14) and (15).

$$T_{{{\text{a}},k}} = T_{{{\text{m}},k}} n_{k} - \frac{{J_{{{\text{eqv}},k}} }}{{n_{k} }}\frac{{{\text{d}}\omega_{{{\text{m}},k}} }}{{{\text{d}}t}},$$
(14)
$$\frac{{{\text{d}}\omega_{{{\text{m}},k}} }}{{{\text{d}}t}} = \frac{{T_{{{\text{m}},k}} n_{k}^{2} - T_{{{\text{a}},k}} n_{k} }}{{J_{{{\text{eqv}},k}} }},$$
(15)

where Jeqv,k is the equivalent moment of inertia of the wheelset projected into the motor side:

$$J_{{{\text{eqv}},k}} = J_{{{\text{m}},k}} + \frac{{J_{{{\text{t}},k}} + J_{{{\text{w}},k}}^{\text{L}} + J_{{{\text{w}},k}}^{\text{R}} + J_{{{\text{x}},k + }} J_{{{\text{br}},k}} }}{{n_{k}^{2} }},$$

To evaluate the adhesion coefficient and analyze the wheel slip ratio by comparing with the wheel velocities, the velocity of the railway vehicle should be estimated. The railway vehicle velocity is evaluated based on the Newton’s second law of motion as in Eq. (16) [21, 22]:

$$m_{\text{dyn}} \frac{{{\text{d}}V}}{{{\text{d}}t}} = \mathop \sum \limits_{k = 1}^{l} \left( {F_{{{\text{a}},k}}^{\text{L}} + F_{{{\text{a}},k}}^{\text{R}} } \right) - F_{\text{L}} ,$$
(16)

where \(m_{\text{dyn}}\) is the dynamic (effective) mass, which refers to the particular drive shaft to be accelerated:

$$m_{\text{dyn}} = m_{\text{stc}} + \frac{{\eta n_{ij}^{2} l}}{{\left( {1 - \bar{\lambda }} \right)^{2} \bar{r}^{2} }}J_{{{\text{m}},k}} + \frac{n}{{\left( {1 - \bar{\lambda }} \right)^{2} \bar{r}^{2} }}\left( {J_{{{\text{w}},k}}^{\text{L}} + J_{{{\text{w}},k}}^{\text{R}} } \right),$$

η is the gear efficiency, \(\bar{\lambda }\) is the mean value of the slip ratio for each wheel and is calculated as in Eq. (17):

$$\bar{\lambda } = \frac{{\left( {\frac{{\mathop \sum \nolimits_{k = 1}^{l} \left( {V_{{{\text{w}},k}}^{\text{L}} + V_{{{\text{w}},k}}^{\text{R}} } \right)}}{2l} - V} \right)}}{{{ \hbox{max} }\left( {\frac{{\mathop \sum \nolimits_{k = 1}^{l} \left( {V_{{{\text{w}},k}}^{\text{L}} + V_{{{\text{w}},k}}^{\text{R}} } \right)}}{2l} , V} \right)}},$$
(17)

where

$$V_{{{\text{w}},k}}^{\text{L}} = \omega_{{{\text{w}},k}}^{\text{L}} r_{{{\text{w}},k}}^{\text{L}} ,\, V_{{{\text{w}},k}}^{\text{R}} = \omega_{{{\text{w}},k}}^{\text{R}} r_{{{\text{w}},k}}^{\text{R}} ,$$

and \(\bar{r}\) is the nominal wheel radius and defined as in Eq. (18):

$$\bar{r} = \frac{{\mathop \sum \nolimits_{k = 1}^{l} \left( {r_{{{\text{w}},k}}^{\text{L}} + r_{{{\text{w}},k}}^{\text{R}} } \right)}}{2l};$$
(18)

\(F_{\text{L}}\) is the sum of various outer losses, as represented in Eq. (19) [23]:

$$F_{\text{L}} = F_{\text{air}} + F_{\text{roll}} + F_{\text{crv}} + F_{\text{grv}} ,$$
(19)

where \(F_{\text{air}} ,F_{\text{roll}} ,F_{\text{crv}}\;{\text{and}}\;F_{\text{grv}}\) denote, respectively, the losses due to air resistance, roll, cornering and the angle of the lateral slope in which the railway vehicle is running.

The loss due to roll depends on the dynamic mass of the vehicle and the current vehicle velocity:

$$F_{\text{roll}} = m_{\text{dyn}} \left( {C_{{{\text{r}}1}} + C_{{{\text{r}}2}} V} \right),$$

where \(C_{{{\text{r}}1}} \;{\text{and}}\;C_{{{\text{r}}2}}\) are vehicle specific parameters related to the wheel characteristic.

The cornering loss is originated from the increased friction between the wheel and rail while the railway vehicle is moving along a curve. It is calculated through an empirical formula, called as Röckl formula [23, 24]:

$$F_{\text{crv}} = \frac{{k_{1} }}{{R_{y} - k_{2} }},$$

where R y is the radius of the track curvature; k1 and k2 are parameters which change with the radius of track curvature as

$$R_{y} > 350 \;{\text{m}} \Rightarrow k_{1} = 650,k_{2} = 55,$$
$$R_{y} < 350 \;{\text{m}} \Rightarrow k_{1} = 500,k_{2} = 30.$$

The air and roll resistance forces can be combined into the propulsion force using Davis formula, evaluated as follows [24]:

$$F_{\text{p}} = F_{\text{roll}} + F_{\text{air}} = \left[ {A_{\text{p}} + \frac{{B_{\text{p}} }}{{W_{{{\text{x}},k}} }} + C_{\text{p}} V + \frac{{\left( {D_{\text{p}} A_{\text{v}} V^{2} } \right)}}{{W_{{{\text{x}},k}} nm}}} \right]gnmW_{{{\text{x}},k}} ,$$

where \(A_{\text{p}} ,B_{\text{p}} ,C_{\text{p}} \;{\text{and}}\;D_{\text{p}}\) are resistance coefficients; Av is front section area of the vehicle; and \(W_{{{\text{x}},k}}\) is the wheelset axle load, defined as

$$W_{{{\text{x}},k}} = \left( {m_{{{\text{a}},k}}^{\text{R}} + m_{{{\text{a}},k}}^{\text{L}} } \right)g.$$

The loss due to the lateral slope angle of the rail is described as follows:

$$F_{\text{grv}} = m_{\text{dyn}} g{ \sin }\left( \zeta \right),$$

where ζ is the lateral slope angle of the rail.

In order to build a realistic model, the values of parameters ought to be determined accurately. The derivative of slip velocity \(\left( {\dot{\nu }_{{{\text{s}},k}} } \right)\) with respect to time can be stated as in Eq. (20):

$$\dot{\nu }_{{{\text{s}},k}} = \frac{{\bar{r}}}{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }}\left\{ {n_{k} T_{{{\text{m}},k}} - \left( {1 + \frac{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }}{{J_{\text{dyn}} }}} \right)T_{{{\text{a}},k}} + \frac{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }}{{J_{\text{dyn}} }}\bar{r}F_{\text{L}} } \right\},$$
(20)

where the moment of inertia \(J_{\text{dyn}}\) is equal to \(m_{\text{dyn}} \bar{r}^{2}\). According to Eq. (20), one can deduce that the longitudinal slip velocity depends on the traction motor torque, adhesion torque and resistance torque. The slip velocity must be limited by designing a re-adhesion controller to prevent the unstable operation region due to a sudden increase in the slip velocity and must be driven to the safe and optimal operation region. The re-adhesion control can be achieved provided that the asymptotic tracking in the sense of \(\nu_{{{\text{s}},k}} \to \nu_{{{\text{s}},k}}^{*}\) is ensured, where \(\nu_{{{\text{s}},k}}^{ *}\) denotes the optimal slip velocity in the stable region of the kth wheelset. Therefore, in this paper, a robust adaptive nonlinear control with a second-order sliding mode observer which satisfies the optimal tracking performance goal under some parameter uncertainty and unmodeled dynamic conditions is proposed.

3 Proposed control strategy

The primary objective of the re-adhesion control methodology is to adjust the slip velocity \(\nu_{{{\text{s}},k}}\) via controlling the traction motor torque under the assumption that all signals are restricted.

In the first step of the controller design, the slip velocity tracking error (es) is defined as

$$e_{\text{s}} = \nu_{{{\text{s}},k}} - \nu_{{{\text{s}},k}}^{*} .$$
(21)

The traction motor torque is controlled by considering a task driving the slip velocity tracking error convergence to the small neighborhood of zero value as time goes to infinity [25]. The time derivative of the tracking error is taken as in Eq. (22):

$$\dot{e}_{\text{s}} = \dot{\nu }_{{{\text{s}},k}} - \dot{\nu }_{{{\text{s}},k}}^{ *} .$$
(22)

By substituting Eq. (20) into Eq. (22), one obtains

$$\dot{e}_{\text{s}} = \frac{{\bar{r}n_{k} }}{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }}T_{{{\text{m}},k}} + \bar{r}\varPsi \left( \cdot \right),$$
(23)

where

$$\varPsi \left( \cdot \right) = - \left( {\frac{1}{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }} + \frac{1}{{J_{\text{dyn}} }}} \right)T_{{{\text{a}},k}} + \frac{1}{{J_{\text{dyn}} }}\mathop r\limits^{{_{{}} }} F_{\text{L}} - \dot{\nu }_{{{\text{s}},k}}^{*} .$$

If the exact value of the Ψ(·) is known, the slip velocity tracking can be achieved perfectly.

On the other hand, the adhesion coefficient of the railway vehicle changes with the wheel–rail interaction condition. The adhesion torque is full of uncertainty and behaves nonlinearly. The resistance force is also time-varying, and its certain value cannot be acquired. Therefore, a robust adaptive control strategy is proposed to handle the effect of Ψ(·) indirectly. This problem can be solved by bounding \(\varPsi \left( \cdot \right)\) without focusing on it. The determination of adhesion torque \(\left( {T_{{{\text{a}},k}} } \right)\) and the resistance force \(\left( {F_{\text{L}} } \right)\) should abide by the following inequality:

$$\left| {T_{a,k}} \right| \leqslant \left| {T_{a,k}} \right|_{\max},\quad \left| {F_{L}} \right| \leqslant \left| {F_{L}} \right|_{\max} .$$
(24)

A scalar function φ(·) is defined as in Eq. (25):

$$ \varphi ( \cdot ) = 1 + {p | {V} |} + {q | {V^2} |} + { | {\dot{\nu}_{{{\text{s}},k}}^{*} } |}. $$
(25)

Although Ψ(·) is composed of nonlinear, uncertain and time-varying terms, it can be bounded by multiplication of Eq. (25) and an unknown positive constant κ, as follows:

$$\left| {\varPsi \left(\cdot \right)} \right| \leqslant \kappa \varphi \left(\cdot \right),$$
(26)

where p and q are unknown and positive constants, and κ can be selected as in Eq. (27).

$$\kappa = { \hbox{max} }\left\{ {\frac{{\bar{r}}}{{J_{\text{dyn}} }}\kappa_{0} + \left( {\frac{1}{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }} + \frac{1}{{J_{\text{dyn}} }}} \right)\left| {\mu_{ \hbox{max} } } \right|m_{\text{dyn}} g\bar{r},\, \frac{{\bar{r}}}{{J_{\text{dyn}} }}\kappa_{1} ,\frac{{\bar{r}}}{{J_{\text{dyn}} }}\kappa_{2} ,1} \right\},$$
(27)

where κ0, κ1 and κ2 are nonnegative constants.

Equation (26) is independent of any system parameters or operating condition. For this reason, the control strategy provides a highly robust and adaptive control scheme even if the adhesion conditions or system parameters of railway vehicle shift. The robust adaptive tracking control is generated by

$$T_{{{\text{m}},k}} = - k_{0} e_{\text{s}} - \hat{\kappa }\varphi \left( \cdot \right){\text{sign}}\left( {e_{\text{s}} } \right),$$
(28)

in which k0 > 0 is a free parameter, and \(\hat{\kappa }\) is the estimate of κ, obtained using the following adaptive algorithm:

$$\mathop {\hat{\kappa }}\limits^{.} = \sigma_{0} \left| {e_{\text{s}} } \right|\varphi \left( \cdot \right),$$
(29)

where \(\sigma_{0}\) is a positive constant for adaptation rate; then asymptotically stable trajectory tracking is fulfilled in that \(e_{\text{s}} \to 0\;{\text{as}}\;t \to \infty\) [26].

From Eqs. (23) and (26), one can derive

$$\dot{e}_{\text{s}} = \frac{{n_{k} }}{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }}\left( { - k_{0} e_{\text{s}} - \hat{\kappa }\varphi \left( \cdot \right){\text{sign}}\left( {e_{\text{s}} } \right)} \right) + \varPsi \left( \cdot \right).$$
(30)

There always exists a positive constant λ which satisfies \(0 < \lambda \le \frac{{n_{k} }}{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }}\). Inspecting the Lyapunov function candidate stated as below:

$$L\left( \cdot \right) = \frac{1}{2}e_{\text{s}}^{2} + \frac{1}{{2\sigma_{0} \lambda }}\left( {\kappa - \lambda \hat{\kappa }} \right)^{2} ,$$
(31)

we know that L(·) is a positive definite function and its derivative with respect to time is

$$L\left( \cdot \right) = e_{\text{s}} \left( {\dot{e}_{\text{s}} } \right) + \frac{1}{{\sigma_{0} }}\left( {\kappa - \lambda \hat{\kappa }} \right)\left( { - \mathop {\hat{\kappa }}\limits^{.} } \right).$$
(32)

Since k0 > 0 and \(0 < \lambda \le \frac{{n_{k} }}{{J_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} }}\) are specified in controller design, \(\dot{L}(\cdot) \leqslant 0\) is guaranteed. Thus, it can be deduced that the re-adhesion control strategy is stable.

4 Optimal slip velocity seeking method

To realize the proposed control strategy, foreknowledge about the optimal slip velocity must be acquired, but in the practical applications the optimal slip velocity cannot be accessible. There is no opportunity to get all the adhesion relationships under various railway conditions. Both of the adhesion model and the optimal slip velocity are unknown in real-time applications. For this reason, an optimal slip velocity seeking method must be developed to estimate the exact value of the optimal slip velocity [27].

According to the characteristic curve presented in Fig. 3, if one knows that \(\frac{{\partial \mu_{\text{a}} }}{{\partial \nu_{\text{s}} }} > 0\) while \(\nu_{\text{s}} < \nu_{\text{s}}^{*}\), and \(\frac{{\partial \mu_{\text{a}} }}{{\partial \nu_{\text{s}} }} < 0\) while \(\nu_{\text{s}} > \nu_{\text{s}}^{*}\), then \(\frac{{\partial \mu_{\text{a}} }}{{\partial \nu_{\text{s}} }} \approx 0\) while \(\nu_{\text{s}} \approx \nu_{\text{s}}^{*}\). Therefore, \({\mathop {\hat{\nu}}\limits^{.}}_{\text{s}} = 0\) if and only if \(\hat{\nu }_{\text{s}} = \nu_{\text{s}}^{*}\).

The proposed estimator of optimal \(\nu_{\text{s}}^{ *}\) is given by [28]

$${\mathop {\hat{\nu}}\limits^{.}}_{\text{s}} = \gamma {\mathcal{G}}\left( t \right),$$
(33)
$$\hat{\nu }_{\text{s}} \left( {t_{k}^{ + } } \right) = \nu_{\text{s}} \left( {t_{k} } \right),$$
(34)

where γ > 0 is an adaptable parameter, t k is the switching point in which the values of the estimated slip velocity \(\hat{\nu }_{\text{s}}\) are switched to the current value of \(\nu_{\text{s}}\) according to Eq. (35):

$${{\mathcal{G}}}(t) = \left\{{\begin{array}{l} {\frac{{\mathop {\mu_{a}}\limits^{.}}}{{\dot{\nu}_{s}}},\,\left| {\dot{\nu}_{s}} \right| \geqslant \epsilon} \\ {0,\,\left| {\dot{\nu}_{s}} \right| < \epsilon} \\ \end{array}} \right.,$$
(35)

in which \(\epsilon\) is a small threshold value to evade numerical drawbacks. Based on the estimate \(\hat{\nu }_{\text{s}}\, {\text{of }}\,\nu_{\text{s}}^{*}\), Eq. (36) can be obtained:

$$\hat{e}_{\text{s}} = \frac{{\left( {\frac{{\omega_{{{\text{w}},k}}^{{{\text{R}},{\text{L}}}} . \bar{r} - V}}{V} - \hat{\lambda }} \right)V}}{{\bar{r}}}.$$
(36)

For the estimated value \(\hat{\nu }_{\text{s}}\), the term \({\mathcal{G}}\left( t \right)\) demands the information of \(\mathop {\mu_{\text{a}} }\limits^{.}\) and \(\dot{\nu }_{\text{s}}\), which can be retrieved by utilizing the second-order sliding mode observer. The sliding mode observer method was explained in detail in the literature [29,30,31,32]. The observer can be constructed independently from the controller information.

5 Simulation results

The mechanical transmission, re-adhesion controller and the optimal slip velocity estimator were implemented in MATLAB and Simulink, and the simulations were carried out by using the Runge–Kutta fourth-order method with a fixed step time of 0.0001 s. It is assumed that a wheel slip was experienced after the rail condition changes suddenly in traction mode. The parameters used in simulation are listed in “Appendix 1.”

The adhesion coefficient is related to the slip velocity as follows [33, 34]:

$$\mu_{\text{a}} = c{\text{e}}^{{ - a\nu_{\text{s}} }} - d{\text{e}}^{{ - b\nu_{\text{s}} }} ,$$

where a, b, c and d are friction model parameters which are designed with respect to the wheel–rail contact condition, and their values are listed in “Appendix 2.” Initial states of the railway vehicle velocity and wheel angular velocity are given as

$$\omega_{{{\text{w}},k}} \left( 0 \right) = 50\;{\text{rad/s,}}\quad V\left( 0 \right) = 10.5\;{\text{m/s}}.$$

It is assumed that the estimated value of slip velocity switches every 10 s. The trajectories of the railway vehicle forward speed and wheel speed are given in Fig. 5, and trajectories of the adhesion coefficient are presented in Fig. 6.

Fig. 5
figure 5

Trajectories of wheel speed and railway vehicle speed under different adhesion conditions

Full size image
Fig. 6
figure 6

Trajectories of the adhesion coefficient under different adhesion conditions

Full size image

The optimal slip velocities change with the adhesion conditions. The adhesion conditions switch every 10 s, and the controller works until the optimal slip velocities for each condition are achieved. It can be seen that the value of the wheel speed changes suddenly at t = 10 s and t = 20 s, which correspond to the switching points of the estimated value of slip velocity. The adhesion coefficient decreases abruptly and wheel slip emerges because of the rail conditions change from “dry to wet,” “dry to low” and “wet to low” at t = 10 s and from “wet to low,” “wet to very low” and “low to very low” at t = 20 s, respectively. The wheel velocity become much faster than the vehicle velocity, and the slip velocity goes from the safety limit to the dangerous area gradually. Afterward, the wheel slippage is detected and the re-adhesion control strategy regulates the control traction motor torque to attenuate the wheel slip and drives the railway vehicle at the optimal slip velocity.

Figure 7 shows the traction motor torque control trajectories. There exists a saturation point in the motor traction torque at 20 s, but the effect time of the peak is very short and can be negligible. Consequently, the adhesion coefficient and speed values are not affected by the sudden increase in the motor torque.

Fig. 7
figure 7

Control torques of the traction motor

Full size image

The trajectories of the actual \((\nu_{\text{s}} )\) and estimated \(\left( {\hat{\nu }_{\text{s}} } \right)\) slip velocities, as shown in Fig. 8, converge to some value near the optimal \(\left( {\nu_{\text{s}}^{*} } \right)\) slip velocities. It can be seen from the results that the actual slip velocities are able to track the optimal slip velocities with a low error band. Optimal slip velocity values are 1.1841 m/s for the dry condition, 1.1852 m/s for the wet condition, 1.1864 m/s for the low condition and 1.3272 m/s for the very low condition. The root mean square (RMS) values of the deviations of the actual slip velocities from the optimal slip velocities, which refer to the slip velocity tracking errors, and the RMS values of the deviations of the estimated slip velocities from the actual slip velocities, which refer to the slip velocity estimation errors, are also shown under the given wheel–rail contact conditions in Table 1. Both of the estimator and controller exhibit the worst performance when the wheel–rail contact condition switches from “dry to very low.” The estimator achieves its best performance in the adhesion condition switching from “dry to low,” whereas the controller performs the best in the switching from “dry to wet.”

Fig. 8
figure 8

Trajectories of the actual and optimal slip velocities under different adhesion conditions: a dry to low, b dry to low to very low, c dry to very low, d dry to wet, e dry to wet to low, and f dry to wet to very low

Full size image
Table 1 RMS values of the slip velocity tracking and estimation errors under switching adhesion conditions (m/s)
Full size table

The whole adhesion performance is illustrated in Fig. 9. The actual slip velocity can precisely track the optimal slip velocity through the adhesion characteristic map. The full detail of adhesion coefficient varying in the re-adhesion control is captured. The adhesion coefficient converges to a neighborhood of the maximum adhesion value for the “dry” condition in the initial acceleration phase; after that it suddenly declines to the safe region in the “wet, low or very low” condition adhesion characteristic and converges to the maximum adhesion value of this characteristic function. By using a re-adhesion control, the adhesion coefficient remains in the safe operation region and high traction ability is guaranteed. The stability of the re-adhesion control is preserved through the full simulation case from the view point of the Lyapunov, and this is also verified in Fig. 10.

Fig. 9
figure 9

Full adhesion map in different wheel–rail contact conditions: a dry to low, b dry to low to very low, c dry to very low, d dry to wet, e dry to wet to low, and f dry to wet to very low

Full size image
Fig. 10
figure 10

Trajectories of the Lyapunov function candidate (a) and its derivative (b)

Full size image

6 Conclusion

A robust adaptive re-adhesion control scheme with second-order sliding mode observer-based Lyapunov theorem was presented for the railway vehicles under the existence of nonlinear and uncertain parameters. The main superiority of this kind of control strategy is that it does not necessitates exact information of system parameters and is versatile to maintain high traction performance under subsequently switching adhesion conditions as well. The adaptive control scheme and optimal slip estimator, which are built with the second-order sliding mode observer, can overcome all of the drawbacks in the studies in the existing literature. Four different wheel–rail conditions are modeled, and the railway vehicle adhesion is examined during simulation by switching these conditions sequentially. Through the optimal slip velocity seeking method, the railway vehicle adhesion can rapidly converge to the optimal slip velocity even if the wheel–rail contact condition degenerates abruptly. The proposed method is validated both theoretically and numerically in the simulation by high performance and robustness criteria. Simulation results show that this kind of robust adaptive approach provides a rapid response to suddenly changing adhesion conditions and driver requests while maximizing the adhesion utilization even if poor adhesion conditions exist. It was proven that this control strategy could solve possible stability problems of the wheel acceleration-based strategies.