1 Introduction

In order to improve the efficiency of rescuing high-speed trains disabled on the railway lines, the train to train rescue method has been proposed. There exist significant differences in the form of in-train connections for domestic electric multiple units (EMU) [1]. Therefore, different types of transition couplers are designed to enable mechanical connections between the CRH series and inspection EMUs. However, the train configuration, coupler structure, braking curve, boundary limitation and in-train stability of domestic EMUs are all different. There also exist difficulties in transmitting braking signal and pressure between the assisting and disabled train. Once the emergency braking (EB) is applied by the assisting train, significant longitudinal impacts are produced because the assisted train is still running forward. The occurrence of compressed coupler angling behavior will further lead to local destructions and in-train interference, which affects the running safety of the coupled train [2].

The in-train stability problems have been reported in the area of long freight cars and locomotives. The signal synchronization, in-train forces and rotational angles of couplers are the main indicators to train derailment accident. A large number of scholars has focused on the theoretical and testing studies of longitudinal train dynamics. In Australia, Cole [3, 4] studied the in-train stability problems of freight cars. It was indicated that the lateral and vertical rotational behavior of coupler occurred during compressed in-train forces, which further arose train derailment accidents. Similar safety issues due to coupler jackknifing behavior had also been reported in Canada [5]. In China, the investigation of derailment accident in Da-Qin heavy haul railway showed that the coupler lateral rotations occurred under compressed forces. The lateral force components lead to a dramatic increase in wheel axle lateral forces which even causes the rail shift and rollover phenomenon [6,7,8]. The Association of American Railroads stipulates that the freight car should be able to pass the curve with a radius of 175 m under the buffer force of 890 kN [9]. According to UIC530-2 [10], the allowable coupler force of freight cars is determined on the S-shaped curve with a radius of 150 m. Normally, the longitudinal impacts of EMUs in normal operations are not noticeable. However, according to previous studies, the in-train stability problem for train to train rescue scenarios cannot be neglected. Significant in-train force occurs due to the braking applied by the assisting train. The combination of coupler force and pitch motion leads to a vertical force component, which further causes the destruction to coupler yoke and the interference of in-train equipment. Based on theoretical and dynamic calculations, the coupler length, free rotational angle, braking level, train configuration as well as suspension clearance will affect the longitudinal train dynamic performance [11, 12].

As the structural diversity of domestic EMUs, especially the coupler and draft gear system, the possible combinations of train to train rescue scenarios are complicated. This makes it difficult to formulate the operation regulation for train to train rescue. Thus, the systemic studies of longitudinal train dynamics for EMUs under rescue are conducted to give insight into its occurring mechanism and safety relevant issues. In this paper, the field and laboratory tests were introduced to investigate the longitudinal impact and coupler rotational behavior. The dynamic models of train and coupler system were developed considering accurate boundary conditions and braking characteristic. The safety indices and its allowable limits for the EMUs under rescue were defined. The running safety for different train to train rescue scenarios was evaluated.

2 Research background of train to train rescue

2.1 Coupler structures of different types of EMUs

The multiple units to multiple units rescue can improve the efficiency of railway operations. However, there exist different types of EMUs in China, which vary a lot in the train and coupler system. The detail technological parameters of train and coupler structures for CRH series EMUs are listed in Table 1, e.g., the train configuration, coupler types and installing height, braking deceleration and stop clearance. It is indicated that there exist two typical types of coupler and draft gear structures, i.e., Japanese Shibata coupler as well as European type 10 coupler. The coupler length of Shibata coupler is relatively short, while that of type 10 coupler longer. The installing height of Shibata coupler is lower than that of type 10 coupler. The EB deceleration of the train installed with Shibata coupler is higher. The two types of typical coupler and draft gear structures are shown in Fig. 1a, b. The Shibata couplers are commonly used in Shinkansen and Chinese CRH2 series EMUs. This type of coupler consists of coupler body, circular pins as well as coupler yoke structure supported by beams. The type 10 coupler has been standardized in Europe railway vehicles, which is also applied to Chinese CRH1, CHR3 and CRH5 series EMUs. This type coupler is not equipped with the coupler yoke structure. In order to realize mechanical connections between different types of trains, transition couplers should be specially designed, (see Fig. 1c–e). The detail introduction of the transition coupler modules can be seen in Refs. [13, 14]. Except for the mechanical connections, there also exist some other problems for the train to train rescue condition, e.g., driver operations, signal synchronization and air pressure transition during braking.

Table 1 Technological parameters of train and coupler system for CRH series EMUs
Full size table
Fig. 1
figure 1

Typical coupler and draft gear structures of domestic EMUs. a Shibata coupler. b Type 10 coupler. c Transition coupler module 1. d Transition coupler module 2. e Transition coupler module 3

Full size image

2.2 Longitudinal dynamic issues for EMUs under rescue

In this section, the dynamic issues for EMUs under rescue are introduced. The longitudinal dynamic performance for domestic EMUs under rescue is verified by field tests since 2013. The first-stage test for train to train rescue was carried out in Guangzhou South Depot at June 7, 2013. Three typical EMUs, i.e., CRH1A, CRH380A and CRH380BL, are selected to verify the functions of transition coupler modules at the speed of 15 km/h, see Fig. 2a. The tests showed that the transition couplers worked well and realized the basic connecting functions between two coupled trains.

Fig. 2
figure 2

Field tests of coupled multiple units under rescue scenarios. a CRH1A–CRH380A. b CRH380BL–CRH1A. c CRH2E–CRH1B. d CRH380A–CRH380A

Full size image

The second-stage test for train to train rescue was conducted in the main railway line from Guangzhou South to Guangzhou North Station at June 13, 2013, see Fig. 2b. In case of CRH1A–CRH380BL rescue scenario, the measured coupler force was 422 kN when EB was applied by CRH1A at the speed of 80 km/h. In case of CRH380BL–CRH1A scenario, the measured coupler force was 345 kN when EB was applied by CRH380BL at the speed of 80 km/h. According to camera videos, the connection section of two coupled trains kept normal.

The third-stage test for train to train rescue was conducted at the loop test line of Qingdao Sifang Company at July 6, 2013. Two typical EMUs, i.e., CRH1B and CRH2E, are connected to validate the longitudinal dynamic performance of the coupled train, see Fig. 2c. In case of CRH1B–CRH2E scenario, the measured coupler force was 721 kN when EB was applied by CRH1B at the speed of 20 km/h, see Fig. 3a. No abnormal phenomenon was observed in the coupler train. While in the case of CRH2E–CRH1B scenario, the measured coupler force was 736 kN when EB was applied by CRH2E at the speed of 20 km/h, see Fig. 3b. However, significant pitch motions of the coupler occurred during the braking process, which further lead to severe local destructions in the coupler yoke, see Fig. 4. The vertical force component of braking-induced in-train force combined with coupler pitch behavior is the main indicator to this phenomenon. The carbody pitch motions and interference of in-train devices also happened [11].

Fig. 3
figure 3

Measured in-train forces of train to train rescue scenarios. a CRH2E–CRH1B. b CRH1B–CRH2E

Full size image
Fig. 4
figure 4

Illustration of braking-induced impact during train to train rescue test. a Coupler pitching behavior. b Local destructions

Full size image

The fourth-stage test for CRH380A–CRH380A rescue was conducted to give insight into the coupler jackknifing mechanism as well as to verify the longitudinal dynamic model, see Fig. 2d. The instrumented couplers were used to measure the in-train forces. The displacement transducers were arranged to determine the relative movement in the train and coupler system. The accelerometers were also installed on the carbody to measure the braking deceleration. The indirect method for the wheel–rail force measurement was adopted to obtain the wheel unloading ratio [15]. It was indicated that the pitch motion of train and couplers only occurred under compressed coupler forces. Consequently, the pitch motion of the carbody generated a vertical displacement between adjacent carbodies, which further led to geometric interference of in-train devices.

In order to investigate the coupler jackknifing behavior under compressed coupler forces, the laboratory test was conducted in Sifang Rolling Stock Research Institute. The illustration of test rig is shown in Fig. 5a. The boundary limitations of the coupler and yoke were actually simulated. The longitudinal compressed force was gradually applied by the actuator. In test case 1, the upper part of tolling is decoupled from the test rig, while the lower supporting beam fixed to the rig. When the force was increased to a certain level, the upper climbing phenomenon of the tolling occurred, see Fig. 5b. This phenomenon can be repeated, but the critical forces of coupler instability were different every time. In case 2, the upper part of tolling is fixed to the test rig, while the lower supporting beam is decoupled, which allowed a larger rotational angle of the coupler. An installing height of 56 mm was set up to provide an initial pitch angle. When the longitudinal force was gradually increased to 900 kN, no upper climbing phenomenon of the tolling occurred. However, significant coupler jackknifing behavior occurred when the applied force was decreased to 200 kN. The lower supporting beam flied away from the test rig, which reproduced the local destructions of coupler yoke in the field test.

Fig. 5
figure 5

Compressed stability test of coupler. a Illustration of test rig. b Coupler jackknifing behavior

Full size image

2.3 Quasi-static geometric analyses of train and coupler

In this section, the quasi-static analyses of train and coupler are carried out to study the coupler jackknifing mechanism. The geometric and force analyses are shown in Fig. 6. In general, the pitch moment is produced by the in-train forces at two ends of the carbody, while the anti-pitch moment by the suspension system.

Fig. 6
figure 6

Quasi-static geometric analyses of train and coupler

Full size image

The pitch angle of the carbody \(\gamma_{1}\) is determined by

$$\gamma_{1} = \arcsin ({{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } {l_{1} }}} \right. \kern-0pt} {l_{1} }}) ,$$
(1)

where \(d_{s}\) is the overall vertical deflection of the secondary and primary springs and \(l_{1}\) is the bogie center distance. The vertical distance between coupler pins at two ends of the carbody is written as

$$h_{1} = \sin \gamma_{1} \cdot l_{2} ,$$
(2)

where \(l_{2}\) is the distance between coupler rotational pins at two ends of the carbody. The pitch angle of two coupled couplers can be written as

$$\gamma_{2} = \arcsin ({{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {l_{3} }}} \right. \kern-0pt} {l_{3} }}) ,$$
(3)

where \(l_{3}\) is the distance between coupler rotational pins at adjacent carbodies. With respect to the gravity center of carbody, the pitch moment due to in-train forces is given by:

$$M_{p} = T_{1} \cos \gamma_{2} \cdot h_{2} { + }T_{1} \sin \gamma_{2} \cdot l_{2} /2 - T_{2} \cos \gamma_{2} \cdot h_{2} {\kern 1pt} { + }T_{2} \sin \gamma_{2} \cdot l_{2} /2 .$$
(4)

If T 1 equals to T 2, the pitch moment can be written as

$$M_{p} = T\sin \gamma_{2} \cdot l_{2} .$$
(5)

The anti-pitch moment provided by suspensions is given by:

$$M_{\text{s}} = \left( {F_{{{\text{z}}0}} - \Delta F_{\text{z}} \cdot 2} \right) \cdot \left( {l_{2} + d_{\text{l}} } \right) - \left( {F_{{{\text{z}}0}} + \Delta F_{\text{z}} \cdot 2} \right) \cdot \left( {l_{2} - d_{\text{l}} } \right) .$$
(6)

Ignoring the minim value d l, Eq. (6) can be written as:

$$M_{\text{s}} = - 4\Delta F_{\text{z}} \cdot l_{2}.$$
(7)

Based on the moment equilibrium, the unloading force of secondary suspension is derived.

$$\Delta F_{\text{z}} { = }\frac{{T\sin \gamma_{2} }}{{4l_{2} }} .$$
(8)

It can be indicated from Eq. (1), the pitch angle of carbody decreases with decreasing suspension deflections or increasing bogie center distance. According to Eqs. (2) and (3), the pitch angle of carbody and distance between coupler rotational pins at two ends of the carbody should be as small as possible to lower the pitch angle of coupler. The distance between coupler rotational pins at adjacent carbodies should be longer. The unloading force of secondary suspension is relevant to the in-train force and pitch angle of coupler, i.e., the vertical force component.

3 Dynamic modeling

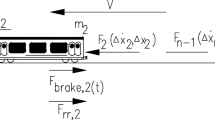
In order to accurately study the longitudinal dynamics of EMUs under rescue, the train and coupler dynamic models are developed in the simulation package SIMPACK. In the model, the three assisting and three assisted vehicles are considered to be with full degree of freedom (DoF), while other vehicles simplified as dummy body with only longitudinal DoF, see Fig. 7. The in-train connections consist of coupler, draft gear and supporting beams. The dynamic model of the coupler system is built based on actual kinetic relations and boundary limitations. The illustration of a pair of coupled Shibata couplers is also shown in Fig. 7. The relative movements and rotations between two coupled couplers in the longitudinal direction are locked. For a Shibata coupler, the relative rotations between the coupler body and yoke are free, including rotations with respect to vertical and lateral axis. The relative movement between the coupler and yoke are locked. The rotation with respect to vertical axis and the relative movement in vertical and longitudinal directions between the yoke and carbody are free. For a type 10 coupler, the coupler is simplified as a rod with longitudinal DoF. The characteristic curve of force–deflection relations of draft gears is given in Fig. 8a. According to coupler structures, the CRH2 series EMUs are divided into type A, while CRH1, CRH3 and CRH5 series EMUs into type B. The look-up table approach is utilized to model the nonlinear hysteresis characteristic of draft gear [12]. The hysteresis characteristic of draft gear means the dissimilarity between its loading and unloading curve. The envelop area between the loading and unloading curve indicates the energy that is absorbed within an operating cycle. In the coupler system model, the boundary limitations between the coupler yoke and carbody are negligible. In normal conditions, the coupler yoke is supported by the supporting beam and limited by the anti-jumping beam. As the supporting beam was destroyed due to the large impact force during the braking test, the nonlinear stiffness of the supporting beam was determined by laboratory test.

Fig. 7
figure 7

Train and coupler system dynamic models

Full size image
Fig. 8
figure 8

Characteristic curves. a Force–deflection relations of draft gear. b EB braking

Full size image

The braking decelerations with respect to train speeds are shown in Fig. 8b. The braking forces or torques are applied by the assisting train, while the assisted train does not possess the ability of braking. It is indicated the EB deceleration of type A is higher than that of type B. The braking deceleration at lower speed is higher. Thus, the braking-induced impact at low speed is mainly discussed in this paper.

According to both the field tests and numerical simulations, low-frequency longitudinal vibrations are arisen due to the application of EB. Figure 9 shows the comparison of tested and simulated coupler forces in the time history. It is indicated that the tested and simulated peak values are 721.23 and 719.47 kN, respectively. The relative error of peak values between simulation and testing are lower than 5%. In general, the simulated results in the time history show good coincidence with the tested ones. Due to the occurrence of collision, the damping effect in the field testing seems to be more significant than that of simulation.

Fig. 9
figure 9

Comparison of tested and simulated coupler force under CRH2E–CRH1B train to train rescue scenario

Full size image

4 Longitudinal dynamics of EMUs under rescue

4.1 Safety indices

According to structural characteristic and theoretical analysis, the limit values of safety evaluation are determined as below:

  1. 1.

    Type A EMUs

    • The coupler force is lower than 800 kN.

    • The deflection of single draft gear in the front section is lower than 96 mm.

    • The deflection of single draft gear in the central section is lower than 56 mm.

    • The wheel unloading ratio is lower than 0.65.

    • The vertical distance between the coupler in the front section and carbody is lower than 80 mm.

    • The interference between the in-train damper and carbody does not occur.

    • The vertical force component at the coupler yoke does not exceed 80 kN.

  2. 2.

    Type B EMUs

    • The coupler force is lower than 800 kN.

    • The wheel unloading ratio is lower than 0.65.

    • The vertical displacement between adjacent carbodies is lower than 200 mm.

4.2 Longitudinal dynamics and safety evaluation of different EMUs under rescue

During the train to train rescue process, the EB is applied by the rescue train while the disabled train is out of the ability of applying braking. The train models for different combinations of train to train rescue conditions are built, including type A–A, B–A as well as A–B scenarios. The short-group train is abbreviated to AS or BS, while long-group train to AL or BL. Herein, the AS and AL train refer to the type A EMU consisted of 8 and 16 vehicles, respectively. The train to train rescue scenario of ‘AL–AS’ refers to the AL train is assisting train with the braking ability, while AS train is disabled without braking.

The train speed before applying EB on the tangent track is 80 km/h. The braking-induced in-train force of type A–A train to train rescue scenario is as high as 944.1 kN in the AL–AL train configuration, see Fig. 10. The in-train forces of AL–AS and AS–AL train configurations are smaller than that of AL–AL but are higher than that of AS–AS train configuration. It is indicated that significant coupler jackknifing behavior occurs. As a consequence of that, the vertical force component is generated due to the combination of in-train forces and coupler pitch angle. Besides, the longer the train configuration, the larger the in-train force. The rescue scenarios for the coupled train consisted of 24 or 32 vehicles have safety concerns when the EB is applied the assisting train. The phenomena of wheel unloading, dynamic interference and local structural destruction may happen. The running safety indices of the AS–AS train configuration are within allowable limits. On tangent and large-radium curved tracks, only the vertical coupler jackknifing behavior occurs, while the lateral coupler jackknifing does not happen. Thus, the wheel unloading ratio is adopted to evaluate the derailment risk. However, the lateral coupler jackknifing behavior on small-radius curved tracks may occur in an extremely coincidental condition. The derailment risk of train to train rescue on small-radius curved tracks will be discussed in future works.

Fig. 10
figure 10

Calculated results of rescue. a In-train force. b Normalized safety indexes

Full size image

The EB induced in-train force of type A–B train to train rescue scenario is given in Fig. 11. The in-train forces of AL–BS and BS–AL train configurations reach a maximum value of 718.6 kN, while that of AS–BS is 449.0 kN. Similarly, the longer the train configuration, the larger the in-train force. The train to train rescue for AL–BS and BS–AL scenarios has safety concerns when the EB is applied the assisting train. The wheel unloading, dynamic interference and local structural destruction may happen. The running safety indices of AS–BS scenario are within limits.

Fig. 11
figure 11

Calculated results of rescue. a In-train force. b Normalized safety indexes

Full size image

The EB induced in-train force of type B–A scenario for train to train rescue is given in Fig. 12. The in-train forces of BL–AS and BS–AL train configurations reach a maximum value of 813.6 kN. The train to train rescue for BL–AL scenario have safety concerns when the EB is applied the assisting train. The wheel unloading, dynamic interference and local structural destruction may happen. The running safety indices of BL–AS, BS–AL and BS–AS scenarios are within limits.

Fig. 12
figure 12

Calculated results of rescue. a In-train force. b Normalized safety indexes

Full size image

5 Outlook

For existing high-speed electric multiple units in China, the braking-induced impacts may occur in the train to train rescue scenarios. Thus, one key technical improvement for the next-generation high-speed vehicles is to realize the mechanical and electrical connections between high-speed trains provided by different manufacturers. The illustration of two coupled new-generation high-speed train, e.g., CR400AF and CR400BF, is shown in Fig. 13. The coupler and draft gear system of the two types of high-speed train have been uniformly redesigned in mechanical and electrical aspects. A series of field tests were conducted before commercial operations. The highest testing speed of two coupled train was 420 km/h under normal conditions. The braking signal of one train is synchronous to another train. In terms of train to train rescue scenario, a disable train can be easily rescued by another train without extra manipulations. The coupler structures and braking characteristics are redesigned to avoid braking-induced impact and further affects. The longitudinal dynamic performance of the new-generation high-speed trains can be significantly improved.

Fig. 13
figure 13

Illustration of two coupled new-generation high-speed trains

Full size image

6 Conclusions

According to the testing and numerical analyses of longitudinal train dynamics for EMUs under rescue, the following conclusions can be drawn:

  1. 1.

    During process of the train to train rescue, the in-train forces are generated by the braking force applied by the assisting train while the assisted train does not possess the braking ability. The in-train force is closely relevant to the weight of train configuration and the braking deceleration.

  2. 2.

    The field and laboratory tests show that coupler vertical jackknifing behavior occurs under compressed in-train force. The coupler pitch combined with longitudinal force produce a vertical force component, which is the main indicator to local destruction and carbody pitch motion. The carbody pitch can even result in the interference of in-train devices.

  3. 3.

    In terms of coupler forces, deflections of draft gear, wheel unloading, in-train interference as well as local destructions, the allowable values of safety indices for EMUs under rescue are determined. The running safety for different train to train rescue scenarios was evaluated based on the developed train and coupler system dynamic models. In terms of EB conditions, the running safeties for the train configurations, i.e., A–A(16 cars), A–B(16 cars), B–A(24 cars), are within allowable limits. For other train configurations, especially for long coupled trains with 32 cars, the longitudinal dynamic issues, e.g., wheel unloading, dynamic interference and local structural destruction, may happen during EB process.