1 Introduction

Quantum information processing in complex networks is based on the assumption that parties (or agents) acting in the network can utilize quantum carriers of information to control the execution of protocols or algorithms. In this scenario, it is reasonable to assume that the integrity of protocol execution should be secure even against the attacker possessing the ability to operate on quantum data. In other words, one has to revise the results concerning the security of classical distributed protocols taking into account the quantum model of computation [1].

Suppose we have a reflexive graph G (i.e. with an edge joining a vertex to itself at each vertex) and two players. We define a game as follows: the first player, usually called Cop or Pursuer, chooses a vertex on which he starts and then the second player, called Robber or Evader, chooses his vertex. After that, each player changes his position to a neighbouring vertex, sequentially. If, after a finite number of rounds, the Cop and the Robber meet in the same vertex, we say that the Cop wins the game. Otherwise, we say that the Robber is the winner.

The game called Cop and Robber game was first analysed by Quilliot [2] and Nowakowski and Winkler [3]. The first author provided a beautiful characterization of finite copwin graphs, i.e. graphs on which the Cop has a winning strategy. The other authors extended it to the case of infinite graphs. Since then, many variants of the game have been proposed, including the game where the players do not see each other [4], the players move simultaneously [5], the Cop plays heuristically [6, 7], or the play is continuous in time [8, 9]. The game provides many stimulating mathematical problems. Among the best-known of them are the characterization of the multi-copwin graph [10] and Meyniel conjecture [11]. Furthermore, the game provides an interesting algorithmic problem: demonstrating that a graph needs at most k Cops for winning the game is NP-hard. The game has also found its applications in robotics [12], modelling graph searching [13], and analysing the security in complex networks [14]. For a survey of the game and its properties see [15].

In this work, we introduce the quantum games based on the assumption that both parties possess full information about the strategy of the second party. In quantum game theory, this assumption is rare as the main motivation to study quantum games is to extend the space of possible moves [16], utilise entanglement for the synchronization of the moves [17], or to share a quantum state for providing the means for cooperation [18]. Such an approach was used in [19] to analyse the quantum Prisoner’s Dilemma as a pursuit game on a graph, where the Cops utilise a shared entangled state.

In contrast, this paper contributes to the field of combinatorial games, where all players (or parties) have full knowledge of the state of the system. In the case of quantum combinatorial games, this is to say that both players possess the complete knowledge of the previous moves of the opponent. In other words, we are interested in the existence of the strategies, which are optimal in some sense. The properties of such games, defined in quantum information systems, were previously studied in the context of network exploration problems [20] and modelling of trapping mechanism in quantum networks [21]. Moreover, the possibility of using the superposition of moves in a combinatorial game has been considered [22].

Here we consider the possibility to define a quantum extension of Cop and Robber game, which describes the general protocol for tracking (or controlling) mobile agents in the scenario with dynamical information. The main question arising in this context concerns the possibility of constructing a strategy for the Cop to catch the Robber, taking into account the probabilistic nature of the quantum measurement. We analyse this problem by introducing suitable winning conditions.

The main contribution of the presented paper is obtaining a nontrivial quantum version of the game. We propose and investigate graph-preserving quantum evolution, which can be used in extending other graph-based games e.g. simple stochastic games [23]. We prove the tight bound for the number of required operations. Moreover, we show that quantum controlled gates, and hence quantum entanglement, provide new strategies which diametrically change the course of the game. Consequently, we provide an argument confirming the crucial role of entanglement in quantum information processing.

The paper is organised as follows. In Sect. 2, we introduce mathematical apparatus, including the concepts necessary to deal with the quantum measurement. We achieve this by introducing a classical game called open probabilistic Cop and Robber game. We show that the game trivialises in the sense of the winning strategy. In Sect. 3, we define a graph-preserving quantum evolution, and by applying it, we introduce classically controlled quantum Cop and Robber game. We show that such a game cannot be used to obtain an advantage in the sense of the broader class of winning strategies. We also provide a tight bound for state obtainability. In Sect. 4, we extend the graph-preserving quantum evolution to describe the non-trivial extension of the game, namely quantum controlled Cop and Robber game. We demonstrate that such version provides an advantage over the classically controlled quantum scheme. Finally, in Sect. 5, we provide a summary of the presented results.

2 Preliminaries

We start by introducing mathematical apparatus required for the analysis of the quantum Cop and Robber game. In particular, we provide some facts related to the probabilistic version of the game that offer some insights into the behaviour of the players in the quantum realm.

2.1 Graph terminology

Suppose we have a digraph G with vertex set V and arcs \(A\subset V\times V\). We say that the vertex \(v\in V\) is a neighbour of \(u\in V\) iff \((u,v)\in A\). The set of all neighbours of u is denoted by S(u). A graph is called reflexive, iff for each \(v\in V\) we have \((v,v)\in A\). The reflexive graphs are the only ones considered here. We say that the vertex v is a corner if there exists the vertex u such that \(S(v)\subset S(u)\). A spanning tree is a sub-graph that is a tree which includes all of the vertices of G. A directed graph is called reversible, if for arbitrary \(v,w\in V\) there is path from v to w.

Suppose we have an undirected graph G with vertex set V and edges E. We call \(V_1\subset V\) a dominating set iff for an arbitrary vertex \(v\in V\) we have \(v\in V_1\) or \(N(v)\cap V_1\ne \emptyset \), where N(v) denotes the set of neighbours of v. The vertex which itself forms a dominating set is called universal vertex.

A graph homomorphism from a graph G to \(G'\) is an arc-preserving mapping from V to \(V'\). We call a graph homomorphism f a retraction if for each \(v'\in V'\) we have \(f(v')=v'\). Then we call \(G'\) a retract of G and denote it by \(G\upharpoonright V'\).

2.2 Open probabilistic Cop and Robber game

As it has already been mentioned, many variations of the game can be proposed. One of the most popular versions is Hunter and Rabbit game [4], where players do not see each other until they are at the same vertex. In that case, the strategy needs to be described with the stochastic operations, and the players’ positions are represented with probability vectors. Note that the probabilistic version of Cop and Robber game is no longer open since both the positions of the players, even in the sense of probability vector, and the performed stochastic operations are unknown to the opponent.

To introduce the open probabilistic version of Cop and Robber game, we use the following scheme. Suppose that the graph is known to both players. The Cop and the Robber, in that order, choose their initial positions randomly, i.e. they select the probabilistic vector of a position. Next, they sequentially perform stochastic operations preserving the graph structure on their states. In each step, both the Cop and the Robber do not know their position and their opponent’s position, but they know the current probability of a player being in all vertices. The Cop when to perform a measurement, that is when he uncovers the board.

To consider probabilistic versions of Cop and Robber game, including the variant with quantum strategies, we need to take into account the probabilistic nature of quantum measurement. To this end, we define the following classes of winning conditions.

Definition 1

(p-copwin graphs) We say that the graph is p-copwin, if there is such strategy for the Cop that after a finite number of steps the probability of measuring the players in the same vertex is greater than p.

Definition 2

(Nearlyp-copwin graphs) We say that the graph is nearly p-copwin, if for arbitrary \(\varepsilon >0\) there is a strategy for the Cop such that he can win with the probability at least \(p-\varepsilon \).

It is worth noting that in the sense of the strategy set, the probabilistic version expands the original, deterministic Cop and Robber game. Every move in the original one can be described as a stochastic operation. When we restrict players to deterministic probability vectors, each course of the original game can be described with open probabilistic Cop and Robber formalism.

However, it is easy to see that the open probabilistic model narrows the set of feasible strategies. To demonstrate this let us suppose that directed graph \(G=(V,A)\) is given. The Cop chooses vector \(p_{\mathcal {C}}(v) =\frac{1}{|V|}\) as the initial state. For arbitrary Robber’s position \(p_\mathcal {R}\) the probability of measuring the players in the same vertex equals

$$\begin{aligned} p_{\text {copwin}} = \sum _{v\in V}p_\mathcal {C}(v)p_\mathcal {R}(v) = \frac{1}{|V|}\sum _{v\in V} p_\mathcal {R}(v) = \frac{1}{|V|}. \end{aligned}$$
(1)

Note that the probability of winning with this strategy does not depend on the Robber’s position. Hence, an arbitrary directed graph is at least \(\frac{1}{|V|}\)-copwin. If the Robber chooses the same initial state, we can show that the arbitrary graph is precisely \(\frac{1}{|V|}\)-copwin. Note that the strategy does not depend on the arcs set, and henceforth the graph does not need to be even connected. The probability depends on the size of V only.

2.3 Probabilistic versus deterministic strategy

Let us now analyse how the introduced scheme influences the class of cop-win graphs. To achieve this let us examine an unfair game on cop-win graphs. It is easy to see that if the Robber is limited to deterministic strategies while the Cop is allowed to use randomised strategies, the latter can win with probability arbitrarily close to one. The following theorem gives the full characterisation of this situation.

Theorem 1

In open probabilistic Cop and Robber game on an undirected graph G with the Robber using deterministic moves, the Cop can win with probability one if and only if G is cop-win. Otherwise, the Cop can win with the probability arbitrarily close to one.

Proof

The sufficiency of a graph being copwin comes from the fact that the Cop can use the deterministic strategy to win. In the not cop-win graph case, the Robber can always evade a part of the probability of the Cop localised in some vertex. Hence we have necessity.

Now we show that an arbitrary graph is nearly 1-copwin. The Cop spreads uniquely on the arbitrary dominating set of the graph. Next, he can ‘catch’ the evader with probability one over the cardinality of the dominating set. The part of probability which is on the Robber’s position will now follow him, while the rest of the probability repeat the strategy. Each round needs the linear time of single steps on a number of vertices, and one can show that the probability of winning for the Robber decreases geometrically with the number of rounds. \(\square \)

If we swap the limitations, the Cop can win with probability at most \(\frac{1}{|V|}\), since the Robber can choose the uniform distribution as the initial state. However, if a graph is not copwin, the Robber can use deterministic strategies to avoid the pursuer entirely. We have not found the full characterization of this situation for copwin graphs.

3 Graph-preserving discrete evolution

The first quantum version of the Cop and Robber game considered in this paper is defined by using quantum operation, preserving the structure of a graph. In this section, we use such operations to introduce a direct quantum version of the open probabilistic Cop and Robber game. We call this game the classically controlled quantum Cop and Robber game to emphasise the fact that the introduced scheme is based on the full knowledge of the quantum state of the opponent. We show that in the context of winning strategy the game does not change in comparison to the probabilistic version. We also show that for arbitrary connected, reflexive and undirected graph every quantum state is obtainable in O(|V|) steps, which is tight bound. We also provide examples demonstrating that finding a graph preserving discrete evolution is not always trivial and can lead to some unintuitive results.

3.1 Direct approach

In the probabilistic version of Cop and Robber game, the players can choose arbitrary stochastic operations preserving the graph structure. Such operations are defined as follows.

Definition 3

(Graph preserving stochastic operation) We say that the stochastic operation M preserves the graph, if for arbitrary disconnected vertices v and w, represented by orthogonal states \(| v \rangle \) and \(| w \rangle \) respectively, we have \(\langle w | M | v \rangle =0\).

In a similar manner, one can define a quantum operation preserving the graph structure.

Definition 4

(Graph preserving quantum operation) We say that the unitary operator U is graph preserving quantum operation, if for arbitrary disconnected vertices v and w, represented by orthogonal states \(| v \rangle \) and \(| w \rangle \) respectively, we have \( \langle w | U | v \rangle =0\).

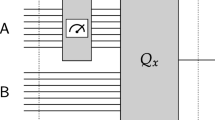
Using the above definition one can introduce the quantized version of Cop and Robber game, called classically controlled quantum Cop and Robber game. At the beginning of this game, both players choose ar arbitrary pure quantum state. The evolution of pure states is described with graph preserving quantum operation U. The \(\mathbf U_G\) denotes the set of all quantum operations preserving the graph G. The \(\mathbf U_G\) contains the identity and is closed under Hermitian transposition. However, it does not form a group because it is not closed under multiplication.

Fig. 1
figure 1

Classically controlled quantum Cop and Robber game. The Cop chooses his initial state first, and then the Robber chooses his state. Double line denotes classical control since both parties possess the full knowledge of their and their opponent’s current state. The measurement is performed in the basis \(\{| v \rangle : v \in V \}\)

Full size image

More precisely, we can define the game as follows. Each player has their own system \(\mathcal {H}_\mathcal {R}\) and \(\mathcal {H}_\mathcal {C}\) spanned by orthogonal set \(\{| v \rangle :v\in V\}\) and chooses the initial quantum state \(| \mathcal {R}_0 \rangle \) and \(| \mathcal {C}_0 \rangle \). The combined system is of the form \(\mathcal {H}_\mathcal {R}\otimes \mathcal {H}_\mathcal {C}\) and the initial state is of the form \(| \mathcal {R}_0 \rangle \otimes | \mathcal {C}_0 \rangle \). Then, in each iteration the Cop and the Robber perform operations \(\mathrm {I}_\mathcal {R}\otimes U_\mathcal {C}\) and \(U_\mathcal {R}\otimes \mathrm {I}_{\mathcal {C}}\), respectively, where \(U_\mathcal {C},U_\mathcal {R}\in \mathbf U_G\). In the end, they perform the measurement in basis \(\{| v \rangle : v\in V\}\). The Cop wins if, after t steps and his move, both players are measured in the same vertex. In this situation, if \(| S_t \rangle \) denotes the game state after t steps, then the probability of the Cop being a winner reads

$$\begin{aligned} p_{\mathrm {copwin}} = \sum _{v\in V} |(\langle v | \otimes \langle v |)| S_t \rangle |^2. \end{aligned}$$
(2)

One should note that by local operation one cannot entangle the registers. For this reason the state is of the form \(| S_t \rangle = | \mathcal {R}_t \rangle \otimes | \mathcal {C}_t \rangle \) and the formula above simplifies to

$$\begin{aligned} p_{\mathrm {copwin}} = \sum _{v\in V} |\langle v |{\mathcal {R}_t}\rangle \langle v |{\mathcal {C}_t}\rangle |^2. \end{aligned}$$
(3)

Quantum circuit for the above game is presented in Fig. 1.

The quantized version of Cop and Robber game introduced above can be understood as a reformulation of the open probabilistic Cop and Robber game in the language of quantum computing. It can be seen that the ability to utilise local quantum moves does not provide any party with an advantage. To demonstrate this one can observe that the Cop and the Robber can choose the equal superposition of the base states, \(\frac{1}{|V|} \sum _{v\in V} | v \rangle \), as the initial state. It is easy to observe that every graph is \(\frac{1}{|V|}\)-copwin. One should note that this example suggests that the triviality does not depend even on the evolution form—similar results will be obtained if we choose discrete quantum walk model or other models as an evolution.

The unfair game yields the same results as an open probabilistic game. We can conclude the results as follows: in order to provide interesting, non-trivial quantized Cop and Robber game, we need to enrich the structure of correlations between the players’ systems. This motivates the quantum model based on the ability to execute non-local quantum gates, developed in Sect. 4.

3.2 Tight bound for state obtainability

It was shown [24] that in order to evolve using operations from \(\mathbf U_G\) the graph may be directed but it must be reversible, i.e. if there is a path from v to w, then there is a path from w to v. However, it is not enough for obtaining an arbitrary result state. Suppose \(G=(\{0,\dots ,n-1\},A)\) is a directed, clockwise cycle. Then, \(\mathbf U_G\) consist of identity operations and clockwise permutations changing at most the amplitude phase, i.e.

$$\begin{aligned} U = \sum _{i=0}^{n-1} e^{\mathrm i\alpha _i}| i\oplus 1 \rangle \langle i |, \end{aligned}$$
(4)

where \(\oplus \) denotes addition modulo n, and \(\alpha _i\in \mathbb R\). As an example, if a state \(| 0 \rangle \) is given, it is impossible to obtain superposition \(\frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )\). Below we present a sufficient condition for an arbitrary state obtainability.

Theorem 2

Let \(G=(V,E)\) be such a reflexive, reversible digraph that contains an undirected spanning tree. Then, for arbitrary states \(| \varphi \rangle \) and \(| \psi \rangle \), there exists a sequence \(U_1,\dots ,U_{2|V|-2}\in \mathbf U_G\) such that

$$\begin{aligned} | \psi \rangle = U_{2|V|-2} \dots U_1| \varphi \rangle . \end{aligned}$$
(5)

Proof

Suppose v and w are connected vertices, and \(| \varphi \rangle = \alpha _v | v \rangle + \alpha _w | w \rangle \). It is simple to show that for arbitrary \(| \psi \rangle = \beta _v | v \rangle + \beta _w | w \rangle \) such that \(\langle \psi |{\psi }\rangle = \langle \varphi |{\varphi }\rangle \), there exists a quantum operation U preserving the graph such that \(| \psi \rangle = U| \varphi \rangle \). This is equivalent to the fact that, if v and w are connected, their arbitrary superposition can be changed to an arbitrary superposition with the same norm.

Let \(n=|V|\). The proof goes as follows. First, we show constructively that for an arbitrary state \(| \varphi \rangle \) and vertex \(v\in V\) we can find a sequence of quantum operations preserving the graph structure, changing \(| \varphi \rangle \) to \(| v \rangle \). Similarly, one can reverse the method to obtain \(| \psi \rangle \) from \(| v \rangle \). In both stages, we need \(n-1\) operations. As the result, we obtain a sequence of length \(2n-2\).

Let T be an arbitrary spanning tree of G and v be its arbitrary vertex. Let \(v_1,\dots ,v_n\) be an arbitrary order such that if \(i>j\), then \(d_T(v,v_i) < d_T(v,v_j)\) (hence \(v_n=v\)). We define \(\mathrm {suc}_T(v_i)= v_j\) such that \(j>i\) and \(v_i\) and \(v_j\) are connected in T for \(i\in {1,\dots ,n}\), and \(\mathrm {suc}(v_n)=v_n\). Since T is a tree, function is well-defined. Moreover, \(\mathbf {U}_T\subseteq \mathbf {U}_G\).

Suppose \(| \varphi \rangle \) is given. The algorithm goes as follows. At each step \(i\in [n-1]\) we choose quantum operation \(U_i \in \mathbf {U}_T\) changing superposition \(\alpha _{v_i}| v_i \rangle +\alpha _{\mathrm {suc}(v_i)}| \mathrm {suc}(v_i) \rangle \) into \(\beta _{\mathrm {suc}(v_i)}| \mathrm {suc}(v_i) \rangle \) such that \(|\beta _{\mathrm {suc}(v_i)}|^2= |\alpha _{v_{i}}|^2+|\alpha _{\mathrm {suc}(v_i)}|^2\) and acting trivially on the other canonical states. Simple induction shows that, after \(n-1\) steps, we obtain state \(| v \rangle \). The reversed method enables us to obtain state \(| \psi \rangle \). \(\square \)

The above theorem shows that the arbitrary state can be obtained with O(|V|) steps. For some graphs, we need much fewer steps. Even the algorithm from the proof can be optimised since in some cases the operations can be performed simultaneously. In the case of the complete graph, an arbitrary state can be obtained in one step. However, one should note that this bound cannot be decreased in general. It can be verified by analysing the path graph.

3.3 Nontriviality of the operations

While it is straightforward to construct proper stochastic operations preserving the graph structure, it is not the case for quantum operations. It is because the construction of stochastic operations can be done independently for each column. In the case of quantum operations, we need to check whether the columns are pair-ways orthogonal.

Suppose the graph in Fig. 2a is given. Let us start with state \(| \varphi \rangle =\alpha | 0 \rangle +\beta | 1 \rangle + \gamma | 2 \rangle \), where \(\alpha ,\beta ,\gamma \ne 0\). Our goal is to find a single graph-preserving quantum operation which will change the state into \(e^{\mathrm i\psi }| 1 \rangle \). Note that all quantum operations need to be of the form

$$\begin{aligned} \begin{bmatrix} \times\times & {} 0 \\ \times\times & {} \times \\ 0\times & {} \times \end{bmatrix}, \end{aligned}$$
(6)

where mark ‘\(\times \)’ denotes the possibly nonzero value. In order to preserve the unitarity of the matrix, the first and the last columns need to be orthogonal. Hence, \(\langle 0 | A | 1 \rangle \) or \(\langle 2 |A | 1 \rangle \) equals 0. In this case, the matrix preserves \(\alpha | 0 \rangle \) or \(\gamma | 2 \rangle \) part of the state up to phase, respectively. The result can be generalized to the star graphs with number of vertices at least 3. Therefore, it is impossible to obtain the goal. At the same time, it is easy to find a stochastic operation which changes arbitrary probability vector \([p_0,p_1,p_2]\) into [0, 1, 0].

The situation changes diametrically in the case of the graph in Fig. 2b. Suppose that we again start in state \(| \varphi \rangle =r_\alpha e^{\mathrm ik_\alpha }| 0 \rangle +r_\beta e^{\mathrm ik_\beta }| 1 \rangle + r_\gamma e^{\mathrm ik_\gamma }| 2 \rangle \), where all the parameters are nonnegative. Then for

$$\begin{aligned} V= \begin{bmatrix} -e^{i ({k_\beta }-{k_\gamma }+\psi )} {r_\beta }&\quad e^{i ({k_\alpha }-{k_\gamma }+\psi )} {r_\alpha }&\quad 0&\quad e^{-i (-{k_\alpha }+{k_\gamma }+\alpha +\pi )} {r_\gamma } \\ e^{-i ({k_\alpha }-{k_\gamma }+\psi )} {r_\alpha }&\quad e^{-i ({k_\beta }-{k_\gamma }+\psi )} {r_\beta }&\quad e^{-i \psi } {r_\gamma }&\quad 0 \\ 0&\quad e^{i \psi } {r_\gamma }&\quad -e^{i ({k_\beta }-{k_\gamma }+\psi )} {r_\beta }&\quad e^{-i \alpha } {r_\alpha } \\ -e^{-i ({k_\alpha }-{k_\gamma }-\alpha )} {r_\gamma }&\quad 0&\quad e^{i \alpha }{r_\alpha }&\quad e^{-i ({k_\beta }-{k_\gamma }+\psi )} {r_\beta } \\ \end{bmatrix} \end{aligned}$$
(7)

we have \(V| \varphi \rangle =e^{\mathrm i(k_\gamma -\psi )}| 1 \rangle \). Note that

$$\begin{aligned} V| 3 \rangle = - e^{-i (-k_\alpha +k_\gamma +\alpha )} r_\gamma | 0 \rangle + e^{-i \alpha } r_\alpha | 2 \rangle + e^{-i (k_\beta -k_\gamma +\psi )} r_\beta | 3 \rangle , \end{aligned}$$
(8)

the amplitudes are fixed and we can only change the local phase.

Fig. 2
figure 2

a An example of a graph for which it is impossible to find graph-preserving quantum operation changing state state \(\alpha | 0 \rangle +\beta | 1 \rangle + \gamma | 2 \rangle \) to state \(| 1 \rangle \). At the same time it is simple to find a stochastic operation which performs similar operation. b An example of a graph for which it is possible to find an operation which changes the state \(\alpha | 0 \rangle +\beta | 1 \rangle + \gamma | 2 \rangle \) to \(| 1 \rangle \), for \(\alpha ,\beta ,\gamma \ne 0\)

Full size image

4 Quantum controlled Cop and Robber game

Taking into account the discussion in Sect. 3 we can now define and analyse another quantized version of Cop and Robber game. Using graph-preserving quantum operations, we generalise the available strategies into controlled graph-preserving quantum operations. Such game differs significantly from the previously mentioned ones, at least in the sense of the probability of winning available for the Cop. We show that a controlled graph preserving quantum operations generalise the original graph-preserving quantum operations.

4.1 Model definition

Similarly to classically controlled quantum Cop and Robber game, each player has their own quantum system spanned by \(\{| v \rangle : v \in V\}\). In the beginning, the Cop and the Robber, in that order, choose their initial states. However, in contrast to the previously defined game, the Robber can entangle arbitrarily with the Cop at the beginning, by performing the controlled operation. In this model, the players do not possess the knowledge about the global states and are allowed to perform controlled graph-preserving quantum operations only. For this reason, we call this model quantum controlled Cop and Robber game.

We define the set of the allowed operations as follows. Let G be an arbitrary reflexive, connected directed graph. By \(\mathbf U_G\) we denote the set of graph-preserving quantum operations. Moreover, let \(U:V\rightarrow \mathbf U_G\) be an arbitrary function. Then the operation

$$\begin{aligned} {\tilde{U}} = \sum _{v\in V} | v \rangle \langle v |\otimes U(v) \end{aligned}$$
(9)

is the controlled graph-preserving quantum operation. Note that \({\tilde{U}}\) is a unitary operation. We denote the set of all such operations as \(\mathbf {cU}_G\). One can verify that

$$\begin{aligned} \mathbf {cU}_G = \mathbf U_{\underbrace{G+G+\cdots +G}_{n\text { times}}}, \end{aligned}$$
(10)

where \(+\) denotes the disjoint union of the graphs.

In the quantum controlled Cop and Robber game, both players can perform arbitrary operations from \(\mathbf {cU}_G\). The control part is performed on the opponent’s system, while the quantum operations are performed on the player’s system.

The probability of the Cop to win is the same as in the classically controlled quantum Cop and Robber game, i.e. if after t-th round the state of \(\mathcal {H}_\mathcal {R}\otimes \mathcal {H}_\mathcal {C}\) is \(| S_t \rangle \), then

$$\begin{aligned} p_{\mathrm {copwin}} = \sum _{v\in V} |(\langle v | \otimes \langle v |)| S_t \rangle |^2. \end{aligned}$$
(11)

However, the formula cannot be simplified due to possible entanglement between the players’ systems. The representation of the game in the form of a quantum circuit is presented in Fig. 3. Note that in this game both players do not know the current global state. For this reason, both players can prepare the strategies before the game.

The quantum-controlled game expands the classically controlled one in the sense of the possible operations. Let \(U\in \mathbf U_G\). Then

$$\begin{aligned} {\tilde{U}} = \sum _{v\in V}| v \rangle \langle v | \otimes U = \left( \sum _{v\in V} | v \rangle \langle v | \right) \otimes U = \mathrm {I}\otimes U. \end{aligned}$$
(12)
Fig. 3
figure 3

Quantum controlled Cop and Robber game. The Cop chooses his initial state first, then the Robber chooses his state. The vertical lines denote quantum control, since both the Robber and the Cop know their and their opponent’s current state. The measurement is performed in basis \(\{| v \rangle : v \in V \}\). \(V\in \mathbf U(\mathcal {H}_\mathcal {R})\) is an arbitrary quantum gate

Full size image

4.2 Non-triviality of the game

The crucial difference between classically controlled and quantum controlled versions of the quantum Cop and Robber game is observed in the possible set of strategies. The ability to introduce entanglement between the systems enables the Cop to win in one step for a large class of graphs.

Theorem 3

An arbitrary graph which contains a universal vertex is 1-copwin in quantum controlled Cop and Robber game.

Proof

The game goes as follows. The Cop starts in a universal vertex \(| v_\mathcal {C} \rangle \). Since the Cop starts in the cannonical state, the Robber can only start in an arbitrary, separated state \(| R \rangle = \sum _{v\in V} \alpha _v | v \rangle \).

Now we define the strategy for the Cop. Let \(U_{v\leftrightarrow v'}\) denote a transposition matrix, i.e.

$$\begin{aligned} U_{v\leftrightarrow v'} = | v \rangle \langle v' | + | v' \rangle \langle v | + \sum _{w\ne v,v'}| w \rangle \langle w |. \end{aligned}$$
(13)

If \(v,v'\) are connected in G, then \(U_{v\leftrightarrow v'}\in \mathbf U_G \). Obviously, if v is a universal vertex then for an arbitrary vertex \(v'\) the operation preserves the graph structure. The Cop chooses the operation

$$\begin{aligned} {\tilde{U}}_\mathcal {C}= \sum _{v\in V} | v \rangle \langle v | \otimes U_{v \leftrightarrow v_\mathcal {C}}. \end{aligned}$$
(14)

The state changes into

$$\begin{aligned} \tilde{U}_\mathcal {C}= \left( \sum _{v\in V} | v \rangle \langle v | \otimes U_{v \leftrightarrow v_\mathcal {C}} \right) | R \rangle \otimes | v_\mathcal {C} \rangle = \sum _{v\in V}\alpha _v | v \rangle \otimes | v \rangle . \end{aligned}$$
(15)

By applying Eq. 11 we obtain the result. \(\square \)

Note that with the above strategy the Cop wins with probability one in a single step. The situation differs significantly in comparison to the situation when both play open probabilistic Cop and Robber game and the classically controlled quantum Cop and Robber games. In these cases, the Cop wins with probability \(\frac{1}{n}\) only.

Because of the above and the result from [25] we have the following collorary.

Corollary 1

Almost all classical copwin graphs are 1-copwin in the quantum controlled Cop and Robber game.

On the other hand it can be seen that the Cop cannot win in the general case. Let us use a cycle graph \(C_4\) as an example. The Cop chooses \(\sum _{i=0}^{3}\alpha _i | i \rangle \) as the initial state. Then, it is optimal for the Robber to choose state \(\sum _{i=0}^{3}\alpha _i | i,i\oplus 2 \rangle \). Simple analysis shows that for an arbitrary Cop’s strategy there always exists a Robber’s strategy such that the state before the Cop’s move is of the form \(\sum _{i=0}^{3}\beta _i | i,i\oplus 2 \rangle \). Hence, the Cop cannot win the game with nonzero probability. This example shows that the probability of winning depends on the graph.

4.3 Local versus non-local game

Let us now consider the following unfair game. The Cop is allowed to perform operations from \(\mathbf {cU_{C_4}}\), while the Robber can only perform local operations from \(\mathbf {U_{C_4}}\). Suppose the Cop starts in vertex \(\frac{1}{2}\sum _{i=0}^3 | i \rangle \). Suppose the Robber chooses an arbitrary state \(\sum _{i=0}^3 \alpha _i| i \rangle \). Then the Cop chooses the controlled operations described in Sect. 3. The state is now of the form

$$\begin{aligned} \sum _{i=0}\sqrt{\frac{3}{4}}\alpha _i | i,i \rangle + \sum _{i,j=0:i\ne j}^{3} \gamma _{i,j}| i,j \rangle , \end{aligned}$$
(16)

where \(\gamma _{i,j}\) comes from the performed operation. Note that

$$\begin{aligned} p_{\mathrm {copwin}} = \sum _{i=0}^{3} \frac{3}{4} |\alpha _i|^2 = \frac{3}{4}. \end{aligned}$$
(17)

Comparing to the classically-controlled quantum Cop and Robber game, where the Cop can achieve the probability \(\frac{1}{4}\) at most, the Cop has much better possibilities.

5 Concluding remarks

In this paper, we have introduced the quantum versions of Cop and Robber game. As a tool, we use quantum operations preserving the structure of the graph. We show that we can prepare an arbitrary state using such operations for arbitrary connected, reflexive digraph which contains an undirected spanning tree. Moreover, we have demonstrated that for arbitrary initial and resulting states we need a sequence of \(2n-2\) operations at most, which is tight in the sense of complexity. We have also proposed a simple algorithm for obtaining such sequence.

Using the introduced operations, we quantized Cop and Robber game. We propose two different quantum models. The classically controlled quantum Cop and Robber game trivialises in the sense of winning strategies and in this case both the Cop and the Robber can choose equal superposition as the initial state and achieve Nash equilibrium. Hence, the probability of winning for the Cop depends only on the vertex set size and not on any other properties of the graph or the evolution model. In that sense, the game is similar to open probabilistic Cop and Robber game. Moreover, we show that both the classically controlled quantum Cop and Robber game and the open probabilistic Cop and Robber game expand the original game in the sense of available strategies. In the case of quantum controlled Cop and Robber game, we allow both players to perform quantum controlled operations, preserving the graph structure. We argue that the game differs significantly from both previously defined models in the sense of winning strategy. By this, we show that the classical control varies considerably from the quantum control. Moreover, we demonstrate that the quantum controlled Cop and Robber game expands the original game in the sense of available strategies.

Unfortunately, we have not found any dependence between the graph-preserving stochastic operations and the quantum operations.

We have also analysed the case of unfair games. We show that the strategies available in the open probabilistic and classically controlled quantum Cop and Robber games are stronger than in the case of deterministic games. We also demonstrate that the strategies available in the quantum controlled Cop and Robber game are stronger than in the classically controlled quantum Cop and Robber game. While in the first one, the result of our analysis is applied to an arbitrary undirected graph, the latter has been shown by offering some examples. This analysis demonstrated that the utilization of quantum resources can extend the space of possible moves. A similar result has been obtained in [22], where it has been proved that the utilization of superposition of moves leads to rulesets that may alter the outcomes of games.

The results presented in this paper may be extended in different directions. First, further analysis of the quantum controlled Cop and Robber game can be made. Moreover, the various classical generalisations of original Cop and Robber game can be applied to the quantized version. Further analysis may provide new information concerning the quantum controlled operations and offer more insight into the differences between the classical and the quantum versions of pursuit-evasion games.