1 Introduction

This paper studies dominance solvability in multicriteria games, i.e. games in which the players’ payoffs are generally multidimensional or vector-valued. Such higher payoff dimensionality may be relevant, for example, when modeling firms that compete in prices for profits as well as market share (Bade 2005; Mármol et al. 2017) or in quantities under demand uncertainty (Caraballo et al. 2015). It is also relevant in the analysis of commons exploitation when players have equity considerations in addition to a payoff capturing their personal gains (Lejano and Ingram 2012). Other potential domains of application of such games are multi-product auctions, multi-issue voting and bargaining among altruistic players.

The paper’s main motivation for studying dominance solvability in the general class of multicriteria games comes from noting that, owing to the often severe multiplicity of generalized Nash equilibria in such games (Shapley 1959), there appears to be a need for solution concepts that offer plausible equilibrium refinements. Such refinements would allow for increased predictive sharpness and, possibly, descriptive relevance within the context of this modeling apparatus. Potentially, they may also help towards making multicriteria games more “friendly” in the economic analysis of strategic interaction.

A reasonable starting point in this endeavour is to turn to the influential notion of sophisticated equilibrium that was introduced in Moulin (1979, 1986) for standard real-payoff games. In that context, dominance solvability can lead the analyst to discard equilibria in which some player employs a strategy that is iteratively weakly dominated. Similar to Moulin’s work, the goal of this paper is to provide a solution concept that builds on a notion of generalized weak dominance which, whenever applicable, eliminates generalized equilibria in which some player’s strategy is iteratively dominated.

To this end, the most direct generalization of weakly dominated strategies in the class of multicriteria games is considered first, requiring one strategy to dominate another for some player if it results in a weakly greater vector payoff against all opponent profiles and strictly so against some such profile. A notion of iterative dominance solvability that builds on this definition is then introduced, extending Moulin’s (1979) notion to the present environment. The paper’s main result is that finite multicriteria games that are dominance solvable in this sense are necessarily generalized equilibria. As such, it includes the main result in Moulin (1979) as a special case where all players’ payoffs are real-valued.

A less demanding solution concept of iterative dominance that is based on the more general notion of partially dominated strategies is introduced next. A strategy is said to be partially dominated by another for some player, if there is no opponent strategy profile at which the former does better (in the vector-dominance sense) and at the same time there is some such profile where the latter does better. This can be thought of as a “reason-based” decision rule (see also Gerasimou 2016 for a related choice-theoretic analysis) that a possibly bounded-rational player in such an environment might employ to make strategic choices. It is shown by example, however, that, when applicable, the solution concept associated with this notion of dominance may fail to select a set of generalized equilibria.

2 Multicriteria games and generalized equilibria

A multicriteria game is a collection \((S_i,v_i)_{i=1}^I\), where I is the number of players, \(S_i\) is player i’s pure strategy set, \(S=\prod _{i=1}^I S_i\) is the set of all strategy profiles, and \(v_i:S\rightarrow \mathbb {R}^{n_i}\) is player i’s payoff function, with \(n_i\ge 1\) holding for every \(i\le I\). It will be assumed that players, strategies and payoff dimensionalities are all finite. Such a multicriteria game will, therefore, be referred to as finite.

For \(s,s'\in S\) and \(i\le I\), the following notation will be used:

(1)

As is standard in this literature (Zhao 2018 is a recent survey), it is assumed throughout that all players’ payoffs are ordered as in (1), and that this is common knowledge. Such an assumption is obviously suitable when the modeler knows that all players’ true preferences do actually coincide with the canonical partial ordering on the Euclidean space that pertains to their payoffs—intuitively, when they are unable to resolve trade-offs across their different payoff dimensions—and this fact is commonly known in the game. Moreover, as pointed out in Bade (2005), the assumption is also relevant when the modeler is actually ignorant about the players’ true (and possibly complete) preferences. In this case, employing the vector-dominance partial ordering—and allowing, in principle, for the possibility that the associated partial preferences may be completed in player-specific ways—ensures that no plausible preference profiles are a priori ruled out.

A strategy profile \(s\in S\) in a multicriteria game is a (pure strategy) generalized Nash equilibrium if, for all \(i\le I\),

$$\begin{aligned} v_i(s_i',s_{-i}) \ngtr v_i(s_i,s_{-i})\qquad \text {for all }s_i'\in S_i. \end{aligned}$$
(2)

If s is a generalized equilibrium, then a unilateral deviation by some player that results in a gain in some payoff dimension also results in a loss in some other dimension. When \(n_i=1\), for all i, this definition reduces to that of ordinary pure-strategy Nash equilibrium.

Focusing on zero-sum, two-person multicriteria games, Shapley (1959) was the first to analyze the above solution concept, which is sometimes referred to as Pareto equilibrium in the literature (Voorneveld et al. 1999). Also focusing on this class of games, Blackwell (1956) studied the minimax solution. An important result that goes back to Shapley (1959) is that if the players’ vector payoffs are “scalarized” by means of a suitable, player-specific vector of convex weights that are attached in a consistent manner to each player’s payoff dimensions, then every generalized Nash equilibrium of the game can be obtained as the possibly unique equilibrium of the corresponding scalarized game under some set of scalarization weights for all players.

3 Weak dominance solvability as an equilibrium refinement

Given a multicriteria game \((S_i,v_i)_{i=1}^I\), a strategy \(s_i'\) of player i will be said to weakly dominate\(s_i''\) in S if

$$\begin{aligned} \begin{array}{lll} v_i(s_i',s_{-i}) &{} \ge &{} v_i(s_i'',s_{-i})\qquad \text {for all }s_{-i}\in S_{-i}\\ &{}&{} \text {and} \\ v_i(s_i',s_{-i}) &{} > &{} v_i(s_i'',s_{-i})\qquad \text {for some } s_{-i}\in S_{-i} \end{array} \end{aligned}$$
(3)

This obviously coincides with the standard definition of weak dominance whenever \(n_i=1\). For \(S'\subseteq S\), let \(U(S')\) denote the set of strategy profiles \(s\in S\) such that \(s_i\) is not weakly dominated for any player \(i\le I\). It will then be said that a multicriteria game is weakly dominance solvable if there exist \(S^1,S^2,\ldots ,S^k\subseteq S\), \(k<\infty \), such that \(S=S^1\), \(S^{j+1}=U(S^j)\) for all \(j\in \{1,\ldots ,k-1\}\), \(U(S^k)=S^k\) and, for every player i and all \(\widetilde{s}_i,\widehat{s}_i\in S_i^k\), for all \(s_{-i}\in S^{k}_{-i}\).

The above definition encompasses that of dominance solvability in the sense of Moulin (1979) as a special case when \(n_i=1\) for all \(i\le I\). Moreover, as in Moulin (1979), the dominated strategies of all players are eliminated in each round. As is well known, this assumption is not without loss of generality. Contrary to what happens when payoffs are real-valued, however, in general situations where a multicriteria game is weakly dominance solvable, the players’ payoff functions are not required to be constant at the solution set. Intuitively, when payoffs are real-valued, the players’ indifference between two strategies conditional on an opponent strategy profile is captured by equality of their payoffs. When the latter are multidimensional, the proposed notion of weak dominance solvability effectively extends the definition of indifference to vector equality or incomparability according to the canonical partial ordering in Euclidean space. As such, this indifference relation is generally intransitive.

The set of pure-strategy-generalized Nash equilibria of a multicriteria game will be denoted by N(S). If such a game is weakly dominance solvable, its solution set will be denoted by \(D^w(S)\).

Proposition 1

If a finite multicriteria game is weakly dominance solvable, then \(D^w(S)\subseteq N(S)\).

Proof

Suppose S is weakly dominance solvable. Let \(\widehat{S}\subseteq S\) and assume to the contrary that there is \(s\in \widehat{S}\) such that \(s\in N(U(\widehat{S}))\) and \(s\not \in N(\widehat{S})\). Then, for some player i and strategy \(s_i'\in \widehat{S}_i\setminus U_i(\widehat{S}_i)\) it holds that

$$\begin{aligned} v_i(s_i',s_{-i})> v_i(s_i,s_{-i}). \end{aligned}$$
(4)

Since \(s'_i\in \widehat{S}_i\setminus U_i(\widehat{S}_i)\), there exists \(s''_i\in \widehat{S}_i\) that weakly dominates \(s'_i\) in \(\widehat{S}\). In particular,

$$\begin{aligned} v_i(s''_i,\widehat{s}_{-i})\ge v_i(s'_i,\widehat{s}_{-i})\qquad \text {for all }\widehat{s}_{-i}\in \widehat{S}_{-i}. \end{aligned}$$
(5)

It follows from (4) and (5) that

$$\begin{aligned} v_i(s''_i,s_{-i})>v_i(s_i,s_{-i}). \end{aligned}$$
(6)

Since \(s\in N(U(\widehat{S}))\), (6) implies \(s''_i\in \widehat{S}_i\setminus U_i(\widehat{S}_i)\). Therefore, \(s''_i\) is also weakly dominated in \(\widehat{S}\) by another strategy \(\overline{s}_i\in \widehat{S}_i\) which, in view of the above, is such that \(\overline{s}_i\not \in U_i(\widehat{S}_i)\) too. Upon applying this argument recursively and recalling that \(\widehat{S}_i\) is finite one concludes that there exists \(s_i^*\in \widehat{S}_i\setminus U_i(\widehat{S})\) such that \(s_i^*\) weakly dominates in \(\widehat{S}\) every \(\widetilde{s}_i\in \widehat{S}_i\setminus U_i(\widehat{S})\). Since \(s_i^*\in \widehat{S}_i\setminus U_i(\widehat{S})\), there exists \(s_i^{**}\in U_i(\widehat{S})\) such that \(s_i^{**}\) weakly dominates \(s_i^*\) in \(\widehat{S}\). Moreover, since \(s_i,s_i^{**}\in U_i(\widehat{S})\) and \(s\in N(U(\widehat{S}))\), it follows that

(7)

From (4) and also from the definitions of \(s_i^{**},s'_i\) we get

$$\begin{aligned} v_i(s_i^{**},s_{-i})\ge v_i(s'_i,s_{-i})> v_i(s_i,s_{-i}). \end{aligned}$$
(8)

This implies

$$\begin{aligned} v_i(s_i^{**},s_{-i}) > v_i(s_i,s_{-i}) \end{aligned}$$
(9)

which contradicts (9). Therefore, it holds that

$$\begin{aligned} N(U(\widehat{S}))\subseteq N(\widehat{S}). \end{aligned}$$
(10)

Now, since the game is weakly dominance solvable, there exist \(S^1,\ldots ,S^k\) such that \(S=S^1\), \(S^{j+1}=U(S^j)\) for all \(j\in \{1,\ldots ,k-1\}\), and \(S^k=U(S^k)\equiv D^w(S)\). It follows from the definition of \(D^w(S)\) that

$$\begin{aligned} D^w(S)=N(D^w(S)). \end{aligned}$$
(11)

Since \(N(U(\widehat{S}))\subseteq N(\widehat{S})\) for all \(\widehat{S}\subseteq S\) and \(S^{j+1}=U(S^j)\), it follows from (10) and (11) that

$$\begin{aligned} N(S)=N(S^1)\supseteq N(S^2)\supseteq \cdots \supseteq N(S^k)=D^w(S). \end{aligned}$$

\(\square \)

Proposition 1 includes Moulin’s (1979) Proposition 1 as a special case when all players’ payoffs are real-valued. In the spirit of Moulin (1986), in those dominance-solvable multicriteria games where the solution set is a proper subset of the game’s set of equilibria, one may refer to those selected by the above solution concept as sophisticated generalized equilibria. An example illustrating the elicitation of such equilibria is given in the game below:

figure a

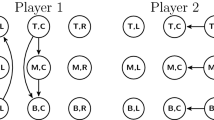
Here, the pure-strategy-generalized equilibria are (U, L) and (M, R). In the first round, M is eliminated by both players as weakly dominated by U and L, respectively, while D and R are removed in the second round as dominated by U and L, respectively. This leads to the unique prediction (U, L).

4 Partial dominance solvability and non-equilibrium solutions

Towards examining the robustness of the above equilibrium refinement in the class of multicriteria games, a generalization of the notion of weak dominance between a player’s strategies is now introduced. Specifically, given such a game \((S_i,v_i)_{i=1}^I\), a strategy \(s_i'\) will be said to partially dominate another strategy \(s''_i\) in S if

$$\begin{aligned} \begin{array}{lll} v_i(s''_i,s_{-i}) &{} \ngtr &{} v_i(s_i',s_{-i})\qquad \text {for all }s_{-i}\in S_{-i}\\ &{} \text {and} &{}\\ v_i(s_i',s_{-i}) &{} > &{} v_i(s''_i,s_{-i})\qquad \text {for some } s_{-i}\in S_{-i}\\ \end{array} \end{aligned}$$

Partial dominance generalizes weak dominance in multicriteria games whenever \(n_i>1\), while it reduces to it—and hence to the standard definition of weak dominance—when \(n_i=1\). A strategy \(s'_i\) will be referred to as partially dominant inS if \(s'_i\) partially dominates every other \(s_i\in S_i\) and the opponents’ strategy profiles are drawn from \(S_{-i}\). A strategy profile \(s\in S\) will also bear this name whenever \(s_i\) is partially dominant in S for every player \(i\le I\).

The next claim follows immediately from the definitions.

Observation 1

If \(s\in S\) is a partially dominant strategy profile in a multicriteria game, then \(s\in N(S)\).

Now, for \(S'\subseteq S\) let \(P(S')\subseteq S'\) denote the set of all strategy profiles \(s\in S'\) that obtain after every partially dominated strategy \(s'_i\in S'_i\) has been removed by every player \(i\le I\). Also, write \(P_i(S')\) for the set of player i’s strategies in \(S_i'\) that are not partially dominated in \(S'\). A multicriteria game \((S_i,v_i)_{i=1}^I\) is said to be partially dominance solvable if there exist \(S^1,S^2,\ldots ,S^k\), \(k<\infty \), such that \(S=S^1\), \(S^{j+1}=P(S^j)\) for all \(j\le k-1\), \(P(S^k)=S^k\), and for every player i and all \(s_i,s'_i\in S_i^k\), for all \(s_{-i}\in S^{k}_{-i}\). If such a game is partially dominance solvable, its solution set will be denoted by \(D^p(S)\).

Observation 2

There exist partially dominance solvable multicriteria games such that

$$\begin{aligned} N(S)\ne \emptyset \quad \text {and}\quad D^p(S)\cap N(S)=\emptyset . \end{aligned}$$

To verify, consider the following game:

figure b

Its pure-strategy-generalized equilibria are (M, A) and (M, C). In the first round of elimination, D is removed by the row player as partially dominated by M, and C by the column player as partially dominated by D. In the second round, A is removed as partially dominated by D. In the third round, M is removed as partially dominated by U, while in the final round, D is removed as dominated by B. The unique partial-dominance solution is, therefore, (U, B), at which profile the row player profitably deviates to D.