Dynamics behavior of a novel infectious disease model considering population mobility on complex network

Abstract

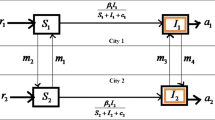
To describe the impact of population mobility between different cities on the spread of infectious disease, a new infectious disease complex dynamical model is proposed. Moreover, we obtain the basic regeneration number of the model based on applied spectral analysis. And the disease-free equilibrium points and local equilibrium points of the model are discussed, and it is found that two kind equilibrium points are globally asymptotically stable. In addition, the final scale of the presented model is analyzed and an expression for the final scale is obtained. Furthermore, we analyze the impact of population mobility on the spread of infectious diseases via numerical simulations. Our results reveal that the increase of population mobility between two cities leads to more intense disease transmission. Finally, the influence of media effects on the spread of infectious diseases is investigated. It is shown that the spread of diseases is suppressed because of the increase of individual's self-isolation rate. Therefore, controlling the population mobility is an effective initiative to curb outbreaks of infectious diseases throughout the network. These results can provide a theoretical basis for preventing and controlling the spreading of infectious diseases.

Appendix A: Specific derivation of stability analysis

Stability plays a crucial role in the dynamic analysis of infectious disease models. The following content is the theoretical derivation of stability analysis. Let's first derive the global stability of the disease-free equilibrium point at $R_{0} < 1$.

Firstly, the disease-free equilibrium $E_{0}$ of system (2) is $\left( {S_{i,k}^{0} ,S_{{q_{i,k} }}^{0} ,0,0,0} \right)$.

Where

$$ S_{i,k}^{0} = \frac{{\delta_{i,k} A_{i} \left( {d_{1} + q_{1} } \right)}}{{d_{1} + q_{1} - qq_{1} }} $$

(A1)

$$S_{{q_{{i,k}} }}^{0} = \frac{{q\delta _{{i,k}} A_{i} }}{{d_{1} + q_{1} - qq_{1} }}.$$

(A2)

System (2) is rewritten in the form.

$$ \left\{ \begin{gathered} \frac{{{\text{d}}X}}{{{\text{d}}t}} = F\left( {X,Z} \right) \hfill \\ \frac{{{\text{d}}Z}}{{{\text{d}}t}} = G\left( {X,Z} \right) \hfill \\ \end{gathered} \right.. $$

(A3)

Where $X = \left( {S_{i,k} \left( t \right),S_{{q_{i,k} }} \left( t \right)} \right)^{\prime }$$Z = \left( {E_{i,k} \left( t \right),I_{i,k} \left( t \right),Q_{i,k} \left( t \right)} \right)^{\prime }$.

$$ \begin{aligned} F\left( {X,Z} \right) & = \left( \begin{gathered} \delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} - \left( {q + d_{1} } \right)S_{i,k} - \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} S_{i,k} - \omega_{i} k\xi_{i} \left( {\beta_{{i{\prime} }} + \lambda_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)S_{i,k} \\ qS_{i,k} - d_{1} S_{{q_{i,k} }} - q_{1} S_{{q_{i,k} }} \\ \end{gathered} \right). \\ G\left( {X,Z} \right) & = \left( \begin{gathered} \theta_{i} \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)S_{i,k} + \left( {\beta_{{i{\prime} }} + \lambda_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)k\omega_{i} \xi_{i} S_{i,k} - \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)E_{i,k} \\ \varepsilon_{i} E_{i,k} - \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right)I_{i,k} \\ \alpha_{i}^{1} E_{i,k} + \alpha_{i}^{2} I_{i.k} - \gamma_{i}^{1} Q_{i,k} - \left( {d_{1} + d_{2} } \right)Q_{i,k} \\ \end{gathered} \right). \\ \end{aligned} $$

$U_{0} = \left( {X_{0} ,0} \right) = \left( {S_{i,k}^{0} ,S_{{q_{i,k} }}^{0} ,0,0,0} \right)$ denotes the disease-free equilibrium of system.

Then, we have the following two conditions:

$\left( {H_{1} } \right)$ For $\frac{dX}{{dt}} = F\left( {X,0} \right) = \left( \begin{gathered} \delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} - \left( {q + d_{1} } \right)S_{i,k} \hfill \\ qS_{i,k} - d_{1} S_{{q_{i,k} }} - q_{1} S_{{q_{i,k} }} \hfill \\ \end{gathered} \right)$,$x_{0} = \left( {S_{i,k}^{0} ,S_{{q_{i,k} }}^{0} ,0,0,0} \right)$ is a globally asymptomatically stable equilibrium of $\frac{dx}{{dt}} = F\left( {x,0} \right)$. Hence,$U_{0}$ is globally asymptomatically stable.

$$ \left( {H_{2} } \right)\;G\left( {X,Z} \right) = {\varvec{A}}Z - \tilde{G}\left( {X,Z} \right). $$

$$ \user2{A = }\left( {\begin{array}{*{20}c} {{\varvec{A}}_{11} } & {{\varvec{A}}_{12} } & {\varvec{0}} \\ {{\varvec{A}}_{21} } & {{\varvec{A}}_{22} } & {\varvec{0}} \\ {{\varvec{A}}_{31} } & {{\varvec{A}}_{32} } & {{\varvec{A}}_{33} } \\ \end{array} } \right). $$

$$ {\varvec{A}}_{11} = \left( {\begin{array}{*{20}c} { - \eta_{1} } & \cdots & 0 & {\rho_{11} } & \cdots & {\rho_{11} } \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & { - \eta_{1} } & {\rho_{1m} } & \cdots & {\rho_{1m} } \\ {\rho_{21} } & \cdots & {\rho_{21} } & { - \eta_{2} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {\rho_{2m} } & \cdots & {\rho_{2m} } & 0 & \cdots & { - \eta_{2} } \\ \end{array} } \right),\;{\varvec{A}}_{12} = \left( {\begin{array}{*{20}c} {f_{11} } & \cdots & 0 & {\rho_{11} } & \cdots & {\rho_{11} } \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {f_{1m} } & \cdots & {f_{1m} } & {\rho_{1m} } & \cdots & {\rho_{1m} } \\ {\rho_{21} } & \cdots & {\rho_{21} } & {f_{21} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {\rho_{2m} } & \cdots & {\rho_{2m} } & {f_{2m} } & \cdots & {f_{2m} } \\ \end{array} } \right) $$

And ${\varvec{A}}_{21} \user2{ = - V}_{21}$, ${\mathbf{A}}_{22} {\mathbf{ = }} - {\mathbf{V}}_{22}$, ${\varvec{A}}_{31} \user2{ = } - {\varvec{V}}_{31}$, ${\varvec{A}}_{32} \user2{ = } - {\varvec{V}}_{32}$, ${\varvec{A}}_{33} \user2{ = } - {\varvec{V}}_{33}$.

Where $\rho_{1l} = \left( {\beta_{2} + \lambda_{2} } \right)k\xi_{2} \omega_{2} \frac{{S_{1,l}^{0} }}{{N_{2} }},\rho_{2l} = \left( {\beta_{1} + \lambda_{1} } \right)k\xi_{1} \omega_{1} \frac{{S_{2,l}^{0} }}{{N_{1} }},l = 1 \cdots m.$

Note that ${\varvec{A}}$ is an Metzler matrix,$\user2{ - A}$ is an M-matrix, and all eigenvalues with respect to ${\varvec{A}}$ have negative real parts when $R_{0} < 1$.We derive that $Z\left( t \right)$ is globally asymptomatically stable, which means.

$$ \mathop {\lim }\limits_{t \to \infty } Z\left( t \right) = 0, $$

$$ \mathop {\lim }\limits_{t \to \infty } \left( {X\left( t \right),Z\left( t \right)} \right) = \left( {x_{0} ,0} \right) = U_{0} . $$

Then, the disease-free equilibrium $E_{0}$ is globally asymptomatically stable when $R_{0} < 1$.

Next, we discuss the global stability of the local equilibrium point at $R_{0} { > }1$.

Proof

Consider the following Lyapunov function candidate

$$ \begin{gathered} L = \left( {S_{i,k} - S_{i,k}^{*} - S_{i,k}^{*} \ln \frac{{S_{i,k} }}{{S_{i,k}^{*} }}} \right) + h_{1} \left( {S_{{q_{i,k} }} - S_{{q_{i,k} }}^{*} - S_{{q_{i,k} }}^{*} \ln \frac{{S_{{q_{i,k} }} }}{{S_{{q_{i,k} }}^{*} }}} \right) \\ \quad + h_{2} \left( {E_{i,k} - E_{i,k}^{*} - E_{i,k}^{*} \ln \frac{{E_{i,k} }}{{E_{i,k}^{*} }}} \right) \hfill \\ \quad + h_{3} \left( {I_{i,k} - I_{i,k}^{*} - I_{i,k}^{*} \ln \frac{{I_{i,k} }}{{I_{i,k}^{*} }}} \right) + h_{4} \left( {Q_{i,k} - Q_{i,k}^{*} - Q_{i,k}^{*} \ln \frac{{Q_{i,k} }}{{Q_{i,k}^{*} }}} \right). \hfill \\ \end{gathered} $$

(A4)

where $h_{1} ,h_{2} ,h_{3} ,h_{4}$ and $h_{5}$ are positive constants to be determined later. Differentiating the function with respect to time yields.

$$ L^{\prime} = (1 - \frac{{S_{i,k}^{*} }}{{S_{i,k} }})S^{\prime}_{i,k} + h_{1} (1 - \frac{{S_{{q_{i,k} }}^{*} }}{{S_{{q_{i,k} }} }})S^{\prime}_{{q_{i,k} }} + h_{2} (1 - \frac{{E_{i,k}^{*} }}{{E_{i,k} }})E^{\prime}_{i,k} + h_{3} (1 - \frac{{I_{i,k}^{*} }}{{I_{i,k} }})I^{\prime}_{i,k} + h_{4} (1 - \frac{{Q_{i,k}^{*} }}{{Q_{i,k} }})Q^{\prime}_{i,k} . $$

(A5)

Substituting system (A5) into the above formula and sorted out:

$$ \begin{aligned} L^{\prime} & = \left( {1 - \frac{1}{{x_{1} }}} \right)\left( {\delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} } \right) + \left( {1 - x_{1} } \right)S_{i,k}^{*} \left[ {\left( {q + d_{1} } \right) + \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] \\ & \quad + h_{1} qS_{i,k}^{*} \left( {x_{1} - \frac{{x_{1} }}{{x_{2} }}} \right) + \left( {1 - x_{2} } \right)h_{1} \left( {d_{1} + q_{1} } \right)S_{{q_{i,k} }}^{*} + \left( {1 - x_{3} } \right)h_{2} E_{i,k}^{*} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right) \\ & \quad + \left( {x_{1} - \frac{{x_{1} }}{{x_{3} }}} \right)h_{2} S_{i,k}^{*} \left[ {\left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] + \left( {1 - x_{4} } \right)h_{3} I_{i,k}^{*} \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right) \\ & \quad + \left( {x_{3} - \frac{{x_{3} }}{{x_{4} }}} \right)h_{3} \varepsilon_{i} E_{i,k}^{*} + \left( {1 - x_{5} } \right)h_{4} Q_{i,k}^{*} \left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right) + \left( {x_{3} - \frac{{x_{3} }}{{x_{5} }}} \right)h_{4} \alpha_{i}^{1} E_{i,k}^{*} + \left( {x_{4} - \frac{{x_{4} }}{{x_{5} }}} \right)h_{4} \alpha_{i}^{2} I_{i,k}^{*} . \\ \end{aligned} $$

(A6)

where $x_{1} = \frac{{S_{i,k} }}{{S_{i,k}^{*} }},x_{2} = \frac{{S_{{q_{i,k} }} }}{{S_{{q_{i,k} }}^{*} }},x_{3} = \frac{{E_{i,k} }}{{E_{i,k}^{*} }},x_{4} = \frac{{I_{i,k} }}{{I_{i,k}^{*} }},x_{5} = \frac{{Q_{i,k} }}{{Q_{i,k}^{*} }}$.

The above formula can be simplified

$$ \begin{aligned} L^{\prime} & = \delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} + S_{i,k}^{*} \left[ {\left( {q + d_{1} } \right) + \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] \\ & \quad + h_{1} \left( {d_{1} + q_{1} } \right)S_{{q_{i,k} }}^{*} + h_{2} E_{i,k}^{*} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right) + h_{3} I_{i,k}^{*} \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right) + h_{4} Q_{i,k}^{*} \left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right) \\ & \quad - \left( {\delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} } \right)\frac{1}{{x_{1} }} + \left[ {h_{1} q - \left( {q + d_{1} } \right) + \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right]x_{1} S_{i,k}^{*} \\ & \quad + h_{2} S_{i,k}^{*} \left[ {\left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] - x_{2} h_{1} \left( {d_{1} + q_{1} } \right)S_{{q_{i,k} }}^{*} \\ & \quad + x_{3} E_{i,k}^{*} \left[ {h_{3} \varepsilon_{i} + h_{4} \alpha_{i}^{1} - h_{2} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)} \right] + x_{4} I_{i,k}^{*} \left[ {h_{4} \alpha_{i}^{2} - h_{3} \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right)} \right] \\ & \quad - x_{5} Q_{i,k}^{*} \left[ {\left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right)} \right] - \frac{{x_{1} }}{{x_{2} }}h_{1} qS_{i,k}^{*} - \frac{{x_{1} }}{{x_{3} }}S_{i,k}^{*} h_{2} \left[ {\left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] \\ & \quad - \frac{{x_{3} }}{{x_{4} }}h_{3} \varepsilon_{i} E_{i,k}^{*} - \frac{{x_{3} }}{{x_{5} }}h_{4} \alpha_{i}^{1} E_{i,k}^{*} - \frac{{x_{4} }}{{x_{5} }}h_{4} \alpha_{i}^{2} I_{i,k}^{*} . \\ \end{aligned} $$

(A7)

Considering $h_{3} = 1$, by setting the coefficients of $x_{2} ,x_{3} ,x_{4} ,x_{5}$ to 0 and solving for $h_{1} ,h_{2} ,h_{4}$ yields.

$h_{1} = {{\left[ {\left( {q + d_{1} } \right) + a} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {q + d_{1} } \right) + a} \right]} q}} \right. \kern-0pt} q}.$$h_{2} = {{\left[ {\alpha_{i}^{2} \varepsilon_{i} + \alpha_{i}^{1} \left( {d_{1} + d_{2} + \alpha_{i}^{2} + \gamma_{i}^{2} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\alpha_{i}^{2} \varepsilon_{i} + \alpha_{i}^{1} \left( {d_{1} + d_{2} + \alpha_{i}^{2} + \gamma_{i}^{2} } \right)} \right]} {\left[ {\alpha_{i}^{2} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)} \right]}}} \right. \kern-0pt} {\left[ {\alpha_{i}^{2} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)} \right]}}$.$h_{4} = {{\left[ {\left( {d_{1} + d_{2} + \alpha_{i}^{2} + \gamma_{i}^{2} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {d_{1} + d_{2} + \alpha_{i}^{2} + \gamma_{i}^{2} } \right)} \right]} {\alpha_{i}^{2} }}} \right. \kern-0pt} {\alpha_{i}^{2} }}.$$a = \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)k\xi_{i} \omega_{i}$.

Using the arithmetic–geometric means inequality, it is found that $L$ is less or equal to zero with equality only if $x_{1} = 1,x_{2} = 1,x_{3} = 1,x_{4} = 1,x_{5} = 1$. By LaSalle’s invariance principle, we know the largest invariant set in $\Omega$ is reduced to the endemic equilibrium $E^{*}$, and the largest invariant set contained in

$$ \left\{ {\left( {S_{i,k} ,S_{{q_{i,k} }} ,E_{i,k} ,Q_{i,k} ,I_{i,k} ,R_{i,k} } \right) \in \Omega |L^{\prime} = 0} \right\} $$

(A8)

Then, we conclude that the endemic equilibrium is globally asymptotically stable in $\Omega$.