Dynamics of stability, bifurcation and control for a commensal symbiosis model

Abstract

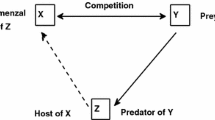
This article investigates a three-species delayed population model comprising a generalist predator and two prey populations, one of which is commensal. The conditions for the uniqueness and local stability of the equilibria are derived. Additionally, a suitable Lyapunov function is constructed to demonstrate the local stability of the interior equilibrium point in the presence of the delay values. The existence of Hopf bifurcation is investigated with respect to the delay parameters, and the necessary conditions are obtained. The Z-type control mechanism is applied to the system so that the controllers can drive the populations to the desired states. Numerical simulations are conducted to validate the results for specific parameter values.

Appendices

Appendix A.

$$\begin{aligned} J_{E_8}= & {} \begin{bmatrix} 1-2x^*+by^*-\frac{2a_1^2m_1x^*z^*}{\left( {x^*}^2+a_1^2\right) ^2} &{} bx^* &{} -\frac{m_1{x^*}^2}{{x^*}^2+a_1^2} \\ 0 &{} r-\frac{2ry^*}{k}-\frac{2a_2^2m_2y^*z^*}{\left( {y^*}^2+a_2^2\right) ^2} &{} -\frac{m_2{y^*}^2}{{y^*}^2+a_2^2} \\ d^2 &{} d^2 &{} -d \end{bmatrix}\\ Q_{61}= & {} d-r-1+2{\tilde{x}}+\frac{2a_1^2m_1{\tilde{x}}{\tilde{z}}}{\left( {\tilde{x}}^2+a_1^2\right) ^2},\\ Q_{62}= & {} (r-d)\left( 1-2{\tilde{x}}-\frac{2a_1^2m_1{\tilde{x}}{\tilde{z}}}{\left( {\tilde{x}}^2+a_1^2\right) ^2}\right) +\frac{d^2m_1{\tilde{x}}^2}{{\tilde{x}}^2+a_1^2}-rd,\\ Q_{63}= & {} rd\left( 1-2{\tilde{x}}-\frac{2a_1^2m_1{\tilde{x}}{\tilde{z}}}{\left( {\tilde{x}}^2+a_1^2\right) ^2}\right) -\frac{rd^2m_1{\tilde{x}}^2}{{\tilde{x}}^2+a_1^2},\\ Q_{71}= & {} d-b{\hat{y}}-r\left( 1-\frac{2{\hat{y}}}{k}\right) +\frac{2m_2a_2^2{\hat{y}}{\hat{z}}}{\left( {\hat{y}}^2+a_2^2\right) ^2},\\ Q_{72}= & {} (b{\hat{y}}-d)\left( r\left( 1-\frac{2{\hat{y}}}{k}\right) -\frac{2m_2a_2^2{\hat{y}}{\hat{z}}}{\left( {\hat{y}}^2+a_2^2\right) ^2}\right) +\frac{d^2m_2{\hat{y}}^2}{{\hat{y}}^2+a_2^2}-bd{\hat{y}},\\ Q_{73}= & {} bd{\hat{y}}\left( r\left( 1-\frac{2{\hat{y}}}{k}\right) -\frac{2m_2a_2^2{\hat{y}}{\hat{z}}}{\left( {\hat{y}}^2+a_2^2\right) ^2}\right) -\frac{bd^2m_2{\hat{y}}^3}{{\hat{y}}^2+a_2^2},\\ Q_{82}= & {} \left( 1-2x^*+by^*-\frac{2a_1^2m_1x^*z^*}{\left( {x^*}^2+a_1^2\right) ^2}\right) \left( r-\frac{2ry^*}{k}-\frac{2a_2^2m_2y^*z^*}{\left( {y^*}^2+a_2^2\right) ^2}\right) \\{} & {} -d\left( 1-2x^*+by^*-\frac{2a_1^2m_1x^*z^*}{\left( {x^*}^2 +a_1^2\right) ^2}+r-\frac{2ry^*}{k}-\frac{2a_2^2m_2y^*z^*}{\left( {y^*}^2+a_2^2\right) ^2}\right) \\{} & {} +d^2\left( \frac{m_1{x^*}^2}{{x^*}^2+a_1^2}+\frac{m_2{y^*}^2}{{y^*}^2+a_2^2}\right) ,\\ Q_{83}= & {} \text {det}(J_{E_8}), \quad Q_{81}= \text {tr}(J_{E_8}). \end{aligned}$$

Appendix B.

$$\begin{aligned} k_1 ={} & {} \frac{k_4}{2by^*z^*}\left[ \frac{2 a_1^2 m_1 x^* {z^*}^2}{\left( a_1^2+{x^*}^2\right) ^2}+\frac{2 a_2^2 m_2 y^* {z^*}^2}{\left( a_2^2+{y^*}^2\right) ^2}\right. \\{} & {} \left. +\left( \frac{2 r}{k}-b\right) y^* z^* -d^2 (x^*+y^*)-(r+1) z^*\right] \\ k_3 ={} & {} \frac{k_4}{2d^2x^*} \left[ \frac{2 a_1^2 m_1 x^* {z^*}^2}{\left( a_1^2+{x^*}^2\right) ^2}+\frac{m_2 y^* {z^*}^2}{a_2^2+{y^*}^2}-b y^* z^*+ \left( d+2 x^*-1\right) z^*\right] \\{} & {} +\frac{2m_1 x^* {z^*}^2}{a_1^2+{x^*}^2}\frac{k_1}{2d^2x^*} \\ k_2 ={} & {} \frac{\left( a_2^2+{y^*}^2\right) ^2}{2m_2 y^* {z^*}^2} \left[ k_4\left( x^*z^*- \left( 1+d+\frac{r y^*}{k}\right) z^*\right. \right. \\{} & {} \left. \left. +\frac{m_2 y^* {z^*}^2}{a_2^2+{y^*}^2}-\frac{2 a_2^2 m_2 y^* {z^*}^2}{\left( a_2^2+{y^*}^2\right) ^2}\right) +2 d^2 y^* k_3\right] \\ {\mathcal {V}}_1={} & {} k_1\left( \frac{2a_{11}}{x^*}+2a_{11}\tau _1+a_{12}\tau _1 +a_{13}\tau _1+a_{11}a_{12}\tau _2\right) \\{} & {} +k_4\left( \frac{a_{22}\tau _1}{2}+\frac{a_{23}\tau _1}{2}\right) \\{} & {} +k_6\left( \frac{a_{31}}{x^*}+a_{31}\tau _1+\frac{ba_{31}\tau _2}{2} +\frac{a_{32}\tau _1}{2}+\frac{a_{33}\tau _1}{2}\right) ,\\ {\mathcal {V}}_2={} & {} k_1\left( a_{12}\tau _1+a_{11}a_{12}\tau _2 +2a_{12}^2\tau _2+a_{13}a_{12}\tau _2\right) \\{} & {} +k_2\frac{2a_{22}}{y^*}+k_4\left( \frac{a_{12}}{y^*} +\frac{a_{22}\tau _1}{2}+ba_{22}\tau _2+\frac{ba_{23}\tau _2}{2}\right) \\{} & {} +k_5\frac{a_{32}}{y^*} +k_6\left( \frac{a_{32}\tau _1}{2}\right. \\{} & {} \left. +\frac{ba_{31}\tau _2}{2}+ba_{32}\tau _2 +\frac{ba_{33}\tau _2}{2}\right) ,\\ {\mathcal {V}}_3={} & {} k_1\left( a_{13}\tau _1+a_{12}a_{13}\tau _2\right) +k_3\frac{2a_{33}}{z^*} +k_4\left( \frac{a_{23}\tau _1}{2}+\frac{ba_{23}\tau _2}{2}\right) \\{} & {} +k_5\frac{a_{23}}{z^*} +k_6\left( \frac{a_{13}}{z^*}+\frac{a_{33}\tau _1}{2}\right. \\{} & {} \left. +\frac{ba_{33}\tau _2}{2}\right) . \end{aligned}$$